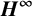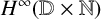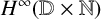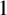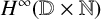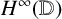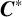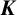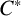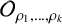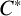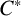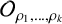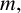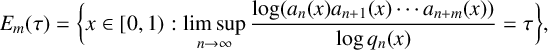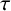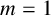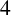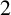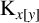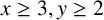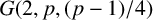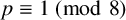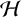Research Article
DENSE STABLE RANK AND RUNGE-TYPE APPROXIMATION THEOREMS FOR
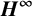 ${\boldsymbol H}^{\boldsymbol{\infty}}$
MAPS
${\boldsymbol H}^{\boldsymbol{\infty}}$
MAPS
- Part of:
-
- Published online by Cambridge University Press:
- 12 May 2021, pp. 289-317
-
- Article
- Export citation
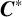 $\boldsymbol {C}^{*}$
-ALGEBRAS FROM
$\boldsymbol {C}^{*}$
-ALGEBRAS FROM 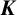 $\boldsymbol {K}$
GROUP REPRESENTATIONS
$\boldsymbol {K}$
GROUP REPRESENTATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2022, pp. 318-338
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN EFFECTIVE ANALYTIC FORMULA FOR THE NUMBER OF DISTINCT IRREDUCIBLE FACTORS OF A POLYNOMIAL
- Part of:
-
- Published online by Cambridge University Press:
- 09 December 2021, pp. 339-356
-
- Article
- Export citation
A DIMENSIONAL RESULT ON THE PRODUCT OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 11 October 2021, pp. 357-385
-
- Article
- Export citation
FINITE TWO-DISTANCE-TRANSITIVE DIHEDRANTS
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2022, pp. 386-401
-
- Article
- Export citation
ON SEPARABILITY FINITENESS CONDITIONS IN SEMIGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2021, pp. 402-430
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Other
INDEX
-
- Published online by Cambridge University Press:
- 11 November 2022, pp. 431-432
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JAZ volume 113 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 11 November 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JAZ volume 113 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 11 November 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation