Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-27T06:38:35.326Z Has data issue: false hasContentIssue false
  • English
  • Français

Round subsets of Wallman-type compactifications*

Published online by Cambridge University Press:  09 April 2009

Li Pu Su
Li Pu Su
Affiliation:
Department of MathematicsThe University of Oklahoma Norman, Oklahoma 73069, U.S.A. The University of British ColumbiaVancouver, Canada.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ℒ be a normal base of a Tychonoff space X and ωℒ denote the Wallman-type (real-) compactification of X generated by ℒ. This Wallman-type compactification is known to associate with a unique proximity δ. A ℒ-filter ℒ is round if for each F ∈ ℒ there is an Fo ∈ ℒ there is an Fo ∈ ℒ such that Fo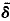(X-F). A subset A of ω(£) is called a round subset of ω (£) iff for each Z ∈ ℒ, if C1w(x)Z contains A, then it is a neighborhood of A. Properties of round ℒ-filters and round sets of ω(ℒ) are introduced. We also prove that the intersection of all the free ℒ-ultrafilters is ℒ= {Z ∈ ℒ: C1x(X-Z) is compact} iff ω(ℒ) – X is a round subset of ω(ℒ) if ℒ is a separating nest generated intersection ring with property (α) then ω(ℒ) - v(ℒ) is a round subset of ω(ℒ).

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 21 , Issue 2 , March 1976 , pp. 224 - 233
Copyright
Copyright © Australian Mathematical Society 1976

References

Alo, R. A. and Shapiro, H. L. (1968), ‘A note on compactifications and seminormal spaces’, J. Austral. Math. Soc. 8, 102–108.CrossRefGoogle Scholar
Alo, R. A. and Shapiro, H. L. (1968), ‘Normal bases and compactifications’, Math. Ann. 175, 337–340.CrossRefGoogle Scholar
Alo, R. A. and Shapiro, H. L. (1969), ‘ℒ-realcompactifications and normal bases’, J. Austral. Math. Soc. 9, 489–495.CrossRefGoogle Scholar
Alo, R. A. and Shapiro, H. L. (1969), ‘Wallman compact and realcompact spaces’, Proc. of the Inter. Symp. on Extension Theory of Top. Structures and Its Application in Berlin, 1967, VEB Deutscher Verlag der Wiss., Berlin.Google Scholar
Alo, R. A., Shapiro, H. L. and Weir, Maurice, ‘Realcompactness and Wallman-realcompactifications’, (to appear).Google Scholar
Frink, O., (1964), ‘Compactifications and semi-normal spaces’, Amer. J. Math. 86, 602–607.Google Scholar
Gagrat, M. S. and Naimpally, S. A., (1973), ‘Wallman compactifications and Wallman realcompactifications’, J. Austral. Math. Soc. 15, 417–426.CrossRefGoogle Scholar
Gillman, L. and Jerison, M., (1960), Rings of Continuous Functions (D. Van Nostrand Co., Inc., Princeton, N. J., 1960).CrossRefGoogle Scholar
Kelley, J. L., (1955), General Topology, D. Van Nostrand Co., Inc., Princeton, N. J., (1955).Google Scholar
Mandelker, M., (1969), ‘Round z-filters and round subsets of βX’, Isr. J. Math. 2, 1–8.CrossRefGoogle Scholar
Mrowka, S., (1957), ‘Some properties of Q-spaces’, Bull. de L'Acad. Pola. des Sci. 5, 947–950.Google Scholar
Naimpally, S. A. and Warrack, B. D., (1970), Proximity Spaces (Cambridge Univ. Press, London, Britain, 1970).Google Scholar
Njåstad, O., (1966), ‘On Wallman-type compactifications’, Math. Zeit. 91, 267–276.Google Scholar
Smirnov, Yu. M., (1964), ‘On proximity spaces’, English Trans. A.M.S. Transl. 38, 5–35.Google Scholar
Steiner, E. F. (1966), ‘Normal families and completely regular spaces’, Duke Math. J. 33, 743–745.Google Scholar
Steiner, A. K. and Steiner, E. F., (1970), ‘Nest generated intersection rings in Tychonoff spaces’, A.M.S. Trans. 148, 589–601.Google Scholar
Su, L. P., (1974), ‘Wallman-type compactifications on zero-dimensional spaces’, Proc. A.M.S., 43, 455–460.CrossRefGoogle Scholar
Su, L. P. (to appear) ‘A characterization of realcompactness’, Proc. A.M.S.Google Scholar