Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-26T04:30:21.641Z Has data issue: false hasContentIssue false
  • English
  • Français

On values taken by the largest prime factor of shifted primes

Part of: Multiplicative number theory

Published online by Cambridge University Press:  09 April 2009

William D. Banks  and
Igor E. Shparlinski
William D. Banks
Affiliation:
Department of Mathematics University of MissouriColumbia, MO 65211USA e-mail: bbanks@math.missouri.edu
Igor E. Shparlinski
Affiliation:
Department of Computing Macquarie UniversitySydney, NSW 2109Australia e-mail: igor@ics.mq.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let P denote the set of prime numbers, and let P(n) denote the largest prime factor of an integer n > 1. We show that, for every real number 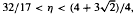, there exists a constant c(η) > 1 such that for every integer a ≠ 0, the set 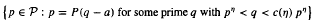has relative asymptotic density one in the set of all prime numbers. Moreover, in the range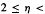 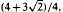, one can take c(η) = 1+ε for any fixed ε > 0. In particular, our results imply that for every real number 0.486 ≤ b.thetav; ≤ 0.531, the relation P(q − a) ≍ qθ holds for infinitely many primes q. We use this result to derive a lower bound on the number of distinct prime divisor of the value of the Carmichael function taken on a product of shifted primes. Finally, we study iterates of the map q ↦ P(q - a) for a > 0, and show that for infinitely many primes q, this map can be iterated at least (log logq)1+o(1) times before it terminates.

MSC classification

Secondary: 11N25: Distribution of integers with specified multiplicative constraints 11N64: Other results on the distribution of values or the characterization of arithmetic functions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 82 , Issue 1 , February 2007 , pp. 133 - 147
Copyright
Copyright © Australian Mathematical Society 2007

References

[1]Alford, W. R., Granville, A. and Pomerance, C., ‘There are infinitely many Carmichael numbers’, Annals Math. 140 (1994), 703–722.CrossRefGoogle Scholar
[2]Baker, R. C. and Harman, G., ‘The brun-titchmarsh theorem on average’, in: Proc. Conf. in Honor of Heini Halberstam (Allerton Park, IL, 1995), Progr. Math. 138 (Birkhäuser, Boston, 1996) pp. 39–103.Google Scholar
[3]Baker, R. C. and Harman, G., ‘Shifted primes wihtout large prime factors’, Acta Arith. 83 (1998), 331–361.CrossRefGoogle Scholar
[4]Balog, A., ‘p+a wihtout large prime factors’, in: Seminar on Number Theory, 1983–84 Talence (Univ. Bordeaux, Thalence, 1984).Google Scholar
[5]Banks, W., Friedlander, J. B., Pomerance, C. and Shparlinski, I. E., ‘Multiplicative structure of values of the Euler function’, in: High Primes and Misdemeanours: Lectures in Honour of the 60th Birthday of Hugh Cowie Williams, Fields institute Communications 41 (Amer.Math. Soc., Providence, RI, 2004) pp. 29–48.Google Scholar
[6]Banks, W., Harman, G. and Shparlinski, I. E., ‘Distributional properties of the largers prime factor’, Michigan Math. J. 53 (2005), 665–681.CrossRefGoogle Scholar
[7]Canfield, E. R., Erdős, P. and Pomerance, C., ‘On a problem of Oppenheim concerning “;Factorisatio Numerorum”’, J. Number Theory 17 (1983), 1–28.CrossRefGoogle Scholar
[8]Dartyge, C., Martin, G. and Tenenbaum, G., ‘Polynomial values free of large prime factors’, Periodica Math. Hungar 43 (2001), 111–119.CrossRefGoogle Scholar
[9]Davenport, H., Multiplicative number theory, 2nd, edition (Springer, New York, 1980).CrossRefGoogle Scholar
[10]Deshouillers, J.-M. and Iwaniec, H., ‘On the Brun-Titchmarsh theorem on average’ in: Topic in classical number theory Vol. I, II (Budapest, 1981), Colloq. Math. Soc. János Bolyai 34 (Nothr-Holland, Amsterdam, 1984) pp. 319–333.Google Scholar
[11]Fouvry, E., ‘Théorème de Brun-Titchmarsh; application au théorème de Fermat’, Invent. Math. 79 (1985), 383–407.Google Scholar
[12]Fouvry, E. and Grupp, F., ‘On the switching principle in sieve theory’ J. Reine Angew. Math. 370 (1986), 101–126.Google Scholar
[13]Friedlander, J. B., Shifted primes without large prime factors, Number Theory and Applications 1989 (Kluwer, Berlin, 1990) pp. 393–401.Google Scholar
[14]Granville, A., ‘Smooth number: Computational number theory and beyond’, in: Algorithmic Number Thoery (eds.Buhler, J. and Stevenhagen, P.), MSRI Publications 44 (Cambrige Univ. Press, to appear).Google Scholar
[15]Halberstam, H. and Richert, H.-E., Sieve Methods (Academic Press, Lodon, 1974).Google Scholar
[16]Hildebrand, A., ‘On the number of positive integers ≤ x and free of prime factors > y’, J. Number Theory 22 (1986), 289–307.CrossRefGoogle Scholar
[17]Hildebrand, A. and Tenebaum, G., ‘Integers without large prime factors’, J. Théor. Nombers Bordeaux 5 (1993), 411–484.CrossRefGoogle Scholar
[18]Hmyrova, N. A., ‘On polynomials with small prime divisors, II’, lzv. Akad. Nauk SSSR Ser. Mat. 30 (1966), 1367–1372 (in Russian).Google Scholar
[19]Hooley, C., ‘On the largest prime factor of p+1’, Mathematika 20 (1973), 135–143.CrossRefGoogle Scholar
[20]Ivić, A., ‘On sums involving reciprocals of the largest prime facator of an interger, II’, Acta Arith. 71 (1995), 229–251.CrossRefGoogle Scholar
[21]Iwaniec, H. and Kowalski, E., Analytic number theory (Amer. Math. Soc., Providence, RI, 2004).Google Scholar
[22]Luca, F. and Pomerance, C., ‘Irreducible redical extensions and the Euler-function chains’, Preprint, 2005.Google Scholar
[23]Mikawa, H., ‘On primes in arithmetic progresseions’, Tsukuba J.Math 25 (2001), 121–153.CrossRefGoogle Scholar
[24]Oon, S.-M., ‘Pseudorandom properties of prime factors’, Period. Math. Hungar 49 (2004), 45–63.CrossRefGoogle Scholar
[25]Pomerance, C., ‘Popular values of eluer's, function’ Mathematika. 27 (1980), 84–89.Google Scholar
[26]Partt, V., ‘Every prime has a succinct certificate’, SIAM J. Comput. 4 (1975), 214–220.CrossRefGoogle Scholar
[27]Tenenbaurn, G., Introduction to analytic and probabilistic number theory (Cambridge University Press, 1995).Google Scholar
[28]Timofeev, N. M., Polynomials with small prime divisors, Taškent. Gos. Univ. Naučn. Trudy 548, Voprosy Mat. (Taškent Gos. Univ., Taškent, 1977) pp. 87–91 (Russian).Google Scholar
[29]Vishnoi, N. K., Theoretical aspects of randomization in computation (Ph.D. Thesis, Georgia Inst. of Technology, 2004), available from http://smartech.gatech.edu:8282/dspace/handle/1853/5049.Google Scholar