Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-05-13T16:36:48.328Z Has data issue: false hasContentIssue false
  • English
  • Français

NORMING SETS AND RELATED REMEZ-TYPE INEQUALITIES

Part of: Approximations and expansions

Published online by Cambridge University Press:  17 November 2015

A. BRUDNYI  and
Y. YOMDIN
A. BRUDNYI*
Affiliation:
Department of Mathematics & Statistics, University of Calgary, Calgary, Alberta, T2N 1N4, Canada email abrudnyi@ucalgary.ca
Y. YOMDIN
Affiliation:
Department of Mathematics, The Weizmann Institute of Science, Rehovot 76100, Israel email yosef.yomdin@weizmann.ac.il
*
✉abrudnyi@ucalgary.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The classical Remez inequality [‘Sur une propriété des polynomes de Tchebycheff’, Comm. Inst. Sci. Kharkov13 (1936), 9–95] bounds the maximum of the absolute value of a real polynomial 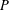$P$ of degree 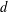$d$ on 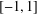$[-1,1]$ through the maximum of its absolute value on any subset 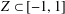$Z\subset [-1,1]$ of positive Lebesgue measure. Extensions to several variables and to certain sets of Lebesgue measure zero, massive in a much weaker sense, are available (see, for example, Brudnyi and Ganzburg [‘On an extremal problem for polynomials of $n$ variables’, Math. USSR Izv.37 (1973), 344–355], Yomdin [‘Remez-type inequality for discrete sets’, Israel. J. Math.186 (2011), 45–60], Brudnyi [‘On covering numbers of sublevel sets of analytic functions’, J. Approx. Theory162 (2010), 72–93]). Still, given a subset 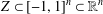$Z\subset [-1,1]^{n}\subset \mathbb{R}^{n}$, it is not easy to determine whether it is 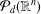${\mathcal{P}}_{d}(\mathbb{R}^{n})$-norming (here 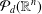${\mathcal{P}}_{d}(\mathbb{R}^{n})$ is the space of real polynomials of degree at most 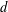$d$ on 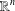$\mathbb{R}^{n}$), that is, satisfies a Remez-type inequality: 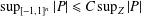$\sup _{[-1,1]^{n}}|P|\leq C\sup _{Z}|P|$ for all 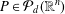$P\in {\mathcal{P}}_{d}(\mathbb{R}^{n})$ with 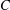$C$ independent of 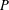$P$. (Although 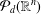${\mathcal{P}}_{d}(\mathbb{R}^{n})$-norming sets are precisely those not contained in any algebraic hypersurface of degree 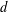$d$ in 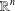$\mathbb{R}^{n}$, there are many apparently unrelated reasons for 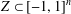$Z\subset [-1,1]^{n}$ to have this property.) In the present paper we study norming sets and related Remez-type inequalities in a general setting of finite-dimensional linear spaces 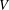$V$ of continuous functions on 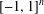$[-1,1]^{n}$, remaining in most of the examples in the classical framework. First, we discuss some sufficient conditions for 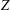$Z$ to be 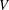$V$-norming, partly known, partly new, restricting ourselves to the simplest nontrivial examples. Next, we extend the Turán–Nazarov inequality for exponential polynomials to several variables, and on this basis prove a new fewnomial Remez-type inequality. Finally, we study the family of optimal constants 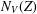$N_{V}(Z)$ in the Remez-type inequalities for 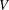$V$, as the function of the set 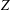$Z$, showing that it is Lipschitz in the Hausdorff metric.

Keywords

norming setnorming constantRemez-type inequalitypolynomialsanalytic functions

MSC classification

Primary: 41A17: Inequalities in approximation (Bernstein, Jackson, Nikol'skiĭ-type inequalities)
Secondary: 41A63: Multidimensional problems (should also be assigned at least one other classification number in this section)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 2 , April 2016 , pp. 163 - 181
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Alexander, H. and Taylor, B. A., ‘Comparison of two capacities in ℂn’, Math. Z. 186 (1984), 407–417.CrossRefGoogle Scholar
Andrievskii, V. V., ‘Local Remez-type inequalities for exponentials of a potential on a piecewise analytic arc’, J. Anal. Math. 100(1) (2006), 323–336.CrossRefGoogle Scholar
Aronszajn, N., ‘A unique continuation theorem for solutions of elliptic partial differential equations of second order’, J. Math. Pures Appl. 36 (1957), 235–249.Google Scholar
Batenkov, D., Sarig, N. and Yomdin, Y., ‘Accuracy of algebraic Fourier reconstruction for shifts of several signals’, Sampl. Theory Signal Image Process. (STSIP) 13(2) (2014), 151–173.CrossRefGoogle Scholar
Bernstein, S., ‘Sur la limitation des valeurs d’un polynôme P n(x) de degré n sur tout un segment par ses valeurs en (n + 1) points du segment’, Isvestiya AN SSSR (1931), 1025–1050.Google Scholar
Borwein, P. B. and Erdélyi, T., ‘Generalizations of Müntz’s theorem via a Remez-type inequality for Müntz spaces’, J. Amer. Math. Soc. 10 (1997), 327–349.CrossRefGoogle Scholar
Bos, L., De Marchi, S., Sommariva, A. and Vianello, M., ‘Weakly admissible meshes and discrete extremal sets’, Numer. Math. Theory Methods Appl. 4 (2011), 1–12.CrossRefGoogle Scholar
Brudnyi, A., ‘On local behavior of analytic functions’, J. Funct. Anal. 169(2) (1999), 481–493.CrossRefGoogle Scholar
Brudnyi, A., ‘Local inequalities for plurisubharmonic functions’, Ann. of Math. (2) 149 (1999), 511–533.CrossRefGoogle Scholar
Brudnyi, A., ‘On local behavior of holomorphic functions along complex submanifolds of ℂN’, Invent. Math. 173(2) (2008), 315–363.CrossRefGoogle Scholar
Brudnyi, A., ‘On covering numbers of sublevel sets of analytic functions’, J. Approx. Theory 162 (2010), 72–93.CrossRefGoogle Scholar
Brudnyi, A. and Brudnyi, Yu., ‘Remez type inequalities and Morrey–Campanato spaces on Ahlfors regular sets’, Contemp. Math. 445 (2007), 19–44.CrossRefGoogle Scholar
Brudnyi, A. and Brudnyi, Yu., Methods of Geometric Analysis in Lipschitz Extension and Trace Problems, Vols. I, II (Birkhäuser, Basel, 2012).Google Scholar
Brudnyi, Yu. and Ganzburg, M., ‘On an extremal problem for polynomials of n variables’, Math. USSR Izv. 37 (1973), 344–355.Google Scholar
Coman, D. and Poletsky, E. A., ‘Transcendence measures and algebraic growth of entire functions’, Invent. Math. 170(1) (2007), 103–145.CrossRefGoogle Scholar
Coppersmith, D. and Rivlin, T. J., ‘The growth of polynomials bounded at equally spaced points’, SIAM J. Math. Anal. 23(4) (1992), 970–983.CrossRefGoogle Scholar
Dudley, R. and Randol, B., ‘Implications of pointwise bounds on polynomials’, Duke Math. J. 29 (1962), 455–458.CrossRefGoogle Scholar
Erdelyi, T., ‘Remez-type inequalities and their applications’, J. Comput. Appl. Math. 47 (1993), 167–209.CrossRefGoogle Scholar
Favard, J., ‘Sur l’interpolation’, Bull. de la S. M. F. 67 (1939), 103–113.Google Scholar
Federer, H., Geometric Measure Theory (Springer, Berlin, 1969).Google Scholar
Fefferman, Ch., Israel, A. and Luli, G., ‘Sobolev extension by linear operators’, J. Amer. Math. Soc. 27(1) (2014), 69–145.CrossRefGoogle Scholar
Friedland, O. and Yomdin, Y., ‘An observation on Turán–Nazarov inequality’, Studia Math. 218(1) (2013), 27–39.CrossRefGoogle Scholar
Friedland, O. and Yomdin, Y., ‘Vitushkin-type theorems’, in: Geometric Aspects of Functional Analysis, Lecture Notes in Mathematics, 2116 (eds. Klartag, B. and Milman, E.) (Springer, 2014), 47–57.Google Scholar
Friedland, O. and Yomdin, Y., ‘$(s,p)$-valent functions’, Preprint, 2015, arXiv:1503.00325.Google Scholar
Hardt, R. and Simon, L., ‘Nodal sets for solutions of elliptic equations’, J. Differential Geom. 30 (1989), 505–522.CrossRefGoogle Scholar
Klimek, M., Pluripotential Theory (Oxford University Press, New York, 1991).CrossRefGoogle Scholar
Kolmogorov, A. N. and Tihomirov, V. M., ‘𝜀-entropy and 𝜀-capacity of sets in functional space’, Amer. Math. Soc. Transl. 17 (1961), 277–364.Google Scholar
Kroó, A., ‘Bernstein type inequalities on star-like domains in ℝd with application to norming sets’, Bull. Math. Sci. 3 (2013), 349–361.CrossRefGoogle Scholar
Labutin, D., ‘Pluripolarity of sets with small Hausdorff measure’, Manuscripta Math. 102 (2000), 163–167.CrossRefGoogle Scholar
Lorentz, R., Multivariate Birkhoff Interpolation (Springer, Berlin, 1992).CrossRefGoogle Scholar
Nazarov, F. L., ‘Local estimates for exponential polynomials and their applications to inequalities of the uncertainty principle type’, Algebra i Analiz 5(4) (1993), 3–66; translation in St. Petersburg Math. J. 5(4) (1994), 663–717.Google Scholar
Nazarov, F., Nishry, A. and Sodin, M., ‘Log-integrability of Rademacher Fourier series, with applications to random analytic functions’, Algebra i Analiz 25(3) (2013), 147–184; translation in St. Petersburg Math. J. 25(3) (2014), 467–494.Google Scholar
Rakhmanov, E. A., ‘Bounds for polynomials with a unit discrete norm’, Ann. of Math. (2) 165(1) (2007), 55–88.CrossRefGoogle Scholar
Remez, E. J., ‘Sur une propriété des polynomes de Tchebycheff’, Comm. Inst. Sci. Kharkov 13 (1936), 93–95.Google Scholar
Taylor, B. A. and Levenberg, N., ‘Comparison of capacities in ℂn’, in: Analyse Complexe, Lecture Notes in Mathematics, 1094 (eds. Amar, E., Gay, R. and Van Nguyen, T.) (Springer, Berlin, 1984), 162–172.Google Scholar
Timan, A. F., Theory of Approximation of Functions of Real Variable (Pergamon Press, Oxford, 1963).Google Scholar
Turán, P., Eine neue Methode in der Analysis und deren Anwendungen (Akadémiai Kiadó, Budapest, 1953).Google Scholar
Vitushkin, A. G., ‘O mnogomernyh variaciyah’, in: Gosudarstv. Izdat. Tehn.-Teor. Lit. (Moscow, 1955), (in Russian).Google Scholar
Weierstraß, K., ‘Zu Hrn. Lindemanns Abhandlung:‘Über die Ludolph’sche Zahl’’, Sitzungber. Königl. Preuss. Akad. Wissensch. zu Berlin 2 (1885), 1067–1086.Google Scholar
Yomdin, Y., ‘Remez-type inequality for discrete sets’, Israel J. Math. 186 (2011), 45–60.CrossRefGoogle Scholar
Yomdin, Y., ‘Remez-type inequality for smooth functions’, in: Geometry and its Applications, Springer Proceedings in Mathematics & Statistics, 72 (eds. Rovenski, V. and Walczak, P.) (Springer, 2014), 235–243.CrossRefGoogle Scholar
Zeriahi, A., ‘A minimum principle for plurisubharmonic functions’, Indiana Univ. Math. J. 56(6) (2007), 2671–2696.CrossRefGoogle Scholar