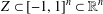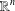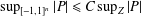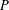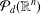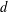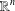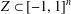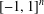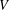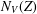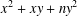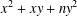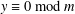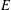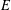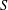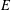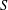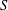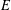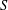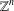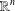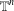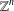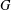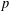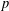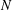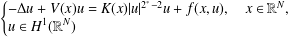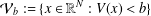To the memory of Professor Garth Gaudry
Research Article
SECOND-ORDER NONCOMMUTATIVE DIFFERENTIAL AND LIPSCHITZ STRUCTURES DEFINED BY A CLOSED SYMMETRIC OPERATOR
- Part of:
-
- Published online by Cambridge University Press:
- 25 November 2015, pp. 145-162
-
- Article
-
- You have access
- Export citation
NORMING SETS AND RELATED REMEZ-TYPE INEQUALITIES
- Part of:
-
- Published online by Cambridge University Press:
- 17 November 2015, pp. 163-181
-
- Article
-
- You have access
- Export citation
REPRESENTATIONS OF INTEGERS BY THE BINARY QUADRATIC FORM
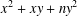 $x^{2}+xy+ny^{2}$
$x^{2}+xy+ny^{2}$
- Part of:
-
- Published online by Cambridge University Press:
- 17 November 2015, pp. 182-191
-
- Article
-
- You have access
- Export citation
ON GENERALISED FC-GROUPS IN WHICH NORMALITY IS A TRANSITIVE RELATION
- Part of:
-
- Published online by Cambridge University Press:
- 29 October 2015, pp. 192-198
-
- Article
-
- You have access
- Export citation
COMPLETE LATTICE HOMOMORPHISM OF STRONGLY REGULAR CONGRUENCES ON
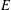 $E$-INVERSIVE SEMIGROUPS
$E$-INVERSIVE SEMIGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 28 October 2015, pp. 199-215
-
- Article
-
- You have access
- Export citation
MAXIMAL SEMIGROUP SYMMETRY AND DISCRETE RIESZ TRANSFORMS
- Part of:
-
- Published online by Cambridge University Press:
- 14 December 2015, pp. 216-240
-
- Article
-
- You have access
- Export citation
RELATIVE ELEMENTARY ABELIAN GROUPS AND A CLASS OF EDGE-TRANSITIVE CAYLEY GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 20 November 2015, pp. 241-251
-
- Article
-
- You have access
- Export citation
CONVERGENCE OF SOLUTIONS TO SOME ELLIPTIC EQUATIONS IN BOUNDED NEUMANN THIN DOMAINS
- Part of:
-
- Published online by Cambridge University Press:
- 20 November 2015, pp. 252-271
-
- Article
-
- You have access
- Export citation
WEAK POTENTIAL CONDITIONS FOR SCHRÖDINGER EQUATIONS WITH CRITICAL NONLINEARITIES
- Part of:
-
- Published online by Cambridge University Press:
- 28 October 2015, pp. 272-288
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
JAZ volume 100 Issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 03 March 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JAZ volume 100 Issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 03 March 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation