Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-25T02:12:52.497Z Has data issue: false hasContentIssue false
  • English
  • Français

Omitting types in 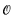-minimal theories

Published online by Cambridge University Press:  12 March 2014

David Marker
David Marker*
Affiliation:
Department of Mathematics, University of California, Berkeley, California 94720
*
Department of Mathematics, University of Illinois at Chicago, Chicago, Illinois 60680
Get access Rights & Permissions [Opens in a new window]

Extract

Let L be a first order language containing a binary relation symbol <.

Definition. Suppose ℳ is an L-structure and < is a total ordering of the domain of ℳ. ℳ is ordered minimal (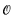-minimal) if and only if any parametrically definable X ⊆ ℳ can be represented as a finite union of points and intervals with endpoints in ℳ.

In any ordered structure every finite union of points and intervals is definable. Thus the 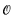-minimal structures are the ones with no unnecessary definable sets. If T is a complete L-theory we say that T is strongly (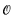-minimal if and only if every model of T is 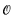-minimal.

The theory of real closed fields is the canonical example of a strongly 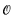-minimal theory. Strongly 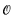-minimal theories were introduced (in a less general guise which we discuss in §6) by van den Dries in [1]. Extending van den Dries' work, Pillay and Steinhorn (see [3], [4] and [2]) developed an extensive structure theory for definable sets in strongly 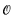-minimal theories, generalizing the results for real closed fields. They also established several striking analogies between strongly 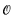-minimal theories and ω-stable theories (most notably the existence and uniqueness of prime models). In this paper we will examine the construction of models of strongly 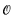-minimal theories emphasizing the problems involved in realizing and omitting types. Among other things we will prove that the Hanf number for omitting types for a strongly 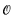-minimal theory T is at most (2∣T∣)+, and characterize the strongly 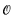-minimal theories with models order isomorphic to (R, <).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 1 , March 1986 , pp. 63 - 74
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCE

[1]van den Dries, L., Remarks on Tarski's problem concerning (R, +, ·, exp), Logic Colloquium '82, North-Holland, Amsterdam, 1984, pp. 97–121.CrossRefGoogle Scholar
[2]Knight, J., Pillay, A. and Steinhorn, C., Definable sets in ordered structures. II, Transactions of the American Mathematical Society (to appear).Google Scholar
[3]Pillay, A. and Steinhorn, C., Definable sets in ordered structures, Bulletin (New Series) of the American Mathematical Society, vol. 11 (1984), pp. 159–162.Google Scholar
[4]Pillay, A. and Steinhorn, C., Definable sets in ordered structures. I, Transactions of the American Mathematical Society (to appear).Google Scholar
[5]Pillay, A. and Steinhorn, C., Discrete -minimal structures (in preparation).Google Scholar