Research Article
A saturation property of ideals and weakly compact cardinals1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 513-525
-
- Article
- Export citation
Recursion in Kolmogorov's R-operator and the ordinal σ3
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-11
-
- Article
- Export citation
Other
Survey/expository papers
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 865
-
- Article
- Export citation
Research Article
Lattice embeddings into the recursively enumerable degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 257-272
-
- Article
- Export citation
Partitions and filters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 12-21
-
- Article
- Export citation
Other
Alfred Tarski
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 866-868
-
- Article
- Export citation
Research Article
Small filter forcing
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 526-546
-
- Article
- Export citation
A generalization of the limit lemma and clopen games
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 273-291
-
- Article
- Export citation
research-article
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 22-32
-
- Article
- Export citation
Combinatorial and recursive aspects of the automorphism group of the countable atomless Boolean algebra
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 292-301
-
- Article
- Export citation
Between strong and superstrong
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 547-559
-
- Article
- Export citation
Alfred Tarski's work in model theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 869-882
-
- Article
- Export citation
On ideals of subsets of the plane and on Cohen reals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 560-569
-
- Article
- Export citation
The contributions of Alfred Tarski to general algebra
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 883-889
-
- Article
- Export citation
Weak partition relations and measurability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 33-38
-
- Article
- Export citation
On the number of nonisomorphic models of an infinitary theory which has the infinitary order property. Part A
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 302-322
-
- Article
- Export citation
0# and some forcing principles
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 39-46
-
- Article
- Export citation
Alfred Tarski and undecidable theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 890-898
-
- Article
- Export citation
Attention à la marche!
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 570-585
-
- Article
- Export citation
Maximal chains in the fundamental order
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 323-326
-
- Article
- Export citation



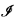 is a
is a 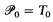
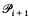 = the set of partial functions from
= the set of partial functions from 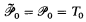
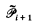 = the set of consistent partial functions from
= the set of consistent partial functions from 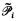 to
to 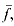 , where
, where 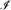 be any proper ideal of subsets of the real line
be any proper ideal of subsets of the real line 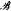 as follows:
as follows: 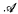 ⊂
⊂ 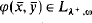 . Now define
. Now define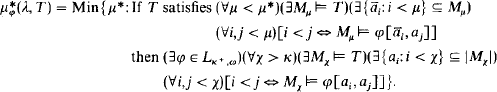
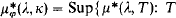 is a theory in
is a theory in 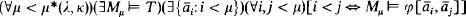
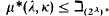 . Here we continue that work by proving
. Here we continue that work by proving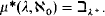 .
.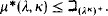 .
.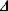 ⊆
⊆ 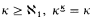 , then
, then