No CrossRef data available.
Article contents
A saturation property of ideals and weakly compact cardinals1
Published online by Cambridge University Press: 12 March 2014
Extract
Suppose κ is a regular uncountable cardinal, λ is a cardinal > 1, and 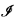 is a κ-complete uniform ideal on κ. This paper deals with a saturation property Sat(κ, λ,
is a κ-complete uniform ideal on κ. This paper deals with a saturation property Sat(κ, λ, 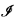 ) of
) of 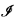 , which is a weakening of usual λ-saturatedness. Roughly speaking, Sat(κ, λ,
, which is a weakening of usual λ-saturatedness. Roughly speaking, Sat(κ, λ, 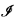 ) means that
) means that 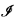 can be densely extended to λ-saturated ideals on small fields of subsets of κ. We will show that some consequences of the existence of a λ-saturated ideal on κ follow from weaker ∃
can be densely extended to λ-saturated ideals on small fields of subsets of κ. We will show that some consequences of the existence of a λ-saturated ideal on κ follow from weaker ∃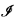 : Sat(κ, λ,
: Sat(κ, λ, 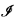 ), and that ∃
), and that ∃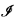 : Sat(κ, λ,
: Sat(κ, λ, 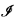 ) is connected with weak compactness and complete ineffability of κ in much the same way as the existence of a saturated ideal on κ is connected with measurability of κ.
) is connected with weak compactness and complete ineffability of κ in much the same way as the existence of a saturated ideal on κ is connected with measurability of κ.
In §2, we define Sat(κ, λ, 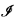 ), mention a few results that can be proved by straightforward adaptation of known methods, and discuss generic ultrapowers of ZFC−, which will be used repeatedly in the subsequent sections as a main technical tool. A related concept Sat(κ, λ) is also defined and shown to be equivalent to ∃
), mention a few results that can be proved by straightforward adaptation of known methods, and discuss generic ultrapowers of ZFC−, which will be used repeatedly in the subsequent sections as a main technical tool. A related concept Sat(κ, λ) is also defined and shown to be equivalent to ∃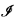 : Sat(κ, λ,
: Sat(κ, λ, 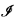 ) under a certain condition.
) under a certain condition.
In §3, we show that ∃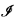 : Sat(κ, κ,
: Sat(κ, κ, 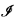 ) implies that κ is highly Mahlo, improving results in [KT] and [So].
) implies that κ is highly Mahlo, improving results in [KT] and [So].
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1986
Footnotes
The results in this paper are from the author's Ph.D. thesis [Ta] written under the supervision of Karel Prikry, to whom the author is grateful.




