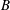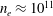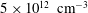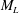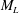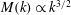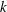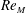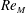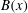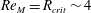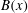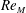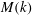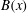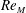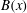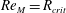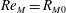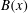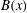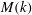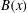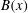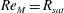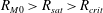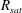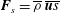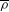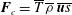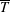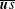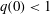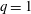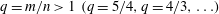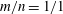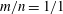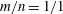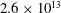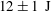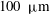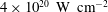Zeldovich’s stretch–twist–fold (STF) dynamo provided a breakthrough in conceptual understanding of fast dynamos, including the small-scale fluctuation dynamos. We study the evolution and saturation behaviour of two types of generalized Baker’s map dynamos, which have been used to model Zeldovich’s STF dynamo process. Using such maps allows one to analyse dynamos at much higher magnetic Reynolds numbers 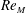 $\mathit{Re}_{M}$ as compared to direct numerical simulations. In the two-strip map dynamo there is constant constructive folding, while the four-strip map dynamo also allows the possibility of a destructive reversal of the field. Incorporating a diffusive step parametrized by
$\mathit{Re}_{M}$ as compared to direct numerical simulations. In the two-strip map dynamo there is constant constructive folding, while the four-strip map dynamo also allows the possibility of a destructive reversal of the field. Incorporating a diffusive step parametrized by 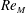 $\mathit{Re}_{M}$ into the map, we find that the magnetic field
$\mathit{Re}_{M}$ into the map, we find that the magnetic field 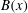 $B(x)$ is amplified only above a critical
$B(x)$ is amplified only above a critical 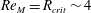 $\mathit{Re}_{M}=R_{\mathit{crit}}\sim 4$ for both types of dynamos. The growing
$\mathit{Re}_{M}=R_{\mathit{crit}}\sim 4$ for both types of dynamos. The growing 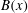 $B(x)$ approaches a shape-invariant eigenfunction independent of initial conditions, whose fine structure increases with increasing
$B(x)$ approaches a shape-invariant eigenfunction independent of initial conditions, whose fine structure increases with increasing 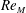 $\mathit{Re}_{M}$. Its power spectrum
$\mathit{Re}_{M}$. Its power spectrum 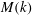 $M(k)$ displays sharp peaks reflecting the fractal nature of
$M(k)$ displays sharp peaks reflecting the fractal nature of 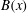 $B(x)$ above the diffusive scale. We explore the saturation of these dynamos in three ways: via a renormalized reduced effective
$B(x)$ above the diffusive scale. We explore the saturation of these dynamos in three ways: via a renormalized reduced effective 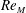 $\mathit{Re}_{M}$ (case I) or due to a decrease in the efficiency of the field amplification by stretching, without changing the map (case IIa), or changing the map (case IIb), and a combination of both effects (case III). For case I, we show that
$\mathit{Re}_{M}$ (case I) or due to a decrease in the efficiency of the field amplification by stretching, without changing the map (case IIa), or changing the map (case IIb), and a combination of both effects (case III). For case I, we show that 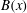 $B(x)$ in the saturated state, for both types of maps, approaches the marginal eigenfunction, which is obtained for
$B(x)$ in the saturated state, for both types of maps, approaches the marginal eigenfunction, which is obtained for 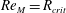 $\mathit{Re}_{M}=R_{\mathit{crit}}$ independent of the initial
$\mathit{Re}_{M}=R_{\mathit{crit}}$ independent of the initial 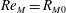 $\mathit{Re}_{M}=R_{M0}$. On the other hand, in case II, for the two-strip map, we show that
$\mathit{Re}_{M}=R_{M0}$. On the other hand, in case II, for the two-strip map, we show that 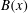 $B(x)$ saturates, preserving the structure of the kinematic eigenfunction. Thus the energy is transferred to larger scales in case I but remains at the smallest resistive scales in case II, as can be seen from both
$B(x)$ saturates, preserving the structure of the kinematic eigenfunction. Thus the energy is transferred to larger scales in case I but remains at the smallest resistive scales in case II, as can be seen from both 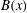 $B(x)$ and
$B(x)$ and 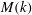 $M(k)$. For the four-strip map,
$M(k)$. For the four-strip map, 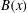 $B(x)$ oscillates with time, although with a structure similar to the kinematic eigenfunction. Interestingly, the saturated state in case III shows an intermediate behaviour, with
$B(x)$ oscillates with time, although with a structure similar to the kinematic eigenfunction. Interestingly, the saturated state in case III shows an intermediate behaviour, with 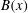 $B(x)$ similar to the kinematic eigenfunction at an intermediate
$B(x)$ similar to the kinematic eigenfunction at an intermediate 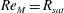 $\mathit{Re}_{M}=R_{\mathit{sat}}$, with
$\mathit{Re}_{M}=R_{\mathit{sat}}$, with 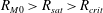 $R_{M0}>R_{\mathit{sat}}>R_{\mathit{crit}}$. The
$R_{M0}>R_{\mathit{sat}}>R_{\mathit{crit}}$. The 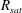 $R_{\mathit{sat}}$ value is determined by the relative importance of the increased diffusion versus the reduced stretching. These saturation properties are akin to the range of possibilities that have been discussed in the context of fluctuation dynamos.
$R_{\mathit{sat}}$ value is determined by the relative importance of the increased diffusion versus the reduced stretching. These saturation properties are akin to the range of possibilities that have been discussed in the context of fluctuation dynamos.