I. INTRODUCTION
Scintillator radiation detectors have many important applications in the context of high-energy physics, medicine, as well as homeland security. Reference Rodnyi1,Reference Knoll2 Examples of inorganic crystal scintillators used for gamma or x-ray detection include halides, oxides, and chalcogenides, Reference Knoll2,Reference Rodnyi3 whereas plastic scintillators are often used for neutron/gamma differentiation. Reference Zaitseva, Glenn, Carman, Hatarik, Hamel, Faust, Schabes, Cherepy and Payne4 Developing more accurate and faster radiation detectors requires successful materials design: certain applications, such as radioactive isotope identification, require particularly high-energy resolution, Reference Nelson, Gosnell and Knapp5 i.e., very high specificity of the optical response depending on the energy of incoming radiation. This is currently one of the major design criteria used in the search for new scintillator materials that also need to withstand incoming radiation and, at the same time, provide an easily detectable, optical response.
Sodium iodide (NaI) has been traditionally used in many devices, due ease of fabrication and low cost. To achieve higher energy resolution, new materials are currently investigated, such as Ce-doped lanthanum bromide (LaBr3), Reference van Loef, Dorenbos, van Eijk, Krämer and Güdel6 Eu-doped strontium iodide (SrI2), Reference Cherepy, Hull, Drobshoff, Payne, van Loef, Wilson, Shah, Roy, Burger, Boatner, Choong and Moses7,Reference Wilson, van Loef, Glodo, Cherepy, Hull, Payne, Choong, Moses and Shah8 and undoped cesium hafnium chloride (Cs2HfCl6). Reference Burger, Rowe, Groza, Figueroa, Cherepy, Beck, Hunter and Payne9 Lately, co-doping of scintillators has also proven to be a successful route to improved scintillation properties. Reference Alekhin, Biner, Krämer and Dorenbos10–Reference Khodyuk, Messina, Hayden, Bourret and Bizarri14
Unfortunately, the complex physics underlying the energy resolution of scintillators presently is still only understood at a qualitative level. Better fundamental, quantitative insight is needed, to enable targeted materials design for scintillators. Furthermore, the length and time scales involved in the entire scintillation mechanism dictate that multiscale modeling has to be used to develop a fully comprehensive picture. Existing models depend on external parameters, such as dielectric functions, stopping power, migration barriers, defect properties, polaron formation, and migration, as well as nonradiative recombination rates. Reference Vasil'ev15–Reference Payne, Hunter, Ahle, Cherepy and Swanberg21 Another example is the Monte-Carlo model of gamma-ray response that requires accurate knowledge of the electron-energy loss function. Reference Gao, Xie, Wang, Kerisit, Wu, Campbell, Van Ginhoven and Prange22
In principle, all these quantities can be deduced either from experiment or from first-principles modeling. Both the exponential growth of computational resources as well as development of sophisticated and predictive computational approaches renders the second option very attractive. Modern first-principles and theoretical spectroscopy techniques are clearly advanced enough to thoroughly study some of the mechanisms at play. While we and others started to apply these techniques to scintillator materials, Reference Åberg, Sadigh, Schleife and Erhart12,Reference Klintenberg, Derenzo and Weber23–Reference Wu, Prange, Gao and Kerisit34 in most cases, even basic quantities such as the dielectric function, optical absorption, or electron-energy loss function are still unknown. The influence of quasiparticle effects and excitons, for instance, is very well studied, e.g., for transparent conducting oxides, Reference Schleife, Rödl, Fuchs, Furthmüller and Bechstedt35–Reference Varley and Schleife39 but it is largely unknown for scintillator materials. Experiments alone cannot always mitigate this situation: LaBr3 is an example for a material where measuring the optical properties is particularly difficult because high-quality, optically polished crystals are practically unavailable. Reference van Dam, Seifert, Drozdowski, Dorenbos and Schaart40
In some cases, thorough experimental and theoretical investigations, targeted at studying the role of excitonic effects, are currently underway: Ucer et al. presented a detailed study on time-resolved pump-probe experiments on pristine and Tl-doped CsI and concluded that self-trapped excitons (STEs) are only present in the former case and that electrons and holes rapidly become trapped on Tl atoms. Reference Ucer, Bizarri, Burger, Gektin, Trefilova and Williams41 On the other hand, the scintillation mechanism of undoped, recently discovered Reference Burger, Rowe, Groza, Figueroa, Cherepy, Beck, Hunter and Payne9 cesium hafnium chloride (Cs2HfCl6) is believed to consist of luminescence from an STE consisting of a hole centered at a Cl-dimer and an electron at a Hf d-orbital. Reference Kang and Biswas42 More work is needed to quantitatively model these processes and to incorporate this information into multiscale models that can achieve computational materials design of scintillator materials.
In this light, it is the goal of our research to employ and develop cutting-edge theoretical spectroscopy techniques to establish fundamental knowledge. Here we apply many-body perturbation theory to scintillator materials, to provide predictions for optical properties, such as dielectric functions, for NaI, LaBr3, BaI2, and SrI2. We disentangle the influence of excitonic effects by comparing to the independent-particle approximation, and we provide quantitative insight into optical anisotropy via the complex frequency-dependent dielectric tensor. Furthermore, in the present work, we aim to alleviate the absence of experimental data for electron-energy loss spectra and we discuss trends across the different scintillator materials. At the same time, by providing detailed insight into free excitons in scintillator materials, we lay the ground-work for studying STEs in more complicated scintillator materials in the future.
The remainder of this work is structured as follows: in Sec. II the theoretical framework and computational approach is summarized briefly. Results for optical properties and electron-energy loss functions are presented in Sec. III. Section IV summarizes and concludes our work.
II. THEORETICAL AND COMPUTATIONAL APPROACH
In this work, we use density functional theory Reference Hohenberg and Kohn43,Reference Kohn and Sham44 (DFT) to compute Kohn–Sham states and eigenvalues as starting electronic structure for many-body perturbation theory. We use the local-density approximation Reference Ceperley and Alder45 to describe exchange and correlation for SrI2 and the generalized-gradient approximation by Perdew, Burke, and Ernzerhof Reference Perdew, Burke and Ernzerhof46 (PBE) is used for the other three materials. The electron–ion interaction was described within the projector-augmented wave method Reference Blöchl47 and a plane-wave basis 48 is used for the wave function expansion. All calculations are carried out within the Vienna Ab-initio Simulation Package Reference Gajdoš, Hummer, Kresse, Furthmüller and Bechstedt49–Reference Kresse and Furthmüller51 and the Bethe–Salpeter equation (BSE) implementation discussed in Refs. Reference Rödl, Fuchs, Furthmüller and Bechstedt52 and Reference Fuchs, Rödl, Schleife and Bechstedt53.
A. Atomic geometries
In this work we adopt experimental atomic geometries for NaI and SrI2 as described in Ref. Reference Erhart, Schleife, Sadigh and Åberg29 and for LaBr3 as described in Ref. Reference Åberg, Sadigh and Erhart28. NaI crystallizes in the rocksalt structure in equilibrium, SrI2 belongs to the Pbca space group Reference Erhart, Schleife, Sadigh and Åberg29 (no. 61 of the International Tables of Crystallography Reference Hahn54 ), and LaBr3 adopts a hexagonal lattice (P63/m, no. 176 in Ref. Reference Hahn54).
For orthorhombic BaI2 (space group Pnma, no. 62 in Ref. Reference Hahn54), we fully relaxed the atomic positions until all Hellman–Feynman force components on any atoms were less than 0.02 eV/Å. This leads to a = 9.01 Å, b = 5.43 Å, and c = 10.87 Å. The Ba atom and both iodine atoms occupy the 4c Wyckoff site with x = 0.244, z = 0.112 (for Ba), x = 0.142, z = 0.425 (for the first I), and x = 0.020, z = 0.836 (for the second I). All unit cells for the materials studied in this work are visualized in Fig. 1.

FIG. 1. Unit cells of the materials studied in this work: (a) NaI, (b) LaBr3, (c) BaI2, and (d) SrI2.
B. Single-particle electronic structure
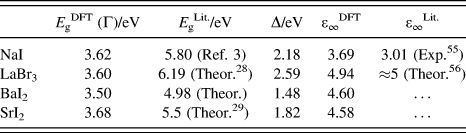
DFT does not provide an accurate description of the electronic structure, since it neglects quasiparticle effects, which manifests itself for instance in the infamous band-gap underestimation. Reference Onida, Reining and Rubio57 In the present work, we need to include quasiparticle effects to accurately describe both band gaps and electronic structure as the foundation of a reliable description of optical properties. Here, we use a scissor operator Δ that shifts all conduction bands to higher energies. The shift Δ is determined using band gaps available in the literature for NaI, LaBr3, and SrI2 (see Table I). For BaI2 we carry out generalized-gradient approximation (GGA) + G 0 W 0 calculations of quasiparticle energies using a Γ-centered 3 × 6 × 3 Monkhorst–Pack Reference Monkhorst and Pack58 (MP) k-point grid and 1024 bands (out of which 54 are occupied) to achieve convergence of the screened interaction. Reference Shishkin and Kresse59 This yields a band gap of 4.98 eV for BaI2 (see Table I).
TABLE I. Kohn–Sham results and literature values for the fundamental band gaps (in eV) are given as well as the scissor value (in eV) used in this work. In addition, DFT results and literature values are given for the static electronic dielectric constants.
In addition, local or semilocal approximations to exchange and correlation suffer from self-interaction errors. This error particularly affects localized orbitals such as d and f states. Hence, we compute the electronic structure of LaBr3 within the rotationally invariant GGA + U approach, Reference Liechtenstein, Anisimov and Zaanen60 to correct for the La 4f states that incorrectly appear within the band gap in DFT-PBE calculations. Reference Åberg, Sadigh and Erhart28 Here we use U = 11.0 eV and J = 0.68 eV, acting on these La 4f electrons. Reference Czyżyk and Sawatzky61
C. Two-particle excitations: excitons
To achieve an accurate description of optical properties (including excitonic and local-field effects) from first principles, we solve the BSE for the optical polarization function. Reference Onida, Reining and Rubio57 This allows us to include two-particle (electron–hole) excitations in the description of the dielectric function. The underlying DFT Kohn–Sham states are used to compute the optical transition matrix elements in the longitudinal approximation Reference Gajdoš, Hummer, Kresse, Furthmüller and Bechstedt49 and the statically screened Coulomb attraction as well as the unscreened exchange terms that determine the excitonic Hamiltonian. Reference Rödl, Fuchs, Furthmüller and Bechstedt52,Reference Fuchs, Rödl, Schleife and Bechstedt53,Reference Onida, Reining and Rubio57 After constructing this Hamiltonian, the dielectric function is computed from it using a time-propagation technique. Reference Schmidt, Glutsch, Hahn and Bechstedt62 The model dielectric function of Bechstedt et al. Reference Bechstedt, Del Sole, Cappellini and Reining63 is used to compute the screened Coulomb interaction W in the excitonic Hamiltonian, using the static electronic dielectric constants obtained on DFT level (see Table I).
Such calculations of converged results for optical properties across a large energy range are numerically very challenging, since different competing requirements have to be fulfilled: the sampling of the Brillouin zone needs to be fine enough to converge the onset of the optical absorption spectrum, but at the same time a large number of conduction bands is required to compute optical properties for high-energy optical transitions. Due to the large computational cost of the BSE approach, we employ the BSE cutoff energies (maximum noninteracting electron–hole pair energy taken into account) and MP k-point grids as listed in Ref. 64. Convergence is improved by displacing each grid by a small random vector to lift degeneracies that occur for unshifted MP meshes.
For computing the electron-energy loss function, we also need to converge the real part of the dielectric function (i.e., related to the imaginary part via a Kramers–Kronig relation) at low photon energies. This is achieved by including optical transitions with transition energies between the BSE cutoff and 200 eV on the level of DFT (as described in Refs. Reference Schleife, Rödl, Fuchs, Furthmüller and Bechstedt35 and Reference Schleife65).
III. OPTICAL PROPERTIES
A. Dielectric functions
Using the computational framework described in Sec. II, we computed the optical properties (dielectric functions) of ideal crystals of NaI (see Fig. 2), LaBr3 (see Fig. 3), BaI2 (see Fig. 4), and SrI2 (see Fig. 5). Due to the absence of experimentally determined (for instance via ellipsometry) dielectric functions, these results represent highly accurate predictions. In these figures, we compare the results within the independent-quasiparticle approximation, i.e., where quasiparticle effects on the Kohn–Sham eigenvalues are taken into account using the DFT + Δ scheme, to the solution of the BSE, that, in addition, includes excitonic and local-field effects. This allows us to draw conclusions about the influence of excitonic effects in the following.
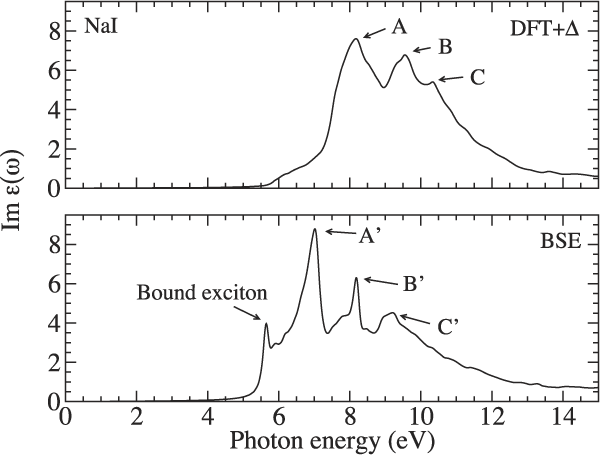
FIG. 2. Imaginary part of the dielectric function ε(ω) computed using the DFT + Δ approximation (top) as well as the BSE approach (bottom) for NaI.
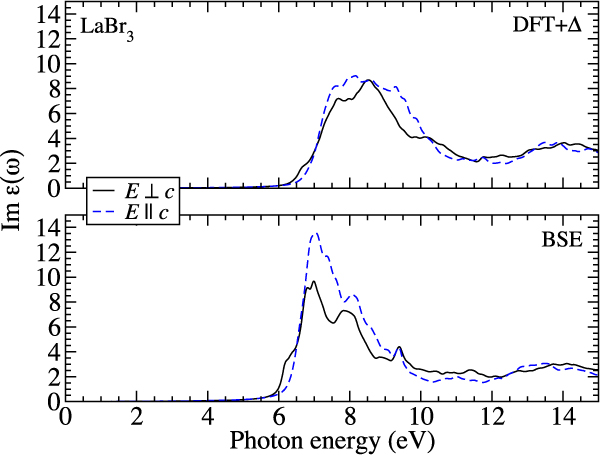
FIG. 3. Imaginary part of the dielectric function ε(ω) computed using the DFT + Δ approximation (top) as well as the BSE approach (bottom) for LaBr3. The optical anisotropy is shown for both.
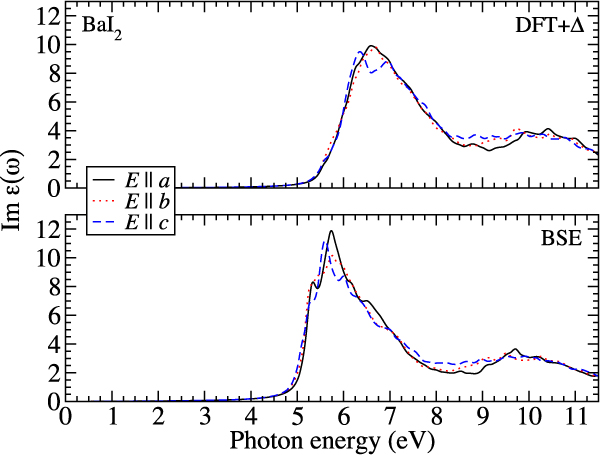
FIG. 4. Imaginary part of the dielectric function ε(ω) computed using the DFT + Δ approximation (top) as well as the BSE approach (bottom) for BaI2. The optical anisotropy is shown for both.
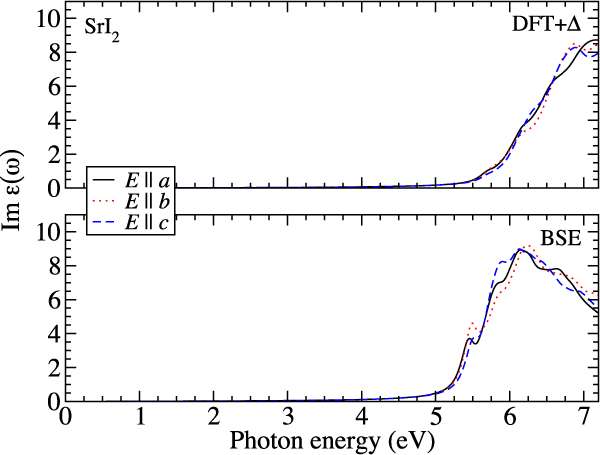
FIG. 5. Imaginary part of the dielectric function ε(ω) computed using the DFT + Δ approximation (top) as well as the BSE approach (bottom) for SrI2. The optical anisotropy is shown for both.
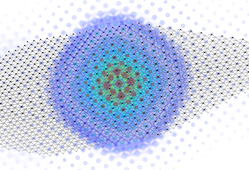
Excitonic effects are particularly dramatic for NaI (see Fig. 2), where the onset of optical absorption is dominated by a bound-excitonic state that occurs as a pronounced peak in the spectrum. It can be seen that this is an additional peak at about 5.5 eV in the lower panel of Fig. 2, that is absent in the upper panel. We visualize part of the two-particle electron–hole wave function of this bound-exciton state in Fig. 6 by fixing the position of the hole at an iodine atom and plotting the resulting electron distribution. The spherical shape confirms its similarity to a 1 s state within a hydrogen-like Wannier–Mott-exciton picture. In Fig. 6, it can be clearly seen that this electron density is centered around the iodine atom at which the hole is fixed. We previously studied this bound-excitonic state in more detail and determined the exciton-binding energy to be 216 meV and the Bohr radius to be 9 Å. Reference Erhart, Schleife, Sadigh and Åberg29

FIG. 6. The two-particle electron–hole wave function is visualized for the lowest bound-exciton state in NaI. The position of the hole is fixed on a I atom in the center of the spherical structure that represents the electronic part.
Furthermore, comparing the upper and lower panels in Fig. 2 shows that peaks that appear in the DFT + Δ spectrum at higher energies (labeled A, B, C in the figure) are shifted to lower photon energies and show slightly redistributed spectral weight when excitonic effects are taken into account. This red shift as well as the spectral redistribution has been traced back to excitonic effects for other materials (e.g., GaN, MgO, or ZnO) that show a similar structure of the uppermost valence and the lowest conduction band. Reference Schleife, Rödl, Fuchs, Furthmüller and Bechstedt35,Reference Benedict and Shirley66 In our calculations, we found that the peaks A, B, and C are attributed to transitions from the I 5p electrons into the conduction bands. The largest contribution to A is transitions into empty Na s states and to B and C transitions into empty I d states. Empty I s states contribute significantly only to A, while B and C also include important contributions from transitions into empty Na and I p states.
The spectra of the other three materials show either much weaker additional peaks/spectral features attributed to bound-excitonic states (see BaI2 and SrI2 in Figs. 4 and 5) or none is visible at all (see LaBr3 in Fig. 3). Partly, this can be attributed to the larger dielectric screening in these materials (see Table I): NaI has the lowest electronic dielectric constant of all four cases investigated here. Consequently the electron–hole interaction is strongest in this material, which is confirmed by the strong excitonic effects observed in the dielectric function. In addition, also the band structures of the materials differ: especially in the case of LaBr3, we attribute the lack of a bound-exciton peak at the absorption onset to the more complicated band structure (see Ref. Reference Åberg, Sadigh and Erhart28) that does not have a pronounced valence-band maximum and conduction-band minimum but rather dispersionless bands. The spectral red shift of higher-energy peaks due to excitonic effects is clearly visible for all materials.
In Figs. 3–5, it can be seen that the spectra of LaBr3, BaI2, and SrI2 feature a fairly broad (more than 2 eV of full width at half maximum) single peak structure starting right above the respective absorption onsets. This clearly distinguishes the spectra of these three materials from the one of NaI (see Fig. 2). Using our data, we are able to trace this feature back to transitions into empty d states that do not occur in NaI but in the other three materials. For LaBr3 this feature arises mostly due to transitions from Br 4p electrons into empty La d states and for BaI2 it is mostly transitions from I 5p into empty Ba d states. In the case of SrI2, it is transitions from I 5p electrons into empty Sr d states that cause the appearance of this spectral feature.
The four different scintillator materials also differ regarding their optical anisotropy: cubic NaI is optically isotropic due to its lattice symmetry. However, also the spectra of the noncubic materials BaI2 and SrI2 show almost no dependence on the light polarization (see Figs. 4 and 5). This agrees well with the dielectric functions computed by Singh using the random phase approximation. Reference Singh67 In the case of LaBr3, the overall anisotropy is still not very strong; however, the energy position and the spectral shape of the absorption edge depend on the polarization of the light (see Fig. 3). This is due to the energy splitting of the uppermost Br 4p derived valence bands by about 88 meV.
B. Electron-energy loss function
To understand the energy loss processes of electrons in the scintillator materials, we use the complex dielectric function to compute the electron-energy loss function for zero momentum transfer according to
For all four materials studied in this work, the results are shown in Fig. 7. In this figure, we compare results computed within the independent-particle approximation, i.e., neglecting excitonic effects, to electron-loss functions derived from the BSE data (i.e., taking excitonic effects into account).
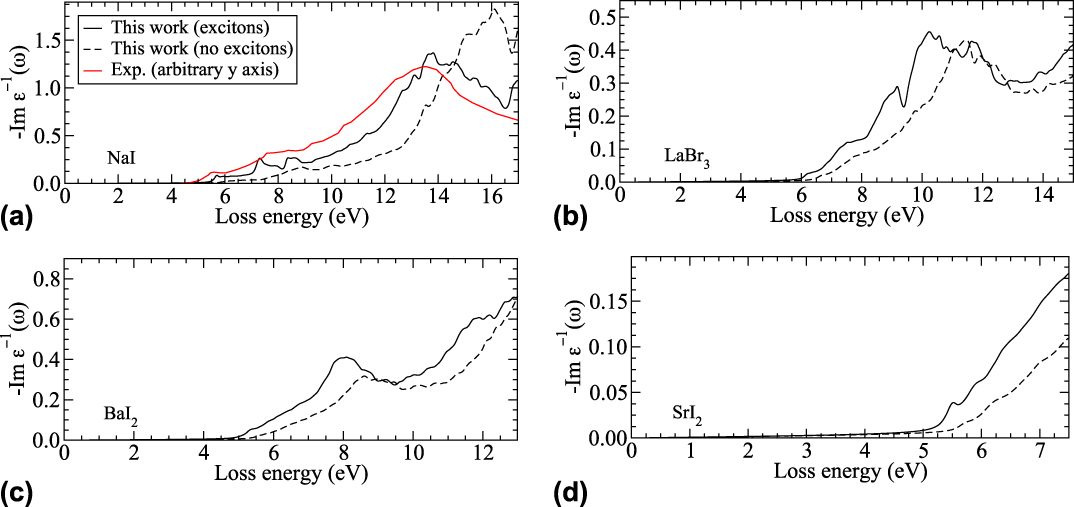
FIG. 7. Electron-energy loss function −Im ε−1(ω) computed from the dielectric function including (solid lines) and excluding (dashed lines) excitonic effects, according to Eq. (1) for NaI (a), LaBr3 (b), BaI2 (c), and SrI2 (d). For NaI, a measured curve Reference Creuzburg68 is included for comparison.
Figure 7 clearly illustrates the impact of excitonic effects on −Im ε−1 across the entire energy range studied here. For all four materials, we observe a remarkable red shift when the electron–hole interaction is included, along with significant spectral redistribution. In particular for NaI, which shows the strongest excitonic effects due the weak screening of the electron–hole interaction, the difference between both computational results are large: a peak that occurs at around 16 eV in independent-particle approximation occurs at ≈13.5 eV due to excitonic effects and also its height is significantly reduced. In the case of NaI, we also compare to an experimental result Reference Creuzburg68 and find very good agreement with our theoretical data that takes excitonic effects into account. Even though the y axis scaling of the experiment is arbitrary, it is immediately clear that both absolute peak positions and relative peak heights agree very well with our computational result. The data for all four materials illustrate that both quasiparticle and excitonic effects need to be treated accurately, to achieve reliable predictions of electron-energy loss function that can be used, for instance, in multiscale modeling approaches. Reference Gao, Xie, Wang, Kerisit, Wu, Campbell, Van Ginhoven and Prange22
IV. CONCLUSIONS
In summary, we have used cutting-edge theoretical spectroscopy techniques to investigate the frequency-dependent, complex dielectric functions, and electron-energy loss functions for zero momentum transfer for four different scintillator materials. Using these results, we illustrate the influence of excitonic effects, which we find to be very strong in NaI, due to the weak screening of the electron–hole interaction. We also point out the formation of bound-excitonic states that are visible near the absorption onset. These first-principles results allow us to explain the origin of three sub peaks in the dielectric function of NaI, and to trace back a broad, peak-like feature in the spectra of LaBr3, BaI2, and SrI2 to the presence of d electrons in these materials. At the same time, the optical anisotropy is small for these four scintillator materials.
We compute electron-energy loss functions for all materials and also find a strong influence of excitonic effects. This result clearly illustrates the importance of accurately describing electronic many-body effects when using first-principles techniques to predict quantities for multiscale modeling approaches. Furthermore, these data constitute the foundation for future studies of STEs, for instance in doped materials or in undoped cesium hafnium chloride, all of which are currently attracting attention in the scintillator community.
Overall, it is our goal to use and develop efficient and accurate computational techniques that provide deep insight into the fundamental properties of materials for scintillator-radiation detectors. One of the biggest challenges in this field is to achieve computational accuracy and efficiency: in many cases the materials of interest are complicated with large unit cells and localized d or f electrons. At the same time, predictions need to be accurate enough to allow the results to be used in larger length scale models. The techniques discussed here and demonstrated for four materials have excellent application potential and promise exciting progress to address some of the challenges of the scintillator community.
ACKNOWLEDGMENTS
We acknowledge fruitful discussions with B. Sadigh and R. T. Williams. Part of this work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344 with support from the National Nuclear Security Administration Office of Nonproliferation Research and Development (NA-22). This research is part of the Blue Waters sustained-petascale computing project, which is supported by the National Science Foundation (awards OCI-0725070 and ACI-1238993) and the state of Illinois. Blue Waters is a joint effort of the University of Illinois at Urbana–Champaign and its National Center for Supercomputing Applications.