Article contents
Shear and shuffle in 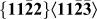 $\left\{ {{\bf 11}\bar {\bf2}{\bf 2}} \right\}\left\langle {{\bf11}\bar {\bf 2}\bar {\bf 3}} \right\rangle$ twinning in titanium
$\left\{ {{\bf 11}\bar {\bf2}{\bf 2}} \right\}\left\langle {{\bf11}\bar {\bf 2}\bar {\bf 3}} \right\rangle$ twinning in titanium
Published online by Cambridge University Press: 22 December 2015
Abstract
In classical twinning theory, the K2 plane of  $\left\{ {11\bar 22} \right\}\left\langle {11\bar 2\bar 3} \right\rangle$ twinning mode was predicted to be
$\left\{ {11\bar 22} \right\}\left\langle {11\bar 2\bar 3} \right\rangle$ twinning mode was predicted to be  $\left\{ {11\bar 2\bar 4} \right\}$, with a twinning shear of ∼0.22 which was experimentally “confirmed”. However, these twinning elements cannot be reproduced or verified in atomistic simulations. The K2 plane in the simulations is always (0001), but this K2 plane would lead to a nominal twining shear of 1.26 which is unrealistically large. In this work, atomistic simulations were performed to investigate the migration of
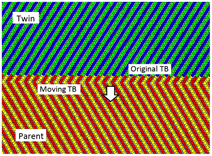
$\left\{ {11\bar 2\bar 4} \right\}$, with a twinning shear of ∼0.22 which was experimentally “confirmed”. However, these twinning elements cannot be reproduced or verified in atomistic simulations. The K2 plane in the simulations is always (0001), but this K2 plane would lead to a nominal twining shear of 1.26 which is unrealistically large. In this work, atomistic simulations were performed to investigate the migration of  $\left\{ {11\bar 22} \right\}$ twin boundary in titanium (Ti). Shear and atomic shuffles for three different, reported K2 planes were analyzed in great detail, for the first time. The analyses show that
$\left\{ {11\bar 22} \right\}$ twin boundary in titanium (Ti). Shear and atomic shuffles for three different, reported K2 planes were analyzed in great detail, for the first time. The analyses show that  ${K_2} = \{ 11\bar 2\bar 4\}$ leads to very complex shuffles despite the small twinning shear and is unfavorable. If
${K_2} = \{ 11\bar 2\bar 4\}$ leads to very complex shuffles despite the small twinning shear and is unfavorable. If  ${K_2} = \{ 11\bar 2\bar 2\}$, only half of the parent atoms are involved in the shuffling, but the twinning shear is very large (0.96) and is also unfavorable. When K2 = (0001), the parent atoms are carried to twin positions partly by shear and partly by a simple shuffle. Because shuffling makes no contribution to the twinning shear, the actual twinning shear is 0.66, instead of 1.26. Thus, K2 = (0001) is the most favorable and the conflict between the simulation results and the classical twinning theory can be reconciled.
${K_2} = \{ 11\bar 2\bar 2\}$, only half of the parent atoms are involved in the shuffling, but the twinning shear is very large (0.96) and is also unfavorable. When K2 = (0001), the parent atoms are carried to twin positions partly by shear and partly by a simple shuffle. Because shuffling makes no contribution to the twinning shear, the actual twinning shear is 0.66, instead of 1.26. Thus, K2 = (0001) is the most favorable and the conflict between the simulation results and the classical twinning theory can be reconciled.
- Type
- Articles
- Information
- Copyright
- Copyright © Materials Research Society 2015
Footnotes
Contributing Editor: Susan B. Sinnott
References
REFERENCES
- 3
- Cited by




