Article contents
On the numerical modeling of nucleation and growth of microstructurally short cracks in polycrystals under cyclic loading
Published online by Cambridge University Press: 17 September 2019
Abstract
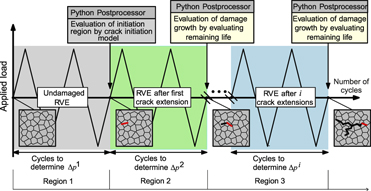
In the scope of this work, a micromechanical model based on the crystal plasticity finite element method is proposed and applied to describe the nucleation and growth of microstructurally short fatigue cracks in polycrystalline materials under cyclic loads. The microstructure is generated in the form of a representative volume element of a polycrystalline material with equiaxed grains having columnar structure along thickness and random crystallographic texture. With this model, we investigate the influence of loading amplitude on the crack growth behavior. It is shown that for smaller strain amplitudes, a single crack nucleates and propagates, while for larger strain amplitudes several independent crack nucleation sites form, from which microcracks start propagating. It is also observed that the global plastic strain amplitude decreases from the initial to the final cycle, during total strain-controlled loading. However, this can even increase the crack growth rate because the crack advance is governed by the local plastic slip which accumulates at the crack tip over the number of cycles. With this work, it is shown that micromechanical modeling can strongly improve our understanding of the mechanisms of short-crack nucleation and growth under fatigue loading.
Keywords
- Type
- Article
- Information
- Copyright
- Copyright © Materials Research Society 2019
References
- 5
- Cited by




