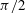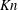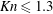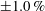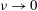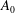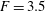Papers
Two-dimensional numerical study of vortex shedding regimes of oscillatory flow past two circular cylinders in side-by-side and tandem arrangements at low Reynolds numbers
-
- Published online by Cambridge University Press:
- 16 June 2014, pp. 1-37
-
- Article
- Export citation
On the structure and origin of pressure fluctuations in wall turbulence: predictions based on the resolvent analysis
-
- Published online by Cambridge University Press:
- 16 June 2014, pp. 38-70
-
- Article
- Export citation
The role of advance ratio and aspect ratio in determining leading-edge vortex stability for flapping flight
-
- Published online by Cambridge University Press:
- 16 June 2014, pp. 71-105
-
- Article
- Export citation
Electrohydrodynamics of particle-covered drops
-
- Published online by Cambridge University Press:
- 16 June 2014, pp. 106-120
-
- Article
- Export citation
The Burnett equations in cylindrical coordinates and their solution for flow in a microtube
-
- Published online by Cambridge University Press:
- 16 June 2014, pp. 121-141
-
- Article
- Export citation
Effect of large bulk viscosity on large-Reynolds-number flows
-
- Published online by Cambridge University Press:
- 17 June 2014, pp. 142-163
-
- Article
- Export citation
How flexibility affects the wake symmetry properties of a self-propelled plunging foil
-
- Published online by Cambridge University Press:
- 18 June 2014, pp. 164-183
-
- Article
- Export citation
Drops of power-law fluids falling on a coated vertical fibre
-
- Published online by Cambridge University Press:
- 19 June 2014, pp. 184-215
-
- Article
- Export citation
Quasi-geostrophic approximation of anelastic convection
-
- Published online by Cambridge University Press:
- 18 June 2014, pp. 216-227
-
- Article
- Export citation
The quiescent core of turbulent channel flow
-
- Published online by Cambridge University Press:
- 18 June 2014, pp. 228-254
-
- Article
- Export citation
Inertial wave excitation and focusing in a liquid bounded by a frustum and a cylinder
-
- Published online by Cambridge University Press:
- 18 June 2014, pp. 255-297
-
- Article
- Export citation
Scaling of the turbulent/non-turbulent interface in boundary layers
-
- Published online by Cambridge University Press:
- 19 June 2014, pp. 298-328
-
- Article
- Export citation
Reconnection of skewed vortices
-
- Published online by Cambridge University Press:
- 20 June 2014, pp. 329-345
-
- Article
- Export citation
Analysis of a model for foam improved oil recovery
-
- Published online by Cambridge University Press:
- 20 June 2014, pp. 346-405
-
- Article
- Export citation
Long-wave dynamics of an inextensible planar membrane in an electric field
-
- Published online by Cambridge University Press:
- 20 June 2014, pp. 406-431
-
- Article
- Export citation
Perturbation theory and numerical modelling of weakly and moderately nonlinear dynamics of the incompressible Richtmyer–Meshkov instability
-
- Published online by Cambridge University Press:
- 23 June 2014, pp. 432-479
-
- Article
- Export citation
The coalescence of liquid drops in a viscous fluid: interface formation model
-
- Published online by Cambridge University Press:
- 24 June 2014, pp. 480-499
-
- Article
- Export citation
Discrete-vortex method with novel shedding criterion for unsteady aerofoil flows with intermittent leading-edge vortex shedding
-
- Published online by Cambridge University Press:
- 23 June 2014, pp. 500-538
-
- Article
- Export citation
Critical layer and radiative instabilities in shallow-water shear flows
-
- Published online by Cambridge University Press:
- 23 June 2014, pp. 539-569
-
- Article
- Export citation
Low-Reynolds-number wakes of elliptical cylinders: from the circular cylinder to the normal flat plate
-
- Published online by Cambridge University Press:
- 24 June 2014, pp. 570-600
-
- Article
- Export citation