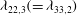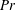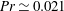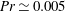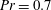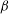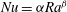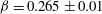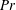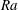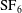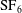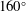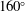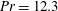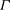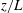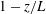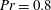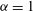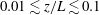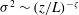Focus on Fluids
From snapshots to modal expansions – bridging low residuals and pure frequencies
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Papers
Nonlinear dynamics of surfactant-laden two-fluid Couette flows in the presence of inertia
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 5-36
-
- Article
- Export citation
Bubbly shock propagation as a mechanism for sheet-to-cloud transition of partial cavities
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 37-78
-
- Article
- Export citation
Interactions of large-scale free-stream turbulence with turbulent boundary layers
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 79-107
-
- Article
- Export citation
Rapid distortion theory analysis on the interaction between homogeneous turbulence and a planar shock wave
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 108-146
-
- Article
- Export citation
Global and local statistics in turbulent convection at low Prandtl numbers
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 147-173
-
- Article
- Export citation
Settling of an asymmetric dumbbell in a quiescent fluid
-
- Published online by Cambridge University Press:
- 03 August 2016, pp. 174-185
-
- Article
- Export citation
The Richtmyer–Meshkov instability of a ‘V’ shaped air/
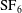 $\text{SF}_{6}$ interface
$\text{SF}_{6}$ interface
-
- Published online by Cambridge University Press:
- 03 August 2016, pp. 186-202
-
- Article
- Export citation
On the nature of fluctuations in turbulent Rayleigh–Bénard convection at large Prandtl numbers
-
- Published online by Cambridge University Press:
- 03 August 2016, pp. 203-244
-
- Article
- Export citation
Dynamics of ferrofluid drop deformations under spatially uniform magnetic fields
-
- Published online by Cambridge University Press:
- 03 August 2016, pp. 245-262
-
- Article
- Export citation
Scaling laws for jets of single cavitation bubbles
-
- Published online by Cambridge University Press:
- 03 August 2016, pp. 263-293
-
- Article
- Export citation
Bypassing slip velocity: rotational and translational velocities of autophoretic colloids in terms of surface flux
-
- Published online by Cambridge University Press:
- 03 August 2016, pp. 294-304
-
- Article
- Export citation
Evolution of detonation formation initiated by a spatially distributed, transient energy source
-
- Published online by Cambridge University Press:
- 04 August 2016, pp. 305-332
-
- Article
- Export citation
Balanced solutions for an ellipsoidal vortex in a rotating stratified flow
-
- Published online by Cambridge University Press:
- 03 August 2016, pp. 333-358
-
- Article
- Export citation
Modulation of turbulence by dispersed solid particles in a spatially developing flat-plate boundary layer
-
- Published online by Cambridge University Press:
- 03 August 2016, pp. 359-394
-
- Article
- Export citation
Vorticity and mixing in Rayleigh–Taylor Boussinesq turbulence
-
- Published online by Cambridge University Press:
- 03 August 2016, pp. 395-436
-
- Article
- Export citation
Forced fountains
-
- Published online by Cambridge University Press:
- 03 August 2016, pp. 437-463
-
- Article
- Export citation
Very large scale motions in the atmospheric surface layer: a field investigation
-
- Published online by Cambridge University Press:
- 04 August 2016, pp. 464-489
-
- Article
- Export citation
3D flow measurements in regular breaking waves past a fixed submerged bar on an impermeable plane slope
-
- Published online by Cambridge University Press:
- 03 August 2016, pp. 490-527
-
- Article
- Export citation
Short-wave instability of an elastic plate in supersonic flow in the presence of the boundary layer
-
- Published online by Cambridge University Press:
- 05 August 2016, pp. 528-552
-
- Article
- Export citation