Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-25T00:11:06.472Z Has data issue: false hasContentIssue false
  • English
  • Français

Vorticity and mixing in Rayleigh–Taylor Boussinesq turbulence

Published online by Cambridge University Press:  03 August 2016

Nicolas Schneider  and
Serge Gauthier
Nicolas Schneider
Affiliation:
CEA, DAM, DIF, Bruyères-Le-Châtel, 91297 Arpajon, EU, France
Serge Gauthier*
Affiliation:
CEA, DAM, DIF, Bruyères-Le-Châtel, 91297 Arpajon, EU, France
*
†Email addresses for correspondence: Serge.Gauthier@orange.fr, Serge.Gauthier@cea.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The Rayleigh–Taylor instability induced turbulence is studied under the Boussinesq approximation focusing on vorticity and mixing. A direct numerical simulation has been carried out with an auto-adaptive multidomain Chebyshev–Fourier–Fourier numerical method. The spatial resolution is increased up to 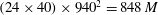$(24\times 40)\times 940^{2}=848\,M$ collocation points. The Taylor Reynolds number is 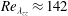$\mathit{Re}_{\unicode[STIX]{x1D706}_{zz}}\approx 142$ and a short inertial range is observed. The nonlinear growth rate of the turbulent mixing layer is found to be close to 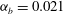$\unicode[STIX]{x1D6FC}_{b}=0.021$. Our conclusions may be summarized as follows.

(i) The simulation data are in agreement with the scalings for the pressure (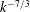$k^{-7/3}$) and the vertical mass flux (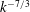$k^{-7/3}$).

(ii) Mean quantities have a self-similar behaviour, but some inhomogeneity is still present. For higher-order quantities the self-similar regime is not fully achieved.

(iii) In the self-similar regime, the mean dissipation rate and the enstrophy behave as 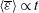$\langle \overline{\unicode[STIX]{x1D700}}\rangle \propto t$ and 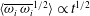$\langle \overline{\unicode[STIX]{x1D714}_{i}\,\unicode[STIX]{x1D714}_{i}}^{1/2}\rangle \propto t^{1/2}$, respectively.

(iv) The large-scale velocity fluctuation probability density function (PDF) is Gaussian, while vorticity and dissipation PDFs show large departures from Gaussianity.

(v) The pressure PDF exhibits strong departures from Gaussianity and is skewed. This is related to vortex coherent structures.

(vi) The intermediate scales of the mixing are isotropic, while small scales remain anisotropic. This leaves open the possibility of a small-scale buoyancy. Velocity intermediate scales are also isotropic, while small scales remain anisotropic. Mixing and dynamics are therefore consistent.

(vii) Properties and behaviours of vorticity and enstrophy are detailed. In particular, equations for these quantities are written down under the Boussinesq approximation.

(viii) The concentration PDF is quasi-Gaussian. The vertical concentration gradient is both non-Gaussian and strongly skewed.

JFM classification

Turbulent Flows: Intermittency Turbulent Flows: Turbulence simulation Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , pp. 395 - 436
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abarzhi, S. I. 2010 On fundamentals of Rayleigh–Taylor turbulent mixing. Europhys. Lett. 91, 35001.CrossRefGoogle Scholar
Abarzhi, S. I., Gauthier, S. & Sreenivasan, K. R. 2013 Turbulent mixing and beyond: non-equilibrium processes from atomistic to astrophysical scales II, introduction. Phil. Trans. R. Soc. Lond. A 371, 200320130268.Google Scholar
Atzeni, S. & Meyer-Ter-Vhen, J. 2004 The Physics of Inertial Fusion. Oxford University Press.CrossRefGoogle Scholar
Barber, J. L., Kadau, K., Germann, T. C. & Alde, B. J. 2008 Initial growth of the Rayleigh–Taylor instability via molecular dynamics. Eur. Phys. J. B 64, 271–276.CrossRefGoogle Scholar
Batchelor, G. K. 1971 Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Batchelor, G. K., Howells, I. D. & Townsend, A. A. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 2. The case of large conductivity. J. Fluid Mech. 5 (1), 134–139.CrossRefGoogle Scholar
Biferale, L., Mantovani, F., Sbragaglia, M., Scagliarini, A., Toschi, F. & Tripiccione, R. 2010 High resolution numerical study of Rayleigh–Taylor turbulence using a thermal lattice Boltzmann scheme. Phys. Fluids 22, 115112.CrossRefGoogle Scholar
Boffetta, G., Mazzino, A., Musacchio, S. & Vozella, L. 2009 Kolmogorov scaling and intermittency in Rayleigh–Taylor turbulence. Phys. Rev. E 79, 065301R.Google ScholarPubMed
Boffetta, G., Mazzino, A., Musacchio, S. & Vozella, L. 2010 Statistics of mixing in three-dimensional Rayleigh–Taylor turbulence at low Atwood number and Prandtl number one. Phys. Fluids 25, 085107.Google Scholar
Bolgiano, R. 1959 Turbulent spectra in a stably stratified atmosphere. J. Geophys. Res. 64 (12), 2226–2229.CrossRefGoogle Scholar
Boussinesq, J. 1903 Théorie Analytique de la Chaleur. Gauthier-Villars.Google Scholar
Brachet, M.-E. 1991 Direct simulation of three-dimensional turbulence in the Taylor–Green vortex. Fluid Dyn. Res. 8, 1–4.CrossRefGoogle Scholar
Cabot, W. & Zhou, Y. 2013 Statistical measurements of scaling and anisotropy of turbulent flows induced by Rayleigh–Taylor instability. Phys. Fluids 25, 015107.CrossRefGoogle Scholar
Cabot, W. H. & Cook, A. W. 2006 Reynolds number effects on Rayleigh–Taylor instability with possible implications for type-Ia supernovae. Nat. Phys. 2, 5621.CrossRefGoogle Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1988 Spectral Methods in Fluid Dynamics. Springer.CrossRefGoogle Scholar
Canuto, V. M. & Goldman, I. 1985 Analytical model for large-scale turbulence. Phys. Rev. Lett. 54 (5), 430–433.CrossRefGoogle ScholarPubMed
Cao, N., Chen, S. & Doolen, D. 1999 Statistics and structures of pressure in isotropic turbulence. Phys. Fluids 11, 2235–2250.CrossRefGoogle Scholar
Celani, A. 2007 The frontiers of computing in turbulence: challenges and perspectives. J. Turbul. 8 (34), 1–9.Google Scholar
Celani, A., Mazzino, A. & Vozella, L. 2006 Rayleigh–Taylor turbulence in two dimensions. Phys. Rev. Lett. 96, 134504.CrossRefGoogle ScholarPubMed
Chertkov, M. 2003 Phenomenology of Rayleigh–Taylor turbulence. Phys. Rev. Lett. 91, 115001.CrossRefGoogle ScholarPubMed
Chu, B.-T. & Kovásznay, L. S. G. 1958 Non-linear interactions in a viscous heat-conducting compressible gas. J. Fluid Mech. 3, 494–514.CrossRefGoogle Scholar
Cook, A. W. 2009 Enthalpy diffusion in multicomponent flows. Phys. Fluids 21, 055109.CrossRefGoogle Scholar
Cook, A. W., Cabot, W. & Miller, P. L. 2004 The mixing transition in Rayleigh–Taylor instability. J. Fluid Mech. 511, 026312.CrossRefGoogle Scholar
Dalziel, S. B., Linden, P. F. & Youngs, D. L. 1999 Self-similarity and internal structure of turbulence induced by Rayleigh–Taylor instability. J. Fluid Mech. 399, 1–48.CrossRefGoogle Scholar
Dalziel, S. B., Patterson, M. D., Caulfield, C. P. & Coomaraswamy, I. A. 2008 Mixing efficiency in high-aspect-ratio Rayleigh–Taylor experiments. Phys. Fluids 20, 065106.CrossRefGoogle Scholar
Dimonte, G., Youngs, D. L., Dimits, A., Weber, S., Marinak, M., Wunsch, S., Garasi, C., Robinson, A., Andrews, M. J., Ramaprabhu, P. et al. 2004 Comparative study of the turbulent Rayleigh–Taylor instability using high-resolution simulations: the alpha-group collaboration. Phys. Fluids 16, 1668–1692.CrossRefGoogle Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.CrossRefGoogle Scholar
Dubief, Y. & Delcayre, F. 2000 On coherent-vortex identification in turbulence. J. Turbul. 11, 1–22.Google Scholar
Duff, R. E., Harlow, F. H. & Hirt, C. W. 1962 Effects of diffusion on interface instability between gases. Phys. Fluids 5, 417.CrossRefGoogle Scholar
Gauthier, S., Guillard, H., Lumpp, T., Malé, J.-M., Peyret, R. & Renaud, F. 1996 A spectral domain decomposition technique with moving interfaces for viscous compressible flows. In Proceedings of the Third ECCOMAS Computational Fluid Dynamics Conference (ed. Désidéri, J.-A., Hirsch, C., Le Tallec, P., Pandolfi, M. & Périaux, J.), pp. 839–844. John Wiley & Sons.Google Scholar
Gauthier, S., Le Creurer, B., Abéguilé, F., Boudesocque-Dubois, C. & Clarisse, J.-M. 2005 A self-adaptative domain decomposition method with Chebyshev method. Intl J. Pure Appl. Maths 24 (4), 553–577.Google Scholar
Glimm, J., Sharp, D. H., Kaman, T. & Lim, H. 2013 New directions for Rayleigh–Taylor mixing. Phil. Trans. R. Soc. Lond. A 371, 20120183.Google ScholarPubMed
Grégoire, O.1997 Modèle multiéchelle pour des écoulements turbulents compressibles en présence de forts gradients de densité. Thèse de l’Université de la Méditerrannée Aix-Marseille II.CrossRefGoogle Scholar
Guillard, H., Malé, J.-M. & Peyret, R. 1992 Adaptive spectral methods with application to mixing layer computations. J. Comput. Phys. 102, 114–127.CrossRefGoogle Scholar
Hinze, J. O. 1959 Turbulence. McGraw-Hill.Google Scholar
Hirschfelder, J. O., Curtiss, C. F. & Bird, R. B. 1954 Molecular Theory of Gases and Liquids. John Wiley & Sons.Google Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.CrossRefGoogle Scholar
Jacobs, J. W. & Dalziel, S. B. 2005 Rayleigh–Taylor instability in complex stratifications. J. Fluid Mech. 542, 251–279.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–95.CrossRefGoogle Scholar
Kalelkar, C. 2006 Statistics of pressure fluctuations in decaying isotropic turbulence. Phys. Rev. E 73, 046301.Google ScholarPubMed
Kaneda, Y. & Yoshida, K. 2004 Small-scale anisotropy in stably stratified turbulence. New J. Phys. 6 (34), 1–16.CrossRefGoogle Scholar
Kaus, B. J. P. & Becker, T. W. 2007 Effects of elasticity on the Rayleigh–Taylor instability: implications for large-scale geodynamics. Geophys. J. Intl 168, 843–862.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941a Energy dissipation in locally isotropic turbulence. Dokl. Akad. Nauk USSR 1 (32), 19–21.Google Scholar
Kolmogorov, A. N. 1941b Local structure of turbulence in an incompressible fluid at very high Reynolds numbers. Dokl. Akad. Nauk USSR 4 (30), 299–303.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 1 (13), 82–85.CrossRefGoogle Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbitrary prandtl number. Phys. Fluids 5, 1374.CrossRefGoogle Scholar
Lafay, M.-A., Le Creurer, B. & Gauthier, S. 2007 Compressibility effects on the Rayleigh–Taylor instability growth between miscible fluids. Europhys. Lett. 79, 64002.CrossRefGoogle Scholar
Le Creurer, B. & Gauthier, S. 2008 A return toward equilibrium in a two-dimensional Rayleigh–Taylor flows instability for compressible miscible fluids. Theor. Comput. Fluid Dyn. 22, 125–144.CrossRefGoogle Scholar
Lesieur, M. 1997 Turbulence in Fluids. Kluwer.CrossRefGoogle Scholar
Leslie, D. C. 1973 Developments in the Theory of Turbulence. Oxford University Press, Clarendon Press.Google Scholar
Lin, Z., Thiffeault, J.-L. & Doering, C. R. 2011 Optimal stirring strategies for passive scalar mixing. J. Fluid Mech. 675, 465–476.CrossRefGoogle Scholar
Linden, P. F., Redondo, J. M. & Youngs, D. L. 1994 Molecular mixing in Rayleigh–Taylor instability. J. Fluid Mech. 265, 97–124.CrossRefGoogle Scholar
Livescu, D. 2013 Numerical simulations of two-fluid turbulent mixing at large density ratios and applications to the Rayleigh–Taylor instability. Phil. Trans. R. Soc. Lond. A 371, 200320120185.Google Scholar
Livescu, D., Ristorcelli, J. R., Petersen, M. R. & Gore, R. A. 2010 New phenomena in variable-density Rayleigh–Taylor turbulence. Phys. Scr. T 142, 014015.Google Scholar
Lumley, A. 1967 Similarity and the turbulent energy spectrum. Phys. Fluids 10 (4), 855–858.CrossRefGoogle Scholar
Mikaelian, K. O. 1989 Turbulent mixing generated by Rayleigh–Taylor and Richtmyer-Meshkov instabilities. Physica D 36 (3), 343–357.Google Scholar
Monin, A. S. & Yaglom, A. M. 1962 Statistical Fluid Mechanics: Mechanics of Turbulence. MIT Press.Google Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.CrossRefGoogle ScholarPubMed
Obukhov, A. 1959 Effect of Archimedean forces on the structure of the temperature field in a turbulent flow. Dokl. Akad. Nauk SSSR 125, 1246.Google Scholar
Olson, D. H. & Jacobs, J. W. 2009 Experimental study of Rayleigh–Taylor instability with a complex initial perturbation. Phys. Fluids 21, 034103.CrossRefGoogle Scholar
Orszag, S. & Patterson, G. S. Jr. 1972 Numerical simulation of three-dimensional homogeneous isotropic turbulence. Phys. Rev. Lett. 28, 76–79.CrossRefGoogle Scholar
Peyret, R. 2002 Spectral Methods for Incompressible Fluids. Springer.CrossRefGoogle Scholar
Plohr, B. J. & Sharp, D. H. 1984 Instability of accelerated elastic metal plates. A. Angew. Math. Phys. 49, 786–804.CrossRefGoogle Scholar
Poujade, O. 2006 Rayleigh–Taylor turbulence is nothing like Kolmogorov Turbulence in the self-similar regime. Phys. Rev. Lett. 97, 185002.CrossRefGoogle ScholarPubMed
Poujade, O. & Peybernes, M. 2010 Growth rate of Rayleigh–Taylor turbulent mixing layers with the foliation approach. Phys. Rev. E 81, 0163168.Google ScholarPubMed
Pumir, A. 1994a A numerical study of pressure fluctuations in three-dimensional, incompressible, homogeneous, isotropic turbulence. Phys. Fluids 6 (6), 2071–2083.CrossRefGoogle Scholar
Pumir, A. 1994b A numerical study of the mixing of a passive scalar in three dimensions in the presence of a mean gradient. Phys. Fluids 6 (6), 2118–2132.CrossRefGoogle Scholar
Pumir, A. 1994c Small-scale properties of scalar and velocity differences in three-dimensional turbulence. Phys. Fluids 6 (12), 3974–3984.CrossRefGoogle Scholar
Ramaprabhu, P. & Andrews, M. J. 2004 Experimental investigation of Rayleigh–Taylor mixing at small Atwood numbers. J. Fluid Mech. 502, 233–271.CrossRefGoogle Scholar
Renaud, F. & Gauthier, S. 1997 A dynamical pseudo-spectral domain decomposition technique: application to viscous compressible flows. J. Comput. Phys. 131, 89–108.CrossRefGoogle Scholar
Ristorcelli, J. R. 2006 Passive scalar mixing: analytic study of time scale ratio, variance, and mix rate. Phys. Fluids 18, 075101.CrossRefGoogle Scholar
Ristorcelli, J. R. & Clark, T. T. 2004 Rayleigh–Taylor turbulence: self-similar analysis and direct numerical simulations. J. Fluid Mech. 507, 213–253.CrossRefGoogle Scholar
Sandoval, D. L.1995 The dynamics of variable-density turbulence. PhD thesis, University of Washington.CrossRefGoogle Scholar
Schneider, N. & Gauthier, S. 2015a Asymptotic analysis of Rayleigh–Taylor flow for Newtonian miscible fluids. J. Engng Maths 92 (1), 55–71.CrossRefGoogle Scholar
Schneider, N. & Gauthier, S. 2015b Visualization of Rayleigh–Taylor flows from Boussinesq approximation to fully compressible Navier–Stokes model. Fluid Dyn. Res. 48, 015504.Google Scholar
Schneider, N., Hammouch, Z., Labrosse, G. & Gauthier, S. 2015 A spectral anelastic Navier–Stokes solver for a stratified two-miscible-layer system in infinite horizontal channel. J. Comput. Phys. 299, 374–403.CrossRefGoogle Scholar
Sharp, D. H. 1984 An overview of Rayleigh–Taylor instability. Physica D 12, 32–44.Google Scholar
She, Z.-S., Jackson, E. & Orszag, S. A. 1990 Intermittent vortex structures in homogeneous isotropic turbulence. Nature 344, 226–228.CrossRefGoogle Scholar
Siggia, E. D. 1981 Numerical study of small scale intermittency in three dimensional turbulence. J. Fluid Mech. 107, 375.CrossRefGoogle Scholar
Souffland, D., Grégoire, O., Gauthier, S. & Schiestel, R. 2002 A two-time-scale turbulence model for turbulent mixing flows induced by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Flow Turbul. Combust. 69, 123–160.CrossRefGoogle Scholar
Soulard, O. & Griffond, J. 2012 Inertial-range anisotropy in Rayleigh–Taylor turbulence. Phys. Fluids 24, 025101.CrossRefGoogle Scholar
Sreenivasan, K. R. 1998 An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 10 (2), 528–529.CrossRefGoogle Scholar
Thompson, P. A. 1972 Compressible Fluid Dynamics. Academic.CrossRefGoogle Scholar
Vincent, A. & Meneguzzi, M. 1991 The spatial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 225, 1–20.CrossRefGoogle Scholar
Vincent, A. & Meneguzzi, M. 1994 The dynamics of vorticity tubes in homogeneous turbulence. J. Fluid Mech. 258, 245–254.CrossRefGoogle Scholar
Vladimirova, N. & Chertkov, M. 2009 Self-similarity and universality in Rayleigh–Taylor, Boussinesq turbulence. Phys. Fluids 21, 015102.CrossRefGoogle Scholar
Waddell, J. T., Niederhaus, C. E. & Jacobs, J. W. 2001 Experimental study of Rayleigh–Taylor instability: low Atwood number liquid systems with single-mode initial perturbations. Phys. Fluids 13 (5), 1263–1273.CrossRefGoogle Scholar
Young, Y. N., Tufo, H., Dubey, A. & Rosner, R. 2001 On the miscible Rayleigh–Taylor instability: two and three dimensions. J. Fluid Mech. 447, 377–408.CrossRefGoogle Scholar
Youngs, D. L. 1984 Numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Physica D 12, 32–44.Google Scholar
Youngs, D. L. 2013 The density ratio dependence of self-similar Rayleigh–Taylor mixing. Phil. Trans. R. Soc. Lond. A 371, 20120173.Google ScholarPubMed
Zeytounian, R. 1990 Asymptotic Modeling of Atmospheric Flows. Springer.CrossRefGoogle Scholar
Zhou, Q. 2013 Temporal evolution and scaling of mixing in two-dimensional Rayleigh–Taylor turbulence. Phys. Fluids 25, 085107.CrossRefGoogle Scholar
Zhou, Y. 2001 A scaling analysis of turbulent flows driven by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Phys. Fluids 13 (2), 538–543.CrossRefGoogle Scholar
Zingale, M., Woosley, S. E., Rendleman, C. A., Day, M. S. & Bell, J. B. 2005 Three-dimensional numerical simulations of Rayleigh–Taylor unstable flames in Type Ia supernovae. Astrophys. J. 632, 1021–1034.CrossRefGoogle Scholar