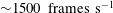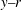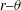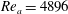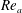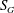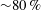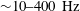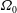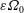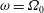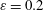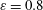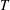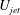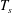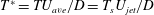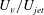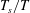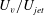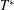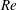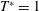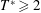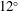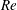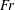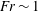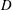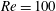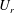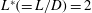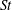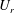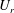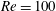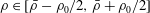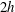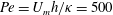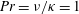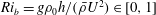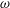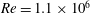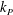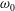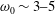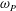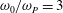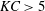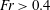JFM Papers
Transition in a separation bubble under tonal and broadband acoustic excitation
-
- Published online by Cambridge University Press:
- 16 August 2018, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cones of silence, complex rays and catastrophes: high-frequency flow–acoustic interaction effects
-
- Published online by Cambridge University Press:
- 16 August 2018, pp. 37-71
-
- Article
- Export citation
Insights into the dynamics of conical breakdown modes in coaxial swirling flow field
-
- Published online by Cambridge University Press:
- 22 August 2018, pp. 72-110
-
- Article
- Export citation
Mean flow generation by an intermittently unstable boundary layer over a sloping wall
-
- Published online by Cambridge University Press:
- 22 August 2018, pp. 111-149
-
- Article
- Export citation
On the scaling of propagation of periodically generated vortex rings
-
- Published online by Cambridge University Press:
- 22 August 2018, pp. 150-170
-
- Article
- Export citation
Confinement effects on regular–irregular transition in shock-wave–boundary-layer interactions
-
- Published online by Cambridge University Press:
- 22 August 2018, pp. 171-204
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The linear instability of the stratified plane Couette flow
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 205-234
-
- Article
- Export citation
Spatio-temporal intermittency of the turbulent energy cascade
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 235-252
-
- Article
- Export citation
Approximate solutions to droplet dynamics in Hele-Shaw flows
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 253-270
-
- Article
- Export citation
Clarifying the relationship between efficiency and resonance for flexible inertial swimmers
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 271-300
-
- Article
- Export citation
Vibrations of a square cylinder submerged in a wake
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 301-332
-
- Article
- Export citation
Jet–flap interaction tones
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 333-358
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal mixing in two-dimensional stratified plane Poiseuille flow at finite Péclet and Richardson numbers
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 359-385
-
- Article
- Export citation
Saturation of a turbulent mixing layer over a cavity: response to harmonic forcing around mean flows
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 386-418
-
- Article
- Export citation
On the over-production of turbulence beneath surface waves in Reynolds-averaged Navier–Stokes models
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 419-460
-
- Article
- Export citation
A volume integral implementation of the Goldstein generalised acoustic analogy for unsteady flow simulations
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 461-487
-
- Article
- Export citation
Turbulent channel flow of an elastoviscoplastic fluid
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 488-514
-
- Article
- Export citation
An analytic solution for the noise generated by gust–aerofoil interaction for plates with serrated leading edges
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 515-536
-
- Article
- Export citation
Large-eddy simulation of flow over an axisymmetric body of revolution
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 537-563
-
- Article
- Export citation
High frequency resonant response of a monopile in irregular deep water waves
-
- Published online by Cambridge University Press:
- 23 August 2018, pp. 564-586
-
- Article
- Export citation