Papers
Large eddy simulation of a pulsed jet in cross-flow
-
- Published online by Cambridge University Press:
- 07 February 2012, pp. 1-34
-
- Article
- Export citation
Cyclic steps and roll waves in shallow water flow over an erodible bed
-
- Published online by Cambridge University Press:
- 08 February 2012, pp. 35-62
-
- Article
- Export citation
Three-dimensional river bed forms
-
- Published online by Cambridge University Press:
- 07 February 2012, pp. 63-80
-
- Article
- Export citation
Escaping mass approach for inclined plane and round buoyant jets
-
- Published online by Cambridge University Press:
- 12 March 2012, pp. 81-111
-
- Article
- Export citation
Global vorticity shedding for a vanishing wing
-
- Published online by Cambridge University Press:
- 13 February 2012, pp. 112-134
-
- Article
- Export citation
Transition to chaos in the wake of a rolling sphere
-
- Published online by Cambridge University Press:
- 22 February 2012, pp. 135-148
-
- Article
- Export citation
A fully adaptive wavelet-based approach to homogeneous turbulence simulation
-
- Published online by Cambridge University Press:
- 08 February 2012, pp. 149-172
-
- Article
- Export citation
Horizontal and vertical motions of barotropic vortices over a submarine mountain
-
- Published online by Cambridge University Press:
- 08 February 2012, pp. 173-198
-
- Article
- Export citation
Effect of non-parallel mean flow on the Green’s function for predicting the low-frequency sound from turbulent air jets
-
- Published online by Cambridge University Press:
- 13 February 2012, pp. 199-234
-
- Article
- Export citation
Instability and hydraulics of turbulent stratified shear flows
-
- Published online by Cambridge University Press:
- 20 February 2012, pp. 235-256
-
- Article
- Export citation
Turbulence dynamics near a turbulent/non-turbulent interface
-
- Published online by Cambridge University Press:
- 13 February 2012, pp. 257-287
-
- Article
- Export citation
Water waves over a variable bottom: a non-local formulation and conformal mappings
-
- Published online by Cambridge University Press:
- 24 February 2012, pp. 288-309
-
- Article
- Export citation
Air trapping at impact of a rigid sphere onto a liquid
-
- Published online by Cambridge University Press:
- 14 February 2012, pp. 310-320
-
- Article
- Export citation
Monolith formation and ring-stain suppression in low-pressure evaporation of poly(ethylene oxide) droplets
-
- Published online by Cambridge University Press:
- 09 February 2012, pp. 321-329
-
- Article
- Export citation
An inertia ‘paradox’ for incompressible stratified Euler fluids
-
- Published online by Cambridge University Press:
- 16 February 2012, pp. 330-340
-
- Article
- Export citation
A multi-layer model for nonlinear internal wave propagation in shallow water
-
- Published online by Cambridge University Press:
- 09 February 2012, pp. 341-365
-
- Article
- Export citation
Anomalous dispersion in chemically heterogeneous media induced by long-range disorder correlation
-
- Published online by Cambridge University Press:
- 13 February 2012, pp. 366-389
-
- Article
- Export citation
Three-dimensional instability of the flow over a forward-facing step
-
- Published online by Cambridge University Press:
- 21 February 2012, pp. 390-404
-
- Article
- Export citation
High-enthalpy flow over a rearward-facing step – a computational study
-
- Published online by Cambridge University Press:
- 20 February 2012, pp. 405-438
-
- Article
- Export citation
Stability of reactive interfaces in saturated porous media under gravity in the presence of transverse flows
-
- Published online by Cambridge University Press:
- 16 February 2012, pp. 439-466
-
- Article
- Export citation




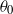 from 90 to
from 90 to 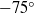 with respect to the horizontal plane. This complementary approach introduces a concentration coefficient, which is calibrated using experimental evidence. The present model has incorporated the second-order approach and, regarding the jet-core region, a jet-core model based on the advanced integral model for the production of more correct transverse profiles of the mean axial velocities and mean concentrations than the common Gaussian or top-hat profiles. The partial differential equations for momentum and tracer conservation are written in orthogonal and cylindrical curvilinear coordinates for inclined plane and round buoyant jets, respectively, and they are integrated under the closure assumptions of (a) quasi-linear spreading of the mean flow and mixing fields, and (b) known transverse profile distributions. The integral forms are solved by employing the Runge–Kutta algorithm. Since the most important contribution in the present model is the simulation of the escaping masses, the model has been called the escaping mass approach (EMA). Herein EMA is applied to predict the mean flow properties (trajectory characteristics, mean axial velocities and mean concentrations) for inclined plane and round buoyant jets. The results predicted are compared with experimental data available in the literature, and the accuracy obtained is more than satisfactory. The performance of the EMA is up to 56 % better than using classical integral procedures. EMA can be used for design purposes and for environmental impact assessment studies.
with respect to the horizontal plane. This complementary approach introduces a concentration coefficient, which is calibrated using experimental evidence. The present model has incorporated the second-order approach and, regarding the jet-core region, a jet-core model based on the advanced integral model for the production of more correct transverse profiles of the mean axial velocities and mean concentrations than the common Gaussian or top-hat profiles. The partial differential equations for momentum and tracer conservation are written in orthogonal and cylindrical curvilinear coordinates for inclined plane and round buoyant jets, respectively, and they are integrated under the closure assumptions of (a) quasi-linear spreading of the mean flow and mixing fields, and (b) known transverse profile distributions. The integral forms are solved by employing the Runge–Kutta algorithm. Since the most important contribution in the present model is the simulation of the escaping masses, the model has been called the escaping mass approach (EMA). Herein EMA is applied to predict the mean flow properties (trajectory characteristics, mean axial velocities and mean concentrations) for inclined plane and round buoyant jets. The results predicted are compared with experimental data available in the literature, and the accuracy obtained is more than satisfactory. The performance of the EMA is up to 56 % better than using classical integral procedures. EMA can be used for design purposes and for environmental impact assessment studies.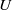 , and constant angle of attack, then rapidly pulled out of the fluid in the spanwise direction. Viewed within a fixed plane perpendicular to the span, the cross-sectional area of the foil seemingly disappears. The rapid spanwise motion results in the nearly instantaneous shedding of the boundary layer into the surrounding fluid. Particle image velocimetry measurements show that the shed layers quickly transition from free shear layers to form two strong, unequal-strength vortices, formed within non-dimensional time
, and constant angle of attack, then rapidly pulled out of the fluid in the spanwise direction. Viewed within a fixed plane perpendicular to the span, the cross-sectional area of the foil seemingly disappears. The rapid spanwise motion results in the nearly instantaneous shedding of the boundary layer into the surrounding fluid. Particle image velocimetry measurements show that the shed layers quickly transition from free shear layers to form two strong, unequal-strength vortices, formed within non-dimensional time 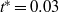 , based on the foil chord and forward velocity. These vortices are connected to, and interact with, the foil’s tip vortex through additional streamwise vorticity formed during the rapid pulling of the foil. Numerical simulations show that two strong spanwise vortices form from the shed vorticity of the boundary layer. The three-dimensional effects of the foil removal process are restricted to the tip of the foil. This method of vorticity transfer may be used for quickly introducing circulation to a fluid to provide forcing for biologically inspired flow control.
, based on the foil chord and forward velocity. These vortices are connected to, and interact with, the foil’s tip vortex through additional streamwise vorticity formed during the rapid pulling of the foil. Numerical simulations show that two strong spanwise vortices form from the shed vorticity of the boundary layer. The three-dimensional effects of the foil removal process are restricted to the tip of the foil. This method of vorticity transfer may be used for quickly introducing circulation to a fluid to provide forcing for biologically inspired flow control. -effect associated with the topographic slope. On arriving, they turn around the obstacle in an anticyclonic direction, whilst anticyclonic vorticity is generated over the summit. The long-term vorticity distribution is dominated by the original cyclone elongated around the topographic contours and the generated anticyclone over the tip of the topography. In the vertical plane an oscillatory uphill–downhill flow is generated, which is directly related to the drift of the cyclone around the mountain. Depending on the vortex characteristics, the period of the oscillation ranges from 4 to 10 times the rotation period of the system. The horizontal and vertical flow fields are reproduced numerically by using a shallow-water formulation, which allows a detailed view of the vertical motions, hence facilitating the interpretation of the experimental results. In addition, the cyclone–anticyclone pair over the mountain is compared with analytical solutions of topographically trapped waves. A general conclusion is that vertical motions persist for several days (or rotation periods), which implies that this mechanism might be potentially important for the vertical transport over seamounts.
-effect associated with the topographic slope. On arriving, they turn around the obstacle in an anticyclonic direction, whilst anticyclonic vorticity is generated over the summit. The long-term vorticity distribution is dominated by the original cyclone elongated around the topographic contours and the generated anticyclone over the tip of the topography. In the vertical plane an oscillatory uphill–downhill flow is generated, which is directly related to the drift of the cyclone around the mountain. Depending on the vortex characteristics, the period of the oscillation ranges from 4 to 10 times the rotation period of the system. The horizontal and vertical flow fields are reproduced numerically by using a shallow-water formulation, which allows a detailed view of the vertical motions, hence facilitating the interpretation of the experimental results. In addition, the cyclone–anticyclone pair over the mountain is compared with analytical solutions of topographically trapped waves. A general conclusion is that vertical motions persist for several days (or rotation periods), which implies that this mechanism might be potentially important for the vertical transport over seamounts.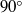 to the downstream axis. The present paper is concerned with the effects of non-parallel mean flows on the adjoint vector Green’s function. We obtain a low-frequency asymptotic solution for that function by solving a very simple second-order hyperbolic equation for a composite dependent variable (which is directly proportional to a pressure-like component of this Green’s function and roughly corresponds to the strength of a monopole source within the jet). Our numerical calculations show that this quantity remains fairly close to the corresponding parallel flow result at low Mach numbers and that, as expected, it converges to that result when an appropriately scaled frequency parameter is increased. But the convergence occurs at progressively higher frequencies as the Mach number increases and the supersonic solution never actually converges to the parallel flow result in the vicinity of a critical- layer singularity that occurs in that solution. The dominant contribution to the propagator comes from the radial derivative of a certain component of the adjoint vector Green’s function. The non-parallel flow has a large effect on this quantity, causing it (and, therefore, the radiated sound) to increase at subsonic speeds and decrease at supersonic speeds. The effects of acoustic source location can be visualized by plotting the magnitude of this quantity, as function of position. These ‘altitude plots’ (which represent the intensity of the radiated sound as a function of source location) show that while the parallel flow solutions exhibit a single peak at subsonic speeds (when the source point is centred on the initial shear layer), the non-parallel solutions exhibit a double peak structure, with the second peak occurring about two potential core lengths downstream of the nozzle. These results are qualitatively consistent with the numerical calculations reported in Karabasov
to the downstream axis. The present paper is concerned with the effects of non-parallel mean flows on the adjoint vector Green’s function. We obtain a low-frequency asymptotic solution for that function by solving a very simple second-order hyperbolic equation for a composite dependent variable (which is directly proportional to a pressure-like component of this Green’s function and roughly corresponds to the strength of a monopole source within the jet). Our numerical calculations show that this quantity remains fairly close to the corresponding parallel flow result at low Mach numbers and that, as expected, it converges to that result when an appropriately scaled frequency parameter is increased. But the convergence occurs at progressively higher frequencies as the Mach number increases and the supersonic solution never actually converges to the parallel flow result in the vicinity of a critical- layer singularity that occurs in that solution. The dominant contribution to the propagator comes from the radial derivative of a certain component of the adjoint vector Green’s function. The non-parallel flow has a large effect on this quantity, causing it (and, therefore, the radiated sound) to increase at subsonic speeds and decrease at supersonic speeds. The effects of acoustic source location can be visualized by plotting the magnitude of this quantity, as function of position. These ‘altitude plots’ (which represent the intensity of the radiated sound as a function of source location) show that while the parallel flow solutions exhibit a single peak at subsonic speeds (when the source point is centred on the initial shear layer), the non-parallel solutions exhibit a double peak structure, with the second peak occurring about two potential core lengths downstream of the nozzle. These results are qualitatively consistent with the numerical calculations reported in Karabasov 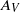 and
and 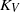 , respectively, are assumed to be equal and are expressed in terms of the buoyancy frequency of the flow,
, respectively, are assumed to be equal and are expressed in terms of the buoyancy frequency of the flow, 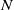 , and the dissipation rate of turbulent kinetic energy per unit mass,
, and the dissipation rate of turbulent kinetic energy per unit mass,  , quantities that can be measured in the sea. The horizontal eddy coefficients,
, quantities that can be measured in the sea. The horizontal eddy coefficients, 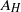 and
and 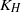 , are taken to be proportional to the dimensionally correct form,
, are taken to be proportional to the dimensionally correct form, 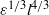 , found appropriate in the description of horizontal dispersion of a field of passive markers of scale
, found appropriate in the description of horizontal dispersion of a field of passive markers of scale 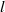 . The extended T–G equation is applied to examine the stability and greatest growth rates in a turbulent shear flow in stratified waters near a sill, that at the entrance to the Clyde Sea in the west of Scotland. Here the main effect of turbulence is a tendency towards stabilizing the flow; the greatest growth rates of small unstable disturbances decrease, and in some cases flows that are unstable in the absence of turbulence are stabilized when its effects are included. It is conjectured that stabilization of a flow by turbulence may lead to a repeating cycle in which a flow with low levels of turbulence becomes unstable, increasing the turbulent dissipation rate and so stabilizing the flow. The collapse of turbulence then leads to a condition in which the flow may again become unstable, the cycle repeating. Two parameters are used to describe the ‘marginality’ of the observed flows. One is based on the proximity of the minimum flow Richardson number to the critical Richardson number, the other on the change in dissipation rate required to stabilize or destabilize an observed flow. The latter is related to the change needed in the flow Reynolds number to achieve zero growth rate. The unstable flows, typical of the Clyde Sea site, are relatively further from neutral stability in Reynolds number than in Richardson number. The effects of turbulence on the hydraulic state of the flow are assessed by examining the speed and propagation direction of long waves in the Clyde Sea. Results are compared to those obtained using the T–G equation without turbulent viscosity or diffusivity. Turbulence may change the state of a flow from subcritical to supercritical.
. The extended T–G equation is applied to examine the stability and greatest growth rates in a turbulent shear flow in stratified waters near a sill, that at the entrance to the Clyde Sea in the west of Scotland. Here the main effect of turbulence is a tendency towards stabilizing the flow; the greatest growth rates of small unstable disturbances decrease, and in some cases flows that are unstable in the absence of turbulence are stabilized when its effects are included. It is conjectured that stabilization of a flow by turbulence may lead to a repeating cycle in which a flow with low levels of turbulence becomes unstable, increasing the turbulent dissipation rate and so stabilizing the flow. The collapse of turbulence then leads to a condition in which the flow may again become unstable, the cycle repeating. Two parameters are used to describe the ‘marginality’ of the observed flows. One is based on the proximity of the minimum flow Richardson number to the critical Richardson number, the other on the change in dissipation rate required to stabilize or destabilize an observed flow. The latter is related to the change needed in the flow Reynolds number to achieve zero growth rate. The unstable flows, typical of the Clyde Sea site, are relatively further from neutral stability in Reynolds number than in Richardson number. The effects of turbulence on the hydraulic state of the flow are assessed by examining the speed and propagation direction of long waves in the Clyde Sea. Results are compared to those obtained using the T–G equation without turbulent viscosity or diffusivity. Turbulence may change the state of a flow from subcritical to supercritical. ), turbulence length scales, and pressure statistics are derived, showing an excellent agreement with results from direct numerical simulations (DNS). Interestingly, the normalized inviscid flow statistics at the T/NT interface do not depend on the form of the assumed TKE spectrum. Outside the turbulent region, where the flow is irrotational (except inside a thin viscous boundary layer),
), turbulence length scales, and pressure statistics are derived, showing an excellent agreement with results from direct numerical simulations (DNS). Interestingly, the normalized inviscid flow statistics at the T/NT interface do not depend on the form of the assumed TKE spectrum. Outside the turbulent region, where the flow is irrotational (except inside a thin viscous boundary layer),  decays as
decays as 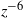 , where
, where  is the distance from the T/NT interface. The mean pressure distribution is calculated using RDT, and exhibits a decrease towards the turbulence region due to the associated velocity fluctuations, consistent with the generation of a mean entrainment velocity. The vorticity variance and
is the distance from the T/NT interface. The mean pressure distribution is calculated using RDT, and exhibits a decrease towards the turbulence region due to the associated velocity fluctuations, consistent with the generation of a mean entrainment velocity. The vorticity variance and  display large maxima at the T/NT interface due to the inviscid discontinuities of the tangential velocity variances existing there, and these maxima are quantitatively related to the thickness
display large maxima at the T/NT interface due to the inviscid discontinuities of the tangential velocity variances existing there, and these maxima are quantitatively related to the thickness 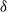 of the viscous boundary layer (VBL). For an equilibrium VBL, the RDT analysis suggests that
of the viscous boundary layer (VBL). For an equilibrium VBL, the RDT analysis suggests that 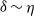 (where
(where 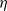 is the Kolmogorov microscale), which is consistent with the scaling law identified in a very recent DNS study for shear-free T/NT interfaces.
is the Kolmogorov microscale), which is consistent with the scaling law identified in a very recent DNS study for shear-free T/NT interfaces.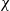 . By experimentally varying concentration and flux (using a low-pressure drying chamber), the prediction is tested over nearly two orders of magnitude in both variables and shown to be in good agreement with the boundary between disks and monoliths at
. By experimentally varying concentration and flux (using a low-pressure drying chamber), the prediction is tested over nearly two orders of magnitude in both variables and shown to be in good agreement with the boundary between disks and monoliths at 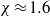 .
. -layer fluid system in which a constant density is assumed in each layer. This allows the model to investigate higher-mode internal waves. Furthermore, the model is capable of simulating large-amplitude internal waves up to the breaking point. However, the model is limited by the assumption that the total water depth is shallow in comparison with the wavelength of interest. Furthermore, the vertical vorticity must vanish, while the horizontal vorticity components are weak. Numerical examples for strongly nonlinear waves are compared with laboratory data and other numerical studies in a two-layer fluid system. Good agreement is observed. The generation and propagation of mode-1 and mode-2 internal waves and their interactions with bottom topography are also investigated.
-layer fluid system in which a constant density is assumed in each layer. This allows the model to investigate higher-mode internal waves. Furthermore, the model is capable of simulating large-amplitude internal waves up to the breaking point. However, the model is limited by the assumption that the total water depth is shallow in comparison with the wavelength of interest. Furthermore, the vertical vorticity must vanish, while the horizontal vorticity components are weak. Numerical examples for strongly nonlinear waves are compared with laboratory data and other numerical studies in a two-layer fluid system. Good agreement is observed. The generation and propagation of mode-1 and mode-2 internal waves and their interactions with bottom topography are also investigated.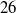 and
and 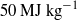 , are considered. The Mach number and unit Reynolds number per metre were 7.6, 11.0 and
, are considered. The Mach number and unit Reynolds number per metre were 7.6, 11.0 and 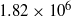 ,
, 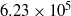 respectively. The Reynolds number based on the step height was correspondingly
respectively. The Reynolds number based on the step height was correspondingly 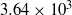 and
and 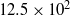 . The computations were carried out assuming the flow to be laminar throughout and the real gas effects such as thermal and chemical non-equilibrium are studied using Park’s two-temperature model with finite-rate chemistry and Gupta’s finite-rate chemistry models. In the close vicinity of the step, detailed quantification of flow features is emphasised. In particular, the presence of the Goldstein singularity at the lip and separation on the face of the step have been elucidated. Within the separated region and downstream of reattachment, the influence of real gas effects has been identified and shown to be negligible. The numerical results are compared with the available experimental data of surface heat flux downstream of the step and reasonable agreement is shown up to 30 step heights downstream.
. The computations were carried out assuming the flow to be laminar throughout and the real gas effects such as thermal and chemical non-equilibrium are studied using Park’s two-temperature model with finite-rate chemistry and Gupta’s finite-rate chemistry models. In the close vicinity of the step, detailed quantification of flow features is emphasised. In particular, the presence of the Goldstein singularity at the lip and separation on the face of the step have been elucidated. Within the separated region and downstream of reattachment, the influence of real gas effects has been identified and shown to be negligible. The numerical results are compared with the available experimental data of surface heat flux downstream of the step and reasonable agreement is shown up to 30 step heights downstream.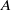 on top of another solution of reactant
on top of another solution of reactant 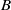 is analysed. A chemical product
is analysed. A chemical product 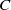 is generated at the interface as a result of a bimolecular chemical reaction
is generated at the interface as a result of a bimolecular chemical reaction 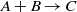 . In general, all chemical components are assumed to have different densities and viscosities, and a transverse velocity is introduced parallel to the interface between the reactants. Although the transverse flow is known for its stabilizing effect in viscously unstable non-reactive systems in the presence of an injection velocity, it is shown here that it can actually destabilize an initially stable reactive front. An expression for the critical transverse velocity beyond which an initially stable interface is destabilized is derived in the case of an initial sharp interface for reactants of the same viscosity. The analysis is extended to a diffused profile, and purely buoyancy-driven flows are analysed first in the absence of viscosity contrast and then in the presence of transverse flows and viscosity contrast. Various possible density fingering scenarios are determined based on the relative contribution of each chemical component to the density profile. It is found that the chemical reaction can destabilize a buoyancy-stable initial interface by generating a non-monotonic density profile. Unlike the viscous fingering of a reactive interface, a symmetry in the stability characteristics with respect to density increase or decrease by chemical reaction product is observed in the case of chemically buoyancy-driven flows for identical reactants.
. In general, all chemical components are assumed to have different densities and viscosities, and a transverse velocity is introduced parallel to the interface between the reactants. Although the transverse flow is known for its stabilizing effect in viscously unstable non-reactive systems in the presence of an injection velocity, it is shown here that it can actually destabilize an initially stable reactive front. An expression for the critical transverse velocity beyond which an initially stable interface is destabilized is derived in the case of an initial sharp interface for reactants of the same viscosity. The analysis is extended to a diffused profile, and purely buoyancy-driven flows are analysed first in the absence of viscosity contrast and then in the presence of transverse flows and viscosity contrast. Various possible density fingering scenarios are determined based on the relative contribution of each chemical component to the density profile. It is found that the chemical reaction can destabilize a buoyancy-stable initial interface by generating a non-monotonic density profile. Unlike the viscous fingering of a reactive interface, a symmetry in the stability characteristics with respect to density increase or decrease by chemical reaction product is observed in the case of chemically buoyancy-driven flows for identical reactants.