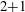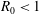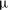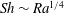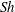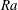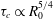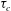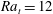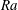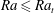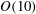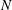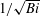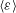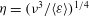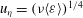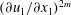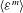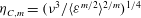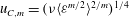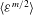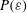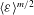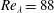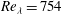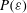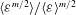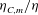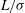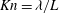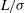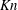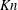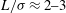Focus on Fluids
Exact coherent structures at extreme Reynolds number
-
- Published online by Cambridge University Press:
- 04 April 2016, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Papers
On the use of the Reynolds decomposition in the intermittent region of turbulent boundary layers
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 5-16
-
- Article
- Export citation
Long ring waves in a stratified fluid over a shear flow
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 17-44
-
- Article
- Export citation
Role of natural convection in the dissolution of sessile droplets
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 45-67
-
- Article
- Export citation
A local scattering theory for the effects of isolated roughness on boundary-layer instability and transition: transmission coefficient as an eigenvalue
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 68-108
-
- Article
- Export citation
Sphere oscillating in a rarefied gas
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 109-153
-
- Article
- Export citation
The impact of imperfect heat transfer on the convective instability of a thermal boundary layer in a porous media
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 154-174
-
- Article
- Export citation
On the steady-state nearly resonant waves
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 175-199
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thin, binary liquid droplets, containing polymer: an investigation of the parameters controlling film shape
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 200-232
-
- Article
- Export citation
Generalised higher-order Kolmogorov scales
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 233-251
-
- Article
- Export citation
Non-equilibrium dynamics of dense gas under tight confinement
-
- Published online by Cambridge University Press:
- 30 March 2016, pp. 252-266
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Droplet–turbulence interaction in a confined polydispersed spray: effect of turbulence on droplet dispersion
-
- Published online by Cambridge University Press:
- 04 April 2016, pp. 267-309
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Consistent nonlinear stochastic evolution equations for deep to shallow water wave shoaling
-
- Published online by Cambridge University Press:
- 04 April 2016, pp. 310-342
-
- Article
- Export citation
Sensitivity of Saffman–Taylor fingers to channel-depth perturbations
-
- Published online by Cambridge University Press:
- 04 April 2016, pp. 343-368
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dissipative random velocity field for fully developed fluid turbulence
-
- Published online by Cambridge University Press:
- 04 April 2016, pp. 369-408
-
- Article
- Export citation
The interaction between two oppositely travelling, horizontally offset, antisymmetric quasi-geostrophic hetons
-
- Published online by Cambridge University Press:
- 04 April 2016, pp. 409-443
-
- Article
- Export citation
A local analysis of the axisymmetric Navier–Stokes flow near a saddle point and no-slip flat boundary
-
- Published online by Cambridge University Press:
- 04 April 2016, pp. 444-459
-
- Article
- Export citation
Asymmetric breaking size-segregation waves in dense granular free-surface flows
-
- Published online by Cambridge University Press:
- 04 April 2016, pp. 460-505
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Crown sealing and buckling instability during water entry of spheres
-
- Published online by Cambridge University Press:
- 05 April 2016, pp. 506-529
-
- Article
- Export citation
Homoclinic snaking in plane Couette flow: bending, skewing and finite-size effects
-
- Published online by Cambridge University Press:
- 06 April 2016, pp. 530-551
-
- Article
- Export citation