Two tandem flexible flags in viscous flow were modelled by numerical simulation using an improved version of the immersed boundary method. The flexible flapping flag and the vortices produced by an upstream flag were found to interact via either a constructive or destructive mode. These interaction modes gave rise to significant differences in the drag force acting on the downstream flapping flag in viscous flow. The constructive mode increased the drag force, while the destructive mode decreased the drag force. Drag on the downstream flexible body was investigated as a function of the streamwise and spanwise gap distances, and the bending coefficient of the flexible flags at intermediate Reynolds numbers (200 ≤ Re ≤ 400).

An ultra-thin viscous film on a substrate is susceptible to rupture instabilities driven by van der Waals attractions. When a unidirectional ‘wind’ shear τ is applied to the free surface, the rupture instability in two dimensions is suppressed when τ exceeds a critical value τc and is replaced by a permanent finite-amplitude structure, an intermolecular-capillary wave, that travels at approximately the speed of the surface. For small amplitudes, the wave is governed by the Kuramoto–Sivashinsky equation. If three-dimensional disturbances are allowed, the shear is decoupled from disturbances perpendicular to the flow, and line rupture would occur. In this case, replacing the unidirectional shear with a shear whose direction rotates with angular speed, 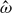, suppresses the rupture if τ ≳ 2τc. For the most dangerous wavenumber, τc ≈ 10−2 dyn cm−2 at 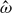≈ 1 rad s−1 for a film with physical properties similar to water at a thickness of 100 nm.