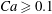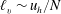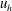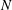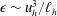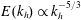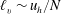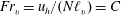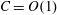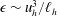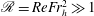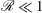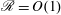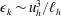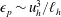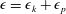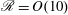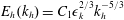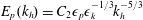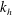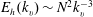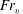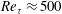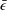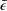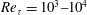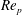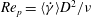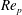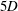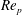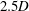Focus on Fluids
The fate of random initial vorticity distributions for two-dimensional Euler equations on a sphere
-
- Published online by Cambridge University Press:
- 24 November 2015, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Papers
Experimental study of rotating-disk boundary-layer flow with surface roughness
-
- Published online by Cambridge University Press:
- 24 November 2015, pp. 5-28
-
- Article
- Export citation
Flutter instability of a thin flexible plate in a channel
-
- Published online by Cambridge University Press:
- 24 November 2015, pp. 29-46
-
- Article
- Export citation
Universality of finger growth in two-dimensional Rayleigh–Taylor and Richtmyer–Meshkov instabilities with all density ratios
-
- Published online by Cambridge University Press:
- 25 November 2015, pp. 47-61
-
- Article
- Export citation
Theoretical model of scattering from flow ducts with semi-infinite axial liner splices
-
- Published online by Cambridge University Press:
- 30 November 2015, pp. 62-83
-
- Article
- Export citation
Streaming-potential phenomena in the thin-Debye-layer limit. Part 3. Shear-induced electroviscous repulsion
-
- Published online by Cambridge University Press:
- 26 November 2015, pp. 84-109
-
- Article
- Export citation
Rheology of a dense suspension of spherical capsules under simple shear flow
-
- Published online by Cambridge University Press:
- 30 November 2015, pp. 110-127
-
- Article
- Export citation
Dynamics of shear-induced migration of spherical particles in oscillatory pipe flow
-
- Published online by Cambridge University Press:
- 30 November 2015, pp. 128-153
-
- Article
- Export citation
Linear and nonlinear receptivity of the boundary layer in transonic flows
-
- Published online by Cambridge University Press:
- 30 November 2015, pp. 154-189
-
- Article
- Export citation
Periodic saltation over hydrodynamically rough beds: aeolian to aquatic
-
- Published online by Cambridge University Press:
- 30 November 2015, pp. 190-209
-
- Article
- Export citation
Dynamics of stratified turbulence decaying from a high buoyancy Reynolds number
-
- Published online by Cambridge University Press:
- 01 December 2015, pp. 210-233
-
- Article
- Export citation
On the universality of local dissipation scales in turbulent channel flow
-
- Published online by Cambridge University Press:
- 01 December 2015, pp. 234-252
-
- Article
- Export citation
Complete self-preservation along the axis of a circular cylinder far wake
-
- Published online by Cambridge University Press:
- 01 December 2015, pp. 253-274
-
- Article
- Export citation
Boundary layer structure in a rough Rayleigh–Bénard cell filled with air
-
- Published online by Cambridge University Press:
- 03 December 2015, pp. 275-293
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scale-to-scale energy and enstrophy transport in two-dimensional Rayleigh–Taylor turbulence
-
- Published online by Cambridge University Press:
- 02 December 2015, pp. 294-308
-
- Article
- Export citation
Uniform momentum zones in turbulent boundary layers
-
- Published online by Cambridge University Press:
- 02 December 2015, pp. 309-331
-
- Article
- Export citation
Particle dispersion by nonlinearly damped random waves
-
- Published online by Cambridge University Press:
- 02 December 2015, pp. 332-347
-
- Article
- Export citation
Rapids
Linear stability analysis for monami in a submerged seagrass bed
-
- Published online by Cambridge University Press:
- 24 November 2015, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The stability of a rising droplet: an inertialess non-modal growth mechanism
-
- Published online by Cambridge University Press:
- 24 November 2015, R2
-
- Article
- Export citation
Preferred interparticle spacings in trains of particles in inertial microchannel flows
-
- Published online by Cambridge University Press:
- 25 November 2015, R3
-
- Article
- Export citation