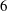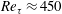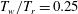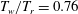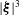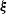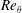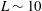Focus on Fluids
Mixed thermal conditions in convection: how do continents affect the mantle’s circulation?
-
- Published online by Cambridge University Press:
- 01 June 2017, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Papers
Effect of wall cooling on boundary-layer-induced pressure fluctuations at Mach 6
-
- Published online by Cambridge University Press:
- 31 May 2017, pp. 5-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computational fluid dynamics model of rhythmic motion of charged droplets between parallel electrodes
-
- Published online by Cambridge University Press:
- 06 June 2017, pp. 31-53
-
- Article
- Export citation
Three-dimensional wave evolution on electrified falling films
-
- Published online by Cambridge University Press:
- 06 June 2017, pp. 54-79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Instabilities and transient growth of the stratified Taylor–Couette flow in a Rayleigh-unstable regime
-
- Published online by Cambridge University Press:
- 31 May 2017, pp. 80-108
-
- Article
- Export citation
On the identification of well-behaved turbulent boundary layers
-
- Published online by Cambridge University Press:
- 31 May 2017, pp. 109-138
-
- Article
- Export citation
Resonant three-dimensional nonlinear sloshing in a square-base basin. Part 4. Oblique forcing and linear viscous damping
-
- Published online by Cambridge University Press:
- 02 June 2017, pp. 139-169
-
- Article
- Export citation
Linear stability of a viscoelastic liquid flow on an oscillating plane
-
- Published online by Cambridge University Press:
- 31 May 2017, pp. 170-185
-
- Article
- Export citation
Spanwise turbulence structure over permeable walls
-
- Published online by Cambridge University Press:
- 01 June 2017, pp. 186-201
-
- Article
- Export citation
Regularized string model for nanofibre formation in centrifugal spinning methods
-
- Published online by Cambridge University Press:
- 01 June 2017, pp. 202-234
-
- Article
-
- You have access
- HTML
- Export citation
Direct numerical simulation of the oscillatory flow around a sphere resting on a rough bottom
-
- Published online by Cambridge University Press:
- 01 June 2017, pp. 235-266
-
- Article
- Export citation
Transitions to different kinds of turbulence in a channel with soft walls
-
- Published online by Cambridge University Press:
- 01 June 2017, pp. 267-306
-
- Article
- Export citation
Perturbation analysis of subphase gas and meniscus curvature effects for longitudinal flows over superhydrophobic surfaces
-
- Published online by Cambridge University Press:
- 01 June 2017, pp. 307-326
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pulsating turbulence in a marginally unstable stratified shear flow
-
- Published online by Cambridge University Press:
- 01 June 2017, pp. 327-341
-
- Article
- Export citation
Flow control of weakly non-parallel flows: application to trailing vortices
-
- Published online by Cambridge University Press:
- 01 June 2017, pp. 342-363
-
- Article
- Export citation
Critical transitions in thin layer turbulence
-
- Published online by Cambridge University Press:
- 01 June 2017, pp. 364-385
-
- Article
- Export citation
Scaling the propulsive performance of heaving and pitching foils
-
- Published online by Cambridge University Press:
- 02 June 2017, pp. 386-397
-
- Article
-
- You have access
- HTML
- Export citation
On the apparent permeability of porous media in rarefied gas flows
-
- Published online by Cambridge University Press:
- 05 June 2017, pp. 398-417
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The long-wave vorticity dynamics of rotating buoyant outflows
-
- Published online by Cambridge University Press:
- 05 June 2017, pp. 418-443
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A local scattering approach for the effects of abrupt changes on boundary-layer instability and transition: a finite-Reynolds-number formulation for isolated distortions
-
- Published online by Cambridge University Press:
- 06 June 2017, pp. 444-483
-
- Article
- Export citation