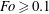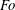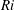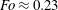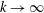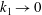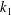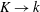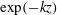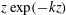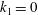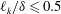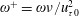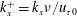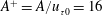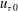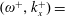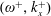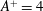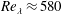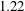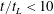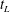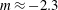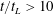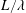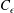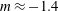JFM Rapids
Prandtl–Batchelor theorem for flows with quasiperiodic time dependence
-
- Published online by Cambridge University Press:
- 07 January 2019, R1
-
- Article
- Export citation
The onset of transient turbulence in minimal plane Couette flow
-
- Published online by Cambridge University Press:
- 10 January 2019, R2
-
- Article
- Export citation
Water entry of spheres with various contact angles
-
- Published online by Cambridge University Press:
- 10 January 2019, R3
-
- Article
- Export citation
Nonlinear aspects of focusing internal waves
-
- Published online by Cambridge University Press:
- 11 January 2019, R4
-
- Article
- Export citation
On the decay of dispersive motions in the outer region of rough-wall boundary layers
-
- Published online by Cambridge University Press:
- 25 January 2019, R5
-
- Article
- Export citation
Focus on Fluids
Dropping slender-body theory into the mud
-
- Published online by Cambridge University Press:
- 04 January 2019, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
A rarefied gas flow around a rotating sphere: diverging profiles of gradients of macroscopic quantities
-
- Published online by Cambridge University Press:
- 04 January 2019, pp. 5-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hydrodynamics of periodic wave energy converter arrays
-
- Published online by Cambridge University Press:
- 04 January 2019, pp. 34-74
-
- Article
- Export citation
Drag reduction in turbulent flows along a cylinder by streamwise-travelling waves of circumferential wall velocity
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 75-98
-
- Article
- Export citation
Laboratory experiments on the temporal decay of homogeneous anisotropic turbulence
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 99-127
-
- Article
- Export citation
The role of gravity in the prediction of the circular hydraulic jump radius for high-viscosity liquids
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 128-161
-
- Article
- Export citation
A simple system for moist convection: the Rainy–Bénard model
-
- Published online by Cambridge University Press:
- 09 January 2019, pp. 162-199
-
- Article
- Export citation
System identification of a low-density jet via its noise-induced dynamics
-
- Published online by Cambridge University Press:
- 08 January 2019, pp. 200-215
-
- Article
- Export citation
Separated rows structure of vortex streets behind triangular objects
-
- Published online by Cambridge University Press:
- 10 January 2019, pp. 216-226
-
- Article
- Export citation
Large eddy simulation of transient upstream/downstream vortex interactions
-
- Published online by Cambridge University Press:
- 09 January 2019, pp. 227-260
-
- Article
- Export citation
Droplet levitation over a moving wall with a steady air film
-
- Published online by Cambridge University Press:
- 08 January 2019, pp. 261-282
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Macroscopic model for unsteady flow in porous media
-
- Published online by Cambridge University Press:
- 10 January 2019, pp. 283-311
-
- Article
- Export citation
Thermophoresis of a spherical particle: modelling through moment-based, macroscopic transport equations
-
- Published online by Cambridge University Press:
- 10 January 2019, pp. 312-347
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of heavy and buoyant underwater pendulums
-
- Published online by Cambridge University Press:
- 16 January 2019, pp. 348-363
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the breakup of spiralling liquid jets
-
- Published online by Cambridge University Press:
- 15 January 2019, pp. 364-384
-
- Article
- Export citation