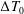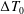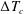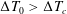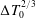1 Introduction
When a drop falls onto a bath of a miscible liquid, one expects it to coalesce immediately upon impact. However, such is not always the case, owing to the presence of a thin lubricating air layer between drop and bath that must drain to a critical thickness before coalescence is initiated by intermolecular forces (Walker Reference Walker1978). Careful observation of raindrops hitting a puddle, lake or sea surface reveal that some millimetric droplets may bounce, leap and roll along the surface prior to coalescence (Reynolds Reference Reynolds1881; Rayleigh Reference Rayleigh1899). Everyday experience indicates that a temperature difference may further delay coalescence. When milk is poured into hot tea or coffee, drops may linger on the surface, levitating there for up to a few seconds before merging.
Coalescence has been studied extensively and the influence of relevant physical quantities (fluid density
![]() $\unicode[STIX]{x1D70C}$
, surface tension
$\unicode[STIX]{x1D70C}$
, surface tension
![]() $\unicode[STIX]{x1D70E}$
, viscosity
$\unicode[STIX]{x1D70E}$
, viscosity
![]() $\unicode[STIX]{x1D707}$
, surface charges, etc.) has been characterized (e.g. Charles & Mason Reference Charles and Mason1960a
,Reference Charles and Mason
b
; Jeffreys & Davis Reference Jeffreys and Davis1971), leading to a classification of different dynamical regimes (Aryafar & Kavehpour Reference Aryafar and Kavehpour2006). Advances in high-speed imaging (Thoroddsen & Takehara Reference Thoroddsen and Takehara2000), experimental techniques (Mohamed-Kassim & Longmire Reference Mohamed-Kassim and Longmire2004), and numerical simulations (Blanchette & Bigioni Reference Blanchette and Bigioni2006, Reference Blanchette and Bigioni2009) have furthered our understanding of coalescence in various circumstances, including the effects of concentration-induced Marangoni stresses (Blanchette, Messio & Bush Reference Blanchette, Messio and Bush2009). The myriad aspects of coalescence were recently reviewed by Kavehpour (Reference Kavehpour2015).
$\unicode[STIX]{x1D707}$
, surface charges, etc.) has been characterized (e.g. Charles & Mason Reference Charles and Mason1960a
,Reference Charles and Mason
b
; Jeffreys & Davis Reference Jeffreys and Davis1971), leading to a classification of different dynamical regimes (Aryafar & Kavehpour Reference Aryafar and Kavehpour2006). Advances in high-speed imaging (Thoroddsen & Takehara Reference Thoroddsen and Takehara2000), experimental techniques (Mohamed-Kassim & Longmire Reference Mohamed-Kassim and Longmire2004), and numerical simulations (Blanchette & Bigioni Reference Blanchette and Bigioni2006, Reference Blanchette and Bigioni2009) have furthered our understanding of coalescence in various circumstances, including the effects of concentration-induced Marangoni stresses (Blanchette, Messio & Bush Reference Blanchette, Messio and Bush2009). The myriad aspects of coalescence were recently reviewed by Kavehpour (Reference Kavehpour2015).
The influence of thermal effects on drop coalescence has received relatively less attention. A series of experimental studies have examined the non-coalescence of two drops maintained at different temperatures owing to the presence of thermally induced Marangoni stresses (Dell’Aversana, Banavar & Koplik Reference Dell’Aversana, Banavar and Koplik1996; Dell’Aversana, Tontodonato & Carotenuto Reference Dell’Aversana, Tontodonato and Carotenuto1997; Dell’Aversana & Neitzel Reference Dell’Aversana and Neitzel1998). These studies demonstrate that above a critical temperature difference, coalescence is precluded by Marangoni stresses driving recirculating flows inside the drops that enhance the intervening lubrication pressure (as in figure 1) – a physical picture supported by the numerical simulations of Monti, Savino & Cicala (Reference Monti, Savino and Cicala1996) and Monti & Savino (Reference Monti and Savino1997). Savino, Paterna & Lappa (Reference Savino, Paterna and Lappa2003) confirmed that coalescence of drops floating on a liquid bath could be delayed by a temperature difference between drop and bath, and the sustenance of the intervening air film by the associated thermocapillary flows. Neitzel & Dell’Aversana (Reference Neitzel and Dell’Aversana2002) and Lappa (Reference Lappa2005) have reviewed studies of different aspects of non-coalescence.
While it has been established that the influence of thermocapillary flows in the lubricating air layer will resist coalescence between two drops with a temperature difference above some critical value (Neitzel & Dell’Aversana Reference Neitzel and Dell’Aversana2002; Savino et al.
Reference Savino, Paterna and Lappa2003), no theoretical model has provided a rationale for this critical temperature difference. Moreover, previous studies have neither characterized nor rationalized the dependence of the residence time of a floating droplet (denoted
![]() $\unicode[STIX]{x1D70F}_{r}$
henceforth) on the temperature difference between drop and bath. We focus here on the coalescence of a drop into a bath of the same liquid, when an initial temperature difference
$\unicode[STIX]{x1D70F}_{r}$
henceforth) on the temperature difference between drop and bath. We focus here on the coalescence of a drop into a bath of the same liquid, when an initial temperature difference
![]() $\unicode[STIX]{x0394}T_{0}$
is imposed between the bath and the drop (figure 1
a). In § 2 we provide experimental evidence of a functional relationship between
$\unicode[STIX]{x0394}T_{0}$
is imposed between the bath and the drop (figure 1
a). In § 2 we provide experimental evidence of a functional relationship between
![]() $\unicode[STIX]{x1D70F}_{r}$
and
$\unicode[STIX]{x1D70F}_{r}$
and
![]() $\unicode[STIX]{x0394}T_{0}$
. In § 3, we rationalize our observations through theoretical consideration of the thermocapillary flows arising within the drop, the bath and the intervening air layer.
$\unicode[STIX]{x0394}T_{0}$
. In § 3, we rationalize our observations through theoretical consideration of the thermocapillary flows arising within the drop, the bath and the intervening air layer.
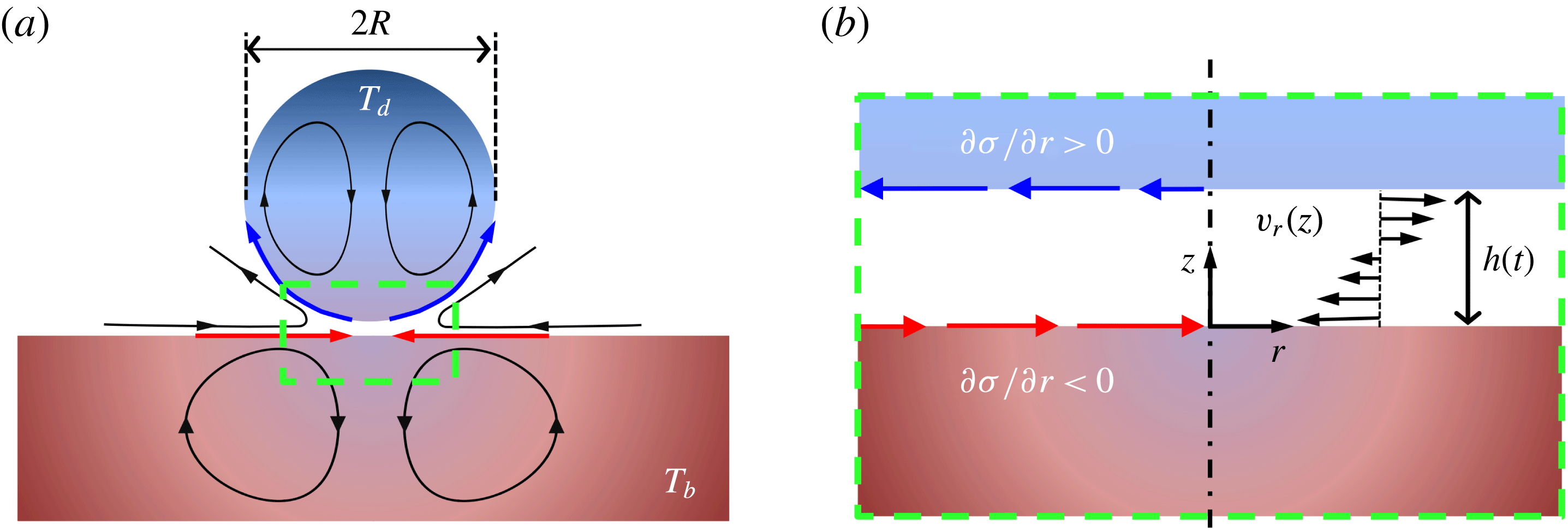
Figure 1. A schematic of thermally delayed drop coalescence. (a) A drop approaches a bath of the same liquid with initial temperature difference
![]() $\unicode[STIX]{x0394}T_{0}=T_{b}-T_{d}$
. Thermal gradients induce Marangoni stresses that drive thermocapillary flows within both the liquid and gas phases. (b) A close-up of the lubrication layer of air between drop and bath.
$\unicode[STIX]{x0394}T_{0}=T_{b}-T_{d}$
. Thermal gradients induce Marangoni stresses that drive thermocapillary flows within both the liquid and gas phases. (b) A close-up of the lubrication layer of air between drop and bath.
2 Experiments
Consider a drop with initial temperature
![]() $T_{d}$
approaching a bath of the same liquid with temperature
$T_{d}$
approaching a bath of the same liquid with temperature
![]() $T_{b}$
(figure 1
a). The drop is released sufficiently close to the bath surface that the effect of its initial velocity is negligible. The initial temperature difference between the drop and the bath,
$T_{b}$
(figure 1
a). The drop is released sufficiently close to the bath surface that the effect of its initial velocity is negligible. The initial temperature difference between the drop and the bath,
![]() $\unicode[STIX]{x0394}T_{0}=T_{b}-T_{d}$
, is prescribed. Owing to the dependence of surface tension
$\unicode[STIX]{x0394}T_{0}=T_{b}-T_{d}$
, is prescribed. Owing to the dependence of surface tension
![]() $\unicode[STIX]{x1D70E}$
on temperature
$\unicode[STIX]{x1D70E}$
on temperature
![]() $T$
, thermal gradients along the interface result in Marangoni stresses that drive thermocapillary flows within both the liquid and gas phases, of the general form sketched in figure 1. The majority of our experiments were performed with
$T$
, thermal gradients along the interface result in Marangoni stresses that drive thermocapillary flows within both the liquid and gas phases, of the general form sketched in figure 1. The majority of our experiments were performed with
![]() $\unicode[STIX]{x0394}T_{0}>0$
, as in the case of a cold milk drop on the surface of hot coffee. We also performed several experiments with
$\unicode[STIX]{x0394}T_{0}>0$
, as in the case of a cold milk drop on the surface of hot coffee. We also performed several experiments with
![]() $\unicode[STIX]{x0394}T_{0}<0$
.
$\unicode[STIX]{x0394}T_{0}<0$
.

Figure 2. (a) Schematic of the experimental set-up. (b) Image showing a drop sitting on a bath of 1 cSt silicone oil with
![]() $\unicode[STIX]{x0394}T_{0}=0$
prior to coalescence (see movie 1). (c) Image captured with a green laser light sheet reveals a recirculating Marangoni flow within a cold drop (see movie 2).
$\unicode[STIX]{x0394}T_{0}=0$
prior to coalescence (see movie 1). (c) Image captured with a green laser light sheet reveals a recirculating Marangoni flow within a cold drop (see movie 2).
2.1 Materials and methods
Figure 2(a) shows a schematic of our experimental set-up. The bath consists of a liquid pool in a customized square cell of dimensions 3.175 cm by 3.175 cm by 1.9 cm deep. The cell, with acrylic walls and a metallic substrate, is placed on a dual cold/hot plate (Teca AHP-301 CPV) that allows for precise control of the temperature at the base of the cell. The temperature of the bath surface (
![]() $T_{b}$
) and that of the drop (
$T_{b}$
) and that of the drop (
![]() $T_{d}$
) are monitored with a hand-held thermometer equipped with a K-type thermocouple. In the range of
$T_{d}$
) are monitored with a hand-held thermometer equipped with a K-type thermocouple. In the range of
![]() $\unicode[STIX]{x0394}T_{0}$
considered, the influence of convective overturning within the bath was negligible. Drops are dispensed through a needle centred above the cell at a height of approximately one drop diameter above the bath. The liquid is pushed by a syringe pump at a flow rate of
$\unicode[STIX]{x0394}T_{0}$
considered, the influence of convective overturning within the bath was negligible. Drops are dispensed through a needle centred above the cell at a height of approximately one drop diameter above the bath. The liquid is pushed by a syringe pump at a flow rate of
![]() $0.07~\text{ml}~\text{min}^{-1}$
, the drop then gently released onto the bath in order to insure a negligible approach speed. A BD stainless steel standard bevel needle 16G was used, fixing the drop radius to be
$0.07~\text{ml}~\text{min}^{-1}$
, the drop then gently released onto the bath in order to insure a negligible approach speed. A BD stainless steel standard bevel needle 16G was used, fixing the drop radius to be
![]() $R=0.6~\text{mm}$
. A Phantom high-speed camera, mounted on a 3-axis positioning stage, recorded each experiment, typically at 2000 f.p.s. Figure 2(b) shows a digital video frame of a drop floating on a bath prior to coalescence (see movie 1 as a supplementary material available online at https://doi.org/10.1017/jfm.2017.686). Back-lighting with a white LED was used in all measurements (see movie 3), but a halogen lamp proved more effective in visualizing the rapid dynamics of the coalescence process, as shown in figure 3 (see also movies 4 and 5). The residence time
$R=0.6~\text{mm}$
. A Phantom high-speed camera, mounted on a 3-axis positioning stage, recorded each experiment, typically at 2000 f.p.s. Figure 2(b) shows a digital video frame of a drop floating on a bath prior to coalescence (see movie 1 as a supplementary material available online at https://doi.org/10.1017/jfm.2017.686). Back-lighting with a white LED was used in all measurements (see movie 3), but a halogen lamp proved more effective in visualizing the rapid dynamics of the coalescence process, as shown in figure 3 (see also movies 4 and 5). The residence time
![]() $\unicode[STIX]{x1D70F}_{r}$
was measured as the interval between drop detachment from the needle and the onset of coalescence (see first two images in figure 3
a,b), which is readily identified by the appearance of capillary waves on the surface of the droplet. The acquisition rate guarantees that the error on
$\unicode[STIX]{x1D70F}_{r}$
was measured as the interval between drop detachment from the needle and the onset of coalescence (see first two images in figure 3
a,b), which is readily identified by the appearance of capillary waves on the surface of the droplet. The acquisition rate guarantees that the error on
![]() $\unicode[STIX]{x1D70F}_{r}$
is on the order of 1 ms, and so negligible relative to the variability between successive measurements.
$\unicode[STIX]{x1D70F}_{r}$
is on the order of 1 ms, and so negligible relative to the variability between successive measurements.

Figure 3. Montage of typical experiments for two different silicone oils with kinematic viscosities (a)
![]() $\unicode[STIX]{x1D708}_{o}=20~\text{cSt}$
and (b)
$\unicode[STIX]{x1D708}_{o}=20~\text{cSt}$
and (b)
![]() $\unicode[STIX]{x1D708}_{o}=1~\text{cSt}$
(see also movies 4 and 5). The first two frames correspond to drop detachment from the needle (
$\unicode[STIX]{x1D708}_{o}=1~\text{cSt}$
(see also movies 4 and 5). The first two frames correspond to drop detachment from the needle (
![]() $t=0$
) and initiation of coalescence (
$t=0$
) and initiation of coalescence (
![]() $t=\unicode[STIX]{x1D70F}_{r}$
). Subsequent images show the coalescence process. The difference between the two sequences is striking: the
$t=\unicode[STIX]{x1D70F}_{r}$
). Subsequent images show the coalescence process. The difference between the two sequences is striking: the
![]() $20~\text{cSt}$
drop coalesces directly, while the
$20~\text{cSt}$
drop coalesces directly, while the
![]() $1~\text{cSt}$
drop executes a coalescence cascade (Thoroddsen & Takehara Reference Thoroddsen and Takehara2000) with up to five to six daughter droplets, only two of which are shown here.
$1~\text{cSt}$
drop executes a coalescence cascade (Thoroddsen & Takehara Reference Thoroddsen and Takehara2000) with up to five to six daughter droplets, only two of which are shown here.
In order to visualize the thermocapillary flow within the drop, the 5 cSt oil was seeded with
![]() $\text{TiO}_{2}$
particles with an average diameter of
$\text{TiO}_{2}$
particles with an average diameter of
![]() $3~\unicode[STIX]{x03BC}\text{m}$
. A drop was then formed, pinned in place by the dispensing needle and illuminated with a green laser sheet (see movie 2). A synthetic streak image obtained by superposing 100 digital video frames taken at 30 f.p.s. prior to coalescence is shown in figure 2(c). The particle pathlines are clearly evident and reveal a poloidal motion with characteristic speed of
$3~\unicode[STIX]{x03BC}\text{m}$
. A drop was then formed, pinned in place by the dispensing needle and illuminated with a green laser sheet (see movie 2). A synthetic streak image obtained by superposing 100 digital video frames taken at 30 f.p.s. prior to coalescence is shown in figure 2(c). The particle pathlines are clearly evident and reveal a poloidal motion with characteristic speed of
![]() ${\sim}5~\text{mm}~\text{s}^{-1}$
in the interior of the drop for
${\sim}5~\text{mm}~\text{s}^{-1}$
in the interior of the drop for
![]() $\unicode[STIX]{x0394}T_{0}=5\,^{\circ }\text{C}$
. This vortical circulation is initiated when the droplet detaches from the needle (see movie 2). A complementary thermocapillary flow is expected to arise within the bath (Savino et al.
Reference Savino, Paterna and Lappa2003, see figure 1).
$\unicode[STIX]{x0394}T_{0}=5\,^{\circ }\text{C}$
. This vortical circulation is initiated when the droplet detaches from the needle (see movie 2). A complementary thermocapillary flow is expected to arise within the bath (Savino et al.
Reference Savino, Paterna and Lappa2003, see figure 1).
Silicone oils allowed us to tune viscosity without substantially altering other properties of the liquid phase (see table 1 in Kavehpour, Ovryn & McKinley Reference Kavehpour, Ovryn and McKinley2002). Five different silicone oils were tested, with kinematic viscosities (
![]() $\unicode[STIX]{x1D708}_{o}$
) of 1, 5, 10, 20 and
$\unicode[STIX]{x1D708}_{o}$
) of 1, 5, 10, 20 and
![]() $500~\text{cSt}$
. All the oils are assumed to have density
$500~\text{cSt}$
. All the oils are assumed to have density
![]() $\unicode[STIX]{x1D70C}_{o}=0.9~\text{g}~\text{cm}^{-3}$
and thermal diffusivity
$\unicode[STIX]{x1D70C}_{o}=0.9~\text{g}~\text{cm}^{-3}$
and thermal diffusivity
![]() $\unicode[STIX]{x1D6FC}_{o}=7\times 10^{-4}~\text{cm}^{2}~\text{s}^{-1}$
. The surface tension is assumed to decrease linearly with increasing temperature:
$\unicode[STIX]{x1D6FC}_{o}=7\times 10^{-4}~\text{cm}^{2}~\text{s}^{-1}$
. The surface tension is assumed to decrease linearly with increasing temperature:
![]() $\unicode[STIX]{x1D70E}(T)=\unicode[STIX]{x1D70E}_{0}-\unicode[STIX]{x1D70E}_{T}(T-T_{0})$
where
$\unicode[STIX]{x1D70E}(T)=\unicode[STIX]{x1D70E}_{0}-\unicode[STIX]{x1D70E}_{T}(T-T_{0})$
where
![]() $\unicode[STIX]{x1D70E}_{0}=20~\text{dyn}~\text{cm}^{-1}$
and
$\unicode[STIX]{x1D70E}_{0}=20~\text{dyn}~\text{cm}^{-1}$
and
![]() $\unicode[STIX]{x1D70E}_{T}=\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}/\unicode[STIX]{x2202}T=5\times 10^{-2}~\text{dyn}~(\text{cm}\,^{\circ }\text{C})^{-1}$
. The air is characterized by its dynamic viscosity
$\unicode[STIX]{x1D70E}_{T}=\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}/\unicode[STIX]{x2202}T=5\times 10^{-2}~\text{dyn}~(\text{cm}\,^{\circ }\text{C})^{-1}$
. The air is characterized by its dynamic viscosity
![]() $\unicode[STIX]{x1D707}_{a}=0.018~\text{cP}$
, density
$\unicode[STIX]{x1D707}_{a}=0.018~\text{cP}$
, density
![]() $\unicode[STIX]{x1D70C}_{a}=1.2\times 10^{-3}~\text{g}~\text{cm}^{-3}$
and thermal diffusivity
$\unicode[STIX]{x1D70C}_{a}=1.2\times 10^{-3}~\text{g}~\text{cm}^{-3}$
and thermal diffusivity
![]() $\unicode[STIX]{x1D6FC}_{a}=0.2~\text{cm}^{2}~\text{s}^{-1}$
. In our theoretical developments, density and viscosity are assumed to be independent of temperature: the only property that changes significantly over the range of temperatures considered is surface tension.
$\unicode[STIX]{x1D6FC}_{a}=0.2~\text{cm}^{2}~\text{s}^{-1}$
. In our theoretical developments, density and viscosity are assumed to be independent of temperature: the only property that changes significantly over the range of temperatures considered is surface tension.
2.2 Measurements of the residence time
In figure 4(a) we report the residence times
![]() $\unicode[STIX]{x1D70F}_{r}$
for the five oils at different
$\unicode[STIX]{x1D70F}_{r}$
for the five oils at different
![]() $\unicode[STIX]{x0394}T_{0}$
. The dashed line indicates the isothermal reference value that is independent of the oil viscosity and assumes a nearly constant value
$\unicode[STIX]{x0394}T_{0}$
. The dashed line indicates the isothermal reference value that is independent of the oil viscosity and assumes a nearly constant value
![]() $\unicode[STIX]{x1D70F}_{r}^{0}\simeq 160\pm 50~\text{ms}$
for all liquids considered and for the given
$\unicode[STIX]{x1D70F}_{r}^{0}\simeq 160\pm 50~\text{ms}$
for all liquids considered and for the given
![]() $R$
. Two important features should be noted. First, as in the case of complete non-coalescence of drops (Dell’Aversana et al.
Reference Dell’Aversana, Banavar and Koplik1996), there is a critical temperature difference below which the residence time
$R$
. Two important features should be noted. First, as in the case of complete non-coalescence of drops (Dell’Aversana et al.
Reference Dell’Aversana, Banavar and Koplik1996), there is a critical temperature difference below which the residence time
![]() $\unicode[STIX]{x1D70F}_{r}$
is comparable to
$\unicode[STIX]{x1D70F}_{r}$
is comparable to
![]() $\unicode[STIX]{x1D70F}_{r}^{0}$
, as indicated by the points lying close to the reference dashed line. This critical value, henceforth denoted
$\unicode[STIX]{x1D70F}_{r}^{0}$
, as indicated by the points lying close to the reference dashed line. This critical value, henceforth denoted
![]() $\unicode[STIX]{x0394}T_{c}$
, increases monotonically with the fluid viscosity. While the 5 cSt oil has
$\unicode[STIX]{x0394}T_{c}$
, increases monotonically with the fluid viscosity. While the 5 cSt oil has
![]() $\unicode[STIX]{x0394}T_{c}\simeq 1\,^{\circ }\text{C}$
, the 500 cSt oil has a value of
$\unicode[STIX]{x0394}T_{c}\simeq 1\,^{\circ }\text{C}$
, the 500 cSt oil has a value of
![]() $\unicode[STIX]{x0394}T_{c}$
much higher than those accessible with our set-up; thus we never observed delayed coalescence with this oil. Second, above
$\unicode[STIX]{x0394}T_{c}$
much higher than those accessible with our set-up; thus we never observed delayed coalescence with this oil. Second, above
![]() $\unicode[STIX]{x0394}T_{c}$
, for all viscosities the residence time monotonically increases with the initial temperature difference with a characteristic power law such that
$\unicode[STIX]{x0394}T_{c}$
, for all viscosities the residence time monotonically increases with the initial temperature difference with a characteristic power law such that
![]() $\unicode[STIX]{x1D70F}_{r}\sim \unicode[STIX]{x0394}T_{0}^{0.66\pm 0.10}$
.
$\unicode[STIX]{x1D70F}_{r}\sim \unicode[STIX]{x0394}T_{0}^{0.66\pm 0.10}$
.
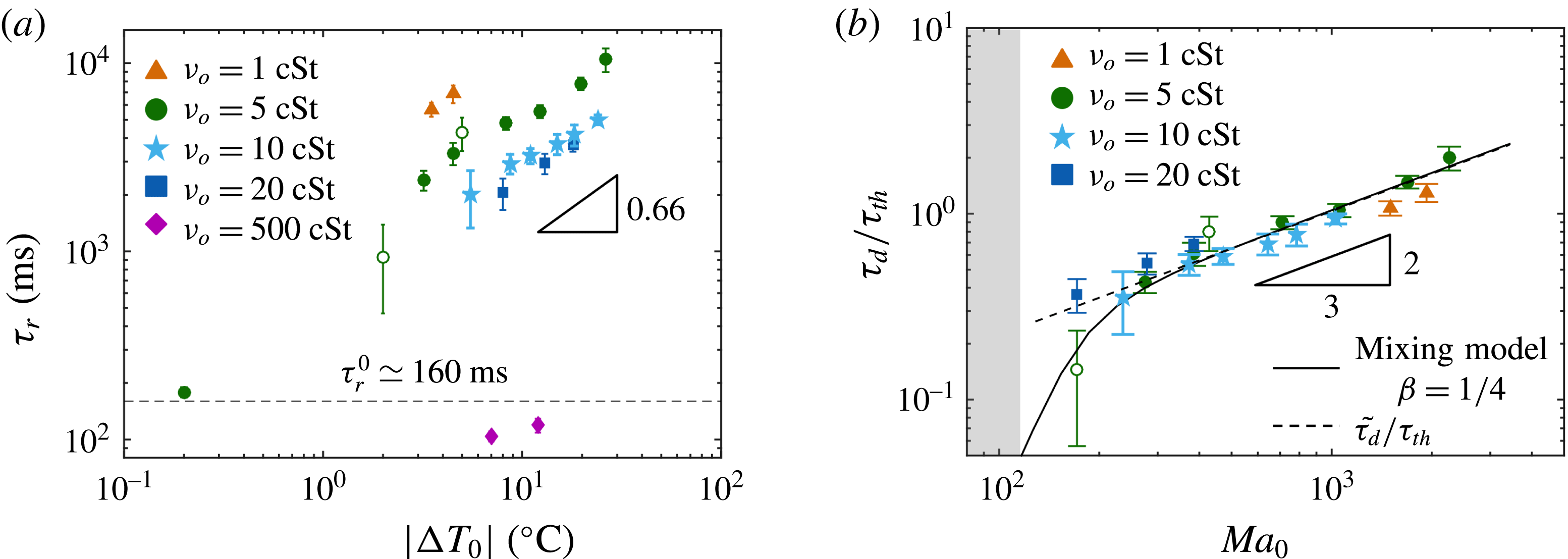
Figure 4. (a) Measurements of the residence time
![]() $\unicode[STIX]{x1D70F}_{r}$
as a function of the absolute value of the initial temperature difference
$\unicode[STIX]{x1D70F}_{r}$
as a function of the absolute value of the initial temperature difference
![]() $|\unicode[STIX]{x0394}T_{0}|$
for the five different silicone oils considered. Open symbols represent the cases where
$|\unicode[STIX]{x0394}T_{0}|$
for the five different silicone oils considered. Open symbols represent the cases where
![]() $\unicode[STIX]{x0394}T_{0}<0$
. Each data point corresponds to an average over
$\unicode[STIX]{x0394}T_{0}<0$
. Each data point corresponds to an average over
![]() $30$
drops and error bars are equivalent to two standard deviations. (b) The delay time
$30$
drops and error bars are equivalent to two standard deviations. (b) The delay time
![]() $\unicode[STIX]{x1D70F}_{d}$
, non-dimensionalized by the characteristic thermal diffusion time
$\unicode[STIX]{x1D70F}_{d}$
, non-dimensionalized by the characteristic thermal diffusion time
![]() $\unicode[STIX]{x1D70F}_{th}=R^{2}/\unicode[STIX]{x1D6FC}_{o}$
, as a function of the initial Marangoni number
$\unicode[STIX]{x1D70F}_{th}=R^{2}/\unicode[STIX]{x1D6FC}_{o}$
, as a function of the initial Marangoni number
![]() $Ma_{0}$
. Symbols correspond to data from (a). The solid line is the theoretical prediction from the model described in § 3.2 with
$Ma_{0}$
. Symbols correspond to data from (a). The solid line is the theoretical prediction from the model described in § 3.2 with
![]() $\unicode[STIX]{x1D6FD}=1/4$
. The dashed line is an approximate closed-form expression derived in the limit of
$\unicode[STIX]{x1D6FD}=1/4$
. The dashed line is an approximate closed-form expression derived in the limit of
![]() $t>\sqrt{3}/\dot{\unicode[STIX]{x1D6FE}}$
.
$t>\sqrt{3}/\dot{\unicode[STIX]{x1D6FE}}$
.
To isolate the influence of thermocapillary flows, we introduce the delay time
![]() $\unicode[STIX]{x1D70F}_{d}=\unicode[STIX]{x1D70F}_{r}-\unicode[STIX]{x1D70F}_{r}^{0}$
and rescale the initial temperature difference in terms of the initial Marangoni number
$\unicode[STIX]{x1D70F}_{d}=\unicode[STIX]{x1D70F}_{r}-\unicode[STIX]{x1D70F}_{r}^{0}$
and rescale the initial temperature difference in terms of the initial Marangoni number
![]() $Ma_{0}=|\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}_{o}|R/\unicode[STIX]{x1D707}_{o}\unicode[STIX]{x1D6FC}_{o}=|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T_{0}|R/\unicode[STIX]{x1D707}_{o}\unicode[STIX]{x1D6FC}_{o}$
, which prescribes the relative magnitudes of the characteristic time scales of thermal diffusion and convection within the drop – respectively,
$Ma_{0}=|\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}_{o}|R/\unicode[STIX]{x1D707}_{o}\unicode[STIX]{x1D6FC}_{o}=|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T_{0}|R/\unicode[STIX]{x1D707}_{o}\unicode[STIX]{x1D6FC}_{o}$
, which prescribes the relative magnitudes of the characteristic time scales of thermal diffusion and convection within the drop – respectively,
![]() $\unicode[STIX]{x1D70F}_{th}=R^{2}/\unicode[STIX]{x1D6FC}_{o}$
and
$\unicode[STIX]{x1D70F}_{th}=R^{2}/\unicode[STIX]{x1D6FC}_{o}$
and
![]() $\unicode[STIX]{x1D70F}_{conv}=R\unicode[STIX]{x1D707}_{o}/(\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T_{0})$
. In figure 4(b) we recast the data of figure 4(a) in terms of these two variables, with the delay time non-dimensionalized by the characteristic thermal diffusion time
$\unicode[STIX]{x1D70F}_{conv}=R\unicode[STIX]{x1D707}_{o}/(\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T_{0})$
. In figure 4(b) we recast the data of figure 4(a) in terms of these two variables, with the delay time non-dimensionalized by the characteristic thermal diffusion time
![]() $\unicode[STIX]{x1D70F}_{th}$
. The data all collapse onto a single curve that approaches a line with slope
$\unicode[STIX]{x1D70F}_{th}$
. The data all collapse onto a single curve that approaches a line with slope
![]() $2/3$
at large
$2/3$
at large
![]() $Ma$
. We note that the threshold below which no delayed coalescence is observed, previously characterized in terms of a viscosity-dependent
$Ma$
. We note that the threshold below which no delayed coalescence is observed, previously characterized in terms of a viscosity-dependent
![]() $\unicode[STIX]{x0394}T_{c}$
, may now be expressed in terms of a single critical Marangoni number,
$\unicode[STIX]{x0394}T_{c}$
, may now be expressed in terms of a single critical Marangoni number,
![]() $Ma_{c}\simeq 100\pm 50$
. Consequently, the delay time may be expressed as
$Ma_{c}\simeq 100\pm 50$
. Consequently, the delay time may be expressed as
![]() $\unicode[STIX]{x1D70F}_{d}/\unicode[STIX]{x1D70F}_{th}\simeq 0.01(Ma_{0}-Ma_{c})^{2/3}$
. We also note that the points in figure 4(a) with
$\unicode[STIX]{x1D70F}_{d}/\unicode[STIX]{x1D70F}_{th}\simeq 0.01(Ma_{0}-Ma_{c})^{2/3}$
. We also note that the points in figure 4(a) with
![]() $\unicode[STIX]{x1D70F}_{r}\sim \unicode[STIX]{x1D70F}_{r}^{0}$
are automatically shifted to
$\unicode[STIX]{x1D70F}_{r}\sim \unicode[STIX]{x1D70F}_{r}^{0}$
are automatically shifted to
![]() $Ma\ll Ma_{c}$
and so are beyond the limits of the plot. In order to rationalize both
$Ma\ll Ma_{c}$
and so are beyond the limits of the plot. In order to rationalize both
![]() $Ma_{c}$
and the resulting power law scaling of
$Ma_{c}$
and the resulting power law scaling of
![]() $\unicode[STIX]{x1D70F}_{d}$
with
$\unicode[STIX]{x1D70F}_{d}$
with
![]() $Ma$
, we proceed by considering the thermocapillary flows generated within the system.
$Ma$
, we proceed by considering the thermocapillary flows generated within the system.
3 Theoretical modelling
In § 3.1, we first describe the air flow in the gap between the drop and the bath using a lubrication analysis from which the critical Marangoni number
![]() $Ma_{c}$
is deduced. In § 3.2, we then rationalize the functional relationship between the residence time and the initial temperature difference through a description of the mixing dynamics within the drop.
$Ma_{c}$
is deduced. In § 3.2, we then rationalize the functional relationship between the residence time and the initial temperature difference through a description of the mixing dynamics within the drop.
3.1 Lubrication flow within the air gap
Our analysis rests on a series of simplifying assumptions. Figure 2(b,c) suggest that the geometry of the flow is non-trivial due to the bath curvature induced locally by the drop’s weight. Previous studies (Dell’Aversana et al.
Reference Dell’Aversana, Tontodonato and Carotenuto1997; Neitzel & Dell’Aversana Reference Neitzel and Dell’Aversana2002; Savino et al.
Reference Savino, Paterna and Lappa2003) have pointed out that in these conditions the underside of the drop may deform such that the height of the gap is not constant. We avoid such geometrical complexities by treating the gap as a cylindrical disk with height
![]() $h(t)$
and radius
$h(t)$
and radius
![]() $R_{d}$
, where
$R_{d}$
, where
![]() $R_{d}=R^{2}/l_{c}$
is the effective contact radius (Mahadevan & Pomeau Reference Mahadevan and Pomeau1999), and
$R_{d}=R^{2}/l_{c}$
is the effective contact radius (Mahadevan & Pomeau Reference Mahadevan and Pomeau1999), and
![]() $l_{c}=\sqrt{\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}_{o}g}$
is the capillary length of the oil; an approximation one expects to be valid provided
$l_{c}=\sqrt{\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D70C}_{o}g}$
is the capillary length of the oil; an approximation one expects to be valid provided
![]() $Bo=\unicode[STIX]{x1D70C}_{o}gR^{2}/\unicode[STIX]{x1D70E}<1$
. In our experiments
$Bo=\unicode[STIX]{x1D70C}_{o}gR^{2}/\unicode[STIX]{x1D70E}<1$
. In our experiments
![]() $Bo=0.17$
and
$Bo=0.17$
and
![]() $R_{d}=0.25~\text{mm}\simeq 0.4R$
. The initial height of the gap is
$R_{d}=0.25~\text{mm}\simeq 0.4R$
. The initial height of the gap is
![]() $h(0)$
and
$h(0)$
and
![]() $h(t)\ll (R,R_{d})$
at all times.
$h(t)\ll (R,R_{d})$
at all times.
We also assume that
![]() $Re_{a}(h/R)\ll 1$
, where
$Re_{a}(h/R)\ll 1$
, where
![]() $Re_{a}=\unicode[STIX]{x1D70C}_{a}Vh_{0}/\unicode[STIX]{x1D707}_{a}$
is the Reynolds number of the air flow, so that the lubrication approximation can be invoked and the Navier–Stokes equations simplified to:
$Re_{a}=\unicode[STIX]{x1D70C}_{a}Vh_{0}/\unicode[STIX]{x1D707}_{a}$
is the Reynolds number of the air flow, so that the lubrication approximation can be invoked and the Navier–Stokes equations simplified to:
where
![]() $p$
is the pressure field and
$p$
is the pressure field and
![]() $v_{r}$
the radial velocity. While both boundaries are free,
$v_{r}$
the radial velocity. While both boundaries are free,
![]() $\unicode[STIX]{x1D707}_{o}/\unicode[STIX]{x1D707}_{a}\gg 1$
so we can apply no-slip boundary conditions, specifically
$\unicode[STIX]{x1D707}_{o}/\unicode[STIX]{x1D707}_{a}\gg 1$
so we can apply no-slip boundary conditions, specifically
![]() $v_{r}(0)=v_{b}$
, the surface speed of the bath, and
$v_{r}(0)=v_{b}$
, the surface speed of the bath, and
![]() $v_{r}(h(t))=v_{d}$
, the surface speed of the drop. Note that
$v_{r}(h(t))=v_{d}$
, the surface speed of the drop. Note that
![]() $v_{b}$
and
$v_{b}$
and
![]() $v_{d}$
can be positive or negative depending on the sign of
$v_{d}$
can be positive or negative depending on the sign of
![]() $\unicode[STIX]{x0394}T_{0}$
. If
$\unicode[STIX]{x0394}T_{0}$
. If
![]() $\unicode[STIX]{x0394}T_{0}>0$
,
$\unicode[STIX]{x0394}T_{0}>0$
,
![]() $v_{b}<0$
while
$v_{b}<0$
while
![]() $v_{d}>0$
, and vice versa (see figure 1). In isothermal conditions, one may assume that
$v_{d}>0$
, and vice versa (see figure 1). In isothermal conditions, one may assume that
![]() $v_{b}=0=v_{d}$
, and the problem reduces to the classic lubrication squeezing flow between two parallel disks (Stefan Reference Stefan1874). However, in the presence of thermal gradients, both interfaces have radial flows driven by Marangoni stresses with characteristic magnitude
$v_{b}=0=v_{d}$
, and the problem reduces to the classic lubrication squeezing flow between two parallel disks (Stefan Reference Stefan1874). However, in the presence of thermal gradients, both interfaces have radial flows driven by Marangoni stresses with characteristic magnitude
![]() $U_{0}\sim \unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T/\unicode[STIX]{x1D707}_{o}$
, leading to the following mixed Couette–Poiseuille velocity profile within the gap:
$U_{0}\sim \unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T/\unicode[STIX]{x1D707}_{o}$
, leading to the following mixed Couette–Poiseuille velocity profile within the gap:
After imposing conservation of mass for a control volume within the gap and the kinematic boundary condition
![]() $v_{z}=-{\dot{h}}$
at
$v_{z}=-{\dot{h}}$
at
![]() $z=h$
, one can use the velocity profile to derive an ordinary differential equation (ODE) for the pressure field:
$z=h$
, one can use the velocity profile to derive an ordinary differential equation (ODE) for the pressure field:
where
![]() $\unicode[STIX]{x0394}v=-(v_{d}+v_{b})>0$
regardless of the sign of
$\unicode[STIX]{x0394}v=-(v_{d}+v_{b})>0$
regardless of the sign of
![]() $\unicode[STIX]{x0394}T_{0}$
(Monti et al.
Reference Monti, Savino and Cicala1996). Integrating (3.3) with the boundary condition
$\unicode[STIX]{x0394}T_{0}$
(Monti et al.
Reference Monti, Savino and Cicala1996). Integrating (3.3) with the boundary condition
![]() $p(R_{d})=p_{a}$
yields:
$p(R_{d})=p_{a}$
yields:
The form of the pressure field indicates that the Marangoni flow augments the pressure within the gap, thus resisting the settling of the drop, independent of the sign of
![]() $\unicode[STIX]{x0394}T_{0}$
. Assuming that the drop acceleration is negligible, so that its weight is supported quasistatically by the pressure field, we deduce:
$\unicode[STIX]{x0394}T_{0}$
. Assuming that the drop acceleration is negligible, so that its weight is supported quasistatically by the pressure field, we deduce:
We thus obtain an ODE for the height of the gap
![]() $h(t)$
. We define a dimensionless height
$h(t)$
. We define a dimensionless height
![]() $h^{\star }=h/h_{0}$
, and a dimensionless time
$h^{\star }=h/h_{0}$
, and a dimensionless time
![]() $t^{\star }=t/\unicode[STIX]{x1D70F}_{s}$
, where
$t^{\star }=t/\unicode[STIX]{x1D70F}_{s}$
, where
![]() $\unicode[STIX]{x1D70F}_{s}=9\unicode[STIX]{x1D707}_{a}R_{d}^{4}/(16\unicode[STIX]{x1D70C}_{o}gR^{3}h_{0}^{2})$
is the characteristic settling time that would arise in the absence of thermocapillary effects. A balance between thermocapillary and viscous stresses at the interface allows us to express
$\unicode[STIX]{x1D70F}_{s}=9\unicode[STIX]{x1D707}_{a}R_{d}^{4}/(16\unicode[STIX]{x1D70C}_{o}gR^{3}h_{0}^{2})$
is the characteristic settling time that would arise in the absence of thermocapillary effects. A balance between thermocapillary and viscous stresses at the interface allows us to express
![]() $\unicode[STIX]{x0394}v$
as
$\unicode[STIX]{x0394}v$
as
![]() $\unicode[STIX]{x0394}v=K|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T|/\unicode[STIX]{x1D707}_{o}$
, with
$\unicode[STIX]{x0394}v=K|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T|/\unicode[STIX]{x1D707}_{o}$
, with
![]() $K\sim \mathit{O}(1)$
. In the absence of direct measurements of the surface velocity, we set the constant
$K\sim \mathit{O}(1)$
. In the absence of direct measurements of the surface velocity, we set the constant
![]() $K$
to unity. We thus write the ODE in dimensionless form as:
$K$
to unity. We thus write the ODE in dimensionless form as:
where
![]() $\unicode[STIX]{x1D70F}_{th}=R^{2}/\unicode[STIX]{x1D6FC}_{o}$
is the thermal diffusion time and
$\unicode[STIX]{x1D70F}_{th}=R^{2}/\unicode[STIX]{x1D6FC}_{o}$
is the thermal diffusion time and
![]() $Ma=|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T|R/\unicode[STIX]{x1D707}_{o}\unicode[STIX]{x1D6FC}_{o}$
is the Marangoni number. Under isothermal conditions (
$Ma=|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T|R/\unicode[STIX]{x1D707}_{o}\unicode[STIX]{x1D6FC}_{o}$
is the Marangoni number. Under isothermal conditions (
![]() $Ma=0$
), equation (3.6) yields the well-known solution
$Ma=0$
), equation (3.6) yields the well-known solution
![]() $h^{\star }(t^{\star })=1/\sqrt{1+t^{\star }}$
for squeezing flow between two disks under constant force (Stefan Reference Stefan1874).
$h^{\star }(t^{\star })=1/\sqrt{1+t^{\star }}$
for squeezing flow between two disks under constant force (Stefan Reference Stefan1874).
If
![]() $Ma\neq 0$
, equation (3.6) indicates that there is a critical value
$Ma\neq 0$
, equation (3.6) indicates that there is a critical value
![]() $Ma_{c}$
above which the gap height does not decrease in time. Using values of fluid properties listed in § 2.1 and an estimated initial height of
$Ma_{c}$
above which the gap height does not decrease in time. Using values of fluid properties listed in § 2.1 and an estimated initial height of
![]() $h_{0}=1.5~\unicode[STIX]{x03BC}\text{m}$
(Monti & Savino Reference Monti and Savino1997) we obtain
$h_{0}=1.5~\unicode[STIX]{x03BC}\text{m}$
(Monti & Savino Reference Monti and Savino1997) we obtain
![]() $\unicode[STIX]{x1D70F}_{s}=0.0078~\text{s}$
and
$\unicode[STIX]{x1D70F}_{s}=0.0078~\text{s}$
and
![]() $\unicode[STIX]{x1D70F}_{th}=5.14~\text{s}$
, which gives
$\unicode[STIX]{x1D70F}_{th}=5.14~\text{s}$
, which gives
![]() $Ma_{c}=3\unicode[STIX]{x1D70F}_{th}R_{d}/(8\unicode[STIX]{x1D70F}_{s}R)\simeq 100$
, in good agreement with the experimental results. The value of
$Ma_{c}=3\unicode[STIX]{x1D70F}_{th}R_{d}/(8\unicode[STIX]{x1D70F}_{s}R)\simeq 100$
, in good agreement with the experimental results. The value of
![]() $Ma_{c}$
can be used to estimate
$Ma_{c}$
can be used to estimate
![]() $\unicode[STIX]{x0394}T_{c}$
for any viscosity. In particular, for
$\unicode[STIX]{x0394}T_{c}$
for any viscosity. In particular, for
![]() $\unicode[STIX]{x1D708}_{o}=5~\text{cSt}$
the critical temperature difference is
$\unicode[STIX]{x1D708}_{o}=5~\text{cSt}$
the critical temperature difference is
![]() $\unicode[STIX]{x0394}T_{c}=Ma_{c}\unicode[STIX]{x1D707}_{o}\unicode[STIX]{x1D6FC}_{o}/\unicode[STIX]{x1D70E}_{T}R\simeq 1\,^{\circ }\text{C}$
, in agreement with our experiments, while for
$\unicode[STIX]{x0394}T_{c}=Ma_{c}\unicode[STIX]{x1D707}_{o}\unicode[STIX]{x1D6FC}_{o}/\unicode[STIX]{x1D70E}_{T}R\simeq 1\,^{\circ }\text{C}$
, in agreement with our experiments, while for
![]() $\unicode[STIX]{x1D708}_{o}=500~\text{cSt}$
,
$\unicode[STIX]{x1D708}_{o}=500~\text{cSt}$
,
![]() $\unicode[STIX]{x0394}T_{c}\simeq 115\,^{\circ }\text{C}$
, which is well beyond the maximum accessible
$\unicode[STIX]{x0394}T_{c}\simeq 115\,^{\circ }\text{C}$
, which is well beyond the maximum accessible
![]() $\unicode[STIX]{x0394}T_{0}$
and so again consistent with our experiments. We further note that the exact value of
$\unicode[STIX]{x0394}T_{0}$
and so again consistent with our experiments. We further note that the exact value of
![]() $Ma_{c}$
depends on the quantities
$Ma_{c}$
depends on the quantities
![]() $h_{0}$
and
$h_{0}$
and
![]() $K$
, which have only been estimated here. Precise measurements of both would be required for a more accurate estimate of
$K$
, which have only been estimated here. Precise measurements of both would be required for a more accurate estimate of
![]() $Ma_{c}$
.
$Ma_{c}$
.
3.2 Mixing and its effect on the residence time
The flow induced by Marangoni stresses acting on the air within the gap accounts for the existence of a critical Marangoni number. To rationalize the dependence of the thermal delay time on
![]() $\unicode[STIX]{x0394}T_{0}$
, we need to estimate the time required for such stresses to diminish, i.e. for temperature differences to decrease such that
$\unicode[STIX]{x0394}T_{0}$
, we need to estimate the time required for such stresses to diminish, i.e. for temperature differences to decrease such that
![]() $Ma<Ma_{c}$
. Formally, this requires the combined solution of the energy equation and the Navier–Stokes equations. However, a relatively expedient route may be found with appropriate simplifications.
$Ma<Ma_{c}$
. Formally, this requires the combined solution of the energy equation and the Navier–Stokes equations. However, a relatively expedient route may be found with appropriate simplifications.
Figure 5. (a) Streamlines (blue) and velocity field (red) of the potential flow solution corresponding to Hill’s spherical vortex. (b) Simulation of a fluid element being deformed and convected with the assumed potential flow (with
![]() $\unicode[STIX]{x0394}T_{0}=10\,^{\circ }\text{C}$
,
$\unicode[STIX]{x0394}T_{0}=10\,^{\circ }\text{C}$
,
![]() $\unicode[STIX]{x1D708}_{o}=5~\text{cSt}$
, see also movie 6). The accompanying schematic indicates the reference system of (3.9). (c) Predicted decay of temperature obtained through (3.12) for
$\unicode[STIX]{x1D708}_{o}=5~\text{cSt}$
, see also movie 6). The accompanying schematic indicates the reference system of (3.9). (c) Predicted decay of temperature obtained through (3.12) for
![]() $\unicode[STIX]{x0394}T_{0}=26\,^{\circ }\text{C}$
and
$\unicode[STIX]{x0394}T_{0}=26\,^{\circ }\text{C}$
and
![]() $\unicode[STIX]{x1D708}_{o}=5~\text{cSt}$
(solid black line). Approximation of the solution for early times (
$\unicode[STIX]{x1D708}_{o}=5~\text{cSt}$
(solid black line). Approximation of the solution for early times (
![]() $t\rightarrow 0$
, solid blue line) and for long times (
$t\rightarrow 0$
, solid blue line) and for long times (
![]() $t>\sqrt{3}/\dot{\unicode[STIX]{x1D6FE}}$
, dashed red line).
$t>\sqrt{3}/\dot{\unicode[STIX]{x1D6FE}}$
, dashed red line).
Figure 2(c) provides direct evidence of convection and the resulting thermal homogenization by highlighting the recirculating flow inside the drop prior to coalescence. Assuming that the characteristic velocity is that of the interface
![]() $U_{0}\sim |\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T_{0}|/\unicode[STIX]{x1D707}_{o}$
, one obtains an estimate of the convective time scale
$U_{0}\sim |\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T_{0}|/\unicode[STIX]{x1D707}_{o}$
, one obtains an estimate of the convective time scale
![]() $\unicode[STIX]{x1D70F}_{conv}\sim R/U_{0}\sim R\unicode[STIX]{x1D707}_{o}/|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T_{0}|\sim \unicode[STIX]{x1D70F}_{th}/Ma_{0}$
. Given that
$\unicode[STIX]{x1D70F}_{conv}\sim R/U_{0}\sim R\unicode[STIX]{x1D707}_{o}/|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T_{0}|\sim \unicode[STIX]{x1D70F}_{th}/Ma_{0}$
. Given that
![]() $Ma_{0}\geqslant Ma_{c}\simeq 100$
, we infer that
$Ma_{0}\geqslant Ma_{c}\simeq 100$
, we infer that
![]() $\unicode[STIX]{x1D70F}_{conv}\ll \unicode[STIX]{x1D70F}_{th}$
so that convection dominates in the initial stages of thermalization. This suggests that when the drop gets close to the bath its lower extremities are warmed up (or cooled down, depending on the sign of
$\unicode[STIX]{x1D70F}_{conv}\ll \unicode[STIX]{x1D70F}_{th}$
so that convection dominates in the initial stages of thermalization. This suggests that when the drop gets close to the bath its lower extremities are warmed up (or cooled down, depending on the sign of
![]() $\unicode[STIX]{x0394}T_{0}$
) and a poloidal convective motion is established that rapidly transports these fluid elements while deforming them into elongated filaments, or lamellae. Only on longer time scales does thermal diffusion become effective and the drop equilibrate thermally.
$\unicode[STIX]{x0394}T_{0}$
) and a poloidal convective motion is established that rapidly transports these fluid elements while deforming them into elongated filaments, or lamellae. Only on longer time scales does thermal diffusion become effective and the drop equilibrate thermally.
A mathematical framework to study related advection–diffusion problems has been developed in the context of mixing by Ottino, Ranz & Macosko (Reference Ottino, Ranz and Macosko1979) and Ranz (Reference Ranz1979), and recently applied by Meunier & Villermaux (Reference Meunier and Villermaux2003) to describe scalar mixing in an axisymmetric vortex flow. In the following, we apply this method to the case of thermal homogenization within the drop, assuming that a roughly symmetric process is also taking place in the bath (Savino et al.
Reference Savino, Paterna and Lappa2003). We assume that the velocity field is expressible in terms of the Hill’s spherical vortex (Batchelor Reference Batchelor1967, p. 237). Defining a dimensionless velocity field as
![]() $\boldsymbol{v}^{\star }=\boldsymbol{v}/\bar{U}$
, where
$\boldsymbol{v}^{\star }=\boldsymbol{v}/\bar{U}$
, where
![]() $\bar{U}$
is a characteristic velocity proportional to
$\bar{U}$
is a characteristic velocity proportional to
![]() $U_{0}$
and a dimensionless radial coordinate as
$U_{0}$
and a dimensionless radial coordinate as
![]() $r^{\star }=r/R$
, the dimensionless velocity components for this potential flow are
$r^{\star }=r/R$
, the dimensionless velocity components for this potential flow are
![]() $v_{r}^{\star }=-(1-r^{\star \,2})\cos \unicode[STIX]{x1D703}$
and
$v_{r}^{\star }=-(1-r^{\star \,2})\cos \unicode[STIX]{x1D703}$
and
![]() $v_{\unicode[STIX]{x1D703}}^{\star }=(1-2r^{\star \,2})\sin \unicode[STIX]{x1D703}$
, which are plotted together with the streamlines (
$v_{\unicode[STIX]{x1D703}}^{\star }=(1-2r^{\star \,2})\sin \unicode[STIX]{x1D703}$
, which are plotted together with the streamlines (
![]() $\unicode[STIX]{x1D713}^{\star }=1/2(r^{\star \,2}-1)r^{\star \,2}\sin ^{2}\unicode[STIX]{x1D703}=\text{const.}$
) in figure 5(a). From these expressions, we compute the dimensionless strain rate tensor within the drop:
$\unicode[STIX]{x1D713}^{\star }=1/2(r^{\star \,2}-1)r^{\star \,2}\sin ^{2}\unicode[STIX]{x1D703}=\text{const.}$
) in figure 5(a). From these expressions, we compute the dimensionless strain rate tensor within the drop:
Accounting for the evident spatial variations would substantially complicate the analysis; hence, we consider an average flow by performing an area-weighted average of the local shear rate tensor over all angles
![]() $\unicode[STIX]{x1D703}$
in the range
$\unicode[STIX]{x1D703}$
in the range
![]() $[0,\unicode[STIX]{x03C0}]$
, obtaining
$[0,\unicode[STIX]{x03C0}]$
, obtaining
Equation (3.8) suggests that, on average, each element of fluid undergoes a shearing deformation. To find the dimensional average shear rate
![]() $\dot{\unicode[STIX]{x1D6FE}}$
we consider the shear rate at the interface to be that imposed by the gradient in surface tension,
$\dot{\unicode[STIX]{x1D6FE}}$
we consider the shear rate at the interface to be that imposed by the gradient in surface tension,
![]() $\dot{\unicode[STIX]{x1D6FE}}_{R}=(\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})/2\unicode[STIX]{x1D707}_{o}R=|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T|/2R\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}_{o}$
. Computing the maximum shear rate at the interface (
$\dot{\unicode[STIX]{x1D6FE}}_{R}=(\unicode[STIX]{x2202}\unicode[STIX]{x1D70E}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})/2\unicode[STIX]{x1D707}_{o}R=|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T|/2R\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}_{o}$
. Computing the maximum shear rate at the interface (
![]() $r^{\star }=1$
,
$r^{\star }=1$
,
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
) from (3.7), we deduce
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$
) from (3.7), we deduce
![]() $\bar{U}=U_{0}/3\unicode[STIX]{x03C0}$
and
$\bar{U}=U_{0}/3\unicode[STIX]{x03C0}$
and
![]() $\dot{\unicode[STIX]{x1D6FE}}=U_{0}/(3\unicode[STIX]{x03C0}^{2}R)$
. Following the method introduced by Ottino et al. (Reference Ottino, Ranz and Macosko1979), we write the energy equation in the frame of reference (
$\dot{\unicode[STIX]{x1D6FE}}=U_{0}/(3\unicode[STIX]{x03C0}^{2}R)$
. Following the method introduced by Ottino et al. (Reference Ottino, Ranz and Macosko1979), we write the energy equation in the frame of reference (
![]() $X,Y$
) of a material element that is convected and deformed as shown in figure 5(b). Neglecting variations in the
$X,Y$
) of a material element that is convected and deformed as shown in figure 5(b). Neglecting variations in the
![]() $X$
-direction, we write:
$X$
-direction, we write:
The velocity field
![]() $V$
can be written in terms of the thickness of the lamella
$V$
can be written in terms of the thickness of the lamella
![]() $s(t)$
based on the rate of stretching
$s(t)$
based on the rate of stretching
![]() $\dot{\unicode[STIX]{x1D716}}=\text{d}\ln s(t)/\text{d}t$
as
$\dot{\unicode[STIX]{x1D716}}=\text{d}\ln s(t)/\text{d}t$
as
![]() $V=\dot{\unicode[STIX]{x1D716}}Y$
. For a flow dominated by shear,
$V=\dot{\unicode[STIX]{x1D716}}Y$
. For a flow dominated by shear,
![]() $s(t)=s_{0}/\sqrt{1+\dot{\unicode[STIX]{x1D6FE}}^{2}t^{2}}$
, where
$s(t)=s_{0}/\sqrt{1+\dot{\unicode[STIX]{x1D6FE}}^{2}t^{2}}$
, where
![]() $s_{0}$
is the initial size of the blob of fluid that has been warmed up (or cooled down) to a temperature close to
$s_{0}$
is the initial size of the blob of fluid that has been warmed up (or cooled down) to a temperature close to
![]() $T_{b}$
as the drop approaches the bath. An estimate of
$T_{b}$
as the drop approaches the bath. An estimate of
![]() $s_{0}$
can be derived by considering that convection can be induced only when a temperature gradient is established on the drop surface. Consequently,
$s_{0}$
can be derived by considering that convection can be induced only when a temperature gradient is established on the drop surface. Consequently,
![]() $s_{0}$
is prescribed by the local balance, at early times, between diffusion from the bath, at a rate
$s_{0}$
is prescribed by the local balance, at early times, between diffusion from the bath, at a rate
![]() $\unicode[STIX]{x1D6FC}_{o}/(\text{d}\ell )^{2}$
with
$\unicode[STIX]{x1D6FC}_{o}/(\text{d}\ell )^{2}$
with
![]() $\text{d}\ell \sim \sqrt{\unicode[STIX]{x1D6FC}_{o}t}$
independent of the temperature difference, and deformation by Marangoni stresses, at a rate
$\text{d}\ell \sim \sqrt{\unicode[STIX]{x1D6FC}_{o}t}$
independent of the temperature difference, and deformation by Marangoni stresses, at a rate
![]() $|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T_{0}|/(\unicode[STIX]{x1D707}_{o}s_{0})$
. When
$|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T_{0}|/(\unicode[STIX]{x1D707}_{o}s_{0})$
. When
![]() $|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T_{0}|/(\unicode[STIX]{x1D707}_{o}s_{0})\geqslant \unicode[STIX]{x1D6FC}_{o}/(\text{d}\ell )^{2}$
, that is for
$|\unicode[STIX]{x1D70E}_{T}\unicode[STIX]{x0394}T_{0}|/(\unicode[STIX]{x1D707}_{o}s_{0})\geqslant \unicode[STIX]{x1D6FC}_{o}/(\text{d}\ell )^{2}$
, that is for
![]() $s_{0}\simeq Ma_{0}(\text{d}\ell )^{2}/R$
, the fluid blob will start moving. As convection is established, this initial blob of fluid at
$s_{0}\simeq Ma_{0}(\text{d}\ell )^{2}/R$
, the fluid blob will start moving. As convection is established, this initial blob of fluid at
![]() $T\sim T_{b}$
is stretched into a thin lamella that is wrapped around the drop (see movie 6). Ultimately, the drop is characterized by a series of alternating warm and cold layers.
$T\sim T_{b}$
is stretched into a thin lamella that is wrapped around the drop (see movie 6). Ultimately, the drop is characterized by a series of alternating warm and cold layers.
By changing variables such that
![]() $\unicode[STIX]{x1D709}=Y/s(t)$
and
$\unicode[STIX]{x1D709}=Y/s(t)$
and
![]() $\unicode[STIX]{x1D70F}=\int _{0}^{t}\unicode[STIX]{x1D6FC}_{o}/s^{2}(t^{\prime })\,\text{d}t^{\prime }$
, we can reduce (3.9) to:
$\unicode[STIX]{x1D70F}=\int _{0}^{t}\unicode[STIX]{x1D6FC}_{o}/s^{2}(t^{\prime })\,\text{d}t^{\prime }$
, we can reduce (3.9) to:
where
![]() $\unicode[STIX]{x1D703}=(T_{b}-T)/\unicode[STIX]{x0394}T_{0}$
and
$\unicode[STIX]{x1D703}=(T_{b}-T)/\unicode[STIX]{x0394}T_{0}$
and
![]() $\unicode[STIX]{x1D709}\in [-1/2,1/2]$
. The change of variables effectively rescales the convection–diffusion equation in order to capture the correct length and time scales over which thermalization acts, specifically those of a stretching and thinning lamella. By definition, convection dominates diffusion when
$\unicode[STIX]{x1D709}\in [-1/2,1/2]$
. The change of variables effectively rescales the convection–diffusion equation in order to capture the correct length and time scales over which thermalization acts, specifically those of a stretching and thinning lamella. By definition, convection dominates diffusion when
![]() $\unicode[STIX]{x1D70F}\ll 1$
. As
$\unicode[STIX]{x1D70F}\ll 1$
. As
![]() $\unicode[STIX]{x1D70F}$
approaches
$\unicode[STIX]{x1D70F}$
approaches
![]() $\mathit{O}(1)$
, the two become comparable so that conduction across the lamella becomes important.
$\mathit{O}(1)$
, the two become comparable so that conduction across the lamella becomes important.
To characterize the thermal equilibration of the drop, we solve (3.10) from the perspective of a lamella originally at
![]() $T_{d}$
, in contact at its boundaries with fluid at
$T_{d}$
, in contact at its boundaries with fluid at
![]() $T_{b}$
. In terms of dimensionless quantities this means that
$T_{b}$
. In terms of dimensionless quantities this means that
![]() $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70F}=0)=1$
inside the lamella (for
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70F}=0)=1$
inside the lamella (for
![]() $|\unicode[STIX]{x1D709}|<1/2$
), and
$|\unicode[STIX]{x1D709}|<1/2$
), and
![]() $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70F}=0)=0$
outside (for
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D70F}=0)=0$
outside (for
![]() $|\unicode[STIX]{x1D709}|>1/2$
). The resulting analytical solution of (3.10) thus emerges:
$|\unicode[STIX]{x1D709}|>1/2$
). The resulting analytical solution of (3.10) thus emerges:
From (3.11) we can compute the evolution of the maximum temperature difference arising at the centre of the lamella
![]() $\unicode[STIX]{x1D709}=0$
:
$\unicode[STIX]{x1D709}=0$
:
Equation (3.12) is plotted in figure 5(c) for the case of
![]() $\unicode[STIX]{x0394}T_{0}=26\,^{\circ }\text{C}$
and
$\unicode[STIX]{x0394}T_{0}=26\,^{\circ }\text{C}$
and
![]() $\unicode[STIX]{x1D708}_{o}=5~\text{cSt}$
. The temperature difference is initially constant since fluid elements are first convected and deformed into lamellae before diffusion becomes significant. When
$\unicode[STIX]{x1D708}_{o}=5~\text{cSt}$
. The temperature difference is initially constant since fluid elements are first convected and deformed into lamellae before diffusion becomes significant. When
![]() $4\sqrt{\unicode[STIX]{x1D70F}}\sim 1$
, thermal diffusion acts effectively across the thickness of the lamella, altering the local temperature and ultimately leading to thermal homogenization of the drop. At long times (3.12) shows that
$4\sqrt{\unicode[STIX]{x1D70F}}\sim 1$
, thermal diffusion acts effectively across the thickness of the lamella, altering the local temperature and ultimately leading to thermal homogenization of the drop. At long times (3.12) shows that
![]() $\unicode[STIX]{x0394}T(t)_{lamella}\sim \unicode[STIX]{x0394}T_{0}\sqrt{3/(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FC}_{o})}(s_{0}/(\dot{\unicode[STIX]{x1D6FE}}t^{3/2}))$
. This suggests that the delay time should scale as
$\unicode[STIX]{x0394}T(t)_{lamella}\sim \unicode[STIX]{x0394}T_{0}\sqrt{3/(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FC}_{o})}(s_{0}/(\dot{\unicode[STIX]{x1D6FE}}t^{3/2}))$
. This suggests that the delay time should scale as
![]() $\unicode[STIX]{x1D70F}_{d}\sim \unicode[STIX]{x0394}T_{0}^{2/3}\sim Ma_{0}^{2/3}$
. We note that the same scaling applies provided the kinematics of the flow field do not have elongational characteristics such that fluid elements separate exponentially quickly in time.
$\unicode[STIX]{x1D70F}_{d}\sim \unicode[STIX]{x0394}T_{0}^{2/3}\sim Ma_{0}^{2/3}$
. We note that the same scaling applies provided the kinematics of the flow field do not have elongational characteristics such that fluid elements separate exponentially quickly in time.
Using (3.12) for a fixed viscosity, we can obtain an estimate for the delay time as a function of
![]() $\unicode[STIX]{x0394}T_{0}$
. We expect the temperature difference across a lamella before coalescence (at
$\unicode[STIX]{x0394}T_{0}$
. We expect the temperature difference across a lamella before coalescence (at
![]() $t\simeq \unicode[STIX]{x1D70F}_{d}$
) to be comparable to the critical temperature difference measured for the entire drop at uniform temperature, i.e.
$t\simeq \unicode[STIX]{x1D70F}_{d}$
) to be comparable to the critical temperature difference measured for the entire drop at uniform temperature, i.e.
![]() $\unicode[STIX]{x0394}T_{lamella}(\unicode[STIX]{x1D70F}_{d})=\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}T_{c}$
with
$\unicode[STIX]{x0394}T_{lamella}(\unicode[STIX]{x1D70F}_{d})=\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}T_{c}$
with
![]() $\unicode[STIX]{x1D6FD}\sim \mathit{O}(1)$
. The resulting estimate for the delay time
$\unicode[STIX]{x1D6FD}\sim \mathit{O}(1)$
. The resulting estimate for the delay time
![]() $\unicode[STIX]{x1D70F}_{d}$
obtained by solving this nonlinear equation is shown in figure 4(b) with a solid curve computed with
$\unicode[STIX]{x1D70F}_{d}$
obtained by solving this nonlinear equation is shown in figure 4(b) with a solid curve computed with
![]() $\unicode[STIX]{x1D6FD}=1/4$
. Comparison with the data shows that, notwithstanding the simplifying assumptions, our analytical model effectively captures the main physical phenomena, rationalizing the observed dependence of
$\unicode[STIX]{x1D6FD}=1/4$
. Comparison with the data shows that, notwithstanding the simplifying assumptions, our analytical model effectively captures the main physical phenomena, rationalizing the observed dependence of
![]() $\unicode[STIX]{x1D70F}_{d}$
on
$\unicode[STIX]{x1D70F}_{d}$
on
![]() $Ma_{0}$
. Finally, we note that a closed form for
$Ma_{0}$
. Finally, we note that a closed form for
![]() $\unicode[STIX]{x1D70F}_{d}$
can be obtained from
$\unicode[STIX]{x1D70F}_{d}$
can be obtained from
![]() $\unicode[STIX]{x0394}T_{lamella}(\unicode[STIX]{x1D70F}_{d})=\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}T_{c}$
in the limit
$\unicode[STIX]{x0394}T_{lamella}(\unicode[STIX]{x1D70F}_{d})=\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}T_{c}$
in the limit
![]() $t>\sqrt{3}/\dot{\unicode[STIX]{x1D6FE}}$
. In this case we have
$t>\sqrt{3}/\dot{\unicode[STIX]{x1D6FE}}$
. In this case we have
![]() $\tilde{\unicode[STIX]{x1D70F}}_{d}=(\sqrt{3}\unicode[STIX]{x0394}T_{0}s_{0}/(\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FC}_{o}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}T_{c}\dot{\unicode[STIX]{x1D6FE}}))^{2/3}$
, as shown as a dashed line in figure 4(b). As
$\tilde{\unicode[STIX]{x1D70F}}_{d}=(\sqrt{3}\unicode[STIX]{x0394}T_{0}s_{0}/(\sqrt{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FC}_{o}}\unicode[STIX]{x1D6FD}\unicode[STIX]{x0394}T_{c}\dot{\unicode[STIX]{x1D6FE}}))^{2/3}$
, as shown as a dashed line in figure 4(b). As
![]() $Ma_{0}\rightarrow Ma_{c}$
, this approximation is no longer valid because it is based on the neglect of the linear term in
$Ma_{0}\rightarrow Ma_{c}$
, this approximation is no longer valid because it is based on the neglect of the linear term in
![]() $t$
in (3.12) that becomes significant for small
$t$
in (3.12) that becomes significant for small
![]() $\dot{\unicode[STIX]{x1D6FE}}$
.
$\dot{\unicode[STIX]{x1D6FE}}$
.
4 Summary and conclusions
We have investigated the role of temperature differences between drop and bath in delaying drop coalescence. Experiments indicate a minimum temperature difference, dependent on the oil viscosity, below which no appreciable difference with the isothermal case exists and above which the residence time increases as a function of the initial temperature difference. We have demonstrated that the observed behaviour is described by a unique curve: above a critical Marangoni number
![]() $Ma_{c}$
the delay time
$Ma_{c}$
the delay time
![]() $\unicode[STIX]{x1D70F}_{d}$
increases as
$\unicode[STIX]{x1D70F}_{d}$
increases as
![]() $\unicode[STIX]{x1D70F}_{d}/\unicode[STIX]{x1D70F}_{th}\sim (Ma_{0}-Ma_{c})^{2/3}$
.
$\unicode[STIX]{x1D70F}_{d}/\unicode[STIX]{x1D70F}_{th}\sim (Ma_{0}-Ma_{c})^{2/3}$
.
By analysing the lubrication air flow within the gap, we have shown that the critical Marangoni number is prescribed by the minimum velocity that must be established for the pressure field, induced by the recirculating air flow within the gap, to sustain the drop’s weight. Due to the symmetry of the pressure field, the effect is independent of the sign of
![]() $\unicode[STIX]{x0394}T_{0}$
, as indicated by our experiments. By considering the kinematics of thermal mixing in a frame deforming with the fluid elements, we have calculated the characteristic time scale for thermal homogenization within the drop, rationalizing the observed dependence of
$\unicode[STIX]{x0394}T_{0}$
, as indicated by our experiments. By considering the kinematics of thermal mixing in a frame deforming with the fluid elements, we have calculated the characteristic time scale for thermal homogenization within the drop, rationalizing the observed dependence of
![]() $\unicode[STIX]{x1D70F}_{d}$
on
$\unicode[STIX]{x1D70F}_{d}$
on
![]() $Ma_{0}$
(and therefore on
$Ma_{0}$
(and therefore on
![]() $\unicode[STIX]{x0394}T_{0}$
).
$\unicode[STIX]{x0394}T_{0}$
).
Our study suggests that a similar formulation can be applied to the case of drop flotation (Savino et al. Reference Savino, Paterna and Lappa2003) and also to the case of impinging drops (Dell’Aversana et al. Reference Dell’Aversana, Banavar and Koplik1996) provided the drop weight is replaced by the applied load. The onset of the coalescence cascade should be delayed but otherwise largely unaffected by an initial temperature difference between the mother droplet and the bath. Once the first drop has coalesced, following the thermal mixing process elucidated here, the temperature of its daughter droplets should be comparable to that of the bath. Finally, we note that thermally delayed drop coalescence may prove useful in levitating drops on vibrating baths (Bush Reference Bush2015).
Acknowledgements
J.B. thanks the NSF for financial support through grants CMMI-1727565 and DMS-1614043, while M.G. and G.H.M. gratefully acknowledge the MIT Energy Initiative and Chevron ETC. M.G. thanks Professor A. E. (Peko) Hosoi for her encouragement and enthusiasm.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2017.686.