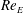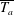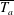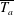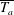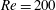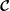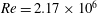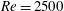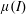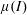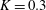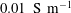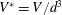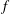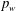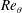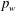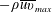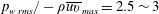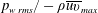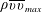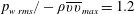Papers
Shallow-water models for a vibrating fluid
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 1-28
-
- Article
- Export citation
The role of surface charge convection in the electrohydrodynamics and breakup of prolate drops
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 29-53
-
- Article
- Export citation
Molecular dynamics study of multicomponent droplet dissolution in a sparingly miscible liquid
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 54-69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Development of gravity currents on rapidly changing slopes
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 70-97
-
- Article
- Export citation
Flow-induced vibration of two cylinders in tandem and staggered arrangements
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 98-130
-
- Article
- Export citation
Tilted incompressible Coriolis modes in spheroids
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 131-163
-
- Article
- Export citation
Conditioning of cross-flow instability modes using dielectric barrier discharge plasma actuators
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 164-205
-
- Article
- Export citation
Revisiting ignited–quenched transition and the non-Newtonian rheology of a sheared dilute gas–solid suspension
-
- Published online by Cambridge University Press:
- 03 November 2017, pp. 206-246
-
- Article
- Export citation
Numerical analysis of high speed wind tunnel flow disturbance measurements using stagnation point probes
-
- Published online by Cambridge University Press:
- 03 November 2017, pp. 247-273
-
- Article
- Export citation
Relative periodic orbits form the backbone of turbulent pipe flow
-
- Published online by Cambridge University Press:
- 06 November 2017, pp. 274-301
-
- Article
- Export citation
On the stability of the μ(I) rheology for granular flow
-
- Published online by Cambridge University Press:
- 03 November 2017, pp. 302-331
-
- Article
- Export citation
Richtmyer–Meshkov instability of a thermal interface in a two-fluid plasma
-
- Published online by Cambridge University Press:
- 03 November 2017, pp. 332-363
-
- Article
- Export citation
Coherent clusters of inertial particles in homogeneous turbulence
-
- Published online by Cambridge University Press:
- 03 November 2017, pp. 364-398
-
- Article
- Export citation
Recovering water wave elevation from pressure measurements
-
- Published online by Cambridge University Press:
- 06 November 2017, pp. 399-429
-
- Article
- Export citation
Effect of a homogeneous magnetic field on the electrospraying characteristics of sulfolane ferrofluids
-
- Published online by Cambridge University Press:
- 06 November 2017, pp. 430-444
-
- Article
- Export citation
Path instabilities of oblate spheroids
-
- Published online by Cambridge University Press:
- 06 November 2017, pp. 445-468
-
- Article
- Export citation
Inviscid instabilities in rotating ellipsoids on eccentric Kepler orbits
-
- Published online by Cambridge University Press:
- 06 November 2017, pp. 469-511
-
- Article
- Export citation
Wave boundary layers in a stratified fluid
-
- Published online by Cambridge University Press:
- 07 November 2017, pp. 512-537
-
- Article
- Export citation
Oblique internal-wave chain resonance over seabed corrugations
-
- Published online by Cambridge University Press:
- 07 November 2017, pp. 538-562
-
- Article
- Export citation
Reynolds-number dependence of wall-pressure fluctuations in a pressure-induced turbulent separation bubble
-
- Published online by Cambridge University Press:
- 07 November 2017, pp. 563-598
-
- Article
- Export citation