1. Introduction
Fluid–structure-interaction (FSI) studies span a vast and diverse range of applications – from natural phenomenon such as the fluttering of flags (Shelley & Zhang Reference Shelley and Zhang2011), phonation (Heil & Hazel Reference Heil and Hazel2011), blood flow in arteries (Freund Reference Freund2014), path of rising bubbles (Ern et al. Reference Ern, Frédéric, Fabre and Magnaudet2012), to the more engineering applications of aircraft stability (Dowell & Hall Reference Dowell and Hall2001), vortex induced vibrations (Williamson & Govardhan Reference Williamson and Govardhan2004), compliant surfaces (Riley, Gad-el Hak & Metcalfe Reference Riley, Gad-el Hak and Metcalfe1988; Kumaran Reference Kumaran2003) etc. The phenomena that emerge out of an FSI problem often exhibit a highly nonlinear, dynamically rich and complex behaviour with different flow regimes such as fluttering and tumbling of plates falling under gravity (Mittal, Seshadri & Udaykumar Reference Mittal, Seshadri and Udaykumar2004), or the unsteady path of rising bubbles (Mougin & Magnaudet Reference Mougin and Magnaudet2001; Ern et al. Reference Ern, Frédéric, Fabre and Magnaudet2012). Despite its nonlinear nature, the initial transitions from one state to another may often be governed by a linear instability mechanism. The simplified case of a linear instability of a parallel boundary layer over a compliant surface was first derived and investigated by Benjamin (Reference Benjamin1959, Reference Benjamin1960) and Landahl (Reference Landahl1962). For boundary layers over Krammer-type compliant surfaces, the linear hydrodynamic instability study was performed by Carpenter & Garrad (Reference Carpenter and Garrad1985, Reference Carpenter and Garrad1986) using this formulation and subsequently several studies have used the same formulation for studying flow instabilities over flexible surfaces, for example, Carpenter & Morris (Reference Carpenter and Morris1990) and Davies & Carpenter (Reference Davies and Carpenter1997).
When the parallel flow assumption is no longer valid a global approach needs to be taken. From the perspective of global instabilities in FSI problems, the first such study was reported by Cossu & Morino (Reference Cossu and Morino2000) for the instability of a spring-mounted cylinder. The authors considered a rigid two-dimensional cylinder that was free to oscillate in the cross-stream direction, subject to the action of a spring-mass-damper system. The linearized equations were solved in a non-inertial frame of reference attached to the cylinder. For low (solid to fluid) mass density ratios, the authors report that the critical Reynolds number for vortex shedding drops to ![]() $Re_{c}\approx 23$. Mittal & Singh (Reference Mittal and Singh2005) also reported a similarly low critical
$Re_{c}\approx 23$. Mittal & Singh (Reference Mittal and Singh2005) also reported a similarly low critical ![]() $Re$ for a cylinder oscillating in both streamwise and transverse directions. A non-inertial reference is also used by Navrose & Mittal (Reference Navrose and Mittal2016) to study the lock-in phenomenon of cylinders oscillating in cross-stream through the linear stability analysis. More recently, Magnaudet and co-workers approached the problem of rising and falling bodies through the perspective of linear instability. Fabre, Assemat & Magnaudet (Reference Fabre, Assemat and Magnaudet2011) developed a quasi-static model to describe the stability of heavy bodies falling in a viscous fluid. Assemat, Fabre & Magnaudet (Reference Assemat, Fabre and Magnaudet2012) performed a linear study of thin and thick two-dimensional plates falling under gravity. The problem is again formulated in a non-inertial frame of reference of the moving body undergoing both translation and rotation. The authors showed a quantitative agreement between the quasi-static model of Fabre et al. (Reference Fabre, Assemat and Magnaudet2011) and the linear stability results for high mass-ratio cases, although the agreement systematically deteriorated as the mass ratio was reduced. Tchoufag, Fabre & Magnaudet (Reference Tchoufag, Fabre and Magnaudet2014a) performed similar studies for three-dimensional disks and thin cylinders, Tchoufag, Magnaudet & Fabre (Reference Tchoufag, Magnaudet and Fabre2014b) applied the linear stability analysis to spheroidal bubbles and Cano-Lozano et al. (Reference Cano-Lozano, Tchoufag, Magnaudet and Martínez-Bazán2016) to oblate bubbles.
$Re$ for a cylinder oscillating in both streamwise and transverse directions. A non-inertial reference is also used by Navrose & Mittal (Reference Navrose and Mittal2016) to study the lock-in phenomenon of cylinders oscillating in cross-stream through the linear stability analysis. More recently, Magnaudet and co-workers approached the problem of rising and falling bodies through the perspective of linear instability. Fabre, Assemat & Magnaudet (Reference Fabre, Assemat and Magnaudet2011) developed a quasi-static model to describe the stability of heavy bodies falling in a viscous fluid. Assemat, Fabre & Magnaudet (Reference Assemat, Fabre and Magnaudet2012) performed a linear study of thin and thick two-dimensional plates falling under gravity. The problem is again formulated in a non-inertial frame of reference of the moving body undergoing both translation and rotation. The authors showed a quantitative agreement between the quasi-static model of Fabre et al. (Reference Fabre, Assemat and Magnaudet2011) and the linear stability results for high mass-ratio cases, although the agreement systematically deteriorated as the mass ratio was reduced. Tchoufag, Fabre & Magnaudet (Reference Tchoufag, Fabre and Magnaudet2014a) performed similar studies for three-dimensional disks and thin cylinders, Tchoufag, Magnaudet & Fabre (Reference Tchoufag, Magnaudet and Fabre2014b) applied the linear stability analysis to spheroidal bubbles and Cano-Lozano et al. (Reference Cano-Lozano, Tchoufag, Magnaudet and Martínez-Bazán2016) to oblate bubbles.
In general, linear FSI investigations have largely followed one of two methodologies. Either through the parallel flow approach or through frames of reference attached to the rigid body in motion. There are a few exceptions to this. Lesoinne et al. (Reference Lesoinne, Sarkis, Hetmaniuk and Farhat2001) formulated the linear FSI problem in the arbitrary-Eulerian–Lagrangian (ALE) form of the inviscid Navier–Stokes where they treated the grid velocity as a pseudo-variable. Fanion, Fernández & Le Tallec (Reference Fanion, Fernández and Le Tallec2000) derived a more general formulation starting from the ALE equations in the weak form, which has been used by Fernández & Le Tallec (Reference Fernández and Le Tallec2003a,Reference Fernández and Le Tallecb). The authors derive a formulation independent of the fluid grid velocity, but both the boundary conditions and the fluid stresses at the FSI interface are modified. The velocity continuity boundary condition transforms to a transpiration boundary condition while additional stress terms at the interface are obtained comprising of higher-order derivatives of the base flow. These additional stresses have been termed as ‘added stiffness’ terms (Fernández & Le Tallec Reference Fernández and Le Tallec2003a,Reference Fernández and Le Tallecb). Goza, Colonius & Sader (Reference Goza, Colonius and Sader2018) used an immersed boundary method for the global stability analysis of inverted flag flapping. In a very recent development, Pfister, Marquet & Carini (Reference Pfister, Marquet and Carini2019) also derived the linear FSI formulation with the ALE framework. In their formulation the fluid and structural quantities are solved on the moving material points. The standard Navier–Stokes and divergence equations are therefore modified to account for the motion of the material points. Using this formulation on moving material points, the authors have investigated several different FSI problems including ones with nonlinear structural models, elastic flutter instabilities and finite aspect ratio structures (Pfister et al. Reference Pfister, Marquet and Carini2019; Pfister & Marquet Reference Pfister and Marquet2020).
In the current work we follow the methodology of Fanion et al. (Reference Fanion, Fernández and Le Tallec2000) and Fernández & Le Tallec (Reference Fernández and Le Tallec2003a) which, in spirit, is similar to the methodology used by Benjamin (Reference Benjamin1960) and Landahl (Reference Landahl1962) for compliant wall cases. However, unlike Fanion et al. (Reference Fanion, Fernández and Le Tallec2000) we proceed with the linearization of the equations in their strong form. The final expressions for the linearized equations are all evaluated on a stationary grid (Eulerian formulation). The resulting expressions for the linearized FSI problem are very similar to the ones obtained by Fanion et al. (Reference Fanion, Fernández and Le Tallec2000); however, some crucial differences arise for the stresses at the interface. The ‘added stiffness’ terms arising in the work of Fanion et al. (Reference Fanion, Fernández and Le Tallec2000) are shown to vanish at first order. While we invoke no special assumptions for the linearization of the fluid equations (other than small-amplitude perturbations), the current capabilities of our numerical solver limits the class of FSI problems that can be validated. Therefore, we confine the focus of the current work to FSI problems undergoing rigid-body motion and defer a more general formulation and validation to future work. The derived formulation for rigid-body linear FSI is numerically validated by comparing linear and nonlinear evolution of different cases which are started from the same base flow state, perturbed by identical small-amplitude disturbances. It is shown that the linear and nonlinear simulations evolve nearly identically through several orders of magnitude of growth of the perturbations. The nonlinear cases eventually reach a saturated state while the linear simulations continue with the exponential growth. The derived equations are then used to investigate the instability of an oscillating cylinder at subcritical Reynolds numbers, for an ellipse in both pure translation and pure rotation, and for the case of symmetry breaking in a cylinder with an attached splitter plate. Finally, in § 4 we investigate the structural sensitivity of the least stable eigenvalue in the coupled FSI problem of an oscillating cylinder at ![]() $Re=50$, with varying structural parameters.
$Re=50$, with varying structural parameters.
The remainder of the paper is organized as follows. In § 2 we describe the problem in a general setting and derive the linearized equations for a FSI problem for rigid-body motion. Numerical validation and results for the derived formulation are presented in § 3. In § 4 we introduce the adjoint problem for the linear FSI system of a cylinder oscillating in cross-flow and show the changes in structural sensitivity of the unstable eigenvalue. Section 5 concludes the paper.
2. Linearization of FSI
2.1. General problem description
We primarily follow the index notation with the implied Einstein summation. Bold face notation is used to represent vectors where necessary. Consider a FSI problem as illustrated in figure 1. The bounded region in white marked by ![]() $\varOmega ^{f}$ represents the fluid part of the domain and the grey region marked by
$\varOmega ^{f}$ represents the fluid part of the domain and the grey region marked by ![]() $\varOmega ^{s}$ represents the structural domain. The combined fluid and structural regions are bounded by the boundaries represented by
$\varOmega ^{s}$ represents the structural domain. The combined fluid and structural regions are bounded by the boundaries represented by ![]() $\partial \varOmega ^{f}_{v}$ and
$\partial \varOmega ^{f}_{v}$ and ![]() $\partial \varOmega ^{f}_{o}$. Here
$\partial \varOmega ^{f}_{o}$. Here ![]() $\partial \varOmega ^{f}_{v}$ represents the far-field boundary conditions which define the problem and
$\partial \varOmega ^{f}_{v}$ represents the far-field boundary conditions which define the problem and ![]() $\partial \varOmega ^{f}_{o}$ represents the open boundary condition applied for computations performed on a finite sized domain. The structural domain is bounded by the time varying FSI interface
$\partial \varOmega ^{f}_{o}$ represents the open boundary condition applied for computations performed on a finite sized domain. The structural domain is bounded by the time varying FSI interface ![]() $\varGamma (t)$ on which the fluid forces act. The Navier–Stokes equations, along with the incompressibility constraint govern the evolution of the fluid in
$\varGamma (t)$ on which the fluid forces act. The Navier–Stokes equations, along with the incompressibility constraint govern the evolution of the fluid in ![]() $\varOmega ^{f}$. For a problem with moving interfaces, the Navier–Stokes is usually formulated in the ALE formulation (Ho & Patera Reference Ho and Patera1990, Reference Ho and Patera1991) defined on moving material points as
$\varOmega ^{f}$. For a problem with moving interfaces, the Navier–Stokes is usually formulated in the ALE formulation (Ho & Patera Reference Ho and Patera1990, Reference Ho and Patera1991) defined on moving material points as
Here ![]() $\boldsymbol {U}$ and
$\boldsymbol {U}$ and ![]() $P$ represents the fluid velocity and pressure, respectively, while
$P$ represents the fluid velocity and pressure, respectively, while ![]() $\boldsymbol {W^{g}}$ represents the velocity of the material points. We refer to the time derivative in this formulation
$\boldsymbol {W^{g}}$ represents the velocity of the material points. We refer to the time derivative in this formulation ![]() $(\partial U_{i}/\partial t\vert _{\boldsymbol {W^{g}}})$ as the ALE time derivative evaluated when following a material point with velocity
$(\partial U_{i}/\partial t\vert _{\boldsymbol {W^{g}}})$ as the ALE time derivative evaluated when following a material point with velocity ![]() $\boldsymbol {W^{g}}$. Note that
$\boldsymbol {W^{g}}$. Note that ![]() $\boldsymbol {W^{g}}$ is not uniquely defined. The only restriction on material point velocity is for the points on the interface
$\boldsymbol {W^{g}}$ is not uniquely defined. The only restriction on material point velocity is for the points on the interface ![]() $\varGamma (t)$, where the fluid velocity is equal to the velocity of the interface points. Typically
$\varGamma (t)$, where the fluid velocity is equal to the velocity of the interface points. Typically ![]() $\boldsymbol {W^{g}}$ is defined by some function which smoothly extends the velocity at the interface to the rest of the fluid domain.
$\boldsymbol {W^{g}}$ is defined by some function which smoothly extends the velocity at the interface to the rest of the fluid domain.

Figure 1. Domain for a general FSI problem. The equilibrium position of the interface is marked by ![]() $\varGamma ^{0}$ and the perturbed position is marked by
$\varGamma ^{0}$ and the perturbed position is marked by ![]() $\varGamma (t)$.
$\varGamma (t)$.
The equations governing the structural motion depend on the type of modelling or degrees of freedom of the structure being considered. Confining the discussion to rigid-body motion problems, we represent the structural equations in a general form as
Here ![]() $\mathcal {M}$ is a generalized inertia,
$\mathcal {M}$ is a generalized inertia, ![]() $\mathcal {D}$ is a generalized damping,
$\mathcal {D}$ is a generalized damping, ![]() $\mathcal {K}$ is a generalized stiffness and
$\mathcal {K}$ is a generalized stiffness and ![]() $\mathcal {F}_{i}$ represents the fluid forces acting on
$\mathcal {F}_{i}$ represents the fluid forces acting on ![]() $\varGamma (t)$. The equation represents a typical linear spring-mass-damper system for rigid-body motion. The structural degrees of freedom are represented by
$\varGamma (t)$. The equation represents a typical linear spring-mass-damper system for rigid-body motion. The structural degrees of freedom are represented by ![]() $\eta _{i}$, whose definition depends on the type of modelling used for the structure. For example, for a cylinder free to oscillate in one direction subject to a spring-damper action (as in Cossu & Morino Reference Cossu and Morino2000),
$\eta _{i}$, whose definition depends on the type of modelling used for the structure. For example, for a cylinder free to oscillate in one direction subject to a spring-damper action (as in Cossu & Morino Reference Cossu and Morino2000), ![]() $\eta _{i}$ represents the position of the centre of mass in that direction,
$\eta _{i}$ represents the position of the centre of mass in that direction, ![]() $\mathcal {M}$ is the cylinder mass,
$\mathcal {M}$ is the cylinder mass, ![]() $\mathcal {D}$ is the damping coefficient,
$\mathcal {D}$ is the damping coefficient, ![]() $\mathcal {K}$ is the spring stiffness constant and
$\mathcal {K}$ is the spring stiffness constant and ![]() $\mathcal {F}_{i}$ is the integral of the fluid forces acting on the cylinder in the
$\mathcal {F}_{i}$ is the integral of the fluid forces acting on the cylinder in the ![]() $i$th direction.
$i$th direction.
The fluid and structural domains are coupled at the FSI interface through a no-slip and no penetration condition. Defining ![]() $\boldsymbol {x}^{\varGamma }$ as the (time-dependent) position of points on the interface
$\boldsymbol {x}^{\varGamma }$ as the (time-dependent) position of points on the interface ![]() $\varGamma (t)$ and
$\varGamma (t)$ and ![]() $\boldsymbol {v}^{\varGamma }$ as their instantaneous velocity, we may write the boundary condition as
$\boldsymbol {v}^{\varGamma }$ as their instantaneous velocity, we may write the boundary condition as
The coupled problem is now defined by (2.1a) and (2.1b) in the fluid domain, (2.2) in the structural domain, coupled with the no-slip condition at the interface (2.3). The problem is completed by the application of appropriate Dirichlet boundary conditions on ![]() $\partial \varOmega ^{f}_{v}$ and open boundary conditions on
$\partial \varOmega ^{f}_{v}$ and open boundary conditions on ![]() $\partial \varOmega ^{f}_{o}$. We assume that the outer domain boundaries always remain stationary.
$\partial \varOmega ^{f}_{o}$. We assume that the outer domain boundaries always remain stationary.
2.2. Steady state
For the problem described in § 2.1, consider a full system state given by ![]() $(\boldsymbol {U}^{0},P^{0},\boldsymbol {{\eta }}^{0})$ (referred to as the base flow state), defined on material points
$(\boldsymbol {U}^{0},P^{0},\boldsymbol {{\eta }}^{0})$ (referred to as the base flow state), defined on material points ![]() $\boldsymbol {x}^{0}$, which satisfies the time-independent incompressible Navier–Stokes and structural equations (along with the respective boundary conditions), i.e.
$\boldsymbol {x}^{0}$, which satisfies the time-independent incompressible Navier–Stokes and structural equations (along with the respective boundary conditions), i.e.
Here ![]() $\mathcal {F}^{0}_{i}$ are the fluid forces acting on the structure at equilibrium and
$\mathcal {F}^{0}_{i}$ are the fluid forces acting on the structure at equilibrium and ![]() $\varGamma ^{0}$ is the equilibrium position of the FSI interface.
$\varGamma ^{0}$ is the equilibrium position of the FSI interface.
2.3. Linearization of the structure
We begin with the linearization of the structural equations. In defining the generalized structural equation (2.2) we make an implicit assumption that the structural equations are inherently linear, which we consider appropriate for the class of rigid-body motion problems that are being considered. In principle, nonlinear spring-mass-damper systems may also be considered but for the moment we restrict the discussion to linear spring-mass-damper systems. Given an initial stationary solution ![]() $\eta ^{0}_{i}$ of the structural equation, we may introduce a perturbed state given by the superposition of the stationary state and small-amplitude perturbations, i.e.
$\eta ^{0}_{i}$ of the structural equation, we may introduce a perturbed state given by the superposition of the stationary state and small-amplitude perturbations, i.e. ![]() $\eta _{i} = \eta ^{0}_{i} + \eta '_{i}$. Similarly, we decompose the fluid forces acting on the structure as
$\eta _{i} = \eta ^{0}_{i} + \eta '_{i}$. Similarly, we decompose the fluid forces acting on the structure as ![]() $\mathcal {F}_{i} = \mathcal {F}^{0}_{i} + \mathcal {F}'_{i}$, where
$\mathcal {F}_{i} = \mathcal {F}^{0}_{i} + \mathcal {F}'_{i}$, where ![]() $\mathcal {F}'_{i}$ are the fluid forces acting on the structure due to the (yet unknown) linearized fluid perturbations. Introducing the decomposition into (2.2), we obtain the equations for the structural perturbations
$\mathcal {F}'_{i}$ are the fluid forces acting on the structure due to the (yet unknown) linearized fluid perturbations. Introducing the decomposition into (2.2), we obtain the equations for the structural perturbations
Equation (2.5) will be completed if we can evaluate the expression for the term ![]() $\mathcal {F}'_{i}$ arising due to the linearized fluid perturbations. The two systems (fluid and structure) are coupled through the term
$\mathcal {F}'_{i}$ arising due to the linearized fluid perturbations. The two systems (fluid and structure) are coupled through the term ![]() $\mathcal {F}'_{i}$ and the velocity boundary conditions at the interface.
$\mathcal {F}'_{i}$ and the velocity boundary conditions at the interface.
2.4. Taylor expansion based linearization of the fluid equations
To begin with, we define an affine mapping between the material points in the reference (equilibrium) configuration and the perturbed points as
Here ![]() $b$ is a vector representing a constant translation of the material points,
$b$ is a vector representing a constant translation of the material points, ![]() $\mathcal {I}$ is the identity matrix and
$\mathcal {I}$ is the identity matrix and ![]() $\mathcal {R}'$ can be considered to be a ‘perturbation matrix’ for the material points. Using such a decomposition allows us to conveniently express the inverse mapping
$\mathcal {R}'$ can be considered to be a ‘perturbation matrix’ for the material points. Using such a decomposition allows us to conveniently express the inverse mapping
For a small deformation, we may assume that ![]() $||\mathcal {R'}||\ll 1$ and the matrix inverse may then be written as
$||\mathcal {R'}||\ll 1$ and the matrix inverse may then be written as
Retaining only the first-order term of the expansion, we obtain the approximate inverse as
We refer to (2.9) as the geometric linearization of the problem. This allows us to conveniently reformulate all derivative terms evaluated on the perturbed grid in terms of the derivatives in the reference configuration. In addition, since ![]() $\mathcal {R}'$ is a perturbation matrix, this allows us to identify higher-order terms arising due to this geometric nonlinearity and later discard them when we retain only the first-order terms. In what follows, all quantities of the form
$\mathcal {R}'$ is a perturbation matrix, this allows us to identify higher-order terms arising due to this geometric nonlinearity and later discard them when we retain only the first-order terms. In what follows, all quantities of the form ![]() $\partial /\partial x_{j}^{0}$ represent the evaluation of derivatives in the reference configuration.
$\partial /\partial x_{j}^{0}$ represent the evaluation of derivatives in the reference configuration.
Next we define a perturbation field for the fluid components ![]() $(\boldsymbol {u}',p')$. The perturbation field is also defined on the same equilibrium grid
$(\boldsymbol {u}',p')$. The perturbation field is also defined on the same equilibrium grid ![]() $\boldsymbol {x}^{0}$ on which the base flow
$\boldsymbol {x}^{0}$ on which the base flow ![]() $(\boldsymbol {U}^{0},P^{0})$ has been defined. The total velocity and pressure fields on the perturbed locations are then evaluated using a superposition of the first-order Taylor expansions for the base flow and the perturbation field, i.e.
$(\boldsymbol {U}^{0},P^{0})$ has been defined. The total velocity and pressure fields on the perturbed locations are then evaluated using a superposition of the first-order Taylor expansions for the base flow and the perturbation field, i.e.
 \begin{gather} U_{i}(x,y,z) = U^{0}_{i} + \left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right) + u'_{i} + \left(\frac{\partial u'_{i}}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right), \end{gather}
\begin{gather} U_{i}(x,y,z) = U^{0}_{i} + \left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right) + u'_{i} + \left(\frac{\partial u'_{i}}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right), \end{gather} \begin{gather}P(x,y,z) = P^{0} + \left(\frac{\partial P^{0}}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right) + p' + \left(\frac{\partial p'}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right) . \end{gather}
\begin{gather}P(x,y,z) = P^{0} + \left(\frac{\partial P^{0}}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right) + p' + \left(\frac{\partial p'}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right) . \end{gather}The last term in (2.10a) and (2.10b) is dropped since it represents a second-order quantity arising due to the interaction of fluid and geometric perturbation terms. This results in the expressions for the total velocity and pressure as
 \begin{equation} u^{\xi}_{i}(x,y,z) = \left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right),\quad p^{\xi}(x,y,z) = \left(\frac{\partial P^{0}}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right), \end{equation}
\begin{equation} u^{\xi}_{i}(x,y,z) = \left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right),\quad p^{\xi}(x,y,z) = \left(\frac{\partial P^{0}}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right), \end{equation}
Where (2.12a) and (2.12b) are derived from (2.10a) and (2.10b), respectively, after dropping the second-order terms, and using the compact notations ![]() $u^{\xi }_{i}$ and
$u^{\xi }_{i}$ and ![]() $p^{\xi }$ to represent the first-order quantities of the Taylor expansion of the base flow velocity and pressure, respectively. Physically, this means that, for a point moving in space, we ignore changes in the perturbation field experienced due to the motion of the point, however, we include the first-order changes in the base flow field. The expressions in (2.12a) amount to a triple decomposition of the total velocity field, where the three terms
$p^{\xi }$ to represent the first-order quantities of the Taylor expansion of the base flow velocity and pressure, respectively. Physically, this means that, for a point moving in space, we ignore changes in the perturbation field experienced due to the motion of the point, however, we include the first-order changes in the base flow field. The expressions in (2.12a) amount to a triple decomposition of the total velocity field, where the three terms ![]() $U^{0}_{i},u^{\xi }_{i}$ and
$U^{0}_{i},u^{\xi }_{i}$ and ![]() $u'_{i}$ signify the base flow field, the perturbation of the base field observed by a point due to its motion and the perturbation velocity field, respectively. Additionally, associated with the motion of the material points, a velocity of the material points can also be defined such that
$u'_{i}$ signify the base flow field, the perturbation of the base field observed by a point due to its motion and the perturbation velocity field, respectively. Additionally, associated with the motion of the material points, a velocity of the material points can also be defined such that
Taking the time derivative of (2.12a), we obtain the ALE time derivative of the total velocity along the trajectory of the material point motion
 \begin{align} \left.\frac{\partial U_{i}}{\partial t}\right\vert_{\boldsymbol{w}} &= \frac{\partial U^{0}_{i}}{\partial t} + \frac{\partial }{\partial t} \left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right) +\frac{\partial u'_{i}}{\partial t} \nonumber\\ &\implies\left.\frac{\partial U_{i}}{\partial t}\right\vert_{\boldsymbol{w}} = \left(w_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}}\right) +\frac{\partial u'_{i}}{\partial t}. \end{align}
\begin{align} \left.\frac{\partial U_{i}}{\partial t}\right\vert_{\boldsymbol{w}} &= \frac{\partial U^{0}_{i}}{\partial t} + \frac{\partial }{\partial t} \left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}}{\rm \Delta} x_{j} \right) +\frac{\partial u'_{i}}{\partial t} \nonumber\\ &\implies\left.\frac{\partial U_{i}}{\partial t}\right\vert_{\boldsymbol{w}} = \left(w_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}}\right) +\frac{\partial u'_{i}}{\partial t}. \end{align}Next we substitute the triple decomposition of the velocity and pressure fields into the governing equations for the fluid motion and perform the geometric linearization so that all derivative quantities are consistently evaluated based on the reference configuration. Starting with the divergence-free constraint at the perturbed configuration leads to the following set of expressions:
 \begin{equation} \frac{\partial U_{i}}{\partial x_{i}} =\left\lbrace \begin{aligned} & \underbrace{\frac{\partial U^{0}_{i}}{\partial x^{0}_{i}}}_{I} + \underbrace{{\rm \Delta} x_{j}\frac{\partial }{\partial x^{0}_{j}} \left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{i}}\right)}_{II} +\underbrace{\frac{\partial u'_{i}}{\partial x^{0}_{i}}}_{III} \\ & \quad -\underbrace{\frac{\partial u'_{i}}{\partial x^{0}_{k}}\mathcal{R'}_{ki} }_{IV} -\underbrace{\frac{\partial }{\partial x^{0}_{k}}\left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}}\right) {\rm \Delta} x_{j}\mathcal{R'}_{ki}}_{V}-\underbrace{\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} \frac{\partial {\rm \Delta} x_{j}}{\partial x^{0}_{k}}\mathcal{R'}_{ki}}_{VI}. \end{aligned}\right. \end{equation}
\begin{equation} \frac{\partial U_{i}}{\partial x_{i}} =\left\lbrace \begin{aligned} & \underbrace{\frac{\partial U^{0}_{i}}{\partial x^{0}_{i}}}_{I} + \underbrace{{\rm \Delta} x_{j}\frac{\partial }{\partial x^{0}_{j}} \left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{i}}\right)}_{II} +\underbrace{\frac{\partial u'_{i}}{\partial x^{0}_{i}}}_{III} \\ & \quad -\underbrace{\frac{\partial u'_{i}}{\partial x^{0}_{k}}\mathcal{R'}_{ki} }_{IV} -\underbrace{\frac{\partial }{\partial x^{0}_{k}}\left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}}\right) {\rm \Delta} x_{j}\mathcal{R'}_{ki}}_{V}-\underbrace{\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} \frac{\partial {\rm \Delta} x_{j}}{\partial x^{0}_{k}}\mathcal{R'}_{ki}}_{VI}. \end{aligned}\right. \end{equation}
Term ![]() $I$ vanishes since it represents the divergence-free constraint of the base flow in the reference configuration. Similarly, term
$I$ vanishes since it represents the divergence-free constraint of the base flow in the reference configuration. Similarly, term ![]() $II$ contains the same divergence-free constraint inside the brackets and hence also vanishes. Terms
$II$ contains the same divergence-free constraint inside the brackets and hence also vanishes. Terms ![]() $IV,V$ and
$IV,V$ and ![]() $VI$ all represent terms that are second order in the perturbations quantities
$VI$ all represent terms that are second order in the perturbations quantities ![]() $\boldsymbol {u}',\boldsymbol {{\rm \Delta} x}$ and
$\boldsymbol {u}',\boldsymbol {{\rm \Delta} x}$ and ![]() $\mathcal {R'}$. Therefore, to a first-order approximation these quantities can be dropped. This leaves the final divergence constraint as
$\mathcal {R'}$. Therefore, to a first-order approximation these quantities can be dropped. This leaves the final divergence constraint as
Note that the derivative is evaluated in the reference configuration (but satisfies the divergence-free constraint on the perturbed locations up to a first-order approximation).
In a similar manner, we may introduce the triple decomposition of the velocity and pressure field into the ALE form of the Navier–Stokes evaluated at the perturbed locations as
 \begin{align} & \left(U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}} + U^{0}_{j}\frac{\partial u^{\xi}_{i}}{\partial x_{j}} + u^{\xi}_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}}\right) + \left( U^{0}_{j}\frac{\partial u'_{i}}{\partial x_{j}} + u'_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}}\right) +\left( \left.\frac{\partial U_{i}}{\partial t}\right\vert_{\boldsymbol{w}} - w_{j}\frac{\partial U_{i}}{\partial x_{j}} \right) \nonumber\\ &\quad =\left(-\frac{\partial P^{0}}{\partial x_{i}} + \frac{1}{Re}\frac{\partial^{2}U^{0}_{i}}{\partial x_{j}\partial x_{j}}\right) + \left(-\frac{\partial p^{\xi}}{\partial x_{i}} + \frac{1}{Re}\frac{\partial^{2}u^{\xi}_{i}}{\partial x_{j}\partial x_{j}}\right) +\left(-\frac{\partial p'}{\partial x_{i}} + \frac{1}{Re}\frac{\partial^{2}u'_{i}}{\partial x_{j}\partial x_{j}}\right). \end{align}
\begin{align} & \left(U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}} + U^{0}_{j}\frac{\partial u^{\xi}_{i}}{\partial x_{j}} + u^{\xi}_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}}\right) + \left( U^{0}_{j}\frac{\partial u'_{i}}{\partial x_{j}} + u'_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}}\right) +\left( \left.\frac{\partial U_{i}}{\partial t}\right\vert_{\boldsymbol{w}} - w_{j}\frac{\partial U_{i}}{\partial x_{j}} \right) \nonumber\\ &\quad =\left(-\frac{\partial P^{0}}{\partial x_{i}} + \frac{1}{Re}\frac{\partial^{2}U^{0}_{i}}{\partial x_{j}\partial x_{j}}\right) + \left(-\frac{\partial p^{\xi}}{\partial x_{i}} + \frac{1}{Re}\frac{\partial^{2}u^{\xi}_{i}}{\partial x_{j}\partial x_{j}}\right) +\left(-\frac{\partial p'}{\partial x_{i}} + \frac{1}{Re}\frac{\partial^{2}u'_{i}}{\partial x_{j}\partial x_{j}}\right). \end{align}The nonlinear transport terms have already been dropped. We now substitute the ALE time derivative from (2.14) and introduce the geometric linearization to consistently evaluate derivatives based on the original configuration. A full expansion of all the terms can be found in appendix A. We write the final form of the Navier–Stokes obtained after the expansion and simplification of the terms and dropping all terms higher than first order:
 \begin{align} & \left[U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} + \frac{\partial P^{0}}{\partial x^{0}_{i}} -\frac{1}{Re}\frac{\partial^{2} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right] + {\rm \Delta} x_{l}\frac{\partial }{\partial x^{0}_{l}}\left[U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} + \frac{\partial P^{0}}{\partial x^{0}_{i}} -\frac{1}{Re}\frac{\partial^{2} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right] \nonumber\\ &+\quad \left[\frac{\partial u'_{i}}{\partial t} +U^{0}_{j}\frac{\partial u'_{i}}{\partial x^{0}_{j}} + u'_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} +\frac{\partial p'}{\partial x^{0}_{i}} - \frac{1}{Re}\frac{\partial^{2} u'_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right] = 0. \end{align}
\begin{align} & \left[U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} + \frac{\partial P^{0}}{\partial x^{0}_{i}} -\frac{1}{Re}\frac{\partial^{2} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right] + {\rm \Delta} x_{l}\frac{\partial }{\partial x^{0}_{l}}\left[U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} + \frac{\partial P^{0}}{\partial x^{0}_{i}} -\frac{1}{Re}\frac{\partial^{2} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right] \nonumber\\ &+\quad \left[\frac{\partial u'_{i}}{\partial t} +U^{0}_{j}\frac{\partial u'_{i}}{\partial x^{0}_{j}} + u'_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} +\frac{\partial p'}{\partial x^{0}_{i}} - \frac{1}{Re}\frac{\partial^{2} u'_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right] = 0. \end{align}
The terms in the first square bracket may be identified as the steady-state equation for the base flow in the reference configuration. The terms inside the second square bracket are also the steady-state equations in the reference configuration. In fact, the set of terms from the first two brackets together represent the first-order Taylor expansion of the steady-state equations for the base flow at the perturbed points. Thus, all the terms in the first two brackets vanish. In hindsight, the final set of expressions obtained seems rather obvious. In fact one may observe the first three terms in the expansion of the divergence-free constraint and realize that they amount to a similar expression. Terms ![]() $I$ and
$I$ and ![]() $II$ in (2.15) together form the first-order Taylor expansion of the base flow divergence-free constraint at the perturbed locations. Since the solution of the steady-state equations and the base field divergence is identically zero everywhere, their Taylor expansions also vanish at the perturbed locations. Thus, we are left with the final linear equations for the perturbed quantities which is also independent of the arbitrarily defined velocity of the grid motion
$II$ in (2.15) together form the first-order Taylor expansion of the base flow divergence-free constraint at the perturbed locations. Since the solution of the steady-state equations and the base field divergence is identically zero everywhere, their Taylor expansions also vanish at the perturbed locations. Thus, we are left with the final linear equations for the perturbed quantities which is also independent of the arbitrarily defined velocity of the grid motion ![]() $\boldsymbol {w}$:
$\boldsymbol {w}$:
2.5. Linearized boundary conditions
Before proceeding to evaluate the total linearized forces on the perturbed points, we consider the global balance of fluxes for the base flow at the equilibrium and the perturbed positions. This allows us to evaluate the forces arising due to the variation of the boundary in a steady base flow. We use the conservative form of the equations, starting with the base flow state in the equilibrium configuration and evaluate the integral over the whole domain:
 \begin{align} & \frac{\partial}{\partial x^{0}_{j}} (U^{0}_{i}U^{0}_{j} - \sigma^{0}_{ij}) = 0 \nonumber\\ &\quad \implies \int_{\varOmega^{0}}\frac{\partial}{\partial x^{0}_{j}} (U^{0}_{i}U^{0}_{j} - \sigma^{0}_{ij})\,\textrm{d}\varOmega = 0 \nonumber\\ &\quad \implies \int_{\partial \varOmega^{f}_{v}} (U^{0}_{i}U^{0}_{j} - \sigma^{0}_{ij})n^{0}_{j}\,\textrm{d} S + \int_{\partial \varOmega^{f}_{o}} (U^{0}_{i}U^{0}_{j} - \sigma^{0}_{ij})n^{0}_{j}\,\textrm{d} S - \int_{\varGamma^{0}}\sigma^{0}_{ij}n^{0}_{j}\,\textrm{d} S = 0. \end{align}
\begin{align} & \frac{\partial}{\partial x^{0}_{j}} (U^{0}_{i}U^{0}_{j} - \sigma^{0}_{ij}) = 0 \nonumber\\ &\quad \implies \int_{\varOmega^{0}}\frac{\partial}{\partial x^{0}_{j}} (U^{0}_{i}U^{0}_{j} - \sigma^{0}_{ij})\,\textrm{d}\varOmega = 0 \nonumber\\ &\quad \implies \int_{\partial \varOmega^{f}_{v}} (U^{0}_{i}U^{0}_{j} - \sigma^{0}_{ij})n^{0}_{j}\,\textrm{d} S + \int_{\partial \varOmega^{f}_{o}} (U^{0}_{i}U^{0}_{j} - \sigma^{0}_{ij})n^{0}_{j}\,\textrm{d} S - \int_{\varGamma^{0}}\sigma^{0}_{ij}n^{0}_{j}\,\textrm{d} S = 0. \end{align}
Here ![]() $n^{0}_{j}\,\textrm {d} S$ represents the local surface vector in the equilibrium configuration. For compact notation, we have denoted the stresses due to the fluid at equilibrium as
$n^{0}_{j}\,\textrm {d} S$ represents the local surface vector in the equilibrium configuration. For compact notation, we have denoted the stresses due to the fluid at equilibrium as ![]() $\sigma ^{0}_{ij}$, defined as
$\sigma ^{0}_{ij}$, defined as
 \begin{equation} \sigma^{0}_{ij} = -P^{0}\delta_{ij} +\frac{1}{Re}\left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} + \frac{\partial U^{0}_{j}}{\partial x^{0}_{i}} \right) . \end{equation}
\begin{equation} \sigma^{0}_{ij} = -P^{0}\delta_{ij} +\frac{1}{Re}\left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} + \frac{\partial U^{0}_{j}}{\partial x^{0}_{i}} \right) . \end{equation}
The three integrals in (2.20) represent the momentum flux through the far field (![]() $\partial \varOmega ^{f}_{v}$), outflow (
$\partial \varOmega ^{f}_{v}$), outflow (![]() $\partial \varOmega ^{f}_{o}$) and FSI interface (
$\partial \varOmega ^{f}_{o}$) and FSI interface (![]() $\varGamma ^{0}$), respectively. Of course it is not necessary to integrate over the whole domain, and the integral may be performed over any arbitrarily chosen part of the domain. The use of divergence theorem will then provide us with the flux balance across the surfaces of this arbitrarily chosen volume. Accordingly, we may choose an arbitrary volume enclosed by three surfaces. Two of the surfaces of this arbitrary volume are chosen such that they coincide with
$\varGamma ^{0}$), respectively. Of course it is not necessary to integrate over the whole domain, and the integral may be performed over any arbitrarily chosen part of the domain. The use of divergence theorem will then provide us with the flux balance across the surfaces of this arbitrarily chosen volume. Accordingly, we may choose an arbitrary volume enclosed by three surfaces. Two of the surfaces of this arbitrary volume are chosen such that they coincide with ![]() $\partial \varOmega _{v}$ and
$\partial \varOmega _{v}$ and ![]() $\partial \varOmega _{o}$ and a third surface may be chosen arbitrarily, which we denote as
$\partial \varOmega _{o}$ and a third surface may be chosen arbitrarily, which we denote as ![]() $C$. Performing the volume integral over this arbitrary volume and using the divergence theorem gives the relation between the fluxes across the boundaries,
$C$. Performing the volume integral over this arbitrary volume and using the divergence theorem gives the relation between the fluxes across the boundaries,
We highlight here that at this point we are not calculating the balance of total momentum in a flow field that has been perturbed. But rather, we are evaluating the expressions for the momentum flux, across different enclosing surfaces, for the same steady base flow. Comparing (2.20) and (2.22) it is easy to see that the fluxes through the arbitrary surface ![]() $C$ and the FSI interface
$C$ and the FSI interface ![]() $\varGamma ^{0}$ must be equal, i.e.
$\varGamma ^{0}$ must be equal, i.e.
Up to this point no assumptions have been invoked and (2.23) is simply a result of momentum flux conservation. The surface ![]() $C$ is arbitrary and can be deformed in any desired fashion. Therefore, the surface can be assumed to be a perturbation of the equilibrium FSI interface
$C$ is arbitrary and can be deformed in any desired fashion. Therefore, the surface can be assumed to be a perturbation of the equilibrium FSI interface ![]() $\varGamma ^{0}$ (for example, the perturbed interface obtained during an unsteady FSI problem). For the exact evaluation of the base-flow momentum flux across the perturbed surfaces, the exact values at the perturbed points would be required. However, following the Taylor expansion based procedure, these may be evaluated using the truncated Taylor series. Noting that
$\varGamma ^{0}$ (for example, the perturbed interface obtained during an unsteady FSI problem). For the exact evaluation of the base-flow momentum flux across the perturbed surfaces, the exact values at the perturbed points would be required. However, following the Taylor expansion based procedure, these may be evaluated using the truncated Taylor series. Noting that ![]() $\boldsymbol {U^{0}}$ is identically zero on
$\boldsymbol {U^{0}}$ is identically zero on ![]() $\varGamma ^{0}$, the resulting linearized expression for the surface integral over this perturbed interface may be evaluated as
$\varGamma ^{0}$, the resulting linearized expression for the surface integral over this perturbed interface may be evaluated as
 \begin{align} & \int_{\varGamma^{0}}\sigma^{0}_{ij}n^{0}_{j}\,\textrm{d} S + \int_{\varGamma^{0}}\sigma^{0}_{ij}n'_{j}\,\textrm{d} S + \int_{\varGamma^{0}}\sigma^{\xi}_{ij}n^{0}_{j}\,\textrm{d} S = \int_{\varGamma^{0}}\sigma^{0}_{ij}n^{0}_{j}\,\textrm{d} S \nonumber\\ &\quad \implies \int_{\varGamma^{0}}\big[\sigma^{0}_{ij}n'_{j} + \sigma^{\xi}_{ij}n^{0}_{j}\big]\,\textrm{d} S = 0. \end{align}
\begin{align} & \int_{\varGamma^{0}}\sigma^{0}_{ij}n^{0}_{j}\,\textrm{d} S + \int_{\varGamma^{0}}\sigma^{0}_{ij}n'_{j}\,\textrm{d} S + \int_{\varGamma^{0}}\sigma^{\xi}_{ij}n^{0}_{j}\,\textrm{d} S = \int_{\varGamma^{0}}\sigma^{0}_{ij}n^{0}_{j}\,\textrm{d} S \nonumber\\ &\quad \implies \int_{\varGamma^{0}}\big[\sigma^{0}_{ij}n'_{j} + \sigma^{\xi}_{ij}n^{0}_{j}\big]\,\textrm{d} S = 0. \end{align}
Here ![]() $n'_{j}\,\textrm {d} S$ represents the first-order change in the surface vector due to the perturbation of the boundary and we have dropped the second-order terms for convection
$n'_{j}\,\textrm {d} S$ represents the first-order change in the surface vector due to the perturbation of the boundary and we have dropped the second-order terms for convection ![]() $u^{\xi }_{i}u^{\xi }_{j}$ and the surface force
$u^{\xi }_{i}u^{\xi }_{j}$ and the surface force ![]() $\sigma ^{\xi }_{ij}n'_{j}$. The expression
$\sigma ^{\xi }_{ij}n'_{j}$. The expression ![]() $\sigma ^{\xi }_{ij}$ is simply the first-order term of the Taylor expansion of the base flow stresses, defined as
$\sigma ^{\xi }_{ij}$ is simply the first-order term of the Taylor expansion of the base flow stresses, defined as
 \begin{equation} \sigma^{\xi}_{ij} = {\rm \Delta} x_{k}\frac{\partial }{\partial x^{0}_{k}} \left[-P^{0}\delta_{ij} +\frac{1}{Re}\left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} + \frac{\partial U^{0}_{j}}{\partial x^{0}_{i}} \right)\right] . \end{equation}
\begin{equation} \sigma^{\xi}_{ij} = {\rm \Delta} x_{k}\frac{\partial }{\partial x^{0}_{k}} \left[-P^{0}\delta_{ij} +\frac{1}{Re}\left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} + \frac{\partial U^{0}_{j}}{\partial x^{0}_{i}} \right)\right] . \end{equation}The first term in (2.24) represents the variation of the base flow forces due to the change in surface normal and the second term represents the variation due to the change in boundary position. To a first-order approximation, these terms balance to zero. Note that no assumption has been made on the type of deformation at the boundary and the condition holds for any arbitrary deformation of the boundary. We note that these are precisely the terms that arise in Fanion et al. (Reference Fanion, Fernández and Le Tallec2000) and Fernández & Le Tallec (Reference Fernández and Le Tallec2003a,Reference Fernández and Le Tallecb) that have been termed as ‘added stiffness’. To a first-order approximation, they simply sum up to zero and play no role in the linear dynamics. However, we note that it is the integral of the added stiffness terms that vanishes and not necessarily the point wise values. One may now evaluate the total linearized forces arising from (2.18) on the perturbed FSI interface and obtain the linearized boundary conditions for the stress balance (2.5) as
 \begin{align} & \left.\begin{aligned} & \mathcal{M}\frac{\partial^{2} \eta'_{i}}{\partial t^{2}} + \mathcal{D}\frac{\partial\eta'_{i}}{\partial t} + \mathcal{K} (\eta^{0}_{i} + \eta'_{i}) + \int_{\varGamma^{0}}\sigma^{0}_{ij}n^{0}_{j}\,\textrm{d} S \nonumber\\ & \quad + \int_{\varGamma^{0}}\sigma^{0}_{ij}n'_{j}\,\textrm{d} S + \int_{\varGamma^{0}}\sigma^{\xi}_{ij}n^{0}_{j}\,\textrm{d} S + \int_{\varGamma^{0}}\sigma'_{ij}n^{0}_{j}\,\textrm{d} S \end{aligned}\right\rbrace = 0, \nonumber\\ &\quad \implies \mathcal{M}\frac{\partial^{2} \eta'_{i}}{\partial t^{2}} + \mathcal{D}\frac{\partial\eta'_{i}}{\partial t} + \mathcal{K}\eta'_{i} + \int_{\varGamma^{0}}\sigma'_{ij}n^{0}_{j}\,\textrm{d} S = 0, \end{align}
\begin{align} & \left.\begin{aligned} & \mathcal{M}\frac{\partial^{2} \eta'_{i}}{\partial t^{2}} + \mathcal{D}\frac{\partial\eta'_{i}}{\partial t} + \mathcal{K} (\eta^{0}_{i} + \eta'_{i}) + \int_{\varGamma^{0}}\sigma^{0}_{ij}n^{0}_{j}\,\textrm{d} S \nonumber\\ & \quad + \int_{\varGamma^{0}}\sigma^{0}_{ij}n'_{j}\,\textrm{d} S + \int_{\varGamma^{0}}\sigma^{\xi}_{ij}n^{0}_{j}\,\textrm{d} S + \int_{\varGamma^{0}}\sigma'_{ij}n^{0}_{j}\,\textrm{d} S \end{aligned}\right\rbrace = 0, \nonumber\\ &\quad \implies \mathcal{M}\frac{\partial^{2} \eta'_{i}}{\partial t^{2}} + \mathcal{D}\frac{\partial\eta'_{i}}{\partial t} + \mathcal{K}\eta'_{i} + \int_{\varGamma^{0}}\sigma'_{ij}n^{0}_{j}\,\textrm{d} S = 0, \end{align}
where ![]() $\sigma '_{ij}$ is the fluid stress due to the perturbation field
$\sigma '_{ij}$ is the fluid stress due to the perturbation field ![]() $(\boldsymbol {u}',p')$ defined as
$(\boldsymbol {u}',p')$ defined as
 \begin{equation} \sigma'_{ij} = -p'\delta_{ij} +\frac{1}{Re}\left(\frac{\partial u'_{i}}{\partial x^{0}_{j}} + \frac{\partial u'_{j}}{\partial x^{0}_{i}} \right) . \end{equation}
\begin{equation} \sigma'_{ij} = -p'\delta_{ij} +\frac{1}{Re}\left(\frac{\partial u'_{i}}{\partial x^{0}_{j}} + \frac{\partial u'_{j}}{\partial x^{0}_{i}} \right) . \end{equation} The velocity continuity boundary conditions on the moving interface ![]() $\varGamma (t)$ simply become
$\varGamma (t)$ simply become
 \begin{align} & U_{i} = v^{\varGamma}_{i}\quad \textrm{on}\ \varGamma(t) \nonumber\\ &\quad \implies {\rm \Delta} x^{\varGamma}_{k}\frac{\partial U^{0}_{i}} {\partial x_{k}} + u'_{i} = v^{\varGamma}_{i}. \end{align}
\begin{align} & U_{i} = v^{\varGamma}_{i}\quad \textrm{on}\ \varGamma(t) \nonumber\\ &\quad \implies {\rm \Delta} x^{\varGamma}_{k}\frac{\partial U^{0}_{i}} {\partial x_{k}} + u'_{i} = v^{\varGamma}_{i}. \end{align}Thus, the perturbation velocities must account for the Taylor expansion term of the base flow at the perturbed boundary. Fanion et al. (Reference Fanion, Fernández and Le Tallec2000) and Fernández & Le Tallec (Reference Fernández and Le Tallec2003a,Reference Fernández and Le Tallecb) refer to this as the transpiration boundary condition.
The linear FSI problem for the perturbations is turned into a standard linear perturbation problem with the exception of the modified boundary conditions (transpiration instead of no-slip). The additional forces at the perturbed boundary are simply due to the perturbation field ![]() $(\boldsymbol {u}',p')$ and no ‘added stiffness’ terms arise in a linear approximation. One may immediately notice that the final form is a generalization of the form derived by Benjamin (Reference Benjamin1959, Reference Benjamin1960) and Landahl (Reference Landahl1962) for parallel flow cases. Finally, we highlight an assumption that is inherent throughout the mathematical derivation. When evaluating the base flow terms at the perturbed points, a first-order Taylor expansion has been used. This is perfectly valid when the perturbed points are inside the equilibrium fluid domain however, when the perturbed points move outside this domain, the validity of the Taylor expansion is less clear. The implicit validity of the Taylor expansion beyond the equilibrium fluid domain underpins the mathematical results of both the unsteady problem in § 2.4 as well as for the steady problem in the current subsection. To the best of our knowledge,we are unaware of any previous work which may resolve this conundrum. We provide a heuristic answer in the next section where several examples are considered for rigid-body motion in symmetric and asymmetric configurations to show the validity of the current approach.
$(\boldsymbol {u}',p')$ and no ‘added stiffness’ terms arise in a linear approximation. One may immediately notice that the final form is a generalization of the form derived by Benjamin (Reference Benjamin1959, Reference Benjamin1960) and Landahl (Reference Landahl1962) for parallel flow cases. Finally, we highlight an assumption that is inherent throughout the mathematical derivation. When evaluating the base flow terms at the perturbed points, a first-order Taylor expansion has been used. This is perfectly valid when the perturbed points are inside the equilibrium fluid domain however, when the perturbed points move outside this domain, the validity of the Taylor expansion is less clear. The implicit validity of the Taylor expansion beyond the equilibrium fluid domain underpins the mathematical results of both the unsteady problem in § 2.4 as well as for the steady problem in the current subsection. To the best of our knowledge,we are unaware of any previous work which may resolve this conundrum. We provide a heuristic answer in the next section where several examples are considered for rigid-body motion in symmetric and asymmetric configurations to show the validity of the current approach.
3. Linear instability results
3.1. Numerical method
Numerical tests are performed to validate the linear equations for FSI derived in the previous section. The cases considered are an oscillating cylinder with a spring-damper action, oscillating and rotating ellipse initially held at an angle to the flow, and rotating cylinder-splitter body. All computations were performed using a high-order spectral-element method code (Fischer, Lottes & Kerkemeier Reference Fischer, Lottes and Kerkemeier2008). The code uses ![]() $n$th-order Lagrange interpolants at Gauss–Lobatto–Legendre (GLL) points for the representation of the velocity and
$n$th-order Lagrange interpolants at Gauss–Lobatto–Legendre (GLL) points for the representation of the velocity and ![]() $(n-2)$th-order interpolants at Gauss–Legendre points for the representation of the pressure in a
$(n-2)$th-order interpolants at Gauss–Legendre points for the representation of the pressure in a ![]() $\mathbb {P}_{n}-\mathbb {P}_{n-2}$ formulation (Maday & Patera Reference Maday and Patera1989). A third-order backward difference is used for the time integration of the equations. The viscous terms are evaluated implicitly while extrapolation is used for the nonlinear terms. Over integration is used for a consistent evaluation of the nonlinear terms and a relaxation term based on the high-pass filtered velocity field is used to stabilize the method (Negi Reference Negi2017). The stabilization method is based on the approximate deconvolution model with relaxation term (ADM-RT) method used for the large-eddy simulation of transitional flows (Schlatter, Stolz & Kleiser Reference Schlatter, Stolz and Kleiser2004, Reference Schlatter, Stolz and Kleiser2006) and has been validated with channel flows and flow over wings in Negi et al. (Reference Negi, Vinuesa, Hanifi, Schlatter and Henningson2018). Moving boundaries are treated using the ALE formulation (Ho & Patera Reference Ho and Patera1990, Reference Ho and Patera1991) and the fluid and structural equations are coupled using the Green's function decomposition approach whereby the geometrical nonlinearity is evaluated explicitly via extrapolation, while the added-mass effects are treated implicitly (Fischer, Schmitt & Tomboulides Reference Fischer, Schmitt and Tomboulides2017). In addition, we have also implemented a fully implicit fixed-point nonlinear iteration method (Küttler & Wall Reference Küttler and Wall2008) for coupling of the fluid and structural equations. Both methods give nearly identical results in all tested cases. For the nonlinear and linear stability results reported in this work, the semi-implicit method of Fischer et al. (Reference Fischer, Schmitt and Tomboulides2017) has been used. For the case of adjoint analysis, the fully implicit fixed-point iterations have been used. All quantities are non-dimensionalized using the fluid density
$\mathbb {P}_{n}-\mathbb {P}_{n-2}$ formulation (Maday & Patera Reference Maday and Patera1989). A third-order backward difference is used for the time integration of the equations. The viscous terms are evaluated implicitly while extrapolation is used for the nonlinear terms. Over integration is used for a consistent evaluation of the nonlinear terms and a relaxation term based on the high-pass filtered velocity field is used to stabilize the method (Negi Reference Negi2017). The stabilization method is based on the approximate deconvolution model with relaxation term (ADM-RT) method used for the large-eddy simulation of transitional flows (Schlatter, Stolz & Kleiser Reference Schlatter, Stolz and Kleiser2004, Reference Schlatter, Stolz and Kleiser2006) and has been validated with channel flows and flow over wings in Negi et al. (Reference Negi, Vinuesa, Hanifi, Schlatter and Henningson2018). Moving boundaries are treated using the ALE formulation (Ho & Patera Reference Ho and Patera1990, Reference Ho and Patera1991) and the fluid and structural equations are coupled using the Green's function decomposition approach whereby the geometrical nonlinearity is evaluated explicitly via extrapolation, while the added-mass effects are treated implicitly (Fischer, Schmitt & Tomboulides Reference Fischer, Schmitt and Tomboulides2017). In addition, we have also implemented a fully implicit fixed-point nonlinear iteration method (Küttler & Wall Reference Küttler and Wall2008) for coupling of the fluid and structural equations. Both methods give nearly identical results in all tested cases. For the nonlinear and linear stability results reported in this work, the semi-implicit method of Fischer et al. (Reference Fischer, Schmitt and Tomboulides2017) has been used. For the case of adjoint analysis, the fully implicit fixed-point iterations have been used. All quantities are non-dimensionalized using the fluid density ![]() $\rho$, free stream velocity
$\rho$, free stream velocity ![]() $U_{\infty }$ and the cylinder/ellipse diameter
$U_{\infty }$ and the cylinder/ellipse diameter ![]() $D$.
$D$.
3.2. Oscillating cylinder at subcritical Reynolds numbers
For the first case, we investigate a two-dimensional circular cylinder free to oscillate in the cross-stream direction subject to the action of a spring-damper system. The Reynolds number of the flow based on the cylinder diameter is ![]() $Re=23.512$. The inlet of the computational domain is
$Re=23.512$. The inlet of the computational domain is ![]() $25$ diameters upstream of the cylinder while the outflow boundary is
$25$ diameters upstream of the cylinder while the outflow boundary is ![]() $60$ diameters downstream of the cylinder. The lateral boundaries are 50 diameters away on either side. A uniform inflow Dirichlet boundary condition is applied on the inflow and the lateral boundaries while the stress-free boundary condition is applied on the outflow boundary. The computational domain is discretized using
$60$ diameters downstream of the cylinder. The lateral boundaries are 50 diameters away on either side. A uniform inflow Dirichlet boundary condition is applied on the inflow and the lateral boundaries while the stress-free boundary condition is applied on the outflow boundary. The computational domain is discretized using ![]() $2284$ spectral elements which are further discretized into
$2284$ spectral elements which are further discretized into ![]() $10\times 10$ GLL points for a ninth-order polynomial representation for the velocity. This amounts to a total of 228 400 degrees of freedom in the domain. The base flow for all cases was calculated by keeping the structure fixed at its initial position. At
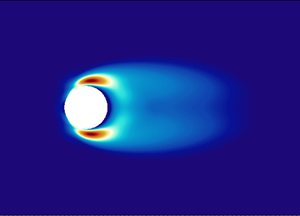
$10\times 10$ GLL points for a ninth-order polynomial representation for the velocity. This amounts to a total of 228 400 degrees of freedom in the domain. The base flow for all cases was calculated by keeping the structure fixed at its initial position. At ![]() $Re=23.512$, the flow with a fixed cylinder is linearly stable. The convergence to steady state was accelerated by using BoostConv (Citro et al. Reference Citro, Luchini, Giannetti and Auteri2017). Figure 2 shows the calculated base flow state (streamwise velocity). Sen, Mittal & Biswas (Reference Sen, Mittal and Biswas2009) report a linear empirical relation for the length of the reverse flow region behind the cylinder which predicts
$Re=23.512$, the flow with a fixed cylinder is linearly stable. The convergence to steady state was accelerated by using BoostConv (Citro et al. Reference Citro, Luchini, Giannetti and Auteri2017). Figure 2 shows the calculated base flow state (streamwise velocity). Sen, Mittal & Biswas (Reference Sen, Mittal and Biswas2009) report a linear empirical relation for the length of the reverse flow region behind the cylinder which predicts ![]() $L/D=1.146$ for the given Reynolds number. The length of the reverse flow region was found to be
$L/D=1.146$ for the given Reynolds number. The length of the reverse flow region was found to be ![]() $L/D=1.150$ for the calculated steady flow, matching well with the results of Sen et al. (Reference Sen, Mittal and Biswas2009).
$L/D=1.150$ for the calculated steady flow, matching well with the results of Sen et al. (Reference Sen, Mittal and Biswas2009).
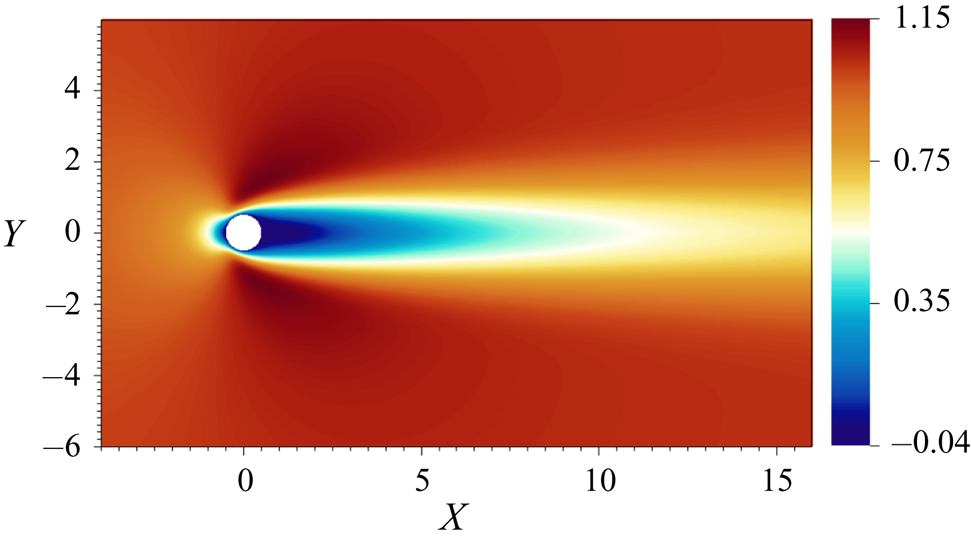
Figure 2. Streamwise velocity of the base flow state for a cylinder in cross-flow at ![]() $Re=23.512$.
$Re=23.512$.
We denote ![]() $\eta$ as the vertical position of the cylinder and the structural equation is modelled using a spring-mass-damper system for the vertical displacement of the cylinder. Following the earlier notation, we denote the fluid domain as
$\eta$ as the vertical position of the cylinder and the structural equation is modelled using a spring-mass-damper system for the vertical displacement of the cylinder. Following the earlier notation, we denote the fluid domain as ![]() $\varOmega ^{f}$, the structural domain as
$\varOmega ^{f}$, the structural domain as ![]() $\varOmega ^{s}$ and the FSI interface as
$\varOmega ^{s}$ and the FSI interface as ![]() $\varGamma$. In all our cases, the structural equation contains a second-order derivative in time. The order of the time derivative is reduced by introducing a variable substitution for the velocity
$\varGamma$. In all our cases, the structural equation contains a second-order derivative in time. The order of the time derivative is reduced by introducing a variable substitution for the velocity ![]() $\varphi$ of the structure. The combined nonlinear equations for the FSI system can be written as
$\varphi$ of the structure. The combined nonlinear equations for the FSI system can be written as
The parameters for the structural system are specified in table 1. The mass ![]() $\mathcal {M}$ corresponds to a density ratio of
$\mathcal {M}$ corresponds to a density ratio of ![]() $7$ (solid to fluid), and the damping constant
$7$ (solid to fluid), and the damping constant ![]() $\mathcal {D}$ is set to
$\mathcal {D}$ is set to ![]() $0.754\,\%$ of the critical damping. Here
$0.754\,\%$ of the critical damping. Here ![]() $\omega _{n} = \sqrt {\mathcal {K}/\mathcal {M}}$ represents the undamped natural frequency of the spring-mass system,
$\omega _{n} = \sqrt {\mathcal {K}/\mathcal {M}}$ represents the undamped natural frequency of the spring-mass system, ![]() $\lambda _{s}=-\omega _{n}(\zeta \pm \textrm {i}\sqrt {1-\zeta ^{2}})$ represents the damped structural eigenvalue of the spring-mass-damper system, with
$\lambda _{s}=-\omega _{n}(\zeta \pm \textrm {i}\sqrt {1-\zeta ^{2}})$ represents the damped structural eigenvalue of the spring-mass-damper system, with ![]() $\zeta =\mathcal {D}/(2\sqrt {\mathcal {K}\mathcal {M} })$ being the damping ratio.
$\zeta =\mathcal {D}/(2\sqrt {\mathcal {K}\mathcal {M} })$ being the damping ratio.
Table 1. Structural parameters for a two-dimensional cylinder oscillating in the cross-stream direction.
Following the Taylor expansion based triple decomposition of the total fluid velocity and pressure, the linearized system of equations governing the fluid and structural perturbations ![]() $(\boldsymbol {u}',p',\eta ',\varphi ')$ can be written as
$(\boldsymbol {u}',p',\eta ',\varphi ')$ can be written as
 \begin{gather}\mathcal{F}'_{i} - \oint_{\varGamma^{0}}\left[p'\delta_{ij} -\frac{1}{Re}\left(\frac{\partial u'_{i}}{\partial x^{0}_{j}} + \frac{\partial u'_{j}}{\partial x^{0}_{i}} \right)\right]n^{0}_{j} \partial\varOmega = 0\quad \text{fluid forces on } \varGamma. \end{gather}
\begin{gather}\mathcal{F}'_{i} - \oint_{\varGamma^{0}}\left[p'\delta_{ij} -\frac{1}{Re}\left(\frac{\partial u'_{i}}{\partial x^{0}_{j}} + \frac{\partial u'_{j}}{\partial x^{0}_{i}} \right)\right]n^{0}_{j} \partial\varOmega = 0\quad \text{fluid forces on } \varGamma. \end{gather}
Note that even though the cylinder is free to move only in the vertical direction, the streamwise perturbation velocity ![]() $u'_{1}$ is non-zero at the cylinder surface due to the Taylor expansion term of the base flow. Additionally, when evaluating the fluid forces in (3.2i), the direction of the normal
$u'_{1}$ is non-zero at the cylinder surface due to the Taylor expansion term of the base flow. Additionally, when evaluating the fluid forces in (3.2i), the direction of the normal ![]() $n^{0}_{j}$ is based on the equilibrium position of the FSI interface.
$n^{0}_{j}$ is based on the equilibrium position of the FSI interface.
Before calculating the spectra of the linearized problem, we compare the evolution of the linear and nonlinear flow cases when the base flow is perturbed by identical small-amplitude perturbations. If the perturbation amplitude is small then nonlinear effects will be negligible and one can expect the linear and nonlinear evolution to be the same. The solutions would eventually diverge due to amplitude saturation in the nonlinear case. Performing this comparison has another advantage in this particular case. Given the low Reynolds number of the case, we expect the dynamics of be governed by a single least damped global mode. Therefore, by tracking the growth in perturbation amplitude through the linear regime, one can determine both the frequency and the growth rate of the unstable mode from the nonlinear simulations. This allows us to validate both the frequency and the growth rate obtained from the linearized equations.
The base flow is disturbed by pseudo-random perturbations of order ![]() $O(10^{-6})$ and the flow evolution is tracked. Figure 3(a) shows the variation of
$O(10^{-6})$ and the flow evolution is tracked. Figure 3(a) shows the variation of ![]() $\eta$ with time during the initial stages of the evolution. Both the linear and nonlinear results fall on top of each other providing the first evidence of the validity of the derived linear equations. Note that the nonlinear simulations have been performed using the ALE framework including the mesh movement, while there is no mesh motion in the linear equations which have been derived to be independent of the grid velocity
$\eta$ with time during the initial stages of the evolution. Both the linear and nonlinear results fall on top of each other providing the first evidence of the validity of the derived linear equations. Note that the nonlinear simulations have been performed using the ALE framework including the mesh movement, while there is no mesh motion in the linear equations which have been derived to be independent of the grid velocity ![]() $\boldsymbol {W^{g}}$. The time evolution of
$\boldsymbol {W^{g}}$. The time evolution of ![]() $\eta$ clearly indicates a single growing mode in the flow. By tracking the peak amplitudes of the oscillations, denoted as
$\eta$ clearly indicates a single growing mode in the flow. By tracking the peak amplitudes of the oscillations, denoted as ![]() $\eta ^{pks}$, one can determine the growth rate and the frequency of the unstable mode. Figure 3(b) shows the time evolution of
$\eta ^{pks}$, one can determine the growth rate and the frequency of the unstable mode. Figure 3(b) shows the time evolution of ![]() $\eta ^{pks}$ in a semi-log plot. After an initial transient phase both the growth rate and angular frequency of the disturbances stabilize to a constant value and the
$\eta ^{pks}$ in a semi-log plot. After an initial transient phase both the growth rate and angular frequency of the disturbances stabilize to a constant value and the ![]() $\eta ^{pks}$ plot traces a straight line in the semi-log plot, signifying exponential growth in time.
$\eta ^{pks}$ plot traces a straight line in the semi-log plot, signifying exponential growth in time.
Figure 3. Comparison of linear and nonlinear evolution of cylinder position ![]() $\eta$ for identical small-amplitude disturbance. (a) The time evolution of
$\eta$ for identical small-amplitude disturbance. (a) The time evolution of ![]() $\eta$ in the first few cycles of the oscillation. (b) The evolution of peak amplitudes of the oscillation in a semi-log scale.
$\eta$ in the first few cycles of the oscillation. (b) The evolution of peak amplitudes of the oscillation in a semi-log scale.
Finally, we introduce the ansatz ![]() $(\boldsymbol {u}',p',\eta ',\varphi ') = (\hat {\boldsymbol {u}},\hat {p},\hat {\eta },\hat {\varphi })\,\textrm {e}^{\lambda t}$ to reduce the linear equations into an eigenvalue problem for the angular frequency
$(\boldsymbol {u}',p',\eta ',\varphi ') = (\hat {\boldsymbol {u}},\hat {p},\hat {\eta },\hat {\varphi })\,\textrm {e}^{\lambda t}$ to reduce the linear equations into an eigenvalue problem for the angular frequency ![]() $\lambda$. The system is solved by estimating the eigenvalues of the time-stepping operator. The method was first used by Eriksson & Rizzi (Reference Eriksson and Rizzi1985) and has been used in several previous works by Barkley, Gomes & Henderson (Reference Barkley, Gomes and Henderson2002), Bagheri et al. (Reference Bagheri, Schlatter, Schmid and Henningson2009b) and Brynjell-Rahkola et al. (Reference Brynjell-Rahkola, Shahriari, Schlatter, Hanifi and Henningson2017) etc. The eigenvalue estimation is done using the implicitly restarted Arnoldi method (Sorensen Reference Sorensen1992) implemented in the open source software package ARPACK (Lehoucq, Sorensen & Yang Reference Lehoucq, Sorensen and Yang1998). Figure 4 shows the one-sided eigenspectra obtained with a single unstable mode. Here
$\lambda$. The system is solved by estimating the eigenvalues of the time-stepping operator. The method was first used by Eriksson & Rizzi (Reference Eriksson and Rizzi1985) and has been used in several previous works by Barkley, Gomes & Henderson (Reference Barkley, Gomes and Henderson2002), Bagheri et al. (Reference Bagheri, Schlatter, Schmid and Henningson2009b) and Brynjell-Rahkola et al. (Reference Brynjell-Rahkola, Shahriari, Schlatter, Hanifi and Henningson2017) etc. The eigenvalue estimation is done using the implicitly restarted Arnoldi method (Sorensen Reference Sorensen1992) implemented in the open source software package ARPACK (Lehoucq, Sorensen & Yang Reference Lehoucq, Sorensen and Yang1998). Figure 4 shows the one-sided eigenspectra obtained with a single unstable mode. Here ![]() $\lambda _{r}$ represents the real part of the eigenvalue (growth rate) and
$\lambda _{r}$ represents the real part of the eigenvalue (growth rate) and ![]() $\lambda _{i}$ represents the imaginary part of the eigenvalue (angular frequency). In table 2 we report the comparison of estimates obtained through the nonlinear simulations, linear simulations and the Arnoldi method. For both the linear and nonlinear simulations, the initial transient period of 10 oscillation cycles was discarded and the estimates are evaluated from the time period when both the growth rate and frequency have stabilized. All three methods have a very good agreement with each other, with the relative difference in the growth rate being less than
$\lambda _{i}$ represents the imaginary part of the eigenvalue (angular frequency). In table 2 we report the comparison of estimates obtained through the nonlinear simulations, linear simulations and the Arnoldi method. For both the linear and nonlinear simulations, the initial transient period of 10 oscillation cycles was discarded and the estimates are evaluated from the time period when both the growth rate and frequency have stabilized. All three methods have a very good agreement with each other, with the relative difference in the growth rate being less than ![]() $0.1\,\%$. The streamwise velocity component of the eigenvector for the unstable frequency is shown in figure 5.
$0.1\,\%$. The streamwise velocity component of the eigenvector for the unstable frequency is shown in figure 5.
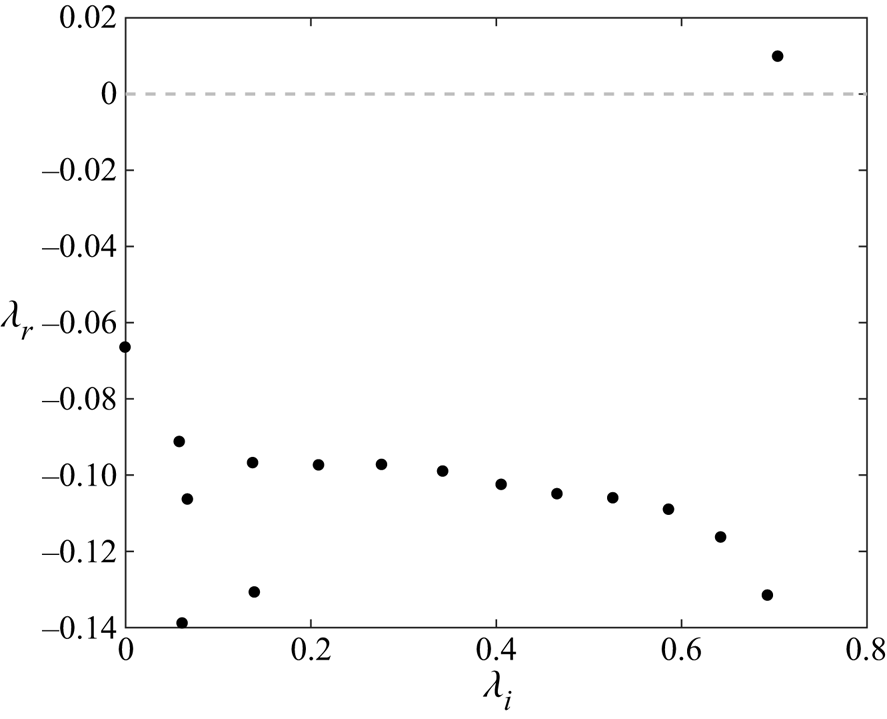
Figure 4. One-sided eigenspectrum for a cylinder in cross-flow at ![]() $Re=23.512$.
$Re=23.512$.

Figure 5. (a) Real and (b) imaginary parts of the streamwise velocity component of the eigenvector corresponding to the unstable eigenvalue for ![]() $Re=23.512$.
$Re=23.512$.
Table 2. Unstable eigenvalue estimates obtained from different methods for an oscillating cylinder at ![]() $Re=23.512$.
$Re=23.512$.
Thus, we find the flow is unstable for an oscillating cylinder at nearly half the critical Reynolds number for the stationary case. Cossu & Morino (Reference Cossu and Morino2000) also found instability at the same Reynolds number for a cylinder oscillating in the cross-flow direction, albeit for slightly different structural parameters.
The undamped natural frequency of the structural system ![]() $\omega _{n}$ is varied parametrically to investigate the changes in instability while keeping the density ratio constant. The damping constant is also varied such that the damping is always equal to
$\omega _{n}$ is varied parametrically to investigate the changes in instability while keeping the density ratio constant. The damping constant is also varied such that the damping is always equal to ![]() $0.754\,\%$ of the critical damping of the spring-mass-damper system. The one-sided spectra of the various cases is shown in figure 6. The instability of the system arises for a narrow range of
$0.754\,\%$ of the critical damping of the spring-mass-damper system. The one-sided spectra of the various cases is shown in figure 6. The instability of the system arises for a narrow range of ![]() $\omega _{n}$ with the peak of the instability centred around
$\omega _{n}$ with the peak of the instability centred around ![]() $\omega _{n}\approx 0.796$. The system rapidly becomes stable again as the structural frequency is varied away from the peak value. In the range where the system is unstable, the unstable frequency of the combined FSI system is close to the undamped frequency
$\omega _{n}\approx 0.796$. The system rapidly becomes stable again as the structural frequency is varied away from the peak value. In the range where the system is unstable, the unstable frequency of the combined FSI system is close to the undamped frequency ![]() $\omega _{n}$. Much of the low frequency spectra remains unaffected by the variation of
$\omega _{n}$. Much of the low frequency spectra remains unaffected by the variation of ![]() $\omega _{n}$. We note that some of the results are in contrast with some of the findings of Cossu & Morino (Reference Cossu and Morino2000) who performed global stability of the oscillating cylinder at the same Reynolds number and density ratio. In their study, the authors find a low frequency unstable mode with eigenvalue
$\omega _{n}$. We note that some of the results are in contrast with some of the findings of Cossu & Morino (Reference Cossu and Morino2000) who performed global stability of the oscillating cylinder at the same Reynolds number and density ratio. In their study, the authors find a low frequency unstable mode with eigenvalue ![]() $\lambda = 1.371\pm 0.194i$ for a structural eigenvalue of
$\lambda = 1.371\pm 0.194i$ for a structural eigenvalue of ![]() $\lambda _{s}=-0.01 \pm 1.326i$. The flow case marked with diamonds in figure 6 corresponds to the same case investigated by Cossu & Morino (Reference Cossu and Morino2000). While we find the system to be unstable at the subcritical Reynolds number of
$\lambda _{s}=-0.01 \pm 1.326i$. The flow case marked with diamonds in figure 6 corresponds to the same case investigated by Cossu & Morino (Reference Cossu and Morino2000). While we find the system to be unstable at the subcritical Reynolds number of ![]() $Re=23.512$, we do not find the instability for the same structural parameters. Unlike Cossu & Morino (Reference Cossu and Morino2000), we also do not find the existence of a low frequency unstable mode within the investigated structural parameters. In all our investigated cases, the effect of the structure on the spectrum remains confined close to the angular frequency of the spring-mass-damper system. (Note that the non-dimensionalization of length in Cossu & Morino (Reference Cossu and Morino2000) is with respect to the radius of the cylinder, while it is with respect to the diameter in the current study. Hence, the respective angular frequencies are doubled in the current study.)
$Re=23.512$, we do not find the instability for the same structural parameters. Unlike Cossu & Morino (Reference Cossu and Morino2000), we also do not find the existence of a low frequency unstable mode within the investigated structural parameters. In all our investigated cases, the effect of the structure on the spectrum remains confined close to the angular frequency of the spring-mass-damper system. (Note that the non-dimensionalization of length in Cossu & Morino (Reference Cossu and Morino2000) is with respect to the radius of the cylinder, while it is with respect to the diameter in the current study. Hence, the respective angular frequencies are doubled in the current study.)
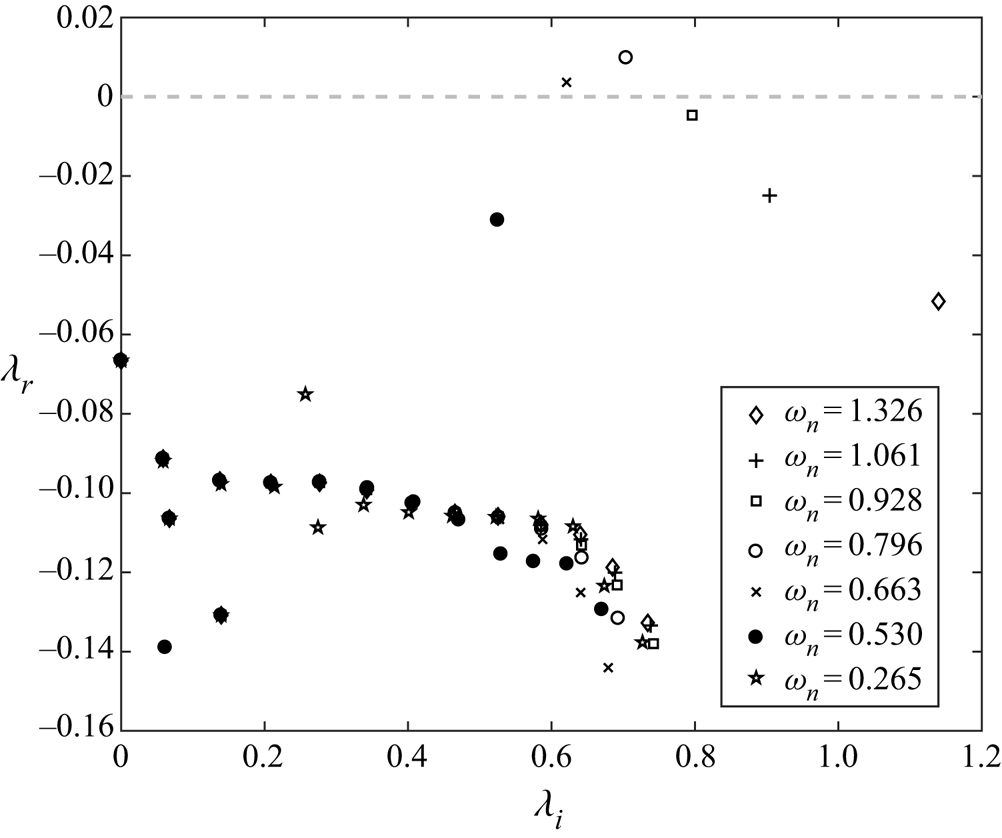
Figure 6. One-sided eigenspectra for a cylinder in cross-flow at ![]() $Re=23.512$ for varying undamped frequency,
$Re=23.512$ for varying undamped frequency, ![]() $\omega _{n}$, of the spring-mass system.
$\omega _{n}$, of the spring-mass system.
We consider another subcritical case at ![]() $Re=40$ which has been investigated in Navrose & Mittal (Reference Navrose and Mittal2016). In this case the authors consider an oscillating cylinder in cross-flow, with a mass ratio of 10 and without any structural damping (
$Re=40$ which has been investigated in Navrose & Mittal (Reference Navrose and Mittal2016). In this case the authors consider an oscillating cylinder in cross-flow, with a mass ratio of 10 and without any structural damping (![]() $\mathcal {D}=0$). The results are reported for the variation of the reduced velocity
$\mathcal {D}=0$). The results are reported for the variation of the reduced velocity ![]() $U^{*}$ which is defined as
$U^{*}$ which is defined as ![]() $U^{*}=U_{\infty }/(\,f_{n}D)$, where
$U^{*}=U_{\infty }/(\,f_{n}D)$, where ![]() $f_{n}=\omega _{n}/(2{\rm \pi} )$ is the natural frequency of the spring-mass system. We investigate the case with
$f_{n}=\omega _{n}/(2{\rm \pi} )$ is the natural frequency of the spring-mass system. We investigate the case with ![]() $U^{*}=8$, again comparing evolution of small-amplitude perturbations in the linear and the nonlinear cases. The initial cycles and the evolution of peak amplitude is shown in figures 7(a) and 7(b). The estimated eigenvalues from the linear, nonlinear and Arnoldi method are reported in table 3. The estimates match to within
$U^{*}=8$, again comparing evolution of small-amplitude perturbations in the linear and the nonlinear cases. The initial cycles and the evolution of peak amplitude is shown in figures 7(a) and 7(b). The estimated eigenvalues from the linear, nonlinear and Arnoldi method are reported in table 3. The estimates match to within ![]() $0.1\,\%$ accuracy. For the nonlinear simulations, the amplitude of oscillations saturates at
$0.1\,\%$ accuracy. For the nonlinear simulations, the amplitude of oscillations saturates at ![]() $y/D=0.4$. This compares well with the saturation amplitude reported in Navrose & Mittal (Reference Navrose and Mittal2016) for this case.
$y/D=0.4$. This compares well with the saturation amplitude reported in Navrose & Mittal (Reference Navrose and Mittal2016) for this case.
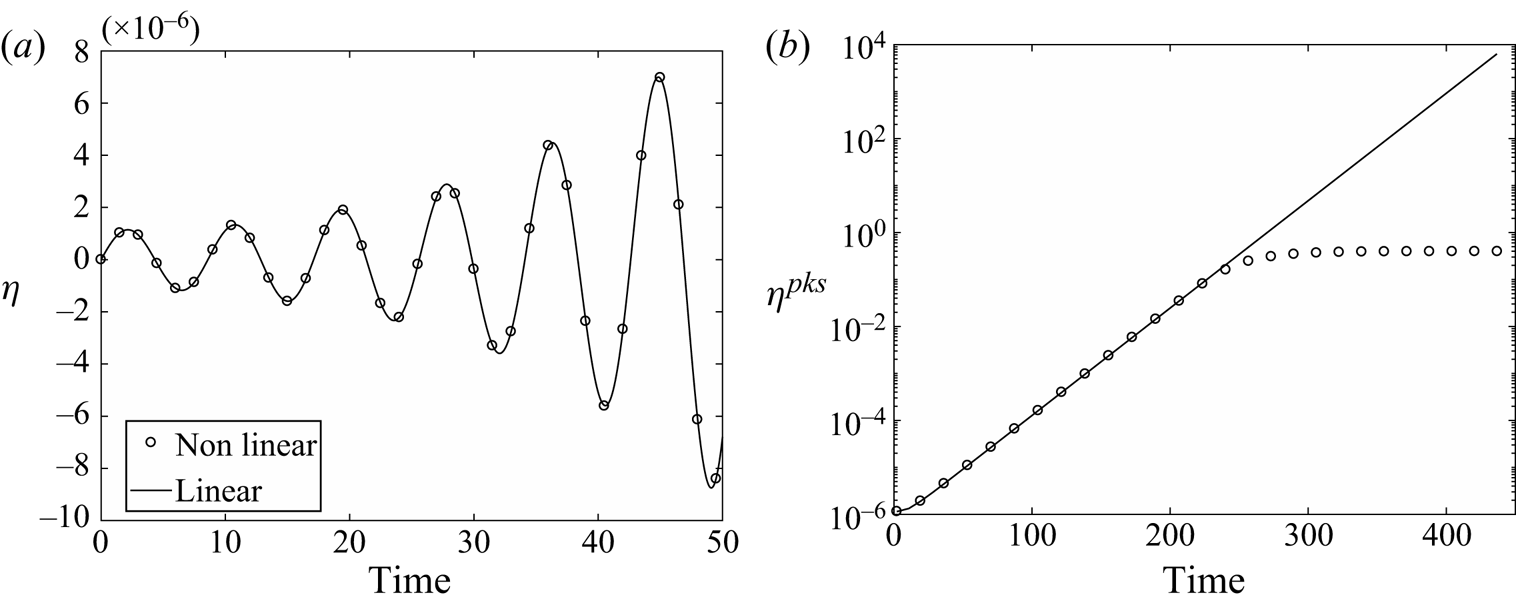
Figure 7. Comparison of linear and nonlinear evolution of cylinder position ![]() $\eta$ at
$\eta$ at ![]() $Re=40$ and
$Re=40$ and ![]() $U^{*}=8$. (a) Time evolution of
$U^{*}=8$. (a) Time evolution of ![]() $\eta$ in the first few cycles of the oscillation. (b) Evolution of peak amplitudes in a semi-log scale.
$\eta$ in the first few cycles of the oscillation. (b) Evolution of peak amplitudes in a semi-log scale.
Table 3. Unstable eigenvalue estimates obtained from different methods for an oscillating cylinder at ![]() $Re=40$ and
$Re=40$ and ![]() $U^{*}=8$.
$U^{*}=8$.
The variation of stability characteristics with varying reduced velocities is also investigated through the evaluation of the eigenvalue spectra for several different cases. The variation of spectra for different parameters is shown in figure 8(a). Similar to the trend seen for the ![]() $Re=23.512$ case, the flow exhibits unstable eigenvalues within a narrow band of frequencies. The variation of growth rate with the reduced velocities is shown in figure 8(b). The growth rates for
$Re=23.512$ case, the flow exhibits unstable eigenvalues within a narrow band of frequencies. The variation of growth rate with the reduced velocities is shown in figure 8(b). The growth rates for ![]() $U^{*}=6$ and
$U^{*}=6$ and ![]() $U^{*}=10$ lie just above the stability threshold. This compares very well with the results of Navrose & Mittal (Reference Navrose and Mittal2016) who report the unstable range as
$U^{*}=10$ lie just above the stability threshold. This compares very well with the results of Navrose & Mittal (Reference Navrose and Mittal2016) who report the unstable range as ![]() $5.9<U^{*}<10.1$ as the parameter range of instability for the oscillating cylinder at
$5.9<U^{*}<10.1$ as the parameter range of instability for the oscillating cylinder at ![]() $Re=40$. The peak growth rates occur at
$Re=40$. The peak growth rates occur at ![]() $U^{*}\approx 8.0$ in Navrose & Mittal (Reference Navrose and Mittal2016), which is also the case in the current work.
$U^{*}\approx 8.0$ in Navrose & Mittal (Reference Navrose and Mittal2016), which is also the case in the current work.

Figure 8. (a) One-sided spectra for an oscillating cylinder at ![]() $Re=40$ for varying reduced velocities
$Re=40$ for varying reduced velocities ![]() $U^{*}$. (b) Variation of the growth rate with reduced velocity
$U^{*}$. (b) Variation of the growth rate with reduced velocity ![]() $U^{*}$.
$U^{*}$.
3.3. Confined oscillating cylinder
In the previous two cases we simulated physical scenarios with effectively unbounded domains. In this subsection we consider the case of an FSI instability in a bounded domain. We replicate the physical set-up studied in Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2012), where a cylinder is free to oscillate in the vertical direction and is confined between two parallel walls. The channel height is denoted at ![]() $h$ and the ratio of the cylinder diameter to channel height is
$h$ and the ratio of the cylinder diameter to channel height is ![]() $D/h=0.66$. The computational domain is set up to match the simulations of Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2012), with the inlet located at
$D/h=0.66$. The computational domain is set up to match the simulations of Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2012), with the inlet located at ![]() $-5h$ and the outflow boundary located at
$-5h$ and the outflow boundary located at ![]() $7h$. A parabolic profile is imposed on the inlet for the streamwise velocity and the mean streamwise velocity (
$7h$. A parabolic profile is imposed on the inlet for the streamwise velocity and the mean streamwise velocity (![]() $\bar {U}$) at the inlet is used for the normalization of the velocity scales. The length scale is normalized by the channel height
$\bar {U}$) at the inlet is used for the normalization of the velocity scales. The length scale is normalized by the channel height ![]() $h$, and the Reynolds number is defined using these two scales as
$h$, and the Reynolds number is defined using these two scales as ![]() $Re=\bar {U}h/\nu$. The solid to fluid density ratio is set to
$Re=\bar {U}h/\nu$. The solid to fluid density ratio is set to ![]() $1.19$, which corresponds to the density ratio studied by Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2012) both numerically and experimentally. The cylinder is free to oscillate in the vertical direction without any external restoring forces or damping. Thus, the only forces acting on the cylinder are the fluid forces. We investigate the loss of stability in the FSI system for three different Reynolds numbers of
$1.19$, which corresponds to the density ratio studied by Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2012) both numerically and experimentally. The cylinder is free to oscillate in the vertical direction without any external restoring forces or damping. Thus, the only forces acting on the cylinder are the fluid forces. We investigate the loss of stability in the FSI system for three different Reynolds numbers of ![]() $Re=25, 22$ and
$Re=25, 22$ and ![]() $20$.
$20$.
Following the usual procedure outlined earlier, the base flow for the three different Reynolds numbers is obtained for a stationary cylinder. Small-amplitude perturbations are then seeded into the system and the linear and nonlinear evolution of the system is tracked in time. The base flow state for ![]() $Re=25$ is shown in figure 9. Figure 10(a) shows the evolution of the peak amplitudes of the oscillation. Again, evident from the graph is the fact that exponential growth is well captured by the linear formulation, and both linear and nonlinear regimes undergo the same amplification through several orders of magnitude. Figure 10(b) shows the eigenvalue spectra for the three cases. A comparison of the linear, nonlinear and Arnoldi approximations of the unstable eigenvalue is given in table 4 and the unstable eigenvector is shown in figure 11. The saturated limit-cycle amplitudes saturate at
$Re=25$ is shown in figure 9. Figure 10(a) shows the evolution of the peak amplitudes of the oscillation. Again, evident from the graph is the fact that exponential growth is well captured by the linear formulation, and both linear and nonlinear regimes undergo the same amplification through several orders of magnitude. Figure 10(b) shows the eigenvalue spectra for the three cases. A comparison of the linear, nonlinear and Arnoldi approximations of the unstable eigenvalue is given in table 4 and the unstable eigenvector is shown in figure 11. The saturated limit-cycle amplitudes saturate at ![]() $\eta _{max}=0.090, 0.076$ and
$\eta _{max}=0.090, 0.076$ and ![]() $0.062$ for
$0.062$ for ![]() $Re=25, 22$ and
$Re=25, 22$ and ![]() $20$, respectively. The corresponding Strouhal numbers, defined as
$20$, respectively. The corresponding Strouhal numbers, defined as ![]() $Sr=fh/\bar {U}$, with
$Sr=fh/\bar {U}$, with ![]() $f$ being the saturated oscillation frequency, are calculated as
$f$ being the saturated oscillation frequency, are calculated as ![]() $Sr=1.13, 1.17$ and
$Sr=1.13, 1.17$ and ![]() $1.22$. The values correspond well with the results of Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2012) for the given density ratio.
$1.22$. The values correspond well with the results of Semin et al. (Reference Semin, Decoene, Hulin, François and Auradou2012) for the given density ratio.
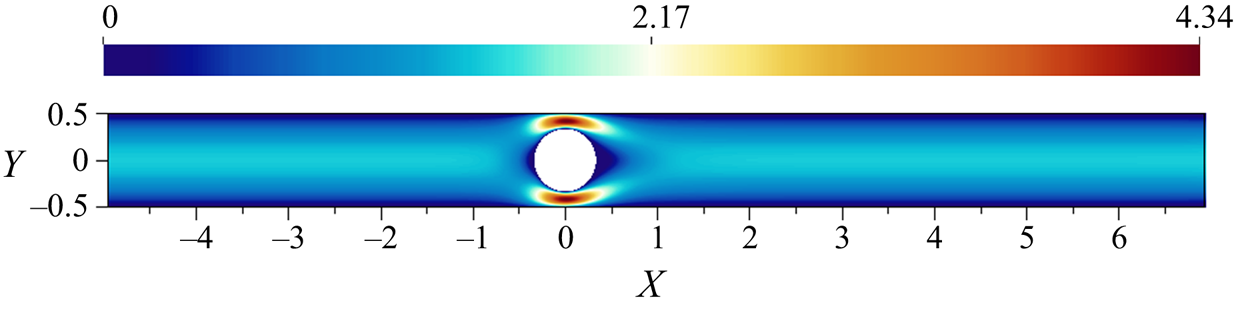
Figure 9. Streamwise velocity of the base flow state for a confined cylinder at ![]() $Re=25$.
$Re=25$.

Figure 10. (a) Comparison of linear and nonlinear evolution of peak amplitudes vertical displacement ![]() $\eta$ for a confined cylinder at three different Reynolds numbers. (b) One-sided eigenvalue spectra for the three different Reynolds number cases.
$\eta$ for a confined cylinder at three different Reynolds numbers. (b) One-sided eigenvalue spectra for the three different Reynolds number cases.

Figure 11. Real (a) and imaginary (b) parts of the streamwise velocity component of the unstable eigenvector for a confined cylinder at ![]() $Re=25$.
$Re=25$.
Table 4. Unstable eigenvalue estimates for a confined cylinder at different Reynolds numbers.

3.4. Asymmetric flow case of a rotated ellipse
The previous subsections investigated the flow around an oscillating circular cylinder through the linear stability analysis. The base flow for these cases exhibits symmetry about the horizontal axis passing through the origin. In order to test the linear formulation a case where no such symmetries arise we consider the case of a rotated ellipse in an open flow. The ellipse geometry is generated with the minor axis length of ![]() $a=0.25$ aligned with the streamwise direction, the major axis length of
$a=0.25$ aligned with the streamwise direction, the major axis length of ![]() $b=0.5$ aligned in the cross-flow direction and the centre of the ellipse located at the origin of the coordinate system
$b=0.5$ aligned in the cross-flow direction and the centre of the ellipse located at the origin of the coordinate system ![]() $(0,0)$. The ellipse is then rotated by an angle of
$(0,0)$. The ellipse is then rotated by an angle of ![]() $30^{\circ }$ clockwise. The stabilized base flow around the rotated ellipse is calculated at
$30^{\circ }$ clockwise. The stabilized base flow around the rotated ellipse is calculated at ![]() $Re=50$, where the diameter along the major axis is used as the length scale for the Reynolds number. The streamwise velocity for the stabilized base flow is shown in figure 12, which clearly shows the lack of symmetry of the base flow close to the ellipse.
$Re=50$, where the diameter along the major axis is used as the length scale for the Reynolds number. The streamwise velocity for the stabilized base flow is shown in figure 12, which clearly shows the lack of symmetry of the base flow close to the ellipse.

Figure 12. Streamwise velocity of the base flow state for a rotated ellipse at ![]() $Re=50$.
$Re=50$.
We consider two cases of FSI: an ellipse free to oscillate in the cross-flow direction and a case with the ellipse free to rotate about the out-of-plane axis passing through its centre. In both cases the ellipse is considered to be held stationary due to a constant external force which balances the fluid forces at equilibrium. The density ratio is set to 10 for the ellipse and no spring or damping forces are considered. Thus, the ellipse motion is governed entirely due to fluid forces and the inertia of the ellipse. We expect any modelling errors in fluid forces to show up strongly for such a case. Proceeding in the usual manner, the comparison of small-amplitude linear and nonlinear evolution for the oscillating case is shown in figures 13(a) and 13(b), while the comparison for the rotational case is shown in figures 13(c) and 13(d). The eigenvalue estimates for both cases are shown in table 5. A good agreement is found for all the cases considered. We note that for the case with vertical oscillations, a zero frequency unstable mode also exists. This was deduced from the time evolution of the simulations since the positive and negative peaks showed a marginally different growth rate. The Arnoldi procedure also showed the existence of both an oscillatory and zero frequency unstable mode. A nonlinear least squares procedure was then used to estimate the growth rate and the unstable frequencies. The one-sided spectra for the two cases is shown in figure 14 and the streamwise components of the eigenvector associated with the (oscillatory) unstable eigenvalues are shown in figure 15. We mention that we have evaluated the ‘added stiffness’ terms of Fanion et al. (Reference Fanion, Fernández and Le Tallec2000) and Fernández & Le Tallec (Reference Fernández and Le Tallec2003a,Reference Fernández and Le Tallecb) for all of the tested cases and we find that these terms always remain several orders of magnitude smaller than the forces arising due to the fluid perturbations. This further confirms the earlier mathematical result (2.24) that the ‘added stiffness’ terms represent a higher-order correction and do not play a role in the linearized dynamics.

Figure 13. Comparison of linear and nonlinear evolution of the position of a rotated ellipse at ![]() $Re=50$. The top two panels represent the vertical translation cases while the bottom two represent the rotational cases. (a) Time evolution of vertical position
$Re=50$. The top two panels represent the vertical translation cases while the bottom two represent the rotational cases. (a) Time evolution of vertical position ![]() $\eta$ in the first few cycles of the oscillation. (b) Evolution of peak amplitudes in a semi-log scale for vertical oscillations. (c) Time evolution of rotational angle
$\eta$ in the first few cycles of the oscillation. (b) Evolution of peak amplitudes in a semi-log scale for vertical oscillations. (c) Time evolution of rotational angle ![]() $\eta$. (d) Evolution of peak amplitudes of the rotational angle in a semi-log scale.
$\eta$. (d) Evolution of peak amplitudes of the rotational angle in a semi-log scale.

Figure 14. One-sided spectra for a rotated ellipse at ![]() $Re=50$. (a) Spectrum for an ellipse free to oscillate in the vertical direction and (b) spectrum for the ellipse free to rotate about its centre.
$Re=50$. (a) Spectrum for an ellipse free to oscillate in the vertical direction and (b) spectrum for the ellipse free to rotate about its centre.

Figure 15. Streamwise velocity component of the eigenvector for (a,b) vertical oscillation and (c,d) rotational FSI cases. The left panels show the real part of the eigenvector and the right panels show the imaginary part of the eigenvector corresponding to the unstable eigenvalue.
Table 5. Unstable eigenvalue estimates for vertical oscillation and rotational cases for a rotated ellipse at ![]() $Re=50$, obtained with three different methods.
$Re=50$, obtained with three different methods.
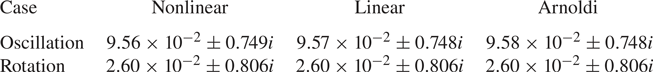
3.5. Spontaneous symmetry breaking
We use the derived linear formulation to investigate the case of a circular cylinder with an attached splitter plate set at zero incidence to the oncoming flow. The structural equations take the same form as in (3.1c), with ![]() $\eta$ now representing the deviation of the rotational angle from the equilibrium position. The terms
$\eta$ now representing the deviation of the rotational angle from the equilibrium position. The terms ![]() $\mathcal {M}, \mathcal {D}, \mathcal {K}$ and
$\mathcal {M}, \mathcal {D}, \mathcal {K}$ and ![]() $\mathcal {F}$ represent the moment of inertia, rotational damping, rotational stiffness and the out-of-plane moment acting on the body, respectively. The cylinder is free to rotate about its centre and the rotational stiffness
$\mathcal {F}$ represent the moment of inertia, rotational damping, rotational stiffness and the out-of-plane moment acting on the body, respectively. The cylinder is free to rotate about its centre and the rotational stiffness ![]() $\mathcal {K}$ and damping
$\mathcal {K}$ and damping ![]() $\mathcal {D}$ are both set to zero. Thus, the cylinder rotates only due to the action of the fluid forces. The particular set-up, along with a variant where the splitter plate is flexible, has been a subject of investigation by several previous authors (Xu, Sen & Gad-el Hak Reference Xu, Sen and Gad-el Hak1990, Reference Xu, Sen and Gad-el Hak1993; Bagheri, Mazzino & Bottaro Reference Bagheri, Mazzino and Bottaro2012; Lācis et al. Reference Lācis, Brosse, Ingremeau, Mazzino, Lundell, Kellay and Bagheri2014). For certain lengths of the cylinder-splitter body, the system exhibits an interesting dynamic where the body spontaneously breaks symmetry and the splitter plate settles at a non-zero angle to the oncoming flow. The breaking of symmetry leads to the generation of lift force which could play a role in locomotion through passive mechanisms (Bagheri et al. Reference Bagheri, Mazzino and Bottaro2012). The symmetry breaking phenomenon is known to occur for both subcritical and supercritical Reynolds numbers (Lācis et al. Reference Lācis, Brosse, Ingremeau, Mazzino, Lundell, Kellay and Bagheri2014) and in both two- and three-dimensional configurations (Lācis et al. Reference Lācis, Olivieri, Mazzino and Bagheri2017). We investigate the phenomenon through our linear FSI framework. According to the results of Lācis et al. (Reference Lācis, Brosse, Ingremeau, Mazzino, Lundell, Kellay and Bagheri2014), symmetry breaking is expected to occur for splitter-plate lengths of less than
$\mathcal {D}$ are both set to zero. Thus, the cylinder rotates only due to the action of the fluid forces. The particular set-up, along with a variant where the splitter plate is flexible, has been a subject of investigation by several previous authors (Xu, Sen & Gad-el Hak Reference Xu, Sen and Gad-el Hak1990, Reference Xu, Sen and Gad-el Hak1993; Bagheri, Mazzino & Bottaro Reference Bagheri, Mazzino and Bottaro2012; Lācis et al. Reference Lācis, Brosse, Ingremeau, Mazzino, Lundell, Kellay and Bagheri2014). For certain lengths of the cylinder-splitter body, the system exhibits an interesting dynamic where the body spontaneously breaks symmetry and the splitter plate settles at a non-zero angle to the oncoming flow. The breaking of symmetry leads to the generation of lift force which could play a role in locomotion through passive mechanisms (Bagheri et al. Reference Bagheri, Mazzino and Bottaro2012). The symmetry breaking phenomenon is known to occur for both subcritical and supercritical Reynolds numbers (Lācis et al. Reference Lācis, Brosse, Ingremeau, Mazzino, Lundell, Kellay and Bagheri2014) and in both two- and three-dimensional configurations (Lācis et al. Reference Lācis, Olivieri, Mazzino and Bagheri2017). We investigate the phenomenon through our linear FSI framework. According to the results of Lācis et al. (Reference Lācis, Brosse, Ingremeau, Mazzino, Lundell, Kellay and Bagheri2014), symmetry breaking is expected to occur for splitter-plate lengths of less than ![]() $2D$. Accordingly, we set the splitter-plate length to be
$2D$. Accordingly, we set the splitter-plate length to be ![]() $1D$ and a thickness of
$1D$ and a thickness of ![]() $0.02D$. Following Lācis et al. (Reference Lācis, Brosse, Ingremeau, Mazzino, Lundell, Kellay and Bagheri2014) we use a solid to fluid density ratio of
$0.02D$. Following Lācis et al. (Reference Lācis, Brosse, Ingremeau, Mazzino, Lundell, Kellay and Bagheri2014) we use a solid to fluid density ratio of ![]() $1.001$ for
$1.001$ for ![]() $Re=45$ and
$Re=45$ and ![]() $1.01$ for
$1.01$ for ![]() $Re=156$. Figures 16(a) and 16(b) show the base flow states for the diameter based Reynolds numbers of
$Re=156$. Figures 16(a) and 16(b) show the base flow states for the diameter based Reynolds numbers of ![]() $Re=45$ (subcritical) and
$Re=45$ (subcritical) and ![]() $Re=156$ (supercritical).
$Re=156$ (supercritical).

Figure 16. Base flow state for a cylinder with splitter plate at (a) ![]() $Re=45.0$ and (b)
$Re=45.0$ and (b) ![]() $Re=156$. Note that the splitter plate is not discernible in the visualization due to its very small thickness (
$Re=156$. Note that the splitter plate is not discernible in the visualization due to its very small thickness (![]() $0.02D$).
$0.02D$).
Figure 17 shows the spectra for the two different Reynolds numbers. Both cases have an eigenvalue lying on the positive ![]() $y$-axis (
$y$-axis (![]() $\lambda =0.10+0i$ for
$\lambda =0.10+0i$ for ![]() $Re=45$ and
$Re=45$ and ![]() $\lambda =0.19+0i$ for
$\lambda =0.19+0i$ for ![]() $Re=156$). This represents the symmetry breaking eigenmode of the system since it does not oscillate about a zero mean but rather leads to a monotonic growth in the rotational angle. For the higher Reynolds number, several other modes of instability exist in the flow which represent the von-Kármán modes of the flow. From the perspective of linear analysis, these modes simply oscillate about the mean angle with growing oscillation amplitudes. However, the zero frequency mode leads to a monotonic rise in the angle and, thus, causes the symmetry breaking effect. For
$Re=156$). This represents the symmetry breaking eigenmode of the system since it does not oscillate about a zero mean but rather leads to a monotonic growth in the rotational angle. For the higher Reynolds number, several other modes of instability exist in the flow which represent the von-Kármán modes of the flow. From the perspective of linear analysis, these modes simply oscillate about the mean angle with growing oscillation amplitudes. However, the zero frequency mode leads to a monotonic rise in the angle and, thus, causes the symmetry breaking effect. For ![]() $Re=45$, we also simulate the linear and nonlinear cases after adding a random small-amplitude perturbations to both flow cases. Figure 18 shows the time evolution of the angle
$Re=45$, we also simulate the linear and nonlinear cases after adding a random small-amplitude perturbations to both flow cases. Figure 18 shows the time evolution of the angle ![]() $\eta$ of the cylinder-splitter body. Both the simulations undergo the same exponential growth of about five orders of magnitude before the nonlinear case saturates, while the linear case continues its exponential growth. The saturation of the nonlinear simulations occur at
$\eta$ of the cylinder-splitter body. Both the simulations undergo the same exponential growth of about five orders of magnitude before the nonlinear case saturates, while the linear case continues its exponential growth. The saturation of the nonlinear simulations occur at ![]() $\eta \approx 15.5^{\circ }$, which is the same turn angle reported by Lācis et al. (Reference Lācis, Brosse, Ingremeau, Mazzino, Lundell, Kellay and Bagheri2014) for a splitter plate of length
$\eta \approx 15.5^{\circ }$, which is the same turn angle reported by Lācis et al. (Reference Lācis, Brosse, Ingremeau, Mazzino, Lundell, Kellay and Bagheri2014) for a splitter plate of length ![]() $1D$. Thus, the linear FSI framework predicts the onset of symmetry breaking instability. Of course for the system to finally exhibit symmetry breaking a nonlinear mechanism is required since the flow must equilibrate at the new position. However, the onset can be traced to the zero frequency unstable mode.
$1D$. Thus, the linear FSI framework predicts the onset of symmetry breaking instability. Of course for the system to finally exhibit symmetry breaking a nonlinear mechanism is required since the flow must equilibrate at the new position. However, the onset can be traced to the zero frequency unstable mode.

Figure 17. One-sided spectra for the cases exhibiting spontaneous symmetry breaking at ![]() $Re=45$ and
$Re=45$ and ![]() $Re=156$ for a rotatable cylinder with splitter plate.
$Re=156$ for a rotatable cylinder with splitter plate.

Figure 18. Time evolution of the angle for a rotatable cylinder with the splitter plate at ![]() $Re=45$.
$Re=45$.
As noted earlier, the work of Pfister et al. (Reference Pfister, Marquet and Carini2019) also considered the problem of linear instability in FSI problems and considered more general structural models including nonlinear structural models and finite aspect ratio geometries. The approach towards linearization of the fluid quantities however has been different from the one taken in the current study. It is therefore interesting to contrast the linearization approaches of the two studies. In particular, both studies start with the ALE form of the full Navier–Stokes and clearly realize the importance of treating the motion of material points consistently. The point of departure between the two studies has been on the approach towards the treatment of the material point motion in the fluid domain. Pfister et al. (Reference Pfister, Marquet and Carini2019) take the approach of incorporating the changes into the equations itself. On the other hand, in the current work the linearized operator at the deformed material points is further approximated by way of a Taylor series expansion and geometric linearization. The final form of the linearized Navier–Stokes obtained is the obvious conclusion of these different approaches. Pfister et al. (Reference Pfister, Marquet and Carini2019) obtain a modified linear operator on a moving grid which incorporates the effects of domain deformation, while the current work obtains the modified linear operator defined on the original stationary grid (the modification arising only at the boundaries). It appears the crucial aspect in the FSI linearization is the consistent treatment of material point motion. Finally, we make a note that the PhD thesis of Pfister (Reference Pfister2019) reports some cases with more complex structural models where the added stiffness terms appear to have a non-trivial effect on the instability characteristics of the FSI problems.
4. Structural sensitivity of the eigenvalue
As noted in figures 6 and 8(a), the unstable eigenvalue of the coupled FSI system changes as the structural parameters are varied, while the base flow is held constant. The variation occurs both for the growth rate as well as the frequency of the eigenvalue. One might expect the sensitivity of the eigenvalue to structural perturbations to change as well. We investigate the eigenvalue sensitivity to structural perturbations for different values of the structural parameters for a spring-mounted two-dimensional circular cylinder, which is free to oscillate in the cross-stream direction. The linear FSI problem is defined by (3.2a)–(3.2i). In the following sections we assume all derivatives are evaluated in the reference configuration and we drop the superscript ![]() $^{0}$ from the derivative terms. In addition, uppercase letters denote base flow quantities and lowercase letters denote perturbation quantities, and the superscripts
$^{0}$ from the derivative terms. In addition, uppercase letters denote base flow quantities and lowercase letters denote perturbation quantities, and the superscripts ![]() $^{0}$ and
$^{0}$ and ![]() $'$ are dropped from the base flow and perturbation quantities.
$'$ are dropped from the base flow and perturbation quantities.
The eigenvalue sensitivity is typically studied through the use of adjoint equations (Giannetti & Luchini Reference Giannetti and Luchini2007; Luchini & Bottaro Reference Luchini and Bottaro2014). For any linear operator ![]() $\mathcal {L}$, the adjoint operator
$\mathcal {L}$, the adjoint operator ![]() $\mathcal {L}^{\dagger }$ is defined such that it satisfies the Lagrange identity
$\mathcal {L}^{\dagger }$ is defined such that it satisfies the Lagrange identity
for any arbitrary vectors ![]() $q$ and
$q$ and ![]() $p$ in the domain of
$p$ in the domain of ![]() $\mathcal {L}$ and
$\mathcal {L}$ and ![]() $\mathcal {L}^{\dagger }$, respectively. The symbol
$\mathcal {L}^{\dagger }$, respectively. The symbol ![]() $\langle \cdot ,\cdot \rangle$ denotes the inner product under which the above identity holds. In the current context the operator
$\langle \cdot ,\cdot \rangle$ denotes the inner product under which the above identity holds. In the current context the operator ![]() $\mathcal {L}$ represents the linearized Navier–Stokes equations for FSI, also referred to as the direct problem,
$\mathcal {L}$ represents the linearized Navier–Stokes equations for FSI, also referred to as the direct problem, ![]() $\mathcal {L}^{\dagger }$ is the corresponding adjoint operator with the definition of the inner product as the integral over the domain
$\mathcal {L}^{\dagger }$ is the corresponding adjoint operator with the definition of the inner product as the integral over the domain ![]() $\varOmega$ and time horizon
$\varOmega$ and time horizon ![]() $T$:
$T$:
Defining the vector ![]() $\boldsymbol {q}=(\boldsymbol {u},p,\eta ,\varphi )$, which lies in the domain of
$\boldsymbol {q}=(\boldsymbol {u},p,\eta ,\varphi )$, which lies in the domain of ![]() $\mathcal {L}$, and an adjoint vector
$\mathcal {L}$, and an adjoint vector ![]() $\boldsymbol {q}^{\dagger }=(\boldsymbol {u}^{\dagger },p^{\dagger },\eta ^{\dagger },\varphi ^{\dagger })$ which lies in the domain of
$\boldsymbol {q}^{\dagger }=(\boldsymbol {u}^{\dagger },p^{\dagger },\eta ^{\dagger },\varphi ^{\dagger })$ which lies in the domain of ![]() $\mathcal {L^{\dagger }}$, the adjoint equations may be found by taking the inner product between the adjoint variables and the direct equations. The use of integration by parts, divergence theorem and a judicious manipulation of terms leads to a set of expressions for the adjoint equations. The full derivation of the equations along with the boundary conditions may be found in appendix B. The final form of the adjoint equations is expressed as
$\mathcal {L^{\dagger }}$, the adjoint equations may be found by taking the inner product between the adjoint variables and the direct equations. The use of integration by parts, divergence theorem and a judicious manipulation of terms leads to a set of expressions for the adjoint equations. The full derivation of the equations along with the boundary conditions may be found in appendix B. The final form of the adjoint equations is expressed as
 \begin{gather} -\frac{\partial u^{\dagger}_{i}}{\partial t} + u^{\dagger}_{j} \frac{\partial U_{j}}{\partial x_{i}}-U_{j}\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial p^{\dagger}}{\partial x_{i}} - \frac{1}{Re}\frac{\partial }{\partial x_{j}} \left(\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial u^{\dagger}_{j}}{\partial x_{i}}\right) =0\quad \text{in } \varOmega^{f}, \end{gather}
\begin{gather} -\frac{\partial u^{\dagger}_{i}}{\partial t} + u^{\dagger}_{j} \frac{\partial U_{j}}{\partial x_{i}}-U_{j}\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial p^{\dagger}}{\partial x_{i}} - \frac{1}{Re}\frac{\partial }{\partial x_{j}} \left(\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial u^{\dagger}_{j}}{\partial x_{i}}\right) =0\quad \text{in } \varOmega^{f}, \end{gather} \begin{gather}\sigma_{ij}^{\dagger} - \left[-p^{\dagger}\delta_{ij} + \frac{1}{Re}\left(\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial u^{\dagger}_{j}}{\partial x_{i}} \right)\right] = 0\quad \text{adjoint forces on } \varGamma, \end{gather}
\begin{gather}\sigma_{ij}^{\dagger} - \left[-p^{\dagger}\delta_{ij} + \frac{1}{Re}\left(\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial u^{\dagger}_{j}}{\partial x_{i}} \right)\right] = 0\quad \text{adjoint forces on } \varGamma, \end{gather}
Here ![]() $\sigma _{ij}^{\dagger }$ is referred to as the adjoint fluid stresses acting on the cylinder. Unlike in the direct equations, the adjoint fluid velocities are spatially homogeneous on the FSI interface
$\sigma _{ij}^{\dagger }$ is referred to as the adjoint fluid stresses acting on the cylinder. Unlike in the direct equations, the adjoint fluid velocities are spatially homogeneous on the FSI interface ![]() $\varGamma$. The sign of the diffusive term indicates the equations evolve an adjoint field backward in time. A variable substitution
$\varGamma$. The sign of the diffusive term indicates the equations evolve an adjoint field backward in time. A variable substitution ![]() $\tau = - t$ can be made to return the equations to forward (in
$\tau = - t$ can be made to return the equations to forward (in ![]() $\tau$) propagation.
$\tau$) propagation.
A validation of the adjoint equations can be found by comparing the spectra of the direct and adjoint problems. The eigenvalues of the adjoint problem are the complex conjugate of the eigenvalues of the direct problem. For real matrices, the spectra for both problems is the same. Figure 19 shows the direct and adjoint spectra for a spring-mounted two-dimensional cylinder at a diameter based Reynolds number of ![]() $Re=50$, mass ratio of
$Re=50$, mass ratio of ![]() $10$, corresponding to
$10$, corresponding to ![]() $\mathcal {M}=7.854$,
$\mathcal {M}=7.854$, ![]() $\mathcal {K}=1.1537$ which corresponds to the natural frequency of the spring-mass system of
$\mathcal {K}=1.1537$ which corresponds to the natural frequency of the spring-mass system of ![]() $\omega _{n}=0.3833$. The damping is set to zero (
$\omega _{n}=0.3833$. The damping is set to zero (![]() $\mathcal {D}=0$). As observed in the figure, the spectra for both the direct and adjoint problems have a very good agreement with each other.
$\mathcal {D}=0$). As observed in the figure, the spectra for both the direct and adjoint problems have a very good agreement with each other.

Figure 19. Comparison of the eigenspectra for the direct and adjoint problems for a density ratio of ![]() $10$ and natural frequency
$10$ and natural frequency ![]() $\omega _{n}=0.3833$.
$\omega _{n}=0.3833$.
For a general linear eigenvalue problem ![]() $\mathcal {L}q = \lambda q$, a first-order approximation to the perturbed eigenvalue problem
$\mathcal {L}q = \lambda q$, a first-order approximation to the perturbed eigenvalue problem ![]() $(\mathcal {L} +{\rm \Delta} \mathcal {L})(q + {\rm \Delta} q) = (\lambda + {\rm \Delta} \lambda )(q +{\rm \Delta} q)$ can be obtained by making use of the corresponding adjoint eigenvector vector field
$(\mathcal {L} +{\rm \Delta} \mathcal {L})(q + {\rm \Delta} q) = (\lambda + {\rm \Delta} \lambda )(q +{\rm \Delta} q)$ can be obtained by making use of the corresponding adjoint eigenvector vector field ![]() $q^{\dagger }$ (Giannetti & Luchini Reference Giannetti and Luchini2007), resulting in an expression for the eigenvalue perturbation as
$q^{\dagger }$ (Giannetti & Luchini Reference Giannetti and Luchini2007), resulting in an expression for the eigenvalue perturbation as
where ![]() $^{*}$ implies complex conjugation and
$^{*}$ implies complex conjugation and ![]() $q^{\dagger }$ represents the right eigenvector of the adjoint operator
$q^{\dagger }$ represents the right eigenvector of the adjoint operator ![]() $\mathcal {L}^{\dagger }$ with the eigenvalue of
$\mathcal {L}^{\dagger }$ with the eigenvalue of ![]() $\lambda ^{*}$. To estimate the drift in eigenvalue, knowledge of the specific operator perturbation
$\lambda ^{*}$. To estimate the drift in eigenvalue, knowledge of the specific operator perturbation ![]() ${\rm \Delta} \mathcal {L}$ is required. However, as shown by Giannetti & Luchini (Reference Giannetti and Luchini2007), a spatial sensitivity map of the eigenvalue perturbation can be found by assuming the perturbation operator to be of the form of a spatially localized feedback, with the feedback being proportional to the local values of the field variables (velocities). For such a case, we may estimate the eigenvalue drift along with its upper bound for each spatially localized operator perturbation as
${\rm \Delta} \mathcal {L}$ is required. However, as shown by Giannetti & Luchini (Reference Giannetti and Luchini2007), a spatial sensitivity map of the eigenvalue perturbation can be found by assuming the perturbation operator to be of the form of a spatially localized feedback, with the feedback being proportional to the local values of the field variables (velocities). For such a case, we may estimate the eigenvalue drift along with its upper bound for each spatially localized operator perturbation as
where ![]() $C_{0}$ is a matrix that defines the feedback due to the localized operator perturbation and the local coupling between different velocity components. The quantity
$C_{0}$ is a matrix that defines the feedback due to the localized operator perturbation and the local coupling between different velocity components. The quantity ![]() $\boldsymbol {\varTheta }(x,y)$ gives an indication of regions where the localized feedback will produce a large drift in the eigenvalue, thus representing the sensitivity of the eigenvalue to structural perturbations.
$\boldsymbol {\varTheta }(x,y)$ gives an indication of regions where the localized feedback will produce a large drift in the eigenvalue, thus representing the sensitivity of the eigenvalue to structural perturbations.
The structural sensitivity of a spring-mounted cylinder is investigated for varying natural frequencies ![]() $\omega _{n}$ of the spring-mass system. In all subsequent cases the structural damping is set to zero and the density ratio is set to
$\omega _{n}$ of the spring-mass system. In all subsequent cases the structural damping is set to zero and the density ratio is set to ![]() $10$. The natural frequency of the spring-mass system is varied and the sensitivity map
$10$. The natural frequency of the spring-mass system is varied and the sensitivity map ![]() $\boldsymbol {\varTheta }$ of the least stable eigenvalue is evaluated. Table 6 shows the variation of the natural frequency
$\boldsymbol {\varTheta }$ of the least stable eigenvalue is evaluated. Table 6 shows the variation of the natural frequency ![]() $\omega _{n}$ and the corresponding least stable eigenvalue. The table also shows the unstable eigenvalue for a stationary cylinder at
$\omega _{n}$ and the corresponding least stable eigenvalue. The table also shows the unstable eigenvalue for a stationary cylinder at ![]() $Re=50$. Figure 20 shows the corresponding changes in structural sensitivity of the least stable eigenvalue. When the structural frequency is much lower than the unstable frequency (figure 20b), the sensitivity map resembles the sensitivity map of the stationary cylinder with small changes close to the cylinder. A small region of sensitivity is generated close to the cylinder, which is located symmetrically with respect to the horizontal axis. This region grows in intensity as
$Re=50$. Figure 20 shows the corresponding changes in structural sensitivity of the least stable eigenvalue. When the structural frequency is much lower than the unstable frequency (figure 20b), the sensitivity map resembles the sensitivity map of the stationary cylinder with small changes close to the cylinder. A small region of sensitivity is generated close to the cylinder, which is located symmetrically with respect to the horizontal axis. This region grows in intensity as ![]() $\omega _{n}$ approaches closer to the unstable frequency (20c). Close to resonance (20d), the dominant region shifts to the cylinder, lying symmetrically on the top and bottom. The near wake region is still sensitive to structural perturbations, however, it is no longer the dominant region. As
$\omega _{n}$ approaches closer to the unstable frequency (20c). Close to resonance (20d), the dominant region shifts to the cylinder, lying symmetrically on the top and bottom. The near wake region is still sensitive to structural perturbations, however, it is no longer the dominant region. As ![]() $\omega _{n}$ is increased to be much larger than the unstable frequency, the sensitivity map resembles the stationary case again. In all cases with FSI, the sensitivity is non-zero at the cylinder surface. However, the values remain small if
$\omega _{n}$ is increased to be much larger than the unstable frequency, the sensitivity map resembles the stationary case again. In all cases with FSI, the sensitivity is non-zero at the cylinder surface. However, the values remain small if ![]() $\omega _{n}$ is far from resonance. Close to resonance, small regions on the cylinder surface have high sensitivities. A close-up of the sensitivity map for
$\omega _{n}$ is far from resonance. Close to resonance, small regions on the cylinder surface have high sensitivities. A close-up of the sensitivity map for ![]() $\omega _{n}=0.7665$ is shown in figure 21, which shows non-zero values of
$\omega _{n}=0.7665$ is shown in figure 21, which shows non-zero values of ![]() $\boldsymbol {\varTheta }$ at the cylinder surface. The non-zero sensitivity on the cylinder surface has implications for control of vortex induced vibrations. In particular, it is found that control techniques for elimination of vortex streets which apply to stationary cylinders do not always work for vibrating cylinders (Dong, Triantafyllou & Karniadakis Reference Dong, Triantafyllou and Karniadakis2008).
$\boldsymbol {\varTheta }$ at the cylinder surface. The non-zero sensitivity on the cylinder surface has implications for control of vortex induced vibrations. In particular, it is found that control techniques for elimination of vortex streets which apply to stationary cylinders do not always work for vibrating cylinders (Dong, Triantafyllou & Karniadakis Reference Dong, Triantafyllou and Karniadakis2008).

Figure 20. Comparison of the structural sensitivity map for the least stable eigenvalue for different values of the natural frequency ![]() $\omega _{n}$. The top panel (a) is the structural sensitivity for the stationary cylinder case. The bottom four panels (b–e) represent the cases with FSI. (a) Stationary cylinder; (b)
$\omega _{n}$. The top panel (a) is the structural sensitivity for the stationary cylinder case. The bottom four panels (b–e) represent the cases with FSI. (a) Stationary cylinder; (b) ![]() $\omega _{n}=0.0767$; (c)
$\omega _{n}=0.0767$; (c) ![]() $\omega _{n}=0.3833$; (d)
$\omega _{n}=0.3833$; (d) ![]() $\omega _{n}=0.7665$ and (e)
$\omega _{n}=0.7665$ and (e) ![]() $\omega _{n}=3.8327$.
$\omega _{n}=3.8327$.

Figure 21. Close-up of the sensitivity map for ![]() $\omega _{n}=0.7665$.
$\omega _{n}=0.7665$.
Table 6. Unstable eigenvalue corresponding to the structural natural frequency ![]() $\omega _{n}$ for the oscillating cylinder cases.
$\omega _{n}$ for the oscillating cylinder cases.

5. Conclusions
An Eulerian formulation for the linear stability analysis of rigid-body motion FSI problems is rigorously derived and validated. The final form of the linear equations is evaluated on the equilibrium grid on which the base state is defined and the first-order effects of moving interfaces are captured by the modification of the interface boundary conditions. The ‘added stiffness’ terms that arise in the formulation of Fanion et al. (Reference Fanion, Fernández and Le Tallec2000) and Fernández & Le Tallec (Reference Fernández and Le Tallec2003a,Reference Fernández and Le Tallecb) are shown to vanish to a first-order approximation and play no role in the linearized perturbation dynamics. The formulation is validated for rigid-body motion FSI problems by comparing the evolution of the linear equations with the nonlinear system when both systems are perturbed with identical small-amplitude disturbances. This has been performed for several different cases for both rotation and translation motion, in symmetric as well as asymmetric flow cases, and bounded and unbounded flows. The linear and nonlinear equations evolve in a near identical manner and the extracted frequency and growth rates for the two cases match to within ![]() $0.1\,\%$ relative difference.
$0.1\,\%$ relative difference.
The FSI linear framework is used to analyse the case of symmetry breaking for a rotating cylinder with a rigid splitter plate. The linear stability analysis predicts the existence of a zero frequency unstable mode. This mode is identified as the cause of symmetry breaking since it causes the system to monotonically deviate from the equilibrium position and thus causing the onset of the symmetry breaking effect. The zero frequency unstable mode can be found for both the subcritical and supercritical Reynolds numbers.
Finally, the eigenvalue sensitivity to structural perturbations is investigated using the adjoint equations for FSI, for a two-dimensional cylinder oscillating in the cross-stream direction at ![]() $Re=50$, for varying natural frequencies of the spring-mass system. When the structural frequencies are far from the unstable frequency, the sensitivity is hardly affected. However, close to resonance, the sensitivity map changes completely and the dominant region of sensitivity lies close to the cylinder, located symmetrically above and below. In all cases of FSI, the sensitivity at the surface is non-zero, however, it attains large values only close to the resonance condition between the fluid and the structure.
$Re=50$, for varying natural frequencies of the spring-mass system. When the structural frequencies are far from the unstable frequency, the sensitivity is hardly affected. However, close to resonance, the sensitivity map changes completely and the dominant region of sensitivity lies close to the cylinder, located symmetrically above and below. In all cases of FSI, the sensitivity at the surface is non-zero, however, it attains large values only close to the resonance condition between the fluid and the structure.
Acknowledgements
Financial support for this work was provided by the European Research Council under grant agreement 694452-TRANSEP-ERC-2015-AdG. The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the PDC Center for High Performance Computing at the Royal Institute of Technology (KTH). The authors would like to thank Dr Lācis for his helpful comments on the manuscript.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Navier–Stokes of Taylor expansion terms
We evaluate the Navier–Stokes at the perturbed locations using the Taylor expansion of the velocity and pressure fields and then use the geometric linearization to consistently evaluate derivatives at the perturbed configuration. Nonlinear terms arising due to the interaction of perturbations terms ![]() $\boldsymbol {u}', p', \mathcal {R}'$ and
$\boldsymbol {u}', p', \mathcal {R}'$ and ![]() $\boldsymbol {{\rm \Delta} x}'$ are dropped, and the equation may be expanded as
$\boldsymbol {{\rm \Delta} x}'$ are dropped, and the equation may be expanded as
 \begin{align} & \left[U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}} + U^{0}_{j}\frac{\partial u^{\xi}_{i}}{\partial x_{j}} + u^{\xi}_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}} + \frac{\partial P^{0}}{\partial x_{i}} + \frac{\partial p^{\xi}}{\partial x_{i}} - \frac{1}{Re}\frac{\partial^{2}U^{0}_{i}}{\partial x_{j}\partial x_{j}} - \frac{1}{Re}\frac{\partial^{2}u^{\xi}_{i}}{\partial x_{j}\partial x_{j}}\right] \nonumber\\ &\qquad +\left[ \left.\frac{\partial U_{i}}{\partial t}\right\vert_{\boldsymbol{w}} -w_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}} + U^{0}_{j}\frac{\partial u'_{i}}{\partial x_{j}} + u'_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}} + \frac{\partial p'}{\partial x_{i}} -\frac{1}{Re}\frac{\partial^{2}u'_{i}}{\partial x_{j}\partial x_{j}}\right] = 0, \nonumber\\ &\quad \implies \overbrace{\left[U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{k}}(\mathcal{I}_{kj} - \mathcal{R'}_{kj})\right]}^{I} + \overbrace{\left[U^{0}_{j}\frac{\partial }{\partial x^{0}_{k}} \left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{l}}{\rm \Delta} x_{l}\right)(\mathcal{I}_{kj} - \mathcal{R'}_{kj})\right]}^{II} \nonumber\\ &\qquad + \overbrace{\left[\left(\frac{\partial U^{0}_{j}}{\partial x^{0}_{l}}{\rm \Delta} x_{l}\right) \frac{\partial U^{0}_{i}}{\partial x^{0}_{k}}(\mathcal{I}_{kj} - \mathcal{R'}_{kj})\right]}^{III} \nonumber\\ &\qquad + \overbrace{\left[\frac{\partial P^{0}}{\partial x^{0}_{k}}(\mathcal{I}_{ki} - \mathcal{R'}_{ki})\right]}^{IV} +\overbrace{\left[u'_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{k}}(\mathcal{I}_{kj} - \mathcal{R'}_{kj})\right]}^{V} \nonumber\\ &\qquad +\overbrace{\left[U^{0}_{j}\frac{\partial u'_{i}}{\partial x^{0}_{k}}(\mathcal{I}_{kj} - \mathcal{R'}_{kj})\right]}^{VI} + \overbrace{\left[\frac{\partial p'}{\partial x^{0}_{k}}(\mathcal{I}_{ki} - \mathcal{R'}_{ki})\right]}^{VII} + \overbrace{\left[\frac{\partial }{\partial x^{0}_{k}}\left(\frac{\partial P^{0}}{\partial x_{l}}{\rm \Delta} x_{l} \right)(\mathcal{I}_{ki} - \mathcal{R'}_{ki})\right]}^{VIII} \nonumber\\ &\qquad -\overbrace{\left[\frac{1}{Re}\frac{\partial^{2}U^{0}_{i}}{\partial x^{0}_{k}\partial x^{0}_{n}}(\mathcal{I}_{kj}\mathcal{I}_{nj} - \mathcal{I}_{kj}\mathcal{R'}_{nj} -\mathcal{R'}_{kj}\mathcal{I}_{nj} + \mathcal{R'}_{kj}\mathcal{R'}_{nj})\right]}^{IX} \nonumber\\ &\qquad -\overbrace{\left[\frac{1}{Re}\left\lbrace\frac{\partial }{\partial x^{0}_{k}}\left\lbrace \frac{\partial }{\partial x^{0}_{n}}\left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{l}} {\rm \Delta} x_{l}\right) \right\rbrace\right\rbrace(\mathcal{I}_{kj}\mathcal{I}_{nj} - \mathcal{I}_{kj}\mathcal{R'}_{nj} -\mathcal{R'}_{kj}\mathcal{I}_{nj} + \mathcal{R'}_{kj}\mathcal{R'}_{nj})\right]}^{X} \nonumber\\ &\qquad -\overbrace{\left[\frac{1}{Re}\frac{\partial^{2}u'_{i}}{\partial x^{0}_{k}\partial x^{0}_{n}}(\mathcal{I}_{kj} \mathcal{I}_{nj} - \mathcal{I}_{kj}\mathcal{R'}_{nj} -\mathcal{R'}_{kj}\mathcal{I}_{nj} + \mathcal{R'}_{kj}\mathcal{R'}_{nj})\right]}^{XI} \nonumber\\ &\qquad -\overbrace{\left[w_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{k}}(\mathcal{I}_{kj} - \mathcal{R'}_{kj})\right]}^{XII} + \left.\frac{\partial U_{i}}{\partial t}\right\vert_{\boldsymbol{w}} =0. \end{align}
\begin{align} & \left[U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}} + U^{0}_{j}\frac{\partial u^{\xi}_{i}}{\partial x_{j}} + u^{\xi}_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}} + \frac{\partial P^{0}}{\partial x_{i}} + \frac{\partial p^{\xi}}{\partial x_{i}} - \frac{1}{Re}\frac{\partial^{2}U^{0}_{i}}{\partial x_{j}\partial x_{j}} - \frac{1}{Re}\frac{\partial^{2}u^{\xi}_{i}}{\partial x_{j}\partial x_{j}}\right] \nonumber\\ &\qquad +\left[ \left.\frac{\partial U_{i}}{\partial t}\right\vert_{\boldsymbol{w}} -w_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}} + U^{0}_{j}\frac{\partial u'_{i}}{\partial x_{j}} + u'_{j}\frac{\partial U^{0}_{i}}{\partial x_{j}} + \frac{\partial p'}{\partial x_{i}} -\frac{1}{Re}\frac{\partial^{2}u'_{i}}{\partial x_{j}\partial x_{j}}\right] = 0, \nonumber\\ &\quad \implies \overbrace{\left[U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{k}}(\mathcal{I}_{kj} - \mathcal{R'}_{kj})\right]}^{I} + \overbrace{\left[U^{0}_{j}\frac{\partial }{\partial x^{0}_{k}} \left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{l}}{\rm \Delta} x_{l}\right)(\mathcal{I}_{kj} - \mathcal{R'}_{kj})\right]}^{II} \nonumber\\ &\qquad + \overbrace{\left[\left(\frac{\partial U^{0}_{j}}{\partial x^{0}_{l}}{\rm \Delta} x_{l}\right) \frac{\partial U^{0}_{i}}{\partial x^{0}_{k}}(\mathcal{I}_{kj} - \mathcal{R'}_{kj})\right]}^{III} \nonumber\\ &\qquad + \overbrace{\left[\frac{\partial P^{0}}{\partial x^{0}_{k}}(\mathcal{I}_{ki} - \mathcal{R'}_{ki})\right]}^{IV} +\overbrace{\left[u'_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{k}}(\mathcal{I}_{kj} - \mathcal{R'}_{kj})\right]}^{V} \nonumber\\ &\qquad +\overbrace{\left[U^{0}_{j}\frac{\partial u'_{i}}{\partial x^{0}_{k}}(\mathcal{I}_{kj} - \mathcal{R'}_{kj})\right]}^{VI} + \overbrace{\left[\frac{\partial p'}{\partial x^{0}_{k}}(\mathcal{I}_{ki} - \mathcal{R'}_{ki})\right]}^{VII} + \overbrace{\left[\frac{\partial }{\partial x^{0}_{k}}\left(\frac{\partial P^{0}}{\partial x_{l}}{\rm \Delta} x_{l} \right)(\mathcal{I}_{ki} - \mathcal{R'}_{ki})\right]}^{VIII} \nonumber\\ &\qquad -\overbrace{\left[\frac{1}{Re}\frac{\partial^{2}U^{0}_{i}}{\partial x^{0}_{k}\partial x^{0}_{n}}(\mathcal{I}_{kj}\mathcal{I}_{nj} - \mathcal{I}_{kj}\mathcal{R'}_{nj} -\mathcal{R'}_{kj}\mathcal{I}_{nj} + \mathcal{R'}_{kj}\mathcal{R'}_{nj})\right]}^{IX} \nonumber\\ &\qquad -\overbrace{\left[\frac{1}{Re}\left\lbrace\frac{\partial }{\partial x^{0}_{k}}\left\lbrace \frac{\partial }{\partial x^{0}_{n}}\left(\frac{\partial U^{0}_{i}}{\partial x^{0}_{l}} {\rm \Delta} x_{l}\right) \right\rbrace\right\rbrace(\mathcal{I}_{kj}\mathcal{I}_{nj} - \mathcal{I}_{kj}\mathcal{R'}_{nj} -\mathcal{R'}_{kj}\mathcal{I}_{nj} + \mathcal{R'}_{kj}\mathcal{R'}_{nj})\right]}^{X} \nonumber\\ &\qquad -\overbrace{\left[\frac{1}{Re}\frac{\partial^{2}u'_{i}}{\partial x^{0}_{k}\partial x^{0}_{n}}(\mathcal{I}_{kj} \mathcal{I}_{nj} - \mathcal{I}_{kj}\mathcal{R'}_{nj} -\mathcal{R'}_{kj}\mathcal{I}_{nj} + \mathcal{R'}_{kj}\mathcal{R'}_{nj})\right]}^{XI} \nonumber\\ &\qquad -\overbrace{\left[w_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{k}}(\mathcal{I}_{kj} - \mathcal{R'}_{kj})\right]}^{XII} + \left.\frac{\partial U_{i}}{\partial t}\right\vert_{\boldsymbol{w}} =0. \end{align}For clarity, the terms are numbered and the expansions of the individual terms (after dropping the higher order terms) are evaluated as
 \begin{equation*} \begin{gathered} I = U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} - \mathcal{R'}_{kj}U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{k}},\quad VII = \frac{\partial p'}{\partial x^{0}_{i}}, \\ II = {\rm \Delta} x_{l}U^{0}_{j}\frac{\partial^{2} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{l}} + U^{0}_{j} \frac{\partial U^{0}_{i}}{\partial x^{0}_{l}}\mathcal{R'}_{lj},\quad VIII = \frac{\partial^{2} P^{0}}{\partial x^{0}_{i}\partial x^{0}_{l}}{\rm \Delta} x_{l} + \frac{\partial P^{0}}{\partial x^{0}_{l}}\mathcal{R'}_{li}, \\ III ={\rm \Delta} x_{l}\frac{\partial U^{0}_{j}}{\partial x^{0}_{l}}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}},\quad IX =-\frac{1}{Re}\left[\frac{\partial^{2}U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}} -2\frac{\partial^{2}U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{k}}\mathcal{R'}_{kj}\right], \\ IV = \frac{\partial P^{0}}{\partial x^{0}_{i}} - \frac{\partial P^{0}}{\partial x^{0}_{k}}\mathcal{R'}_{ki},\quad X = -\frac{1}{Re}\left[\frac{\partial^{3} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}\partial x^{0}_{l}}{\rm \Delta} x_{l} + 2\frac{\partial^{2} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{l}}\mathcal{R'}_{lj}\right], \\ V = u'_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}},\quad XI = -\frac{1}{Re}\left[\frac{\partial^{2}u'_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right], \\ VI = U^{0}_{j}\frac{\partial u'_{i}}{\partial x^{0}_{j}},\quad XII = -w_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}}. \end{gathered}\end{equation*}
\begin{equation*} \begin{gathered} I = U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} - \mathcal{R'}_{kj}U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{k}},\quad VII = \frac{\partial p'}{\partial x^{0}_{i}}, \\ II = {\rm \Delta} x_{l}U^{0}_{j}\frac{\partial^{2} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{l}} + U^{0}_{j} \frac{\partial U^{0}_{i}}{\partial x^{0}_{l}}\mathcal{R'}_{lj},\quad VIII = \frac{\partial^{2} P^{0}}{\partial x^{0}_{i}\partial x^{0}_{l}}{\rm \Delta} x_{l} + \frac{\partial P^{0}}{\partial x^{0}_{l}}\mathcal{R'}_{li}, \\ III ={\rm \Delta} x_{l}\frac{\partial U^{0}_{j}}{\partial x^{0}_{l}}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}},\quad IX =-\frac{1}{Re}\left[\frac{\partial^{2}U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}} -2\frac{\partial^{2}U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{k}}\mathcal{R'}_{kj}\right], \\ IV = \frac{\partial P^{0}}{\partial x^{0}_{i}} - \frac{\partial P^{0}}{\partial x^{0}_{k}}\mathcal{R'}_{ki},\quad X = -\frac{1}{Re}\left[\frac{\partial^{3} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}\partial x^{0}_{l}}{\rm \Delta} x_{l} + 2\frac{\partial^{2} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{l}}\mathcal{R'}_{lj}\right], \\ V = u'_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}},\quad XI = -\frac{1}{Re}\left[\frac{\partial^{2}u'_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right], \\ VI = U^{0}_{j}\frac{\partial u'_{i}}{\partial x^{0}_{j}},\quad XII = -w_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}}. \end{gathered}\end{equation*}On collecting all terms of the expansions, several terms cancel and we obtain the following simplified expression:
 \begin{align} & \left[U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} + \frac{1}{\rho}\frac{\partial P^{0}}{\partial x^{0}_{i}} - \frac{1}{Re}\frac{\partial^{2} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right] + {\rm \Delta} x_{l}\frac{\partial }{\partial x^{0}_{l}}\left[U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} + \frac{1}{\rho}\frac{\partial P^{0}}{\partial x^{0}_{i}} - \frac{1}{Re}\frac{\partial^{2} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right] \nonumber\\ &\quad +\left[\left.\frac{\partial U_{i}}{\partial t}\right\vert_{\boldsymbol{w}} -w_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} +U^{0}_{j}\frac{\partial u'_{i}}{\partial x^{0}_{j}} + u'_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} +\frac{\partial p'}{\partial x^{0}_{i}} -\frac{1}{Re}\frac{\partial^{2}u'_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right]=0. \end{align}
\begin{align} & \left[U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} + \frac{1}{\rho}\frac{\partial P^{0}}{\partial x^{0}_{i}} - \frac{1}{Re}\frac{\partial^{2} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right] + {\rm \Delta} x_{l}\frac{\partial }{\partial x^{0}_{l}}\left[U^{0}_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} + \frac{1}{\rho}\frac{\partial P^{0}}{\partial x^{0}_{i}} - \frac{1}{Re}\frac{\partial^{2} U^{0}_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right] \nonumber\\ &\quad +\left[\left.\frac{\partial U_{i}}{\partial t}\right\vert_{\boldsymbol{w}} -w_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} +U^{0}_{j}\frac{\partial u'_{i}}{\partial x^{0}_{j}} + u'_{j}\frac{\partial U^{0}_{i}}{\partial x^{0}_{j}} +\frac{\partial p'}{\partial x^{0}_{i}} -\frac{1}{Re}\frac{\partial^{2}u'_{i}}{\partial x^{0}_{j}\partial x^{0}_{j}}\right]=0. \end{align}
The first two bracketed terms together in (A 2) represent the first-order Taylor expansion of the steady-state Navier–Stokes evaluated at the perturbed location ![]() $\boldsymbol {{\rm \Delta} x}$. Since the steady-state equation for the base flow is identically zero everywhere, the Taylor expansion also vanishes.
$\boldsymbol {{\rm \Delta} x}$. Since the steady-state equation for the base flow is identically zero everywhere, the Taylor expansion also vanishes.
Appendix B. Derivation of adjoint
The adjoint equations are derived for the linearized FSI equations under the inner product defined as the integral over the domain ![]() $\varOmega$ and time horizon
$\varOmega$ and time horizon ![]() $T$:
$T$:
In the context of FSI, ![]() $\mathcal {L}$ represents the linearized FSI equations defined by (3.2a)–(3.2i) and
$\mathcal {L}$ represents the linearized FSI equations defined by (3.2a)–(3.2i) and ![]() $\mathcal {L}^{\dagger }$ represents the adjoint operator satisfying the Lagrange identity under the inner product defined in (B 1)
$\mathcal {L}^{\dagger }$ represents the adjoint operator satisfying the Lagrange identity under the inner product defined in (B 1)
For linear FSI, we consider the case of a two-dimensional circular cylinder free to oscillate in the vertical direction subject to the action of a spring-mass-damper system and the fluid forces. The structural system is then defined by the position ![]() $\eta$ and velocity
$\eta$ and velocity ![]() $\varphi$ of its centre of mass in the vertical direction. In the following
$\varphi$ of its centre of mass in the vertical direction. In the following ![]() $i=2$ represents the vertical direction. The vectors are defined as
$i=2$ represents the vertical direction. The vectors are defined as ![]() $\boldsymbol {q}=(\boldsymbol {u},p,\eta ,\varphi )$, which lies in the domain of
$\boldsymbol {q}=(\boldsymbol {u},p,\eta ,\varphi )$, which lies in the domain of ![]() $\mathcal {L}$, and
$\mathcal {L}$, and ![]() $\boldsymbol {q}=(\boldsymbol {u}^{\dagger },p^{\dagger },\eta ^{\dagger },\varphi ^{\dagger })$, which lies in the domain of
$\boldsymbol {q}=(\boldsymbol {u}^{\dagger },p^{\dagger },\eta ^{\dagger },\varphi ^{\dagger })$, which lies in the domain of ![]() $\mathcal {L}^{\dagger }$. The Lagrange identity may be written as
$\mathcal {L}^{\dagger }$. The Lagrange identity may be written as
 \begin{align} & \langle \mathcal{L}^{\dagger}\boldsymbol{q}^{\dagger},\boldsymbol{q}\rangle = \langle \boldsymbol{q}^{\dagger},\mathcal{L}\boldsymbol{q}\rangle, \nonumber\\ &\quad \implies \langle \mathcal{L}^{\dagger}\boldsymbol{q}^{\dagger},\boldsymbol{q}\rangle = \left\{\begin{aligned} & \int_{T}\int_{\varOmega} u^{\dagger}_{i}\left[\frac{\partial u_{i}}{\partial t} + u_{j} \frac{\partial U_{i}}{\partial x_{j}} + U_{j}\frac{\partial u_{i}}{\partial x_{j}}\right] \textrm{d}\varOmega \,\textrm{d} t \\ & \quad +\int_{T}\int_{\varOmega}u^{\dagger}_{i}\left[\frac{\partial p}{\partial x_{i}} - \frac{1}{Re}\frac{\partial }{\partial x_{j}}\left( \frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}}\right) \right] \textrm{d}\varOmega \,\textrm{d} t\\ & \quad -\int_{T}\int_{\varOmega} p^{\dagger}\frac{\partial u_{i}}{\partial x_{i}}\textrm{d}\varOmega \,\textrm{d} t + \int_{T}\eta^{\dagger}\left(\frac{\textrm{d}\eta}{\textrm{d} t} - \varphi\right)\textrm{d} t\\ & \quad + \int_{T}\varphi^{\dagger}\left(\mathcal{M}\frac{\textrm{d} \varphi}{\textrm{d} t} +\mathcal{D}\varphi + \mathcal{K}\eta + \oint_{\partial\varOmega} \sigma_{2j}n_{j}\,\textrm{d}\varOmega\right)\textrm{d} t. \end{aligned}\right. \end{align}
\begin{align} & \langle \mathcal{L}^{\dagger}\boldsymbol{q}^{\dagger},\boldsymbol{q}\rangle = \langle \boldsymbol{q}^{\dagger},\mathcal{L}\boldsymbol{q}\rangle, \nonumber\\ &\quad \implies \langle \mathcal{L}^{\dagger}\boldsymbol{q}^{\dagger},\boldsymbol{q}\rangle = \left\{\begin{aligned} & \int_{T}\int_{\varOmega} u^{\dagger}_{i}\left[\frac{\partial u_{i}}{\partial t} + u_{j} \frac{\partial U_{i}}{\partial x_{j}} + U_{j}\frac{\partial u_{i}}{\partial x_{j}}\right] \textrm{d}\varOmega \,\textrm{d} t \\ & \quad +\int_{T}\int_{\varOmega}u^{\dagger}_{i}\left[\frac{\partial p}{\partial x_{i}} - \frac{1}{Re}\frac{\partial }{\partial x_{j}}\left( \frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}}\right) \right] \textrm{d}\varOmega \,\textrm{d} t\\ & \quad -\int_{T}\int_{\varOmega} p^{\dagger}\frac{\partial u_{i}}{\partial x_{i}}\textrm{d}\varOmega \,\textrm{d} t + \int_{T}\eta^{\dagger}\left(\frac{\textrm{d}\eta}{\textrm{d} t} - \varphi\right)\textrm{d} t\\ & \quad + \int_{T}\varphi^{\dagger}\left(\mathcal{M}\frac{\textrm{d} \varphi}{\textrm{d} t} +\mathcal{D}\varphi + \mathcal{K}\eta + \oint_{\partial\varOmega} \sigma_{2j}n_{j}\,\textrm{d}\varOmega\right)\textrm{d} t. \end{aligned}\right. \end{align}Integrating by parts and using the divergence theorem leads to
 \begin{equation} \langle \mathcal{L}^{\dagger}\boldsymbol{q}^{\dagger},\boldsymbol{q}\rangle =\left\{\begin{aligned} & \int_{T}\int_{\varOmega} u_{i}\left[-\frac{\partial u^{\dagger}_{i}}{\partial t} + u^{\dagger}_{j}\frac{\partial U_{j}}{\partial x_{i}}-U_{j}\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} \right.\\ & \quad \left.-\frac{1}{Re} \frac{\partial }{\partial x_{j}}\left( \frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial u^{\dagger}_{j}}{\partial x_{i}}\right)+ \frac{\partial p^{\dagger}}{\partial x_{i}}\right]\textrm{d}\varOmega \,\textrm{d} t \\ & \quad - \int_{T}\int_{\varOmega}p\left[\frac{\partial u^{\dagger}_{i}}{\partial x_{i}}\right]\textrm{d}\varOmega \,\textrm{d} t\\ & \quad + \int_{T}\oint_{\partial\varOmega} \left[u^{\dagger}_{i}u_{i}U_{j} + u^{\dagger}_{i} \sigma_{ij} - u_{i} \sigma^{\dagger}_{ij}\right]n_{j}\,\textrm{d}\varOmega \,\textrm{d} t \\ & \quad +\int_{T}\left[\varphi\left(-\mathcal{M}\frac{\textrm{d} \varphi^{\dagger}}{\textrm{d} t} +\mathcal{D}\varphi^{\dagger} -\eta^{\dagger}\right) + \eta\left(-\frac{\textrm{d}\eta^{\dagger}}{\textrm{d} t} + \mathcal{K}\varphi^{\dagger}\right) \right.\\ & \quad \left.+ \varphi^{\dagger}\oint_{\partial\varOmega} \sigma_{2j}n_{j}\,\textrm{d}\varOmega \right]\textrm{d} t \\ & \quad + \left[\int_{\varOmega} (u^{\dagger}_{i}u_{i}) \,\textrm{d}\varOmega\right]_{0}^{\textrm{T}} +\left[\mathcal{M}\frac{\textrm{d} (\varphi^{\dagger}\varphi)}{\textrm{d} t} + \frac{\textrm{d} (\eta^{\dagger}\eta)}{\textrm{d} t} \right]_{0}^{\textrm{T}}, \end{aligned}\right. \end{equation}
\begin{equation} \langle \mathcal{L}^{\dagger}\boldsymbol{q}^{\dagger},\boldsymbol{q}\rangle =\left\{\begin{aligned} & \int_{T}\int_{\varOmega} u_{i}\left[-\frac{\partial u^{\dagger}_{i}}{\partial t} + u^{\dagger}_{j}\frac{\partial U_{j}}{\partial x_{i}}-U_{j}\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} \right.\\ & \quad \left.-\frac{1}{Re} \frac{\partial }{\partial x_{j}}\left( \frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial u^{\dagger}_{j}}{\partial x_{i}}\right)+ \frac{\partial p^{\dagger}}{\partial x_{i}}\right]\textrm{d}\varOmega \,\textrm{d} t \\ & \quad - \int_{T}\int_{\varOmega}p\left[\frac{\partial u^{\dagger}_{i}}{\partial x_{i}}\right]\textrm{d}\varOmega \,\textrm{d} t\\ & \quad + \int_{T}\oint_{\partial\varOmega} \left[u^{\dagger}_{i}u_{i}U_{j} + u^{\dagger}_{i} \sigma_{ij} - u_{i} \sigma^{\dagger}_{ij}\right]n_{j}\,\textrm{d}\varOmega \,\textrm{d} t \\ & \quad +\int_{T}\left[\varphi\left(-\mathcal{M}\frac{\textrm{d} \varphi^{\dagger}}{\textrm{d} t} +\mathcal{D}\varphi^{\dagger} -\eta^{\dagger}\right) + \eta\left(-\frac{\textrm{d}\eta^{\dagger}}{\textrm{d} t} + \mathcal{K}\varphi^{\dagger}\right) \right.\\ & \quad \left.+ \varphi^{\dagger}\oint_{\partial\varOmega} \sigma_{2j}n_{j}\,\textrm{d}\varOmega \right]\textrm{d} t \\ & \quad + \left[\int_{\varOmega} (u^{\dagger}_{i}u_{i}) \,\textrm{d}\varOmega\right]_{0}^{\textrm{T}} +\left[\mathcal{M}\frac{\textrm{d} (\varphi^{\dagger}\varphi)}{\textrm{d} t} + \frac{\textrm{d} (\eta^{\dagger}\eta)}{\textrm{d} t} \right]_{0}^{\textrm{T}}, \end{aligned}\right. \end{equation}where we have denoted the direct and adjoint stresses in compact notation as
 \begin{equation} \sigma_{ij} = -p\delta_{ij} +\frac{1}{Re}\left( \frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}} \right);\quad \sigma_{ij}^{\dagger} = -p^{\dagger}\delta_{ij} + \frac{1}{Re}\left(\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial u^{\dagger}_{j}}{\partial x_{i}} \right). \end{equation}
\begin{equation} \sigma_{ij} = -p\delta_{ij} +\frac{1}{Re}\left( \frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}} \right);\quad \sigma_{ij}^{\dagger} = -p^{\dagger}\delta_{ij} + \frac{1}{Re}\left(\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial u^{\dagger}_{j}}{\partial x_{i}} \right). \end{equation}The temporal boundary terms for appropriately defined direct and adjoint operators vanish (Bagheri, Brandt & Henningson Reference Bagheri, Brandt and Henningson2009a). For the outer boundaries of the domain, the structural variables play no role and the boundary terms may be written compactly as
For homogeneous Dirichlet and stress-free conditions for the direct problem, the boundary conditions for the adjoint problem reduce to
On the interface boundary ![]() $\varGamma$, the structural equations are part of the boundary terms. The base flow
$\varGamma$, the structural equations are part of the boundary terms. The base flow ![]() $\boldsymbol {U}$ is identically zero and using the velocity boundary condition at the interface for the direct variables, we obtain (for an oscillating cylinder case)
$\boldsymbol {U}$ is identically zero and using the velocity boundary condition at the interface for the direct variables, we obtain (for an oscillating cylinder case)
 \begin{align} & -\left[\int_{T}\oint_{\partial\varOmega} u^{\dagger}_{i}\sigma_{ij}n_{j}\,\textrm{d}\varOmega \,\textrm{d} t\right] + \left[\int_{T}\eta\left(-\frac{\textrm{d}\eta^{\dagger}}{\textrm{d} t} + \mathcal{K}\varphi^{\dagger} - \oint_{\partial\varOmega}\frac{\partial U_{k}}{\partial x_{2}}\sigma^{\dagger}_{kj}n_{j}\,\textrm{d}\varOmega\right)\textrm{d} t\right] \nonumber\\ &\quad +\left[\int_{T}\varphi\left(-\mathcal{M}\frac{\textrm{d} \varphi^{\dagger}}{\textrm{d} t} +\mathcal{D}\varphi^{\dagger} -\eta^{\dagger} + \oint_{\partial\varOmega}\sigma^{\dagger}_{ij}n_{j}\,\textrm{d}\varOmega \right) \textrm{d} t \right] \nonumber\\ &\quad +\left[\int_{T} \oint_{\partial\varOmega} \varphi^{\dagger} \sigma_{2j}n_{j}\,\textrm{d}\varOmega \,\textrm{d} t\right] = 0. \end{align}
\begin{align} & -\left[\int_{T}\oint_{\partial\varOmega} u^{\dagger}_{i}\sigma_{ij}n_{j}\,\textrm{d}\varOmega \,\textrm{d} t\right] + \left[\int_{T}\eta\left(-\frac{\textrm{d}\eta^{\dagger}}{\textrm{d} t} + \mathcal{K}\varphi^{\dagger} - \oint_{\partial\varOmega}\frac{\partial U_{k}}{\partial x_{2}}\sigma^{\dagger}_{kj}n_{j}\,\textrm{d}\varOmega\right)\textrm{d} t\right] \nonumber\\ &\quad +\left[\int_{T}\varphi\left(-\mathcal{M}\frac{\textrm{d} \varphi^{\dagger}}{\textrm{d} t} +\mathcal{D}\varphi^{\dagger} -\eta^{\dagger} + \oint_{\partial\varOmega}\sigma^{\dagger}_{ij}n_{j}\,\textrm{d}\varOmega \right) \textrm{d} t \right] \nonumber\\ &\quad +\left[\int_{T} \oint_{\partial\varOmega} \varphi^{\dagger} \sigma_{2j}n_{j}\,\textrm{d}\varOmega \,\textrm{d} t\right] = 0. \end{align}The second and the third brackets form the two adjoint structural equations, while the first and the fourth brackets together form the boundary conditions for the coupling between the fluid and the structure in the adjoint equations. The final set of adjoint equations for FSI of the two-dimensional oscillating cylinder can be written as
 \begin{gather} -\frac{\partial u^{\dagger}_{i}}{\partial t} + u^{\dagger}_{j}\frac{\partial U_{j}}{\partial x_{i}}-U_{j}\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial p^{\dagger}}{\partial x_{i}} - \frac{1}{Re}\frac{\partial }{\partial x_{j}} \left(\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial u^{\dagger}_{j}}{\partial x_{i}}\right) = 0\quad \text{in } \varOmega^{f}, \end{gather}
\begin{gather} -\frac{\partial u^{\dagger}_{i}}{\partial t} + u^{\dagger}_{j}\frac{\partial U_{j}}{\partial x_{i}}-U_{j}\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial p^{\dagger}}{\partial x_{i}} - \frac{1}{Re}\frac{\partial }{\partial x_{j}} \left(\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial u^{\dagger}_{j}}{\partial x_{i}}\right) = 0\quad \text{in } \varOmega^{f}, \end{gather} \begin{gather}\sigma_{ij}^{\dagger} - \left[-p^{\dagger}\delta_{ij} + \frac{1}{Re}\left(\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial u^{\dagger}_{j}}{\partial x_{i}} \right) \right] = 0\quad \text{adjoint forces on } \varGamma, \end{gather}
\begin{gather}\sigma_{ij}^{\dagger} - \left[-p^{\dagger}\delta_{ij} + \frac{1}{Re}\left(\frac{\partial u^{\dagger}_{i}}{\partial x_{j}} + \frac{\partial u^{\dagger}_{j}}{\partial x_{i}} \right) \right] = 0\quad \text{adjoint forces on } \varGamma, \end{gather}Appendix C. Convergence tests
The convergence tests for an oscillating cylinder are reported in this section. The convergence test is performed for the case of a spring-mounted two-dimensional cylinder at a diameter based Reynolds number of ![]() $Re=23.512$. The structural parameters are the same as the ones reported in table 1. Table 7 reports the domain size and polynomial order of the various tests performed to ensure converged results. A comparison of the spectra for case
$Re=23.512$. The structural parameters are the same as the ones reported in table 1. Table 7 reports the domain size and polynomial order of the various tests performed to ensure converged results. A comparison of the spectra for case ![]() $1$ and case
$1$ and case ![]() $2$ is shown in figure 22. The panel on the left shows the spectra comparison for two different polynomial orders. The two cases have nearly identical spectra implying the convergence of results with grid resolution. The panel on the right shows the spectra for three different domain sizes. For all three cases, the physical eigenvalue of the system is always converged. The highly damped modes represent the box modes of the system which vary slightly depending on the size of the computational box. A similar behaviour of the damped eigenmodes can be found in Assemat et al. (Reference Assemat, Fabre and Magnaudet2012). Overall, the results show the convergence of the physical eigenvalue both in terms of grid resolution and numerical domain.
$2$ is shown in figure 22. The panel on the left shows the spectra comparison for two different polynomial orders. The two cases have nearly identical spectra implying the convergence of results with grid resolution. The panel on the right shows the spectra for three different domain sizes. For all three cases, the physical eigenvalue of the system is always converged. The highly damped modes represent the box modes of the system which vary slightly depending on the size of the computational box. A similar behaviour of the damped eigenmodes can be found in Assemat et al. (Reference Assemat, Fabre and Magnaudet2012). Overall, the results show the convergence of the physical eigenvalue both in terms of grid resolution and numerical domain.

Figure 22. A comparison of spectra for different domain studies. (a) Spectra for two different polynomial orders of ![]() $N=7$ (case 1) and
$N=7$ (case 1) and ![]() $N=9$ (case 2). (b) Comparison of spectra for three different domain sizes.
$N=9$ (case 2). (b) Comparison of spectra for three different domain sizes.
Table 7. Structural parameters for a two-dimensional cylinder oscillating in the cross-stream direction.