Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-26T02:30:41.742Z Has data issue: false hasContentIssue false
  • English
  • Français

Confinement of rotating convection by a laterally varying magnetic field

Published online by Cambridge University Press:  07 June 2017

Binod Sreenivasan Open the ORCID record for Binod Sreenivasan [Opens in a new window]  and
Venkatesh Gopinath
Binod Sreenivasan*
Affiliation:
Centre for Earth Sciences, Indian Institute of Science, Bangalore 560012, India
Venkatesh Gopinath
Affiliation:
Centre for Earth Sciences, Indian Institute of Science, Bangalore 560012, India
*
†Email address for correspondence: bsreeni@ceas.iisc.ernet.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Spherical shell dynamo models based on rotating convection show that the flow within the tangent cylinder is dominated by an off-axis plume that extends from the inner core boundary to high latitudes and drifts westward. Earlier studies explained the formation of such a plume in terms of the effect of a uniform axial magnetic field that significantly increases the length scale of convection in a rotating plane layer. However, rapidly rotating dynamo simulations show that the magnetic field within the tangent cylinder has severe lateral inhomogeneities that may influence the onset of an isolated plume. Increasing the rotation rate in our dynamo simulations (by decreasing the Ekman number 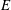$E$) produces progressively thinner plumes that appear to seek out the location where the field is strongest. Motivated by this result, we examine the linear onset of convection in a rapidly rotating fluid layer subject to a laterally varying axial magnetic field. A Cartesian geometry is chosen where the finite dimensions 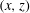$(x,z)$ mimic 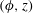$(\unicode[STIX]{x1D719},z)$ in cylindrical coordinates. The lateral inhomogeneity of the field gives rise to a unique mode of instability where convection is entirely confined to the peak-field region. The localization of the flow by the magnetic field occurs even when the field strength (measured by the Elsasser number 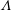$\unicode[STIX]{x1D6EC}$) is small and viscosity controls the smallest length scale of convection. The lowest Rayleigh number at which an isolated plume appears within the tangent cylinder in spherical shell dynamo simulations agrees closely with the viscous-mode Rayleigh number in the plane layer linear magnetoconvection model. The lowest Elsasser number for plume formation in the simulations is significantly higher than the onset values in linear magnetoconvection, which indicates that the viscous–magnetic mode transition point with spatially varying fields is displaced to much higher Elsasser numbers. The localized excitation of viscous-mode convection by a laterally varying magnetic field provides a mechanism for the formation of isolated plumes within the Earth’s tangent cylinder. The polar vortices in the Earth’s core can therefore be non-axisymmetric. More generally, this study shows that a spatially varying magnetic field strongly controls the structure of rotating convection at a Rayleigh number not much different from its non-magnetic value.

JFM classification

MHD and Electrohydrodynamics: Dynamo theory Geophysical and Geological Flows: Geodynamo MHD and Electrohydrodynamics: Magneto convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 822 , 10 July 2017 , pp. 590 - 616
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aujogue, K., Pothérat, A., Bates, I., Debray, F. & Sreenivasan, B. 2016 Little earth experiment: an instrument to model planetary cores. Rev. Sci. Instrum. 87, 084502.Google Scholar
Aujogue, K., Pothérat, A. & Sreenivasan, B. 2015 Onset of plane layer magnetoconvection at low Ekman number. Phys. Fluids 27, 106602.Google Scholar
Aurnou, J., Andreadis, S., Zhu, L. & Olson, P. 2003 Experiments on convection in Earth’s core tangent cylinder. Earth Planet. Sci. Lett. 212, 119–134.CrossRefGoogle Scholar
Calkins, M. A., Julien, K. & Marti, P. 2013 Three-dimensional quasi-geostrophic convection in the rotating cylindrical annulus with steeply sloping endwalls. J. Fluid Mech. 732, 214–244.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon.Google Scholar
Christensen, U. R. & Wicht, J. 2007 Numerical dynamo models. In Treatise on Geophysics (ed. Olson, P.), vol. 8, pp. 245–282. Elsevier.Google Scholar
Davidson, P. A. 2001 An Introduction to Magnetohydrodynamics. Cambridge University Press.CrossRefGoogle Scholar
Fearn, D. R. & Proctor, M. R. E. 1983 Hydromagnetic waves in a differentially rotating sphere. J. Fluid Mech. 128, 1–20.CrossRefGoogle Scholar
Gopinath, V. & Sreenivasan, B. 2015 On the control of rapidly rotating convection by an axially varying magnetic field. Geophys. Astrophys. Fluid Dyn. 109, 567–586.CrossRefGoogle Scholar
Gubbins, D., Willis, A. P. & Sreenivasan, B. 2007 Correlation of Earth’s magnetic field with lower mantle thermal and seismic structure. Phys. Earth Planet. Inter. 358, 957–990.Google Scholar
Holme, R. 2015 Large-scale flow in the core. In Core Dynamics (ed. Olson, P.), Treatise on Geophysics, vol. 8, pp. 91–113. Elsevier.Google Scholar
Hori, K. & Wicht, J. 2013 Subcritical dynamos in the early Mars’ core: implications for cessation of the past Martian dynamo. Phys. Earth Planet. Inter. 219, 21–33.Google Scholar
Hu, J., Henry, D., Yin, X-Y. & BenHadid, H. 2012 Linear biglobal analysis of Rayleigh-Bénard instabilities in binary fluids with and without throughflow. J. Fluid Mech. 713, 216–242.Google Scholar
Huang, L., Ng, C-O. & Chwang, A. T. 2006 A Fourier–Chebyshev collocation method for the mass transport in a layer of power-law fluid mud. Comput. Meth. Appl. Mech. Engng 195, 1136–1153.Google Scholar
Hulot, G., Eymin, C., Langlais, B., Mandea, M. & Olsen, N. 2002 Small-scale structure of the geodynamo inferred from Oersted and Magsat satellite data. Nature 416, 620–623.CrossRefGoogle ScholarPubMed
Jackson, A., Jonkers, A. R. T. & Walker, M. R. 2000 Four centuries of geomagnetic secular variation from historical records. Phil. Trans. R. Soc. Lond. A 358, 957–990.Google Scholar
Jones, C. A. 2015 Thermal and compositional convection in the outer core. In Core Dynamics (ed. Olson, P.), Treatise on Geophysics, vol. 8, pp. 115–159. Elsevier.Google Scholar
Jones, C. A., Mussa, A. I. & Worland, S. J. 2003 Magnetoconvection in a rapidly rotating sphere: the weak-field case. Proc. R. Soc. Lond. A 459, 773–797.Google Scholar
Kono, M. & Roberts, P. H. 2002 Recent geodynamo simulations and observations of the geomagnetic field. Rev. Geophys. 40 (4), 1013.Google Scholar
Kuang, W., Jiang, W. & Wang, T. 2008 Sudden termination of Martian dynamo?: implications from subcritical dynamo simulations. Geophys. Res. Lett. 35, L14284.Google Scholar
Kuang, W. & Roberts, P. H. 1990 Resistive instabilities in rapidly rotating fluids: linear theory of the tearing mode. Geophys. Astrophys. Fluid Dyn. 55, 199–239.Google Scholar
Longbottom, A. W., Jones, C. A. & Hollerbach, R. 1995 Linear magnetoconvection in a rotating spherical shell, incorporating a finitely conducting inner core. Geophys. Astrophys. Fluid Dyn. 80, 205–227.Google Scholar
Malkus, W. V. R. 1967 Hydromagnetic planetary waves. J. Fluid Mech. 28, 793–802.Google Scholar
Morin, V. & Dormy, E. 2009 The dynamo bifurcation in rotating spherical shells. Intl J. Mod. Phys. B 23, 5467–5482.Google Scholar
Muite, B. K. 2010 A numerical comparison of chebyshev methods for solving fourth order semilinear initial boundary value problems. J. Comput. Appl. Maths 234, 317–342.Google Scholar
Nakagawa, Y. 1957 Experiments on the instability of a layer of mercury heated from below and subject to the simultaneous action of a magnetic field and rotation. Proc. R. Soc. Lond. A 242, 81–88.Google Scholar
Olson, P. & Aurnou, J. 1999 A polar vortex in the Earth’s core. Nature 402, 170–173.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics. Springer.Google Scholar
Peyret, R. 2002 Spectral Methods for Incompressible Viscous Flow. Springer.Google Scholar
Soward, A. M. 1979 Thermal and magnetically driven convection in a rapidly rotating fluid layer. J. Fluid Mech. 90, 669–684.Google Scholar
Sreenivasan, B. & Jones, C. A. 2005 Structure and dynamics of the polar vortex in the Earth’s core. Geophys. Res. Lett. 32, L20301.Google Scholar
Sreenivasan, B. & Jones, C. A. 2006a Azimuthal winds, convection and dynamo action in the polar regions of planetary cores. Geophys. Astrophys. Fluid Dyn. 100, 319–339.CrossRefGoogle Scholar
Sreenivasan, B. & Jones, C. A. 2006b The role of inertia in the evolution of spherical dynamos. Geophys. J. Intl 164, 467–476.Google Scholar
Sreenivasan, B. & Jones, C. A. 2011 Helicity generation and subcritical behaviour in rapidly rotating dynamos. J. Fluid Mech. 688, 5–30.Google Scholar
Sreenivasan, B., Sahoo, S. & Dhama, G. 2014 The role of buoyancy in polarity reversals of the geodynamo. Geophys. J. Intl 199, 1698–1708.Google Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.Google Scholar
Trefethen, L. N. 2000 Spectral Methods in Matlab, 1st edn. Society for Industrial and Applied Mathematics (SIAM).Google Scholar
Tucker, P. J. Y. & Jones, C. A. 1997 Magnetic and thermal instabilities in a plane layer: I. Geophys. Astrophys. Fluid Dyn. 86, 201–227.Google Scholar
Willis, A. P., Sreenivasan, B. & Gubbins, D. 2007 Thermal core-mantle interaction: exploring regimes for ‘locked’ dynamo action. Phys. Earth Planet. Inter. 165, 83–92.Google Scholar
Zhang, K. 1995 Spherical shell rotating convection in the presence of a toroidal magnetic field. Proc. R. Soc. Lond. A 448, 243–268.Google Scholar