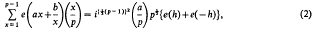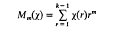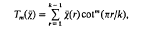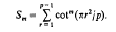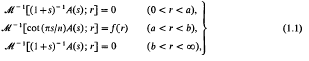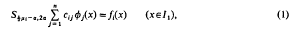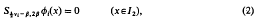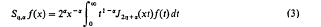Research Article
On the values of the Epstein zeta function
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-12
-
- Article
-
- You have access
- Export citation
Topologies on Boolean algebras defined by ideals and dual ideals
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 13-20
-
- Article
-
- You have access
- Export citation
Any group is a maximal subgroup of the semigroup of binary relations on some set†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 21-24
-
- Article
-
- You have access
- Export citation
On Salié's sum
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 25-26
-
- Article
-
- You have access
- Export citation
Regular semigroups which are subdirect products of a band and a semilattice of groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 27-49
-
- Article
-
- You have access
- Export citation
An elementary proof of some character sum identities of Apostol
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 50-53
-
- Article
-
- You have access
- Export citation
A remark on the divisor function d(n)
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 54-55
-
- Article
-
- You have access
- Export citation
The translational hull of an inverse semigroup
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 56-64
-
- Article
-
- You have access
- Export citation
The solution of certain triple integral equations involving inverse Mellin transforms†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 65-72
-
- Article
-
- You have access
- Export citation
Simultaneous dual integral equations
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 73-76
-
- Article
-
- You have access
- Export citation
Spaces of closed subgroups of a connected Lie group
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 77-79
-
- Article
-
- You have access
- Export citation
A ratio limit theorem for contraction projections and applications
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 80-85
-
- Article
-
- You have access
- Export citation
Factorization and arithmetic functions for orders in composition algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 86-95
-
- Article
-
- You have access
- Export citation
Locally convex spaces with fundamental sequences
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 96-100
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 14 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation

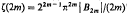 , where
, where 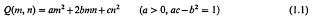
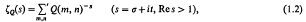
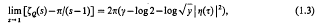
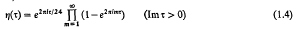
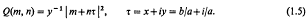
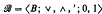 the binary operation
the binary operation 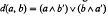 is a “metric“ operation to show that, if
is a “metric“ operation to show that, if 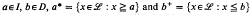 , as sub-base for the open sets. It is these topologies that are studied in this paper.
, as sub-base for the open sets. It is these topologies that are studied in this paper.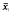 , where
, where 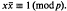 We consider the sum
We consider the sum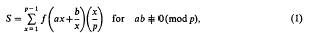
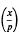 is the Legendre symbol. The sum is zero if
is the Legendre symbol. The sum is zero if 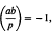 as is clear on replacing
as is clear on replacing