Article contents
THE GEOMETRY OF BLUEPRINTS PART II: TITS–WEYL MODELS OF ALGEBRAIC GROUPS
Published online by Cambridge University Press: 23 October 2018
Abstract
This paper is dedicated to a problem raised by Jacquet Tits in 1956: the Weyl group of a Chevalley group should find an interpretation as a group over what is nowadays called 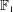 $\mathbb{F}_{1}$, the field with one element. Based on Part I of The geometry of blueprints, we introduce the class of Tits morphisms between blue schemes. The resulting Tits category
$\mathbb{F}_{1}$, the field with one element. Based on Part I of The geometry of blueprints, we introduce the class of Tits morphisms between blue schemes. The resulting Tits category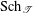 $\text{Sch}_{{\mathcal{T}}}$ comes together with a base extension to (semiring) schemes and the so-called Weyl extension to sets. We prove for
$\text{Sch}_{{\mathcal{T}}}$ comes together with a base extension to (semiring) schemes and the so-called Weyl extension to sets. We prove for 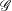 ${\mathcal{G}}$ in a wide class of Chevalley groups—which includes the special and general linear groups, symplectic and special orthogonal groups, and all types of adjoint groups—that a linear representation of
${\mathcal{G}}$ in a wide class of Chevalley groups—which includes the special and general linear groups, symplectic and special orthogonal groups, and all types of adjoint groups—that a linear representation of 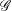 ${\mathcal{G}}$ defines a model
${\mathcal{G}}$ defines a model 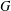 $G$ in
$G$ in 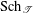 $\text{Sch}_{{\mathcal{T}}}$ whose Weyl extension is the Weyl group
$\text{Sch}_{{\mathcal{T}}}$ whose Weyl extension is the Weyl group 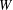 $W$ of
$W$ of 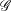 ${\mathcal{G}}$. We call such models Tits–Weyl models. The potential of Tits–Weyl models lies in (a) their intrinsic definition that is given by a linear representation; (b) the (yet to be formulated) unified approach towards thick and thin geometries; and (c) the extension of a Chevalley group to a functor on blueprints, which makes it, in particular, possible to consider Chevalley groups over semirings. This opens applications to idempotent analysis and tropical geometry.
${\mathcal{G}}$. We call such models Tits–Weyl models. The potential of Tits–Weyl models lies in (a) their intrinsic definition that is given by a linear representation; (b) the (yet to be formulated) unified approach towards thick and thin geometries; and (c) the extension of a Chevalley group to a functor on blueprints, which makes it, in particular, possible to consider Chevalley groups over semirings. This opens applications to idempotent analysis and tropical geometry.
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author 2018
References
- 5
- Cited by




