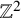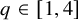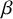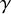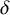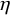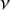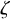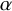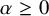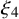1 Introduction
1.1 Motivation
Understanding the behaviour of physical systems undergoing a continuous phase transition at and near their critical point is one of the major challenges of modern statistical physics on both the physics and mathematical sides. In the first half of the twentieth century, the understanding relied essentially on exact computations, as exemplified by the analysis of mean-field systems and Onsager’s revolutionary solution of the 2D Ising model [Reference OnsagerOns44]. In the 1960s, a major advance was achieved by American chemist Benjamin Widom, who proposed in [Reference WidomWid65] that many quantities at and near criticality follow power laws, translating the question of understanding the phase transition into the question of computing so-called critical exponents. Also, the arrival of the renormalisation group (RG) formalism (see [Reference FisherFis98] for a historical exposition) led to a (nonrigorous) deep physical and geometrical understanding of continuous phase transitions. The RG formalism suggests that ‘coarse-graining’ renormalisation transformations correspond to appropriately changing the scale and parameters of the model under study. The large-scale limit of the critical regime then arises as the fixed point of the renormalisation transformations.
A striking consequence of the RG formalism is that because the critical fixed point is usually unique, the scaling limit at the critical point must satisfy translation, rotation, scale and even conformal invariance [Reference PolyakovPol70]. In two dimensions, this prediction allowed for the computation of the critical exponents ruling the behaviour of thermodynamical quantities and the classification of models into universality classes, meaning classes of models undergoing the same critical behaviour.
Another observation related to the previous developments is that the critical exponents are related to each other: if the behaviours of the specific heat, order parameter, susceptibility, source-field, two-point function and correlation length are governed by the exponents
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
,
$\beta $
,
![]() $\gamma $
,
$\gamma $
,
![]() $\delta $
,
$\delta $
,
![]() $\eta $
and
$\eta $
and
![]() $\nu $
, respectively, then the following scaling relations were predicted by physicists; see, for example, [Reference Essam and FisherEF63, Reference FisherFis64, Reference WidomWid65] for some early works on the subject (below, the dimension d of the lattice is assumed to be equal to 2, but we state the relations in this generality as they are predicted to extend to any dimension below the so-called upper critical dimension of the system):
$\nu $
, respectively, then the following scaling relations were predicted by physicists; see, for example, [Reference Essam and FisherEF63, Reference FisherFis64, Reference WidomWid65] for some early works on the subject (below, the dimension d of the lattice is assumed to be equal to 2, but we state the relations in this generality as they are predicted to extend to any dimension below the so-called upper critical dimension of the system):
A striking feature of these relations is that they hold for different universality classes, meaning the critical exponents may vary for different models, but they are always related via equations (1.1) and (1.2).
The aim of this paper is to provide rigorous proofs of these scaling relations for a family of planar percolation models. Percolation models are models of random subgraphs of a given lattice. Bernoulli percolation is perhaps the most-studied such model, and breakthroughs in the understanding of its phase transition have often served as milestones in the exciting history of statistical physics. The random-cluster model (also called Fortuin-Kasteleyn percolation) is another example of a percolation model. It was introduced by Fortuin and Kasteleyn around 1970 [Reference FortuinFor71, Reference Fortuin and KasteleynFK72] as a generalisation of Bernoulli percolation. It was found to be related to many other models of statistical mechanics, including the Ising, Potts and Ashkin-Teller models, and to exhibit a very rich critical behaviour. Of particular importance from the point of view of physics and relevant to our paper is the fact that the scaling limits of the random-cluster models at criticality are expected to fall into different universality classes and to be related to various 2D conformal field theories.
Let us conclude this section by reminding the reader that the theory of Bernoulli percolation is now well developed, with a deep qualitative understanding of the properties of the scaling limit [Reference Aizenman and BurchardAB99] and crossing probabilities [Reference RussoRus78, Reference Seymour and WelshSW78], universal critical exponents [Reference Kesten, Sidoravicius and ZhangKSZ98], scaling relations [Reference KestenKes87, Reference NolinNol08], noise sensitivity, near-critical window [Reference Garban, Pete and SchrammGPS10, Reference Garban, Pete and SchrammGPS18] and so on. For a variant of the model (site percolation on the triangular lattice), the existence of the scaling limit and its conformal invariance was proved [Reference SmirnovSmi01] and critical exponents have been computed [Reference Smirnov and WernerSW01]; see [Reference Beffara and Duminil-CopinBD13] and references therein for an overview of two-dimensional Bernoulli percolation. Deriving all these properties for Bernoulli percolation relies on specific features, such as independence of the states of different edges and geometric interpretations of differential formulae using so-called pivotal events. These features are not satisfied for more general random-cluster models. Another more prosaic goal of this paper is therefore to develop robust tools enabling one to bypass these special characteristics of Bernoulli percolation to extend the results mentioned in the abstract to the whole regime of critical random-cluster models undergoing a continuous phase transition. As such, these tools may have a number of implications that are not mentioned in the present paper, in particular for the study of other planar-dependent percolation models.
1.2 Definition of the random-cluster model
As mentioned in the previous section, the model of interest in this paper is the random-cluster model, which we now define. For background, we direct the reader to the monograph [Reference GrimmettGri06] and the lecture notes [Reference Duminil-CopinDum17] for an exposition of recent results.
Consider the square lattice
![]() $(\mathbb Z^2,\mathbb E)$
that is the graph with vertex-set
$(\mathbb Z^2,\mathbb E)$
that is the graph with vertex-set
![]() $\mathbb Z^2=\{(n,m):n,m\in \mathbb Z\}$
and edges between nearest neighbours. In a slight abuse of notation, we will write
$\mathbb Z^2=\{(n,m):n,m\in \mathbb Z\}$
and edges between nearest neighbours. In a slight abuse of notation, we will write
![]() $\mathbb {Z}^2$
for the graph itself. Consider a finite subgraph
$\mathbb {Z}^2$
for the graph itself. Consider a finite subgraph
![]() $G = (V,E)$
of the square lattice (V denotes the vertex-set and E the edge-set), and let
$G = (V,E)$
of the square lattice (V denotes the vertex-set and E the edge-set), and let
![]() $\partial G$
be the set of vertices in V incident to at most three edges in E. Write
$\partial G$
be the set of vertices in V incident to at most three edges in E. Write
![]() $\Lambda _n$
for the subgraph of
$\Lambda _n$
for the subgraph of
![]() $\mathbb {Z}^2$
spanned by the vertex-set
$\mathbb {Z}^2$
spanned by the vertex-set
![]() $\{-n,\dots , n\}^2$
. For
$\{-n,\dots , n\}^2$
. For
![]() $1 \le r < R$
, write
$1 \le r < R$
, write
![]() $\mathrm {Ann}(r,R)$
for the annulus
$\mathrm {Ann}(r,R)$
for the annulus
![]() $\Lambda _R\smallsetminus \Lambda _{r-1}$
. We also write
$\Lambda _R\smallsetminus \Lambda _{r-1}$
. We also write
![]() $\Lambda _n(x)$
and
$\Lambda _n(x)$
and
![]() $\Lambda _n(e)$
for the boxes of size n recentred around x and the bottom left endpoint of the edge e, respectively.
$\Lambda _n(e)$
for the boxes of size n recentred around x and the bottom left endpoint of the edge e, respectively.
To define the model, consider first a finite graph G. A percolation configuration
![]() $\omega $
on G is an element of
$\omega $
on G is an element of
![]() $\{0,1\}^{E}$
. An edge e is said to be open (in
$\{0,1\}^{E}$
. An edge e is said to be open (in
![]() $\omega $
) if
$\omega $
) if
![]() $\omega _e=1$
; otherwise it is closed. A configuration
$\omega _e=1$
; otherwise it is closed. A configuration
![]() $\omega $
can be seen as a subgraph of G with vertex-set V and edge-set
$\omega $
can be seen as a subgraph of G with vertex-set V and edge-set
![]() $\{e\in E:\omega _e=1\}$
. When speaking of connections in
$\{e\in E:\omega _e=1\}$
. When speaking of connections in
![]() $\omega $
, we view
$\omega $
, we view
![]() $\omega $
as a graph. For sets of vertices A and B, we say that A is connected to B if there exists a path of edges of
$\omega $
as a graph. For sets of vertices A and B, we say that A is connected to B if there exists a path of edges of
![]() $\omega $
that connect a vertex of A to a vertex of B. This event is denoted by
$\omega $
that connect a vertex of A to a vertex of B. This event is denoted by
![]() $A{\longleftrightarrow }B$
. We also speak of connections in a set of vertices C if the endpoints of the edges of the path are all in C.
$A{\longleftrightarrow }B$
. We also speak of connections in a set of vertices C if the endpoints of the edges of the path are all in C.
A cluster is a connected component of
![]() $\omega $
. The boundary conditions
$\omega $
. The boundary conditions
![]() $\xi $
on G are given by a partition of
$\xi $
on G are given by a partition of
![]() $\partial G$
. We say that two vertices of G are wired together if they belong to the same element of the partition
$\partial G$
. We say that two vertices of G are wired together if they belong to the same element of the partition
![]() $\xi $
.
$\xi $
.
Definition 1.1. The random-cluster measure on G with edge-weight p, cluster-weight
![]() $q>0$
and boundary conditions
$q>0$
and boundary conditions
![]() $\xi $
is given by
$\xi $
is given by
where
![]() $|\omega |:=\sum _{e\in E}\omega _e$
,
$|\omega |:=\sum _{e\in E}\omega _e$
,
![]() $k(\omega )$
is the number of connected components of the graph,
$k(\omega )$
is the number of connected components of the graph,
![]() $\omega ^{\xi }$
is the graph obtained from
$\omega ^{\xi }$
is the graph obtained from
![]() $\omega $
by identifying wired vertices together, and
$\omega $
by identifying wired vertices together, and
![]() $Z^{\xi }(G,p,q)$
is a normalising constant called the partition function chosen in such a way that
$Z^{\xi }(G,p,q)$
is a normalising constant called the partition function chosen in such a way that
![]() $\phi _{G,p,q}^{\xi }$
is a probability measure.
$\phi _{G,p,q}^{\xi }$
is a probability measure.
Two specific families of boundary conditions will be of special interest to us. On the one hand, the free boundary conditions, denoted 0, correspond to no wirings between boundary vertices. On the other hand, the wired boundary conditions, denoted 1, correspond to all boundary vertices being wired together.
The random-cluster model may be modified to accommodate an external magnetic field as follows. Add to the lattice
![]() $\mathbb {Z}^2$
a vertex
$\mathbb {Z}^2$
a vertex
![]() $\mathfrak g$
called the ghost vertex, and connect it to each vertex v of
$\mathfrak g$
called the ghost vertex, and connect it to each vertex v of
![]() $\mathbb {Z}^2$
with an edge
$\mathbb {Z}^2$
with an edge
![]() $v\mathfrak g$
. The random-cluster measure
$v\mathfrak g$
. The random-cluster measure
![]() $\phi _{G,p,q,h}^i$
(for
$\phi _{G,p,q,h}^i$
(for
![]() $i=0$
or
$i=0$
or
![]() $1$
and
$1$
and
![]() $h \geq 0$
) is defined exactly as the random-cluster model on G, except that the boundary is now
$h \geq 0$
) is defined exactly as the random-cluster model on G, except that the boundary is now
![]() $\partial G\cup \{\mathfrak g\}$
, and the edge-weight is p for the edges of G and
$\partial G\cup \{\mathfrak g\}$
, and the edge-weight is p for the edges of G and
![]() $1-e^{-h}$
for edges having
$1-e^{-h}$
for edges having
![]() $\mathfrak g$
as an endpoint: that is,
$\mathfrak g$
as an endpoint: that is,
where
![]() $\Delta (\omega ):=\sum _{v\in V}\omega _{v{\mathfrak g}}$
. The probability that
$\Delta (\omega ):=\sum _{v\in V}\omega _{v{\mathfrak g}}$
. The probability that
![]() $\mathfrak g$
is in the cluster of 0 has an interpretation in terms of spin models with a magnetic field: for
$\mathfrak g$
is in the cluster of 0 has an interpretation in terms of spin models with a magnetic field: for
![]() $q=2$
, this probability is equal to the spontaneous magnetisation with an external field h for the Ising model on the square lattice. A similar interpretation holds for the 3-state and 4-state Potts models. For more details on this topic, see [Reference Biskup, Borgs, Chayes and KoteckýBBCK00].
$q=2$
, this probability is equal to the spontaneous magnetisation with an external field h for the Ising model on the square lattice. A similar interpretation holds for the 3-state and 4-state Potts models. For more details on this topic, see [Reference Biskup, Borgs, Chayes and KoteckýBBCK00].
For
![]() $q\ge 1$
and
$q\ge 1$
and
![]() $i=0,1$
, the family of measures
$i=0,1$
, the family of measures
![]() $\phi _{G,p,q,h}^i$
converges weakly as G tends to the whole square lattice [Reference GrimmettGri06, Theorem 4.19]. The limiting measures on
$\phi _{G,p,q,h}^i$
converges weakly as G tends to the whole square lattice [Reference GrimmettGri06, Theorem 4.19]. The limiting measures on
![]() $\{0,1\}^{\mathbb {E}}$
are denoted by
$\{0,1\}^{\mathbb {E}}$
are denoted by
![]() $\phi _{p,q,h}^i$
and are called infinite-volume random-cluster measures with free and wired boundary conditions. They are invariant under translations and ergodic. When
$\phi _{p,q,h}^i$
and are called infinite-volume random-cluster measures with free and wired boundary conditions. They are invariant under translations and ergodic. When
![]() $h=0$
, we simply drop it from the notation.
$h=0$
, we simply drop it from the notation.
The random-cluster model undergoes a phase transition at
![]() $h=0$
and a critical parameter
$h=0$
and a critical parameter
![]() $p_c=p_c(q)$
in the following sense: if
$p_c=p_c(q)$
in the following sense: if
![]() $p>p_c(q)$
, the probability
$p>p_c(q)$
, the probability
is strictly positive, while for
![]() $p<p_c(q)$
, it is equal to 0. In the past 10 years, considerable progress has been made in the understanding of this phase transition: the critical point was proved in [Reference Beffara and Duminil-CopinBD12] (see also [Reference Duminil-Copin and ManolescuDM16, Reference Duminil-Copin, Raoufi and TassionDRT18]) to be equal to
$p<p_c(q)$
, it is equal to 0. In the past 10 years, considerable progress has been made in the understanding of this phase transition: the critical point was proved in [Reference Beffara and Duminil-CopinBD12] (see also [Reference Duminil-Copin and ManolescuDM16, Reference Duminil-Copin, Raoufi and TassionDRT18]) to be equal to
 $$ \begin{align*} p_c(q)=\frac{\sqrt q}{1+\sqrt q}. \end{align*} $$
$$ \begin{align*} p_c(q)=\frac{\sqrt q}{1+\sqrt q}. \end{align*} $$
It was also shown in these papers that the correlation length
is finite as soon as
![]() $p\ne p_c$
, where
$p\ne p_c$
, where
(when
![]() $p=p_c$
, we drop
$p=p_c$
, we drop
![]() $p_c$
from this notation).
$p_c$
from this notation).
For
![]() $q\ge 1$
, it was proved in [Reference Duminil-Copin, Sidoravicius and TassionDST17, Reference Duminil-Copin, Gagnebin, Harel, Manolescu and TassionDGHMT16] (see also [Reference Ray and SpinkaRS20] when
$q\ge 1$
, it was proved in [Reference Duminil-Copin, Sidoravicius and TassionDST17, Reference Duminil-Copin, Gagnebin, Harel, Manolescu and TassionDGHMT16] (see also [Reference Ray and SpinkaRS20] when
![]() $q>4$
) that the correlation length at
$q>4$
) that the correlation length at
![]() $p_c$
is infinite if and only if
$p_c$
is infinite if and only if
![]() $q\le 4$
. As the divergence of the correlation length is one of the characterisations of a continuous phase transition, and as we are interested in this type of phase transition only, in the whole paper we will restrict our attention to the range
$q\le 4$
. As the divergence of the correlation length is one of the characterisations of a continuous phase transition, and as we are interested in this type of phase transition only, in the whole paper we will restrict our attention to the range
![]() $q\in [1,4]$
. Also, since the
$q\in [1,4]$
. Also, since the
![]() $q=1$
case was already treated by Kesten in [Reference KestenKes87] and later solved in numerous other places (see references below), we will often assume that
$q=1$
case was already treated by Kesten in [Reference KestenKes87] and later solved in numerous other places (see references below), we will often assume that
![]() $q>1$
.
$q>1$
.
Two notational conventions
Since
![]() $q\in [1,4]$
will always be fixed, we drop it from notation. For
$q\in [1,4]$
will always be fixed, we drop it from notation. For
![]() $q\in [1,4]$
, there is a unique infinite-volume random-cluster measure, so we omit the superscript corresponding to the boundary condition and denote it simply by
$q\in [1,4]$
, there is a unique infinite-volume random-cluster measure, so we omit the superscript corresponding to the boundary condition and denote it simply by
![]() $\phi _{p}$
.
$\phi _{p}$
.
For two families
![]() $(f_i)_{i\in I}$
and
$(f_i)_{i\in I}$
and
![]() $(g_i)_{i\in I}$
, introduce
$(g_i)_{i\in I}$
, introduce
![]() $ f\asymp g$
(respectively,
$ f\asymp g$
(respectively,
![]() $ f\stackrel{<}{\scriptstyle{\frown}} g$
and
$ f\stackrel{<}{\scriptstyle{\frown}} g$
and
![]() $f\stackrel{>}{\scriptstyle{\frown}} g$
) to refer to the existence of constants
$f\stackrel{>}{\scriptstyle{\frown}} g$
) to refer to the existence of constants
![]() $c,C\in (0,\infty )$
such that for every
$c,C\in (0,\infty )$
such that for every
![]() $i\in I$
,
$i\in I$
,
![]() $cg_i\le f_i\le Cg_i$
(respectively,
$cg_i\le f_i\le Cg_i$
(respectively,
![]() $f_i\le Cg_i$
and
$f_i\le Cg_i$
and
![]() $f_i\ge cg_i$
). In most cases, the family I will be obvious from context and omitted. In the special case where I contains (implicitly or explicitly) the edge-parameter
$f_i\ge cg_i$
). In most cases, the family I will be obvious from context and omitted. In the special case where I contains (implicitly or explicitly) the edge-parameter
![]() $p\in (0,1)$
, we further require that p is not close to 0 or 1 (which is justified for every application we have in mind since we are interested in properties for p close to
$p\in (0,1)$
, we further require that p is not close to 0 or 1 (which is justified for every application we have in mind since we are interested in properties for p close to
![]() $p_c$
).
$p_c$
).
1.3 Stability below the characteristic length
When studying a noncritical system, a natural length-scale is provided by the characteristic length, which appeared in a simplified context of Bernoulli percolation in the work of Kesten [Reference KestenKes87] (see also [Reference Borgs, Chayes, Kesten and SpencerBCKS99]) and was explicit for the random-cluster model in [Reference Duminil-Copin, Garban and PeteDGP14]. To define the characteristic length, we first introduce the notion of crossing probability.
A quad
![]() $(\mathcal {D}; a,b,c,d)$
is a finite subgraph of
$(\mathcal {D}; a,b,c,d)$
is a finite subgraph of
![]() $\mathbb {Z}^2$
whose boundary
$\mathbb {Z}^2$
whose boundary
![]() $\partial \mathcal {D}$
is a simple path of edges of
$\partial \mathcal {D}$
is a simple path of edges of
![]() $\mathbb Z^2$
, along with four points
$\mathbb Z^2$
, along with four points
![]() $a,b,c,d$
found on
$a,b,c,d$
found on
![]() $\partial \mathcal {D}$
in counterclockwise order. These points define four arcs
$\partial \mathcal {D}$
in counterclockwise order. These points define four arcs
![]() $(ab)$
,
$(ab)$
,
![]() $(bc)$
,
$(bc)$
,
![]() $(cd)$
and
$(cd)$
and
![]() $(da)$
corresponding to the parts of the boundary between them. We also see the quad as a domain of
$(da)$
corresponding to the parts of the boundary between them. We also see the quad as a domain of
![]() $\mathbb R^2$
with marked points on its boundary by taking the union of the faces enclosed by
$\mathbb R^2$
with marked points on its boundary by taking the union of the faces enclosed by
![]() $\partial \mathcal {D}$
. The typical example is the case of rectangles
$\partial \mathcal {D}$
. The typical example is the case of rectangles
![]() $[0,n]\times [0,m]$
or
$[0,n]\times [0,m]$
or
![]() $\Lambda _n$
with
$\Lambda _n$
with
![]() $a,b,c,d$
being the corners of the rectangle, oriented in counterclockwise order, starting from the bottom-right corner. In this case, we omit
$a,b,c,d$
being the corners of the rectangle, oriented in counterclockwise order, starting from the bottom-right corner. In this case, we omit
![]() $a,b,c,d$
from the notation. We say that the quad
$a,b,c,d$
from the notation. We say that the quad
![]() $(\mathcal {D},a,b,c,d)$
is crossed if
$(\mathcal {D},a,b,c,d)$
is crossed if
![]() $(ab)$
is connected to
$(ab)$
is connected to
![]() $(cd)$
in
$(cd)$
in
![]() $\mathcal {D}$
. The event is denoted by
$\mathcal {D}$
. The event is denoted by
![]() $\mathcal {C}(\mathcal {D})$
.
$\mathcal {C}(\mathcal {D})$
.
We say that a quad
![]() $(\mathcal {D}; a,b,c,d)$
is
$(\mathcal {D}; a,b,c,d)$
is
![]() $\eta $
-regular at scale R for some
$\eta $
-regular at scale R for some
![]() $\eta> 0$
if
$\eta> 0$
if
![]() $\mathcal {D}$
is contained in
$\mathcal {D}$
is contained in
![]() $\Lambda _R$
and is the union of a finite number of translates of
$\Lambda _R$
and is the union of a finite number of translates of
![]() $\Lambda _{\eta R}$
by points of
$\Lambda _{\eta R}$
by points of
![]() $\eta R\mathbb Z^2$
, and
$\eta R\mathbb Z^2$
, and
![]() $a,b,c,d\in \eta R\mathbb {Z}^2$
.
$a,b,c,d\in \eta R\mathbb {Z}^2$
.
Now, consider
![]() $\delta _L>0$
small enough. How small
$\delta _L>0$
small enough. How small
![]() $\delta _L$
should be is dictated by the proof of equation (RSW), and we simply wish to mention here that
$\delta _L$
should be is dictated by the proof of equation (RSW), and we simply wish to mention here that
![]() $\delta _L$
can be taken independent of
$\delta _L$
can be taken independent of
![]() $q\in [1,4]$
and can easily be estimated (even though the value is irrelevant for our study); see also Remark 2.14.
$q\in [1,4]$
and can easily be estimated (even though the value is irrelevant for our study); see also Remark 2.14.
Definition 1.2 (Characteristic length)
For each
![]() $q\ge 1$
and
$q\ge 1$
and
![]() $p\in (0,1)$
, let
$p\in (0,1)$
, let
We insist on the fact that we consider the unique infinite-volume measure
![]() $\phi _p$
for the definition.
$\phi _p$
for the definition.
Note that
![]() $L(p)<+\infty $
for every
$L(p)<+\infty $
for every
![]() $p\ne p_c$
by [Reference Beffara and Duminil-CopinBD12]; by duality,
$p\ne p_c$
by [Reference Beffara and Duminil-CopinBD12]; by duality,
![]() $L(p_c)=+\infty $
as long as
$L(p_c)=+\infty $
as long as
![]() $\delta _L < 1/2$
, which we will always assume. The interest of the characteristic length lies in its connection with the scaling window: that is, the regime of parameters
$\delta _L < 1/2$
, which we will always assume. The interest of the characteristic length lies in its connection with the scaling window: that is, the regime of parameters
![]() $(R,p)$
for which one expects typical properties of the random-cluster model in
$(R,p)$
for which one expects typical properties of the random-cluster model in
![]() $\Lambda _R$
with parameters p to be similar to the critical ones. In physics, the statement that the system looks critical is usually related to another length-scale: namely, the correlation length
$\Lambda _R$
with parameters p to be similar to the critical ones. In physics, the statement that the system looks critical is usually related to another length-scale: namely, the correlation length
![]() $\xi (p)$
defined in equation (1.3). The correlation length encodes the rate of exponential decay of the probability of being connected to distance n but not to infinity as n tends to infinity; it is not a priori directly related to
$\xi (p)$
defined in equation (1.3). The correlation length encodes the rate of exponential decay of the probability of being connected to distance n but not to infinity as n tends to infinity; it is not a priori directly related to
![]() $L(p)$
. Nevertheless, the following result reunites the two notions of correlation and characteristic lengths, thus affirming that the characteristic length is simply the correlation length in disguise.
$L(p)$
. Nevertheless, the following result reunites the two notions of correlation and characteristic lengths, thus affirming that the characteristic length is simply the correlation length in disguise.
Theorem 1.3 (Equivalence correlation/characteristic lengths)
Fix
![]() $1\le q\le 4$
. We have that for
$1\le q\le 4$
. We have that for
![]() $p\in (0,1)$
,
$p\in (0,1)$
,
The proof is based on a coarse-grained procedure. We wish to highlight that the result is new for every
![]() $1<q\le 4$
– even for
$1<q\le 4$
– even for
![]() $q=2$
, for which [Reference Duminil-Copin, Garban and PeteDGP14, Theorem 1.2] proves almost the same statement, but with a logarithmic control over the ratio of
$q=2$
, for which [Reference Duminil-Copin, Garban and PeteDGP14, Theorem 1.2] proves almost the same statement, but with a logarithmic control over the ratio of
![]() $L(p)/\xi (p)$
rather than a constant one. Combined with [Reference Beffara and Duminil-CopinBD12b], for instance, this enables us to estimate Ising quantities; see Theorem 1.13 below.
$L(p)/\xi (p)$
rather than a constant one. Combined with [Reference Beffara and Duminil-CopinBD12b], for instance, this enables us to estimate Ising quantities; see Theorem 1.13 below.
One of the main results of [Reference KestenKes87] is that the scaling window is simply the set of
![]() $(p;R)$
such that
$(p;R)$
such that
![]() $R=O(L(p))$
. This result is sometimes referred to as stability below the characteristic length; it is the subject of the following theorem in the context of the random-cluster model. Together with Theorem 1.3, the stability result legitimates the two physical interpretations of the correlation length: in terms of rate of decay and in terms of scaling window. We state the result for
$R=O(L(p))$
. This result is sometimes referred to as stability below the characteristic length; it is the subject of the following theorem in the context of the random-cluster model. Together with Theorem 1.3, the stability result legitimates the two physical interpretations of the correlation length: in terms of rate of decay and in terms of scaling window. We state the result for
![]() $q\ne 1$
as the case
$q\ne 1$
as the case
![]() $q=1$
was already treated in [Reference KestenKes87]. Recall the definition of
$q=1$
was already treated in [Reference KestenKes87]. Recall the definition of
![]() $\pi _1(p;R)$
and the fact that we omit p when
$\pi _1(p;R)$
and the fact that we omit p when
![]() $p=p_c$
.
$p=p_c$
.
Theorem 1.4 (Stability below the characteristic length)
Fix
![]() $1< q \le 4$
.
$1< q \le 4$
.
(Stability of crossing probabilities) There exists
![]() $\varepsilon> 0$
such that for every
$\varepsilon> 0$
such that for every
![]() $\eta $
-regular discrete quad
$\eta $
-regular discrete quad
![]() $(\mathcal {D},a,b,c,d)$
at scale
$(\mathcal {D},a,b,c,d)$
at scale
![]() $R\ge 1$
and every
$R\ge 1$
and every
![]() $p \in (0,1)$
(the constant in
$p \in (0,1)$
(the constant in
![]() $\stackrel{<}{\scriptstyle{\frown}}$
depends on
$\stackrel{<}{\scriptstyle{\frown}}$
depends on
![]() $\eta $
but
$\eta $
but
![]() $\varepsilon $
does not),
$\varepsilon $
does not),
(Stability of the one-arm event) For every
![]() $p \in (0,1)$
and every
$p \in (0,1)$
and every
![]() $R\le L(p)$
,
$R\le L(p)$
,
The stability of arm event probabilities given by equation (1.8) extends to more general arm events. Moreover, an improved version may be formulated; see Remark 7.2 for details.
The strategy for proving Theorem 1.4 is related to Kesten’s original one in that it uses Theorem 1.6 below to study the behaviour of derivatives of crossing events. Nevertheless, several additional difficulties occur, mainly due to the replacement of pivotality by influence in the differential formulas for probabilities of events: recall [Reference GrimmettGri06, Theorem 2.46] the general formula, valid for every
![]() $q>0$
,
$q>0$
,
where
![]() $\mathrm {Cov}_p$
denotes the covariance under
$\mathrm {Cov}_p$
denotes the covariance under
![]() $\phi _p$
. For
$\phi _p$
. For
![]() $q=1$
, the sum of covariances gets nicely rewritten in terms of pivotal edges: edges that when switched from closed to open, change the occurrence of the event. In particular, it is possible to prove that for crossing events of a rectangle of size R and edges that are far from the boundary of the rectangle, the probability of being pivotal is of the order of the probability
$q=1$
, the sum of covariances gets nicely rewritten in terms of pivotal edges: edges that when switched from closed to open, change the occurrence of the event. In particular, it is possible to prove that for crossing events of a rectangle of size R and edges that are far from the boundary of the rectangle, the probability of being pivotal is of the order of the probability
![]() $\pi _4(p;R)$
that in the ball of radius R around a given edge e, the two extremities of e belong to different clusters that both reach the boundary of said ball (when
$\pi _4(p;R)$
that in the ball of radius R around a given edge e, the two extremities of e belong to different clusters that both reach the boundary of said ball (when
![]() $p=p_c$
, we simply write
$p=p_c$
, we simply write
![]() $\pi _4(R)$
). This property was used crucially in [Reference KestenKes87] and ultimately leads to Kesten’s scaling relation
$\pi _4(R)$
). This property was used crucially in [Reference KestenKes87] and ultimately leads to Kesten’s scaling relation
![]() $L(p)^2 \pi _4(L(p)) \asymp (p-p_c)^{-1}$
. The description in terms of pivotal edges is wrong for random-cluster models with
$L(p)^2 \pi _4(L(p)) \asymp (p-p_c)^{-1}$
. The description in terms of pivotal edges is wrong for random-cluster models with
![]() $q>1$
as the covariance between an edge and crossing events at scale R is no longer of the order of
$q>1$
as the covariance between an edge and crossing events at scale R is no longer of the order of
![]() $\pi _4(p;R)$
; see [Reference Duminil-Copin, Garban and PeteDGP14].
$\pi _4(p;R)$
; see [Reference Duminil-Copin, Garban and PeteDGP14].
Driven by this different phenomenology, in this paper we introduce a new interpretation of the covariance valid for every
![]() $q>1$
encoding how much an edge is influenced by boundary conditions at a distance R or, equivalently, how fast the model mixes.
$q>1$
encoding how much an edge is influenced by boundary conditions at a distance R or, equivalently, how fast the model mixes.
Definition 1.5 (Mixing rate)
For
![]() $1< q\le 4$
,
$1< q\le 4$
,
![]() $1 \le r < R$
,
$1 \le r < R$
,
![]() $p\in (0,1)$
and e an edge incident to the origin, write
$p\in (0,1)$
and e an edge incident to the origin, write
The quantity
![]() $\Delta _p(R)$
, to which we now refer as the mixing rate, will be crucial in our study, as it will replace the amplitude
$\Delta _p(R)$
, to which we now refer as the mixing rate, will be crucial in our study, as it will replace the amplitude
![]() $\pi _4(p;R)$
of standard pivotal events in the study of Bernoulli percolation. As such, it is very important to derive some of its properties.
$\pi _4(p;R)$
of standard pivotal events in the study of Bernoulli percolation. As such, it is very important to derive some of its properties.
Theorem 1.6 (Properties of the mixing rate)
Fix
![]() $1<q\le 4$
.
$1<q\le 4$
.
(i) (Mixing rate/covariance connection) For every
![]() $\eta>0$
, every
$\eta>0$
, every
![]() $p\in (0,1)$
and every
$p\in (0,1)$
and every
![]() $\eta $
-regular quad
$\eta $
-regular quad
![]() $(\mathcal {D},a,b,c,d)$
at scale
$(\mathcal {D},a,b,c,d)$
at scale
![]() $R\le L(p)$
(below, the constants in
$R\le L(p)$
(below, the constants in
![]() $\asymp $
depend on
$\asymp $
depend on
![]() $\eta $
),
$\eta $
),
(ii) (Quasi-multiplicativity) For every
![]() $p\in (0,1)$
and
$p\in (0,1)$
and
![]() $1\le r\le \rho \le R\le L(p)$
,
$1\le r\le \rho \le R\le L(p)$
,
(iii) (Stability below the characteristic length) For every
![]() $p\in (0,1)$
and
$p\in (0,1)$
and
![]() $1\le R\le L(p)$
,
$1\le R\le L(p)$
,
(iv) (Comparison to pivotality) There exists
![]() $\varepsilon>0$
such that for every
$\varepsilon>0$
such that for every
![]() $1\le r\le R\le L(p)$
,
$1\le r\le R\le L(p)$
,
(v) (Mixing interpretation) For every
![]() $1\le 2r\le R\le L(p)$
,
$1\le 2r\le R\le L(p)$
,
 $$ \begin{align} \Delta_p(r,R)\asymp\max\Big\{\Big|\frac{\phi_p[A\cap B]}{\phi_p[A]\phi_p[B]}-1\Big|\ :\ A\in\mathcal F(\Lambda_r)\text{ and }B\in\mathcal F(\mathbb Z^2\smallsetminus\Lambda_R)\Big\}, \end{align} $$
$$ \begin{align} \Delta_p(r,R)\asymp\max\Big\{\Big|\frac{\phi_p[A\cap B]}{\phi_p[A]\phi_p[B]}-1\Big|\ :\ A\in\mathcal F(\Lambda_r)\text{ and }B\in\mathcal F(\mathbb Z^2\smallsetminus\Lambda_R)\Big\}, \end{align} $$
where
![]() $\mathcal F(S)$
is the
$\mathcal F(S)$
is the
![]() $\sigma $
-algebra generated by the edges with both endpoints in S.
$\sigma $
-algebra generated by the edges with both endpoints in S.
The proof of this theorem is the main innovation of the paper. It is based on new increasing couplings between random-cluster models. While coupling Bernoulli percolation at different parameters is fairly straightforward, coupling different random-cluster models can be quite elaborate. In this paper, we develop several increasing couplings between random-cluster models (typically one at
![]() $p_c$
and one at p, or one at
$p_c$
and one at p, or one at
![]() $p_c$
and another at
$p_c$
and another at
![]() $p_c$
, but conditioned on an event) that satisfy various properties.
$p_c$
, but conditioned on an event) that satisfy various properties.
In the previous theorem, Properties (i)–(v) have crucial interpretations. Property (i) will have the following important application: it states that the covariance between an edge that is deep inside an
![]() $\eta $
-regular quad and the crossing event of said quad is of the order of
$\eta $
-regular quad and the crossing event of said quad is of the order of
![]() $\Delta _p(R)$
. Some more refined results (in particular near the boundary) can be obtained; see Lemma 5.3 and the remarks below. Property (ii) is an analogue of the quasi-multiplicativity of probabilities of arm events and will be popping up everywhere in the applications of
$\Delta _p(R)$
. Some more refined results (in particular near the boundary) can be obtained; see Lemma 5.3 and the remarks below. Property (ii) is an analogue of the quasi-multiplicativity of probabilities of arm events and will be popping up everywhere in the applications of
![]() $\Delta _p(R)$
, in particular when trying to estimate the covariance between a crossing event and an edge close to the boundary of the quad. Property (iii) states the stability below the characteristic length for the mixing rate, analogously to that proved by Kesten for the four-arm event probability. Property (iv) shows that replacing
$\Delta _p(R)$
, in particular when trying to estimate the covariance between a crossing event and an edge close to the boundary of the quad. Property (iii) states the stability below the characteristic length for the mixing rate, analogously to that proved by Kesten for the four-arm event probability. Property (iv) shows that replacing
![]() $\pi _4(p;R)$
by
$\pi _4(p;R)$
by
![]() $\Delta _p(R)$
is really necessary, as the trivial bound stating that the covariance is larger than or equal to pivotality is polynomially far from being sharp for any
$\Delta _p(R)$
is really necessary, as the trivial bound stating that the covariance is larger than or equal to pivotality is polynomially far from being sharp for any
![]() $q>1$
. Finally, (v) justifies the reference to mixing in the name of
$q>1$
. Finally, (v) justifies the reference to mixing in the name of
![]() $\Delta _p$
, as it links this quantity to the error term in the ratio-weak mixing.
$\Delta _p$
, as it links this quantity to the error term in the ratio-weak mixing.
We finish our comments on this theorem with a crucial observation. When trying to compute asymptotics for the covariance between an edge and a crossing event, (i) and (ii) imply that it suffices to understand for every
![]() $\varepsilon>0$
the limit of
$\varepsilon>0$
the limit of
![]() $\Delta _{p_c}(\varepsilon R,R)$
as R tends to infinity. Indeed, these limits allow us to estimate the covariance up to arbitrarily small polynomial terms and therefore estimate the critical exponent. This is very useful as the covariance itself is not easily expressed in terms of properties of large interfaces of the critical system, while
$\Delta _{p_c}(\varepsilon R,R)$
as R tends to infinity. Indeed, these limits allow us to estimate the covariance up to arbitrarily small polynomial terms and therefore estimate the critical exponent. This is very useful as the covariance itself is not easily expressed in terms of properties of large interfaces of the critical system, while
![]() $\Delta _{p_c}(\varepsilon R,R)$
(which is equal to
$\Delta _{p_c}(\varepsilon R,R)$
(which is equal to
![]() $1-2\phi _{\Lambda _R,p_c}^0[\mathcal {C}(\Lambda _{\varepsilon R})]+o(1)$
by duality) is a quantity that can be derived from the scaling limit of the critical model, for instance using the conjectural convergence to the Conformal Loop Ensemble – see also Question 3 below.
$1-2\phi _{\Lambda _R,p_c}^0[\mathcal {C}(\Lambda _{\varepsilon R})]+o(1)$
by duality) is a quantity that can be derived from the scaling limit of the critical model, for instance using the conjectural convergence to the Conformal Loop Ensemble – see also Question 3 below.
It is tempting to deduce from the previous theorem that when
![]() $q>1$
, the derivative of crossing probabilities of
$q>1$
, the derivative of crossing probabilities of
![]() $\eta $
-regular quads at scale
$\eta $
-regular quads at scale
![]() $R\le L(p)$
is of order
$R\le L(p)$
is of order
![]() $R^2\Delta _p(R)$
(exactly like it is of order
$R^2\Delta _p(R)$
(exactly like it is of order
![]() $R^2\pi _4(R)$
for Bernoulli percolation). This statement is not always correct and illustrates the subtle but deep difference with Bernoulli percolation. Indeed, there is a competition on the right-hand side of equation (1.9) between two possible scenarios:
$R^2\pi _4(R)$
for Bernoulli percolation). This statement is not always correct and illustrates the subtle but deep difference with Bernoulli percolation. Indeed, there is a competition on the right-hand side of equation (1.9) between two possible scenarios:
-
• The collective contribution of edges in
 $\mathcal {D}$
is the main part of the right-hand side. In this case, we expect the derivative at
$\mathcal {D}$
is the main part of the right-hand side. In this case, we expect the derivative at
 $p_c$
to exist and to be of order
$p_c$
to exist and to be of order
 $R^2\Delta _{p_c}(R)$
. Moreover, it may be proved in this case that the derivative is stable within the critical window.
$R^2\Delta _{p_c}(R)$
. Moreover, it may be proved in this case that the derivative is stable within the critical window. -
• The collective contribution of edges far from
 $\mathcal {D}$
is the main part of the right-hand side. In this case, the derivative at
$\mathcal {D}$
is the main part of the right-hand side. In this case, the derivative at
 $p_c$
is infinite. For
$p_c$
is infinite. For
 $p\ne p_c$
, the contribution comes mostly from edges at distance
$p\ne p_c$
, the contribution comes mostly from edges at distance
 $L(p)$
, and the derivative is of order
$L(p)$
, and the derivative is of order
 $L(p)^2\Delta _p(L(p))^2/\Delta _p(R)$
.
$L(p)^2\Delta _p(L(p))^2/\Delta _p(R)$
.
Taking into account estimates from Lemma 5.3 to handle covariances with edges near the boundary, an accurate estimate of the derivative, valid in all scenarios, is therefore given by the following statement.
Corollary 1.7. Fix
![]() $1<q\le 4$
and
$1<q\le 4$
and
![]() $\eta>0$
. For every
$\eta>0$
. For every
![]() $p\in (0,1)$
and every
$p\in (0,1)$
and every
![]() $\eta $
-regular quad
$\eta $
-regular quad
![]() $(\mathcal {D},a,b,c,d)$
at scale
$(\mathcal {D},a,b,c,d)$
at scale
![]() $R\le L(p)$
,
$R\le L(p)$
,
 $$ \begin{align} \tfrac{\mathrm{d}}{\mathrm{d}p}\phi_{p}[\mathcal{C}(\mathcal{D})]\asymp R^2\Delta_p(R)+\sum_{\ell=R}^{L(p)}\ell \Delta_p(\ell)\Delta_p(R,\ell), \end{align} $$
$$ \begin{align} \tfrac{\mathrm{d}}{\mathrm{d}p}\phi_{p}[\mathcal{C}(\mathcal{D})]\asymp R^2\Delta_p(R)+\sum_{\ell=R}^{L(p)}\ell \Delta_p(\ell)\Delta_p(R,\ell), \end{align} $$
where the constants in
![]() $\asymp $
depend on
$\asymp $
depend on
![]() $\eta $
.
$\eta $
.
Looking at this sum formula for the derivative, one sees that whether the derivative is governed by the collective contribution of edges in or close to
![]() $\mathcal {D}$
or by that of edges far from
$\mathcal {D}$
or by that of edges far from
![]() $\mathcal {D}$
is related to the way
$\mathcal {D}$
is related to the way
![]() $\ell \Delta _p(\ell )$
decays or not as
$\ell \Delta _p(\ell )$
decays or not as
![]() $\ell $
tends to infinity. This can also be related to whether the specific heat blows up or not at
$\ell $
tends to infinity. This can also be related to whether the specific heat blows up or not at
![]() $p_c$
, as will be seen in the next section. Note that this up-to-constant formula unravelled a third possible scenario where each scale contributes the same amount. This scenario happens for the random-cluster model with
$p_c$
, as will be seen in the next section. Note that this up-to-constant formula unravelled a third possible scenario where each scale contributes the same amount. This scenario happens for the random-cluster model with
![]() $q=2$
, in which the derivative blows up logarithmically in
$q=2$
, in which the derivative blows up logarithmically in
![]() $L(p)$
– the logarithmic blowup of the specific heat may be deduced from the explicit form of the free energy [Reference OnsagerOns44].
$L(p)$
– the logarithmic blowup of the specific heat may be deduced from the explicit form of the free energy [Reference OnsagerOns44].
To derive this corollary, one will need an important result that is reminiscent of the classical claim that the four-arm exponent is strictly smaller than 2 for Bernoulli percolation.
Proposition 1.8 (Lower bound on
 $\Delta _{p}(r,R)$
)
$\Delta _{p}(r,R)$
)
For every
![]() $1<q\le 4$
, there exists
$1<q\le 4$
, there exists
![]() $\delta>0$
such that for every
$\delta>0$
such that for every
![]() $1\le r\le R\le L(p)$
,
$1\le r\le R\le L(p)$
,
While the rest of the paper relies on fairly generic assumptions on the percolation model at hand, the previous proposition harvests a much more specific property of the random-cluster model on
![]() $\mathbb Z^2$
, namely the parafermionic observable. For
$\mathbb Z^2$
, namely the parafermionic observable. For
![]() $1\le q<4$
, the result will follow from crossing estimates that were recently obtained in [Reference Duminil-Copin, Manolescu and TassionDMT20] using this observable. These crossing estimates are uniform in boundary conditions and (possibly fractal) domains. The byproduct of the analysis in [Reference Duminil-Copin, Manolescu and TassionDMT20] is that
$1\le q<4$
, the result will follow from crossing estimates that were recently obtained in [Reference Duminil-Copin, Manolescu and TassionDMT20] using this observable. These crossing estimates are uniform in boundary conditions and (possibly fractal) domains. The byproduct of the analysis in [Reference Duminil-Copin, Manolescu and TassionDMT20] is that
![]() $\pi _4(R)/\pi _4(r)$
is bounded from below by
$\pi _4(R)/\pi _4(r)$
is bounded from below by
![]() $(r/R)^{2-\delta }$
and therefore, by (iv), so is
$(r/R)^{2-\delta }$
and therefore, by (iv), so is
![]() $\Delta _p(r,R)$
. For
$\Delta _p(r,R)$
. For
![]() $q=4$
, the crossing estimates are not uniform in boundary conditions, and a more specific analysis, also based on the parafermionic observable, must be performed. It is the subject of Section 6.2 in this paper.
$q=4$
, the crossing estimates are not uniform in boundary conditions, and a more specific analysis, also based on the parafermionic observable, must be performed. It is the subject of Section 6.2 in this paper.
1.4 Scaling relations
In continuous phase transitions, natural observables of the model decay algebraically. The behaviour at and near criticality is thus expected to be encoded by various critical exponents
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
,
$\beta $
,
![]() $\gamma $
,
$\gamma $
,
![]() $\delta $
,
$\delta $
,
![]() $\eta $
,
$\eta $
,
![]() $\nu $
,
$\nu $
,
![]() $\zeta $
,
$\zeta $
,
![]() $\iota $
,
$\iota $
,
![]() $\xi _1$
and
$\xi _1$
and
![]() $\xi _4$
defined as follows (below,
$\xi _4$
defined as follows (below,
![]() $o(1)$
denotes a quantity tending to 0):
$o(1)$
denotes a quantity tending to 0):
 $$ \begin{align*} f''(p)&=|p-p_c|^{-\alpha+o(1)}&\text{ as } p\rightarrow p_c,\\ \theta(p)&=(p-p_c)^{\beta+o(1)}&\text{as } p\searrow p_c, \\ \chi(p)&=|p-p_c|^{-\gamma+o(1)}&\text{as } p\rightarrow p_c,\\ \phi^1_{p_c,h}[0\longleftrightarrow\mathfrak g]&=h^{1/\delta+o(1)}&\text{as } h\rightarrow 0,\\ \phi_{p_c}[0\longleftrightarrow x]&=|x|^{-\eta+o(1)}&\text{as } |x|\rightarrow\infty,\\ \pi_1(R)&=R^{-\xi_1+o(1)} &\text{as } R\rightarrow\infty,\\ \xi(p)&=|p-p_c|^{-\nu+o(1)}&\text{as } p\rightarrow p_c,\\ \phi_{p_c}[|\mathsf{C}|\ge n]&=n^{-\zeta+o(1)} &\text{as } n\rightarrow \infty,\\ \Delta_{p_c}(R)&=R^{-\iota+o(1)} &\text{as } R\rightarrow\infty,\\ \pi_4(R)&=R^{-\xi_4+o(1)} &\text{as } R\rightarrow\infty, \end{align*} $$
$$ \begin{align*} f''(p)&=|p-p_c|^{-\alpha+o(1)}&\text{ as } p\rightarrow p_c,\\ \theta(p)&=(p-p_c)^{\beta+o(1)}&\text{as } p\searrow p_c, \\ \chi(p)&=|p-p_c|^{-\gamma+o(1)}&\text{as } p\rightarrow p_c,\\ \phi^1_{p_c,h}[0\longleftrightarrow\mathfrak g]&=h^{1/\delta+o(1)}&\text{as } h\rightarrow 0,\\ \phi_{p_c}[0\longleftrightarrow x]&=|x|^{-\eta+o(1)}&\text{as } |x|\rightarrow\infty,\\ \pi_1(R)&=R^{-\xi_1+o(1)} &\text{as } R\rightarrow\infty,\\ \xi(p)&=|p-p_c|^{-\nu+o(1)}&\text{as } p\rightarrow p_c,\\ \phi_{p_c}[|\mathsf{C}|\ge n]&=n^{-\zeta+o(1)} &\text{as } n\rightarrow \infty,\\ \Delta_{p_c}(R)&=R^{-\iota+o(1)} &\text{as } R\rightarrow\infty,\\ \pi_4(R)&=R^{-\xi_4+o(1)} &\text{as } R\rightarrow\infty, \end{align*} $$
where all the quantities above were already defined in previous sections, except that
![]() $0\longleftrightarrow \mathfrak g$
is the event that 0 is connected to the ghost by an open path,
$0\longleftrightarrow \mathfrak g$
is the event that 0 is connected to the ghost by an open path,
![]() $|\mathsf {C}|$
is the number of vertices in the cluster
$|\mathsf {C}|$
is the number of vertices in the cluster
![]() $\mathsf {C}$
of the origin, and
$\mathsf {C}$
of the origin, and
![]() $f(p)$
and
$f(p)$
and
![]() $\chi (p)$
are the thermodynamical quantities, respectively called the free-energy and the susceptibility definedFootnote
1
by
$\chi (p)$
are the thermodynamical quantities, respectively called the free-energy and the susceptibility definedFootnote
1
by

Let us mention that the first equation only applies when
![]() $f''(p)$
diverges as p approaches
$f''(p)$
diverges as p approaches
![]() $p_c$
, which is to say that the phase transition is of second order.
$p_c$
, which is to say that the phase transition is of second order.
These exponents are quantities of central interest in physics and have been the object of many studies. A beautiful prediction (again, see e.g., [Reference Essam and FisherEF63, Reference FisherFis64, Reference WidomWid65]) is that these exponents should depend on each other via scaling relations:
An important feature of the relations above is that they are independent of q: the exponents vary from model to model, but not the formulae. Relations (R1–5) were proved for Bernoulli percolation (i.e., cluster-weight
![]() $q=1$
) in a milestone paper by Harry Kesten [Reference KestenKes87] without any of them being computed or, indeed, even shown to exist (see also [Reference NolinNol08, Reference Garban, Pete and SchrammGPS18, Reference Duminil-Copin, Manolescu and TassionDMT20b]). For the random-cluster with
$q=1$
) in a milestone paper by Harry Kesten [Reference KestenKes87] without any of them being computed or, indeed, even shown to exist (see also [Reference NolinNol08, Reference Garban, Pete and SchrammGPS18, Reference Duminil-Copin, Manolescu and TassionDMT20b]). For the random-cluster with
![]() $q=2$
, critical exponents were calculated independently [Reference McCoy and WuMW83, Reference Duminil-Copin, Garban and PeteDGP14, Reference Duminil-CopinDum13] and observed to satisfy (R1–6). Let us mention that similar relations should hold in all dimensions that are below the so-called upper-critical dimension (with certain values of
$q=2$
, critical exponents were calculated independently [Reference McCoy and WuMW83, Reference Duminil-Copin, Garban and PeteDGP14, Reference Duminil-CopinDum13] and observed to satisfy (R1–6). Let us mention that similar relations should hold in all dimensions that are below the so-called upper-critical dimension (with certain values of
![]() $2$
replaced by the dimension d). We refer to a paper by Borgs, Chayes, Kesten and Spencer [Reference Borgs, Chayes, Kesten and SpencerBCKS99] (see also [Reference Borgs, Chayes, Kesten and SpencerBCKS01]) for a discussion of this phenomenon for Bernoulli percolation.
$2$
replaced by the dimension d). We refer to a paper by Borgs, Chayes, Kesten and Spencer [Reference Borgs, Chayes, Kesten and SpencerBCKS99] (see also [Reference Borgs, Chayes, Kesten and SpencerBCKS01]) for a discussion of this phenomenon for Bernoulli percolation.
Kesten’s analysis in the case of Bernoulli percolation relied on another scaling relation, sometimes referred to as Kesten’s scaling relation, stating that
![]() $\nu (2-\xi _4)=1$
for
$\nu (2-\xi _4)=1$
for
![]() $q=1$
. It was observed in [Reference Duminil-Copin, Garban and PeteDGP14] that this equality fails for
$q=1$
. It was observed in [Reference Duminil-Copin, Garban and PeteDGP14] that this equality fails for
![]() $q=2$
(one can also check this using the table gathering the predicted exponents below). We will show that it should be replaced by the following generalised Kesten’s scaling relation:
$q=2$
(one can also check this using the table gathering the predicted exponents below). We will show that it should be replaced by the following generalised Kesten’s scaling relation:
Note that the second property of Theorem 1.6 shows that
![]() $\xi _4>\iota $
so that
$\xi _4>\iota $
so that
![]() $\nu (2-\xi _4)=1$
fails not only at
$\nu (2-\xi _4)=1$
fails not only at
![]() $q=2$
but for every
$q=2$
but for every
![]() $q>1$
.
$q>1$
.
Before discussing the main results, let us mention the predicted values for the different exponents. The three first scaling relations enable us to express
![]() $\delta $
,
$\delta $
,
![]() $\eta $
and
$\eta $
and
![]() $\zeta $
in terms of
$\zeta $
in terms of
![]() $\xi _1$
only. This is particularly interesting since
$\xi _1$
only. This is particularly interesting since
![]() $\xi _1$
is measurable in terms of the scaling limit of interfaces at criticality. The relations given by equations (
R6
) and (
R7
) link
$\xi _1$
is measurable in terms of the scaling limit of interfaces at criticality. The relations given by equations (
R6
) and (
R7
) link
![]() $\alpha $
,
$\alpha $
,
![]() $\nu $
and
$\nu $
and
![]() $\iota $
. This is again very useful since it was noted in the previous section how
$\iota $
. This is again very useful since it was noted in the previous section how
![]() $\iota $
can be obtained from the understanding of the scaling limit of interfaces. An alternative approach to computing these three exponents would be to first obtain
$\iota $
can be obtained from the understanding of the scaling limit of interfaces. An alternative approach to computing these three exponents would be to first obtain
![]() $\alpha $
, which may perhaps be derived using exact integrability of the random-cluster model; see [Reference BaxterBax89, Section 12.8] and Section 1.6 for more details. Finally, equations (
R4
) and (
R5
) express
$\alpha $
, which may perhaps be derived using exact integrability of the random-cluster model; see [Reference BaxterBax89, Section 12.8] and Section 1.6 for more details. Finally, equations (
R4
) and (
R5
) express
![]() $\beta $
and
$\beta $
and
![]() $\gamma $
in terms of
$\gamma $
in terms of
![]() $\xi _1$
and
$\xi _1$
and
![]() $\nu $
so that one can obtain all the exponents from
$\nu $
so that one can obtain all the exponents from
![]() $\xi _1$
and
$\xi _1$
and
![]() $\iota $
(or
$\iota $
(or
![]() $\alpha $
).
$\alpha $
).
Conformal invariance enables us to predict that the scaling limit of the random-cluster model with cluster-weight
![]() $q\in [0,4]$
is related to CLE
$q\in [0,4]$
is related to CLE
![]() $(\kappa )$
(see [Reference Schramm, Sheffield and WilsonSSW09] and the discussion in [Reference Garban and WuGW19]), from which
$(\kappa )$
(see [Reference Schramm, Sheffield and WilsonSSW09] and the discussion in [Reference Garban and WuGW19]), from which
![]() $\xi _1$
and
$\xi _1$
and
![]() $\iota $
can be deduced. This leads to the following table, where all the exponents are expressed in terms of
$\iota $
can be deduced. This leads to the following table, where all the exponents are expressed in terms of
![]() $\kappa $
.
$\kappa $
.

In this paper, we prove (R1–7) for the random-cluster model with general cluster-weights
![]() $q\in [1,4]$
, except for equation (
R6
) when
$q\in [1,4]$
, except for equation (
R6
) when
![]() $\alpha $
is negative. We insist on the fact that the random-cluster models belong to different universality classes when q varies from
$\alpha $
is negative. We insist on the fact that the random-cluster models belong to different universality classes when q varies from
![]() $q=1$
to
$q=1$
to
![]() $q=4$
, so that this paper provides the first generic derivation of these relations for different universality classes. As in [Reference KestenKes87], we do not claim to show that any of these exponents exist, nor do we compute their values; the actual statements of the scaling relations with no reference to the exponents are given in the following three theorems. Nonetheless, if one makes the assumption of algebraic decay with the proper exponent, the next statements imply the scaling relations mentioned above.
$q=4$
, so that this paper provides the first generic derivation of these relations for different universality classes. As in [Reference KestenKes87], we do not claim to show that any of these exponents exist, nor do we compute their values; the actual statements of the scaling relations with no reference to the exponents are given in the following three theorems. Nonetheless, if one makes the assumption of algebraic decay with the proper exponent, the next statements imply the scaling relations mentioned above.
Below, we assume that
![]() $1<q\le 4$
as the case
$1<q\le 4$
as the case
![]() $q=1$
is already known. We start with the two simplest scaling relations given by equations (
R1
) and (
R2
) involving only quantities at
$q=1$
is already known. We start with the two simplest scaling relations given by equations (
R1
) and (
R2
) involving only quantities at
![]() $p=p_c$
and
$p=p_c$
and
![]() $h=0$
. The theorem is an easy consequence of uniform crossing estimates obtained for the random-cluster at criticality; see, for example, [Reference Duminil-Copin, Sidoravicius and TassionDST17]. While the result is not especially complicated, we chose to include it here for completeness. Introduce the following quantity for every
$h=0$
. The theorem is an easy consequence of uniform crossing estimates obtained for the random-cluster at criticality; see, for example, [Reference Duminil-Copin, Sidoravicius and TassionDST17]. While the result is not especially complicated, we chose to include it here for completeness. Introduce the following quantity for every
![]() $n>0$
,
$n>0$
,
Theorem 1.9 (Scaling relations at criticality)
Fix
![]() $1 < q\le 4$
. For
$1 < q\le 4$
. For
![]() $x\in \mathbb {Z}^2$
and
$x\in \mathbb {Z}^2$
and
![]() $n\ge 1$
,
$n\ge 1$
,
We now turn to the scaling relation given by equation (
R3
) involving the magnetic field. For
![]() $q=2$
, equation (
R3
) was proved in [Reference Camia, Garban and NewmanCGN14] using the GKS inequality, but this inequality is not available for general random-cluster models. A fact that came as a surprise to us is that equation (
R3
) can be derived for every
$q=2$
, equation (
R3
) was proved in [Reference Camia, Garban and NewmanCGN14] using the GKS inequality, but this inequality is not available for general random-cluster models. A fact that came as a surprise to us is that equation (
R3
) can be derived for every
![]() $1\le q\le 4$
without referring to any other result of the paper (see Section 8.3).
$1\le q\le 4$
without referring to any other result of the paper (see Section 8.3).
Theorem 1.10 (Scaling relation with magnetic field)
Fix
![]() $1 < q\le 4$
. For
$1 < q\le 4$
. For
![]() $h>0$
,
$h>0$
,
The scaling relations in equations
R4
–
R7
are the most difficult as they involve the random-cluster model at p near
![]() $p_c$
and rely heavily on the stability in the near-critical regime.
$p_c$
and rely heavily on the stability in the near-critical regime.
Theorem 1.11 (Scaling relations near-critical regime)
Fix
![]() $1< q \le 4$
. For
$1< q \le 4$
. For
![]() $p>p_c$
(and
$p>p_c$
(and
![]() $p\ne p_c$
for the second),
$p\ne p_c$
for the second),
 $$ \begin{align} f''(p)&\asymp\sum_{\ell\le \xi(p)}\ell\Delta_{p_c}(\ell)^2. \end{align} $$
$$ \begin{align} f''(p)&\asymp\sum_{\ell\le \xi(p)}\ell\Delta_{p_c}(\ell)^2. \end{align} $$
Note that assuming that
![]() $\iota $
exists, we get very different behaviour depending on whether it is smaller or larger than
$\iota $
exists, we get very different behaviour depending on whether it is smaller or larger than
![]() $1$
or, correspondingly, whether
$1$
or, correspondingly, whether
![]() $\alpha $
is positive or negative: that is, whether the random-cluster model undergoes a second-order or higher-order phase transition. The former occurs when
$\alpha $
is positive or negative: that is, whether the random-cluster model undergoes a second-order or higher-order phase transition. The former occurs when
![]() $\nu <1$
: that is, conjecturally when
$\nu <1$
: that is, conjecturally when
![]() $q\in (2,4]$
. When
$q\in (2,4]$
. When
![]() $\nu =1$
, which is conjectured to correspond only at
$\nu =1$
, which is conjectured to correspond only at
![]() $q=2$
, all the exponents are known and
$q=2$
, all the exponents are known and
![]() $f''(p)$
blows up logarithmically (in particular, it satisfies the scaling relation as well). When
$f''(p)$
blows up logarithmically (in particular, it satisfies the scaling relation as well). When
![]() $\nu>1$
,
$\nu>1$
,
![]() $f''(p)$
should remain bounded in the vicinity of
$f''(p)$
should remain bounded in the vicinity of
![]() $p_c$
, and the phase transition becomes of third order (or higher). The exponent
$p_c$
, and the phase transition becomes of third order (or higher). The exponent
![]() $\alpha $
may still be defined using the third derivative of f, which is supposed to diverge at
$\alpha $
may still be defined using the third derivative of f, which is supposed to diverge at
![]() $p_c$
. We are currently only able to derive an upper bound on
$p_c$
. We are currently only able to derive an upper bound on
![]() $f'''$
; the lower bound is unavailable even for Bernoulli percolation. We refer to Remark 8.4 for details.
$f'''$
; the lower bound is unavailable even for Bernoulli percolation. We refer to Remark 8.4 for details.
1.5 Three complementary results on the Potts models
This section gathers three satellite results that are of interest on their own and do not necessarily fit into the story line of the previous sections. For
![]() $q=2$
, it is already known that the value of
$q=2$
, it is already known that the value of
![]() $\xi _1$
is equal to
$\xi _1$
is equal to
![]() $1/8$
, so our paper provides a new proof of the following immediate corollary using the Edwards-Sokal coupling [Reference GrimmettGri06, Section 1.4]. We include it since the Ising model with a magnetic field, contrary to the case
$1/8$
, so our paper provides a new proof of the following immediate corollary using the Edwards-Sokal coupling [Reference GrimmettGri06, Section 1.4]. We include it since the Ising model with a magnetic field, contrary to the case
![]() $h= 0$
, is not integrable and hence is notoriously difficult to study. As mentioned previously, it was obtained in [Reference Camia, Garban and NewmanCGN14] using alternative arguments.
$h= 0$
, is not integrable and hence is notoriously difficult to study. As mentioned previously, it was obtained in [Reference Camia, Garban and NewmanCGN14] using alternative arguments.
Theorem 1.12. Let
![]() $m(\beta ,h)$
be the spontaneous magnetisation of the Ising model on
$m(\beta ,h)$
be the spontaneous magnetisation of the Ising model on
![]() $\mathbb {Z}^2$
at inverse-temperature
$\mathbb {Z}^2$
at inverse-temperature
![]() $\beta $
and magnetic field h. For every
$\beta $
and magnetic field h. For every
![]() $h\in (0,1)$
,
$h\in (0,1)$
,
Let us mention here that for
![]() $q=2$
, we can derive from the estimate
$q=2$
, we can derive from the estimate
![]() $\xi (p)\asymp |p-p_c|^{-1}$
(this result was obtained numerous times; see [Reference Beffara and Duminil-CopinBD12b] for a short proof) the following result.
$\xi (p)\asymp |p-p_c|^{-1}$
(this result was obtained numerous times; see [Reference Beffara and Duminil-CopinBD12b] for a short proof) the following result.
Theorem 1.13. For
![]() $q=2$
, we have that for every p,
$q=2$
, we have that for every p,
and for every
![]() $R\le L(p)$
and e and f two edges at a distance R from each other,
$R\le L(p)$
and e and f two edges at a distance R from each other,
In particular, we deduce that
Of course, the last estimate can be obtained by differentiating the exact formula for the free energy due to [Reference OnsagerOns44]. To the best of our knowledge, the other estimates are new.
When
![]() $1\le q\le 3$
, it was proved in [Reference Duminil-Copin, Manolescu and TassionDMT20] that
$1\le q\le 3$
, it was proved in [Reference Duminil-Copin, Manolescu and TassionDMT20] that
![]() $\pi _1(R)\pi _4(R)\ge cR^{c-2}$
for every
$\pi _1(R)\pi _4(R)\ge cR^{c-2}$
for every
![]() $R\ge 1$
and some constant
$R\ge 1$
and some constant
![]() $c> 0$
. In Remark 6.8, we show that
$c> 0$
. In Remark 6.8, we show that
![]() $\pi _1(R)\Delta _{p_c}(R)\ge cR^{c-2}$
also for
$\pi _1(R)\Delta _{p_c}(R)\ge cR^{c-2}$
also for
![]() $q=4$
. From these inequalities, using equations (1.25), (1.27) and (1.20), one may deduce the result below, which should be understood as
$q=4$
. From these inequalities, using equations (1.25), (1.27) and (1.20), one may deduce the result below, which should be understood as
![]() $\beta < 1$
for
$\beta < 1$
for
![]() $1\le q\le 3$
and
$1\le q\le 3$
and
![]() $q=4$
. The result for
$q=4$
. The result for
![]() $q = 1$
(that is, for Bernoulli percolation) was already obtained by Kesten and Zhang [Reference Kesten and ZhangKZ87]; we expect
$q = 1$
(that is, for Bernoulli percolation) was already obtained by Kesten and Zhang [Reference Kesten and ZhangKZ87]; we expect
![]() $\beta < 1$
to be valid for all
$\beta < 1$
to be valid for all
![]() $1 \le q \le 4$
.
$1 \le q \le 4$
.
Theorem 1.14 (Nondifferentiability of the order parameter)
For every
![]() $1\le q\le 3$
or
$1\le q\le 3$
or
![]() $q=4$
, there exists
$q=4$
, there exists
![]() $c>0$
such that for every
$c>0$
such that for every
![]() $p\ge p_c$
,
$p\ge p_c$
,
In particular, the spontaneous magnetisation
![]() $m(\beta )$
of the 2-, 3- and 4-state Potts models satisfies
$m(\beta )$
of the 2-, 3- and 4-state Potts models satisfies
![]() $m(\beta )\ge c(\beta -\beta _c)^{1-c}$
for
$m(\beta )\ge c(\beta -\beta _c)^{1-c}$
for
![]() $\beta \ge \beta _c$
.
$\beta \ge \beta _c$
.
1.6 Open questions
The present paper opens many doors in the study of the critical regime of random-cluster models (and, more generally, planar-dependent percolation models). We now mention a few open questions that in our opinion deserve attention. We refrain from asking the obvious question of proving conformal invariance of the model and focus on questions directly related to the current work.
Let us start with a question concerning scaling relations: whether one can prove equation (
R6
) when
![]() $q\le 2$
. As mentioned above, in this case
$q\le 2$
. As mentioned above, in this case
![]() $f''(p)$
is expected to remain bounded when p tends to
$f''(p)$
is expected to remain bounded when p tends to
![]() $p_c$
, but one may consider the behaviour of
$p_c$
, but one may consider the behaviour of
![]() $f'''(p)$
to make sense of
$f'''(p)$
to make sense of
![]() $\alpha $
. Remark 8.4 of the present paper shows that the critical exponent
$\alpha $
. Remark 8.4 of the present paper shows that the critical exponent
![]() $\alpha $
defined like this satisfies
$\alpha $
defined like this satisfies
![]() $2\nu \le 2-\alpha $
, leaving the following question open (note that this is also open for
$2\nu \le 2-\alpha $
, leaving the following question open (note that this is also open for
![]() $q=1$
).
$q=1$
).
Question 1. Prove that for every
![]() $1\le q<2$
, one has
$1\le q<2$
, one has
![]() $2\nu \ge 2-\alpha $
.
$2\nu \ge 2-\alpha $
.
Another natural question is to derive critical exponents for random-cluster models. The scaling relations enable us to deduce certain exponents from others, and we may therefore choose which exponents to try to derive. From this point of view, the exponent
![]() $\alpha $
is particularly tempting since it directly implies
$\alpha $
is particularly tempting since it directly implies
![]() $\nu $
and also since exact integrability often provides physicists and mathematicians with closed formulae that may lead to
$\nu $
and also since exact integrability often provides physicists and mathematicians with closed formulae that may lead to
![]() $\alpha $
. We refer to [Reference BaxterBax89] for more details on this and summarise the discussion in the following question.
$\alpha $
. We refer to [Reference BaxterBax89] for more details on this and summarise the discussion in the following question.
Question 2. Obtain
![]() $\alpha $
using exact integrability to understand the near-critical behaviour of the free energy.
$\alpha $
using exact integrability to understand the near-critical behaviour of the free energy.
Another approach consists in deriving the exponents having as a basis the assumption of conformal invariance. As already discussed, the scaling limit of the family of boundaries of clusters should then be described by a Conformal Loop Ensemble. The parameter of the CLE may be identified via crossing probabilities and self-duality as the unique
![]() $\kappa \geq 4$
that satisfies
$\kappa \geq 4$
that satisfies
![]() $\sqrt q = - 2 \cos (4\pi /\kappa )$
[Reference Miller and WernerMilWer18].
$\sqrt q = - 2 \cos (4\pi /\kappa )$
[Reference Miller and WernerMilWer18].
Due to the present paper,
![]() $\xi _1$
and
$\xi _1$
and
![]() $\iota $
are sufficient to derive the other exponents. Moreover, they both should be computable using the scaling limit of the critical model, while the exponents
$\iota $
are sufficient to derive the other exponents. Moreover, they both should be computable using the scaling limit of the critical model, while the exponents
![]() $\beta $
,
$\beta $
,
![]() $\gamma $
,
$\gamma $
,
![]() $\delta $
and
$\delta $
and
![]() $\nu $
involve values of
$\nu $
involve values of
![]() $p\ne p_c$
and should not therefore be accessible directly from the critical scaling limit. The question of deriving
$p\ne p_c$
and should not therefore be accessible directly from the critical scaling limit. The question of deriving
![]() $\xi _1$
assuming the convergence to CLE of the interfaces has already been discussed in the literature [Reference Lawler, Schramm and WernerLSW02]. In light of the quasi-multiplicativity property of
$\xi _1$
assuming the convergence to CLE of the interfaces has already been discussed in the literature [Reference Lawler, Schramm and WernerLSW02]. In light of the quasi-multiplicativity property of
![]() $\Delta _{p_c}(r,R)$
, the following question seems tractable.
$\Delta _{p_c}(r,R)$
, the following question seems tractable.
Question 3. Compute
![]() $\iota $
assuming that the scaling limit of the critical model is described by CLE
$\iota $
assuming that the scaling limit of the critical model is described by CLE
![]() $(\kappa )$
.
$(\kappa )$
.
Let us finish this section by mentioning that [Reference Duminil-Copin, Garban and PeteDGP14] emphasises a self-organised mechanism in the way new edges occur as p increases in Grimmett’s monotone coupling (see [Reference GrimmettGri06, Reference Duminil-Copin, Garban and PeteDGP14] for details). The authors argued that edges appear in clouds and that the understanding of these clouds would be crucial towards the construction of the near-critical scaling limit; would anybody manage to construct the conformally invariant scaling limit at
![]() $p_c$
? The current work answers a number of questions and conjectures asked in this paper (including Conjectures 4.1 and 4.2 since
$p_c$
? The current work answers a number of questions and conjectures asked in this paper (including Conjectures 4.1 and 4.2 since
![]() $\xi (p)$
is explicitly known; see, for example, [Reference Beffara and Duminil-CopinBD12b] and references therein) but does not provide direct insight on the structure of these clouds. We therefore include the following question.
$\xi (p)$
is explicitly known; see, for example, [Reference Beffara and Duminil-CopinBD12b] and references therein) but does not provide direct insight on the structure of these clouds. We therefore include the following question.
Question 4. What does the present work tell us about clouds (in the sense of [Reference Duminil-Copin, Garban and PeteDGP14]) in Grimmett’s monotone coupling?
Almost everything is known about the random-cluster model with
![]() $q=2$
on the square lattice, since the conformal invariance of the model and its interfaces was proved [Reference SmirnovSmi10, Reference Chelkak, Duminil-Copin, Hongler, Kemppainen and SmirnovCDHKS14]. It is therefore only natural to discuss the question of the construction of the near-critical scaling limit in this context, especially since one expects subtle differences with the corresponding result for Bernoulli percolation (see [Reference Garban, Pete and SchrammGPS18]).
$q=2$
on the square lattice, since the conformal invariance of the model and its interfaces was proved [Reference SmirnovSmi10, Reference Chelkak, Duminil-Copin, Hongler, Kemppainen and SmirnovCDHKS14]. It is therefore only natural to discuss the question of the construction of the near-critical scaling limit in this context, especially since one expects subtle differences with the corresponding result for Bernoulli percolation (see [Reference Garban, Pete and SchrammGPS18]).
Question 5. Construct the near-critical scaling limit of the model: that is, the limits of random-cluster models on
![]() $\tfrac 1R\mathbb Z^2$
at p such that R is on the order of
$\tfrac 1R\mathbb Z^2$
at p such that R is on the order of
![]() $\lambda L(p)$
, where
$\lambda L(p)$
, where
![]() $\lambda $
is a fixed strictly positive parameter. One may start by studying the case of
$\lambda $
is a fixed strictly positive parameter. One may start by studying the case of
![]() $q=2$
.
$q=2$
.
Recently, the rotational invariance of the critical random-cluster model was obtained in [Reference Duminil-Copin, Kozlowski, Krachun, Manolescu and OulamaraDKKMO20]. This rotational invariance is expected to carry over to the near-critical regime. The arguments developed here, combined with those of [Reference Duminil-Copin, Garban and PeteDGP14], should be relevant for the next question.
Question 6. Prove that the near-critical scaling limit of the model is invariant under rotations.
Organisation of the paper
Section 2 provides the necessary background to our paper. Section 3 studies the dependency of crossing probabilities on boundary conditions (see Theorem 3.6) and introduces the notion of boosting pairs of boundary conditions. Section 4 contains the proof of points (ii), (iv) and (v) of Theorem 1.6. This is the core of our paper and indeed its biggest innovation. Section 5 initiates the connection between the quantity
![]() $\Delta _p$
and covariances, in particular proving Theorem 1.6(i). Section 6 shows the lower bound on
$\Delta _p$
and covariances, in particular proving Theorem 1.6(i). Section 6 shows the lower bound on
![]() $\Delta _p$
given by Proposition 1.8. Section 7 contains the proof of the stability below the correlation length: Theorem 1.4 and Theorem 1.6(iii). Finally, Section 8 contains the derivation of the scaling relations.
$\Delta _p$
given by Proposition 1.8. Section 7 contains the proof of the stability below the correlation length: Theorem 1.4 and Theorem 1.6(iii). Finally, Section 8 contains the derivation of the scaling relations.
A word about constants
We will often work with
![]() $p\in (0,1)$
and a spatial scale
$p\in (0,1)$
and a spatial scale
![]() $R \leq L(p)$
. Unless stated otherwise, constants
$R \leq L(p)$
. Unless stated otherwise, constants
![]() $c, (c_i)_{i\ge 0}, C$
and
$c, (c_i)_{i\ge 0}, C$
and
![]() $(C_i)_{i\ge 0}$
are assumed uniform in
$(C_i)_{i\ge 0}$
are assumed uniform in
![]() $(p;R)$
as above, with the assumption that p is not close to
$(p;R)$
as above, with the assumption that p is not close to
![]() $0$
or
$0$
or
![]() $1$
. They are, however, allowed to depend on the threshold
$1$
. They are, however, allowed to depend on the threshold
![]() $\delta _L$
used in the definition of
$\delta _L$
used in the definition of
![]() $L(p)$
; recall that this threshold is assumed small but fixed. We do not discuss the dependence in q of constants, but the careful reader will notice that they may be rendered uniform in q, potentially outside the vicinity of
$L(p)$
; recall that this threshold is assumed small but fixed. We do not discuss the dependence in q of constants, but the careful reader will notice that they may be rendered uniform in q, potentially outside the vicinity of
![]() $1$
and
$1$
and
![]() $4$
.
$4$
.
We reiterate that the constants in the notation
![]() $\asymp $
,
$\asymp $
,
![]() $\stackrel{<}{\scriptstyle{\frown}}$
and
$\stackrel{<}{\scriptstyle{\frown}}$
and
![]() $\stackrel{>}{\scriptstyle{\frown}}$
also follow the same principle.
$\stackrel{>}{\scriptstyle{\frown}}$
also follow the same principle.
2 Preliminaries
This section briefly recalls some tools for the study of the planar random-cluster model. Some sections are new, for instance Section 2.4. We recommend that the reader quickly browses this section, even if they are already comfortable with the basics of the random-cluster model.
2.1 Elementary properties of the random-cluster model
We will use standard properties of the random-cluster model. They can be found in [Reference GrimmettGri06], and we only recall them briefly below. Fix a subgraph
![]() $G=(V,E)$
of
$G=(V,E)$
of
![]() $\mathbb {Z}^2$
.
$\mathbb {Z}^2$
.
Monotonic properties. An event A is called increasing if for any
![]() $\omega \le \omega '$
(for the partial ordering on
$\omega \le \omega '$
(for the partial ordering on
![]() $\{0,1\}^E$
),
$\{0,1\}^E$
),
![]() $\omega \in A$
implies that
$\omega \in A$
implies that
![]() $\omega '\in A$
. Fix
$\omega '\in A$
. Fix
![]() $q\ge 1$
,
$q\ge 1$
,
![]() $1\ge p'\ge p\ge 0$
,
$1\ge p'\ge p\ge 0$
,
![]() $h'\ge h\ge 0$
and some boundary conditions
$h'\ge h\ge 0$
and some boundary conditions
![]() $\xi '\ge \xi $
, where
$\xi '\ge \xi $
, where
![]() $\xi '\ge \xi $
means that any wired vertices in
$\xi '\ge \xi $
means that any wired vertices in
![]() $\xi $
are also wired in
$\xi $
are also wired in
![]() $\xi '$
. Then for every increasing events A and B,
$\xi '$
. Then for every increasing events A and B,
The inequalities above will, respectively, be referred to as the FKG inequality, the monotonicity in h and p and the comparison between boundary conditions.
Spatial Markov property. For any configuration
![]() $\omega '\in \{0,1\}^E$
and any
$\omega '\in \{0,1\}^E$
and any
![]() $F\subset E$
,
$F\subset E$
,
where H denotes the graph spanned by the edge-set F and
![]() $\xi '$
the boundary conditions on H defined as follows: x and y on
$\xi '$
the boundary conditions on H defined as follows: x and y on
![]() $\partial H$
are wired if they are connected in
$\partial H$
are wired if they are connected in
![]() $(\omega ')_{|E\smallsetminus F}^{\xi }$
.
$(\omega ')_{|E\smallsetminus F}^{\xi }$
.
Dual model. Define the dual graph
![]() $G^*=(V^*,E^*)$
of G in the usual way: place dual sites at the centres of the faces of G, and for every bond
$G^*=(V^*,E^*)$
of G in the usual way: place dual sites at the centres of the faces of G, and for every bond
![]() $e\in E$
, place a dual bond
$e\in E$
, place a dual bond
![]() $e^*$
between the two dual sites corresponding to faces bordering e. Given a subgraph configuration
$e^*$
between the two dual sites corresponding to faces bordering e. Given a subgraph configuration
![]() $\omega $
, construct a configuration
$\omega $
, construct a configuration
![]() $\omega ^*$
on
$\omega ^*$
on
![]() $G^*$
by declaring any bond of the dual graph to be open (respectively, closed) if the corresponding bond of the primal lattice is closed (respectively, open) for the initial configuration. The new configuration is called the dual configuration of
$G^*$
by declaring any bond of the dual graph to be open (respectively, closed) if the corresponding bond of the primal lattice is closed (respectively, open) for the initial configuration. The new configuration is called the dual configuration of
![]() $\omega $
. The dual model on the dual graph given by the dual configurations then corresponds to a random-cluster measure with the same parameter q, a dual parameter
$\omega $
. The dual model on the dual graph given by the dual configurations then corresponds to a random-cluster measure with the same parameter q, a dual parameter
![]() $p^*$
satisfying
$p^*$
satisfying
and dual boundary conditions. We do not want to discuss too much the details of how dual boundary conditions are defined (we refer to [Reference GrimmettGri06]) and simply mention that the dual of free boundary conditions are the wired ones and vice versa. Note that the critical point is self-dual in the sense that
![]() $p_c^*=p_c$
.
$p_c^*=p_c$
.
Loop model. The loop representation of a configuration on G is supported on the medial graph of G defined as follows. Let
![]() $(\mathbb {Z}^2)^{\diamond }$
be the medial lattice with vertex-set given by the midpoints of edges of
$(\mathbb {Z}^2)^{\diamond }$
be the medial lattice with vertex-set given by the midpoints of edges of
![]() $\mathbb {Z}^2$
and edges between pairs of nearest vertices (i.e., vertices at a distance
$\mathbb {Z}^2$
and edges between pairs of nearest vertices (i.e., vertices at a distance
![]() $\sqrt 2/2$
from each other). It is a rotated and rescaled version of
$\sqrt 2/2$
from each other). It is a rotated and rescaled version of
![]() $\mathbb {Z}^2$
. For future reference, note that the faces of
$\mathbb {Z}^2$
. For future reference, note that the faces of
![]() $(\mathbb {Z}^2)^{\diamond }$
contain either a vertex of
$(\mathbb {Z}^2)^{\diamond }$
contain either a vertex of
![]() $\mathbb {Z}^2$
or one of
$\mathbb {Z}^2$
or one of
![]() $(\mathbb {Z}^2)^*$
. The edges of the medial lattice
$(\mathbb {Z}^2)^*$
. The edges of the medial lattice
![]() $(\mathbb {Z}^2)^{\diamond }$
are considered oriented in a counterclockwise direction around each face containing a vertex of
$(\mathbb {Z}^2)^{\diamond }$
are considered oriented in a counterclockwise direction around each face containing a vertex of
![]() $\mathbb {Z}^2$
. Let
$\mathbb {Z}^2$
. Let
![]() $G^{\diamond }$
be the subgraph of
$G^{\diamond }$
be the subgraph of
![]() $(\mathbb {Z}^2)^{\diamond }$
spanned by the edges of
$(\mathbb {Z}^2)^{\diamond }$
spanned by the edges of
![]() $(\mathbb {Z}^2)^{\diamond }$
adjacent to a face corresponding to a vertex of G.
$(\mathbb {Z}^2)^{\diamond }$
adjacent to a face corresponding to a vertex of G.
Let
![]() $\omega $
be a configuration on G. Draw self-avoiding paths on
$\omega $
be a configuration on G. Draw self-avoiding paths on
![]() $G^{\diamond }$
as follows: a path arriving at a vertex of the medial lattice always takes a
$G^{\diamond }$
as follows: a path arriving at a vertex of the medial lattice always takes a
![]() $\pm \pi /2$
turn at vertices so as not to cross the edges of
$\pm \pi /2$
turn at vertices so as not to cross the edges of
![]() $\omega $
or
$\omega $
or
![]() $\omega ^*$
(see Figure 14). The loop configuration thus defined is formed of possibly several paths going from boundary to boundary, as well as disjoint loops; together these form a partition of the edges of
$\omega ^*$
(see Figure 14). The loop configuration thus defined is formed of possibly several paths going from boundary to boundary, as well as disjoint loops; together these form a partition of the edges of
![]() $G^{\diamond }$
.
$G^{\diamond }$
.
2.2 Crossing and arm event probabilities below the characteristic length
As is often the case when investigating the critical behaviour of lattice models, we will need to use crossing estimates in rectangles and more generally in quads, as well as estimates on certain universal and non-universal critical exponents. Such crossing estimates initially emerged in the study of Bernoulli percolation in the late 1970s under the coined name of Russo-Seymour-Welsh theory [Reference RussoRus78, Reference Seymour and WelshSW78].
The main technical tool we will use is the following result on crossing estimates and arm events probabilities.
Theorem 2.1 (Crossing estimates below the characteristic length)
For
![]() $\rho ,\varepsilon>0$
, there exist
$\rho ,\varepsilon>0$
, there exist
![]() $c'>0$
and
$c'>0$
and
![]() $c=c(\rho ,\varepsilon )>0$
such that for every p, every
$c=c(\rho ,\varepsilon )>0$
such that for every p, every
![]() $1 \le n\le L(p)$
, every graph G containing
$1 \le n\le L(p)$
, every graph G containing
![]() $[-\varepsilon n,(\rho +\varepsilon )n]\times [-\varepsilon n,(1+\varepsilon )n]$
and every boundary conditions
$[-\varepsilon n,(\rho +\varepsilon )n]\times [-\varepsilon n,(1+\varepsilon )n]$
and every boundary conditions
![]() $\xi $
,
$\xi $
,
Moreover, if
![]() $A_n$
denotes the event that there exists an open circuit surrounding
$A_n$
denotes the event that there exists an open circuit surrounding
![]() $\Lambda _n$
in
$\Lambda _n$
in
![]() $\mathrm {Ann}(n,2n)$
,
$\mathrm {Ann}(n,2n)$
,
Since the result is not formally proved anywhere, we include it here. It basically consists in gathering different known results.
Proof. We start with equation (RSW). By duality and comparison between boundary conditions given by equation (CBC), it suffices to show that for
![]() $p<p_c$
and
$p<p_c$
and
![]() $\xi =0$
, we have that
$\xi =0$
, we have that
where
![]() $R:=[0,\rho n]\times [0,n]$
and
$R:=[0,\rho n]\times [0,n]$
and
![]() $\overline {R}=[-\varepsilon n,(\rho +\varepsilon )n]\times [-\varepsilon n,(1+\varepsilon )n]$
.
$\overline {R}=[-\varepsilon n,(\rho +\varepsilon )n]\times [-\varepsilon n,(1+\varepsilon )n]$
.
The RSW theorem extracted from [Reference Duminil-Copin and TassionDT19] gives the existence of
![]() $C=C(\rho )>0$
such that for every n and p,
$C=C(\rho )>0$
such that for every n and p,
where in the second inequality, we used the definition of
![]() $L(p)$
and the fact that
$L(p)$
and the fact that
![]() $n\le L(p)$
.
$n\le L(p)$
.
Consider the event
![]() $\mathcal {E}^*$
that there exists a dual-open circuit in the annulus
$\mathcal {E}^*$
that there exists a dual-open circuit in the annulus
![]() $\overline {R}\smallsetminus R$
surrounding R. Then equations (CBC) and (
p-MON) and the fact that
$\overline {R}\smallsetminus R$
surrounding R. Then equations (CBC) and (
p-MON) and the fact that
![]() $\mathcal {E}^*$
is decreasing imply that
$\mathcal {E}^*$
is decreasing imply that
![]() $\phi _p[\mathcal {E}^*|\mathcal {C}(R)] \geq \phi _{\overline {R}\smallsetminus R, p_c}^1[\mathcal {E}^*]$
. The result of [Reference Duminil-Copin, Sidoravicius and TassionDST17] states that the latter probability is bounded from below by
$\phi _p[\mathcal {E}^*|\mathcal {C}(R)] \geq \phi _{\overline {R}\smallsetminus R, p_c}^1[\mathcal {E}^*]$
. The result of [Reference Duminil-Copin, Sidoravicius and TassionDST17] states that the latter probability is bounded from below by
![]() $c_0=c_0(\rho ,\varepsilon )>0$
independently of n. The spatial Markov property and the comparison between boundary conditions allow us to conclude that
$c_0=c_0(\rho ,\varepsilon )>0$
independently of n. The spatial Markov property and the comparison between boundary conditions allow us to conclude that
This concludes the proof of equation (RSW). For equation (RSW′
), use the FKG inequality and the fact that there exists a circuit in
![]() $\mathrm {Ann}(n,2n)$
surrounding the origin if the rectangle
$\mathrm {Ann}(n,2n)$
surrounding the origin if the rectangle
![]() $[-\tfrac 53n,\tfrac 53n]\times [\tfrac 43n,\tfrac 53n]$
as well as its rotations by angles
$[-\tfrac 53n,\tfrac 53n]\times [\tfrac 43n,\tfrac 53n]$
as well as its rotations by angles
![]() $\tfrac \pi 2$
,
$\tfrac \pi 2$
,
![]() $\pi $
and
$\pi $
and
![]() $\tfrac {3\pi }2$
are crossed in the long direction.
$\tfrac {3\pi }2$
are crossed in the long direction.
The previous theorem has classical applications for the probability of so-called arm events. A self-avoiding path of type
![]() $0$
or
$0$
or
![]() $1$
connecting the inner to the outer boundary of an annulus is called an arm. We say that an arm is of type
$1$
connecting the inner to the outer boundary of an annulus is called an arm. We say that an arm is of type
![]() $1$
if it is composed of primal edges that are all open and of type
$1$
if it is composed of primal edges that are all open and of type
![]() $0$
if it is composed of dual edges that are all dual-open. For
$0$
if it is composed of dual edges that are all dual-open. For
![]() $k\ge 1$
and
$k\ge 1$
and
![]() $\sigma \in \{0,1\}^k$
, define
$\sigma \in \{0,1\}^k$
, define
![]() $A_{\sigma }(r,R)$
to be the event that there exist k disjoint arms from the inner to the outer boundary of
$A_{\sigma }(r,R)$
to be the event that there exist k disjoint arms from the inner to the outer boundary of
![]() $\mathrm {Ann}(r,R)$
, which are of type
$\mathrm {Ann}(r,R)$
, which are of type
![]() $\sigma _1,\dots , \sigma _k$
when indexed in counterclockwise order.
$\sigma _1,\dots , \sigma _k$
when indexed in counterclockwise order.
To simplify the notation, we introduce
![]() $\pi _{\sigma }(p;r,R)$
for the
$\pi _{\sigma }(p;r,R)$
for the
![]() $\phi _{p}$
-probability of
$\phi _{p}$
-probability of
![]() $A_{\sigma }(r,R)$
. We drop p or r from the notation when
$A_{\sigma }(r,R)$
. We drop p or r from the notation when
![]() $p=p_c$
or r is the smallest integer such that
$p=p_c$
or r is the smallest integer such that
![]() $\pi _{\sigma }(p;r,R)>0$
for all
$\pi _{\sigma }(p;r,R)>0$
for all
![]() $R>r$
. Finally, when
$R>r$
. Finally, when
![]() $\sigma =1010\dots $
is alternating
$\sigma =1010\dots $
is alternating
![]() $0$
and
$0$
and
![]() $1$
and has length k, we write the subscript k instead of
$1$
and has length k, we write the subscript k instead of
![]() $\sigma $
. For every
$\sigma $
. For every
![]() $\sigma $
,
$\sigma $
,
![]() $ \pi _{\sigma }(R)$
decays algebraically with R [Reference Duminil-Copin, Sidoravicius and TassionDST17], and the scale invariance prediction suggests the existence of a critical exponent
$ \pi _{\sigma }(R)$
decays algebraically with R [Reference Duminil-Copin, Sidoravicius and TassionDST17], and the scale invariance prediction suggests the existence of a critical exponent
![]() $\xi _{\sigma }$
such that
$\xi _{\sigma }$
such that
![]() $ \pi _{\sigma }(R)=R^{-\xi _{\sigma }+o(1)}$
as R tends to infinity.
$ \pi _{\sigma }(R)=R^{-\xi _{\sigma }+o(1)}$
as R tends to infinity.
We also introduce
![]() $A_{\sigma }^+(r,R)$
to be the same event as
$A_{\sigma }^+(r,R)$
to be the same event as
![]() $A_{\sigma }(r,R)$
, except that the paths must lie in the upper half-plane
$A_{\sigma }(r,R)$
, except that the paths must lie in the upper half-plane
![]() $\mathbb H:=\mathbb Z\times \mathbb Z_+$
and are indexed starting from the right-most. Introduce its probability
$\mathbb H:=\mathbb Z\times \mathbb Z_+$
and are indexed starting from the right-most. Introduce its probability
![]() $\pi _{\sigma }^+(p;r,R)$
and the associated exponent
$\pi _{\sigma }^+(p;r,R)$
and the associated exponent
![]() $\xi _{\sigma }^+$
.
$\xi _{\sigma }^+$
.
We will need the following near-critical estimates on certain arm event probabilities.
Proposition 2.2 (Estimates on certain arm events)
Fix
![]() $1\le q\le 4$
. There exists
$1\le q\le 4$
. There exists
![]() $c> 0$
such that for
$c> 0$
such that for
![]() $p\in (0,1)$
and
$p\in (0,1)$
and
![]() $1\le r\le R\le L(p)$
,
$1\le r\le R\le L(p)$
,
Proof. The bound given by equation (2.1) follows from the fractal structure of interfaces, which in turn follows from equation (RSW) and [Reference Aizenman and BurchardAB99, Theorem 1.3]. The argument is classical, and we omit it.
The inequality on the right of equation (2.2) is a standard consequence of equation (RSW). The one on the left follows readily from equation (2.1), the FKG inequality and self-duality.
Proposition 2.3 (Quasi-multiplicativity of arm event probabilities)
Fix
![]() $1\le q\le 4$
. For every
$1\le q\le 4$
. For every
![]() $1\le r\le \rho \le R\le L(p)$
and
$1\le r\le \rho \le R\le L(p)$
and
![]() $k = 1$
or
$k = 1$
or
![]() $k\ge 2$
even,
$k\ge 2$
even,
Proof. This is a standard consequence of equation (RSW). For
![]() $k =1$
, the proof is simple; for
$k =1$
, the proof is simple; for
![]() $k \geq 2$
even, the proof is more tedious but is identical to that for
$k \geq 2$
even, the proof is more tedious but is identical to that for
![]() $q = 1$
[Reference KestenKes87].
$q = 1$
[Reference KestenKes87].
The proof of equation (2.3) goes through the so-called separation of arms (for alternating arm events), which is also a consequence of equation (RSW). We direct the reader to [Reference KestenKes87, Reference NolinNol08, Reference Chelkak, Duminil-Copin and HonglerCDH16] for details.
2.3 Couplings via exploration
In this section, we present a technique for coupling different random-cluster measures in an increasing fashion by exploring the graph edge by edge, which we formalise using decision trees as follows. Consider a graph
![]() $G=(V,E)$
with n edges and
$G=(V,E)$
with n edges and
![]() $U=(U_{e})_{e \in E}$
a family of independent uniform random variables in
$U=(U_{e})_{e \in E}$
a family of independent uniform random variables in
![]() $[0,1]$
. For a n-tuple
$[0,1]$
. For a n-tuple
![]() $e=(e_1,\dots ,e_n)$
of edges and for
$e=(e_1,\dots ,e_n)$
of edges and for
![]() $t\le n$
, write
$t\le n$
, write
![]() $e_{[t]}=(e_1,\dots ,e_t)$
(with the convention
$e_{[t]}=(e_1,\dots ,e_t)$
(with the convention
![]() $e_{[0]}=\emptyset $
) and
$e_{[0]}=\emptyset $
) and
![]() $U_{{[t]}}=(U_{e_1},\dots ,U_{e_t})$
.
$U_{{[t]}}=(U_{e_1},\dots ,U_{e_t})$
.
Definition 2.4 (Decision tree, stopping time)
A decision tree is a pair
![]() $\mathbf {T}=(e_1, (\psi _t)_{2 \le t \le n})$
, where
$\mathbf {T}=(e_1, (\psi _t)_{2 \le t \le n})$
, where
![]() $e_1 \in E$
, and for each
$e_1 \in E$
, and for each
![]() $2 \le t\le n$
the function
$2 \le t\le n$
the function
![]() $\psi _t$
takes a pair
$\psi _t$
takes a pair
![]() $(e_{[t-1]}, U_{{[t-1]}})$
as an input and returns an element
$(e_{[t-1]}, U_{{[t-1]}})$
as an input and returns an element
![]() $e_t\in E\smallsetminus \{e_1,\dots ,e_{t-1}\}$
. A stopping time for
$e_t\in E\smallsetminus \{e_1,\dots ,e_{t-1}\}$
. A stopping time for
![]() $\mathbf {T}$
is a random variable
$\mathbf {T}$
is a random variable
![]() $\tau $
taking values in
$\tau $
taking values in
![]() $\{1,\dots ,n, \infty \}$
, which is such that
$\{1,\dots ,n, \infty \}$
, which is such that
![]() $\{\tau \le t\}$
is measurable in terms of
$\{\tau \le t\}$
is measurable in terms of
![]() $(e_{[t]},U_{{[t]}})$
.
$(e_{[t]},U_{{[t]}})$
.
We will say that the decision tree reveals one by one the edges of E; the edges
![]() $e_{[t]}$
are the edges revealed at time t. Less formally, a decision tree takes
$e_{[t]}$
are the edges revealed at time t. Less formally, a decision tree takes
![]() $U~$
as an input and reveals edges one after the other. It always starts from the same fixed
$U~$
as an input and reveals edges one after the other. It always starts from the same fixed
![]() $e_1\in E$
(which corresponds to the root of the decision tree) and then queries the value of
$e_1\in E$
(which corresponds to the root of the decision tree) and then queries the value of
![]() $U_{e_1}$
. After that, it continues inductively as follows: at step
$U_{e_1}$
. After that, it continues inductively as follows: at step
![]() $t>1$
, the function
$t>1$
, the function
![]() $\psi _t$
, which should be interpreted as the decision rule at time t, takes the locations and the values of the revealed edges at time
$\psi _t$
, which should be interpreted as the decision rule at time t, takes the locations and the values of the revealed edges at time
![]() $t-1$
and decides which edge to reveal next.
$t-1$
and decides which edge to reveal next.
Remark 2.5. The theory of (random) decision trees played a key role in computer science (we refer the reader to the survey [Reference Buhrman and De WolfBW02]) but also found many applications in other fields of mathematics. In particular, random decision trees (sometimes called randomised algorithms) were used in [Reference Schramm and SteifSS10] to study the noise sensitivity of Boolean functions, for instance in the context of percolation theory. It was also used in [Reference Duminil-Copin, Raoufi and TassionDRT19] in combination with the OSSS inequality (which was originally introduced in [Reference O’Donnell, Saks, Schramm and ServedioOSSS05]) to prove sharpness of random-cluster models.
Decision trees may be used to construct random-cluster measures in a step-by-step fashion. This technique is generic and may be applied to so-called monotonic measures (see, e.g., [Reference GrimmettGri06]). A key feature of this construction is that it enables one to do it with two (or more) random-cluster measures simultaneously. In this case, the decision tree produces couplings of these measures. Since we are mostly interested in couplings, we directly explain the construction for a pair of configurations. For
![]() $1\le t\le n$
, we extend the notation
$1\le t\le n$
, we extend the notation
![]() $e_{[t]}$
and
$e_{[t]}$
and
![]() $U_{{[t]}}$
with the notation
$U_{{[t]}}$
with the notation
![]() $\omega _{{[t]}}=(\omega _{e_1},\dots ,\omega _{e_t})$
. Below, we use the notation
$\omega _{{[t]}}=(\omega _{e_1},\dots ,\omega _{e_t})$
. Below, we use the notation
![]() $G_t$
for the graph G minus the edges
$G_t$
for the graph G minus the edges
![]() $e_1,\dots ,e_t$
.
$e_1,\dots ,e_t$
.
Proposition 2.6. Fix a finite subgraph
![]() $G = (V,E)$
of
$G = (V,E)$
of
![]() $\mathbb {Z}^2$
. Consider
$\mathbb {Z}^2$
. Consider
![]() $0 \le p\le p'\le 1$
,
$0 \le p\le p'\le 1$
,
![]() $q\geq 1$
and
$q\geq 1$
and
![]() $\xi \le \xi '$
boundary conditions. Let
$\xi \le \xi '$
boundary conditions. Let
![]() $\mathbf T=(e_1, (\psi _t)_{2 \le t \le n})$
be a decision tree and
$\mathbf T=(e_1, (\psi _t)_{2 \le t \le n})$
be a decision tree and
![]() $(U_e)_{e \in E}$
be a set of independent and identically distributed uniform random variables under some measure
$(U_e)_{e \in E}$
be a set of independent and identically distributed uniform random variables under some measure
![]() $\mathbb {P}_{\mathbf {T}}$
. Define
$\mathbb {P}_{\mathbf {T}}$
. Define
![]() $\omega ,\omega ' \in \{0,1\}^E$
by the following inductive procedure: for every
$\omega ,\omega ' \in \{0,1\}^E$
by the following inductive procedure: for every
![]() $0\le t<n$
,
$0\le t<n$
,

where
![]() $\xi _t$
and
$\xi _t$
and
![]() $\xi ^{\prime }_t$
are the boundary conditions induced by
$\xi ^{\prime }_t$
are the boundary conditions induced by
![]() $\omega _{{[t]}}^{\xi }$
and
$\omega _{{[t]}}^{\xi }$
and
![]() $(\omega ^{\prime }_{{[t]}})^{\xi '}$
, respectively (when
$(\omega ^{\prime }_{{[t]}})^{\xi '}$
, respectively (when
![]() $t=0$
, these are
$t=0$
, these are
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
). Then
$\xi '$
). Then
![]() $\mathbb P_{\mathbf {T}}$
-almost surely, for every stopping time
$\mathbb P_{\mathbf {T}}$
-almost surely, for every stopping time
![]() $\tau $
for
$\tau $
for
![]() $\mathbf T$
, we have that
$\mathbf T$
, we have that
-
•
 $\omega _{{[\tau ]}}\le \omega ^{\prime }_{{[\tau ]}}$
,
$\omega _{{[\tau ]}}\le \omega ^{\prime }_{{[\tau ]}}$
, -
• conditionally on
 $(\tau ,\omega _{{[\tau ]}},\omega ^{\prime }_{{[\tau ]}})$
,
$(\tau ,\omega _{{[\tau ]}},\omega ^{\prime }_{{[\tau ]}})$
,
 $\omega $
and
$\omega $
and
 $\omega '$
on
$\omega '$
on
 $G_{\tau }$
have law
$G_{\tau }$
have law
 $\phi _{G_{\tau }, p}^{\xi _{\tau }}$
and
$\phi _{G_{\tau }, p}^{\xi _{\tau }}$
and
 $\phi _{G_{\tau }, p'}^{\xi ^{\prime }_{\tau }}$
.
$\phi _{G_{\tau }, p'}^{\xi ^{\prime }_{\tau }}$
.
Note that for
![]() $\tau =0$
, we obtain that
$\tau =0$
, we obtain that
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
have laws
$\omega '$
have laws
![]() $\phi _{G,p}^{\xi }$
and
$\phi _{G,p}^{\xi }$
and
![]() $\phi _{G,p'}^{\xi '}$
, respectively, and that
$\phi _{G,p'}^{\xi '}$
, respectively, and that
![]() $\omega \le \omega '$
a.s. The procedure above may be applied to infinite-volume measures as long as
$\omega \le \omega '$
a.s. The procedure above may be applied to infinite-volume measures as long as
![]() ${\mathbf T}$
is such that all edges are eventually queried.
${\mathbf T}$
is such that all edges are eventually queried.
Proof. That
![]() $\omega _{{[\tau ]}}\le \omega ^{\prime }_{{[\tau ]}}$
is proved by induction and uses the monotonic property of random-cluster measures mentioned in Section 2.1. That
$\omega _{{[\tau ]}}\le \omega ^{\prime }_{{[\tau ]}}$
is proved by induction and uses the monotonic property of random-cluster measures mentioned in Section 2.1. That
![]() $\omega _{{[\tau ]}}$
and
$\omega _{{[\tau ]}}$
and
![]() $\omega ^{\prime }_{{[\tau ]}}$
have the right laws is also proved by induction, using the spatial Markov property given by equation (SMP).
$\omega ^{\prime }_{{[\tau ]}}$
have the right laws is also proved by induction, using the spatial Markov property given by equation (SMP).
Remark 2.7. While the definition indicates that
![]() $\mathbf T$
looks at
$\mathbf T$
looks at
![]() $U_{{[t]}}$
in order to decide the next queried edge
$U_{{[t]}}$
in order to decide the next queried edge
![]() $e_{t+1}$
(and hence
$e_{t+1}$
(and hence
![]() $U_{e_{t+1}}$
), we will often describe
$U_{e_{t+1}}$
), we will often describe
![]() $\mathbf T$
as choosing
$\mathbf T$
as choosing
![]() $e_{t+1}$
as a function of
$e_{t+1}$
as a function of
![]() $\omega _{{[t]}}$
and
$\omega _{{[t]}}$
and
![]() $\omega ^{\prime }_{{[t]}}$
, which are in turn functions of
$\omega ^{\prime }_{{[t]}}$
, which are in turn functions of
![]() $( e_{[t]}, U_{{[t]}})$
.
$( e_{[t]}, U_{{[t]}})$
.
Remark 2.8. Due to Proposition 2.6, we may construct an increasing coupling between
![]() $\phi _{G, p}^{\xi }$
and
$\phi _{G, p}^{\xi }$
and
![]() $\phi _{G, p'}^{\xi '}$
by switching between decision trees at stopping times. Indeed, if we start the coupling by following a decision tree
$\phi _{G, p'}^{\xi '}$
by switching between decision trees at stopping times. Indeed, if we start the coupling by following a decision tree
![]() $\mathbf T$
but stop the procedure at some stopping time
$\mathbf T$
but stop the procedure at some stopping time
![]() $\tau $
, then we may complete it with any increasing coupling of
$\tau $
, then we may complete it with any increasing coupling of
![]() $\phi _{G_{\tau }, p}^{\xi _{\tau }}$
and
$\phi _{G_{\tau }, p}^{\xi _{\tau }}$
and
![]() $\phi _{G_{\tau }, p'}^{\xi ^{\prime }_{\tau }}$
. We will often use this property, sometimes continuing with a specific coupling, other times with an arbitrary one.
$\phi _{G_{\tau }, p'}^{\xi ^{\prime }_{\tau }}$
. We will often use this property, sometimes continuing with a specific coupling, other times with an arbitrary one.
We now discuss a few examples of decision trees and the couplings they produce.
Example 1
The deterministic decision tree
![]() $\mathbf T$
for which the order
$\mathbf T$
for which the order
![]() $e_1,\dots ,e_n$
is fixed.
$e_1,\dots ,e_n$
is fixed.
Example 2
The decision tree
![]() $\mathbf T$
explores the clusters of
$\mathbf T$
explores the clusters of
![]() $\partial G$
in
$\partial G$
in
![]() $\omega '$
. Formally, this decision tree is defined using a growing sequence
$\omega '$
. Formally, this decision tree is defined using a growing sequence
![]() $\partial G=V_0\subset V_1\subset \cdots \subset V$
that represents the sets of vertices that the decision tree found to be connected to
$\partial G=V_0\subset V_1\subset \cdots \subset V$
that represents the sets of vertices that the decision tree found to be connected to
![]() $\partial G$
at time t.
$\partial G$
at time t.
Fix an arbitrary ordering of the edges in E, and set
![]() $V_0=\partial G$
. Now, for
$V_0=\partial G$
. Now, for
![]() $t \geq 0$
, assume that
$t \geq 0$
, assume that
![]() $e_{[t]}$
and
$e_{[t]}$
and
![]() $V_t\subset V$
have been constructed, and distinguish between two cases:
$V_t\subset V$
have been constructed, and distinguish between two cases:
-
• If there exists an unrevealed edge connecting a vertex
 $x \in V_t$
to a vertex
$x \in V_t$
to a vertex
 $y \notin V_t$
, then reveal
$y \notin V_t$
, then reveal
 $e_{t+1}= xy$
(if several choices for
$e_{t+1}= xy$
(if several choices for
 $xy$
exists, choose the smallest one in the chosen ordering) and set
$xy$
exists, choose the smallest one in the chosen ordering) and set  $$ \begin{align*} V_{t+1}:=\begin{cases}V_t\cup\{y\}&\text{ if }\omega^{\prime}_{e_{t+1}}=1,\\ V_t&\text{ otherwise}.\end{cases} \end{align*} $$
$$ \begin{align*} V_{t+1}:=\begin{cases}V_t\cup\{y\}&\text{ if }\omega^{\prime}_{e_{t+1}}=1,\\ V_t&\text{ otherwise}.\end{cases} \end{align*} $$
-
• If no edge as above exists, then set
 $ e_{t+1}$
to be the smallest
$ e_{t+1}$
to be the smallest
 $e\in E\smallsetminus e_{[t]}$
for the chosen ordering, and set
$e\in E\smallsetminus e_{[t]}$
for the chosen ordering, and set
 $V_{t+1}:=V_t$
.
$V_{t+1}:=V_t$
.
The coupling
![]() $\mathbb P_{\mathbf T}$
has the following useful property when
$\mathbb P_{\mathbf T}$
has the following useful property when
![]() $p=p'$
. If
$p=p'$
. If
![]() $\tau $
denotes the first time the decision tree finds no unrevealed edge between
$\tau $
denotes the first time the decision tree finds no unrevealed edge between
![]() $V_t$
and
$V_t$
and
![]() $V_t^c$
(note that
$V_t^c$
(note that
![]() $\tau $
is a stopping time), then all edges bounding the unrevealed region
$\tau $
is a stopping time), then all edges bounding the unrevealed region
![]() $E\smallsetminus e_{[\tau ]}$
are closed in
$E\smallsetminus e_{[\tau ]}$
are closed in
![]() $\omega ^{\prime }_{[\tau ]}$
and hence also in
$\omega ^{\prime }_{[\tau ]}$
and hence also in
![]() $\omega _{[\tau ]}$
. As a consequence, at every subsequent step in the coupling process, edges will be sampled with the same rule in the two configurations; hence the configurations will be equal on
$\omega _{[\tau ]}$
. As a consequence, at every subsequent step in the coupling process, edges will be sampled with the same rule in the two configurations; hence the configurations will be equal on
![]() $E\smallsetminus e_{[\tau ]}$
. Equivalently, they will only (possibly) differ for edges that are connected to
$E\smallsetminus e_{[\tau ]}$
. Equivalently, they will only (possibly) differ for edges that are connected to
![]() $\partial G$
in
$\partial G$
in
![]() $\omega '$
, thus leading to the following conclusion when combined with equation (RSW).
$\omega '$
, thus leading to the following conclusion when combined with equation (RSW).
Proposition 2.9 (Mixing)
There exists
![]() $c_{\mathrm {mix}}>0$
such that for every
$c_{\mathrm {mix}}>0$
such that for every
![]() $p\in (0,1)$
and every
$p\in (0,1)$
and every
![]() $r\le R$
with
$r\le R$
with
![]() $R/r$
large enough, every
$R/r$
large enough, every
![]() $G\supset \Lambda _{R}$
and every event A depending on edges in
$G\supset \Lambda _{R}$
and every event A depending on edges in
![]() $\Lambda _r$
, we have that for every two boundary conditions
$\Lambda _r$
, we have that for every two boundary conditions
![]() $\xi $
and
$\xi $
and
![]() $\psi $
,
$\psi $
,
One may be surprised at first sight not to see any reference to the characteristic length in this statement, yet one should remember that the rate of decay is in fact faster when p is away from
![]() $p_c$
. The previous proposition simply states a universal bound on the rate of mixing valid for every
$p_c$
. The previous proposition simply states a universal bound on the rate of mixing valid for every
![]() $p\in (0,1)$
.
$p\in (0,1)$
.
Notice also that in equation (2.4), the event A is not assumed increasing, nor is there any assumption of ordering between the boundary conditions
![]() $\xi $
and
$\xi $
and
![]() $\psi $
. This absence of assumptions would greatly simplify the proof.
$\psi $
. This absence of assumptions would greatly simplify the proof.
The above has the following immediate corollary, which we will use throughout the paper.
Corollary 2.10. There exists a constant
![]() $C_{\mathrm {mix}}> 1$
such that for every
$C_{\mathrm {mix}}> 1$
such that for every
![]() $p \in (0,1)$
, every
$p \in (0,1)$
, every
![]() $R \geq 1$
, every two boundary conditions
$R \geq 1$
, every two boundary conditions
![]() $\xi $
and
$\xi $
and
![]() $\psi $
on
$\psi $
on
![]() $\Lambda _{C_{\mathrm {mix}} R}$
and every event A depending on the edges in
$\Lambda _{C_{\mathrm {mix}} R}$
and every event A depending on the edges in
![]() $\Lambda _R$
,
$\Lambda _R$
,
In particular, for any graph G containing
![]() $\Lambda _{C_{\mathrm {mix}}R}$
, any boundary condition
$\Lambda _{C_{\mathrm {mix}}R}$
, any boundary condition
![]() $\xi $
and any two events A and B depending on the edges inside
$\xi $
and any two events A and B depending on the edges inside
![]() $\Lambda _R$
and outside
$\Lambda _R$
and outside
![]() $\Lambda _{C_{\mathrm {mix}}R}$
, respectively,
$\Lambda _{C_{\mathrm {mix}}R}$
, respectively,
Proof of Proposition 2.9
By duality, it suffices to prove the statement for
![]() $p\le p_c$
. Set
$p\le p_c$
. Set
![]() $\rho = \sqrt {rR}$
, and let
$\rho = \sqrt {rR}$
, and let
![]() $\Omega $
be a subgraph of G containing
$\Omega $
be a subgraph of G containing
![]() $\Lambda _{\rho }$
. We first compare the probability of A under free boundary conditions to that under arbitrary boundary conditions
$\Lambda _{\rho }$
. We first compare the probability of A under free boundary conditions to that under arbitrary boundary conditions
![]() $\psi $
. For reasons that will be apparent later, we do this on
$\psi $
. For reasons that will be apparent later, we do this on
![]() $\Omega $
.
$\Omega $
.
For some boundary conditions
![]() $\psi $
on
$\psi $
on
![]() $\partial \Omega $
, using the increasing coupling
$\partial \Omega $
, using the increasing coupling
![]() $\mathbb P_{\mathbf {T}}$
between
$\mathbb P_{\mathbf {T}}$
between
![]() $\phi _{\Omega ,p}^0$
and
$\phi _{\Omega ,p}^0$
and
![]() $\phi _{\Omega ,p}^{\psi }$
described above, we find
$\phi _{\Omega ,p}^{\psi }$
described above, we find

for some constant
![]() $c>0$
. The first inequality is due to the property of the coupling, the second to equations (SMP), (CBC) and (
p-MON) and the third to equations (2.2) and (2.5). In conclusion,
$c>0$
. The first inequality is due to the property of the coupling, the second to equations (SMP), (CBC) and (
p-MON) and the third to equations (2.2) and (2.5). In conclusion,
The above applies in particular to
![]() $\Omega = G$
; let us now obtain a converse bound in this case.
$\Omega = G$
; let us now obtain a converse bound in this case.
Start by observing that for any fixed
![]() $\Omega $
as above,
$\Omega $
as above,
 $$ \begin{align} \phi_{G,p}^0[A] = \sum_{\xi \text{ b.c. on }\partial \Omega} \phi_{\Omega,p}^{\xi} [A] \phi_{G,p}^0[\omega_{|G\smallsetminus\Omega} \text{ induces } \xi \text{ on }\partial\Omega] \le \phi_{\Omega,p}^0[A]/(1-(r/R)^c). \end{align} $$
$$ \begin{align} \phi_{G,p}^0[A] = \sum_{\xi \text{ b.c. on }\partial \Omega} \phi_{\Omega,p}^{\xi} [A] \phi_{G,p}^0[\omega_{|G\smallsetminus\Omega} \text{ induces } \xi \text{ on }\partial\Omega] \le \phi_{\Omega,p}^0[A]/(1-(r/R)^c). \end{align} $$
Now fix some boundary conditions
![]() $\psi $
on G. For a configuration
$\psi $
on G. For a configuration
![]() $\omega $
on G, let
$\omega $
on G, let
![]() $\Omega (\omega )$
be the set of vertices that are not connected to
$\Omega (\omega )$
be the set of vertices that are not connected to
![]() $\mathbb {Z}^2\smallsetminus \Lambda _{R-1}$
. Then
$\mathbb {Z}^2\smallsetminus \Lambda _{R-1}$
. Then
 $$ \begin{align*} \phi_{G,p}^{\psi} [A]&\ge \phi_{G,p}^{\psi} [A,\partial \Lambda_{\rho} \kern6pt\not\kern-6pt\longleftrightarrow \partial \Lambda_R]\\ &=\sum_{\Omega \supset \Lambda_{\rho} }\phi_{\Omega,p}^0[A]\,\phi_{G,p}^{\psi} [\Omega(\omega)=\Omega]\\ &\ge (1-(r/R)^c)\phi_{G,p}^0[A] \phi_{G,p}^{\psi} [\partial \Lambda_{\rho} \kern6pt\not\kern-6pt\longleftrightarrow \partial \Lambda_R]\\ &\ge (1-(r/R)^c)^2 \phi_{G,p}^0[A], \end{align*} $$
$$ \begin{align*} \phi_{G,p}^{\psi} [A]&\ge \phi_{G,p}^{\psi} [A,\partial \Lambda_{\rho} \kern6pt\not\kern-6pt\longleftrightarrow \partial \Lambda_R]\\ &=\sum_{\Omega \supset \Lambda_{\rho} }\phi_{\Omega,p}^0[A]\,\phi_{G,p}^{\psi} [\Omega(\omega)=\Omega]\\ &\ge (1-(r/R)^c)\phi_{G,p}^0[A] \phi_{G,p}^{\psi} [\partial \Lambda_{\rho} \kern6pt\not\kern-6pt\longleftrightarrow \partial \Lambda_R]\\ &\ge (1-(r/R)^c)^2 \phi_{G,p}^0[A], \end{align*} $$
where in the second inequality, we used equation (2.7) and the fact that
 $$\begin{align*}\sum_{\Omega \supset \Lambda_{\rho} }\phi_{G,p}^{\psi} [\Omega(\omega)=\Omega] = \phi_{G,p}^{\psi} [\partial \Lambda_{\rho} \kern6pt\not\kern-6pt\longleftrightarrow \partial \Lambda_R]. \end{align*}$$
$$\begin{align*}\sum_{\Omega \supset \Lambda_{\rho} }\phi_{G,p}^{\psi} [\Omega(\omega)=\Omega] = \phi_{G,p}^{\psi} [\partial \Lambda_{\rho} \kern6pt\not\kern-6pt\longleftrightarrow \partial \Lambda_R]. \end{align*}$$
In the last inequality, we used that
for some constant
![]() $c> 0$
, by equation (2.2).
$c> 0$
, by equation (2.2).
Using the inequality above and equation (2.6) applied to G, we conclude that
Applying the above to two arbitrary boundary conditions
![]() $\psi $
and
$\psi $
and
![]() $\xi $
on
$\xi $
on
![]() $\partial G$
and using the triangular inequality, we conclude that for all
$\partial G$
and using the triangular inequality, we conclude that for all
![]() $r/R$
large enough,
$r/R$
large enough,
By assuming again that
![]() $r/R$
is small enough and modifying the constant in the exponent, we may eliminate the prefactor
$r/R$
is small enough and modifying the constant in the exponent, we may eliminate the prefactor
![]() $4(1+2(r/R)^c)$
and obtain equation (2.4).
$4(1+2(r/R)^c)$
and obtain equation (2.4).
Example 3
Alternatively, one may consider the decision tree
![]() $\mathbf T$
that explores the dual clusters of
$\mathbf T$
that explores the dual clusters of
![]() $\partial G^*$
in
$\partial G^*$
in
![]() $\omega ^*$
. We do not define this decision tree formally as it is almost identical to that of the previous example. We simply mention that when coupling two measures with
$\omega ^*$
. We do not define this decision tree formally as it is almost identical to that of the previous example. We simply mention that when coupling two measures with
![]() $p=p'$
using
$p=p'$
using
![]() $\mathbf T$
, differences only occur for edges that are connected in
$\mathbf T$
, differences only occur for edges that are connected in
![]() $\omega ^*$
to
$\omega ^*$
to
![]() $\partial G$
.
$\partial G$
.
Remark 2.11. In spite of the constructions above, we are unaware of the existence of a coupling of random-cluster models with boundary conditions
![]() $\xi \le \xi '$
and the same edge-parameter
$\xi \le \xi '$
and the same edge-parameter
![]() $p=p'$
that combines the properties of Examples 2 and 3: namely, a coupling for which only edges connected in both
$p=p'$
that combines the properties of Examples 2 and 3: namely, a coupling for which only edges connected in both
![]() $\omega '$
and
$\omega '$
and
![]() $\omega ^*$
to
$\omega ^*$
to
![]() $\partial G$
may have different states in the two configurations.
$\partial G$
may have different states in the two configurations.
Remark 2.12. Even though the uniform variables
![]() $(U_e)_{e\in E}$
are attached to the edges, the order in which these are revealed by
$(U_e)_{e\in E}$
are attached to the edges, the order in which these are revealed by
![]() $\mathbf T$
influences the final couple of configurations
$\mathbf T$
influences the final couple of configurations
![]() $(\omega , \omega ')$
. Indeed, consider
$(\omega , \omega ')$
. Indeed, consider
![]() $G = \Lambda _R$
, parameters
$G = \Lambda _R$
, parameters
![]() $p = p'$
and boundary conditions
$p = p'$
and boundary conditions
![]() $\xi = 0$
and
$\xi = 0$
and
![]() $\xi ' = 1$
; let e be one of the edges containing the origin. In the coupling produced with the decision tree of Example
$\xi ' = 1$
; let e be one of the edges containing the origin. In the coupling produced with the decision tree of Example
![]() $1$
,
$1$
,
![]() $\omega _e$
may differ from
$\omega _e$
may differ from
![]() $\omega ^{\prime }_e$
when e is not connected to
$\omega ^{\prime }_e$
when e is not connected to
![]() $\partial G$
in
$\partial G$
in
![]() $\omega '$
, while this is impossible with the one produced by Example 2.
$\omega '$
, while this is impossible with the one produced by Example 2.
2.4 Equivalence
 $L(p)-\xi (p)$
: proof of Theorem 1.3
$L(p)-\xi (p)$
: proof of Theorem 1.3
We will show the following proposition.
Proposition 2.13. There exist
![]() $c,C>0$
such that for every
$c,C>0$
such that for every
![]() $p < p_c$
and
$p < p_c$
and
![]() $x\in \mathbb {Z}^2$
,
$x\in \mathbb {Z}^2$
,
Before proving this proposition, we explain how it implies the theorem.
Proof of Theorem 1.3
For
![]() $p < p_c$
, the proof is immediate thanks to the definition of
$p < p_c$
, the proof is immediate thanks to the definition of
![]() $\xi (p)$
and the fact that
$\xi (p)$
and the fact that
(we use the FKG inequality on the left).
For
![]() $p> p_c$
, we proceed by duality. Notice that
$p> p_c$
, we proceed by duality. Notice that

Indeed, any configuration contributing to the second probability contains a dual circuit of length at least n, surrounding
![]() $0$
and passing through some point
$0$
and passing through some point
![]() $(k+\tfrac 12,0)$
on the horizontal axis. The last inequality is due to the subcritical case already established.
$(k+\tfrac 12,0)$
on the horizontal axis. The last inequality is due to the subcritical case already established.
Conversely, due to equation (CBC),
As n tends to infinity, the first term on the right-hand side above decays at most polynomially due to equations (2.2) and (2.5), while the second is lower-bounded by
![]() $\exp [-C|x|/L(p^*)]$
due to the subcritical case and the FKG property.
$\exp [-C|x|/L(p^*)]$
due to the subcritical case and the FKG property.
The two inequalities above show that
![]() $\xi (p)\asymp L(p^*)$
. That
$\xi (p)\asymp L(p^*)$
. That
![]() $L(p^*)\asymp L(p)$
follows directly by duality from the definition of the characteristic length.
$L(p^*)\asymp L(p)$
follows directly by duality from the definition of the characteristic length.
We now turn to the proof of Proposition 2.13.
Proof of Proposition 2.13
Set
![]() $L=L(p)$
. We assume that
$L=L(p)$
. We assume that
![]() $x\in L\mathbb Z^2$
; the general case can be solved similarly. We start with the lower bound. Consider the shortest family of vertices of
$x\in L\mathbb Z^2$
; the general case can be solved similarly. We start with the lower bound. Consider the shortest family of vertices of
![]() $y_i \in L\mathbb Z^2$
with
$y_i \in L\mathbb Z^2$
with
![]() $0=y_0,\dots ,y_k=x$
. Let
$0=y_0,\dots ,y_k=x$
. Let
![]() $A_L(y)$
be the event that there exists a circuit in
$A_L(y)$
be the event that there exists a circuit in
![]() $\Lambda _{2L}(y)$
surrounding
$\Lambda _{2L}(y)$
surrounding
![]() $\Lambda _L(y)$
. If
$\Lambda _L(y)$
. If
![]() $A_L(y_j)$
occurs for every
$A_L(y_j)$
occurs for every
![]() $0\le j\le k$
, then
$0\le j\le k$
, then
![]() $\Lambda _L$
is connected to
$\Lambda _L$
is connected to
![]() $\Lambda _L(x)$
. We deduce from the FKG inequality and equation (RSW) that
$\Lambda _L(x)$
. We deduce from the FKG inequality and equation (RSW) that
where the last inequality follows from equation (RSW) and
![]() $C> 0$
is some universal constant.
$C> 0$
is some universal constant.
For the upper bound, we start by observing that by equation (2.5) and the RSW theorem from [Reference Duminil-Copin and TassionDT19], we have that for some constant C,
 $$ \begin{align} \phi^1_{\Lambda_{2C_{\mathrm{mix}}L},p}[\Lambda_L\longleftrightarrow\partial\Lambda_{2L}] &\le 2\, \phi_{p}[\Lambda_L\longleftrightarrow\partial\Lambda_{2L}] \nonumber\\ &\le 2\, C\phi_{p}[\mathcal{C}(\Lambda_L)]^{1/C} \le 2\, C\delta_L^{1/C}<8^{-(4C_{\mathrm{mix}}+1)^{2}}, \end{align} $$
$$ \begin{align} \phi^1_{\Lambda_{2C_{\mathrm{mix}}L},p}[\Lambda_L\longleftrightarrow\partial\Lambda_{2L}] &\le 2\, \phi_{p}[\Lambda_L\longleftrightarrow\partial\Lambda_{2L}] \nonumber\\ &\le 2\, C\phi_{p}[\mathcal{C}(\Lambda_L)]^{1/C} \le 2\, C\delta_L^{1/C}<8^{-(4C_{\mathrm{mix}}+1)^{2}}, \end{align} $$
provided that
![]() $\delta _L$
in the definition of
$\delta _L$
in the definition of
![]() $L(p)$
is chosen sufficiently small. Now, if
$L(p)$
is chosen sufficiently small. Now, if
![]() $\Lambda _L$
and
$\Lambda _L$
and
![]() $\Lambda _L(x)$
are connected, then there must exist a sequence of
$\Lambda _L(x)$
are connected, then there must exist a sequence of
![]() $N \ge |x|/L$
distinct vertices
$N \ge |x|/L$
distinct vertices
![]() $0=y_1,\dots ,y_N=x$
contained in
$0=y_1,\dots ,y_N=x$
contained in
![]() $L\mathbb {Z}^2$
such that
$L\mathbb {Z}^2$
such that
-
•
 $\|y_i-y_{i+1}\|_{\infty }= L$
for every i;
$\|y_i-y_{i+1}\|_{\infty }= L$
for every i; -
•
 $\Lambda _L(y_i)$
is connected to
$\Lambda _L(y_i)$
is connected to
 $\partial \Lambda _{2L}(y_i)$
for every i.
$\partial \Lambda _{2L}(y_i)$
for every i.
Of these, choose the first subsequence of vertices
![]() $(y_i)_{i \in I}$
for the lexicographical order that contains
$(y_i)_{i \in I}$
for the lexicographical order that contains
![]() $k = N (4C_{\mathrm {mix}}+1)^{-2}$
vertices that are all at a distance at least
$k = N (4C_{\mathrm {mix}}+1)^{-2}$
vertices that are all at a distance at least
![]() $4 C_{\mathrm {mix}}$
from each other (the existence of such a subsequence is due to the pigeonhole principle). The union bound over the possible choices of
$4 C_{\mathrm {mix}}$
from each other (the existence of such a subsequence is due to the pigeonhole principle). The union bound over the possible choices of
![]() $y_1,\dots ,y_N$
(of which there are at most
$y_1,\dots ,y_N$
(of which there are at most
![]() $8^N$
), the spatial Markov property given by equation (SMP) and the comparison between boundary conditions in equation (CBC) imply that
$8^N$
), the spatial Markov property given by equation (SMP) and the comparison between boundary conditions in equation (CBC) imply that
The desired upper bound follows from the above using equation (2.11).
Remark 2.14. The previous proof is where the strongest condition on
![]() $\delta _L$
is imposed; recall that we also require that
$\delta _L$
is imposed; recall that we also require that
![]() $\delta _L<1/2$
to guarantee infinite characteristic length at
$\delta _L<1/2$
to guarantee infinite characteristic length at
![]() $p_c$
.
$p_c$
.
The next corollary is a useful estimate that we will invoke later in the article.
Corollary 2.15. There exists
![]() $c=c(\delta _L)>0$
such that for every
$c=c(\delta _L)>0$
such that for every
![]() $p>p_c$
and
$p>p_c$
and
![]() $k\ge 1$
,
$k\ge 1$
,
Proof. Note that the previous proof implies that for some constant
![]() $c>0$
, we have that for every
$c>0$
, we have that for every
![]() $p>p_c$
,
$p>p_c$
,
By the same counting argument as in the proof of the supercritical case of Theorem 1.3, we deduce from the above that the probability that there exists a circuit in
![]() $\omega ^*$
surrounding
$\omega ^*$
surrounding
![]() $\Lambda _{k L(p)}$
is bounded from above by
$\Lambda _{k L(p)}$
is bounded from above by
![]() $\sum _{j \geq k} \phi _{p^*}[\Lambda _{L(p)}\longleftrightarrow \partial \Lambda _{j L(p)}]\stackrel{<}{\scriptstyle{\frown}} \exp [-ck]$
.
$\sum _{j \geq k} \phi _{p^*}[\Lambda _{L(p)}\longleftrightarrow \partial \Lambda _{j L(p)}]\stackrel{<}{\scriptstyle{\frown}} \exp [-ck]$
.
3 Boosting pairs of boundary conditions for flower domains
Fix
![]() $q \in (1,4]$
for the whole section; we will omit it from the notation. The results of this section do not apply to
$q \in (1,4]$
for the whole section; we will omit it from the notation. The results of this section do not apply to
![]() $q = 1$
. As p will be fixed in all statements, we also remove it from the notation of the measure and write
$q = 1$
. As p will be fixed in all statements, we also remove it from the notation of the measure and write
![]() $\phi $
instead of
$\phi $
instead of
![]() $\phi _p$
.
$\phi _p$
.
3.1 Flower domains
We start by introducing the crucial notion of the flower domain. Figure 1 may be useful in understanding the definition below.

Figure 1 An inner flower domain on the left and an outer one on the right.
Definition 3.1 (Flower domain)
An inner flower domain on
![]() $\Lambda _R$
is a simply connected finite domain
$\Lambda _R$
is a simply connected finite domain
![]() $\mathcal {F}$
containing
$\mathcal {F}$
containing
![]() $\Lambda _R$
, whose boundary is formed of an even sequence of arcs
$\Lambda _R$
, whose boundary is formed of an even sequence of arcs
![]() $(a_{j}a_{j+1})_{j = 1,\dots ,2k}$
(with the convention
$(a_{j}a_{j+1})_{j = 1,\dots ,2k}$
(with the convention
![]() $a_{2k+1} = a_1$
), where each point
$a_{2k+1} = a_1$
), where each point
![]() $a_{j}$
is on
$a_{j}$
is on
![]() $\partial \Lambda _R$
.
$\partial \Lambda _R$
.
An outer flower domain on
![]() $\Lambda _R$
is the complement
$\Lambda _R$
is the complement
![]() $\mathcal {F}$
of a simply connected finite domain, with
$\mathcal {F}$
of a simply connected finite domain, with
![]() $\Lambda _R^c \subset \mathcal {F}$
and whose boundary is formed of an even sequence of arcs
$\Lambda _R^c \subset \mathcal {F}$
and whose boundary is formed of an even sequence of arcs
![]() $(a_{j}a_{j+1})_{j = 1,\dots ,2k}$
(with the convention
$(a_{j}a_{j+1})_{j = 1,\dots ,2k}$
(with the convention
![]() $a_{2k+1} = a_1$
), where each point
$a_{2k+1} = a_1$
), where each point
![]() $a_{j}$
is on
$a_{j}$
is on
![]() $\partial \Lambda _R$
.
$\partial \Lambda _R$
.
The arcs of the boundary are called primal and dual petals depending on whether j is odd or even, respectively. In both cases, we identify
![]() $\mathcal {F}$
as the graph formed of the edges strictly inside
$\mathcal {F}$
as the graph formed of the edges strictly inside
![]() $\mathcal {F}$
plus the edges on the dual petals.
$\mathcal {F}$
plus the edges on the dual petals.
For
![]() $\eta> 0$
, the flower domain
$\eta> 0$
, the flower domain
![]() $\mathcal {F}$
is said to be
$\mathcal {F}$
is said to be
![]() $\eta $
-well-separated if the distance between any two distinct points
$\eta $
-well-separated if the distance between any two distinct points
![]() $a_i$
and
$a_i$
and
![]() $a_j$
is greater than
$a_j$
is greater than
![]() $\eta R$
.
$\eta R$
.
A boundary condition
![]() $\xi $
is said to be coherent with
$\xi $
is said to be coherent with
![]() $\mathcal {F}$
if all vertices of any primal petal are wired together and all vertices of dual petals (except the endpoints) are wired to no other vertex of
$\mathcal {F}$
if all vertices of any primal petal are wired together and all vertices of dual petals (except the endpoints) are wired to no other vertex of
![]() $\partial \mathcal {F}$
.
$\partial \mathcal {F}$
.
Formally, flower domains should be defined as the couple formed of
![]() $\mathcal {F}$
and of the points
$\mathcal {F}$
and of the points
![]() $a_1,\dots , a_{2k}$
; we will, however, allow ourselves this small abuse of notation. When considering a flower domain with a coherent boundary condition, it will be useful to view the flower domain as containing the edges of the primal petals that are conditioned to be opened. We will also often identify dual arcs
$a_1,\dots , a_{2k}$
; we will, however, allow ourselves this small abuse of notation. When considering a flower domain with a coherent boundary condition, it will be useful to view the flower domain as containing the edges of the primal petals that are conditioned to be opened. We will also often identify dual arcs
![]() $(a_ja_{j+1})$
with the dual path made of the dual edges
$(a_ja_{j+1})$
with the dual path made of the dual edges
![]() $e^*$
with e incident to
$e^*$
with e incident to
![]() $x\in (a_ja_{j+1})$
and
$x\in (a_ja_{j+1})$
and
![]() $y\notin \mathcal {F}$
and assume it is made of open dual edges.
$y\notin \mathcal {F}$
and assume it is made of open dual edges.
Notice that when
![]() $\mathcal {F}$
has at least four petals, several boundary conditions are coherent with
$\mathcal {F}$
has at least four petals, several boundary conditions are coherent with
![]() $\mathcal {F}$
as different primal petals may or may not be wired together.
$\mathcal {F}$
as different primal petals may or may not be wired together.
Example
The example that we will most commonly use is that of a flower domain revealed from the inside or outside. Consider
![]() $r < R$
, and let
$r < R$
, and let
![]() $\omega $
be a configuration on the annulus
$\omega $
be a configuration on the annulus
![]() $\mathrm {Ann}(r,R)$
.
$\mathrm {Ann}(r,R)$
.
The inner flower domain
![]() $\mathcal {F}$
from
$\mathcal {F}$
from
![]() $\Lambda _{R}$
to
$\Lambda _{R}$
to
![]() $\Lambda _r$
is obtained as follows. Consider all interfaces of
$\Lambda _r$
is obtained as follows. Consider all interfaces of
![]() $\omega $
contained in
$\omega $
contained in
![]() $\mathrm {Ann}(r,R)$
starting on
$\mathrm {Ann}(r,R)$
starting on
![]() $\partial \Lambda _R$
; these are paths in the loop representation of the random cluster model with endpoints on
$\partial \Lambda _R$
; these are paths in the loop representation of the random cluster model with endpoints on
![]() $\partial \Lambda _R$
or
$\partial \Lambda _R$
or
![]() $\partial \Lambda _r$
. Write
$\partial \Lambda _r$
. Write
![]() $\mathsf {Exp}$
for the set of edges adjacent or intersecting any such interface. Loosely speaking, these are the edges revealed during the exploration of the interfaces starting on
$\mathsf {Exp}$
for the set of edges adjacent or intersecting any such interface. Loosely speaking, these are the edges revealed during the exploration of the interfaces starting on
![]() $\partial \Lambda _R$
.
$\partial \Lambda _R$
.
If at least one such interface has an endpoint on
![]() $\partial \Lambda _r$
, define
$\partial \Lambda _r$
, define
![]() $\mathcal {F}$
as being the connected component of
$\mathcal {F}$
as being the connected component of
![]() $\Lambda _r$
in
$\Lambda _r$
in
![]() $\Lambda _R \smallsetminus \mathsf {Exp}$
. Otherwise,
$\Lambda _R \smallsetminus \mathsf {Exp}$
. Otherwise,
![]() $\mathcal {F}$
is not defined (formally, set
$\mathcal {F}$
is not defined (formally, set
![]() $\mathcal {F} = \emptyset $
in this case). Observe that the number of interfaces between
$\mathcal {F} = \emptyset $
in this case). Observe that the number of interfaces between
![]() $\partial \Lambda _R$
and
$\partial \Lambda _R$
and
![]() $\partial \Lambda _r$
is necessarily even. Their endpoints
$\partial \Lambda _r$
is necessarily even. Their endpoints
![]() $\partial \Lambda _r$
naturally partition
$\partial \Lambda _r$
naturally partition
![]() $\partial \mathcal {F}$
into primal and dual petals. See Figure 1 for an illustration.
$\partial \mathcal {F}$
into primal and dual petals. See Figure 1 for an illustration.
To define the outer flower domain from
![]() $\Lambda _{r}$
to
$\Lambda _{r}$
to
![]() $\Lambda _R$
, similarly explore the interfaces starting on
$\Lambda _R$
, similarly explore the interfaces starting on
![]() $\partial \Lambda _r^c$
.
$\partial \Lambda _r^c$
.
Let us mention an important lemma for what comes next.
Lemma 3.2. For every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $\eta> 0$
such that for any
$\eta> 0$
such that for any
![]() $p \in (0,1)$
, any
$p \in (0,1)$
, any
![]() $R <L(p)$
and any boundary conditions
$R <L(p)$
and any boundary conditions
![]() $\xi $
,
$\xi $
,
when
![]() $\mathcal {F}$
denotes the inner flower domain revealed from
$\mathcal {F}$
denotes the inner flower domain revealed from
![]() $\Lambda _{2R}$
to
$\Lambda _{2R}$
to
![]() $\Lambda _R$
, and
$\Lambda _R$
, and
when
![]() $\mathcal {F}$
denotes the outer flower domain revealed from
$\mathcal {F}$
denotes the outer flower domain revealed from
![]() $\Lambda _{R}$
to
$\Lambda _{R}$
to
![]() $\Lambda _{2R}$
.
$\Lambda _{2R}$
.
Proof. We treat the case of outer flower domains; that of inner domains can be solved similarly. For
![]() $\mathcal {F}$
to exist but not be
$\mathcal {F}$
to exist but not be
![]() $\eta $
-well-separated, it needs to contain a primal or dual petal with
$\eta $
-well-separated, it needs to contain a primal or dual petal with
![]() $|a_i-a_{i+1}|<\eta R$
. We will exclude below the possibility of a small dual petal; the case of a primal one is identical.
$|a_i-a_{i+1}|<\eta R$
. We will exclude below the possibility of a small dual petal; the case of a primal one is identical.
Divide
![]() $\partial \Lambda _{2R}$
into arcs
$\partial \Lambda _{2R}$
into arcs
![]() $\ell _1,\dots ,\ell _N$
of lengths between
$\ell _1,\dots ,\ell _N$
of lengths between
![]() $\eta R$
and
$\eta R$
and
![]() $2\eta R$
successively overlapping on a segment of length
$2\eta R$
successively overlapping on a segment of length
![]() $\eta R$
, each arc being included in a single side of
$\eta R$
, each arc being included in a single side of
![]() $\partial \Lambda _{2R}$
. Let
$\partial \Lambda _{2R}$
. Let
![]() $A_{101}^{\square }(\ell _i)$
be the event that there exist two primal arms with a dual one in between contained in
$A_{101}^{\square }(\ell _i)$
be the event that there exist two primal arms with a dual one in between contained in
![]() $\mathrm {Ann}(R,2R)$
from
$\mathrm {Ann}(R,2R)$
from
![]() $\ell _i$
to
$\ell _i$
to
![]() $\partial \Lambda _{R}$
. Notice that if
$\partial \Lambda _{R}$
. Notice that if
![]() $\mathcal {F}$
contains a dual petal with endpoints at a distance smaller than
$\mathcal {F}$
contains a dual petal with endpoints at a distance smaller than
![]() $\eta R$
of each other, then there exists at least one arc
$\eta R$
of each other, then there exists at least one arc
![]() $\ell _i$
for which
$\ell _i$
for which
![]() $A_{101}^{\square }(\ell _i)$
occurs. Our goal is therefore to bound the probability of the events
$A_{101}^{\square }(\ell _i)$
occurs. Our goal is therefore to bound the probability of the events
![]() $A_{101}^{\square }(\ell _i)$
.
$A_{101}^{\square }(\ell _i)$
.
Fix
![]() $\ell _i$
, and let
$\ell _i$
, and let
![]() $\mathrm {Rect}\subset \Lambda _{2R}$
be the rectangle of size
$\mathrm {Rect}\subset \Lambda _{2R}$
be the rectangle of size
![]() $R\times 4R$
with one of the long sides being the side of
$R\times 4R$
with one of the long sides being the side of
![]() $\partial \Lambda _{2R}$
containing
$\partial \Lambda _{2R}$
containing
![]() $\ell _i$
(we use here that
$\ell _i$
(we use here that
![]() $\ell _i$
is included in one of the sides of
$\ell _i$
is included in one of the sides of
![]() $\Lambda _{2R}$
). Define
$\Lambda _{2R}$
). Define
![]() $\widetilde A_{10}^{\square }(\ell _i)$
as the event that there exist two paths, one primal and one dual, starting on
$\widetilde A_{10}^{\square }(\ell _i)$
as the event that there exist two paths, one primal and one dual, starting on
![]() $\ell _i$
and crossing
$\ell _i$
and crossing
![]() $\mathrm {Rect}$
to its opposite side. See Figure 2 for an illustration. From equation (RSW), it is easily deduced by an exploration argument that
$\mathrm {Rect}$
to its opposite side. See Figure 2 for an illustration. From equation (RSW), it is easily deduced by an exploration argument that
for universal constants
![]() $c_0,C_0> 0$
. Indeed, explore first the interface from
$c_0,C_0> 0$
. Indeed, explore first the interface from
![]() $\ell _i$
to the opposite side of
$\ell _i$
to the opposite side of
![]() $\mathrm {Rect}$
closest to a chosen endpoint of
$\mathrm {Rect}$
closest to a chosen endpoint of
![]() $\ell _i$
. The existence of such an interface is synonymous to
$\ell _i$
. The existence of such an interface is synonymous to
![]() $\widetilde A_{10}^{\square }(\ell _i)$
. Condition next on this interface, and bound the probability of the existence of the second primal arm as follows. Consider disjoint annuli around
$\widetilde A_{10}^{\square }(\ell _i)$
. Condition next on this interface, and bound the probability of the existence of the second primal arm as follows. Consider disjoint annuli around
![]() $\ell _i$
, at dyadic scales between
$\ell _i$
, at dyadic scales between
![]() $2\eta R$
and R, and apply equation (RSW) in each annulus to conclude that under this conditioning, the second primal arm occurs with a polynomially small probability. Observe that the conditioning on the interface induces both positive and negative information on the remaining edges, but the information favourable to the existence of a primal path is, for every dyadic annulus, at a macroscopic distance. This allows one to apply equation (RSW) in the annuli; see also the caption of Figure 2 for explanations.
$2\eta R$
and R, and apply equation (RSW) in each annulus to conclude that under this conditioning, the second primal arm occurs with a polynomially small probability. Observe that the conditioning on the interface induces both positive and negative information on the remaining edges, but the information favourable to the existence of a primal path is, for every dyadic annulus, at a macroscopic distance. This allows one to apply equation (RSW) in the annuli; see also the caption of Figure 2 for explanations.

Figure 2
Left: If there exists a dual petal with both endpoints in an interval
![]() $\ell _i$
, then the three-arm event
$\ell _i$
, then the three-arm event
![]() $A_{101}^{\square }(\ell _i)$
occurs. Right: When
$A_{101}^{\square }(\ell _i)$
occurs. Right: When
![]() $\widetilde A_{10}^{\square }(\ell _i)$
occurs, condition on the lowest horizontal interface crossing
$\widetilde A_{10}^{\square }(\ell _i)$
occurs, condition on the lowest horizontal interface crossing
![]() $\mathrm {Rect}$
from
$\mathrm {Rect}$
from
![]() $\ell _i$
to its left side. Above it, we find order
$\ell _i$
to its left side. Above it, we find order
![]() $\log \eta $
disjoint tubes that when dually crossed, prevent the existence of a second primal arm from
$\log \eta $
disjoint tubes that when dually crossed, prevent the existence of a second primal arm from
![]() $\ell _i$
to the left side of
$\ell _i$
to the left side of
![]() $\mathrm {Rect}$
. Due to equation (RSW), each such tube is dually crossed with positive probability, independently of the others. Indeed, the boundary conditions on
$\mathrm {Rect}$
. Due to equation (RSW), each such tube is dually crossed with positive probability, independently of the others. Indeed, the boundary conditions on
![]() $\partial \Lambda _R^c$
, as well as those induced by the conditioning on the lowest interface, may have both free and wired parts, but only the free boundary conditions border the tubes. This suffices to obtain the polynomial term in equation (3.1).
$\partial \Lambda _R^c$
, as well as those induced by the conditioning on the lowest interface, may have both free and wired parts, but only the free boundary conditions border the tubes. This suffices to obtain the polynomial term in equation (3.1).
To bound the probabilities of the events
![]() $\widetilde A_{10}^{\square }(\ell _i)$
, define
$\widetilde A_{10}^{\square }(\ell _i)$
, define
![]() $\mathbf N$
to be the number of disjoint clusters crossing
$\mathbf N$
to be the number of disjoint clusters crossing
![]() $\mathrm {Rect}$
. Then
$\mathrm {Rect}$
. Then
 $$ \begin{align} \sum_{i=1}^k\phi_{\Lambda_{R}^c}^{\xi}[\widetilde A_{10}^{\square}(\ell_i)]\le 4\phi_{\Lambda_R^c}^{\xi}[\mathbf N]\le C_1, \end{align} $$
$$ \begin{align} \sum_{i=1}^k\phi_{\Lambda_{R}^c}^{\xi}[\widetilde A_{10}^{\square}(\ell_i)]\le 4\phi_{\Lambda_R^c}^{\xi}[\mathbf N]\le C_1, \end{align} $$
where the first inequality is a deterministic bound (obtained by bounding, for each side of
![]() $\partial \Lambda _{2R}$
, the sum of the
$\partial \Lambda _{2R}$
, the sum of the
![]() $\ell _i$
included in it by the random variable
$\ell _i$
included in it by the random variable
![]() $\mathbf N$
or a rotation of it) and the second uniform bound on the expectation of
$\mathbf N$
or a rotation of it) and the second uniform bound on the expectation of
![]() $\mathbf N$
, which is a standard consequence of equation (RSW) sketched below: observe that there exists
$\mathbf N$
, which is a standard consequence of equation (RSW) sketched below: observe that there exists
![]() $c_2>0$
such that for every
$c_2>0$
such that for every
![]() $k\ge 0$
,
$k\ge 0$
,
Indeed, conditionally on the k top-most clusters crossing
![]() $\mathrm {Rect}$
, observe that the complement
$\mathrm {Rect}$
, observe that the complement
![]() $\Omega $
in
$\Omega $
in
![]() $\mathrm { Rect}$
of these clusters is a subset of
$\mathrm { Rect}$
of these clusters is a subset of
![]() $\mathrm {Rect}$
with free boundary conditions on the part of the boundary that lies strictly inside
$\mathrm {Rect}$
with free boundary conditions on the part of the boundary that lies strictly inside
![]() $\mathrm {Rect}$
. Then a dual path disconnecting the two sides of
$\mathrm {Rect}$
. Then a dual path disconnecting the two sides of
![]() $\mathrm {Rect}$
in
$\mathrm {Rect}$
in
![]() $\Omega $
occurs with probability at least
$\Omega $
occurs with probability at least
![]() $c_2>0$
by equation (RSW). This proves equation (3.3), which in turn implies equation (3.2).
$c_2>0$
by equation (RSW). This proves equation (3.3), which in turn implies equation (3.2).
Combining equations (3.1) and (3.2) and adding a factor
![]() $2$
to account for the existence of small primal petals, we find
$2$
to account for the existence of small primal petals, we find
 $$\begin{align*}\phi_{\Lambda_{R}^c}^{\xi} [\mathcal{F} \text{ exists but is not } \eta\text{-well-separated}] \le 2C_0\eta^{c_0} \, \sum_{i=1}^k\phi_{\Lambda_{R}^c}^{\xi}[\widetilde A_{10}^{\square}(\ell_i)]\le 2C_0C_1\eta^{c_0}. \end{align*}$$
$$\begin{align*}\phi_{\Lambda_{R}^c}^{\xi} [\mathcal{F} \text{ exists but is not } \eta\text{-well-separated}] \le 2C_0\eta^{c_0} \, \sum_{i=1}^k\phi_{\Lambda_{R}^c}^{\xi}[\widetilde A_{10}^{\square}(\ell_i)]\le 2C_0C_1\eta^{c_0}. \end{align*}$$
Fixing
![]() $\eta $
small enough concludes the proof.
$\eta $
small enough concludes the proof.
Definition 3.3 (Double four-petal flower domain)
Fix
![]() $1 \le r < R$
. We say that there exists a double four-petal flower domain between
$1 \le r < R$
. We say that there exists a double four-petal flower domain between
![]() $\Lambda _r$
and
$\Lambda _r$
and
![]() $\Lambda _R$
if
$\Lambda _R$
if
-
• the outer flower domain
 $\mathcal {F}_{out}$
revealed from
$\mathcal {F}_{out}$
revealed from
 $\Lambda _{(rR)^{1/2}}$
to
$\Lambda _{(rR)^{1/2}}$
to
 $\Lambda _{R}$
exists, is
$\Lambda _{R}$
exists, is
 $1/2$
-well-separated and has exactly four petals
$1/2$
-well-separated and has exactly four petals
 $P_1^{out},\dots ,P_4^{out}$
;
$P_1^{out},\dots ,P_4^{out}$
; -
• the inner flower domain
 $\mathcal {F}_{in}$
revealed from
$\mathcal {F}_{in}$
revealed from
 $\Lambda _{(rR)^{1/2}}$
to
$\Lambda _{(rR)^{1/2}}$
to
 $\Lambda _{r}$
exists, is
$\Lambda _{r}$
exists, is
 $1/2$
-well-separated and has exactly four petals
$1/2$
-well-separated and has exactly four petals
 $P_1^{in},\dots ,P_4^{in}$
;
$P_1^{in},\dots ,P_4^{in}$
; -
•
 $P_1^{in}$
is connected to
$P_1^{in}$
is connected to
 $P_1^{out}$
and
$P_1^{out}$
and
 $P_3^{in}$
to
$P_3^{in}$
to
 $P_3^{out}$
in
$P_3^{out}$
in
 $\omega \cap \mathcal {F}_{in}^c \cap \mathcal {F}_{out}^c$
;
$\omega \cap \mathcal {F}_{in}^c \cap \mathcal {F}_{out}^c$
; -
•
 $P_2^{in}$
is connected to
$P_2^{in}$
is connected to
 $P_2^{out}$
and
$P_2^{out}$
and
 $P_4^{in}$
to
$P_4^{in}$
to
 $P_4^{out}$
in
$P_4^{out}$
in
 $\omega ^*\cap \mathcal {F}_{in}^c \cap \mathcal {F}_{out}^c$
.
$\omega ^*\cap \mathcal {F}_{in}^c \cap \mathcal {F}_{out}^c$
.
See Figure 3 for an example.

Figure 3 A double four-petal flower domain. The two connected components of the white area are
![]() $\mathcal {F}_{in}$
and
$\mathcal {F}_{in}$
and
![]() $\mathcal {F}_{out}$
.
$\mathcal {F}_{out}$
.
The advantage of the double four-petal flower domain is that it can be revealed from
![]() $\partial \Lambda _{(rR)^{1/2}}$
towards the inside and outside and limits the interaction between the configurations in
$\partial \Lambda _{(rR)^{1/2}}$
towards the inside and outside and limits the interaction between the configurations in
![]() $\mathcal {F}_{in}$
and
$\mathcal {F}_{in}$
and
![]() $\mathcal {F}_{out}$
.
$\mathcal {F}_{out}$
.
Lemma 3.4. For any
![]() $\eta> 0$
, there exists
$\eta> 0$
, there exists
![]() $c = c(\eta )> 0$
such that for any
$c = c(\eta )> 0$
such that for any
![]() $p \in (0,1)$
, any
$p \in (0,1)$
, any
![]() $R <L(p)$
large enough and any boundary conditions
$R <L(p)$
large enough and any boundary conditions
![]() $\xi $
on
$\xi $
on
![]() $\mathrm {Ann} := \mathrm {Ann}((1-\eta )R, (1 + 2\eta )R)$
,
$\mathrm {Ann} := \mathrm {Ann}((1-\eta )R, (1 + 2\eta )R)$
,
Proof. We recommend inspecting Figure 4 while reading this proof. Set
![]() $R'':=(1+\eta )R$
and
$R'':=(1+\eta )R$
and
![]() $R':=(RR'')^{1/2}$
. Consider the rectangles
$R':=(RR'')^{1/2}$
. Consider the rectangles
and their rotations
![]() $\mathrm {Rect}_N$
,
$\mathrm {Rect}_N$
,
![]() $\mathrm {Rect}_W$
,
$\mathrm {Rect}_W$
,
![]() $\mathrm {Rect}_S$
and
$\mathrm {Rect}_S$
and
![]() $\mathrm {Rect}_N'$
,
$\mathrm {Rect}_N'$
,
![]() $\mathrm {Rect}_W'$
,
$\mathrm {Rect}_W'$
,
![]() $\mathrm { Rect}_S'$
by angles
$\mathrm { Rect}_S'$
by angles
![]() $\pi /2$
,
$\pi /2$
,
![]() $\pi $
and
$\pi $
and
![]() $3\pi /2$
, respectively. Also define the L-shaped regions
$3\pi /2$
, respectively. Also define the L-shaped regions
 $$ \begin{align*} &\mathrm{Lshape}_{NE} :=[R,R']\times[- R/2, R'] \cup [- R/2, R'] \times [R,R'] \quad \text{ and }\\ &\mathrm{Lshape}_{NE}':=[R',R'']\times[- R/2, R''] \cup [- R/2, R''] \times [R',R''] \end{align*} $$
$$ \begin{align*} &\mathrm{Lshape}_{NE} :=[R,R']\times[- R/2, R'] \cup [- R/2, R'] \times [R,R'] \quad \text{ and }\\ &\mathrm{Lshape}_{NE}':=[R',R'']\times[- R/2, R''] \cup [- R/2, R''] \times [R',R''] \end{align*} $$
and their rotations
![]() $\mathrm {Lshape}_{NW}$
,
$\mathrm {Lshape}_{NW}$
,
![]() $\mathrm {Lshape}_{SW}$
,
$\mathrm {Lshape}_{SW}$
,
![]() $\mathrm {Lshape}_{SE}$
and
$\mathrm {Lshape}_{SE}$
and
![]() $\mathrm {Lshape}_{NW}'$
,
$\mathrm {Lshape}_{NW}'$
,
![]() $\mathrm { Lshape}_{SW}'$
,
$\mathrm { Lshape}_{SW}'$
,
![]() $\mathrm {Lshape}_{SE}'$
by angles
$\mathrm {Lshape}_{SE}'$
by angles
![]() $\pi /2$
,
$\pi /2$
,
![]() $\pi $
and
$\pi $
and
![]() $3\pi /2$
, respectively. Let
$3\pi /2$
, respectively. Let
![]() $E_{1}$
be the event that there exist
$E_{1}$
be the event that there exist
-
• dual crossings in
 $\mathrm {Rect}_E$
and
$\mathrm {Rect}_E$
and
 $\mathrm {Rect}_N$
between
$\mathrm {Rect}_N$
between
 $ \Lambda _R$
and
$ \Lambda _R$
and
 $\partial \Lambda _{R'}$
,
$\partial \Lambda _{R'}$
, -
• dual crossings in
 $\mathrm {Rect}_E'$
and
$\mathrm {Rect}_E'$
and
 $\mathrm {Rect}_N'$
between
$\mathrm {Rect}_N'$
between
 $ \Lambda _{R'}$
and
$ \Lambda _{R'}$
and
 $\partial \Lambda _{R''}$
,
$\partial \Lambda _{R''}$
, -
• primal crossings in
 $\mathrm {Rect}_E$
and
$\mathrm {Rect}_E$
and
 $\mathrm {Rect}_N$
between
$\mathrm {Rect}_N$
between
 $ \Lambda _R$
and
$ \Lambda _R$
and
 $\partial \Lambda _{R'}$
, connected by a primal path in
$\partial \Lambda _{R'}$
, connected by a primal path in
 $\mathrm {Lshape}_{NE}$
,
$\mathrm {Lshape}_{NE}$
, -
• primal crossings in
 $\mathrm {Rect}_E'$
and
$\mathrm {Rect}_E'$
and
 $\mathrm {Rect}_N'$
between
$\mathrm {Rect}_N'$
between
 $ \Lambda _{R'}$
and
$ \Lambda _{R'}$
and
 $\partial \Lambda _{R''}$
, connected by a primal path in
$\partial \Lambda _{R''}$
, connected by a primal path in
 $\mathrm {Lshape}_{NE}'$
,
$\mathrm {Lshape}_{NE}'$
, -
• a primal path between
 $ \Lambda _{R}$
and
$ \Lambda _{R}$
and
 $\partial \Lambda _{R''}$
contained in
$\partial \Lambda _{R''}$
contained in
 $(\mathrm {Lshape}_{NE} \cup \mathrm {Lshape}_{NE}')\smallsetminus (\mathrm {Rect}_E \cup \mathrm {Rect}_N \cup \mathrm {Rect}_E' \cup \mathrm {Rect}_N ' )$
.
$(\mathrm {Lshape}_{NE} \cup \mathrm {Lshape}_{NE}')\smallsetminus (\mathrm {Rect}_E \cup \mathrm {Rect}_N \cup \mathrm {Rect}_E' \cup \mathrm {Rect}_N ' )$
.
Also, let
![]() $E_{3}$
be the rotation by
$E_{3}$
be the rotation by
![]() $\pi $
of
$\pi $
of
![]() $E_1$
.
$E_1$
.

Figure 4
Left: The event
![]() $E_1 \cap E_3$
. The bold contour delimits
$E_1 \cap E_3$
. The bold contour delimits
![]() $\mathrm {Lshape}_{NW} \cup \mathrm { Lshape}_{NW}'$
. Right: The configuration in the pink area and its boundary are determined by the conditioning on
$\mathrm {Lshape}_{NW} \cup \mathrm { Lshape}_{NW}'$
. Right: The configuration in the pink area and its boundary are determined by the conditioning on
![]() $\mathsf {C}_1$
,
$\mathsf {C}_1$
,
![]() $\mathsf {C}_1'$
,
$\mathsf {C}_1'$
,
![]() $\mathsf {C}_3$
,
$\mathsf {C}_3$
,
![]() $\mathsf {C}_3'$
and
$\mathsf {C}_3'$
and
![]() $\omega $
inside
$\omega $
inside
![]() $(\mathrm {Lshape}_{NE} \cup \mathrm {Lshape}_{NE}') \smallsetminus (\mathrm {Rect}_E \cup \mathrm {Rect}_N \cup \mathrm {Rect}_E' \cup \mathrm {Rect}_N ')$
. This part of the configuration is sufficient to ensure that
$(\mathrm {Lshape}_{NE} \cup \mathrm {Lshape}_{NE}') \smallsetminus (\mathrm {Rect}_E \cup \mathrm {Rect}_N \cup \mathrm {Rect}_E' \cup \mathrm {Rect}_N ')$
. This part of the configuration is sufficient to ensure that
![]() $E_1 \cap E_3$
occurs, and the measure in the rest of the space is an FK-percolation measure with prescribed boundary conditions. The dual blue paths occur with positive probability under this conditioning; they produce
$E_1 \cap E_3$
occurs, and the measure in the rest of the space is an FK-percolation measure with prescribed boundary conditions. The dual blue paths occur with positive probability under this conditioning; they produce
![]() $E_2$
and
$E_2$
and
![]() $E_4$
. When all of
$E_4$
. When all of
![]() $E_1, \dots , E_4$
occur, there exists a double four-petal flower domain between
$E_1, \dots , E_4$
occur, there exists a double four-petal flower domain between
![]() $\Lambda _R$
and
$\Lambda _R$
and
![]() $\Lambda _{R''}$
.
$\Lambda _{R''}$
.
Due to equation (RSW), there exists some
![]() $c_0> 0$
depending only on
$c_0> 0$
depending only on
![]() $\eta $
such that
$\eta $
such that
Now, when
![]() $E_1 \cap E_3$
occurs, let
$E_1 \cap E_3$
occurs, let
![]() $\mathsf {C}_1$
be the unique connected component of
$\mathsf {C}_1$
be the unique connected component of
![]() $\mathrm {Lshape}_{NE}$
that contains both crossings in
$\mathrm {Lshape}_{NE}$
that contains both crossings in
![]() $\mathrm {Rect}_E$
and
$\mathrm {Rect}_E$
and
![]() $\mathrm {Rect}_N$
from
$\mathrm {Rect}_N$
from
![]() $ \Lambda _R$
to
$ \Lambda _R$
to
![]() $\partial \Lambda _{R'}$
. Define
$\partial \Lambda _{R'}$
. Define
![]() $\mathsf {C}_1'$
in the same way for the outer annulus and
$\mathsf {C}_1'$
in the same way for the outer annulus and
![]() $\mathsf {C}_3$
and
$\mathsf {C}_3$
and
![]() $\mathsf {C}_3'$
by the same definition applied to the rotation by
$\mathsf {C}_3'$
by the same definition applied to the rotation by
![]() $\pi $
of the configuration. When
$\pi $
of the configuration. When
![]() $E_1 \cap E_3$
fails to occur, set
$E_1 \cap E_3$
fails to occur, set
![]() $\mathsf {C}_1 = \mathsf {C}_1' = \mathsf {C}_3 = \mathsf {C}_3' = \emptyset $
. Furthermore, when
$\mathsf {C}_1 = \mathsf {C}_1' = \mathsf {C}_3 = \mathsf {C}_3' = \emptyset $
. Furthermore, when
![]() $E_1\cap E_3$
does occur, let
$E_1\cap E_3$
does occur, let
![]() $E_2$
be the event that there exist
$E_2$
be the event that there exist
-
• a dual path between
 $\partial \mathsf {C}_1$
and
$\partial \mathsf {C}_1$
and
 $\partial \mathsf {C}_3$
contained in
$\partial \mathsf {C}_3$
contained in
 $\mathrm {Lshape}_{NW}$
,
$\mathrm {Lshape}_{NW}$
, -
• a dual path between
 $\partial \mathsf {C}_1'$
and
$\partial \mathsf {C}_1'$
and
 $\partial \mathsf {C}_3'$
contained in
$\partial \mathsf {C}_3'$
contained in
 $\mathrm {Lshape}_{NW}'$
,
$\mathrm {Lshape}_{NW}'$
, -
• a dual path between
 $ \Lambda _{R}$
and
$ \Lambda _{R}$
and
 $\partial \Lambda _{R''}$
contained in
$\partial \Lambda _{R''}$
contained in
 $(\mathrm {Lshape}_{NW} \cup \mathrm {Lshape}_{NW}') \smallsetminus (\mathrm {Rect}_N \cup \mathrm {Rect}_W \cup \mathrm {Rect}_N' \cup \mathrm {Rect}_W')$
.
$(\mathrm {Lshape}_{NW} \cup \mathrm {Lshape}_{NW}') \smallsetminus (\mathrm {Rect}_N \cup \mathrm {Rect}_W \cup \mathrm {Rect}_N' \cup \mathrm {Rect}_W')$
.
Define
![]() $E_4$
in the same way for the configuration rotated by
$E_4$
in the same way for the configuration rotated by
![]() $\pi $
.
$\pi $
.
Observe now that conditionally on any realisation of
![]() $\mathsf {C}_1$
,
$\mathsf {C}_1$
,
![]() $\mathsf {C}_1'$
,
$\mathsf {C}_1'$
,
![]() $\mathsf {C}_3$
,
$\mathsf {C}_3$
,
![]() $\mathsf {C}_3'$
different from
$\mathsf {C}_3'$
different from
![]() $\emptyset $
and on the configuration inside
$\emptyset $
and on the configuration inside
![]() $(\mathrm {Lshape}_{NE} \cup \mathrm {Lshape}_{NE}') \smallsetminus (\mathrm {Rect}_E \cup \mathrm {Rect}_N \cup \mathrm {Rect}_E' \cup \mathrm { Rect}_N ')$
, the configuration in the rest of the space is that of an FK-percolation with boundary conditions given by the conditioning. Indeed, the conditioning suffices to guarantee the occurrence of
$(\mathrm {Lshape}_{NE} \cup \mathrm {Lshape}_{NE}') \smallsetminus (\mathrm {Rect}_E \cup \mathrm {Rect}_N \cup \mathrm {Rect}_E' \cup \mathrm { Rect}_N ')$
, the configuration in the rest of the space is that of an FK-percolation with boundary conditions given by the conditioning. Indeed, the conditioning suffices to guarantee the occurrence of
![]() $E_1\cap E_3$
.
$E_1\cap E_3$
.
Thus, due to equation (RSW), by conditioning on
![]() $\mathsf {C}_1$
,
$\mathsf {C}_1$
,
![]() $\mathsf {C}_1'$
,
$\mathsf {C}_1'$
,
![]() $\mathsf {C}_3$
,
$\mathsf {C}_3$
,
![]() $\mathsf {C}_3'$
and the configuration inside
$\mathsf {C}_3'$
and the configuration inside
![]() $(\mathrm {Lshape}_{NE} \cup \mathrm {Lshape}_{NE}') \smallsetminus (\mathrm {Rect}_E \cup \mathrm {Rect}_N \cup \mathrm {Rect}_E' \cup \mathrm { Rect}_N ')$
and then averaging the result, we find that
$(\mathrm {Lshape}_{NE} \cup \mathrm {Lshape}_{NE}') \smallsetminus (\mathrm {Rect}_E \cup \mathrm {Rect}_N \cup \mathrm {Rect}_E' \cup \mathrm { Rect}_N ')$
and then averaging the result, we find that
for some
![]() $c_1> 0$
depending only on
$c_1> 0$
depending only on
![]() $\eta $
. Thus, we conclude that
$\eta $
. Thus, we conclude that
Finally, notice that when
![]() $E_1\cap \dots \cap E_4$
occurs, there exists a double four-petal flower domain between
$E_1\cap \dots \cap E_4$
occurs, there exists a double four-petal flower domain between
![]() $\Lambda _R$
and
$\Lambda _R$
and
![]() $\Lambda _{R''}$
. Indeed, the events
$\Lambda _{R''}$
. Indeed, the events
![]() $E_1$
and
$E_1$
and
![]() $E_3$
guarantee the existence of two primal petals for
$E_3$
guarantee the existence of two primal petals for
![]() $\mathcal {F}^{\mathrm {in}}$
and two primal petals for
$\mathcal {F}^{\mathrm {in}}$
and two primal petals for
![]() $\mathcal {F}^{\mathrm {out}}$
, with endpoints in the rectangles
$\mathcal {F}^{\mathrm {out}}$
, with endpoints in the rectangles
![]() $\mathrm {Rect}_.$
and
$\mathrm {Rect}_.$
and
![]() $\mathrm {Rect}_.'$
, respectively. Moreover,
$\mathrm {Rect}_.'$
, respectively. Moreover,
![]() $E_2$
and
$E_2$
and
![]() $E_4$
guarantee that these primal petals are separated by exactly one dual petal on each side.
$E_4$
guarantee that these primal petals are separated by exactly one dual petal on each side.
3.2 Boosting pair of boundary conditions
The goal of this section is to study how changes in boundary conditions impact crossing probabilities.
Definition 3.5. A boosting pair of boundary conditions for a flower domain
![]() $\mathcal {F}$
is a pair of boundary conditions
$\mathcal {F}$
is a pair of boundary conditions
![]() $(\xi ,\xi ')$
such that
$(\xi ,\xi ')$
such that
-
•
 $\xi $
and
$\xi $
and
 $\xi '$
are compatible with
$\xi '$
are compatible with
 $\mathcal {F}$
;
$\mathcal {F}$
; -
•
 $\xi \le \xi '$
;
$\xi \le \xi '$
; -
• there exist two primal petals of
 $\mathcal {F}$
that are wired together in
$\mathcal {F}$
that are wired together in
 $\xi '$
but not in
$\xi '$
but not in
 $\xi $
.
$\xi $
.
In a slight abuse of notation, we will henceforth also call a pair
![]() $(\zeta ,\zeta ')$
of boundary conditions on
$(\zeta ,\zeta ')$
of boundary conditions on
![]() $\mathcal {F}$
boosting if there exists a boosting pair
$\mathcal {F}$
boosting if there exists a boosting pair
![]() $(\xi ,\xi ')$
of boundary conditions on
$(\xi ,\xi ')$
of boundary conditions on
![]() $\mathcal {F}$
(in the sense of the definition above) such that
$\mathcal {F}$
(in the sense of the definition above) such that
![]() $\zeta \le \xi < \xi '\le \zeta '$
. In particular,
$\zeta \le \xi < \xi '\le \zeta '$
. In particular,
![]() $\zeta $
and
$\zeta $
and
![]() $\zeta '$
need not be compatible with
$\zeta '$
need not be compatible with
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Recall from Section 2.2 that
![]() $A_R$
is the event that there exists a circuit in
$A_R$
is the event that there exists a circuit in
![]() $\mathrm {Ann}(R,2R)$
surrounding
$\mathrm {Ann}(R,2R)$
surrounding
![]() $0$
. The object of this section is to prove the following theorem.
$0$
. The object of this section is to prove the following theorem.
Theorem 3.6. Fix
![]() $q\in (1,4]$
. For every
$q\in (1,4]$
. For every
![]() $\eta>0$
, there exists
$\eta>0$
, there exists
![]() $\delta =\delta (\eta ,q)>0$
such that the following holds.
$\delta =\delta (\eta ,q)>0$
such that the following holds.
-
(i) For every
 $p \in (0,1)$
, every
$p \in (0,1)$
, every
 $R \le L(p)$
, every
$R \le L(p)$
, every
 $\eta $
-well-separated inner flower domain
$\eta $
-well-separated inner flower domain
 $\mathcal {F}$
on
$\mathcal {F}$
on
 $\Lambda _{2R}$
, every boosting pair
$\Lambda _{2R}$
, every boosting pair
 $(\xi ,\xi ')$
of boundary conditions on
$(\xi ,\xi ')$
of boundary conditions on
 $\mathcal {F}$
and every
$\mathcal {F}$
and every
 $\eta $
-regular quad
$\eta $
-regular quad
 $(\mathcal {D},a,b,c,d)$
of size R, (3.7)
$(\mathcal {D},a,b,c,d)$
of size R, (3.7) $$ \begin{align} \phi^{\xi'}_{\mathcal{F}}[\mathcal{C}(\mathcal{D})] &\ge \phi^{\xi}_{\mathcal{F}}[\mathcal{C}(\mathcal{D})]+\delta , \end{align} $$
(3.8)
$$ \begin{align} \phi^{\xi'}_{\mathcal{F}}[\mathcal{C}(\mathcal{D})] &\ge \phi^{\xi}_{\mathcal{F}}[\mathcal{C}(\mathcal{D})]+\delta , \end{align} $$
(3.8) $$ \begin{align} \phi^{\xi'}_{\mathcal{F}}[A_{R}]&\ge \phi^{\xi}_{\mathcal{F}}[A_{R}]+\delta. \end{align} $$
$$ \begin{align} \phi^{\xi'}_{\mathcal{F}}[A_{R}]&\ge \phi^{\xi}_{\mathcal{F}}[A_{R}]+\delta. \end{align} $$
-
(ii) For every
 $p \in (0,1)$
, every
$p \in (0,1)$
, every
 $R \le L(p)$
, every
$R \le L(p)$
, every
 $\eta $
-well-separated outer flower domain
$\eta $
-well-separated outer flower domain
 $\mathcal {F}$
on
$\mathcal {F}$
on
 $\Lambda _R$
, every boosting pair
$\Lambda _R$
, every boosting pair
 $(\xi ,\xi ')$
of boundary conditions on
$(\xi ,\xi ')$
of boundary conditions on
 $\mathcal {F}$
and every
$\mathcal {F}$
and every
 $\eta $
-regular quad
$\eta $
-regular quad
 $(\mathcal {D},a,b,c,d)$
of size R translated in such a way that it is contained in
$(\mathcal {D},a,b,c,d)$
of size R translated in such a way that it is contained in
 $\mathrm { Ann}(2R, 4R)$
, (3.9)
$\mathrm { Ann}(2R, 4R)$
, (3.9) $$ \begin{align} \phi^{\xi'}_{\mathcal{F}}[\mathcal{C}(\mathcal{D})] &\ge \phi^{\xi}_{\mathcal{F}}[\mathcal{C}(\mathcal{D})]+\delta, \end{align} $$
(3.10)
$$ \begin{align} \phi^{\xi'}_{\mathcal{F}}[\mathcal{C}(\mathcal{D})] &\ge \phi^{\xi}_{\mathcal{F}}[\mathcal{C}(\mathcal{D})]+\delta, \end{align} $$
(3.10) $$ \begin{align} \phi^{\xi'}_{\mathcal{F}}[A_R]&\ge \phi^{\xi}_{\mathcal{F}}[A_R]+\delta. \end{align} $$
$$ \begin{align} \phi^{\xi'}_{\mathcal{F}}[A_R]&\ge \phi^{\xi}_{\mathcal{F}}[A_R]+\delta. \end{align} $$
In light of the RSW theory, the crossing probabilities
![]() $\phi ^{\xi }_{\mathcal {F}}[\mathcal {C}(\mathcal {D})]$
and
$\phi ^{\xi }_{\mathcal {F}}[\mathcal {C}(\mathcal {D})]$
and
![]() $\phi ^{\xi '}_{\mathcal {F}}[\mathcal {C}(\mathcal {D})]$
are bounded away from
$\phi ^{\xi '}_{\mathcal {F}}[\mathcal {C}(\mathcal {D})]$
are bounded away from
![]() $0$
and
$0$
and
![]() $1$
by constants depending only on
$1$
by constants depending only on
![]() $\eta $
. Above, we are concerned with the amount by which such crossing probabilities increase when the boundary conditions change from
$\eta $
. Above, we are concerned with the amount by which such crossing probabilities increase when the boundary conditions change from
![]() $\xi $
to
$\xi $
to
![]() $\xi '$
. Indeed, the theorem states that the increase is positive uniformly in the scale, the quad to be crossed and the boosting pair of boundary conditions. The rest of the section is dedicated to proving Theorem 3.6.
$\xi '$
. Indeed, the theorem states that the increase is positive uniformly in the scale, the quad to be crossed and the boosting pair of boundary conditions. The rest of the section is dedicated to proving Theorem 3.6.
The following elementary lemma is the cornerstone for the proof. For a quad
![]() $(\mathcal {D},a,b,c,d)$
, let
$(\mathcal {D},a,b,c,d)$
, let
![]() $\mathrm {mix}$
be the boundary conditions on
$\mathrm {mix}$
be the boundary conditions on
![]() $\mathcal {D}$
corresponding to the partitions containing
$\mathcal {D}$
corresponding to the partitions containing
![]() $(ab)$
,
$(ab)$
,
![]() $(cd)$
and singletons, and
$(cd)$
and singletons, and
![]() $\mathrm {mix}'$
be those containing
$\mathrm {mix}'$
be those containing
![]() $(ab)\cup (cd)$
and singletons.
$(ab)\cup (cd)$
and singletons.
Lemma 3.7. For every
![]() $q>1$
,
$q>1$
,
![]() $p \in (0,1)$
and every quad
$p \in (0,1)$
and every quad
![]() $(\mathcal {D},a,b,c,d)$
, we have
$(\mathcal {D},a,b,c,d)$
, we have
Notice that the ratio on the right-hand side above is always larger than
![]() $1$
, and considerably so when
$1$
, and considerably so when
![]() $\phi _{\mathcal {D}}^{\mathrm {mix}}[\mathcal {C}(\mathcal {D})]$
is far from
$\phi _{\mathcal {D}}^{\mathrm {mix}}[\mathcal {C}(\mathcal {D})]$
is far from
![]() $1$
.
$1$
.
Proof. Let
![]() $w(\omega ):=(\tfrac p{1-p})^{|\omega |}q^{k(\omega ^{\mathrm {mix}})}$
and
$w(\omega ):=(\tfrac p{1-p})^{|\omega |}q^{k(\omega ^{\mathrm {mix}})}$
and
![]() $w'(\omega ):=(\tfrac p{1-p})^{|\omega |}q^{k(\omega ^{\mathrm { mix'}})}$
, and observe that
$w'(\omega ):=(\tfrac p{1-p})^{|\omega |}q^{k(\omega ^{\mathrm { mix'}})}$
, and observe that
 $$ \begin{align*} w(\omega)=\begin{cases} w'(\omega)&\text{if }\omega\in\mathcal{C}(\mathcal{D}),\\ q w'(\omega)&\text{if }\omega\notin\mathcal{C}(\mathcal{D}).\end{cases} \end{align*} $$
$$ \begin{align*} w(\omega)=\begin{cases} w'(\omega)&\text{if }\omega\in\mathcal{C}(\mathcal{D}),\\ q w'(\omega)&\text{if }\omega\notin\mathcal{C}(\mathcal{D}).\end{cases} \end{align*} $$
Now, set
 $$ \begin{align*} Z[\mathcal{C}(\mathcal{D})]&:=\sum_{\omega\in\mathcal{C}(\mathcal{D})}w(\omega), \ \qquad Z[\mathcal{C}(\mathcal{D})^c]:=\sum_{\omega\notin\mathcal{C}(\mathcal{D})}w(\omega),\\ Z'[\mathcal{C}(\mathcal{D})]&:=\sum_{\omega\in\mathcal{C}(\mathcal{D})}w'(\omega),\qquad Z'[\mathcal{C}(\mathcal{D})^c]:=\sum_{\omega\notin\mathcal{C}(\mathcal{D})}w'(\omega). \end{align*} $$
$$ \begin{align*} Z[\mathcal{C}(\mathcal{D})]&:=\sum_{\omega\in\mathcal{C}(\mathcal{D})}w(\omega), \ \qquad Z[\mathcal{C}(\mathcal{D})^c]:=\sum_{\omega\notin\mathcal{C}(\mathcal{D})}w(\omega),\\ Z'[\mathcal{C}(\mathcal{D})]&:=\sum_{\omega\in\mathcal{C}(\mathcal{D})}w'(\omega),\qquad Z'[\mathcal{C}(\mathcal{D})^c]:=\sum_{\omega\notin\mathcal{C}(\mathcal{D})}w'(\omega). \end{align*} $$
Then
 $$ \begin{align*} {\phi^{\mathrm{mix'}}_{\mathcal{D}}[\mathcal{C}(\mathcal{D})]} =\frac{Z'[\mathcal{C}(\mathcal{D})]}{Z'[\mathcal{C}(\mathcal{D})]+Z'[\mathcal{C}(\mathcal{D})^c]} &=\frac{Z[\mathcal{C}(\mathcal{D})]}{Z[\mathcal{C}(\mathcal{D})]+\tfrac1qZ[\mathcal{C}(\mathcal{D})^c]}\\ &=\frac{\phi^{\mathrm{mix}}_{\mathcal{D}}[\mathcal{C}(\mathcal{D})]}{\phi^{\mathrm{mix}}_{\mathcal{D}}[\mathcal{C}(\mathcal{D})]+\tfrac1q(1-\phi^{\mathrm{mix}}_{\mathcal{D}}[\mathcal{C}(\mathcal{D})])}, \end{align*} $$
$$ \begin{align*} {\phi^{\mathrm{mix'}}_{\mathcal{D}}[\mathcal{C}(\mathcal{D})]} =\frac{Z'[\mathcal{C}(\mathcal{D})]}{Z'[\mathcal{C}(\mathcal{D})]+Z'[\mathcal{C}(\mathcal{D})^c]} &=\frac{Z[\mathcal{C}(\mathcal{D})]}{Z[\mathcal{C}(\mathcal{D})]+\tfrac1qZ[\mathcal{C}(\mathcal{D})^c]}\\ &=\frac{\phi^{\mathrm{mix}}_{\mathcal{D}}[\mathcal{C}(\mathcal{D})]}{\phi^{\mathrm{mix}}_{\mathcal{D}}[\mathcal{C}(\mathcal{D})]+\tfrac1q(1-\phi^{\mathrm{mix}}_{\mathcal{D}}[\mathcal{C}(\mathcal{D})])}, \end{align*} $$
which is the desired equality.
Proof of Theorem 3.6
We will focus on inner flower domains; the case of outer flower domains is very similar. Let
![]() $\mathcal {F}$
be an
$\mathcal {F}$
be an
![]() $\eta $
-well-separated inner flower domain on
$\eta $
-well-separated inner flower domain on
![]() $\Lambda _{2R}$
, and let
$\Lambda _{2R}$
, and let
![]() $(\xi ,\xi ')$
be a boosting pair of boundary conditions. Write
$(\xi ,\xi ')$
be a boosting pair of boundary conditions. Write
![]() $P_1,\dots , P_{2k}$
for the petals of
$P_1,\dots , P_{2k}$
for the petals of
![]() $\mathcal {F}$
in counterclockwise order, indexed in such a way that
$\mathcal {F}$
in counterclockwise order, indexed in such a way that
![]() $P_1$
is primal. Fix i and j odd such that
$P_1$
is primal. Fix i and j odd such that
![]() $P_i$
is wired to
$P_i$
is wired to
![]() $P_j$
in
$P_j$
in
![]() $\xi '$
but not in
$\xi '$
but not in
![]() $\xi $
. Below,
$\xi $
. Below,
![]() $c_0,\dots ,c_4$
will denote strictly positive constants depending only on
$c_0,\dots ,c_4$
will denote strictly positive constants depending only on
![]() $\eta $
.
$\eta $
.
We start by proving equation (3.7). We recommend taking a look at Figure 5. Fix an
![]() $\eta $
-regular quad
$\eta $
-regular quad
![]() $(\mathcal {D},a,b,c,d)$
of size R, and translate everything in such a way that the box
$(\mathcal {D},a,b,c,d)$
of size R, and translate everything in such a way that the box
![]() $\Lambda _{\eta R}$
is included in
$\Lambda _{\eta R}$
is included in
![]() $\mathcal {D}$
. Consider the event E that there exists a double four-petal flower domain
$\mathcal {D}$
. Consider the event E that there exists a double four-petal flower domain
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
between
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
between
![]() $\Lambda _{\eta R/4}$
and
$\Lambda _{\eta R/4}$
and
![]() $\Lambda _{\eta R/2}$
and that
$\Lambda _{\eta R/2}$
and that
-
•
 $P_1^{\mathrm {out}}$
and
$P_1^{\mathrm {out}}$
and
 $P_3^{\mathrm {out}}$
are connected to
$P_3^{\mathrm {out}}$
are connected to
 $P_i$
and
$P_i$
and
 $P_j$
in
$P_j$
in
 $\mathcal {F} \cap \mathcal {F}_{\mathrm { out}}$
, respectively;
$\mathcal {F} \cap \mathcal {F}_{\mathrm { out}}$
, respectively; -
•
 $P_1^{\mathrm {out}}$
and
$P_1^{\mathrm {out}}$
and
 $P_3^{\mathrm {out}}$
are not connected to each other or any other primal petal of
$P_3^{\mathrm {out}}$
are not connected to each other or any other primal petal of
 $\mathcal {F}$
in
$\mathcal {F}$
in
 $\mathcal {F} \cap \mathcal {F}_{\mathrm {out}}$
;
$\mathcal {F} \cap \mathcal {F}_{\mathrm {out}}$
; -
•
 $P_1^{\mathrm {out}}$
and
$P_1^{\mathrm {out}}$
and
 $P_3^{\mathrm {out}}$
are connected to the arcs
$P_3^{\mathrm {out}}$
are connected to the arcs
 $(ab)$
and
$(ab)$
and
 $(cd)$
in
$(cd)$
in
 $\mathcal {D} \cap \mathcal {F}_{\mathrm {out}}$
, respectively;
$\mathcal {D} \cap \mathcal {F}_{\mathrm {out}}$
, respectively; -
•
 $P_2^{\mathrm {out}}$
and
$P_2^{\mathrm {out}}$
and
 $P_4^{\mathrm {out}}$
are dually connected to the arcs
$P_4^{\mathrm {out}}$
are dually connected to the arcs
 $(bc)$
and
$(bc)$
and
 $(da)$
in
$(da)$
in
 $\mathcal {D} \cap \mathcal {F}_{\mathrm {out}}$
.
$\mathcal {D} \cap \mathcal {F}_{\mathrm {out}}$
.
The separation of petals together with equation (RSW) and Lemma 3.4 give

Figure 5 The domain
![]() $\mathcal D$
with the four marked points
$\mathcal D$
with the four marked points
![]() $a,b,c,d$
in grey, contained in the flower domain
$a,b,c,d$
in grey, contained in the flower domain
![]() $\mathcal {F}$
. In this case,
$\mathcal {F}$
. In this case,
![]() $P_3$
is assumed to be connected to
$P_3$
is assumed to be connected to
![]() $P_7$
in
$P_7$
in
![]() $\xi '$
but not in
$\xi '$
but not in
![]() $\xi $
. Red depicts the double flower domain
$\xi $
. Red depicts the double flower domain
![]() $(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
, which is revealed first. Then conditionally on the realisation of
$(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
, which is revealed first. Then conditionally on the realisation of
![]() $(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
, the conditions for the event E to occur are depicted in blue (note that the blue connections from
$(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
, the conditions for the event E to occur are depicted in blue (note that the blue connections from
![]() $\mathcal {F}_{\mathrm {out}}$
to
$\mathcal {F}_{\mathrm {out}}$
to
![]() $\mathcal {F}$
do not necessarily need to cross the arcs
$\mathcal {F}$
do not necessarily need to cross the arcs
![]() $(ab)$
and
$(ab)$
and
![]() $(cd)$
of
$(cd)$
of
![]() $\mathcal {D}$
). At the time
$\mathcal {D}$
). At the time
![]() $\tau $
of the procedure, the red and blue parts have been revealed and only the inside of
$\tau $
of the procedure, the red and blue parts have been revealed and only the inside of
![]() $\mathcal {F}_{\mathrm {in}}$
is unrevealed. Then the event
$\mathcal {F}_{\mathrm {in}}$
is unrevealed. Then the event
![]() $\mathcal {C}(\mathcal {D})$
depends on the connection inside
$\mathcal {C}(\mathcal {D})$
depends on the connection inside
![]() $\mathcal {F}_{\mathrm {in}}$
between its primal petals, which, with positive probability, are connected in
$\mathcal {F}_{\mathrm {in}}$
between its primal petals, which, with positive probability, are connected in
![]() $\omega '$
but not in
$\omega '$
but not in
![]() $\omega $
(see the green paths).
$\omega $
(see the green paths).
Consider the coupling
![]() $\mathbb P_{\mathbf {T}}$
between
$\mathbb P_{\mathbf {T}}$
between
![]() $\phi ^{\xi }_{\mathcal {F}}$
and
$\phi ^{\xi }_{\mathcal {F}}$
and
![]() $\phi ^{\xi '}_{\mathcal {F}}$
obtained by first exploring
$\phi ^{\xi '}_{\mathcal {F}}$
obtained by first exploring
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
in
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
in
![]() $\omega $
, then revealing all the edges in
$\omega $
, then revealing all the edges in
![]() $\mathcal {F}_{\mathrm {out}}\cap \mathcal {F}$
, and then revealing all those inside
$\mathcal {F}_{\mathrm {out}}\cap \mathcal {F}$
, and then revealing all those inside
![]() $\mathcal {F}_{\mathrm {in}}$
. Let
$\mathcal {F}_{\mathrm {in}}$
. Let
![]() $\tau $
be the stopping time corresponding to the end of the second step of this exploration.
$\tau $
be the stopping time corresponding to the end of the second step of this exploration.
Suppose that
![]() $\omega _{[\tau ]}\in E$
. Then
$\omega _{[\tau ]}\in E$
. Then
![]() $\mathcal {D}$
is crossed in
$\mathcal {D}$
is crossed in
![]() $\omega $
if and only if the petals
$\omega $
if and only if the petals
![]() $P_1^{\mathrm {in}}$
and
$P_1^{\mathrm {in}}$
and
![]() $P_3^{\mathrm {in}}$
are connected inside
$P_3^{\mathrm {in}}$
are connected inside
![]() $\mathcal {F}_{\mathrm {in}}$
. Write
$\mathcal {F}_{\mathrm {in}}$
. Write
![]() $\zeta < \zeta '$
for the two boundary conditions on
$\zeta < \zeta '$
for the two boundary conditions on
![]() $\mathcal {F}_{\mathrm {in}}$
, which are coherent with the flower domain structure (with
$\mathcal {F}_{\mathrm {in}}$
, which are coherent with the flower domain structure (with
![]() $P_1^{\mathrm {in}}$
wired to
$P_1^{\mathrm {in}}$
wired to
![]() $P_3^{\mathrm {in}}$
in
$P_3^{\mathrm {in}}$
in
![]() $\zeta '$
but not in
$\zeta '$
but not in
![]() $\zeta $
). Then the boundary conditions induced by
$\zeta $
). Then the boundary conditions induced by
![]() $\omega _{[\tau ]}$
and
$\omega _{[\tau ]}$
and
![]() $\xi $
on
$\xi $
on
![]() $\mathcal {F}_{\mathrm {in}}$
are
$\mathcal {F}_{\mathrm {in}}$
are
![]() $\zeta $
. Moreover, since
$\zeta $
. Moreover, since
![]() $\omega ' \geq \omega $
, and due to the wiring of
$\omega ' \geq \omega $
, and due to the wiring of
![]() $P_i$
and
$P_i$
and
![]() $P_j$
in
$P_j$
in
![]() $\xi '$
,
$\xi '$
,
![]() $\omega _{[\tau ]}'$
induces the boundary conditions on
$\omega _{[\tau ]}'$
induces the boundary conditions on
![]() $\mathcal {F}_{\mathrm {in}}$
that dominate
$\mathcal {F}_{\mathrm {in}}$
that dominate
![]() $\zeta '$
. Thus,
$\zeta '$
. Thus,
 $$ \begin{align*} \phi^{\xi'}_{\mathcal{F}}[\mathcal{C}(\mathcal{D})]-\phi^{\xi}_{\mathcal{F}}[\mathcal{C}(\mathcal{D})] &=\mathbb{P}_{\mathbf{T}}[\omega'\in\mathcal{C}(\mathcal{D}),\,\omega\notin\mathcal{C}(\mathcal{D})]\\ &\geq \mathbb{E}_{\mathbf{T}}\Big[\big( \phi_{\mathcal{F}_{\mathrm{in}}}^{\zeta'}[P_1^{\mathrm{in}} \longleftrightarrow P_3^{\mathrm{ in}}]-\phi_{\mathcal{F}_{\mathrm{in}}}^{\zeta}[P_1^{\mathrm{in}} \longleftrightarrow P_3^{\mathrm{in}}]\big) \mathbf 1_{\omega_{[\tau]}\in E}\Big]\\ &\ge c_1 \mathbb{P}_{\mathbf{T}}[\omega_{[\tau]}\in E]\ge c_1c_0>0, \end{align*} $$
$$ \begin{align*} \phi^{\xi'}_{\mathcal{F}}[\mathcal{C}(\mathcal{D})]-\phi^{\xi}_{\mathcal{F}}[\mathcal{C}(\mathcal{D})] &=\mathbb{P}_{\mathbf{T}}[\omega'\in\mathcal{C}(\mathcal{D}),\,\omega\notin\mathcal{C}(\mathcal{D})]\\ &\geq \mathbb{E}_{\mathbf{T}}\Big[\big( \phi_{\mathcal{F}_{\mathrm{in}}}^{\zeta'}[P_1^{\mathrm{in}} \longleftrightarrow P_3^{\mathrm{ in}}]-\phi_{\mathcal{F}_{\mathrm{in}}}^{\zeta}[P_1^{\mathrm{in}} \longleftrightarrow P_3^{\mathrm{in}}]\big) \mathbf 1_{\omega_{[\tau]}\in E}\Big]\\ &\ge c_1 \mathbb{P}_{\mathbf{T}}[\omega_{[\tau]}\in E]\ge c_1c_0>0, \end{align*} $$
where
![]() $c_1>0$
is given by Lemma 3.7 and equation (RSW). This concludes the proof of equation (3.7).
$c_1>0$
is given by Lemma 3.7 and equation (RSW). This concludes the proof of equation (3.7).
We turn to equation (3.8) and refer the reader to Figure 6. Write z for the point
![]() $(3R/2, 0)$
. Consider the coupling
$(3R/2, 0)$
. Consider the coupling
![]() $\mathbb {P}_{\mathbf T}$
between
$\mathbb {P}_{\mathbf T}$
between
![]() $\phi ^{\xi }_{\mathcal {F}}$
and
$\phi ^{\xi }_{\mathcal {F}}$
and
![]() $\phi ^{\xi '}_{\mathcal {F}}$
obtained by first exploring the double flower domain
$\phi ^{\xi '}_{\mathcal {F}}$
obtained by first exploring the double flower domain
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
in
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
in
![]() $\omega $
between
$\omega $
between
![]() $\Lambda _{R/16}(z)$
and
$\Lambda _{R/16}(z)$
and
![]() $\Lambda _{R/8}(z)$
, then the configurations inside
$\Lambda _{R/8}(z)$
, then the configurations inside
![]() $\mathcal {F}_{\mathrm {in}}$
and finally those in
$\mathcal {F}_{\mathrm {in}}$
and finally those in
![]() $\mathcal {F}_{\mathrm {out}}$
. If no double flower domain exists, reveal all remaining edges in arbitrary order. Write
$\mathcal {F}_{\mathrm {out}}$
. If no double flower domain exists, reveal all remaining edges in arbitrary order. Write
![]() $\tau _1$
for the stopping time marking the end of the exploration of
$\tau _1$
for the stopping time marking the end of the exploration of
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
and
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
and
![]() $\tau _2$
for the stopping time after further exploring
$\tau _2$
for the stopping time after further exploring
![]() $\mathcal {F}_{\mathrm {in}}$
.
$\mathcal {F}_{\mathrm {in}}$
.

Figure 6 A depiction of the annulus configuration in the proof of equation (3.8). In black, the flower domain
![]() $\mathcal {F}$
. The red part corresponds to the double flower domain
$\mathcal {F}$
. The red part corresponds to the double flower domain
![]() $(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
revealed at time
$(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
revealed at time
![]() $\tau _1$
. The blue part corresponds to what is revealed at time
$\tau _1$
. The blue part corresponds to what is revealed at time
![]() $\tau _2$
: that is, a connection in
$\tau _2$
: that is, a connection in
![]() $\omega '$
between two wired petals of
$\omega '$
between two wired petals of
![]() $\mathcal {F}_{\mathrm {in}}$
together with a dual connection in
$\mathcal {F}_{\mathrm {in}}$
together with a dual connection in
![]() $\omega ^*$
between two free petals. Then after time
$\omega ^*$
between two free petals. Then after time
![]() $\tau _2$
, we construct the event H (in green).
$\tau _2$
, we construct the event H (in green).
Condition on a pair of configurations
![]() $(\omega _{[\tau _1]}, \omega ^{\prime }_{[\tau _1]})$
such that the double flower domain exists, and write
$(\omega _{[\tau _1]}, \omega ^{\prime }_{[\tau _1]})$
such that the double flower domain exists, and write
![]() $\zeta < \zeta '$
for the two boundary conditions on
$\zeta < \zeta '$
for the two boundary conditions on
![]() $\mathcal {F}_{\mathrm {in}}$
that are coherent with the flower domain structure. The configuration
$\mathcal {F}_{\mathrm {in}}$
that are coherent with the flower domain structure. The configuration
![]() $\omega $
inside
$\omega $
inside
![]() $\mathcal {F}_{\mathrm {in}}$
is sampled according to a convex combination of
$\mathcal {F}_{\mathrm {in}}$
is sampled according to a convex combination of
![]() $\phi _{\mathcal {F}_{\mathrm {in}}}^{\zeta }$
and
$\phi _{\mathcal {F}_{\mathrm {in}}}^{\zeta }$
and
![]() $\phi _{\mathcal {F}_{\mathrm {in}}}^{\zeta '}$
. Indeed, the coefficient
$\phi _{\mathcal {F}_{\mathrm {in}}}^{\zeta '}$
. Indeed, the coefficient
![]() $\lambda $
for the latter measure is given by the probability that
$\lambda $
for the latter measure is given by the probability that
![]() $P_1^{\mathrm {out}}$
is connected to
$P_1^{\mathrm {out}}$
is connected to
![]() $P_3^{\mathrm {out}}$
in
$P_3^{\mathrm {out}}$
in
![]() $\mathcal {F}_{\mathrm {out}}$
, including via the boundary conditions
$\mathcal {F}_{\mathrm {out}}$
, including via the boundary conditions
![]() $\xi $
. Similarly, the law of
$\xi $
. Similarly, the law of
![]() $\omega '$
inside
$\omega '$
inside
![]() $\mathcal {F}_{\mathrm {in}}$
dominates a convex combination of
$\mathcal {F}_{\mathrm {in}}$
dominates a convex combination of
![]() $\phi _{\mathcal {F}_{\mathrm { in}}}^{\zeta }$
and
$\phi _{\mathcal {F}_{\mathrm { in}}}^{\zeta }$
and
![]() $\phi _{\mathcal {F}_{\mathrm {in}}}^{\zeta '}$
, with the coefficient
$\phi _{\mathcal {F}_{\mathrm {in}}}^{\zeta '}$
, with the coefficient
![]() $\lambda '$
for the latter given by the probability that
$\lambda '$
for the latter given by the probability that
![]() $P_1^{\mathrm {out}}$
is connected to
$P_1^{\mathrm {out}}$
is connected to
![]() $P_3^{\mathrm {out}}$
in
$P_3^{\mathrm {out}}$
in
![]() $\mathcal {F}_{\mathrm {out}}$
, including via the boundary conditions
$\mathcal {F}_{\mathrm {out}}$
, including via the boundary conditions
![]() $\xi '$
.
$\xi '$
.
By an argument similar to the first point of the proof involving the event E, it may be shown that there exists a uniformly positive probability
![]() $c_2> 0$
for
$c_2> 0$
for
![]() $P_1^{\mathrm {out}}$
and
$P_1^{\mathrm {out}}$
and
![]() $P_3^{\mathrm {out}}$
to be connected in
$P_3^{\mathrm {out}}$
to be connected in
![]() $\mathcal {F}_{\mathrm {out}}$
to
$\mathcal {F}_{\mathrm {out}}$
to
![]() $P_i$
and
$P_i$
and
![]() $P_j$
, respectively, but not to each other. Thus,
$P_j$
, respectively, but not to each other. Thus,
![]() $\lambda ' \geq \lambda + c_2$
. Applying Lemma 3.7 and equation (RSW), we find
$\lambda ' \geq \lambda + c_2$
. Applying Lemma 3.7 and equation (RSW), we find

for some
![]() $c_3>0$
.
$c_3>0$
.
Write F for the event that
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
exists and that
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
exists and that
![]() $P_1^{\mathrm {in}}$
is connected to
$P_1^{\mathrm {in}}$
is connected to
![]() $P_3^{\mathrm {in}}$
inside
$P_3^{\mathrm {in}}$
inside
![]() $\mathcal {F}_{\mathrm {in}}$
in
$\mathcal {F}_{\mathrm {in}}$
in
![]() $\omega '$
but not in
$\omega '$
but not in
![]() $\omega $
. This event is measurable in terms of the configurations at the stopping time
$\omega $
. This event is measurable in terms of the configurations at the stopping time
![]() $\tau _2$
. Finally, write H for the event that in
$\tau _2$
. Finally, write H for the event that in
![]() $\omega $
,
$\omega $
,
-
• in
 $\mathcal {F}_{\mathrm {out}} \cap \mathrm {Ann}(R,2R)$
,
$\mathcal {F}_{\mathrm {out}} \cap \mathrm {Ann}(R,2R)$
,
 $P_1^{\mathrm {out}}$
is connected to
$P_1^{\mathrm {out}}$
is connected to
 $P_3^{\mathrm {out}}$
by a primal path,
$P_3^{\mathrm {out}}$
by a primal path, -
•
 $P_2^{\mathrm {out}}$
is connected to
$P_2^{\mathrm {out}}$
is connected to
 $\Lambda _{R}$
by a dual path and
$\Lambda _{R}$
by a dual path and -
•
 $P_4^{\mathrm {out}}$
is connected to
$P_4^{\mathrm {out}}$
is connected to
 $\Lambda _{2R}^c$
by a dual path.
$\Lambda _{2R}^c$
by a dual path.
Notice that if H occurs, the primal path connecting
![]() $P_1^{\mathrm {out}}$
to
$P_1^{\mathrm {out}}$
to
![]() $P_3^{\mathrm {out}}$
needs to ‘wind around’
$P_3^{\mathrm {out}}$
needs to ‘wind around’
![]() $\Lambda _{R}$
. Thus, H may be understood as the connection between
$\Lambda _{R}$
. Thus, H may be understood as the connection between
![]() $ P_1^{\mathrm {in}}$
and
$ P_1^{\mathrm {in}}$
and
![]() $P_3^{\mathrm {in}}$
in
$P_3^{\mathrm {in}}$
in
![]() $\mathcal {F}_{\mathrm {in}}$
being ‘pivotal’ for
$\mathcal {F}_{\mathrm {in}}$
being ‘pivotal’ for
![]() $A_{R}$
(for
$A_{R}$
(for
![]() $\omega $
). By equation (RSW),
$\omega $
). By equation (RSW),
for some
![]() $c_4> 0$
. Moreover, when F and H occur, then
$c_4> 0$
. Moreover, when F and H occur, then
![]() $A_{R}$
occurs for
$A_{R}$
occurs for
![]() $\omega '$
but not for
$\omega '$
but not for
![]() $\omega $
. Thus,
$\omega $
. Thus,
which is the desired conclusion.
Remark 3.8. The proof of equation (3.8) may appear contradictory, as we are first arguing that
![]() $P_1^{\mathrm {out}}$
and
$P_1^{\mathrm {out}}$
and
![]() $P_3^{\mathrm {out}}$
may appear wired in
$P_3^{\mathrm {out}}$
may appear wired in
![]() $\omega '$
but not in
$\omega '$
but not in
![]() $\omega $
and then we focus on the event
$\omega $
and then we focus on the event
![]() $\omega \in H$
, which ensures that
$\omega \in H$
, which ensures that
![]() $P_1^{\mathrm {out}}$
and
$P_1^{\mathrm {out}}$
and
![]() $P_3^{\mathrm {out}}$
are connected in both
$P_3^{\mathrm {out}}$
are connected in both
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
. The reader should keep in mind that the configurations
$\omega '$
. The reader should keep in mind that the configurations
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
in
$\omega '$
in
![]() $\mathcal {F}_{\mathrm {in}}$
are sampled before sampling the configurations in
$\mathcal {F}_{\mathrm {in}}$
are sampled before sampling the configurations in
![]() $\mathcal {F}_{\mathrm {out}}$
, and their laws are obtained by averaging over the possible configurations in
$\mathcal {F}_{\mathrm {out}}$
, and their laws are obtained by averaging over the possible configurations in
![]() $\mathcal {F}_{\mathrm {out}}$
.
$\mathcal {F}_{\mathrm {out}}$
.
Alternatively, one may imagine a coupling where
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
is revealed first, then the configurations in
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
is revealed first, then the configurations in
![]() $\mathcal {F}_{\mathrm {out}}$
are revealed, then those in
$\mathcal {F}_{\mathrm {out}}$
are revealed, then those in
![]() $\mathcal {F}_{\mathrm {in}}$
are revealed, and finally the configurations in
$\mathcal {F}_{\mathrm {in}}$
are revealed, and finally the configurations in
![]() $\mathcal {F}_{\mathrm {out}}$
are resampled. In this context, we are investigating the situation where in the first sampling of the configurations in
$\mathcal {F}_{\mathrm {out}}$
are resampled. In this context, we are investigating the situation where in the first sampling of the configurations in
![]() $\mathcal {F}_{\mathrm {out}}$
,
$\mathcal {F}_{\mathrm {out}}$
,
![]() $P_1^{\mathrm {out}}$
and
$P_1^{\mathrm {out}}$
and
![]() $P_3^{\mathrm {out}}$
are connected to
$P_3^{\mathrm {out}}$
are connected to
![]() $P_i$
and
$P_i$
and
![]() $P_j$
, respectively, but not to each other, then, in the sampling inside
$P_j$
, respectively, but not to each other, then, in the sampling inside
![]() $\mathcal {F}_{\mathrm {in}}$
,
$\mathcal {F}_{\mathrm {in}}$
,
![]() $P_1^{\mathrm {in}}$
and
$P_1^{\mathrm {in}}$
and
![]() $P_3^{\mathrm {in}}$
are connected in
$P_3^{\mathrm {in}}$
are connected in
![]() $\omega '$
but not in
$\omega '$
but not in
![]() $\omega $
, and finally, in the second sampling in
$\omega $
, and finally, in the second sampling in
![]() $\mathcal {F}_{\mathrm {out}}$
, H occurs for
$\mathcal {F}_{\mathrm {out}}$
, H occurs for
![]() $\omega $
.
$\omega $
.
3.3 Crossing quads produce boosting pairs
This section is concerned with the following result, which roughly states that conditioning on the existence of the crossing of a quad has the same effect as a boosting pair of boundary conditions.
Proposition 3.9. For any
![]() $\eta> 0$
, there exists a constant
$\eta> 0$
, there exists a constant
![]() $c = c(\eta ,q)> 0$
such that the following holds. Fix p, and let
$c = c(\eta ,q)> 0$
such that the following holds. Fix p, and let
![]() $(\mathcal {D},a,b,c,d)$
be an
$(\mathcal {D},a,b,c,d)$
be an
![]() $\eta $
-regular discrete quad at scale
$\eta $
-regular discrete quad at scale
![]() $R\le L(p)$
. Then there exists a coupling via decision trees
$R\le L(p)$
. Then there exists a coupling via decision trees
![]() $\mathbb {P}$
of
$\mathbb {P}$
of
![]() $\phi $
and
$\phi $
and
![]() $\phi [\cdot \,|\mathcal {C}(\mathcal {D})]$
and a stopping time
$\phi [\cdot \,|\mathcal {C}(\mathcal {D})]$
and a stopping time
![]() $\tau $
such that when
$\tau $
such that when
![]() $\tau < \infty $
,
$\tau < \infty $
,
![]() $\mathcal {F}_{\tau } = \mathbb {Z}^2\smallsetminus e_{[\tau ]}$
is a
$\mathcal {F}_{\tau } = \mathbb {Z}^2\smallsetminus e_{[\tau ]}$
is a
![]() $1/2$
-well-separated outer flower domain on
$1/2$
-well-separated outer flower domain on
![]() $\Lambda _{2R}$
(with
$\Lambda _{2R}$
(with
![]() $\Lambda _{3R/2} \subset \mathcal {F}_{\tau }^c$
), and the boundary conditions induced by
$\Lambda _{3R/2} \subset \mathcal {F}_{\tau }^c$
), and the boundary conditions induced by
![]() $\omega ^{\prime }_{[\tau ]}$
on
$\omega ^{\prime }_{[\tau ]}$
on
![]() $\mathcal {F}_{\tau }$
are a boost of those induced by
$\mathcal {F}_{\tau }$
are a boost of those induced by
![]() $\omega _{[\tau ]}$
. Finally,
$\omega _{[\tau ]}$
. Finally,
Furthermore, the same is true when
![]() $\mathcal {C}(\mathcal {D})$
is replaced by
$\mathcal {C}(\mathcal {D})$
is replaced by
![]() $A_{R/2}$
.
$A_{R/2}$
.
The proof of Proposition 3.9 is based on the following lemma, which allows us to ‘lengthen’ crossings at a small cost. For an
![]() $\eta $
-regular discrete quad
$\eta $
-regular discrete quad
![]() $(\mathcal {D},a,b,c,d)$
at some scale R and for some
$(\mathcal {D},a,b,c,d)$
at some scale R and for some
![]() $m \le \eta R/4$
, define two modified quads
$m \le \eta R/4$
, define two modified quads
![]() $(\mathcal {D}^+,a^+,b^+,c^+,d^+)$
and
$(\mathcal {D}^+,a^+,b^+,c^+,d^+)$
and
![]() $(\mathcal {D}^-,a^-,b^-,c^-,d^-)$
as follows (see Figure 7 for an illustration). The domains
$(\mathcal {D}^-,a^-,b^-,c^-,d^-)$
as follows (see Figure 7 for an illustration). The domains
![]() $\mathcal {D}^+$
and
$\mathcal {D}^+$
and
![]() $\mathcal {D}^-$
are formed by the union of
$\mathcal {D}^-$
are formed by the union of
![]() $\mathcal {D}$
with the set of edges of
$\mathcal {D}$
with the set of edges of
![]() $\mathbb {Z}^2 \smallsetminus \mathcal {D}$
that are at a
$\mathbb {Z}^2 \smallsetminus \mathcal {D}$
that are at a
![]() $\ell ^{\infty }$
distance at most m from the arcs
$\ell ^{\infty }$
distance at most m from the arcs
![]() $(ab)$
and
$(ab)$
and
![]() $(cd)$
(respectively
$(cd)$
(respectively
![]() $(bc)$
and
$(bc)$
and
![]() $(da)$
), but at least distance m from a, b, c and d. The point
$(da)$
), but at least distance m from a, b, c and d. The point
![]() $a^+$
is the first point of
$a^+$
is the first point of
![]() $\partial \mathcal {D}^+$
in counterclockwise order after a that is at a distance m from
$\partial \mathcal {D}^+$
in counterclockwise order after a that is at a distance m from
![]() $\partial \mathcal {D}$
; the point
$\partial \mathcal {D}$
; the point
![]() $b^+$
is the last such point before b. The points
$b^+$
is the last such point before b. The points
![]() $c^+$
and
$c^+$
and
![]() $d^+$
are defined similarly in terms of c and d, respectively. A similar definition applies to
$d^+$
are defined similarly in terms of c and d, respectively. A similar definition applies to
![]() $a^-$
,
$a^-$
,
![]() $b^-$
,
$b^-$
,
![]() $c^-$
and
$c^-$
and
![]() $d^-$
.
$d^-$
.

Figure 7
Left: For a fixed lowest crossing
![]() $\Gamma $
of
$\Gamma $
of
![]() $\mathcal {D}$
with the endpoint x at a distance at least
$\mathcal {D}$
with the endpoint x at a distance at least
![]() $\sqrt { mR}$
from a, one may identify order
$\sqrt { mR}$
from a, one may identify order
![]() $\log R/m$
disjoint quads – such as the pink one – which, if crossed, create a connection between
$\log R/m$
disjoint quads – such as the pink one – which, if crossed, create a connection between
![]() $\Gamma $
and
$\Gamma $
and
![]() $(a^+b^+)$
. Each such quad has a uniformly positive probability of being crossed, independently of the other quads. Middle: At the time
$(a^+b^+)$
. Each such quad has a uniformly positive probability of being crossed, independently of the other quads. Middle: At the time
![]() $\tau _2 < \infty $
, when
$\tau _2 < \infty $
, when
![]() $\Gamma ^+$
and
$\Gamma ^+$
and
![]() $\Gamma ^-$
have been revealed, the region of
$\Gamma ^-$
have been revealed, the region of
![]() $\mathcal {D}^+\smallsetminus \mathcal {D}$
above
$\mathcal {D}^+\smallsetminus \mathcal {D}$
above
![]() $\Gamma ^+$
and that of
$\Gamma ^+$
and that of
![]() $\mathcal {D}^-\smallsetminus \mathcal {D}$
left of
$\mathcal {D}^-\smallsetminus \mathcal {D}$
left of
![]() $\Gamma ^-$
are unrevealed. Right: The unrevealed regions may be used to connect
$\Gamma ^-$
are unrevealed. Right: The unrevealed regions may be used to connect
![]() $\Gamma ^+$
to the primal petals of
$\Gamma ^+$
to the primal petals of
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\omega $
and
$\omega $
and
![]() $\Gamma ^-$
to the dual petals of
$\Gamma ^-$
to the dual petals of
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\omega ^*$
. This ensures that the boundary conditions induced by
$\omega ^*$
. This ensures that the boundary conditions induced by
![]() $\omega ^{\prime }_{[\tau ]}$
on
$\omega ^{\prime }_{[\tau ]}$
on
![]() $\mathcal {F}$
are a boost of those induced by
$\mathcal {F}$
are a boost of those induced by
![]() $\omega _{[\tau ]}$
.
$\omega _{[\tau ]}$
.
Remark 3.10. The choice of
![]() $m\le \eta R/4$
and the fact that
$m\le \eta R/4$
and the fact that
![]() $\mathcal {D}$
is
$\mathcal {D}$
is
![]() $\eta $
-regular guarantee that
$\eta $
-regular guarantee that
![]() $\mathcal {D}^+\smallsetminus \mathcal {D}$
and
$\mathcal {D}^+\smallsetminus \mathcal {D}$
and
![]() $\mathcal {D}^-\smallsetminus \mathcal {D}$
are at a distance at least
$\mathcal {D}^-\smallsetminus \mathcal {D}$
are at a distance at least
![]() $\eta R/4$
from each other and are each made of two separate connected components. In particular, the complement of
$\eta R/4$
from each other and are each made of two separate connected components. In particular, the complement of
![]() $\mathcal {D}^+\cup \mathcal {D}^-$
is connected.
$\mathcal {D}^+\cup \mathcal {D}^-$
is connected.
Notice that
![]() $(\mathcal {D}^+,a^+,b^+,c^+,d^+)$
and
$(\mathcal {D}^+,a^+,b^+,c^+,d^+)$
and
![]() $(\mathcal {D}^-,a^-,b^-,c^-,d^-)$
are both discrete quads and that
$(\mathcal {D}^-,a^-,b^-,c^-,d^-)$
are both discrete quads and that
While the lemma below is valid for all
![]() $m < \eta R/4$
, we will eventually use it for
$m < \eta R/4$
, we will eventually use it for
![]() $m = c_0 R$
for some small constant
$m = c_0 R$
for some small constant
![]() $c_0$
. As such,
$c_0$
. As such,
![]() $\mathcal {D}^+$
and
$\mathcal {D}^+$
and
![]() $\mathcal {D}^-$
are roughlyFootnote
2
$\mathcal {D}^-$
are roughlyFootnote
2
![]() $\eta '$
-regular at scale R for
$\eta '$
-regular at scale R for
![]() $\eta '= c_0 \eta \ll \eta $
.
$\eta '= c_0 \eta \ll \eta $
.
Lemma 3.11. For any
![]() $\eta> 0$
, there exist
$\eta> 0$
, there exist
![]() $C=C(\eta )>0$
,
$C=C(\eta )>0$
,
![]() $\varepsilon =\varepsilon (\eta )> 0$
such that the following holds. For any
$\varepsilon =\varepsilon (\eta )> 0$
such that the following holds. For any
![]() $p \in (0,1)$
,
$p \in (0,1)$
,
![]() $R \le L(p)$
,
$R \le L(p)$
,
![]() $m < \eta R/4$
and any
$m < \eta R/4$
and any
![]() $\eta $
-regular discrete quad
$\eta $
-regular discrete quad
![]() $(\mathcal {D},a,b,c,d)$
at scale
$(\mathcal {D},a,b,c,d)$
at scale
![]() $R \le L(p)$
,
$R \le L(p)$
,
Proof. We will focus on the first inequality; the second one is the same inequality applied to the dual model. Since
![]() $\mathcal {C}(\mathcal {D}^+) \subset \mathcal {C}(\mathcal {D})$
, we are searching for an upper bound on
$\mathcal {C}(\mathcal {D}^+) \subset \mathcal {C}(\mathcal {D})$
, we are searching for an upper bound on
![]() $\phi [\mathcal {C}(\mathcal {D}) \smallsetminus \mathcal {C}(\mathcal {D}^+)]$
. When
$\phi [\mathcal {C}(\mathcal {D}) \smallsetminus \mathcal {C}(\mathcal {D}^+)]$
. When
![]() $\mathcal {C}(\mathcal {D})$
occurs, let
$\mathcal {C}(\mathcal {D})$
occurs, let
![]() $\Gamma $
be the ‘lowest’ crossing of
$\Gamma $
be the ‘lowest’ crossing of
![]() $\mathcal {D}$
: that is, the open path closest to the arc
$\mathcal {D}$
: that is, the open path closest to the arc
![]() $(bc)$
with endpoints
$(bc)$
with endpoints
![]() $x \in (ab)$
and
$x \in (ab)$
and
![]() $y \in (cd)$
. Write
$y \in (cd)$
. Write
![]() $\mathsf {Under}(\Gamma )$
for the set of edges of
$\mathsf {Under}(\Gamma )$
for the set of edges of
![]() $\mathcal {D}$
between
$\mathcal {D}$
between
![]() $\Gamma $
and
$\Gamma $
and
![]() $(bc)$
.
$(bc)$
.
If
![]() $\mathcal {C}(\mathcal {D}) \smallsetminus \mathcal {C}(\mathcal {D}^+)$
occurs, then at least one of the following four events needs to occur:
$\mathcal {C}(\mathcal {D}) \smallsetminus \mathcal {C}(\mathcal {D}^+)$
occurs, then at least one of the following four events needs to occur:
-
(i) x is at a distance at most
 $\sqrt {mR}$
from a;
$\sqrt {mR}$
from a; -
(ii) x is at a distance at least
 $\sqrt {mR}$
from a, but
$\sqrt {mR}$
from a, but
 $\Gamma $
is not connected to
$\Gamma $
is not connected to
 $(a^+b^+)$
in
$(a^+b^+)$
in
 $\mathcal {D}^+$
;
$\mathcal {D}^+$
; -
(iii) y is at a distance at most
 $\sqrt {mR}$
from d;
$\sqrt {mR}$
from d; -
(iv) y is at a distance at least
 $\sqrt {mR}$
from d, but
$\sqrt {mR}$
from d, but
 $\Gamma $
is not connected to
$\Gamma $
is not connected to
 $(c^+d^+)$
in
$(c^+d^+)$
in
 $\mathcal {D}^+$
.
$\mathcal {D}^+$
.
Next, we bound the probability of each of the four events described above.
If the event in (i) occurs, there exists a primal arm, namely
![]() $\Gamma $
, contained in
$\Gamma $
, contained in
![]() $\mathcal {D}$
from
$\mathcal {D}$
from
![]() $\Lambda _{\sqrt {mR}}(a)$
to distance
$\Lambda _{\sqrt {mR}}(a)$
to distance
![]() $\eta R$
; and therefore, using equation (2.2), we get
$\eta R$
; and therefore, using equation (2.2), we get
To control the probability of the event (ii), we claim that there exist constants
![]() $C, \varepsilon>0$
such that
$C, \varepsilon>0$
such that
Indeed, by considering the intersections of
![]() $\mathcal {D}^+$
with the dyadic annuli contained between
$\mathcal {D}^+$
with the dyadic annuli contained between
![]() $\Lambda _{m}(x)$
and
$\Lambda _{m}(x)$
and
![]() $\Lambda _{\sqrt {m R}}(x)$
, one may create order
$\Lambda _{\sqrt {m R}}(x)$
, one may create order
![]() $\log R/m$
disjoint quads such that when any one of them is crossed by a primal path, that induces a connection between
$\log R/m$
disjoint quads such that when any one of them is crossed by a primal path, that induces a connection between
![]() $\Gamma $
and
$\Gamma $
and
![]() $(d^+a^+)$
in
$(d^+a^+)$
in
![]() $\mathcal {D}^+$
. Then equation (RSW) applies in these quads as the conditioning above only induces negative information at a macroscopic distance from the quads; see Figure 7 (left diagram). Therefore, that none of the quads is primally crossed occurs with a probability that is exponential in the number of quads or equivalently polynomial in
$\mathcal {D}^+$
. Then equation (RSW) applies in these quads as the conditioning above only induces negative information at a macroscopic distance from the quads; see Figure 7 (left diagram). Therefore, that none of the quads is primally crossed occurs with a probability that is exponential in the number of quads or equivalently polynomial in
![]() $m/R$
.
$m/R$
.
The bounds above also apply to the events in (iii) and (iv). When combined using a union bound, we find
Changing the value of C gives the proof.
Remark 3.12. Alternatively, one may use bounds on the probability of the three-arm event in the half-plane to prove the above. We prefer the strategy above as it adapts easily to fractal quads of bounded extremal distance; the cases (i) and (ii) (and (iii) and (iv), respectively) should then be distinguished using extremal distance rather than the geometric average of m and R. Above, the quad
![]() $\mathcal {D}$
is assumed to be
$\mathcal {D}$
is assumed to be
![]() $\eta $
-regular simply for convenience.
$\eta $
-regular simply for convenience.
Proof of Proposition 3.9
Fix
![]() $\eta> 0$
, and let
$\eta> 0$
, and let
![]() $C=C(\eta )$
and
$C=C(\eta )$
and
![]() $\varepsilon =\varepsilon (\eta )$
be the constants given by Lemma 3.11 for this value of
$\varepsilon =\varepsilon (\eta )$
be the constants given by Lemma 3.11 for this value of
![]() $\eta $
. Below,
$\eta $
. Below,
![]() $c_0,\dots ,c_3$
denote strictly positive constants depending only on
$c_0,\dots ,c_3$
denote strictly positive constants depending only on
![]() $\eta $
.
$\eta $
.
For p and R with
![]() $R \le L(p)$
, let
$R \le L(p)$
, let
![]() $m = c_0 R$
be such that
$m = c_0 R$
be such that
where the infimum is taken over all
![]() $\eta $
-regular quads
$\eta $
-regular quads
![]() $\mathcal {D}$
at scale R. By equation (RSW), the infimum is uniformly positive, and therefore
$\mathcal {D}$
at scale R. By equation (RSW), the infimum is uniformly positive, and therefore
![]() $c_0>0$
above does indeed depend only on
$c_0>0$
above does indeed depend only on
![]() $\eta $
.
$\eta $
.
Fix
![]() $\mathcal {D}$
as in the statement of the proposition. Then in any increasing coupling
$\mathcal {D}$
as in the statement of the proposition. Then in any increasing coupling
![]() $\mathbb {P}$
of
$\mathbb {P}$
of
![]() $\phi [\cdot ]$
and
$\phi [\cdot ]$
and
![]() $\phi [\cdot \,|\mathcal {C}(\mathcal {D})]$
(note that
$\phi [\cdot \,|\mathcal {C}(\mathcal {D})]$
(note that
![]() $\mathcal {C}(\mathcal {D})$
occurs automatically for
$\mathcal {C}(\mathcal {D})$
occurs automatically for
![]() $\omega '$
),
$\omega '$
),
 $$ \begin{align*} \mathbb{P}[\omega' \in &\mathcal{C}(\mathcal{D}^+), \,\omega \notin \mathcal{C}(\mathcal{D}^-)]\\ &\ge \mathbb P[\omega'\in \mathcal C(\mathcal{D}),\omega\notin \mathcal{C}(\mathcal{D})]-\mathbb P[\omega\in \mathcal{C}(\mathcal{D}^-),\omega\notin \mathcal{C}(\mathcal{D})]-\mathbb P[\omega'\in \mathcal{C}(\mathcal{D}),\omega'\notin \mathcal{C}(\mathcal{D}^+)]\\ & \geq 1-\phi[\mathcal{C}(\mathcal{D})]- \phi[\mathcal{C}(\mathcal{D}^-) \smallsetminus \mathcal{C}(\mathcal{D})] - \frac{\phi[ \mathcal{C}(\mathcal{D})\smallsetminus\mathcal{C}(\mathcal{D}^+)]}{\phi[|\mathcal{C}(\mathcal{D})]} \\ & \geq \phi[\mathcal{C}(\mathcal{D})^c] - C(m/R)^{\varepsilon} - \frac{C(m/R)^{\varepsilon}}{\phi[\mathcal{C}(\mathcal{D})]} \\ & \geq \tfrac12\phi[\mathcal{C}(\mathcal{D})^c] \geq c_1>0. \end{align*} $$
$$ \begin{align*} \mathbb{P}[\omega' \in &\mathcal{C}(\mathcal{D}^+), \,\omega \notin \mathcal{C}(\mathcal{D}^-)]\\ &\ge \mathbb P[\omega'\in \mathcal C(\mathcal{D}),\omega\notin \mathcal{C}(\mathcal{D})]-\mathbb P[\omega\in \mathcal{C}(\mathcal{D}^-),\omega\notin \mathcal{C}(\mathcal{D})]-\mathbb P[\omega'\in \mathcal{C}(\mathcal{D}),\omega'\notin \mathcal{C}(\mathcal{D}^+)]\\ & \geq 1-\phi[\mathcal{C}(\mathcal{D})]- \phi[\mathcal{C}(\mathcal{D}^-) \smallsetminus \mathcal{C}(\mathcal{D})] - \frac{\phi[ \mathcal{C}(\mathcal{D})\smallsetminus\mathcal{C}(\mathcal{D}^+)]}{\phi[|\mathcal{C}(\mathcal{D})]} \\ & \geq \phi[\mathcal{C}(\mathcal{D})^c] - C(m/R)^{\varepsilon} - \frac{C(m/R)^{\varepsilon}}{\phi[\mathcal{C}(\mathcal{D})]} \\ & \geq \tfrac12\phi[\mathcal{C}(\mathcal{D})^c] \geq c_1>0. \end{align*} $$
Next, we create an increasing coupling
![]() $\mathbb {P}$
between
$\mathbb {P}$
between
![]() $\phi $
and
$\phi $
and
![]() $\phi [\cdot \,|\mathcal {C}(\mathcal {D})]$
using the specific decision tree described below. Start by exploring the lowest crossing
$\phi [\cdot \,|\mathcal {C}(\mathcal {D})]$
using the specific decision tree described below. Start by exploring the lowest crossing
![]() $\Gamma ^+$
in
$\Gamma ^+$
in
![]() $\mathcal {D}^+$
from
$\mathcal {D}^+$
from
![]() $(a^+b^+)$
to
$(a^+b^+)$
to
![]() $(c^+d^+)$
(that is, the crossing closest to
$(c^+d^+)$
(that is, the crossing closest to
![]() $(b^+c^+)$
) in the larger configuration
$(b^+c^+)$
) in the larger configuration
![]() $\omega '$
. Write
$\omega '$
. Write
![]() $\tau _1$
for the stopping time when this crossing is found; set
$\tau _1$
for the stopping time when this crossing is found; set
![]() $\tau _1 = \infty $
if no such crossing exists. If
$\tau _1 = \infty $
if no such crossing exists. If
![]() $\tau _1 < \infty $
, explore the ‘right-most’ dual crossing
$\tau _1 < \infty $
, explore the ‘right-most’ dual crossing
![]() $\Gamma ^-$
in
$\Gamma ^-$
in
![]() $\mathcal {D}^-$
from
$\mathcal {D}^-$
from
![]() $(b^-c^-)$
to
$(b^-c^-)$
to
![]() $(d^-a^-)$
(that is, the one closest to
$(d^-a^-)$
(that is, the one closest to
![]() $(c^-d^-)$
) in the configuration
$(c^-d^-)$
) in the configuration
![]() $\omega ^*$
; define
$\omega ^*$
; define
![]() $\tau _2$
for the stopping time when this crossing is found (if
$\tau _2$
for the stopping time when this crossing is found (if
![]() $\tau _1 = \infty $
or no such crossing is found, set
$\tau _1 = \infty $
or no such crossing is found, set
![]() $\tau _2 = \infty $
). Notice that
$\tau _2 = \infty $
). Notice that
Assuming that
![]() $\tau _2 < \infty $
, the revealed edges
$\tau _2 < \infty $
, the revealed edges
![]() $e_{[\tau _2]}$
are those of
$e_{[\tau _2]}$
are those of
![]() $\mathcal {D}^+$
below
$\mathcal {D}^+$
below
![]() $\Gamma ^+$
and those of
$\Gamma ^+$
and those of
![]() $\mathcal {D}^-$
right or
$\mathcal {D}^-$
right or
![]() $\Gamma ^-$
. In particular, the edges of
$\Gamma ^-$
. In particular, the edges of
![]() $\mathcal {D}^+\smallsetminus \mathcal {D}$
that are above
$\mathcal {D}^+\smallsetminus \mathcal {D}$
that are above
![]() $\Gamma ^+$
, as well as those of
$\Gamma ^+$
, as well as those of
![]() $\mathcal {D}^- \smallsetminus \mathcal {D}$
that are left of
$\mathcal {D}^- \smallsetminus \mathcal {D}$
that are left of
![]() $\Gamma ^-$
, are unrevealed. See Figure 7 (middle diagram).
$\Gamma ^-$
, are unrevealed. See Figure 7 (middle diagram).
Next, explore the double four-petal flower domain
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
between
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
between
![]() $\Lambda _{3R/2}$
and
$\Lambda _{3R/2}$
and
![]() $\Lambda _{2R}$
in
$\Lambda _{2R}$
in
![]() $\omega $
; let
$\omega $
; let
![]() $\tau _3$
be the stopping time marking the end of this exploration (with
$\tau _3$
be the stopping time marking the end of this exploration (with
![]() $\tau _3 = \infty $
if no double four-petal flower domain exists or if
$\tau _3 = \infty $
if no double four-petal flower domain exists or if
![]() $\tau _2 = \infty $
). Due to Lemma 3.4,
$\tau _2 = \infty $
). Due to Lemma 3.4,
Finally, reveal the configurations in the unrevealed regions of
![]() $\mathcal {F}_{\mathrm {in}}$
, and write
$\mathcal {F}_{\mathrm {in}}$
, and write
![]() $\tau _4$
for the stopping time marking the end of this stage. Let H be the event that
$\tau _4$
for the stopping time marking the end of this stage. Let H be the event that
![]() $P_1^{\mathrm {in}}$
and
$P_1^{\mathrm {in}}$
and
![]() $P_3^{\mathrm {in}}$
are connected by paths of
$P_3^{\mathrm {in}}$
are connected by paths of
![]() $\omega ' \cap (\mathcal {F}_{\mathrm { in}}^c \smallsetminus \mathcal {D})$
to
$\omega ' \cap (\mathcal {F}_{\mathrm { in}}^c \smallsetminus \mathcal {D})$
to
![]() $\Gamma ^+$
and
$\Gamma ^+$
and
![]() $P_2^{\mathrm {in}}$
and
$P_2^{\mathrm {in}}$
and
![]() $P_4^{\mathrm {in}}$
are connected by paths of
$P_4^{\mathrm {in}}$
are connected by paths of
![]() $\omega ^* \cap (\mathcal {F}_{\mathrm {in}}^c \smallsetminus \mathcal {D})$
to
$\omega ^* \cap (\mathcal {F}_{\mathrm {in}}^c \smallsetminus \mathcal {D})$
to
![]() $\Gamma ^-$
. Due to equation (RSW) (see Figure 7, right diagram),
$\Gamma ^-$
. Due to equation (RSW) (see Figure 7, right diagram),
Special care should be taken as the primal connections occur in
![]() $\omega '$
while the dual ones occur in
$\omega '$
while the dual ones occur in
![]() $\omega $
. This may be easily overcome by considering connections in predetermined disjoint regions.Footnote
3
$\omega $
. This may be easily overcome by considering connections in predetermined disjoint regions.Footnote
3
Now, if
![]() $\tau _3 < \infty $
and H occurs, then
$\tau _3 < \infty $
and H occurs, then
![]() $P_1^{\mathrm {out}}$
and
$P_1^{\mathrm {out}}$
and
![]() $P_3^{\mathrm {out}}$
are disconnected in
$P_3^{\mathrm {out}}$
are disconnected in
![]() $\omega \cap \mathcal {F}_{\mathrm {out}}^c$
but are connected in
$\omega \cap \mathcal {F}_{\mathrm {out}}^c$
but are connected in
![]() $\omega '\cap \mathcal {F}^c_{\mathrm {out}}$
. Set
$\omega '\cap \mathcal {F}^c_{\mathrm {out}}$
. Set
![]() $\tau = \tau _3$
if the above occurs and
$\tau = \tau _3$
if the above occurs and
![]() $\tau = \infty $
otherwise. Then
$\tau = \infty $
otherwise. Then
![]() $\tau $
satisfies the requirements of the proposition and
$\tau $
satisfies the requirements of the proposition and
Finally, let us discuss the case where
![]() $\mathcal {C}(\mathcal {D})$
is replaced by
$\mathcal {C}(\mathcal {D})$
is replaced by
![]() $A_{R/2}$
, for which the proof is much simpler. Consider the following increasing coupling of
$A_{R/2}$
, for which the proof is much simpler. Consider the following increasing coupling of
![]() $\omega \sim \phi $
and
$\omega \sim \phi $
and
![]() $\omega ' \sim \phi [\cdot \,|A_{R/2}]$
. Start by exploring the double four-petal flower domain
$\omega ' \sim \phi [\cdot \,|A_{R/2}]$
. Start by exploring the double four-petal flower domain
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
between
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
between
![]() $\Lambda _{3R/2}$
and
$\Lambda _{3R/2}$
and
![]() $\Lambda _{2R}$
in
$\Lambda _{2R}$
in
![]() $\omega $
; write
$\omega $
; write
![]() $\tau _1$
for the stopping time marking the end of this exploration. When
$\tau _1$
for the stopping time marking the end of this exploration. When
![]() $\tau _1 < \infty $
, reveal the configurations inside
$\tau _1 < \infty $
, reveal the configurations inside
![]() $\mathcal {F}_{\mathrm {in}}$
in any order. At this stage, due to equation (RSW), there is a uniformly positive probability that
$\mathcal {F}_{\mathrm {in}}$
in any order. At this stage, due to equation (RSW), there is a uniformly positive probability that
![]() $P_1^{\mathrm {in}}$
and
$P_1^{\mathrm {in}}$
and
![]() $P_3^{\mathrm {in}}$
are both connected to
$P_3^{\mathrm {in}}$
are both connected to
![]() $\Lambda _{R/2}$
but not to each other in
$\Lambda _{R/2}$
but not to each other in
![]() $\omega \cap \mathcal {F}_{\mathrm {in}}$
. It is then deterministic that
$\omega \cap \mathcal {F}_{\mathrm {in}}$
. It is then deterministic that
![]() $P_1^{\mathrm {in}}$
is connected to
$P_1^{\mathrm {in}}$
is connected to
![]() $P_3^{\mathrm {in}}$
by an open path of
$P_3^{\mathrm {in}}$
by an open path of
![]() $\omega '$
inside
$\omega '$
inside
![]() $\mathcal {F}_{\mathrm {in}}$
. Thus, when this event occurs, the boundary conditions induced by
$\mathcal {F}_{\mathrm {in}}$
. Thus, when this event occurs, the boundary conditions induced by
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
on
$\omega '$
on
![]() $\mathcal {F}_{\mathrm {out}}$
form a boosting pair, and we declare
$\mathcal {F}_{\mathrm {out}}$
form a boosting pair, and we declare
![]() $\tau $
to be the end of this stage of the exploration; otherwise, set
$\tau $
to be the end of this stage of the exploration; otherwise, set
![]() $\tau = \infty $
. Finally, Lemma 3.4 and the use of (RSW) mentioned above show that
$\tau = \infty $
. Finally, Lemma 3.4 and the use of (RSW) mentioned above show that
![]() $\tau < \infty $
with uniformly positive probability.
$\tau < \infty $
with uniformly positive probability.
We conclude this section with the following lemma, which is a straightforward application of equation (RSW) and will be useful in future sections. It is independent of the rest of the section, but we include it here as it also deals with the probability that
![]() $\tau <\infty $
.
$\tau <\infty $
.
Lemma 3.13. For any
![]() $\eta> 0$
, there exists a constant
$\eta> 0$
, there exists a constant
![]() $c = c(\eta )> 0$
such that the following holds. Fix p and
$c = c(\eta )> 0$
such that the following holds. Fix p and
![]() $\mathcal {F}$
an
$\mathcal {F}$
an
![]() $\eta $
-well-separated outer flower domain on
$\eta $
-well-separated outer flower domain on
![]() $\Lambda _{R}$
for some
$\Lambda _{R}$
for some
![]() $R\le L(p)$
. Let
$R\le L(p)$
. Let
![]() $\xi ,\xi '$
be a boosting pair of boundary conditions on
$\xi ,\xi '$
be a boosting pair of boundary conditions on
![]() $\mathcal {F}$
and x be a point of
$\mathcal {F}$
and x be a point of
![]() $\mathrm {Ann}(2R,4R)$
. Then there exists a coupling via decision trees
$\mathrm {Ann}(2R,4R)$
. Then there exists a coupling via decision trees
![]() $\mathbb {P}$
of
$\mathbb {P}$
of
![]() $\phi _{\mathcal {F}}^{\xi }$
and
$\phi _{\mathcal {F}}^{\xi }$
and
![]() $\phi _{\mathcal {F}}^{\xi '}$
and a stopping time
$\phi _{\mathcal {F}}^{\xi '}$
and a stopping time
![]() $\tau $
such that when
$\tau $
such that when
![]() $\tau < \infty $
,
$\tau < \infty $
,
![]() $\mathcal {F}_{\tau } = \mathcal {F}\smallsetminus e_{[\tau ]}$
is a
$\mathcal {F}_{\tau } = \mathcal {F}\smallsetminus e_{[\tau ]}$
is a
![]() $1/2$
-well-separated inner flower domain on
$1/2$
-well-separated inner flower domain on
![]() $\Lambda _{R/4}(x)$
, and the boundary conditions induced by
$\Lambda _{R/4}(x)$
, and the boundary conditions induced by
![]() $\omega ^{\prime }_{[\tau ]}$
on
$\omega ^{\prime }_{[\tau ]}$
on
![]() $\mathcal {F}_{\tau }$
are a boost of those induced by
$\mathcal {F}_{\tau }$
are a boost of those induced by
![]() $\omega _{[\tau ]}$
. Finally,
$\omega _{[\tau ]}$
. Finally,
The proof is similar to (yet much easier than) the one of Theorem 3.6.
Proof. Write
![]() $P_i$
,
$P_i$
,
![]() $P_j$
for two petals of
$P_j$
for two petals of
![]() $\mathcal {F}$
that are wired in
$\mathcal {F}$
that are wired in
![]() $\xi '$
but not in
$\xi '$
but not in
![]() $\xi $
.
$\xi $
.
Start by exploring the double four-petal flower domain
![]() $(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
between
$(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
between
![]() $\Lambda _{R/4}(x)$
and
$\Lambda _{R/4}(x)$
and
![]() $\Lambda _{R/2}(x)$
. If no such double flower domain exists, set
$\Lambda _{R/2}(x)$
. If no such double flower domain exists, set
![]() $\tau = \infty $
and proceed arbitrarily. If
$\tau = \infty $
and proceed arbitrarily. If
![]() $(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
exists, continue by revealing the configurations in
$(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
exists, continue by revealing the configurations in
![]() $\mathcal {F} \cap \mathcal {F}_{\mathrm {out}}$
. Write H for the event that in
$\mathcal {F} \cap \mathcal {F}_{\mathrm {out}}$
. Write H for the event that in
![]() $\omega \cap \mathcal {F}_{\mathrm {out}}$
,
$\omega \cap \mathcal {F}_{\mathrm {out}}$
,
![]() $P^{\mathrm {out}}_1$
is connected to
$P^{\mathrm {out}}_1$
is connected to
![]() $P_i$
,
$P_i$
,
![]() $P^{\mathrm {out}}_3$
is connected to
$P^{\mathrm {out}}_3$
is connected to
![]() $P_j$
, but
$P_j$
, but
![]() $P^{\mathrm {out}}_1$
and
$P^{\mathrm {out}}_1$
and
![]() $P^{\mathrm { out}}_3$
are not connected to each other or any other petal of
$P^{\mathrm { out}}_3$
are not connected to each other or any other petal of
![]() $\mathcal {F}$
. Equation (RSW) implies that
$\mathcal {F}$
. Equation (RSW) implies that
where
![]() $c> 0$
depends only on
$c> 0$
depends only on
![]() $\eta $
. If H occurs, set
$\eta $
. If H occurs, set
![]() $\tau $
to be the stopping time at which the configurations in
$\tau $
to be the stopping time at which the configurations in
![]() $\mathcal {F}_{\mathrm {out}}$
have been revealed; otherwise, set
$\mathcal {F}_{\mathrm {out}}$
have been revealed; otherwise, set
![]() $\tau = \infty $
.
$\tau = \infty $
.
Then due to Lemma 3.4 and equation (3.15),
![]() $\mathbb {P}[H ] \stackrel{>}{\scriptstyle{\frown}} c$
. Finally, when
$\mathbb {P}[H ] \stackrel{>}{\scriptstyle{\frown}} c$
. Finally, when
![]() $\tau < \infty $
, the boundary conditions induced by
$\tau < \infty $
, the boundary conditions induced by
![]() $\omega ^{\prime }_{[\tau ]}$
on
$\omega ^{\prime }_{[\tau ]}$
on
![]() $\mathcal {F}_{\tau } = \mathcal {F}_{\mathrm {in}}$
are indeed a boost of those induced by
$\mathcal {F}_{\tau } = \mathcal {F}_{\mathrm {in}}$
are indeed a boost of those induced by
![]() $\omega _{[\tau ]}$
, since
$\omega _{[\tau ]}$
, since
![]() $P^1_{\mathrm {in}}$
is connected to
$P^1_{\mathrm {in}}$
is connected to
![]() $P^3_{\mathrm {in}}$
in
$P^3_{\mathrm {in}}$
in
![]() $\omega ^{\prime }_{[\tau ]}$
but not in
$\omega ^{\prime }_{[\tau ]}$
but not in
![]() $\omega _{[\tau ]}$
.
$\omega _{[\tau ]}$
.
4 Properties of the mixing rate
Fix
![]() $q \in (1,4]$
and
$q \in (1,4]$
and
![]() $\eta> 0$
for the whole of this section; all constants, including those in
$\eta> 0$
for the whole of this section; all constants, including those in
![]() $\stackrel{<}{\scriptstyle{\frown}}$
and
$\stackrel{<}{\scriptstyle{\frown}}$
and
![]() $\asymp $
, may depend on
$\asymp $
, may depend on
![]() $\eta $
. In this section, we always work with a single edge-parameter
$\eta $
. In this section, we always work with a single edge-parameter
![]() $p\in (0,1)$
, and therefore we often omit it from the measure
$p\in (0,1)$
, and therefore we often omit it from the measure
![]() $\phi _{G,p}$
for notational convenience.
$\phi _{G,p}$
for notational convenience.
4.1 Noncoupling induces boosting boundary conditions
The main result of this subsection is the following; it is the cornerstone of the other results proved later in this and other sections.
Theorem 4.1. For any
![]() $\eta>0$
,
$\eta>0$
,
![]() $p\in (0,1)$
and
$p\in (0,1)$
and
![]() $4r < R \le L(p)$
.
$4r < R \le L(p)$
.
-
(i) Let
 $\mathcal {G}$
be an
$\mathcal {G}$
be an
 $\eta $
-well-separated inner flower domain on
$\eta $
-well-separated inner flower domain on
 $\Lambda _R$
and
$\Lambda _R$
and
 $(\xi ,\xi ')$
be a boosting pair of boundary conditions on
$(\xi ,\xi ')$
be a boosting pair of boundary conditions on
 $\mathcal {G}$
. There exists an increasing coupling
$\mathcal {G}$
. There exists an increasing coupling
 $\mathbb {P}$
of
$\mathbb {P}$
of
 $\phi _{\mathcal {G},p}^{\xi }$
and
$\phi _{\mathcal {G},p}^{\xi }$
and
 $\phi _{\mathcal {G},p}^{\xi '}$
on
$\phi _{\mathcal {G},p}^{\xi '}$
on
 $\mathcal {G} \smallsetminus \Lambda _r$
via decision trees, and a stopping time
$\mathcal {G} \smallsetminus \Lambda _r$
via decision trees, and a stopping time
 $\tau $
with the following property. When
$\tau $
with the following property. When
 $\tau <\infty $
,
$\tau <\infty $
,
 $\mathcal {F}_{\tau } = \mathcal {G} \smallsetminus e_{[\tau ]}$
is a
$\mathcal {F}_{\tau } = \mathcal {G} \smallsetminus e_{[\tau ]}$
is a
 $1/2$
-well-separated inner flower domain on
$1/2$
-well-separated inner flower domain on
 $\Lambda _r$
, and the boundary conditions induced by
$\Lambda _r$
, and the boundary conditions induced by
 $(\omega ^{\prime }_{[\tau ]})^{\xi '}$
on
$(\omega ^{\prime }_{[\tau ]})^{\xi '}$
on
 $\mathcal {F}_{\tau }$
are a boost of those induced by
$\mathcal {F}_{\tau }$
are a boost of those induced by
 $\omega _{[\tau ]}^{\xi }$
. Moreover, if we write
$\omega _{[\tau ]}^{\xi }$
. Moreover, if we write
 $\zeta $
and
$\zeta $
and
 $\zeta '$
for the boundary conditions induced by
$\zeta '$
for the boundary conditions induced by
 $(\omega ')^{\xi '}$
and
$(\omega ')^{\xi '}$
and
 $\omega ^{\xi }$
on
$\omega ^{\xi }$
on
 $\partial \Lambda _r$
, then
$\partial \Lambda _r$
, then  $$ \begin{align*} \mathbb{P}[\tau < \infty] \asymp \mathbb{P}[\zeta \neq\zeta' ]. \end{align*} $$
$$ \begin{align*} \mathbb{P}[\tau < \infty] \asymp \mathbb{P}[\zeta \neq\zeta' ]. \end{align*} $$
-
(ii) Let
 $\mathcal {G}$
be an
$\mathcal {G}$
be an
 $\eta $
-well-separated outer flower domain on
$\eta $
-well-separated outer flower domain on
 $\Lambda _r$
and
$\Lambda _r$
and
 $(\xi ,\xi ')$
be a boosting pair of boundary conditions on
$(\xi ,\xi ')$
be a boosting pair of boundary conditions on
 $\mathcal {G}$
. There exists an increasing coupling
$\mathcal {G}$
. There exists an increasing coupling
 $\mathbb {P}$
of
$\mathbb {P}$
of
 $\phi _{\mathcal {G},p}^{\xi }$
and
$\phi _{\mathcal {G},p}^{\xi }$
and
 $\phi _{\mathcal {G},p}^{\xi '}$
on
$\phi _{\mathcal {G},p}^{\xi '}$
on
 $\mathcal {G} \cap \Lambda _R$
via decision trees, and a stopping time
$\mathcal {G} \cap \Lambda _R$
via decision trees, and a stopping time
 $\tau $
with the following property. When
$\tau $
with the following property. When
 $\tau <\infty $
,
$\tau <\infty $
,
 $\mathcal {F}_{\tau } = \mathcal {G}\smallsetminus e_{[\tau ]}$
is a
$\mathcal {F}_{\tau } = \mathcal {G}\smallsetminus e_{[\tau ]}$
is a
 $1/2$
-well-separated outer flower domain on
$1/2$
-well-separated outer flower domain on
 $\Lambda _R$
, and the boundary conditions induced by
$\Lambda _R$
, and the boundary conditions induced by
 $(\omega ^{\prime }_{[\tau ]})^{\xi '}$
on
$(\omega ^{\prime }_{[\tau ]})^{\xi '}$
on
 $\mathcal {F}_{\tau }$
are a boost of those induced by
$\mathcal {F}_{\tau }$
are a boost of those induced by
 $\omega _{[\tau ]}^{\xi }$
. Moreover, if we write
$\omega _{[\tau ]}^{\xi }$
. Moreover, if we write
 $\zeta $
and
$\zeta $
and
 $\zeta '$
for the boundary conditions induced by
$\zeta '$
for the boundary conditions induced by
 $(\omega ')^{\xi '}$
and
$(\omega ')^{\xi '}$
and
 $\omega ^{\xi }$
on
$\omega ^{\xi }$
on
 $\partial \Lambda _R$
, then
$\partial \Lambda _R$
, then  $$ \begin{align*} \mathbb{P}[\tau < \infty] \asymp \mathbb{P}[\zeta \neq\zeta' ]. \end{align*} $$
$$ \begin{align*} \mathbb{P}[\tau < \infty] \asymp \mathbb{P}[\zeta \neq\zeta' ]. \end{align*} $$
Remark 4.2. In the previous theorem, we sample edges only outside
![]() $\Lambda _r$
in Case (i) and only inside
$\Lambda _r$
in Case (i) and only inside
![]() $\Lambda _R$
in Case (ii), but of course once this is done, one may use an arbitrary coupling inside
$\Lambda _R$
in Case (ii), but of course once this is done, one may use an arbitrary coupling inside
![]() $\Lambda _r$
or outside
$\Lambda _r$
or outside
![]() $\Lambda _R$
to obtain couplings in the whole flower domain
$\Lambda _R$
to obtain couplings in the whole flower domain
![]() $\mathcal {G}$
. We stated the previous theorem in this setting to be able to reuse the coupling in applications we have in mind.
$\mathcal {G}$
. We stated the previous theorem in this setting to be able to reuse the coupling in applications we have in mind.
Remark 4.3. The proofs of Theorem 4.1 (i) and (ii) may be readily adapted to the FK-percolation measure on any graphs containing
![]() $\mathcal {G} \smallsetminus \Lambda _{r/2}$
and
$\mathcal {G} \smallsetminus \Lambda _{r/2}$
and
![]() $\mathcal {G} \cap \Lambda _{2R}$
, respectively, as they essentially only rely on the RSW property in
$\mathcal {G} \cap \Lambda _{2R}$
, respectively, as they essentially only rely on the RSW property in
![]() $\mathrm {Ann}(r,R)$
.
$\mathrm {Ann}(r,R)$
.
The first point of the theorem should be understood as follows. We reveal the configurations
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
in the coupling
$\omega '$
in the coupling
![]() $\mathbb {P}$
starting from the outside and moving inwards; while doing this, we follow the difference between the boundary conditions that the configurations induce on the unrevealed region. If this difference survives until the whole of
$\mathbb {P}$
starting from the outside and moving inwards; while doing this, we follow the difference between the boundary conditions that the configurations induce on the unrevealed region. If this difference survives until the whole of
![]() $\mathcal {G} \smallsetminus \Lambda _r$
is revealed, then there is a positive probability that it survives as a significant difference, namely in the form of a boosting pair of boundary conditions on a well-separated flower domain.
$\mathcal {G} \smallsetminus \Lambda _r$
is revealed, then there is a positive probability that it survives as a significant difference, namely in the form of a boosting pair of boundary conditions on a well-separated flower domain.
The second point is analogous, with the revealment starting inside and moving outwards.
Proof of Theorem 4.1
We will only prove point (i); the proof of point (ii) is identical. Fix
![]() $p \in (0,1)$
,
$p \in (0,1)$
,
![]() $4r \le R \le L(p)$
and
$4r \le R \le L(p)$
and
![]() $\mathcal {G}$
,
$\mathcal {G}$
,
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
as in the statement. All constants below are independent of r, R,
$\xi '$
as in the statement. All constants below are independent of r, R,
![]() $\mathcal {G}$
,
$\mathcal {G}$
,
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
unless explicitly stated. When referring to connections in configurations
$\xi '$
unless explicitly stated. When referring to connections in configurations
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
with laws
$\omega '$
with laws
![]() $\phi _{\mathcal {G},p}^{\xi }$
and
$\phi _{\mathcal {G},p}^{\xi }$
and
![]() $\phi _{\mathcal {G},p}^{\xi '}$
, respectively, we will implicitly include connections that use the boundary conditions. In other words, we omit the superscript in the notation
$\phi _{\mathcal {G},p}^{\xi '}$
, respectively, we will implicitly include connections that use the boundary conditions. In other words, we omit the superscript in the notation
![]() $\omega ^{\xi }$
and
$\omega ^{\xi }$
and
![]() $(\omega ')^{\xi '}$
.
$(\omega ')^{\xi '}$
.
First, for any increasing coupling
![]() $\mathbb {P}$
between
$\mathbb {P}$
between
![]() $\phi _{\mathcal {G}}^{\xi }$
and
$\phi _{\mathcal {G}}^{\xi }$
and
![]() $\phi _{\mathcal {G}}^{\xi '}$
obtained by a decision tree, and any stopping time
$\phi _{\mathcal {G}}^{\xi '}$
obtained by a decision tree, and any stopping time
![]() $\tau $
with the properties of the theorem,
$\tau $
with the properties of the theorem,
![]() $\mathbb {P}[\tau < \infty ] \le \mathbb {P}[\zeta \neq \zeta ']$
. Indeed, the requirement that the boundary conditions induced by
$\mathbb {P}[\tau < \infty ] \le \mathbb {P}[\zeta \neq \zeta ']$
. Indeed, the requirement that the boundary conditions induced by
![]() $\omega ^{\prime }_{[\tau ]}$
on
$\omega ^{\prime }_{[\tau ]}$
on
![]() $\mathcal {F}_{\tau }$
are a boost of those induced by
$\mathcal {F}_{\tau }$
are a boost of those induced by
![]() $\omega _{[\tau ]}$
imposes that the boundary conditions induced by
$\omega _{[\tau ]}$
imposes that the boundary conditions induced by
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
on
$\omega '$
on
![]() $\Lambda _{r}$
are distinct. The rest of the proof is dedicated to the converse bound.
$\Lambda _{r}$
are distinct. The rest of the proof is dedicated to the converse bound.
Assume for simplicity that
![]() $R = 4^k r$
for some integer
$R = 4^k r$
for some integer
![]() $k \geq 2$
. By monotonicity, it suffices to treat the case where
$k \geq 2$
. By monotonicity, it suffices to treat the case where
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
are identical, with the exception of two petals that are wired together in
$\xi '$
are identical, with the exception of two petals that are wired together in
![]() $\xi '$
but not in
$\xi '$
but not in
![]() $\xi $
. Assume this is the case, and write
$\xi $
. Assume this is the case, and write
![]() $P_1$
and
$P_1$
and
![]() $P_3$
for the two primal petals of
$P_3$
for the two primal petals of
![]() $\mathcal {G}$
that are wired together in
$\mathcal {G}$
that are wired together in
![]() $\xi '$
but not in
$\xi '$
but not in
![]() $\xi $
(contrary to what the notation suggests,
$\xi $
(contrary to what the notation suggests,
![]() $P_1$
and
$P_1$
and
![]() $P_3$
need not be separated by a single dual petal).
$P_3$
need not be separated by a single dual petal).
Below, we describe an increasing coupling
![]() $\mathbf P$
of
$\mathbf P$
of
![]() $\phi _{\mathcal {G}}^{\xi }$
and
$\phi _{\mathcal {G}}^{\xi }$
and
![]() $\phi _{\mathcal {G}}^{\xi '}$
on
$\phi _{\mathcal {G}}^{\xi '}$
on
![]() $\mathcal {G} \smallsetminus \Lambda _r$
obtained through a decision tree. The actual coupling of the theorem is a slight variation of
$\mathcal {G} \smallsetminus \Lambda _r$
obtained through a decision tree. The actual coupling of the theorem is a slight variation of
![]() $\mathbf P$
that we will describe at the end of the proof.
$\mathbf P$
that we will describe at the end of the proof.
At any time t, write
![]() $\mathcal {F}_t$
for the connected component of
$\mathcal {F}_t$
for the connected component of
![]() $\Lambda _r$
in
$\Lambda _r$
in
![]() $\mathcal {G} \smallsetminus e_{[t]}$
. We will abusively consider that all edges of
$\mathcal {G} \smallsetminus e_{[t]}$
. We will abusively consider that all edges of
![]() $\mathcal {G}$
that are not revealed at time t and that are not part of
$\mathcal {G}$
that are not revealed at time t and that are not part of
![]() $\mathcal {F}_t$
are revealed instantaneously. Thus, from now on, we have
$\mathcal {F}_t$
are revealed instantaneously. Thus, from now on, we have
![]() $\mathcal {F}_t = \mathcal {G} \smallsetminus e_{[t]}$
. We will identify
$\mathcal {F}_t = \mathcal {G} \smallsetminus e_{[t]}$
. We will identify
![]() $\omega _{[t]}$
and
$\omega _{[t]}$
and
![]() $\omega _{[t]}'$
to the boundary conditions they induce on
$\omega _{[t]}'$
to the boundary conditions they induce on
![]() $\mathcal {F}_t$
.
$\mathcal {F}_t$
.
Write T for the first time t when
![]() $\omega _{[t]}$
and
$\omega _{[t]}$
and
![]() $\omega ^{\prime }_{[t]}$
induce the same boundary conditions on
$\omega ^{\prime }_{[t]}$
induce the same boundary conditions on
![]() $\mathcal {F}_t$
, and
$\mathcal {F}_t$
, and
![]() $T = \infty $
if the boundary conditions are never the same. If
$T = \infty $
if the boundary conditions are never the same. If
![]() $T <\infty $
, the configurations
$T <\infty $
, the configurations
![]() $\omega ,\omega '$
in
$\omega ,\omega '$
in
![]() $\mathcal {F}_{T}$
are identical, regardless of the decision tree used after T. Thus, when this occurs, reveal the rest of the edges using lexicographical order.
$\mathcal {F}_{T}$
are identical, regardless of the decision tree used after T. Thus, when this occurs, reveal the rest of the edges using lexicographical order.
The coupling proceeds in several stages numbered
![]() $j = 0,\dots , k$
. If at any point T occurs, the procedure described below stops, and the revealment by lexicographical order is used. Stage j corresponds to revealing information in
$j = 0,\dots , k$
. If at any point T occurs, the procedure described below stops, and the revealment by lexicographical order is used. Stage j corresponds to revealing information in
![]() $\Lambda _{4^{k-j} r}^c := \mathcal {G} \smallsetminus \Lambda _{4^{k-j} r}$
. We will write
$\Lambda _{4^{k-j} r}^c := \mathcal {G} \smallsetminus \Lambda _{4^{k-j} r}$
. We will write
![]() $\tau _j$
for the stopping time that marks the end of stage j. At time
$\tau _j$
for the stopping time that marks the end of stage j. At time
![]() $\tau _j$
, the revealed edges are those of the cluster of
$\tau _j$
, the revealed edges are those of the cluster of
![]() $P_1$
and
$P_1$
and
![]() $P_3$
in
$P_3$
in
![]() $\omega ' \cap \Lambda _{4^{k-j} r}^c$
, any edges of
$\omega ' \cap \Lambda _{4^{k-j} r}^c$
, any edges of
![]() $\Lambda _{4^{k-j} r}^c$
adjacent to this cluster, as well as any edges separated from
$\Lambda _{4^{k-j} r}^c$
adjacent to this cluster, as well as any edges separated from
![]() $\Lambda _r$
by the two categories of edges mentioned above.
$\Lambda _r$
by the two categories of edges mentioned above.
Let us now describe precisely the revealment algorithm.
Revealment algorithm
Stage 0: Reveal the cluster of
![]() $P_1$
and
$P_1$
and
![]() $P_3$
inside
$P_3$
inside
![]() $\omega ' \cap \Lambda _R^c$
in arbitrary order. Let
$\omega ' \cap \Lambda _R^c$
in arbitrary order. Let
![]() $\tau _{0}$
be the stopping time marking the end of this stage.
$\tau _{0}$
be the stopping time marking the end of this stage.
Stage
![]() $j+1$
: Fix
$j+1$
: Fix
![]() $j\geq 0$
, and assume the coupling defined up to time
$j\geq 0$
, and assume the coupling defined up to time
![]() $\tau _j$
(see Figure 8 for an illustration). Stage
$\tau _j$
(see Figure 8 for an illustration). Stage
![]() $j+1$
is itself formed of two steps. As already mentioned, this is only valid when
$j+1$
is itself formed of two steps. As already mentioned, this is only valid when
![]() $T> \tau _{j}$
. Write
$T> \tau _{j}$
. Write
![]() $\rho = 4^{k-j-1} r$
. In
$\rho = 4^{k-j-1} r$
. In
![]() $\omega ^{\prime }_{[\tau _j]}$
, the boundary of
$\omega ^{\prime }_{[\tau _j]}$
, the boundary of
![]() $\mathcal {F}_{\tau _j}$
is formed of dual arcs outside of
$\mathcal {F}_{\tau _j}$
is formed of dual arcs outside of
![]() $\Lambda _{4\rho }$
with endpoints on
$\Lambda _{4\rho }$
with endpoints on
![]() $\partial \Lambda _{4\rho }$
, along with points on
$\partial \Lambda _{4\rho }$
, along with points on
![]() $\partial \Lambda _{4\rho }$
that are connected in
$\partial \Lambda _{4\rho }$
that are connected in
![]() $\omega ^{\prime }_{\tau _j}$
to
$\omega ^{\prime }_{\tau _j}$
to
![]() $P_1$
or
$P_1$
or
![]() $P_3$
. Call the latter points the ‘wired’ points of
$P_3$
. Call the latter points the ‘wired’ points of
![]() $\partial \mathcal {F}_{\tau _j}$
. Since T has not yet occurred, there exists at least one wired point on
$\partial \mathcal {F}_{\tau _j}$
. Since T has not yet occurred, there exists at least one wired point on
![]() $\partial \mathcal {F}_{\tau _j}$
.
$\partial \mathcal {F}_{\tau _j}$
.

Figure 8 Red solid lines represent open edges in
![]() $\omega '$
, while blue ones represent open edges in
$\omega '$
, while blue ones represent open edges in
![]() $\omega $
. Dotted lines represent closed (or, equivalently, open dual edges) in the configurations corresponding to their colour. Left: At the end of stage j, the revealed edges are those of the cluster of
$\omega $
. Dotted lines represent closed (or, equivalently, open dual edges) in the configurations corresponding to their colour. Left: At the end of stage j, the revealed edges are those of the cluster of
![]() $P_1$
and
$P_1$
and
![]() $P_3$
in
$P_3$
in
![]() $\omega ' \cap \Lambda _{4\rho }^c$
and its boundary. Then by time
$\omega ' \cap \Lambda _{4\rho }^c$
and its boundary. Then by time
![]() $\tau _{j+1/2}$
, the interfaces in
$\tau _{j+1/2}$
, the interfaces in
![]() $\omega $
starting at the wired vertices previously exposed are revealed until they touch
$\omega $
starting at the wired vertices previously exposed are revealed until they touch
![]() $\Lambda _{2\rho }$
. At this time, the unrevealed region is a flower domain that is likely well-separated. Middle: Assuming that the primal petals of
$\Lambda _{2\rho }$
. At this time, the unrevealed region is a flower domain that is likely well-separated. Middle: Assuming that the primal petals of
![]() $\mathcal {F}_{\tau _{j+1/2}}$
are all wired together in
$\mathcal {F}_{\tau _{j+1/2}}$
are all wired together in
![]() $\omega $
, we turn our attention to the set
$\omega $
, we turn our attention to the set
![]() $\mathcal {A}$
of points that lie on dual petals of
$\mathcal {A}$
of points that lie on dual petals of
![]() $\mathcal {F}_{\tau _{j+1/2}}$
but are connected to
$\mathcal {F}_{\tau _{j+1/2}}$
but are connected to
![]() $P_1$
or
$P_1$
or
![]() $P_3$
in
$P_3$
in
![]() $\omega ^{\prime }_{[\tau _{j+1/2}]}$
. If this set has a good probability of being connected to
$\omega ^{\prime }_{[\tau _{j+1/2}]}$
. If this set has a good probability of being connected to
![]() $\Lambda _{\rho }$
, then we call
$\Lambda _{\rho }$
, then we call
![]() $\tau _{j+1/2}$
promising. Right: For
$\tau _{j+1/2}$
promising. Right: For
![]() $\tau _{j+1/2}$
promising, we may connect two separate regions of
$\tau _{j+1/2}$
promising, we may connect two separate regions of
![]() $\mathcal {A}$
to the two primal external petals of a double flower-domain at a smaller scale. Then these petals will be connected in
$\mathcal {A}$
to the two primal external petals of a double flower-domain at a smaller scale. Then these petals will be connected in
![]() $\omega '$
but not in
$\omega '$
but not in
![]() $\omega $
.
$\omega $
.
First, reveal all interfaces in
![]() $\omega \cap \mathcal {F}_{\tau _j} \cap \Lambda _{2\rho }^c$
that start at wired points of
$\omega \cap \mathcal {F}_{\tau _j} \cap \Lambda _{2\rho }^c$
that start at wired points of
![]() $\partial \mathcal {F}_{\tau _j}$
. This may be done by tracking the left and right boundaries of the clusters of each wired point of
$\partial \mathcal {F}_{\tau _j}$
. This may be done by tracking the left and right boundaries of the clusters of each wired point of
![]() $\partial \mathcal {F}_{\tau _j}$
until they finish on
$\partial \mathcal {F}_{\tau _j}$
until they finish on
![]() $\partial \mathcal {F}_{\tau _j}$
or reach
$\partial \mathcal {F}_{\tau _j}$
or reach
![]() $\partial \Lambda _{2\rho }$
. Write
$\partial \Lambda _{2\rho }$
. Write
![]() $\tau _{j+1/2}$
for the stopping time that marks the end of this step. Formally, if T occurs before time
$\tau _{j+1/2}$
for the stopping time that marks the end of this step. Formally, if T occurs before time
![]() $\tau _{j+1/2}$
, set
$\tau _{j+1/2}$
, set
![]() $\tau _{j+1/2} = \infty $
.
$\tau _{j+1/2} = \infty $
.
Next, explore the cluster of
![]() $P_1$
and
$P_1$
and
![]() $P_3$
inside
$P_3$
inside
![]() $\omega ' \cap \Lambda _{\rho }^c$
, and write
$\omega ' \cap \Lambda _{\rho }^c$
, and write
![]() $\tau _{j+1}$
for the stopping time marking the end of this stage (set
$\tau _{j+1}$
for the stopping time marking the end of this stage (set
![]() $\tau _{j+1} = \infty $
if T occurs before the end of this stage). In fact, we will sometimes require that the clusters are revealed in a certain order (see the coupling
$\tau _{j+1} = \infty $
if T occurs before the end of this stage). In fact, we will sometimes require that the clusters are revealed in a certain order (see the coupling
![]() $\mathrm {P}$
defined by Lemma 4.5 for details).
$\mathrm {P}$
defined by Lemma 4.5 for details).
After stage k
: Assuming that
![]() $T> \tau _k$
, reveal all remaining edges in lexicographical order.
$T> \tau _k$
, reveal all remaining edges in lexicographical order.
Each stopping time
![]() $\tau _{j+1/2}$
will be declared promising or not (see the precise definition below) depending on the configuration at that stage and on some constant threshold
$\tau _{j+1/2}$
will be declared promising or not (see the precise definition below) depending on the configuration at that stage and on some constant threshold
![]() $\delta> 0$
to be fixed below. Fix
$\delta> 0$
to be fixed below. Fix
![]() $0\le j <k$
, and assume
$0\le j <k$
, and assume
![]() $\tau _{j+1/2} < \infty $
(otherwise,
$\tau _{j+1/2} < \infty $
(otherwise,
![]() $\tau _{j+1/2}$
is not promising). Then
$\tau _{j+1/2}$
is not promising). Then
![]() $\mathcal {F}_{\tau _{j+1/2}}$
is either a simply connected domain containing
$\mathcal {F}_{\tau _{j+1/2}}$
is either a simply connected domain containing
![]() $\Lambda _{2\rho }$
and
$\Lambda _{2\rho }$
and
![]() $\omega _{[\tau _{j+1/2}]}$
induces free boundary conditions on it, or it is an inner flower domain on
$\omega _{[\tau _{j+1/2}]}$
induces free boundary conditions on it, or it is an inner flower domain on
![]() $\Lambda _{2\rho }$
and
$\Lambda _{2\rho }$
and
![]() $\omega _{[\tau _{j+1/2}]}$
induces coherent boundary conditions on it. The former occurs when none of the revealed interfaces in the first step of stage j reaches
$\omega _{[\tau _{j+1/2}]}$
induces coherent boundary conditions on it. The former occurs when none of the revealed interfaces in the first step of stage j reaches
![]() $\Lambda _{2\rho }$
.
$\Lambda _{2\rho }$
.
First, we analyse the case where
![]() $\omega _{[\tau _{j+1/2}]}$
induces free boundary conditions
$\omega _{[\tau _{j+1/2}]}$
induces free boundary conditions
![]() $\mathcal {F}_{\tau _{j+1/2}}$
. Write
$\mathcal {F}_{\tau _{j+1/2}}$
. Write
![]() $\mathcal A$
for the set of vertices on
$\mathcal A$
for the set of vertices on
![]() $\partial \mathcal {F}_{\tau _{j+1/2}}$
that are connected to
$\partial \mathcal {F}_{\tau _{j+1/2}}$
that are connected to
![]() $P_1\cup P_3$
in
$P_1\cup P_3$
in
![]() $\omega ^{\prime }_{[\tau _{j+1/2}]}$
. Notice that due to the exploration procedure, for any edge
$\omega ^{\prime }_{[\tau _{j+1/2}]}$
. Notice that due to the exploration procedure, for any edge
![]() $uv$
with
$uv$
with
![]() $u \in \partial \mathcal {F}_{\tau _{j+1/2}}$
and
$u \in \partial \mathcal {F}_{\tau _{j+1/2}}$
and
![]() $v \in \mathcal {F}_{\tau _{j+1/2}}^c$
, v is connected in
$v \in \mathcal {F}_{\tau _{j+1/2}}^c$
, v is connected in
![]() $\omega ^{\prime }_{[\tau _{j+1/2}]}$
to
$\omega ^{\prime }_{[\tau _{j+1/2}]}$
to
![]() $P_1$
or
$P_1$
or
![]() $P_3$
. Thus,
$P_3$
. Thus,
![]() $\mathcal A$
is exactly the set of vertices
$\mathcal A$
is exactly the set of vertices
![]() $u \in \partial \mathcal {F}_{\tau _{j+1/2}}$
for which there exists a revealed edge
$u \in \partial \mathcal {F}_{\tau _{j+1/2}}$
for which there exists a revealed edge
![]() $uv$
with
$uv$
with
![]() $v \in \mathcal {F}_{\tau _{j+1/2}}^c$
that is open in
$v \in \mathcal {F}_{\tau _{j+1/2}}^c$
that is open in
![]() $\omega ^{\prime }_{[\tau _{j+1/2}]}$
. In particular, in the boundary conditions induced by
$\omega ^{\prime }_{[\tau _{j+1/2}]}$
. In particular, in the boundary conditions induced by
![]() $\omega ^{\prime }_{[\tau _{j+1/2}]}$
on
$\omega ^{\prime }_{[\tau _{j+1/2}]}$
on
![]() $\mathcal {F}_{\tau _{j+1/2}}$
, all vertices of
$\mathcal {F}_{\tau _{j+1/2}}$
, all vertices of
![]() $\mathcal A$
are wired together, and all other boundary vertices are free (that is, they are not wired to any other boundary vertices).
$\mathcal A$
are wired together, and all other boundary vertices are free (that is, they are not wired to any other boundary vertices).
In this case, we call
![]() $\tau _{j+1/2}$
promising if
$\tau _{j+1/2}$
promising if
Next, we turn our attention to the case where
![]() $\mathcal {F}_{\tau _{j+1/2}}$
is a flower domain. Write
$\mathcal {F}_{\tau _{j+1/2}}$
is a flower domain. Write
![]() $\mathcal {A}$
for the set of points on the dual petals of
$\mathcal {A}$
for the set of points on the dual petals of
![]() $\mathcal {F}_{\tau _{j+1/2}}$
that are connected to
$\mathcal {F}_{\tau _{j+1/2}}$
that are connected to
![]() $P_1$
or
$P_1$
or
![]() $P_3$
in
$P_3$
in
![]() $\omega ^{\prime }_{[\tau _{j+1/2}]}$
. By the same argument as in the previous case, in the boundary conditions imposed by
$\omega ^{\prime }_{[\tau _{j+1/2}]}$
. By the same argument as in the previous case, in the boundary conditions imposed by
![]() $\omega ^{\prime }_{[\tau _{j+1/2}]}$
on
$\omega ^{\prime }_{[\tau _{j+1/2}]}$
on
![]() $\mathcal {F}_{\tau _{j+1/2}}$
, there exists a single wired component formed of
$\mathcal {F}_{\tau _{j+1/2}}$
, there exists a single wired component formed of
![]() $\mathcal {A}$
along with all primal petals of
$\mathcal {A}$
along with all primal petals of
![]() $\mathcal {F}_{\tau _{j+1/2}}$
.
$\mathcal {F}_{\tau _{j+1/2}}$
.
If
![]() $\mathcal {F}_{\tau _{j+1/2}}$
is not
$\mathcal {F}_{\tau _{j+1/2}}$
is not
![]() $\delta $
-well-separated, then we say that
$\delta $
-well-separated, then we say that
![]() $\tau _{j+1/2}$
is not promising. If
$\tau _{j+1/2}$
is not promising. If
![]() $\mathcal {F}_{\tau _{j+1/2}}$
is
$\mathcal {F}_{\tau _{j+1/2}}$
is
![]() $\delta $
-well-separated and contains at least two primal petals that are not wired in
$\delta $
-well-separated and contains at least two primal petals that are not wired in
![]() $\omega _{[\tau _{j+1/2}]}$
, then we call
$\omega _{[\tau _{j+1/2}]}$
, then we call
![]() $\tau _{j+1/2}$
promising. Finally, if
$\tau _{j+1/2}$
promising. Finally, if
![]() $\mathcal {F}_{\tau _{j+1/2}}$
is
$\mathcal {F}_{\tau _{j+1/2}}$
is
![]() $\delta $
-well-separated and all its primal petals are wired together in
$\delta $
-well-separated and all its primal petals are wired together in
![]() $\omega _{[\tau _{j+1/2}]}$
, we call
$\omega _{[\tau _{j+1/2}]}$
, we call
![]() $\tau _{j+1/2}$
promising if
$\tau _{j+1/2}$
promising if
For formal reasons, set
![]() $\tau _{-1/2} = 0$
and call it promising. We now state two results that are instrumental in the proof of the theorem. Roughly speaking, the first one states that if
$\tau _{-1/2} = 0$
and call it promising. We now state two results that are instrumental in the proof of the theorem. Roughly speaking, the first one states that if
![]() $\tau _{j+1/2}$
is not promising, then it is very likely for T to arise before
$\tau _{j+1/2}$
is not promising, then it is very likely for T to arise before
![]() $\tau _{j+1}$
. The second lemma states that as soon as
$\tau _{j+1}$
. The second lemma states that as soon as
![]() $\tau _{j+1/2}$
is promising, there exists a coupling guaranteeing a fairly good probability that the flower domain on
$\tau _{j+1/2}$
is promising, there exists a coupling guaranteeing a fairly good probability that the flower domain on
![]() $\partial \Lambda _r$
is
$\partial \Lambda _r$
is
![]() $1/2$
-well-separated and the boundary conditions in
$1/2$
-well-separated and the boundary conditions in
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
induced on this domain correspond to a boosting pair.
$\omega '$
induced on this domain correspond to a boosting pair.
Lemma 4.4. For any
![]() $\varepsilon> 0$
, we may choose
$\varepsilon> 0$
, we may choose
![]() $\delta =\delta (\varepsilon )>0$
(independent of r, R, p,
$\delta =\delta (\varepsilon )>0$
(independent of r, R, p,
![]() $\mathcal {G}$
,
$\mathcal {G}$
,
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
) so that for every
$\xi '$
) so that for every
![]() $0 \le j < k$
,
$0 \le j < k$
,
Lemma 4.5. For any
![]() $\delta> 0$
, there exists
$\delta> 0$
, there exists
![]() $c(\delta )> 0$
with the following property. Fix some
$c(\delta )> 0$
with the following property. Fix some
![]() $-1 \le j \le k-1$
and a realisation of
$-1 \le j \le k-1$
and a realisation of
![]() $\tau _{j+1/2}$
,
$\tau _{j+1/2}$
,
![]() $\omega _{[\tau _{j+1/2}]}$
,
$\omega _{[\tau _{j+1/2}]}$
,
![]() $\omega ^{\prime }_{[\tau _{j+1/2}]}$
and
$\omega ^{\prime }_{[\tau _{j+1/2}]}$
and
![]() $\mathcal {F}_{\tau _{j+1/2}}$
for which
$\mathcal {F}_{\tau _{j+1/2}}$
for which
![]() $\tau _{j+1/2}$
is promising. Then there exists an increasing coupling
$\tau _{j+1/2}$
is promising. Then there exists an increasing coupling
![]() $\mathrm {P}$
of
$\mathrm {P}$
of
![]() $\phi _{\mathcal {F}_{\tau _{j+1/2}}}^{\omega _{[\tau _{j+1/2}]}}$
and
$\phi _{\mathcal {F}_{\tau _{j+1/2}}}^{\omega _{[\tau _{j+1/2}]}}$
and
![]() $\phi _{\mathcal {F}_{\tau _{j+1/2}}}^{\omega ^{\prime }_{[\tau _{j+1/2}]}}$
via decision trees and a stopping time
$\phi _{\mathcal {F}_{\tau _{j+1/2}}}^{\omega ^{\prime }_{[\tau _{j+1/2}]}}$
via decision trees and a stopping time
![]() $\sigma $
with the following property. When
$\sigma $
with the following property. When
![]() $\sigma <\infty $
,
$\sigma <\infty $
,
![]() $\mathcal {F}_{\sigma }$
is a
$\mathcal {F}_{\sigma }$
is a
![]() $1/2$
-well-separated inner flower domain on
$1/2$
-well-separated inner flower domain on
![]() $\Lambda _r$
, and the boundary conditions induced by
$\Lambda _r$
, and the boundary conditions induced by
![]() $\omega ^{\prime }_{[\sigma ]}$
on
$\omega ^{\prime }_{[\sigma ]}$
on
![]() $\mathcal {F}_{\sigma }$
are a boost of those induced by
$\mathcal {F}_{\sigma }$
are a boost of those induced by
![]() $\omega _{[\sigma ]}$
. Moreover,
$\omega _{[\sigma ]}$
. Moreover,
Remark 4.6. It is essential in the second lemma that
![]() $c(\delta )$
is allowed to depend on
$c(\delta )$
is allowed to depend on
![]() $\delta $
but that it only appears as a multiplicative constant in equation (4.1). Indeed, the upper bound in equation (4.1) depends on the ratio between the scales of
$\delta $
but that it only appears as a multiplicative constant in equation (4.1). Indeed, the upper bound in equation (4.1) depends on the ratio between the scales of
![]() $\mathcal {F}_{\tau _{j+1/2}}$
and
$\mathcal {F}_{\tau _{j+1/2}}$
and
![]() $\mathcal {F}_{\sigma }$
in a way that is uniform in
$\mathcal {F}_{\sigma }$
in a way that is uniform in
![]() $\delta $
.
$\delta $
.
Before proving the two lemmas, let us conclude the proof of the theorem. Fix
![]() $\varepsilon> 0$
so that
$\varepsilon> 0$
so that
![]() $\pi _4(p;r,4^j r) \geq (2\varepsilon )^{j}$
for all
$\pi _4(p;r,4^j r) \geq (2\varepsilon )^{j}$
for all
![]() $j \geq 0$
with
$j \geq 0$
with
![]() $4^j r \le L(p)$
. Due to equation (RSW),
$4^j r \le L(p)$
. Due to equation (RSW),
![]() $\varepsilon $
may be chosen independently of r or p. Let
$\varepsilon $
may be chosen independently of r or p. Let
![]() $\delta = \delta (\varepsilon )$
be the quantity given by Lemma 4.4 for this value of
$\delta = \delta (\varepsilon )$
be the quantity given by Lemma 4.4 for this value of
![]() $\varepsilon $
. Below,
$\varepsilon $
. Below,
![]() $c_0$
and
$c_0$
and
![]() $c_1$
stand for strictly positive constants that may depend on
$c_1$
stand for strictly positive constants that may depend on
![]() $\varepsilon $
but not on r, R or
$\varepsilon $
but not on r, R or
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
First, observe that due to Lemma 4.5 and Theorem 3.6, there exists
![]() $c_0> 0$
such that for any
$c_0> 0$
such that for any
![]() $1 \le j \le k$
,
$1 \le j \le k$
,
Indeed, the first inequality follows from the more general observation that
![]() $\mathbf P[T = \infty ]$
bounds the distance in total variation between the restrictions of
$\mathbf P[T = \infty ]$
bounds the distance in total variation between the restrictions of
![]() $\phi _{\mathcal {G}}^{\xi '}$
and
$\phi _{\mathcal {G}}^{\xi '}$
and
![]() $\phi _{\mathcal {G}}^{\xi }$
to
$\phi _{\mathcal {G}}^{\xi }$
to
![]() $\Lambda _r$
. For the second inequality, consider the increasing coupling of
$\Lambda _r$
. For the second inequality, consider the increasing coupling of
![]() $\phi _{\mathcal {G}}^{\xi '}$
and
$\phi _{\mathcal {G}}^{\xi '}$
and
![]() $\phi _{\mathcal {G}}^{\xi }$
obtained by following
$\phi _{\mathcal {G}}^{\xi }$
obtained by following
![]() $\mathbf P$
up to the stopping time
$\mathbf P$
up to the stopping time
![]() $\tau _{k-j-1/2}$
and then, if
$\tau _{k-j-1/2}$
and then, if
![]() $\tau _{k-j-1/2}$
is promising, using the coupling
$\tau _{k-j-1/2}$
is promising, using the coupling
![]() ${\mathrm P}$
of Lemma 4.5 and applying Theorem 3.6.
${\mathrm P}$
of Lemma 4.5 and applying Theorem 3.6.
Next, we claim that there exists some
![]() $\ell \geq 1$
such that if
$\ell \geq 1$
such that if
![]() $T = \infty $
, then with positive probability, there exists one promising stopping time among the last
$T = \infty $
, then with positive probability, there exists one promising stopping time among the last
![]() $\ell $
ones. It is essential here that
$\ell $
ones. It is essential here that
![]() $\ell $
is independent of
$\ell $
is independent of
![]() $R/r$
. Indeed, fix
$R/r$
. Indeed, fix
![]() $\ell \geq 1$
, and observe that
$\ell \geq 1$
, and observe that
 $$ \begin{align*} &\mathbf P[T = \infty \text{ and } \tau_{k-1/2},\dots,\tau_{k-\ell+1/2} \text{ not promising}] \\ &\quad = \sum_{j = \ell}^{k} \mathbf P[T = \infty ;~\tau_{k-1/2},\dots,\tau_{k-j+1/2} \text{ not promising; } \tau_{k-j-1/2} \text{ promising}] \\ &\quad \le \sum_{j = \ell}^{k}\varepsilon^{j-1} \mathbf P[\tau_{k-j-1/2} \text{ promising}] \\ &\quad \le c_0 \, \mathbf P[T = \infty]\, \sum_{j = \ell}^{k} 2^{-j} \le c_0 \, 2^{-\ell+1} \, \mathbf P[T = \infty]. \end{align*} $$
$$ \begin{align*} &\mathbf P[T = \infty \text{ and } \tau_{k-1/2},\dots,\tau_{k-\ell+1/2} \text{ not promising}] \\ &\quad = \sum_{j = \ell}^{k} \mathbf P[T = \infty ;~\tau_{k-1/2},\dots,\tau_{k-j+1/2} \text{ not promising; } \tau_{k-j-1/2} \text{ promising}] \\ &\quad \le \sum_{j = \ell}^{k}\varepsilon^{j-1} \mathbf P[\tau_{k-j-1/2} \text{ promising}] \\ &\quad \le c_0 \, \mathbf P[T = \infty]\, \sum_{j = \ell}^{k} 2^{-j} \le c_0 \, 2^{-\ell+1} \, \mathbf P[T = \infty]. \end{align*} $$
(Note that this is where we use the convention that
![]() $\tau _{-1/2}$
is promising.) The first inequality is obtained by repeated applications of Lemma 4.4; the second is due to equation (4.2). Thus, if we fix
$\tau _{-1/2}$
is promising.) The first inequality is obtained by repeated applications of Lemma 4.4; the second is due to equation (4.2). Thus, if we fix
![]() $\ell \geq - \log _2 c_0 + 2$
, then indeed
$\ell \geq - \log _2 c_0 + 2$
, then indeed
We are now ready to define the coupling
![]() $\mathbb {P}$
of the theorem. Follow
$\mathbb {P}$
of the theorem. Follow
![]() $\mathbf P$
up to the first promising stopping time
$\mathbf P$
up to the first promising stopping time
![]() $\tau _{j+1/2}$
with
$\tau _{j+1/2}$
with
![]() $j \geq k-\ell $
. Then follow the coupling
$j \geq k-\ell $
. Then follow the coupling
![]() ${\mathrm P}$
of Lemma 4.5; write
${\mathrm P}$
of Lemma 4.5; write
![]() $\tau _{\text {final}}$
for the stopping time described in said lemma. If
$\tau _{\text {final}}$
for the stopping time described in said lemma. If
![]() $\mathbf P$
does not encounter a promising stopping time
$\mathbf P$
does not encounter a promising stopping time
![]() $\tau _{j+1/2}$
with
$\tau _{j+1/2}$
with
![]() $j \geq k-\ell $
, set
$j \geq k-\ell $
, set
![]() $\tau _{\text {final}} = \infty $
. Then due to Lemma 4.5 and equation (4.3),
$\tau _{\text {final}} = \infty $
. Then due to Lemma 4.5 and equation (4.3),
Since
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $\ell $
are independent of r and R, the right-hand side is bounded away from
$\ell $
are independent of r and R, the right-hand side is bounded away from
![]() $0$
uniformly in
$0$
uniformly in
![]() $r \le R/4$
. Moreover,
$r \le R/4$
. Moreover,
![]() $\tau _{\mathrm {final}}$
satisfies the conditions stated in the theorem. Multiply the above by
$\tau _{\mathrm {final}}$
satisfies the conditions stated in the theorem. Multiply the above by
![]() $\mathbb {P}[T = \infty ] = \mathbb {P}[\zeta \neq \zeta ']$
to obtain the desired inequality.
$\mathbb {P}[T = \infty ] = \mathbb {P}[\zeta \neq \zeta ']$
to obtain the desired inequality.
Proof of Lemma 4.4
Fix
![]() $\varepsilon> 0$
, and fix a realisation of
$\varepsilon> 0$
, and fix a realisation of
![]() $\tau _j$
,
$\tau _j$
,
![]() $\omega _{[\tau _j]}$
and
$\omega _{[\tau _j]}$
and
![]() $\omega ^{\prime }_{[\tau _j]}$
. Lemma 3.2 ensures that by choosing
$\omega ^{\prime }_{[\tau _j]}$
. Lemma 3.2 ensures that by choosing
![]() $\delta> 0$
small enough, we have
$\delta> 0$
small enough, we have
Suppose now that either
![]() $\mathcal {F}_{\tau _{j+1/2}}$
is a
$\mathcal {F}_{\tau _{j+1/2}}$
is a
![]() $\delta $
-well-separated flower domain or
$\delta $
-well-separated flower domain or
![]() $\omega _{\tau _{j+1/2}}$
induced free boundary conditions on it. In either case, if
$\omega _{\tau _{j+1/2}}$
induced free boundary conditions on it. In either case, if
![]() $\tau _{j+1/2}$
is not promising, it is because
$\tau _{j+1/2}$
is not promising, it is because
![]() $\mathcal {A}$
has a conditionally small probability of being connected to
$\mathcal {A}$
has a conditionally small probability of being connected to
![]() $\Lambda _{\rho }$
in
$\Lambda _{\rho }$
in
![]() $\omega '$
.
$\omega '$
.
Continue the coupling
![]() $\mathbf P$
by revealing first the connected component
$\mathbf P$
by revealing first the connected component
![]() $\mathsf {C}$
of
$\mathsf {C}$
of
![]() $\mathcal {A}$
in
$\mathcal {A}$
in
![]() $\omega ' \cap \Lambda _{\rho }^c$
and then the rest of the connected components of
$\omega ' \cap \Lambda _{\rho }^c$
and then the rest of the connected components of
![]() $P_1$
and
$P_1$
and
![]() $P_3$
. If
$P_3$
. If
![]() $\mathsf {C}$
does not reach
$\mathsf {C}$
does not reach
![]() $\Lambda _{\rho }$
, then it is entirely surrounded by closed edges of
$\Lambda _{\rho }$
, then it is entirely surrounded by closed edges of
![]() $\omega '$
. Thus, the boundary conditions in
$\omega '$
. Thus, the boundary conditions in
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
on the complement of
$\omega '$
on the complement of
![]() $\mathsf {C}$
are identical, which is to say that T occurs before
$\mathsf {C}$
are identical, which is to say that T occurs before
![]() $\tau _{j+1}$
. Thus
$\tau _{j+1}$
. Thus
By choosing
![]() $\delta> 0$
small enough, the right-hand side may be rendered smaller than
$\delta> 0$
small enough, the right-hand side may be rendered smaller than
![]() $\varepsilon /2$
. Apply the union bound to obtain the desired inequality.
$\varepsilon /2$
. Apply the union bound to obtain the desired inequality.
Proof of Lemma 4.5
Fix
![]() $\delta> 0$
and a realisation
$\delta> 0$
and a realisation
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() $\mathcal {F}_{\tau _{j+1/2}}$
, with boundary conditions
$\mathcal {F}_{\tau _{j+1/2}}$
, with boundary conditions
![]() $\zeta $
and
$\zeta $
and
![]() $\zeta '$
induced by
$\zeta '$
induced by
![]() $\omega _{[\tau _{j+1/2}]}$
and
$\omega _{[\tau _{j+1/2}]}$
and
![]() $\omega ^{\prime }_{[\tau _{j+1/2}]}$
, respectively, on
$\omega ^{\prime }_{[\tau _{j+1/2}]}$
, respectively, on
![]() $\mathcal {F}$
. Assume that
$\mathcal {F}$
. Assume that
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() $\zeta $
and
$\zeta $
and
![]() $\zeta '$
satisfy the assumptions of the lemma. Three situations need to be analysed; we will proceed in increasing order of difficulty. Set
$\zeta '$
satisfy the assumptions of the lemma. Three situations need to be analysed; we will proceed in increasing order of difficulty. Set
![]() $\rho :=4^{k-j}r$
.
$\rho :=4^{k-j}r$
.
Case 1:
![]() $\mathcal {F}$
is a flower domain with two petals wired in
$\mathcal {F}$
is a flower domain with two petals wired in
![]() $\zeta '$
but not in
$\zeta '$
but not in
![]() $\zeta $
. First, assume that
$\zeta $
. First, assume that
![]() $\mathcal {F}$
is a
$\mathcal {F}$
is a
![]() $\delta $
-well-separated flower domain containing two primal petals
$\delta $
-well-separated flower domain containing two primal petals
![]() $P_i$
and
$P_i$
and
![]() $P_j$
that are not wired together in
$P_j$
that are not wired together in
![]() $\zeta $
. Recall that
$\zeta $
. Recall that
![]() $P_i$
and
$P_i$
and
![]() $P_j$
are necessarily wired together in
$P_j$
are necessarily wired together in
![]() $\zeta '$
.
$\zeta '$
.
Then
![]() $\mathrm {P}$
is constructed as follows. Attempt to explore the double four-petal flower domain
$\mathrm {P}$
is constructed as follows. Attempt to explore the double four-petal flower domain
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
between
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
between
![]() $\Lambda _r$
and
$\Lambda _r$
and
![]() $\Lambda _{2r}$
for the configuration
$\Lambda _{2r}$
for the configuration
![]() $\omega $
. If no such double four-petal flower domain exists, set
$\omega $
. If no such double four-petal flower domain exists, set
![]() $\sigma = \infty $
, and reveal the remaining edges in lexicographical order. If it exists, reveal the configurations in
$\sigma = \infty $
, and reveal the remaining edges in lexicographical order. If it exists, reveal the configurations in
![]() $\mathcal {F}_{\mathrm {out}} \cap \mathcal {F}$
, and let
$\mathcal {F}_{\mathrm {out}} \cap \mathcal {F}$
, and let
![]() $\sigma $
be the stopping time marking the end of this stage.
$\sigma $
be the stopping time marking the end of this stage.
Let H be the event that the double four-petal flower domain
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
exists and that the two primal petals
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
exists and that the two primal petals
![]() $P_1^{\mathrm {out}}$
and
$P_1^{\mathrm {out}}$
and
![]() $P_3^{\mathrm {out}}$
of
$P_3^{\mathrm {out}}$
of
![]() $\mathcal {F}_{\mathrm {out}}$
are connected in
$\mathcal {F}_{\mathrm {out}}$
are connected in
![]() $\omega ^{\prime }_{[\sigma ]}$
to
$\omega ^{\prime }_{[\sigma ]}$
to
![]() $P_i$
and
$P_i$
and
![]() $P_j$
, respectively, while
$P_j$
, respectively, while
![]() $P_i$
and
$P_i$
and
![]() $P_j$
are not connected to each other or any primal petal of
$P_j$
are not connected to each other or any primal petal of
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\omega _{[\sigma ]}$
. It is a standard consequence of the separation of arms that there exists a constant
$\omega _{[\sigma ]}$
. It is a standard consequence of the separation of arms that there exists a constant
![]() $c(\delta )> 0$
such that
$c(\delta )> 0$
such that
Lemma 3.4 ensures that the event in the conditioning has uniformly positive probability, and hence so does H. Finally, notice that when H occurs, the boundary conditions induced by
![]() $\omega ^{\prime }_{[\sigma ]}$
on
$\omega ^{\prime }_{[\sigma ]}$
on
![]() $\partial \mathcal {F}_{\mathrm { in}}$
are a boost of those induced by
$\partial \mathcal {F}_{\mathrm { in}}$
are a boost of those induced by
![]() $\omega _{[\sigma ]}$
. This concludes the proof in this case.
$\omega _{[\sigma ]}$
. This concludes the proof in this case.
Case 2:
![]() $\mathcal {F}$
is not a flower domain. Next, assume that
$\mathcal {F}$
is not a flower domain. Next, assume that
![]() $\mathcal {F}$
is not a flower domain and therefore that
$\mathcal {F}$
is not a flower domain and therefore that
![]() $\zeta = 0$
. Start the coupling by attempting to reveal the double four-petal flower domains
$\zeta = 0$
. Start the coupling by attempting to reveal the double four-petal flower domains
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
between
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
between
![]() $\Lambda _{r}$
and
$\Lambda _{r}$
and
![]() $\Lambda _{2r}$
and
$\Lambda _{2r}$
and
![]() $(\overline {\mathcal {F}}_{\mathrm {in}}, \overline {\mathcal {F}}_{\mathrm {out}})$
between
$(\overline {\mathcal {F}}_{\mathrm {in}}, \overline {\mathcal {F}}_{\mathrm {out}})$
between
![]() $\Lambda _{\rho }$
and
$\Lambda _{\rho }$
and
![]() $\Lambda _{3\rho /2}$
, respectively, for the configuration
$\Lambda _{3\rho /2}$
, respectively, for the configuration
![]() $\omega $
(if
$\omega $
(if
![]() $\rho = r$
, only perform the latter exploration). If these two double four-petal flower domains exist, proceed by revealing the configurations in
$\rho = r$
, only perform the latter exploration). If these two double four-petal flower domains exist, proceed by revealing the configurations in
![]() $\overline {\mathcal {F}}_{\mathrm { in}}\cap {\mathcal {F}}_{\mathrm {out}}$
; call
$\overline {\mathcal {F}}_{\mathrm { in}}\cap {\mathcal {F}}_{\mathrm {out}}$
; call
![]() $\sigma _0$
the stopping time marking the end of this stage.
$\sigma _0$
the stopping time marking the end of this stage.
Let H be the event that the two double four-petal flower domains above exist, that
![]() $\overline {P}_1^{\mathrm {in}}$
is connected to
$\overline {P}_1^{\mathrm {in}}$
is connected to
![]() ${P}_1^{\mathrm {out}}$
and
${P}_1^{\mathrm {out}}$
and
![]() $\overline {P}_3^{\mathrm {in}}$
to
$\overline {P}_3^{\mathrm {in}}$
to
![]() ${P}_3^{\mathrm {out}}$
in
${P}_3^{\mathrm {out}}$
in
![]() $\omega \cap \overline {\mathcal {F}}_{\mathrm {in}}\cap {\mathcal {F}}_{\mathrm {out}}$
and that
$\omega \cap \overline {\mathcal {F}}_{\mathrm {in}}\cap {\mathcal {F}}_{\mathrm {out}}$
and that
![]() $\overline {P}_2^{\mathrm {in}}$
is connected to
$\overline {P}_2^{\mathrm {in}}$
is connected to
![]() ${P}_2^{\mathrm {out}}$
and
${P}_2^{\mathrm {out}}$
and
![]() $\overline {P}_4^{\mathrm {in}}$
to
$\overline {P}_4^{\mathrm {in}}$
to
![]() ${P}_4^{\mathrm {out}}$
in
${P}_4^{\mathrm {out}}$
in
![]() $\omega ^* \cap \overline {\mathcal {F}}_{\mathrm {in}}\cap {\mathcal {F}}_{\mathrm {out}}$
. As in the first case, it is a consequence of the separation of arms and Lemma 3.4 that there exists
$\omega ^* \cap \overline {\mathcal {F}}_{\mathrm {in}}\cap {\mathcal {F}}_{\mathrm {out}}$
. As in the first case, it is a consequence of the separation of arms and Lemma 3.4 that there exists
![]() $c_0> 0$
such that
$c_0> 0$
such that
Next we reveal the configurations in
![]() $\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
in a fashion described below. Write
$\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
in a fashion described below. Write
![]() $H'$
for the event that
$H'$
for the event that
![]() $\overline {P}_1^{\mathrm {out}}$
and
$\overline {P}_1^{\mathrm {out}}$
and
![]() $\overline {P}_3^{\mathrm {out}}$
are connected to each other in
$\overline {P}_3^{\mathrm {out}}$
are connected to each other in
![]() $\omega ' \cap \overline {\mathcal {F}}_{\mathrm {out}}$
but not in
$\omega ' \cap \overline {\mathcal {F}}_{\mathrm {out}}$
but not in
![]() $\omega \cap \overline {\mathcal {F}}_{\mathrm {out}}$
. Observe that if H and
$\omega \cap \overline {\mathcal {F}}_{\mathrm {out}}$
. Observe that if H and
![]() $H'$
occur, then the boundary conditions induced on
$H'$
occur, then the boundary conditions induced on
![]() $\mathcal {F}_{\mathrm {in}}$
by
$\mathcal {F}_{\mathrm {in}}$
by
![]() $\omega \cap \mathcal {F}_{\mathrm {in}}$
and
$\omega \cap \mathcal {F}_{\mathrm {in}}$
and
![]() $\omega '\cap \mathcal {F}_{\mathrm {in}}$
, respectively, form a boosting pair. At this stage, it will be useful to introduce the following claim.
$\omega '\cap \mathcal {F}_{\mathrm {in}}$
, respectively, form a boosting pair. At this stage, it will be useful to introduce the following claim.
Claim 4.7. There exist
![]() $c_1 = c_1(\delta )> 0$
and four disjoint domains
$c_1 = c_1(\delta )> 0$
and four disjoint domains
![]() $D_1,\dots , D_4$
contained in
$D_1,\dots , D_4$
contained in
![]() $\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
(they depend on
$\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
(they depend on
![]() $\mathcal {A}$
) such that
$\mathcal {A}$
) such that
where
![]() $\omega ^{\prime }_{[\sigma _0]}, 0$
(and
$\omega ^{\prime }_{[\sigma _0]}, 0$
(and
![]() $\omega _{[\sigma _0]}, 1$
) are the boundary conditions on
$\omega _{[\sigma _0]}, 1$
) are the boundary conditions on
![]() $\partial D_i$
induced by the configuration equal to
$\partial D_i$
induced by the configuration equal to
![]() $\omega '$
(and
$\omega '$
(and
![]() $\omega $
, respectively), completed in the unrevealed region of
$\omega $
, respectively), completed in the unrevealed region of
![]() $D_i^c$
by closed (respectively, open) edges.
$D_i^c$
by closed (respectively, open) edges.
Essentially,
![]() $D_1,\dots , D_4$
should be viewed as disjoint tubes connecting the petals
$D_1,\dots , D_4$
should be viewed as disjoint tubes connecting the petals
![]() $\overline {P}_i^{\mathrm {out}}$
to four disjoint regions of
$\overline {P}_i^{\mathrm {out}}$
to four disjoint regions of
![]() $\partial \mathcal {F}$
. Each tube should be considered thick enough to contain either primal or dual paths with positive probability (for instance, we may think of each tube as being constructed using a finite number of rectangles of aspect ratio
$\partial \mathcal {F}$
. Each tube should be considered thick enough to contain either primal or dual paths with positive probability (for instance, we may think of each tube as being constructed using a finite number of rectangles of aspect ratio
![]() $2$
). Moreover, we should further require that the regions of
$2$
). Moreover, we should further require that the regions of
![]() $\partial \mathcal {F}$
contained in
$\partial \mathcal {F}$
contained in
![]() $D_1$
and
$D_1$
and
![]() $D_3$
contain sufficiently many points of
$D_3$
contain sufficiently many points of
![]() $\mathcal {A}$
that a connection reaches these points with positive probability. Let us delay the proof of this technical result and finish the proof of the lemma in this case.
$\mathcal {A}$
that a connection reaches these points with positive probability. Let us delay the proof of this technical result and finish the proof of the lemma in this case.
Fix the four domains
![]() $D_1,\dots , D_4$
given by the claim. Reveal the configuration in
$D_1,\dots , D_4$
given by the claim. Reveal the configuration in
![]() $\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
by first revealing the configurations outside
$\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
by first revealing the configurations outside
![]() $D_1,\dots , D_4$
and then in each of the quads
$D_1,\dots , D_4$
and then in each of the quads
![]() $D_1,\dots D_4$
. Due to equation (CBC),
$D_1,\dots D_4$
. Due to equation (CBC),
whenever
![]() $(\omega _{[\sigma _0]},\omega _{[\sigma _0]}')$
are such that H occur. Notice now that since all points of
$(\omega _{[\sigma _0]},\omega _{[\sigma _0]}')$
are such that H occur. Notice now that since all points of
![]() $\mathcal {A}$
are wired together in
$\mathcal {A}$
are wired together in
![]() $\omega '$
outside of
$\omega '$
outside of
![]() $\mathcal {F}$
but the entire boundary of
$\mathcal {F}$
but the entire boundary of
![]() $\mathcal {F}$
is free in
$\mathcal {F}$
is free in
![]() $\omega $
, if the event above occurs, then so does
$\omega $
, if the event above occurs, then so does
![]() $H'$
. Thus,
$H'$
. Thus,
If we now set
![]() $\sigma $
to be the stopping time at which all of
$\sigma $
to be the stopping time at which all of
![]() $\mathcal {F}_{\mathrm {in}}^c$
has been revealed and
$\mathcal {F}_{\mathrm {in}}^c$
has been revealed and
![]() $H'$
has been found to occur, and
$H'$
has been found to occur, and
![]() $\sigma = \infty $
otherwise, then
$\sigma = \infty $
otherwise, then
![]() $\sigma $
satisfies the properties claimed in the lemma.
$\sigma $
satisfies the properties claimed in the lemma.
Case 3:
![]() $\mathcal {F}$
is a flower domain, but the petals wired in
$\mathcal {F}$
is a flower domain, but the petals wired in
![]() $\zeta '$
are wired in
$\zeta '$
are wired in
![]() $\zeta $
. The construction in this case is very similar to that of Case 2. Start by revealing the double four-petal flower domains
$\zeta $
. The construction in this case is very similar to that of Case 2. Start by revealing the double four-petal flower domains
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
between
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
between
![]() $\Lambda _{r}$
and
$\Lambda _{r}$
and
![]() $\Lambda _{2r}$
and
$\Lambda _{2r}$
and
![]() $(\overline {\mathcal {F}}_{\mathrm {in}}, \overline {\mathcal {F}}_{\mathrm {out}})$
between
$(\overline {\mathcal {F}}_{\mathrm {in}}, \overline {\mathcal {F}}_{\mathrm {out}})$
between
![]() $\Lambda _{\rho }$
and
$\Lambda _{\rho }$
and
![]() $\Lambda _{3\rho /2}$
, respectively, for the configuration
$\Lambda _{3\rho /2}$
, respectively, for the configuration
![]() $\omega $
. Define H and
$\omega $
. Define H and
![]() $H'$
in the same way as in Case 2. The only difference is in the way in which the configurations in
$H'$
in the same way as in Case 2. The only difference is in the way in which the configurations in
![]() $\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
are revealed so that
$\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
are revealed so that
![]() $\mathrm {P}[H'\,|\, H]$
is bounded below by a constant depending only on
$\mathrm {P}[H'\,|\, H]$
is bounded below by a constant depending only on
![]() $\delta $
.
$\delta $
.
Write
![]() $P_1,\dots , P_{2k}$
for the petals of
$P_1,\dots , P_{2k}$
for the petals of
![]() $\mathcal {F}$
. By the union bound and the assumption on
$\mathcal {F}$
. By the union bound and the assumption on
![]() $\mathcal {A}$
, there exists a free petal
$\mathcal {A}$
, there exists a free petal
![]() $P_j$
such that
$P_j$
such that
Recall that
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $\delta $
-well-separated and therefore k is bounded in terms of
$\delta $
-well-separated and therefore k is bounded in terms of
![]() $\delta $
only. A construction similar to that of the claim may be performed, with
$\delta $
only. A construction similar to that of the claim may be performed, with
![]() $\mathcal {A}$
replaced by
$\mathcal {A}$
replaced by
![]() $\mathcal {A} \cap P_j$
and
$\mathcal {A} \cap P_j$
and
![]() $\partial \mathcal {F}$
replaced by
$\partial \mathcal {F}$
replaced by
![]() $P_j$
. We conclude in the same way as in Case 2.
$P_j$
. We conclude in the same way as in Case 2.
We now turn to the proof of Claim 4.7. This type of construction is usually tedious because of the general form of
![]() $\mathcal {F}$
but may be performed fairly explicitly. We warn the reader of the difficulties arising from the potential bottlenecks of
$\mathcal {F}$
but may be performed fairly explicitly. We warn the reader of the difficulties arising from the potential bottlenecks of
![]() $\mathcal {F}$
and the fact that equation (RSW) is not valid with arbitrary boundary conditions in arbitrary quads when
$\mathcal {F}$
and the fact that equation (RSW) is not valid with arbitrary boundary conditions in arbitrary quads when
![]() $q=4$
. Nevertheless, with sufficient care, the domains
$q=4$
. Nevertheless, with sufficient care, the domains
![]() $D_1,\dots ,D_4$
may be constructed as unions of small squares
$D_1,\dots ,D_4$
may be constructed as unions of small squares
![]() $\Lambda _{c \rho n}(x)$
with
$\Lambda _{c \rho n}(x)$
with
![]() $x \in c\rho \mathbb {Z}^2$
and
$x \in c\rho \mathbb {Z}^2$
and
![]() $c> 0$
a small constant independent of
$c> 0$
a small constant independent of
![]() $\rho $
. We propose below an alternative, more innovative construction of
$\rho $
. We propose below an alternative, more innovative construction of
![]() $D_1,\dots , D_4$
. We will use the following result from [Reference Duminil-Copin, Manolescu and TassionDMT20] (see Remark 4.2 to be precise).
$D_1,\dots , D_4$
. We will use the following result from [Reference Duminil-Copin, Manolescu and TassionDMT20] (see Remark 4.2 to be precise).
The extremal distance between the arcs
![]() $(ab)$
and
$(ab)$
and
![]() $(cd)$
of a quad
$(cd)$
of a quad
![]() $(\mathcal {D}, a,b,c,d)$
is the unique value
$(\mathcal {D}, a,b,c,d)$
is the unique value
![]() $\ell = \ell _{\mathcal {D}}[(ab),(cd)]$
such that there exists a conformal transformation
$\ell = \ell _{\mathcal {D}}[(ab),(cd)]$
such that there exists a conformal transformation
![]() $\psi $
from
$\psi $
from
![]() $\mathcal {D}$
(seen as a domain in the continuum) to
$\mathcal {D}$
(seen as a domain in the continuum) to
![]() $(0, 1)\times (0, \ell )$
, with
$(0, 1)\times (0, \ell )$
, with
![]() $a, b, c, d$
being mapped (by the continuous extension of
$a, b, c, d$
being mapped (by the continuous extension of
![]() $\psi $
) to the corners of
$\psi $
) to the corners of
![]() $[0, 1] \times [0, \ell ]$
, in counterclockwise order, starting with the lower-left corner.
$[0, 1] \times [0, \ell ]$
, in counterclockwise order, starting with the lower-left corner.
Proposition 4.8 (RSW in terms of extremal distance)
For all
![]() $L> 0$
, there exists
$L> 0$
, there exists
![]() $\eta (L)>0$
such that for all
$\eta (L)>0$
such that for all
![]() $1\le q\le 4$
,
$1\le q\le 4$
,
![]() $p \in (0,1)$
,
$p \in (0,1)$
,
![]() $R < L(p)$
and
$R < L(p)$
and
![]() $(\mathcal {D}, a,b,c,d)$
a discrete quad contained in
$(\mathcal {D}, a,b,c,d)$
a discrete quad contained in
![]() $\Lambda _R$
, if
$\Lambda _R$
, if
![]() $\ell _{\mathcal {D}}[(ab),(cd)] \le L$
, then
$\ell _{\mathcal {D}}[(ab),(cd)] \le L$
, then
where
![]() $1/0$
denotes the boundary condition on
$1/0$
denotes the boundary condition on
![]() $\mathcal {D}$
, where the arcs
$\mathcal {D}$
, where the arcs
![]() $(ab)$
and
$(ab)$
and
![]() $(cd)$
are wired and the rest of the boundary is free.
$(cd)$
are wired and the rest of the boundary is free.
While the result is stated only for
![]() $p=p_c$
in [Reference Duminil-Copin, Manolescu and TassionDMT20], the reader will easily check in the corresponding paper that the proof extends to the near-critical regime.
$p=p_c$
in [Reference Duminil-Copin, Manolescu and TassionDMT20], the reader will easily check in the corresponding paper that the proof extends to the near-critical regime.
Proof of Claim 4.7
Write
![]() $B_s$
for the euclidean ball of
$B_s$
for the euclidean ball of
![]() $\mathbb {R}^2$
of radius s centred at
$\mathbb {R}^2$
of radius s centred at
![]() $0$
and
$0$
and
![]() $B_s(z)$
for its translate by
$B_s(z)$
for its translate by
![]() $z \in \mathbb {R}^2$
. Let
$z \in \mathbb {R}^2$
. Let
![]() $\psi $
be a conformal map from
$\psi $
be a conformal map from
![]() $\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
to some
$\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
to some
![]() $B_1 \smallsetminus B_s$
. The existence of such a map is given by the uniformisation theorem for the topological annulus
$B_1 \smallsetminus B_s$
. The existence of such a map is given by the uniformisation theorem for the topological annulus
![]() $\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
. Note that s is determined by
$\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
. Note that s is determined by
![]() $\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
. Moreover, since
$\mathcal {F} \cap \overline {\mathcal {F}}_{\mathrm {out}}$
. Moreover, since
![]() $\partial \mathcal {F}$
intersects
$\partial \mathcal {F}$
intersects
![]() $\Lambda _{2\rho }$
and
$\Lambda _{2\rho }$
and
![]() $\partial \overline {\mathcal {F}}$
is contained in
$\partial \overline {\mathcal {F}}$
is contained in
![]() $\mathrm {Ann}(\rho ,\frac 32\rho )$
, s is bounded uniformly away from
$\mathrm {Ann}(\rho ,\frac 32\rho )$
, s is bounded uniformly away from
![]() $0$
and
$0$
and
![]() $1$
, and the endpoints of
$1$
, and the endpoints of
![]() $P_1,\dots ,P_4$
are far away from each other.
$P_1,\dots ,P_4$
are far away from each other.
Fix some small positive constant
![]() $c_0 = c_0(\delta ) < (1-s)/16$
, which will be chosen below and will depend only on
$c_0 = c_0(\delta ) < (1-s)/16$
, which will be chosen below and will depend only on
![]() $\delta $
. Let
$\delta $
. Let
![]() $a_0,\dots , a_K = a_0$
(with
$a_0,\dots , a_K = a_0$
(with
![]() $K = 2\pi /c_0$
) be points on the circle
$K = 2\pi /c_0$
) be points on the circle
![]() $\partial B_1$
indexed in counterclockwise order and at a distance
$\partial B_1$
indexed in counterclockwise order and at a distance
![]() $c_0$
from each other. Write
$c_0$
from each other. Write
![]() $(a_{i}a_{i+1})$
for the arc of
$(a_{i}a_{i+1})$
for the arc of
![]() $\partial B_1$
contained between
$\partial B_1$
contained between
![]() $a_i$
and
$a_i$
and
![]() $a_{i+1}$
; identify
$a_{i+1}$
; identify
![]() $\psi ^{-1}(a_{i}a_{i+1})$
to the corresponding vertices of
$\psi ^{-1}(a_{i}a_{i+1})$
to the corresponding vertices of
![]() $\partial \mathcal {F}$
. Let
$\partial \mathcal {F}$
. Let
![]() $\mathcal {A}_i:=\mathcal {A} \cap \psi ^{-1}(a_{i}a_{i+1})$
.
$\mathcal {A}_i:=\mathcal {A} \cap \psi ^{-1}(a_{i}a_{i+1})$
.
Next, we argue that there exist two indices
![]() $i,j$
with
$i,j$
with
![]() $|i - j| \geq 8$
(modulo K) such that
$|i - j| \geq 8$
(modulo K) such that
 $$ \begin{align} \phi_{\mathcal{F}}^{\zeta'} [\mathcal{A}_i \longleftrightarrow \psi^{-1}(B_{2c_0}(a_i))^c] &\geq c_0\delta/2,\nonumber\\ \phi_{\mathcal{F}}^{\zeta'} [\mathcal{A}_j\longleftrightarrow \psi^{-1}(B_{2c_0}(a_j))^c] &\geq c_0\delta/2. \end{align} $$
$$ \begin{align} \phi_{\mathcal{F}}^{\zeta'} [\mathcal{A}_i \longleftrightarrow \psi^{-1}(B_{2c_0}(a_i))^c] &\geq c_0\delta/2,\nonumber\\ \phi_{\mathcal{F}}^{\zeta'} [\mathcal{A}_j\longleftrightarrow \psi^{-1}(B_{2c_0}(a_j))^c] &\geq c_0\delta/2. \end{align} $$
Indeed, if the above fails, then there necessarily exists i such that for all
![]() $j \notin \{i,\dots , i+7\}$
,
$j \notin \{i,\dots , i+7\}$
,
Assuming that this is the case, explore the open cluster
![]() $\mathbf C$
of
$\mathbf C$
of
![]() $\mathcal {A} \smallsetminus \psi ^{-1}(a_i a_{i+8})$
. Due to the small value of
$\mathcal {A} \smallsetminus \psi ^{-1}(a_i a_{i+8})$
. Due to the small value of
![]() $c_0$
and to the assumption above, we conclude by the union bound that
$c_0$
and to the assumption above, we conclude by the union bound that
If
![]() $\mathbf C$
does not intersect
$\mathbf C$
does not intersect
![]() $\Lambda _{\rho }$
, the measure on
$\Lambda _{\rho }$
, the measure on
![]() $\mathcal {F}\smallsetminus \mathbf C$
obtained by conditioning on
$\mathcal {F}\smallsetminus \mathbf C$
obtained by conditioning on
![]() $\mathbf C$
has free boundary conditions for all vertices adjacent to
$\mathbf C$
has free boundary conditions for all vertices adjacent to
![]() $\mathbf C$
. Then due to Proposition 4.8 applied repeatedly to the dual model, we conclude that for
$\mathbf C$
. Then due to Proposition 4.8 applied repeatedly to the dual model, we conclude that for
![]() $c_0$
small enough,
$c_0$
small enough,
Combining equations (4.8) and (4.9), we conclude that
![]() $\phi _{\mathcal {F}}^{\zeta '} [\mathcal {A} \leftrightarrow \Lambda _{\rho }] < \delta $
, which contradicts the assumption that the stopping time at which
$\phi _{\mathcal {F}}^{\zeta '} [\mathcal {A} \leftrightarrow \Lambda _{\rho }] < \delta $
, which contradicts the assumption that the stopping time at which
![]() $\mathcal {F}$
was discovered was promising. Thus the existence of
$\mathcal {F}$
was discovered was promising. Thus the existence of
![]() $i,j$
as above, satisfying equation (4.7), is proved.
$i,j$
as above, satisfying equation (4.7), is proved.
For what comes next, we refer to Figure 9. Set
where the quads
![]() $(D_k',a_k',b_k',c_k',d_k')$
satisfy:
$(D_k',a_k',b_k',c_k',d_k')$
satisfy:
-
•
 $D^{\prime }_k\subset B_1\smallsetminus B_s$
for every k;
$D^{\prime }_k\subset B_1\smallsetminus B_s$
for every k; -
• the extremal lengths
 $\ell _{D_k}[(a_kb_k),(c_kd_k)]$
belong to
$\ell _{D_k}[(a_kb_k),(c_kd_k)]$
belong to
 $(\kappa ,1/\kappa )$
with
$(\kappa ,1/\kappa )$
with
 $\kappa =\kappa (c_0)\in (0,\infty )$
;
$\kappa =\kappa (c_0)\in (0,\infty )$
; -
•
 $(a^{\prime }_kb^{\prime }_k)=\psi (\overline {P}_k^{\mathrm {out}}$
);
$(a^{\prime }_kb^{\prime }_k)=\psi (\overline {P}_k^{\mathrm {out}}$
); -
•
 $(a^{\prime }_kb^{\prime }_k)$
is equal to
$(a^{\prime }_kb^{\prime }_k)$
is equal to
 $(a_{i-3}a_{i+3})$
,
$(a_{i-3}a_{i+3})$
,
 $(a_{i+3}a_{j-3})$
,
$(a_{i+3}a_{j-3})$
,
 $(a_{j-3}a_{j+3})$
and
$(a_{j-3}a_{j+3})$
and
 $(a_{j+3}a_{i-3})$
for
$(a_{j+3}a_{i-3})$
for
 $k=1,2,3,4$
, respectively;
$k=1,2,3,4$
, respectively; -
•
 $D^{\prime }_1$
and
$D^{\prime }_1$
and
 $D^{\prime }_3$
contain
$D^{\prime }_3$
contain
 $B_{3c_0}(a_i)$
and
$B_{3c_0}(a_i)$
and
 $B_{3c_0}(a_j)$
, respectively.
$B_{3c_0}(a_j)$
, respectively.
The construction of the domains
![]() $(D^{\prime }_k,a^{\prime }_k,b^{\prime }_k,c^{\prime }_k,d^{\prime }_k)$
is straightforward.
$(D^{\prime }_k,a^{\prime }_k,b^{\prime }_k,c^{\prime }_k,d^{\prime }_k)$
is straightforward.

Figure 9 The uniformisation map
![]() $\Psi $
from
$\Psi $
from
![]() $\mathcal {F}\cap \overline {\mathcal {F}}^{\mathrm {out}}$
into
$\mathcal {F}\cap \overline {\mathcal {F}}^{\mathrm {out}}$
into
![]() $B_1\smallsetminus B_s$
. On the right, the black dots denote the
$B_1\smallsetminus B_s$
. On the right, the black dots denote the
![]() $a_i$
. We depicted the balls
$a_i$
. We depicted the balls
![]() $B_{2c_0}(a_i)$
and
$B_{2c_0}(a_i)$
and
![]() $B_{3c_0}(a_i)$
. The four domains
$B_{3c_0}(a_i)$
. The four domains
![]() $D_1',\dots ,D_4'$
can be chosen in many ways. In brighter red, the path
$D_1',\dots ,D_4'$
can be chosen in many ways. In brighter red, the path
![]() $\ell ^+$
and its preimage
$\ell ^+$
and its preimage
![]() $\psi ^{-1}(\ell ^+)$
. The path
$\psi ^{-1}(\ell ^+)$
. The path
![]() $\Gamma $
from
$\Gamma $
from
![]() $\mathcal A$
into
$\mathcal A$
into
![]() $\psi ^{-1}(\ell ^+)$
is drawn in dark blue.
$\psi ^{-1}(\ell ^+)$
is drawn in dark blue.
We now check equations (4.5) and (4.6). We start with the latter and focus on the first inequality. The boundary conditions induced by
![]() $\{\omega _{[\sigma _0]},1\}$
on
$\{\omega _{[\sigma _0]},1\}$
on
![]() $D_2$
are free on
$D_2$
are free on
![]() $\overline {P}_2^{\mathrm {out}}$
and on
$\overline {P}_2^{\mathrm {out}}$
and on
![]() $\psi ^{-1}((a_{i+3}a_{j-3}))$
. Therefore, the result follows directly from Proposition 4.8 and duality. We now turn to the former and focus on the first inequality. Let
$\psi ^{-1}((a_{i+3}a_{j-3}))$
. Therefore, the result follows directly from Proposition 4.8 and duality. We now turn to the former and focus on the first inequality. Let
First, a mixing-type argument using Proposition 4.8 gives that
Second, if
![]() $\ell ^{\pm }:=\ell \cap \psi ^{-1}(H^{\pm })$
, where
$\ell ^{\pm }:=\ell \cap \psi ^{-1}(H^{\pm })$
, where
![]() $H^+$
is the half-plane on the left of the line going from 0 to
$H^+$
is the half-plane on the left of the line going from 0 to
![]() $\tfrac 12(a_i+a_{i+1})$
(where left is understood when looking in the direction
$\tfrac 12(a_i+a_{i+1})$
(where left is understood when looking in the direction
![]() $\tfrac 12(a_i+a_{i+1})$
) and
$\tfrac 12(a_i+a_{i+1})$
) and
![]() $H^-=\mathbb C\smallsetminus H^+$
, the union bound gives that for
$H^-=\mathbb C\smallsetminus H^+$
, the union bound gives that for
![]() $\#$
equal to
$\#$
equal to
![]() $+$
or
$+$
or
![]() $-$
,
$-$
,
We assume below that
![]() $\#=+$
(the same can be done for
$\#=+$
(the same can be done for
![]() $\#=-$
). Condition on the left-most path
$\#=-$
). Condition on the left-most path
![]() $\Gamma $
going from
$\Gamma $
going from
![]() $\mathcal {A}$
to
$\mathcal {A}$
to
![]() $\ell ^+$
. Then conditioned on
$\ell ^+$
. Then conditioned on
![]() $\Gamma $
, the domain carved from
$\Gamma $
, the domain carved from
![]() $D_1$
by removing
$D_1$
by removing
![]() $\Gamma $
and all the edges revealed to determine
$\Gamma $
and all the edges revealed to determine
![]() $\Gamma $
has wired boundary conditions on
$\Gamma $
has wired boundary conditions on
![]() $\overline {P}_1^{\mathrm {out}}$
, wired on
$\overline {P}_1^{\mathrm {out}}$
, wired on
![]() $\Gamma $
and boundary conditions dominating the free boundary conditions elsewhere. Since the extremal distance between
$\Gamma $
and boundary conditions dominating the free boundary conditions elsewhere. Since the extremal distance between
![]() $\overline {P}_1^{\mathrm {out}}$
and
$\overline {P}_1^{\mathrm {out}}$
and
![]() $\Gamma $
in this new domain is larger than
$\Gamma $
in this new domain is larger than
![]() $\kappa '=\kappa '(\kappa ,\delta )>0$
, we deduce from Proposition 4.8 that
$\kappa '=\kappa '(\kappa ,\delta )>0$
, we deduce from Proposition 4.8 that
Combining the three last displayed equations gives the first inequality of equation (4.5) and therefore concludes the proof.
4.2 Mixing rate versus coupling
In this section, we estimate the probability under the coupling of Theorem 4.1 that
![]() $\tau $
occurs. The relevant result of this section is the following theorem.
$\tau $
occurs. The relevant result of this section is the following theorem.
Theorem 4.9. For any
![]() $p\in (0,1)$
and any
$p\in (0,1)$
and any
![]() $4r < R \le L(p)$
, the following holds. Fix
$4r < R \le L(p)$
, the following holds. Fix
![]() $\mathcal {G}$
an
$\mathcal {G}$
an
![]() $\eta $
-well-separated inner flower domain on
$\eta $
-well-separated inner flower domain on
![]() $\Lambda _R$
or outer flower domain on
$\Lambda _R$
or outer flower domain on
![]() $\Lambda _r$
and
$\Lambda _r$
and
![]() $(\xi ,\xi ')$
a boosting pair of boundary conditions on
$(\xi ,\xi ')$
a boosting pair of boundary conditions on
![]() $\mathcal {G}$
. Let
$\mathcal {G}$
. Let
![]() $\mathbb {P}$
be the coupling of Theorem 4.1 (points (i) or (ii), depending on whether
$\mathbb {P}$
be the coupling of Theorem 4.1 (points (i) or (ii), depending on whether
![]() $\mathcal {G}$
is an inner or outer flower domain), and recall the stopping time
$\mathcal {G}$
is an inner or outer flower domain), and recall the stopping time
![]() $\tau $
associated to
$\tau $
associated to
![]() $\mathbb {P}$
. Then
$\mathbb {P}$
. Then
As a consequence, if
![]() $\mathcal {G}$
is an inner flower domain and H is either the crossing event of an
$\mathcal {G}$
is an inner flower domain and H is either the crossing event of an
![]() $\eta $
-regular quad at scale r or
$\eta $
-regular quad at scale r or
![]() $H = A_{r/2}$
, or if
$H = A_{r/2}$
, or if
![]() $\mathcal {G}$
is an outer flower domain and H is either the crossing event of an
$\mathcal {G}$
is an outer flower domain and H is either the crossing event of an
![]() $\eta $
-regular quad at scale R translated so that it is contained in
$\eta $
-regular quad at scale R translated so that it is contained in
![]() $\mathrm {Ann}(R,2R)$
or
$\mathrm {Ann}(R,2R)$
or
![]() $H = A_{R}$
, then
$H = A_{R}$
, then
When
![]() $\mathcal {G}$
is an inner flower domain, equation (4.11) should be understood as follows. Any boosting pair of boundary conditions at scale R boosts the probability of any crossing event at scale r by a quantity comparable to
$\mathcal {G}$
is an inner flower domain, equation (4.11) should be understood as follows. Any boosting pair of boundary conditions at scale R boosts the probability of any crossing event at scale r by a quantity comparable to
![]() $\Delta _p(r,R)$
. The same holds when the boundary conditions are at scale r and the crossing event is at scale R. Recall that
$\Delta _p(r,R)$
. The same holds when the boundary conditions are at scale r and the crossing event is at scale R. Recall that
![]() $\Delta _p(r,R)$
was defined in terms of the boost that a specific pair of boundary conditions at scale R has on a specific crossing event at scale r. Thus, in addition to stating that the boost of any boosting pair of boundary conditions on any crossing event is comparable, the proposition also links the boost from outside in to that from inside out.
$\Delta _p(r,R)$
was defined in terms of the boost that a specific pair of boundary conditions at scale R has on a specific crossing event at scale r. Thus, in addition to stating that the boost of any boosting pair of boundary conditions on any crossing event is comparable, the proposition also links the boost from outside in to that from inside out.
Remark 4.10. As with Theorem 4.1, Theorem 4.9 also applies to graphs containing
![]() $\mathcal {G} \smallsetminus \Lambda _{r/2}$
and
$\mathcal {G} \smallsetminus \Lambda _{r/2}$
and
![]() $\mathcal {G} \cap \Lambda _{2R}$
, respectively. Note that the probability that
$\mathcal {G} \cap \Lambda _{2R}$
, respectively. Note that the probability that
![]() $\tau <\infty $
is comparable to
$\tau <\infty $
is comparable to
![]() $\Delta _p(r,R)$
, independently of the chosen graph. The proof only requires minor adaptations, which we omit here.
$\Delta _p(r,R)$
, independently of the chosen graph. The proof only requires minor adaptations, which we omit here.
The rest of this section is dedicated to showing Theorem 4.9. The proof is split into several steps, each corresponding to a lemma. First, as a consequence of Theorem 4.1(i), we prove that the influence of boundary conditions at scale R on the crossing of any two regular quads at scale r is comparable.
Lemma 4.11. Fix
![]() $p\in (0,1)$
and
$p\in (0,1)$
and
![]() $2r < R \le L(p)$
. Let
$2r < R \le L(p)$
. Let
![]() $\mathcal {G}$
be an
$\mathcal {G}$
be an
![]() $\eta $
-well-separated inner flower domain on
$\eta $
-well-separated inner flower domain on
![]() $\Lambda _R$
and
$\Lambda _R$
and
![]() $(\xi ,\xi ')$
be a boosting pair of boundary conditions on
$(\xi ,\xi ')$
be a boosting pair of boundary conditions on
![]() $\mathcal {G}$
. Moreover, let H be either the crossing event of an
$\mathcal {G}$
. Moreover, let H be either the crossing event of an
![]() $\eta $
-regular quad at scale r or
$\eta $
-regular quad at scale r or
![]() $H = A_{r/2}$
. Then if
$H = A_{r/2}$
. Then if
![]() $\mathbb P$
is the coupling of Theorem 4.1(i),
$\mathbb P$
is the coupling of Theorem 4.1(i),
In particular,
A particular case of equation (4.13) shows that
![]() $\Delta _p(1,R)\asymp \Delta _p(R)$
. In addition, by taking
$\Delta _p(1,R)\asymp \Delta _p(R)$
. In addition, by taking
![]() $H = \mathcal {C}(\Lambda _{r/2})$
, equation (4.13) also proves that
$H = \mathcal {C}(\Lambda _{r/2})$
, equation (4.13) also proves that
and more generally that replacing r by a multiple of r only affects
![]() $\Delta _p$
by a multiplicative constant.
$\Delta _p$
by a multiplicative constant.
Remark 4.12. As will be apparent from the proof, an equivalent of equation (4.12) may also be proved for outer flower domains on
![]() $\Lambda _r$
and crossing events at scale R. However, an equivalent of equation (4.13) cannot be shown with the same proof, at least for now (but will be later).
$\Lambda _r$
and crossing events at scale R. However, an equivalent of equation (4.13) cannot be shown with the same proof, at least for now (but will be later).
Proof. Fix p, r, R,
![]() $\mathcal {G}$
,
$\mathcal {G}$
,
![]() $\xi $
,
$\xi $
,
![]() $\xi '$
and H as in the statement. Let
$\xi '$
and H as in the statement. Let
![]() $\mathbb {P}$
be the coupling of Theorem 4.1 (i) between
$\mathbb {P}$
be the coupling of Theorem 4.1 (i) between
![]() $\phi _{\Lambda _R}^{\xi '}$
and
$\phi _{\Lambda _R}^{\xi '}$
and
![]() $\phi _{\Lambda _R}^{\xi }$
. Then using the notation of the theorem,
$\phi _{\Lambda _R}^{\xi }$
. Then using the notation of the theorem,
Moreover, by Theorem 3.6,
where
![]() $\mathbb {E}$
stands for the expectation associated to
$\mathbb {E}$
stands for the expectation associated to
![]() $\mathbb {P}$
. The two displays above imply that
$\mathbb {P}$
. The two displays above imply that
Apply this to a generic H and to
![]() $H = \mathcal {C}(\Lambda _r)$
to obtain equation (4.12). Finally, equation (4.12) applied with
$H = \mathcal {C}(\Lambda _r)$
to obtain equation (4.12). Finally, equation (4.12) applied with
![]() $\mathcal {G} = \Lambda _R$
,
$\mathcal {G} = \Lambda _R$
,
![]() $\xi = 0$
,
$\xi = 0$
,
![]() $\xi ' = 1$
gives equation (4.13).
$\xi ' = 1$
gives equation (4.13).
Next, we deduce an interpretation of
![]() $\Delta _p(r,R)$
as a covariance between events at scales r and R. Considering the symmetry between r and R below, this result is used to link the influence from outside in to that from inside out.
$\Delta _p(r,R)$
as a covariance between events at scales r and R. Considering the symmetry between r and R below, this result is used to link the influence from outside in to that from inside out.
Lemma 4.13. For every p and every
![]() $4 r\le R \le L(p)$
,
$4 r\le R \le L(p)$
,
Proof. We start by proving the equivalence between
![]() $\mathrm {Cov}(A_{r/2},A_R)$
and
$\mathrm {Cov}(A_{r/2},A_R)$
and
![]() $\Delta _p(r,R)$
. By the monotonicity of boundary conditions in equation (CBC),
$\Delta _p(r,R)$
. By the monotonicity of boundary conditions in equation (CBC),
where the last inequality is due to Lemma 4.11.
For the converse bound, some additional work is needed. Let
![]() $\mathbb {P}$
denote the coupling between
$\mathbb {P}$
denote the coupling between
![]() $\phi $
and
$\phi $
and
![]() $\phi [\cdot \,|A_{r/2}]$
inside
$\phi [\cdot \,|A_{r/2}]$
inside
![]() $\Lambda _{R/2}$
produced by applying Proposition 3.9 and then Theorem 4.1(ii). Recall that
$\Lambda _{R/2}$
produced by applying Proposition 3.9 and then Theorem 4.1(ii). Recall that
![]() $\zeta $
and
$\zeta $
and
![]() $\zeta '$
denote the boundary conditions on
$\zeta '$
denote the boundary conditions on
![]() $\Lambda _{R/2}^c$
induced by
$\Lambda _{R/2}^c$
induced by
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
, respectively. Complete the coupling outside of
$\omega '$
, respectively. Complete the coupling outside of
![]() $\Lambda _{R/2}$
by an arbitrary increasing coupling. Then Theorems 3.6 and 4.1(ii) show that
$\Lambda _{R/2}$
by an arbitrary increasing coupling. Then Theorems 3.6 and 4.1(ii) show that

Using that
![]() $\phi [A_{r/2}]\stackrel{>}{\scriptstyle{\frown}} 1$
, we deducefrom the display above that
$\phi [A_{r/2}]\stackrel{>}{\scriptstyle{\frown}} 1$
, we deducefrom the display above that
![]() $\mathrm {Cov}(A_{r/2}, A_R) \stackrel{>}{\scriptstyle{\frown}} \mathbb {P}[\zeta ' \neq \zeta ]$
. Moreover, by equation (SMP),
$\mathrm {Cov}(A_{r/2}, A_R) \stackrel{>}{\scriptstyle{\frown}} \mathbb {P}[\zeta ' \neq \zeta ]$
. Moreover, by equation (SMP),
 $$ \begin{align} \mathbb{P}[\zeta' \neq \zeta] &\ge \mathbb{P}[\omega' \in A_{R/2},\, \omega \notin A_{R/2}] \ge \mathrm{Cov}(A_{r/2}, A_{R/2}) \quad \text{ and} \nonumber\\ \mathbb{P}[\zeta' \neq \zeta] &\ge \mathbb{P}[\omega' \notin A_{R/2}^*,\, \omega \in A_{R/2}^*] \ge - \mathrm{Cov}(A_{r/2}, A_{R/2}^*), \end{align} $$
$$ \begin{align} \mathbb{P}[\zeta' \neq \zeta] &\ge \mathbb{P}[\omega' \in A_{R/2},\, \omega \notin A_{R/2}] \ge \mathrm{Cov}(A_{r/2}, A_{R/2}) \quad \text{ and} \nonumber\\ \mathbb{P}[\zeta' \neq \zeta] &\ge \mathbb{P}[\omega' \notin A_{R/2}^*,\, \omega \in A_{R/2}^*] \ge - \mathrm{Cov}(A_{r/2}, A_{R/2}^*), \end{align} $$
where
![]() $A_{R/2}^* = \{\Lambda _{R/2} \not \longleftrightarrow \partial \Lambda _{R}\}$
is the event
$A_{R/2}^* = \{\Lambda _{R/2} \not \longleftrightarrow \partial \Lambda _{R}\}$
is the event
![]() $A_{R/2}$
applied to the dual model. Divide the equations above by
$A_{R/2}$
applied to the dual model. Divide the equations above by
![]() $\phi [A_{R/2}]$
and
$\phi [A_{R/2}]$
and
![]() $\phi [A_{R/2}^*]$
, respectively, both of which are uniformly positive quantities. Using the monotonicity of boundary conditions in equations (CBC) and (4.13), we conclude that
$\phi [A_{R/2}^*]$
, respectively, both of which are uniformly positive quantities. Using the monotonicity of boundary conditions in equations (CBC) and (4.13), we conclude that
Together with equations (4.17) and (4.18), this shows that
Finally, we turn to the equivalence between
![]() $\mathrm {Cov}(A_{r/2}, A_R)$
and
$\mathrm {Cov}(A_{r/2}, A_R)$
and
![]() $\phi _{\Lambda _r^c}^1[A_R] - \phi _{\Lambda _r^c}^0[A_R]$
. The monotonicity of boundary conditions in equation (CBC) shows that
$\phi _{\Lambda _r^c}^1[A_R] - \phi _{\Lambda _r^c}^0[A_R]$
. The monotonicity of boundary conditions in equation (CBC) shows that
Conversely,
 $$ \begin{align*} \phi_{\Lambda_r^c}^1[A_R] - \phi_{\Lambda_r^c}^0[A_R] &\leq \phi[A_R\,|\,A_{r}] - \phi[A_R\,|\, A_r^*] &\text{by equation (CBC)}&\\&\leq (\phi[A_R\,|\,A_{r}] - \phi[A_R]\big) - (\phi[A_R\,|\, A_r^*]- \phi[A_R]) &\\&\stackrel{<}{\scriptstyle{\frown}} \mathrm{Cov}(A_R,A_{r}) - \mathrm{Cov}(A_R,A_{r}^*)&\hspace{-1.5cm}\text{as } \phi[A_{r}]\stackrel{>}{\scriptstyle{\frown}}1 \text{ and } \phi[A_r^*]\stackrel{>}{\scriptstyle{\frown}}1 &\\&\stackrel{<}{\scriptstyle{\frown}} ( \phi[A_r \,|\, A_R] - \phi[A_r])+ ( \phi[A_r^*] - \phi[A_r^* \,|\, A_R])&\text{since } \phi[A_R]\le1 &\\ &\stackrel{<}{\scriptstyle{\frown}} \Delta_p(2r,R) &\hspace{-1cm}\text{by equation (CBC) and Lemma 4.11}&\\&\stackrel{<}{\scriptstyle{\frown}} \Delta_p(r,R) &\text{by equation (4.14)} &\\ &\stackrel{<}{\scriptstyle{\frown}} \mathrm{Cov}[A_{r/2}, A_R] &\text{by equation (4.20).}& \end{align*} $$
$$ \begin{align*} \phi_{\Lambda_r^c}^1[A_R] - \phi_{\Lambda_r^c}^0[A_R] &\leq \phi[A_R\,|\,A_{r}] - \phi[A_R\,|\, A_r^*] &\text{by equation (CBC)}&\\&\leq (\phi[A_R\,|\,A_{r}] - \phi[A_R]\big) - (\phi[A_R\,|\, A_r^*]- \phi[A_R]) &\\&\stackrel{<}{\scriptstyle{\frown}} \mathrm{Cov}(A_R,A_{r}) - \mathrm{Cov}(A_R,A_{r}^*)&\hspace{-1.5cm}\text{as } \phi[A_{r}]\stackrel{>}{\scriptstyle{\frown}}1 \text{ and } \phi[A_r^*]\stackrel{>}{\scriptstyle{\frown}}1 &\\&\stackrel{<}{\scriptstyle{\frown}} ( \phi[A_r \,|\, A_R] - \phi[A_r])+ ( \phi[A_r^*] - \phi[A_r^* \,|\, A_R])&\text{since } \phi[A_R]\le1 &\\ &\stackrel{<}{\scriptstyle{\frown}} \Delta_p(2r,R) &\hspace{-1cm}\text{by equation (CBC) and Lemma 4.11}&\\&\stackrel{<}{\scriptstyle{\frown}} \Delta_p(r,R) &\text{by equation (4.14)} &\\ &\stackrel{<}{\scriptstyle{\frown}} \mathrm{Cov}[A_{r/2}, A_R] &\text{by equation (4.20).}& \end{align*} $$
Note that in the second and third lines above, the second term is negative. The last two displays prove that
![]() $\mathrm {Cov}[A_{r/2}, A_R] \asymp \phi _{\Lambda _r^c}^1[A_R] - \phi _{\Lambda _r^c}^0[A_R]$
.
$\mathrm {Cov}[A_{r/2}, A_R] \asymp \phi _{\Lambda _r^c}^1[A_R] - \phi _{\Lambda _r^c}^0[A_R]$
.
Notice that equations 4.17–4.20 also show that
and more generally that replacing R by a constant multiple of R only affects
![]() $\Delta _p$
by a multiplicative constant.
$\Delta _p$
by a multiplicative constant.
Finally, we claim that all boosting pairs of boundary conditions at scale R influence
![]() $A_{r/2}$
by a similar amount; the same holds from the inside out.
$A_{r/2}$
by a similar amount; the same holds from the inside out.
Lemma 4.14. Fix p and
![]() $4 r\le R \le L(p)$
. Then
$4 r\le R \le L(p)$
. Then
-
(i) for any
 $\eta $
-well-separated inner flower domain
$\eta $
-well-separated inner flower domain
 $\mathcal {G}$
on
$\mathcal {G}$
on
 $\Lambda _R$
and any boosting pair of boundary conditions
$\Lambda _R$
and any boosting pair of boundary conditions
 $\xi ,\xi '$
on
$\xi ,\xi '$
on
 $\mathcal {G}$
, (4.22)
$\mathcal {G}$
, (4.22) $$ \begin{align} \phi_{\mathcal{G}}^{\xi'} [A_{r/2}] - \phi_{\mathcal{G}}^{\xi} [A_{r/2}] \asymp \phi_{\Lambda_R}^1 [A_{r/2}] - \phi_{\Lambda_R}^{0} [A_{r/2}]; \end{align} $$
$$ \begin{align} \phi_{\mathcal{G}}^{\xi'} [A_{r/2}] - \phi_{\mathcal{G}}^{\xi} [A_{r/2}] \asymp \phi_{\Lambda_R}^1 [A_{r/2}] - \phi_{\Lambda_R}^{0} [A_{r/2}]; \end{align} $$
-
(ii) for any
 $\eta $
-well-separated outer flower domain
$\eta $
-well-separated outer flower domain
 $\mathcal {G}$
on
$\mathcal {G}$
on
 $\Lambda _r$
and any boosting pair of boundary conditions
$\Lambda _r$
and any boosting pair of boundary conditions
 $\xi ,\xi '$
on
$\xi ,\xi '$
on
 $\mathcal {G}$
, (4.23)
$\mathcal {G}$
, (4.23) $$ \begin{align} \phi_{\mathcal{G}}^{\xi'} [A_R] - \phi_{\mathcal{G}}^{\xi} [A_R] \asymp \phi_{\Lambda_r^c}^{1} [A_R] - \phi_{\Lambda_r^c}^{0} [A_R]. \end{align} $$
$$ \begin{align} \phi_{\mathcal{G}}^{\xi'} [A_R] - \phi_{\mathcal{G}}^{\xi} [A_R] \asymp \phi_{\Lambda_r^c}^{1} [A_R] - \phi_{\Lambda_r^c}^{0} [A_R]. \end{align} $$
Proof. We will only treat point
![]() $(i)$
as point
$(i)$
as point
![]() $(ii)$
is identical.
$(ii)$
is identical.
By the monotonicity of boundary conditions,
We turn to the converse bound. We recommend taking a look at Figure 10. By monotonicity, we may assume that
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
are both coherent with
$\xi '$
are both coherent with
![]() $\mathcal {G}$
, and that there exists exactly one pair of sets in the partition
$\mathcal {G}$
, and that there exists exactly one pair of sets in the partition
![]() $\xi $
that are wired together in
$\xi $
that are wired together in
![]() $\xi '$
(due to the coherence condition, each such set contains at least one primal petal of
$\xi '$
(due to the coherence condition, each such set contains at least one primal petal of
![]() $\mathcal {G}$
). Consider the graph G obtained from
$\mathcal {G}$
). Consider the graph G obtained from
![]() $\mathcal {G}$
as follows. All vertices contained in a non-singleton set of the partition
$\mathcal {G}$
as follows. All vertices contained in a non-singleton set of the partition
![]() $\xi $
are collapsed to a single point (in particular, all points on each primal petal of
$\xi $
are collapsed to a single point (in particular, all points on each primal petal of
![]() $\mathcal {G}$
are collapsed together). Write
$\mathcal {G}$
are collapsed together). Write
![]() $a_1,\dots , a_k$
for the points thus obtained. Then there exist two distinct points
$a_1,\dots , a_k$
for the points thus obtained. Then there exist two distinct points
![]() $a_i$
and
$a_i$
and
![]() $a_j$
such that the corresponding groups of petals are wired in
$a_j$
such that the corresponding groups of petals are wired in
![]() $\xi '$
. Finally, G is the graph obtained after the collapsing procedure described above, with an additional edge f between
$\xi '$
. Finally, G is the graph obtained after the collapsing procedure described above, with an additional edge f between
![]() $a_i$
and
$a_i$
and
![]() $a_j$
. There is an obvious correspondence between the edges of
$a_j$
. There is an obvious correspondence between the edges of
![]() $\mathcal {G}$
and those of
$\mathcal {G}$
and those of
![]() $G\smallsetminus \{f\}$
, and we will identify them from now on. Let
$G\smallsetminus \{f\}$
, and we will identify them from now on. Let
![]() $\phi _G$
be the random-cluster measure on the finite graph G (note that G is not a subgraph of
$\phi _G$
be the random-cluster measure on the finite graph G (note that G is not a subgraph of
![]() $\mathbb {Z}^2$
).
$\mathbb {Z}^2$
).

Figure 10 The graph G. The black edges between the true vertices of the petals and the vertices in red mean they are all merged into the red vertex or, equivalently, that we added open edges between them and the red vertices. We also depicted the flower domains
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathcal {F}_{\tau }$
, as well as the event H that corresponds to the occurrence of the red paths.
$\mathcal {F}_{\tau }$
, as well as the event H that corresponds to the occurrence of the red paths.
With the construction above,
![]() $\phi ^{\xi }_{\mathcal {G}}$
and
$\phi ^{\xi }_{\mathcal {G}}$
and
![]() $\phi ^{\xi '}_{\mathcal {G}}$
are simply the restrictions of
$\phi ^{\xi '}_{\mathcal {G}}$
are simply the restrictions of
![]() $\phi _G[\cdot \,|\omega _f = 0]$
and
$\phi _G[\cdot \,|\omega _f = 0]$
and
![]() $\phi _G[\cdot \,|\omega _f = 1]$
, respectively, to
$\phi _G[\cdot \,|\omega _f = 1]$
, respectively, to
![]() $\mathcal {G}$
. As such,
$\mathcal {G}$
. As such,
![]() $\phi _G[A_{r/2}] \stackrel{>}{\scriptstyle{\frown}} 1$
and Bayes’s formula imply that
$\phi _G[A_{r/2}] \stackrel{>}{\scriptstyle{\frown}} 1$
and Bayes’s formula imply that
 $$ \begin{align} \phi_{\mathcal{G}}^{\xi'} [A_{r/2}] - \phi_{\mathcal{G}}^{\xi} [A_{r/2}] &= \phi_G [A_{r/2}|\omega_f =1] - \phi_G [A_{r/2}|\omega_f =0] \nonumber\\ &\geq \phi_{G} [A_{r/2}|\omega_f =1] - \phi_G[A_{r/2}]\nonumber\\ & \stackrel{>}{\scriptstyle{\frown}} \phi_{G} [\omega_f =1|A_{r/2}] - \phi_{G}[\omega_f =1]. \end{align} $$
$$ \begin{align} \phi_{\mathcal{G}}^{\xi'} [A_{r/2}] - \phi_{\mathcal{G}}^{\xi} [A_{r/2}] &= \phi_G [A_{r/2}|\omega_f =1] - \phi_G [A_{r/2}|\omega_f =0] \nonumber\\ &\geq \phi_{G} [A_{r/2}|\omega_f =1] - \phi_G[A_{r/2}]\nonumber\\ & \stackrel{>}{\scriptstyle{\frown}} \phi_{G} [\omega_f =1|A_{r/2}] - \phi_{G}[\omega_f =1]. \end{align} $$
Now let
![]() $\mathbb {P}$
be the coupling between
$\mathbb {P}$
be the coupling between
![]() $\phi _{G}$
and
$\phi _{G}$
and
![]() $\phi _{G} [\cdot \,|A_{r/2}]$
obtained as follows:
$\phi _{G} [\cdot \,|A_{r/2}]$
obtained as follows:
-
• reveal the edges of
 $\Lambda _{2r}$
in the order dictated by Proposition 3.9. If this stage produces an outer flower domain with a boosting pair of boundary conditions, apply Theorem 4.1(ii) from scale
$\Lambda _{2r}$
in the order dictated by Proposition 3.9. If this stage produces an outer flower domain with a boosting pair of boundary conditions, apply Theorem 4.1(ii) from scale
 $2r$
to scale
$2r$
to scale
 $R/2$
, up to the associated stopping time
$R/2$
, up to the associated stopping time
 $\tau $
(see Remark 4.3 about applying Theorem 4.1(ii) in G);
$\tau $
(see Remark 4.3 about applying Theorem 4.1(ii) in G); -
• reveal all remaining edges of
 $\mathcal {G}$
;
$\mathcal {G}$
; -
• reveal the state of f.
If
![]() $\tau < \infty $
, there exist two primal petals
$\tau < \infty $
, there exist two primal petals
![]() $P_i$
and
$P_i$
and
![]() $P_j$
of
$P_j$
of
![]() $\mathcal {F}_{\tau }$
that are wired in
$\mathcal {F}_{\tau }$
that are wired in
![]() $\omega _{[\tau ]}'$
but not in
$\omega _{[\tau ]}'$
but not in
![]() $\omega _{[\tau ]}$
. Arbitrarily choose one such pair of petals. Let
$\omega _{[\tau ]}$
. Arbitrarily choose one such pair of petals. Let
![]() $H = H(\mathcal {F}_{\tau }, \omega _{[\tau ]},\omega _{[\tau ]}')$
be the event that
$H = H(\mathcal {F}_{\tau }, \omega _{[\tau ]},\omega _{[\tau ]}')$
be the event that
![]() $a_i$
is connected to
$a_i$
is connected to
![]() $P_i$
in
$P_i$
in
![]() $\omega \cap \mathcal {F}_{\tau }$
, that
$\omega \cap \mathcal {F}_{\tau }$
, that
![]() $a_j$
is connected to
$a_j$
is connected to
![]() $P_j$
in
$P_j$
in
![]() $\omega \cap \mathcal {F}_{\tau }$
but that
$\omega \cap \mathcal {F}_{\tau }$
but that
![]() $a_i$
and
$a_i$
and
![]() $a_j$
are not connected to each other or any other primal petal of
$a_j$
are not connected to each other or any other primal petal of
![]() $\mathcal {F}_{\tau }$
in
$\mathcal {F}_{\tau }$
in
![]() $\omega \cap \mathcal {F}_{\tau }$
.
$\omega \cap \mathcal {F}_{\tau }$
.
Since
![]() $\mathcal {F}_{\tau }$
is
$\mathcal {F}_{\tau }$
is
![]() $1/2$
-well-separated and
$1/2$
-well-separated and
![]() $\mathcal {G}$
is
$\mathcal {G}$
is
![]() $\eta $
-well-separated, and since
$\eta $
-well-separated, and since
![]() $\mathcal {F}_{\tau } \cap \mathcal {G}$
contains the annulus
$\mathcal {F}_{\tau } \cap \mathcal {G}$
contains the annulus
![]() $\mathrm {Ann}(R/2,R)$
, by standard applications of equation (RSW), we find that
$\mathrm {Ann}(R/2,R)$
, by standard applications of equation (RSW), we find that
The occurrence of H may be determined before revealing the state of the edge f. Moreover, if H occurs, then the endpoints
![]() $a_i$
and
$a_i$
and
![]() $a_j$
of f are connected in
$a_j$
of f are connected in
![]() $\omega ' \smallsetminus \{f\}$
but not in
$\omega ' \smallsetminus \{f\}$
but not in
![]() $\omega \smallsetminus \{f\}$
. Indeed,
$\omega \smallsetminus \{f\}$
. Indeed,
![]() $\omega '$
dominates
$\omega '$
dominates
![]() $\omega $
, which implies that
$\omega $
, which implies that
![]() $a_i$
is connected to
$a_i$
is connected to
![]() $P_i$
(in
$P_i$
(in
![]() $\omega ' \cap \mathcal {F}_{\tau }$
), which is connected to
$\omega ' \cap \mathcal {F}_{\tau }$
), which is connected to
![]() $P_j$
(in
$P_j$
(in
![]() $\omega ^{\prime }_{[\tau ]}$
), which in turn is connected to
$\omega ^{\prime }_{[\tau ]}$
), which in turn is connected to
![]() $a_j$
(in
$a_j$
(in
![]() $\omega ' \cap \mathcal {F}_{\tau }$
).
$\omega ' \cap \mathcal {F}_{\tau }$
).
It follows that at the last step of the coupling, if
![]() $\tau < \infty $
and H occurs, there is a probability
$\tau < \infty $
and H occurs, there is a probability
![]() $\frac {p(1-p)(q-1)}{p + (1-p)q}>0$
that f is closed in
$\frac {p(1-p)(q-1)}{p + (1-p)q}>0$
that f is closed in
![]() $\omega $
but open in
$\omega $
but open in
![]() $\omega '$
. To summarise, we find
$\omega '$
. To summarise, we find
Finally, by Theorem 4.1(ii), the fact that
![]() $\phi _{G} [A_{R/2}] \stackrel{>}{\scriptstyle{\frown}} 1$
and the comparison between boundary conditions in equation (CBC), we have
$\phi _{G} [A_{R/2}] \stackrel{>}{\scriptstyle{\frown}} 1$
and the comparison between boundary conditions in equation (CBC), we have
 $$ \begin{align} \mathbb{P}[\tau < \infty] &\stackrel{>}{\scriptstyle{\frown}}\mathbb{P}[\omega \text{ and } \omega' \text{ induce different b.c. on } \Lambda_{R/2}^c]\\&\ge \mathbb{P}[\omega' \in A_{R/2} \text{ and } \omega \notin A_{R/2}]\nonumber\\&\stackrel{>}{\scriptstyle{\frown}} \mathrm{Cov}_G(A_{r/2}, A_{R/2}) \stackrel{>}{\scriptstyle{\frown}} \phi_{\Lambda_R}^{1} [A_{r/2}]- \phi_{\Lambda_R}^{0} [A_{r/2}] , \nonumber \end{align} $$
$$ \begin{align} \mathbb{P}[\tau < \infty] &\stackrel{>}{\scriptstyle{\frown}}\mathbb{P}[\omega \text{ and } \omega' \text{ induce different b.c. on } \Lambda_{R/2}^c]\\&\ge \mathbb{P}[\omega' \in A_{R/2} \text{ and } \omega \notin A_{R/2}]\nonumber\\&\stackrel{>}{\scriptstyle{\frown}} \mathrm{Cov}_G(A_{r/2}, A_{R/2}) \stackrel{>}{\scriptstyle{\frown}} \phi_{\Lambda_R}^{1} [A_{r/2}]- \phi_{\Lambda_R}^{0} [A_{r/2}] , \nonumber \end{align} $$
where
![]() $\mathrm {Cov}_G$
is the covariance under
$\mathrm {Cov}_G$
is the covariance under
![]() $\phi _G$
and the last inequality is given by equations (4.13) and (4.16). Equations (4.24)-(4.26) prove
$\phi _G$
and the last inequality is given by equations (4.13) and (4.16). Equations (4.24)-(4.26) prove
as desired.
We are finally ready to prove Theorem 4.9.
Proof of Theorem 4.9
We start with the case where
![]() $\mathcal {G}$
is an inner flower domain on
$\mathcal {G}$
is an inner flower domain on
![]() $\Lambda _R$
. Recall that
$\Lambda _R$
. Recall that
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
form a boosting pair of boundary conditions on
$\xi '$
form a boosting pair of boundary conditions on
![]() $\mathcal {G}$
and that
$\mathcal {G}$
and that
![]() $\tau $
is the stopping time associated to the coupling of Theorem 4.1 between
$\tau $
is the stopping time associated to the coupling of Theorem 4.1 between
![]() $\phi _{\mathcal {G}}^{\xi '}$
and
$\phi _{\mathcal {G}}^{\xi '}$
and
![]() $\phi _{\mathcal {G}}^{\xi }$
. Due to Lemma 4.11, we find that
$\phi _{\mathcal {G}}^{\xi }$
. Due to Lemma 4.11, we find that
Now, Lemma 4.14 and equation (4.13) indicate that the right-hand side above is of order
![]() $\Delta _p(r,R)$
, and equation (4.10) is proved in this case. Finally, equation (4.11) follows from another application of Lemma 4.11.
$\Delta _p(r,R)$
, and equation (4.10) is proved in this case. Finally, equation (4.11) follows from another application of Lemma 4.11.
Similarly, when
![]() $\mathcal {G}$
is an outer flower domain on
$\mathcal {G}$
is an outer flower domain on
![]() $\Lambda _r$
, due to Lemma 4.11 applied from inside to outside (see Remark 4.12), then to Lemmata 4.14 and 4.13, respectively,
$\Lambda _r$
, due to Lemma 4.11 applied from inside to outside (see Remark 4.12), then to Lemmata 4.14 and 4.13, respectively,
Another application of Lemma 4.11 also proves equation (4.11) in this case.
4.3
 $\Delta _p$
controls the mixing rate: proof of Theorem 1.6(v)
$\Delta _p$
controls the mixing rate: proof of Theorem 1.6(v)
For the lower bound, equation (4.16) gives that
 $$ \begin{align*} \max\Big\{\Big|\frac{\phi_p[A\cap B]}{\phi_p[A]\phi_p[B]}-1\Big|\, :\, A\in\mathcal F(\Lambda_r), B\in\mathcal F(\mathbb Z^2\smallsetminus\Lambda_R)\Big\} \ge \frac{\phi_p[A_{r/2}\cap A_R]}{\phi_p[A_{r/2}]\phi_p[A_R]}-1 \stackrel{>}{\scriptstyle{\frown}} \Delta_p(r,R). \end{align*} $$
$$ \begin{align*} \max\Big\{\Big|\frac{\phi_p[A\cap B]}{\phi_p[A]\phi_p[B]}-1\Big|\, :\, A\in\mathcal F(\Lambda_r), B\in\mathcal F(\mathbb Z^2\smallsetminus\Lambda_R)\Big\} \ge \frac{\phi_p[A_{r/2}\cap A_R]}{\phi_p[A_{r/2}]\phi_p[A_R]}-1 \stackrel{>}{\scriptstyle{\frown}} \Delta_p(r,R). \end{align*} $$
For the upper bound, use the spatial Markov property given by equation (SMP) to get that for every
![]() $A\in \mathcal F(\Lambda _r)$
and
$A\in \mathcal F(\Lambda _r)$
and
![]() $B\in \mathcal F(\mathbb Z^2\smallsetminus \Lambda _R)$
,
$B\in \mathcal F(\mathbb Z^2\smallsetminus \Lambda _R)$
,
 $$ \begin{align} \Big|\frac{\phi_p[A\cap B]}{\phi_p[A]\phi_p[B]}-1\Big|\le \max\Big\{\Big|\frac{\phi_{\Lambda_R,p}^{\xi'}[A]}{\phi_{\Lambda_R,p}^{\xi}[A]}-1\Big|\ :\xi,\xi'\text{ b.c. on }\partial\Lambda_R\Big\}. \end{align} $$
$$ \begin{align} \Big|\frac{\phi_p[A\cap B]}{\phi_p[A]\phi_p[B]}-1\Big|\le \max\Big\{\Big|\frac{\phi_{\Lambda_R,p}^{\xi'}[A]}{\phi_{\Lambda_R,p}^{\xi}[A]}-1\Big|\ :\xi,\xi'\text{ b.c. on }\partial\Lambda_R\Big\}. \end{align} $$
Now, consider the coupling
![]() $\mathbb P$
between
$\mathbb P$
between
![]() $\omega ^0$
and
$\omega ^0$
and
![]() $ \omega ^1$
constructed in Theorem 4.9 on
$ \omega ^1$
constructed in Theorem 4.9 on
![]() $\Lambda _R \smallsetminus \Lambda _{2r}$
and boundary conditions
$\Lambda _R \smallsetminus \Lambda _{2r}$
and boundary conditions
![]() $0$
and
$0$
and
![]() $1$
, respectively, on
$1$
, respectively, on
![]() $\Lambda _{R}$
(which form a boosting pair). By applying the same decision tree for the boundary conditions
$\Lambda _{R}$
(which form a boosting pair). By applying the same decision tree for the boundary conditions
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
, we obtain two additional configurations
$\xi '$
, we obtain two additional configurations
![]() $\omega ^{\xi },\omega ^{\xi '}$
with laws
$\omega ^{\xi },\omega ^{\xi '}$
with laws
![]() $\phi _{\Lambda _R}^{\xi }$
and
$\phi _{\Lambda _R}^{\xi }$
and
![]() $\phi _{\Lambda _R}^{\xi '}$
, respectively, such that
$\phi _{\Lambda _R}^{\xi '}$
, respectively, such that
![]() $\omega ^0 \leq \omega ^{\xi } \leq \omega ^1$
and
$\omega ^0 \leq \omega ^{\xi } \leq \omega ^1$
and
![]() $\omega ^0 \leq \omega ^{\xi '} \leq \omega ^1$
. If
$\omega ^0 \leq \omega ^{\xi '} \leq \omega ^1$
. If
![]() $\zeta $
and
$\zeta $
and
![]() $\zeta '$
are the boundary conditions induced on
$\zeta '$
are the boundary conditions induced on
![]() $\partial \Lambda _{2r}$
by
$\partial \Lambda _{2r}$
by
![]() $\omega ^0$
and
$\omega ^0$
and
![]() $\omega ^1$
, we see that
$\omega ^1$
, we see that
where in the second inequality we used Theorems 4.1 and 4.9 as well as the mixing property to replace
![]() $\phi _{\Lambda _{2r},p}^{\psi }[A]$
by
$\phi _{\Lambda _{2r},p}^{\psi }[A]$
by
![]() $\phi _{\Lambda _R,p}^{\xi }[A]$
. This concludes the proof.
$\phi _{\Lambda _R,p}^{\xi }[A]$
. This concludes the proof.
![]() $\square $
$\square $
4.4 Quasi-multiplicativity of
 $\Delta _p$
: proof of Theorem 1.6(ii)
$\Delta _p$
: proof of Theorem 1.6(ii)
Let
![]() $\mathbb {P}$
be the coupling between
$\mathbb {P}$
be the coupling between
![]() $\phi _{\Lambda _R}^{1}$
and
$\phi _{\Lambda _R}^{1}$
and
![]() $\phi _{\Lambda _R}^{0}$
in
$\phi _{\Lambda _R}^{0}$
in
![]() $\mathrm {Ann}(n,R)$
given by Theorem 4.1(i), and let
$\mathrm {Ann}(n,R)$
given by Theorem 4.1(i), and let
![]() $\zeta $
and
$\zeta $
and
![]() $\zeta '$
be the boundary conditions induced by
$\zeta '$
be the boundary conditions induced by
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
on
$\omega '$
on
![]() $\partial \Lambda _{n}$
. Complete the coupling inside
$\partial \Lambda _{n}$
. Complete the coupling inside
![]() $\Lambda _n$
by an arbitrary increasing coupling of
$\Lambda _n$
by an arbitrary increasing coupling of
![]() $\phi _{\Lambda _n}^{\zeta }$
and
$\phi _{\Lambda _n}^{\zeta }$
and
![]() $\phi _{\Lambda _n}^{\zeta '}$
. Write
$\phi _{\Lambda _n}^{\zeta '}$
. Write
![]() $\mathbb {E}$
for the expectation associated to
$\mathbb {E}$
for the expectation associated to
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
On the one hand, the definition of
![]() $\Delta _p(r,n)$
, Theorems 4.1 and 4.9 and the comparison between boundary conditions in equation (CBC) yield
$\Delta _p(r,n)$
, Theorems 4.1 and 4.9 and the comparison between boundary conditions in equation (CBC) yield

On the other hand, recall that when
![]() $\tau < \infty $
,
$\tau < \infty $
,
![]() $\mathcal {F}_{\tau }$
is a
$\mathcal {F}_{\tau }$
is a
![]() $1/2$
-well-separated inner flower domain on
$1/2$
-well-separated inner flower domain on
![]() $\Lambda _n$
and that
$\Lambda _n$
and that
![]() $\omega _{[\tau ]}$
and
$\omega _{[\tau ]}$
and
![]() $\omega ^{\prime }_{[\tau ]}$
induce a boosting pair of boundary conditions on
$\omega ^{\prime }_{[\tau ]}$
induce a boosting pair of boundary conditions on
![]() $\mathcal {F}_{\tau }$
. Thus, Theorem 4.9 implies
$\mathcal {F}_{\tau }$
. Thus, Theorem 4.9 implies

![]() $\square $
$\square $
4.5 Mixing rate versus pivotality: proof of Theorem 1.6(iv)
This section concerns the proof of equation (1.17). This property is not crucial to the rest of the paper (its use in the proof of Lemma 5.3 may be avoided), but it illustrates that Kesten’s scaling relation does not extend with
![]() $\pi _4(p;r,R)$
instead of
$\pi _4(p;r,R)$
instead of
![]() $\Delta _p(r,R)$
.
$\Delta _p(r,R)$
.
Remark 4.15. Note that the weaker bound
![]() $\Delta _p(r,R)\stackrel{>}{\scriptstyle{\frown}} \pi _4(p;r,R)$
follows readily from Theorems 4.1 and 4.9. Thus, the polynomial improvement of
$\Delta _p(r,R)\stackrel{>}{\scriptstyle{\frown}} \pi _4(p;r,R)$
follows readily from Theorems 4.1 and 4.9. Thus, the polynomial improvement of
![]() $(R/r)^c$
is the core of equation (1.17).
$(R/r)^c$
is the core of equation (1.17).
We will use the following notation. Let
![]() $r < R$
,
$r < R$
,
![]() $\mathcal {F}$
be an outer flower domain on
$\mathcal {F}$
be an outer flower domain on
![]() $\Lambda _r$
and
$\Lambda _r$
and
![]() $\mathcal {G}$
be an inner flower domain on
$\mathcal {G}$
be an inner flower domain on
![]() $\Lambda _R$
, each containing exactly four petals denoted by
$\Lambda _R$
, each containing exactly four petals denoted by
![]() $P_1,\dots , P_4$
and
$P_1,\dots , P_4$
and
![]() $P_1',\dots , P_4'$
, respectively. Then
$P_1',\dots , P_4'$
, respectively. Then
![]() $\xi ^1$
(respectively,
$\xi ^1$
(respectively,
![]() $\xi ^0$
) are the boundary conditions on
$\xi ^0$
) are the boundary conditions on
![]() $\mathcal {F}$
, which are coherent with its flower domain structure and in which the primal petals
$\mathcal {F}$
, which are coherent with its flower domain structure and in which the primal petals
![]() $P_1$
and
$P_1$
and
![]() $P_3$
are wired (respectively, not wired) together. The similarly defined boundary conditions on
$P_3$
are wired (respectively, not wired) together. The similarly defined boundary conditions on
![]() $\mathcal {G}$
are written
$\mathcal {G}$
are written
![]() $\zeta ^1$
and
$\zeta ^1$
and
![]() $\zeta ^0$
, respectively.
$\zeta ^0$
, respectively.
For
![]() $i,j \in \{0,1\}$
, denote by
$i,j \in \{0,1\}$
, denote by
![]() $\phi _{\mathcal {F}\cap \mathcal {G}}^{\xi ^i\cup \zeta ^j}$
the measure on the subgraph
$\phi _{\mathcal {F}\cap \mathcal {G}}^{\xi ^i\cup \zeta ^j}$
the measure on the subgraph
![]() $\mathcal {F}\cap \mathcal {G}$
with the boundary condition
$\mathcal {F}\cap \mathcal {G}$
with the boundary condition
![]() $\xi ^i\cup \zeta ^j$
, which is the partition of
$\xi ^i\cup \zeta ^j$
, which is the partition of
![]() $\partial (\mathcal {F}\cap \mathcal {G})=\partial \mathcal {F}\cup \partial \mathcal {G}$
given by the union of the partitions
$\partial (\mathcal {F}\cap \mathcal {G})=\partial \mathcal {F}\cup \partial \mathcal {G}$
given by the union of the partitions
![]() $\xi ^i$
of the inner boundary and
$\xi ^i$
of the inner boundary and
![]() $\zeta ^j$
of the outer one.
$\zeta ^j$
of the outer one.
For configurations on
![]() $\mathcal {F} \cap \mathcal {G}$
, define the events
$\mathcal {F} \cap \mathcal {G}$
, define the events

Also write
![]() $\phi _{\mathcal {F} \cap \Lambda _R}^{\xi ^i\cup 1}$
and
$\phi _{\mathcal {F} \cap \Lambda _R}^{\xi ^i\cup 1}$
and
![]() $\phi _{\mathcal {F} \cap \Lambda _R}^{\xi ^i\cup 0}$
for the measures on
$\phi _{\mathcal {F} \cap \Lambda _R}^{\xi ^i\cup 0}$
for the measures on
![]() $\mathcal {F} \cap \Lambda _R$
with boundary conditions
$\mathcal {F} \cap \Lambda _R$
with boundary conditions
![]() $\xi ^i$
on
$\xi ^i$
on
![]() $\partial \mathcal {F}$
and, respectively, wired and free boundary conditions on
$\partial \mathcal {F}$
and, respectively, wired and free boundary conditions on
![]() $\partial \Lambda _R$
. Define
$\partial \Lambda _R$
. Define
![]() $A_4(\mathcal {F},R)$
and
$A_4(\mathcal {F},R)$
and
![]() $\tilde A_4(\mathcal {F},R)$
as in the last display, with
$\tilde A_4(\mathcal {F},R)$
as in the last display, with
![]() $P_1',\dots , P_4'$
all replaced by
$P_1',\dots , P_4'$
all replaced by
![]() $\partial \Lambda _R$
.
$\partial \Lambda _R$
.
The following lemma states that the probability of the four-arm event
![]() $A_{4}(\mathcal {F},\mathcal {G})$
increases substantially if we allow the primal arms to be in
$A_{4}(\mathcal {F},\mathcal {G})$
increases substantially if we allow the primal arms to be in
![]() $\omega '$
rather than in
$\omega '$
rather than in
![]() $\omega $
. It is particularly important in the lemma below that
$\omega $
. It is particularly important in the lemma below that
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
are not assumed to be well-separated.
$\mathcal {G}$
are not assumed to be well-separated.
Lemma 4.16. There exists
![]() $\delta> 0$
such that the following holds. For any
$\delta> 0$
such that the following holds. For any
![]() $p \in (0,1)$
and
$p \in (0,1)$
and
![]() $1 \leq r \leq L(p)$
, any outer flower domain
$1 \leq r \leq L(p)$
, any outer flower domain
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\Lambda _r$
and any inner flower domain
$\Lambda _r$
and any inner flower domain
![]() $\mathcal {G}$
on
$\mathcal {G}$
on
![]() $ \Lambda _{2r}$
, both containing exactly four petals, and any
$ \Lambda _{2r}$
, both containing exactly four petals, and any
![]() $i \in \{0,1\}$
, there exists a coupling
$i \in \{0,1\}$
, there exists a coupling
![]() $\mathbb {P}$
of
$\mathbb {P}$
of
![]() $\phi _{\mathcal {F}\cap \mathcal {G}}^{\xi ^i\cup \zeta ^0}$
and
$\phi _{\mathcal {F}\cap \mathcal {G}}^{\xi ^i\cup \zeta ^0}$
and
![]() $\phi _{\mathcal {F}\cap \mathcal {G}}^{\xi ^i\cup \zeta ^1}$
such that
$\phi _{\mathcal {F}\cap \mathcal {G}}^{\xi ^i\cup \zeta ^1}$
such that
Proof. Fix p, r, i,
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
as above. We will first treat the case where both flower domains are well-separated and then use it to solve the general case.
$\mathcal {G}$
as above. We will first treat the case where both flower domains are well-separated and then use it to solve the general case.
Proof when
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
are
$\mathcal {G}$
are
![]() $1/2$
-well-separated. Let
$1/2$
-well-separated. Let
![]() $x = (3n/2,0)$
, and start the coupling by exploring the double four-petal flower domain
$x = (3n/2,0)$
, and start the coupling by exploring the double four-petal flower domain
![]() $(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
between
$(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
between
![]() $\Lambda _{n/8}(x)$
and
$\Lambda _{n/8}(x)$
and
![]() $\Lambda _{n/4}(x)$
in
$\Lambda _{n/4}(x)$
in
![]() $\omega $
. If this stage fails, reveal the rest of the configuration in an arbitrarily increasing fashion. If
$\omega $
. If this stage fails, reveal the rest of the configuration in an arbitrarily increasing fashion. If
![]() $(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
exists, continue by revealing the configuration inside
$(\mathcal {F}_{\mathrm {in}},\mathcal {F}_{\mathrm {out}})$
exists, continue by revealing the configuration inside
![]() $\mathcal {F}_{\mathrm {in}}$
. Write
$\mathcal {F}_{\mathrm {in}}$
. Write
![]() $\xi _{\mathrm {in}}^{0}<\xi _{\mathrm {in}}^{1}$
for the two boundary conditions on
$\xi _{\mathrm {in}}^{0}<\xi _{\mathrm {in}}^{1}$
for the two boundary conditions on
![]() $\mathcal {F}_{\mathrm {in}}$
, which are coherent with the flower domain structure.
$\mathcal {F}_{\mathrm {in}}$
, which are coherent with the flower domain structure.
We now use the same argument as in the proof of equation (3.8) to study the connection probability between
![]() $P_1^{\mathrm {in}}$
and
$P_1^{\mathrm {in}}$
and
![]() $P_3^{\mathrm {in}}$
inside
$P_3^{\mathrm {in}}$
inside
![]() $\mathcal {F}_{\mathrm {in}}$
in
$\mathcal {F}_{\mathrm {in}}$
in
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
. The conditional law of
$\omega '$
. The conditional law of
![]() $\omega $
in
$\omega $
in
![]() $\mathcal {F}_{\mathrm {in}}$
is
$\mathcal {F}_{\mathrm {in}}$
is
while that of
![]() $\omega '$
dominates
$\omega '$
dominates
Thus,
![]() $\lambda ' - \lambda $
may be lower bounded by the probability that
$\lambda ' - \lambda $
may be lower bounded by the probability that
![]() $P_1^{\mathrm {out}}$
and
$P_1^{\mathrm {out}}$
and
![]() $P_3^{\mathrm {out}}$
are connected in
$P_3^{\mathrm {out}}$
are connected in
![]() $\mathcal {F}_{\mathrm {out}}$
to the two primal petals of
$\mathcal {F}_{\mathrm {out}}$
to the two primal petals of
![]() $\mathcal {G}$
but not to each other. By equation (RSW), we conclude that
$\mathcal {G}$
but not to each other. By equation (RSW), we conclude that
![]() $\lambda ' - \lambda \stackrel{>}{\scriptstyle{\frown}} 1$
and by Lemma 3.7 that
$\lambda ' - \lambda \stackrel{>}{\scriptstyle{\frown}} 1$
and by Lemma 3.7 that
Finally, reveal the configurations on
![]() $\mathcal {F}_{\mathrm {out}}$
.
$\mathcal {F}_{\mathrm {out}}$
.
Let H be the event that in
![]() $\mathcal {F}_{\mathrm {out}}$
(see Figure 11, left diagram for an illustration):
$\mathcal {F}_{\mathrm {out}}$
(see Figure 11, left diagram for an illustration):
-
•
 $P_1^{\mathrm {out}}$
is connected to
$P_1^{\mathrm {out}}$
is connected to
 $P_1$
in
$P_1$
in
 $\omega $
,
$\omega $
, -
•
 $P_3^{\mathrm {out}}$
is connected to
$P_3^{\mathrm {out}}$
is connected to
 $P_1'$
in
$P_1'$
in
 $\omega $
,
$\omega $
, -
•
 $P_3$
is connected to
$P_3$
is connected to
 $P_3'$
in
$P_3'$
in
 $\omega $
,
$\omega $
, -
•
 $P_2$
,
$P_2$
,
 $P_2'$
and
$P_2'$
and
 $P_4^{\mathrm {out}}$
are connected in
$P_4^{\mathrm {out}}$
are connected in
 $\omega ^*$
and
$\omega ^*$
and -
•
 $P_4$
,
$P_4$
,
 $P_4'$
and
$P_4'$
and
 $P_2^{\mathrm {out}}$
are connected in
$P_2^{\mathrm {out}}$
are connected in
 $\omega ^*$
.
$\omega ^*$
.
In other words, H is the event that the connection between
![]() $P_1^{\mathrm {in}}$
and
$P_1^{\mathrm {in}}$
and
![]() $P_3^{\mathrm {in}}$
inside
$P_3^{\mathrm {in}}$
inside
![]() $\mathcal {F}_{\mathrm { in}}$
is pivotal for
$\mathcal {F}_{\mathrm { in}}$
is pivotal for
![]() $A_{4}(\mathcal {F},\mathcal {G})$
. Then equation (RSW) and the well-separation of
$A_{4}(\mathcal {F},\mathcal {G})$
. Then equation (RSW) and the well-separation of
![]() $\mathcal {F}$
,
$\mathcal {F}$
,
![]() $\mathcal {F}_{\mathrm {out}}$
and
$\mathcal {F}_{\mathrm {out}}$
and
![]() $\mathcal {G}$
imply that
$\mathcal {G}$
imply that

Figure 11
Left: In the graph
![]() $\mathcal {F}\cap \mathcal {G}$
, we first explore the double four-petal flower domain
$\mathcal {F}\cap \mathcal {G}$
, we first explore the double four-petal flower domain
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
and then reveal the configurations in
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
and then reveal the configurations in
![]() $\mathcal {F}_{\mathrm {in}}$
and
$\mathcal {F}_{\mathrm {in}}$
and
![]() $\mathcal {F}_{\mathrm {out}}$
. If H occurs (see the blue paths), then
$\mathcal {F}_{\mathrm {out}}$
. If H occurs (see the blue paths), then
![]() $A_{4}(\mathcal {F},\mathcal {G})$
depends on the connection inside
$A_{4}(\mathcal {F},\mathcal {G})$
depends on the connection inside
![]() $\mathcal {F}_{\mathrm {in}}$
between its primal petals. If this connection occurs in
$\mathcal {F}_{\mathrm {in}}$
between its primal petals. If this connection occurs in
![]() $\omega '$
but not in
$\omega '$
but not in
![]() $\omega $
, then the configurations are in
$\omega $
, then the configurations are in
![]() $\tilde A_{4}(\mathcal {F},\mathcal {G}) \smallsetminus A_{4}(\mathcal {F},\mathcal {G})$
. Right: When
$\tilde A_{4}(\mathcal {F},\mathcal {G}) \smallsetminus A_{4}(\mathcal {F},\mathcal {G})$
. Right: When
![]() $P_1$
is small, exploring one of the interfaces
$P_1$
is small, exploring one of the interfaces
![]() $\Gamma _1$
or
$\Gamma _1$
or
![]() $\Gamma _2$
produces a long arc that renders the probability that
$\Gamma _2$
produces a long arc that renders the probability that
![]() $P_1$
is connected to
$P_1$
is connected to
![]() $I_1$
uniformly positive. In the picture, this is done by exploring
$I_1$
uniformly positive. In the picture, this is done by exploring
![]() $\Gamma _1$
. However, if
$\Gamma _1$
. However, if
![]() $\Gamma _1$
typically exits
$\Gamma _1$
typically exits
![]() $\Lambda _{\varepsilon r}(x)$
to the right of y, we would explore
$\Lambda _{\varepsilon r}(x)$
to the right of y, we would explore
![]() $\Gamma _2$
.
$\Gamma _2$
.
Now, since
![]() $A_{4}(\mathcal {F},\mathcal {G})$
implies the occurrence of
$A_{4}(\mathcal {F},\mathcal {G})$
implies the occurrence of
![]() $\tilde A_{4}(\mathcal {F},\mathcal {G})$
, we conclude that
$\tilde A_{4}(\mathcal {F},\mathcal {G})$
, we conclude that
Finally, equations (4.29) and (4.30) and Lemma 3.4 together imply that the right-hand side is larger than
![]() $c_0>0$
. This concludes the proof of equation (4.28) when
$c_0>0$
. This concludes the proof of equation (4.28) when
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
are
$\mathcal {G}$
are
![]() $1/2$
-well-separated.
$1/2$
-well-separated.
Proof when
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
are not
$\mathcal {G}$
are not
![]() $1/2$
-well-separated. We will construct the coupling
$1/2$
-well-separated. We will construct the coupling
![]() $\mathbb {P}$
between
$\mathbb {P}$
between
![]() $\phi _{\mathcal {F}\cap \mathcal {G}}^{\xi ^i,\zeta ^0}$
and
$\phi _{\mathcal {F}\cap \mathcal {G}}^{\xi ^i,\zeta ^0}$
and
![]() $\phi _{\mathcal {F}\cap \mathcal {G}}^{\xi ^i,\zeta ^1}$
in two steps. We start by exploring the outer flower domain
$\phi _{\mathcal {F}\cap \mathcal {G}}^{\xi ^i,\zeta ^1}$
in two steps. We start by exploring the outer flower domain
![]() $\overline {\mathcal {F}}$
between
$\overline {\mathcal {F}}$
between
![]() $\Lambda _r$
and
$\Lambda _r$
and
![]() $\Lambda _{5r/8}$
in
$\Lambda _{5r/8}$
in
![]() $\omega $
and the inner flower domain
$\omega $
and the inner flower domain
![]() $\overline {\mathcal {G}}$
from
$\overline {\mathcal {G}}$
from
![]() $\Lambda _{2r}$
to
$\Lambda _{2r}$
to
![]() $\Lambda _{7r/8}$
also in
$\Lambda _{7r/8}$
also in
![]() $\omega $
. Say that
$\omega $
. Say that
![]() $(\overline {\mathcal {F}},\overline {\mathcal {G}})$
is good if
$(\overline {\mathcal {F}},\overline {\mathcal {G}})$
is good if
-
•
 $\overline {\mathcal {F}}$
and
$\overline {\mathcal {F}}$
and
 $\overline {\mathcal {G}}$
each contain exactly four petals and are
$\overline {\mathcal {G}}$
each contain exactly four petals and are
 $1/2$
-well-separated;
$1/2$
-well-separated; -
• the four petals of
 $\overline {\mathcal {F}}$
are connected in
$\overline {\mathcal {F}}$
are connected in
 $\mathcal {F}\smallsetminus \overline {\mathcal {F}}$
to the corresponding petals of
$\mathcal {F}\smallsetminus \overline {\mathcal {F}}$
to the corresponding petals of
 $\mathcal {F}$
by paths of alternating types in
$\mathcal {F}$
by paths of alternating types in
 $\omega $
;
$\omega $
; -
• the four petals of
 $\overline {\mathcal {G}}$
are connected in
$\overline {\mathcal {G}}$
are connected in
 $ \mathcal {G}\smallsetminus \overline {\mathcal {G}}$
to the corresponding petals of
$ \mathcal {G}\smallsetminus \overline {\mathcal {G}}$
to the corresponding petals of
 $\mathcal {G}$
by paths of alternating types in
$\mathcal {G}$
by paths of alternating types in
 $\omega $
.
$\omega $
.
The following claim is a standard but tedious consequence of equation (RSW), similar to the separation of arms. We will sketch its proof below after completing that of Lemma 4.16.
Claim 4.17. There exists a universal constant
![]() $c> 0$
such that
$c> 0$
such that
where the constant in
![]() $\stackrel{>}{\scriptstyle{\frown}}$
does not depend on
$\stackrel{>}{\scriptstyle{\frown}}$
does not depend on
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
If
![]() $(\overline {\mathcal {F}},\overline {\mathcal {G}})$
is not good, complete
$(\overline {\mathcal {F}},\overline {\mathcal {G}})$
is not good, complete
![]() $(\omega ,\omega ')$
inside
$(\omega ,\omega ')$
inside
![]() $\overline {\mathcal {F}}\cap \overline {\mathcal {G}}$
using an arbitrary increasing coupling. When
$\overline {\mathcal {F}}\cap \overline {\mathcal {G}}$
using an arbitrary increasing coupling. When
![]() $(\overline {\mathcal {F}},\overline {\mathcal {G}})$
is good, the first case may be applied to
$(\overline {\mathcal {F}},\overline {\mathcal {G}})$
is good, the first case may be applied to
![]() $\overline {\mathcal {F}}$
and
$\overline {\mathcal {F}}$
and
![]() $\overline {\mathcal {G}}$
and provides a way to complete
$\overline {\mathcal {G}}$
and provides a way to complete
![]() $(\omega ,\omega ')$
inside
$(\omega ,\omega ')$
inside
![]() $\overline {\mathcal {F}}\cap \overline {\mathcal {G}}$
so that
$\overline {\mathcal {F}}\cap \overline {\mathcal {G}}$
so that
Moreover, notice that in this case,
![]() $A_{4}(\mathcal {F},\mathcal {G})$
is equivalent to
$A_{4}(\mathcal {F},\mathcal {G})$
is equivalent to
![]() $A_{4}(\overline {\mathcal {F}},\overline {\mathcal {G}})$
and
$A_{4}(\overline {\mathcal {F}},\overline {\mathcal {G}})$
and
![]() $\tilde A_{4}(\mathcal {F},\mathcal {G})$
to
$\tilde A_{4}(\mathcal {F},\mathcal {G})$
to
![]() $\tilde A_{4}(\overline {\mathcal {F}},\overline {\mathcal {G}})$
. By summing the display above, we conclude that
$\tilde A_{4}(\overline {\mathcal {F}},\overline {\mathcal {G}})$
. By summing the display above, we conclude that
The above, together with Claim 4.17, provide the desired conclusion.
Finally, we turn to the proof of Claim 4.17. As already mentioned, this proof is quite tedious but is only based on the RSW theory and uses somewhat standard techniques. We sketch it below.
Proof of Claim 4.17
Note that all events depend exclusively on
![]() $\omega $
, and we will ignore the configuration
$\omega $
, and we will ignore the configuration
![]() $\omega '$
henceforth. Write
$\omega '$
henceforth. Write
![]() $\phi = \phi _{\mathcal {F}\cap \mathcal {G}}^{\xi ^i\cup \zeta ^0}$
for the law of
$\phi = \phi _{\mathcal {F}\cap \mathcal {G}}^{\xi ^i\cup \zeta ^0}$
for the law of
![]() $\omega $
.
$\omega $
.
Consider the interfaces
![]() $\Gamma _1,\dots , \Gamma _4$
separating the primal clusters of the primal petals of
$\Gamma _1,\dots , \Gamma _4$
separating the primal clusters of the primal petals of
![]() $\mathcal {F}$
from the dual clusters of its dual petals. View these interfaces as directed pathsFootnote
4
starting from the points
$\mathcal {F}$
from the dual clusters of its dual petals. View these interfaces as directed pathsFootnote
4
starting from the points
![]() $x_1,\dots , x_4$
that separate the petals of
$x_1,\dots , x_4$
that separate the petals of
![]() $\mathcal {F}$
and indexed by
$\mathcal {F}$
and indexed by
![]() $t \geq 0$
. When
$t \geq 0$
. When
![]() $A_4(\mathcal {F},\mathcal {G})$
occurs, these interfaces end on
$A_4(\mathcal {F},\mathcal {G})$
occurs, these interfaces end on
![]() $\partial \mathcal {G}$
at the points separating its petals.
$\partial \mathcal {G}$
at the points separating its petals.
For times
![]() $t_1,\dots , t_4$
, the portions of interfaces
$t_1,\dots , t_4$
, the portions of interfaces
![]() $\Gamma _1([0,t_1]), \dots , \Gamma _4([0,t_4])$
may be explored via a standard procedure, and the measure in
$\Gamma _1([0,t_1]), \dots , \Gamma _4([0,t_4])$
may be explored via a standard procedure, and the measure in
![]() $\mathcal {F} \cap \mathcal {G} \smallsetminus \big (\Gamma _1([0,t_1]) \cup \dots \cup \Gamma _4([0,t_4])\big )$
is given by equation (SMP). Fix
$\mathcal {F} \cap \mathcal {G} \smallsetminus \big (\Gamma _1([0,t_1]) \cup \dots \cup \Gamma _4([0,t_4])\big )$
is given by equation (SMP). Fix
![]() $\varepsilon = \frac 1{128}$
, and set
$\varepsilon = \frac 1{128}$
, and set
![]() $r' := (1+2\varepsilon )r$
. Let
$r' := (1+2\varepsilon )r$
. Let
![]() $I_1 := \{r'\} \times [-r'/2,r'/2]$
be an interval along the right side of the box
$I_1 := \{r'\} \times [-r'/2,r'/2]$
be an interval along the right side of the box
![]() $\Lambda _{r'}$
. Call
$\Lambda _{r'}$
. Call
![]() $I_2$
,
$I_2$
,
![]() $I_3$
and
$I_3$
and
![]() $I_3$
the rotations of
$I_3$
the rotations of
![]() $I_1$
by angles
$I_1$
by angles
![]() $\pi /2$
,
$\pi /2$
,
![]() $\pi $
and
$\pi $
and
![]() $3\pi /2$
, respectively. For
$3\pi /2$
, respectively. For
![]() $c> 0$
, we say that
$c> 0$
, we say that
![]() $\Gamma _1([0,t_1]), \dots , \Gamma _4([0,t_4]) \ c$
-expose
$\Gamma _1([0,t_1]), \dots , \Gamma _4([0,t_4]) \ c$
-expose
![]() $\mathcal {F}$
if
$\mathcal {F}$
if
We claim that for some universal
![]() $c>0$
, there exist stopping times
$c>0$
, there exist stopping times
![]() $\tau _1,\dots , \tau _4$
such that
$\tau _1,\dots , \tau _4$
such that
![]() $\Gamma _1([0,\tau _1]), \dots , \Gamma _4([0,\tau _4])$
are all contained in
$\Gamma _1([0,\tau _1]), \dots , \Gamma _4([0,\tau _4])$
are all contained in
![]() $\Lambda _{r'}$
and
$\Lambda _{r'}$
and
The above should be understood as a separation statement. Indeed, it essentially states that conditionally on the interfaces
![]() $\Gamma _1,\dots , \Gamma _4$
reaching
$\Gamma _1,\dots , \Gamma _4$
reaching
![]() $\partial \mathcal {G}$
, one may find a time when they are well-separated.
$\partial \mathcal {G}$
, one may find a time when they are well-separated.
Notice that if
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $\varepsilon /4$
-well-separated, then the above is trivial, as we may take
$\varepsilon /4$
-well-separated, then the above is trivial, as we may take
![]() $\tau _1 = \dots =\tau _4 = 0$
and adjust c. Thus, we only need to consider the case where at least one of the petals of
$\tau _1 = \dots =\tau _4 = 0$
and adjust c. Thus, we only need to consider the case where at least one of the petals of
![]() $\mathcal {F}$
is small.
$\mathcal {F}$
is small.
To start, assume that
![]() $P_1$
has endpoints
$P_1$
has endpoints
![]() $x_1$
and
$x_1$
and
![]() $x_2$
at a distance at most
$x_2$
at a distance at most
![]() $\varepsilon r/4$
from each other, while all other petals have well-separated endpoints (say, at a distance
$\varepsilon r/4$
from each other, while all other petals have well-separated endpoints (say, at a distance
![]() $2\varepsilon r$
from each other). For simplicity of exposition, assume that both endpoints of
$2\varepsilon r$
from each other). For simplicity of exposition, assume that both endpoints of
![]() $P_1$
are on the right side of
$P_1$
are on the right side of
![]() $\Lambda _r$
. We will then take
$\Lambda _r$
. We will then take
![]() $\tau _3 = \tau _4 = 0$
and either
$\tau _3 = \tau _4 = 0$
and either
![]() $\tau _1 = 0$
or
$\tau _1 = 0$
or
![]() $\tau _2 = 0$
, as described below.
$\tau _2 = 0$
, as described below.
Let x denote the centre of the segment
![]() $[x_1,x_2]$
. Let
$[x_1,x_2]$
. Let
![]() $y = x + (\varepsilon r,0)$
be the midpoint of the arc
$y = x + (\varepsilon r,0)$
be the midpoint of the arc
![]() $\partial \Lambda _{\varepsilon r}(x) \cap \Lambda _{r}^c$
. Let
$\partial \Lambda _{\varepsilon r}(x) \cap \Lambda _{r}^c$
. Let
![]() $\tilde \tau _1$
be the first time when
$\tilde \tau _1$
be the first time when
![]() $\Gamma _1$
exits
$\Gamma _1$
exits
![]() $\Lambda _{\varepsilon r}(x)$
and
$\Lambda _{\varepsilon r}(x)$
and
![]() $\tilde \tau _2$
be the first time when
$\tilde \tau _2$
be the first time when
![]() $\Gamma _2$
exits
$\Gamma _2$
exits
![]() $\Lambda _{\varepsilon r}(x)$
. Observe that due to our assumption,
$\Lambda _{\varepsilon r}(x)$
. Observe that due to our assumption,
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
both start inside
$\Gamma _2$
both start inside
![]() $\Lambda _{\varepsilon r/4}(x)$
. Formally,
$\Lambda _{\varepsilon r/4}(x)$
. Formally,
![]() $\Gamma _1$
may end at
$\Gamma _1$
may end at
![]() $x_2$
and never exit
$x_2$
and never exit
![]() $\Lambda _{\varepsilon r}(x)$
– in this case,
$\Lambda _{\varepsilon r}(x)$
– in this case,
![]() $\Gamma _2$
is the reverse of
$\Gamma _2$
is the reverse of
![]() $\Gamma _1$
, and we set
$\Gamma _1$
, and we set
![]() $\tilde \tau _1 = \tilde \tau _2 = \infty $
. For
$\tilde \tau _1 = \tilde \tau _2 = \infty $
. For
![]() $A_{4}(\mathcal {F},\mathcal {G})$
to occur, it is necessary that
$A_{4}(\mathcal {F},\mathcal {G})$
to occur, it is necessary that
![]() $\tilde \tau _1 < \infty $
and
$\tilde \tau _1 < \infty $
and
![]() $\tilde \tau _2 < \infty $
.
$\tilde \tau _2 < \infty $
.
Now, when
![]() $\tilde \tau _1 < \infty $
and
$\tilde \tau _1 < \infty $
and
![]() $\tilde \tau _2 < \infty $
,
$\tilde \tau _2 < \infty $
,
![]() $\Gamma _{1}(\tilde \tau _1)$
is a point on
$\Gamma _{1}(\tilde \tau _1)$
is a point on
![]() $\partial \Lambda _{\varepsilon r}(x)$
to the right of
$\partial \Lambda _{\varepsilon r}(x)$
to the right of
![]() $\Gamma _{2}(\tilde \tau _2)$
– see Figure 11, right diagram. Thus, we have
$\Gamma _{2}(\tilde \tau _2)$
– see Figure 11, right diagram. Thus, we have
If the former is valid, take
![]() $\tau _1 = \tilde \tau _1$
and
$\tau _1 = \tilde \tau _1$
and
![]() $\tau _2 = 0$
. Otherwise, take
$\tau _2 = 0$
. Otherwise, take
![]() $\tau _1 = 0$
and
$\tau _1 = 0$
and
![]() $\tau _2 = \tilde \tau _2$
.
$\tau _2 = \tilde \tau _2$
.
Assume that we are in the first case. When
![]() $\Gamma _1(\tau _1)$
is indeed to the right of y, equation (RSW) proves that
$\Gamma _1(\tau _1)$
is indeed to the right of y, equation (RSW) proves that
![]() $\Gamma _1([0,\tau _1])$
, …,
$\Gamma _1([0,\tau _1])$
, …,
![]() $\Gamma _4([0,\tau _4]) \ c$
-expose
$\Gamma _4([0,\tau _4]) \ c$
-expose
![]() $\mathcal {F}$
for some universal constant
$\mathcal {F}$
for some universal constant
![]() $c> 0$
; see also Figure 11, right diagram.
$c> 0$
; see also Figure 11, right diagram.
This proves equation (4.32) under the particular assumption that
![]() $P_1$
is small, while the other petals are big. To fully prove equation (4.32), one should also consider the cases where more than one petal is small. These may be solved by performing the same procedure two or three times, with radii
$P_1$
is small, while the other petals are big. To fully prove equation (4.32), one should also consider the cases where more than one petal is small. These may be solved by performing the same procedure two or three times, with radii
![]() $r' \gg r'' \gg r'''$
. We leave the details of these to the reader.
$r' \gg r'' \gg r'''$
. We leave the details of these to the reader.
Call
![]() $\overline {\mathcal {F}}$
good if it is
$\overline {\mathcal {F}}$
good if it is
![]() $1/2$
-well-separated and has exactly four petals that are connected to the corresponding ones of
$1/2$
-well-separated and has exactly four petals that are connected to the corresponding ones of
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\mathcal {F}\smallsetminus \overline {\mathcal {F}}$
. A similar definition may be given for
$\mathcal {F}\smallsetminus \overline {\mathcal {F}}$
. A similar definition may be given for
![]() $\overline {\mathcal {G}}$
, so that
$\overline {\mathcal {G}}$
, so that
![]() $(\overline {\mathcal {F}},\overline {\mathcal {G}})$
is good if and only if both
$(\overline {\mathcal {F}},\overline {\mathcal {G}})$
is good if and only if both
![]() $\overline {\mathcal {F}}$
and
$\overline {\mathcal {F}}$
and
![]() $\overline {\mathcal {G}}$
are good. Now, applying Lemma 3.4 in
$\overline {\mathcal {G}}$
are good. Now, applying Lemma 3.4 in
![]() $\mathrm {Ann}(\frac {9}{16}r,\frac {5}{8}r)$
and using equation (RSW), we deduce the existence of a universal constant
$\mathrm {Ann}(\frac {9}{16}r,\frac {5}{8}r)$
and using equation (RSW), we deduce the existence of a universal constant
![]() $c_1> 0$
such that
$c_1> 0$
such that
Combining the above with equation (4.32), we conclude that
for some universal constant
![]() $c_2> 0$
. Apply the same argument for
$c_2> 0$
. Apply the same argument for
![]() $\mathcal {G}$
to show that
$\mathcal {G}$
to show that
Combining the last two inequalities, we obtain the desired conclusion.
The following is a consequence of Lemma 4.16.
Corollary 4.18. For
![]() $\rho $
large enough,
$\rho $
large enough,
![]() $p \in (0,1)$
and
$p \in (0,1)$
and
![]() $r < R \leq L(p)$
with
$r < R \leq L(p)$
with
![]() $R = (\rho ^2 + 2)^k r$
, any outer flower domain
$R = (\rho ^2 + 2)^k r$
, any outer flower domain
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\Lambda _r$
with exactly four petals and any
$\Lambda _r$
with exactly four petals and any
![]() $i \in \{0,1\}$
, there exists an increasing coupling
$i \in \{0,1\}$
, there exists an increasing coupling
![]() $\mathbb {P}$
of
$\mathbb {P}$
of
![]() $\phi _{\mathcal {F} \cap \Lambda _R}^{\xi ^i\cup 0}$
and
$\phi _{\mathcal {F} \cap \Lambda _R}^{\xi ^i\cup 0}$
and
![]() $\phi _{\mathcal {F} \cap \Lambda _R}^{\xi ^i\cup 1}$
such that
$\phi _{\mathcal {F} \cap \Lambda _R}^{\xi ^i\cup 1}$
such that
where
![]() $\delta> 0$
is the constant given by Lemma 4.16.
$\delta> 0$
is the constant given by Lemma 4.16.
Proof. The proof proceeds by induction on k. Consider the value of
![]() $\rho>1$
fixed; it will be chosen at the end of the proof, and it will be apparent that it is independent of p, r, R or
$\rho>1$
fixed; it will be chosen at the end of the proof, and it will be apparent that it is independent of p, r, R or
![]() $\mathcal {F}$
. The case
$\mathcal {F}$
. The case
![]() $k = 0$
is trivially true.
$k = 0$
is trivially true.
Fix
![]() $k \geq 0$
, and assume that equation (4.34) holds for this value of k; we will now prove equation (4.34) for
$k \geq 0$
, and assume that equation (4.34) holds for this value of k; we will now prove equation (4.34) for
![]() $k+1$
. Let
$k+1$
. Let
![]() $\mathcal {F}$
be an inner flower domain on
$\mathcal {F}$
be an inner flower domain on
![]() $\Lambda _r$
, and fix boundary conditions
$\Lambda _r$
, and fix boundary conditions
![]() $\xi \in \{\xi ^0,\xi ^1\}$
on
$\xi \in \{\xi ^0,\xi ^1\}$
on
![]() $\partial \mathcal {F}$
. The coupling
$\partial \mathcal {F}$
. The coupling
![]() $\mathbb {P}$
is built in three steps:
$\mathbb {P}$
is built in three steps:
Step 1: Explore the inner flower domain from
![]() $\partial \Lambda _{2r\rho }$
to
$\partial \Lambda _{2r\rho }$
to
![]() $\partial \Lambda _{2r}$
and the outer one from
$\partial \Lambda _{2r}$
and the outer one from
![]() $\partial \Lambda _{2r\rho }$
to
$\partial \Lambda _{2r\rho }$
to
![]() $\partial \Lambda _{2r\rho ^2}$
in
$\partial \Lambda _{2r\rho ^2}$
in
![]() $\omega $
; call these
$\omega $
; call these
![]() $\mathcal {G}_{\mathrm {in}}$
and
$\mathcal {G}_{\mathrm {in}}$
and
![]() $\mathcal {G}_{\mathrm {out}}$
, respectively. We will abuse notation by identifying
$\mathcal {G}_{\mathrm {out}}$
, respectively. We will abuse notation by identifying
![]() $(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
with the entire configuration
$(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
with the entire configuration
![]() $(\omega ,\omega ')$
on
$(\omega ,\omega ')$
on
![]() $\mathcal {G}_{\mathrm {in}}^c \cap \mathcal {G}_{\mathrm {out}}^c$
. Say that
$\mathcal {G}_{\mathrm {in}}^c \cap \mathcal {G}_{\mathrm {out}}^c$
. Say that
![]() $(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
is good if both
$(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
is good if both
![]() $\mathcal {G}_{\mathrm {in}}$
and
$\mathcal {G}_{\mathrm {in}}$
and
![]() $\mathcal {G}_{\mathrm {out}}$
have exactly four petals
$\mathcal {G}_{\mathrm {out}}$
have exactly four petals
![]() $P^{\mathrm {in}}_1,\dots , P^{\mathrm {in}}_{4}$
and
$P^{\mathrm {in}}_1,\dots , P^{\mathrm {in}}_{4}$
and
![]() $P^{\mathrm {out}}_{1},\dots , P^{\mathrm {out}}_{4}$
, respectively, and if in
$P^{\mathrm {out}}_{1},\dots , P^{\mathrm {out}}_{4}$
, respectively, and if in
![]() $\omega \cap (\mathcal {G}_{\mathrm {in}}^c \cap \mathcal {G}_{\mathrm {out}}^c)$
there exist open paths connecting
$\omega \cap (\mathcal {G}_{\mathrm {in}}^c \cap \mathcal {G}_{\mathrm {out}}^c)$
there exist open paths connecting
![]() $P^{\mathrm {in}}_{1}$
to
$P^{\mathrm {in}}_{1}$
to
![]() $P^{\mathrm {out}}_{1}$
and
$P^{\mathrm {out}}_{1}$
and
![]() $P^{\mathrm {in}}_{3}$
to
$P^{\mathrm {in}}_{3}$
to
![]() $P^{\mathrm {out}}_{3}$
and dual-open paths connecting
$P^{\mathrm {out}}_{3}$
and dual-open paths connecting
![]() $P^{\mathrm {in}}_{2}$
to
$P^{\mathrm {in}}_{2}$
to
![]() $P^{\mathrm {out}}_{2}$
and
$P^{\mathrm {out}}_{2}$
and
![]() $P^{\mathrm {in}}_{4}$
to
$P^{\mathrm {in}}_{4}$
to
![]() $P^{\mathrm {out}}_{4}$
. As before, we use the notation
$P^{\mathrm {out}}_{4}$
. As before, we use the notation
![]() $\zeta _{\mathrm {in}}^{0}$
,
$\zeta _{\mathrm {in}}^{0}$
,
![]() $\zeta _{\mathrm {in}}^{1}$
for the two boundary conditions on
$\zeta _{\mathrm {in}}^{1}$
for the two boundary conditions on
![]() $\mathcal {G}_{\mathrm {in}}$
coherent with it being a flower domain and
$\mathcal {G}_{\mathrm {in}}$
coherent with it being a flower domain and
![]() $\zeta _{\mathrm {out}}^{0}$
and
$\zeta _{\mathrm {out}}^{0}$
and
![]() $\zeta _{\mathrm {out}}^{1}$
for those on
$\zeta _{\mathrm {out}}^{1}$
for those on
![]() $\mathcal {G}_{\mathrm {out}}$
.
$\mathcal {G}_{\mathrm {out}}$
.
Stage 2: If
![]() $(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
is not good, we sample the rest of the configurations according to an arbitrary increasing coupling. If
$(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
is not good, we sample the rest of the configurations according to an arbitrary increasing coupling. If
![]() $(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
is good, observe that the law of
$(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
is good, observe that the law of
![]() $\omega $
in
$\omega $
in
![]() $\mathcal {G}_{\mathrm {out}}$
, conditionally on the revealed set, is a linear combination
$\mathcal {G}_{\mathrm {out}}$
, conditionally on the revealed set, is a linear combination
Moreover, the conditional law of
![]() $\omega '$
dominates
$\omega '$
dominates
for the same value
![]() $\lambda $
.
$\lambda $
.
Since
![]() $\tilde A_4(\mathcal {G}_{\mathrm {out}}, R)$
is increasing in
$\tilde A_4(\mathcal {G}_{\mathrm {out}}, R)$
is increasing in
![]() $\omega '$
and decreasing in
$\omega '$
and decreasing in
![]() $\omega $
, we may use equation (4.34) for k (which is our induction hypothesis) applied between
$\omega $
, we may use equation (4.34) for k (which is our induction hypothesis) applied between
![]() $\mathcal {G}_{\mathrm {out}}$
and
$\mathcal {G}_{\mathrm {out}}$
and
![]() $\Lambda _R$
, once with the boundary conditions
$\Lambda _R$
, once with the boundary conditions
![]() $\zeta _{\mathrm {out}}^{0}$
on
$\zeta _{\mathrm {out}}^{0}$
on
![]() $\mathcal {G}_{\mathrm {out}}$
and once with the boundary conditions
$\mathcal {G}_{\mathrm {out}}$
and once with the boundary conditions
![]() $\zeta _{\mathrm {out}}^{1}$
, to produce an increasing coupling of
$\zeta _{\mathrm {out}}^{1}$
, to produce an increasing coupling of
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
on
$\omega '$
on
![]() $\mathcal {G}_{\mathrm {out}}$
so that
$\mathcal {G}_{\mathrm {out}}$
so that
Step 3: Finally, we sample
![]() $(\omega ,\omega ')$
in
$(\omega ,\omega ')$
in
![]() $\mathcal {G}_{\mathrm {in}} \cap \mathcal {F}$
according to a specific coupling between the measures in this region, with boundary conditions induced by the previously revealed parts of
$\mathcal {G}_{\mathrm {in}} \cap \mathcal {F}$
according to a specific coupling between the measures in this region, with boundary conditions induced by the previously revealed parts of
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
, respectively. Recall that this stage is reached only if
$\omega '$
, respectively. Recall that this stage is reached only if
![]() $(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
is good and that the revealed configurations suffice to decide whether
$(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
is good and that the revealed configurations suffice to decide whether
![]() $\tilde A_4(\mathcal {G}_{\mathrm {out}}, R)$
occurred or not.
$\tilde A_4(\mathcal {G}_{\mathrm {out}}, R)$
occurred or not.
If
![]() $\tilde A_4(\mathcal {G}_{\mathrm {out}}, R)$
did not occur, complete the coupling in an arbitrary increasing way. If
$\tilde A_4(\mathcal {G}_{\mathrm {out}}, R)$
did not occur, complete the coupling in an arbitrary increasing way. If
![]() $\tilde A_4(\mathcal {G}_{\mathrm {out}}, R)$
did occur, then the boundary conditions induced by the already revealed parts of
$\tilde A_4(\mathcal {G}_{\mathrm {out}}, R)$
did occur, then the boundary conditions induced by the already revealed parts of
![]() $\omega $
on
$\omega $
on
![]() $\mathcal {G}_{\mathrm {in}}$
are equal to
$\mathcal {G}_{\mathrm {in}}$
are equal to
![]() $\zeta _{\mathrm {in}}^{0}$
. Indeed, in
$\zeta _{\mathrm {in}}^{0}$
. Indeed, in
![]() $\omega \cap \mathcal {G}_{\mathrm {out}}$
,
$\omega \cap \mathcal {G}_{\mathrm {out}}$
,
![]() $P^{\mathrm {out}}_{1}$
and
$P^{\mathrm {out}}_{1}$
and
![]() $P^{\mathrm {out}}_{3}$
are disconnected from each other due to the dual arms. On the contrary, the boundary conditions induced by the revealed region of
$P^{\mathrm {out}}_{3}$
are disconnected from each other due to the dual arms. On the contrary, the boundary conditions induced by the revealed region of
![]() $\omega '$
on
$\omega '$
on
![]() $\mathcal {G}_{\mathrm {in}}$
dominate
$\mathcal {G}_{\mathrm {in}}$
dominate
![]() $\zeta _{\mathrm {in}}^{1}$
, since in
$\zeta _{\mathrm {in}}^{1}$
, since in
![]() $\omega ' \cap \mathcal {G}_{\mathrm {out}}$
,
$\omega ' \cap \mathcal {G}_{\mathrm {out}}$
,
![]() $P^{\mathrm {out}}_{1}$
and
$P^{\mathrm {out}}_{1}$
and
![]() $P^{\mathrm {out}}_{3}$
are connected to
$P^{\mathrm {out}}_{3}$
are connected to
![]() $\partial \Lambda _R$
, which is wired. Thus, we may apply Lemma 4.16 to continue the coupling so that
$\partial \Lambda _R$
, which is wired. Thus, we may apply Lemma 4.16 to continue the coupling so that
 $$ \begin{align} & \mathbb{P}[\tilde A_4(\mathcal{F},\mathcal{G}_{\mathrm{in}}) | \, (\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ good and }\tilde A_4(\mathcal{G}_{\mathrm{out}}, R)]\nonumber\\ &\quad \geq (1+\delta) \mathbb{P}[ A_4(\mathcal{F},\mathcal{G}_{\mathrm{in}}) | \, (\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ good and } \tilde A_4(\mathcal{G}_{\mathrm{out}}, R)]. \end{align} $$
$$ \begin{align} & \mathbb{P}[\tilde A_4(\mathcal{F},\mathcal{G}_{\mathrm{in}}) | \, (\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ good and }\tilde A_4(\mathcal{G}_{\mathrm{out}}, R)]\nonumber\\ &\quad \geq (1+\delta) \mathbb{P}[ A_4(\mathcal{F},\mathcal{G}_{\mathrm{in}}) | \, (\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ good and } \tilde A_4(\mathcal{G}_{\mathrm{out}}, R)]. \end{align} $$
This concludes the construction of the coupling
![]() $\mathbb {P}$
; next we show that
$\mathbb {P}$
; next we show that
![]() $\mathbb {P}$
satisfies equation (4.34).
$\mathbb {P}$
satisfies equation (4.34).
If
![]() $(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
is good and
$(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
is good and
![]() $\tilde A_4(\mathcal {G}_{\mathrm {out}}, R)$
and
$\tilde A_4(\mathcal {G}_{\mathrm {out}}, R)$
and
![]() $\tilde A_4(\mathcal {F},\mathcal {G}_{\mathrm {in}})$
both occur, then so does
$\tilde A_4(\mathcal {F},\mathcal {G}_{\mathrm {in}})$
both occur, then so does
![]() $\tilde A_4(\mathcal {F},R)$
. By equations (4.36) and (4.37) and the fact that
$\tilde A_4(\mathcal {F},R)$
. By equations (4.36) and (4.37) and the fact that
![]() $(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
are determined by
$(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
are determined by
![]() $\omega $
alone, we find
$\omega $
alone, we find
 $$ \begin{align} &\mathbb{P}[\tilde A_4(\mathcal{F},R)] \nonumber \\&\geq (1+\delta)(1+\tfrac{\delta}2)^{k} \sum_{(\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ good}}\phi_{\mathcal{F}}^{\xi\cup0} [(\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}})] \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{G}_{\mathrm{out}},R) \cap A_4(\mathcal{F},\mathcal{G}_{\mathrm{ in}})|\,(\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}})] \nonumber\\&= (1+\delta)(1+\tfrac{\delta}2)^{k} \sum_{(\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ good}}\phi_{\mathcal{F}}^{\xi\cup0} [(\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}})] \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R)| \, (\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}})] \nonumber\\&= (1+\delta)(1+\tfrac{\delta}2)^{k} \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R) \text{ and } (\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ good}]. \end{align} $$
$$ \begin{align} &\mathbb{P}[\tilde A_4(\mathcal{F},R)] \nonumber \\&\geq (1+\delta)(1+\tfrac{\delta}2)^{k} \sum_{(\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ good}}\phi_{\mathcal{F}}^{\xi\cup0} [(\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}})] \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{G}_{\mathrm{out}},R) \cap A_4(\mathcal{F},\mathcal{G}_{\mathrm{ in}})|\,(\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}})] \nonumber\\&= (1+\delta)(1+\tfrac{\delta}2)^{k} \sum_{(\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ good}}\phi_{\mathcal{F}}^{\xi\cup0} [(\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}})] \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R)| \, (\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}})] \nonumber\\&= (1+\delta)(1+\tfrac{\delta}2)^{k} \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R) \text{ and } (\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ good}]. \end{align} $$
The first equality is due to the fact that conditionally on a good
![]() $(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
,
$(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
,
![]() $A_4(\mathcal {F},R)$
occurs if and only if both
$A_4(\mathcal {F},R)$
occurs if and only if both
![]() $A_4(\mathcal {G}_{\mathrm {out}},R)$
and
$A_4(\mathcal {G}_{\mathrm {out}},R)$
and
![]() $A_4(\mathcal {F},\mathcal {G}_{\mathrm { in}})$
do. The last equality is obtained directly by summation.
$A_4(\mathcal {F},\mathcal {G}_{\mathrm { in}})$
do. The last equality is obtained directly by summation.
Observe now that for
![]() $A_4(\mathcal {F},R)$
to occur,
$A_4(\mathcal {F},R)$
to occur,
![]() $\mathcal {G}_{\mathrm {in}}$
and
$\mathcal {G}_{\mathrm {in}}$
and
![]() $\mathcal {G}_{\mathrm {out}}$
need to have at least four petals each. Moreover, if they each have exactly four petals, then these need to be connected in such a way that
$\mathcal {G}_{\mathrm {out}}$
need to have at least four petals each. Moreover, if they each have exactly four petals, then these need to be connected in such a way that
![]() $(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
is good. Thus
$(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
is good. Thus
 $$ \begin{align} \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R),(\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ not good}] \le &\,\phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R),\mathcal{G}_{\mathrm{in}} \text{ has at least 6 petals}] \nonumber\\ +&\,\phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R),\mathcal{G}_{\mathrm{out}} \text{ has at least 6 petals}]. \end{align} $$
$$ \begin{align} \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R),(\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ not good}] \le &\,\phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R),\mathcal{G}_{\mathrm{in}} \text{ has at least 6 petals}] \nonumber\\ +&\,\phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R),\mathcal{G}_{\mathrm{out}} \text{ has at least 6 petals}]. \end{align} $$
We will argue that both terms on the right-hand side are small compared to the quantity
![]() $\phi _{\mathcal {F}}^{\xi ,0}[A_4(\mathcal {F},R)]$
, provided
$\phi _{\mathcal {F}}^{\xi ,0}[A_4(\mathcal {F},R)]$
, provided
![]() $\rho $
is large enough.
$\rho $
is large enough.
Indeed, due to the quasi-multiplicativity of the four- and six-arm events (the former applied to the slightly unusual event
![]() $A_4(\mathcal {F},R)$
) and the mixing property given by equation (Mix), there exists a universal constant
$A_4(\mathcal {F},R)$
) and the mixing property given by equation (Mix), there exists a universal constant
![]() $C<\infty $
(that does not depend on
$C<\infty $
(that does not depend on
![]() $\mathcal {F}$
, p, r or R) such that
$\mathcal {F}$
, p, r or R) such that
 $$ \begin{align*} \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R),\mathcal{G}_{\mathrm{in}} \text{ has at least 6 petals}] &\le C \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},2r)] \phi_{\mathcal{F}}^{\xi\cup0}[A_4(2\rho r, R)] \pi_6(2r,2\rho r)\\ &\le C^2 \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R)] \frac{\pi_6(2r,2\rho r)}{\pi_4(2r,2\rho r)}. \end{align*} $$
$$ \begin{align*} \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R),\mathcal{G}_{\mathrm{in}} \text{ has at least 6 petals}] &\le C \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},2r)] \phi_{\mathcal{F}}^{\xi\cup0}[A_4(2\rho r, R)] \pi_6(2r,2\rho r)\\ &\le C^2 \phi_{\mathcal{F}}^{\xi\cup0}[A_4(\mathcal{F},R)] \frac{\pi_6(2r,2\rho r)}{\pi_4(2r,2\rho r)}. \end{align*} $$
Due to equation (RSW),
![]() $\rho> 0$
may be chosen independently of
$\rho> 0$
may be chosen independently of
![]() $\mathcal {F}$
, p, r or R so that
$\mathcal {F}$
, p, r or R so that
Assuming this is the case, and by the same reasoning for the second term of equation (4.39), we find
which, when inserted in equation (4.38), proves equation (4.34) for
![]() $R = (\rho ^2 + 2)^{k+1} r$
.
$R = (\rho ^2 + 2)^{k+1} r$
.
Proof of (1.17)
Fix
![]() $\delta> 0$
and
$\delta> 0$
and
![]() $\rho $
given by Corollary 4.18. Due to Theorem 1.6(ii) and equation (2.3), it suffices to prove the statement for
$\rho $
given by Corollary 4.18. Due to Theorem 1.6(ii) and equation (2.3), it suffices to prove the statement for
![]() $R = 2(\rho ^2 + 2)^k r$
. From now on, fix such values r and R.
$R = 2(\rho ^2 + 2)^k r$
. From now on, fix such values r and R.
We use the same notation as in the proof of Corollary 4.18 and construct a coupling
![]() $\mathbb {P}$
between
$\mathbb {P}$
between
![]() $\phi _{\Lambda _R}^0$
and
$\phi _{\Lambda _R}^0$
and
![]() $\phi _{\Lambda _R}^1$
similar to that of the previous proof.
$\phi _{\Lambda _R}^1$
similar to that of the previous proof.
First, explore the double four-petal flower domain between
![]() $\Lambda _{r}$
and
$\Lambda _{r}$
and
![]() $\Lambda _{2r}$
; call it
$\Lambda _{2r}$
; call it
![]() $(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
. If no such double flower domain exists, proceed with an arbitrary coupling. If
$(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
. If no such double flower domain exists, proceed with an arbitrary coupling. If
![]() $(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
exists, use the coupling provided by Corollary 4.18 to complete
$(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
exists, use the coupling provided by Corollary 4.18 to complete
![]() $(\omega ,\omega ')$
in
$(\omega ,\omega ')$
in
![]() $\mathcal {G}_{\mathrm {out}}$
so that
$\mathcal {G}_{\mathrm {out}}$
so that
Finally, use an arbitrary increasing coupling inside
![]() $\mathcal {G}_{\mathrm {in}}$
.
$\mathcal {G}_{\mathrm {in}}$
.
When
![]() $(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
exists and
$(\mathcal {G}_{\mathrm {in}},\mathcal {G}_{\mathrm {out}})$
exists and
![]() $\tilde A_4(\mathcal {G}_{\mathrm {out}},R)$
occurs, the boundary conditions imposed by the revealed portions of
$\tilde A_4(\mathcal {G}_{\mathrm {out}},R)$
occurs, the boundary conditions imposed by the revealed portions of
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
are equal to
$\omega '$
are equal to
![]() $\zeta ^0_{\mathrm {in}}$
and dominate
$\zeta ^0_{\mathrm {in}}$
and dominate
![]() $\zeta ^1_{\mathrm {in}}$
, respectively. Using Theorem 3.6 and Lemma 3.4, we conclude that
$\zeta ^1_{\mathrm {in}}$
, respectively. Using Theorem 3.6 and Lemma 3.4, we conclude that
 $$ \begin{align*} \Delta_p(r,R) &= \mathbb{P}\big[ \omega' \in \mathcal{C}(\Lambda_r), \omega \notin \mathcal{C}(\Lambda_r) \big]\\ &\stackrel{>}{\scriptstyle{\frown}} \mathbb{P} \big[\tilde A_4(\mathcal{G}_{\mathrm{out}},R), \, (\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ exists}\big] \\ &\stackrel{>}{\scriptstyle{\frown}} (1+ \tfrac\delta2)^k \mathbb{P} \big[A_4(\mathcal{G}_{\mathrm{ out}},R), \, (\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ exists}\big] \\ &\stackrel{>}{\scriptstyle{\frown}} (R/2r)^{\varepsilon} \pi_4 (r,R), \end{align*} $$
$$ \begin{align*} \Delta_p(r,R) &= \mathbb{P}\big[ \omega' \in \mathcal{C}(\Lambda_r), \omega \notin \mathcal{C}(\Lambda_r) \big]\\ &\stackrel{>}{\scriptstyle{\frown}} \mathbb{P} \big[\tilde A_4(\mathcal{G}_{\mathrm{out}},R), \, (\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ exists}\big] \\ &\stackrel{>}{\scriptstyle{\frown}} (1+ \tfrac\delta2)^k \mathbb{P} \big[A_4(\mathcal{G}_{\mathrm{ out}},R), \, (\mathcal{G}_{\mathrm{in}},\mathcal{G}_{\mathrm{out}}) \text{ exists}\big] \\ &\stackrel{>}{\scriptstyle{\frown}} (R/2r)^{\varepsilon} \pi_4 (r,R), \end{align*} $$
where
![]() $\varepsilon = \log (1+\frac \delta 2)/\log {(\rho ^2 + 2)}> 0$
. In the last inequality, we also used the so-called separation of arms for the four-arm event.
$\varepsilon = \log (1+\frac \delta 2)/\log {(\rho ^2 + 2)}> 0$
. In the last inequality, we also used the so-called separation of arms for the four-arm event.
5 Derivatives in terms of
 $\Delta _p$
$\Delta _p$
5.1 Derivatives for crossing and arm events
In this section, we obtain expressions for the derivatives of probabilities of crossing events and arm events in terms of
![]() $\Delta _p$
. In addition, we upper-bound the derivative of the mixing rate
$\Delta _p$
. In addition, we upper-bound the derivative of the mixing rate
![]() $\Delta _p$
with similar expressions. The relevant results are Propositions 5.1 and 5.9, respectively. These will hold within the critical window and are instrumental in proving the main stability results, Theorem 1.4 and equation (1.16).
$\Delta _p$
with similar expressions. The relevant results are Propositions 5.1 and 5.9, respectively. These will hold within the critical window and are instrumental in proving the main stability results, Theorem 1.4 and equation (1.16).
We start with a proposition that states a slightly weaker form of Corollary 1.7 but extends the expression to logarithmic derivatives of probabilities of arm events.
Proposition 5.1. Fix
![]() $\eta>0$
. For
$\eta>0$
. For
![]() $p\in (0,1)$
and every
$p\in (0,1)$
and every
![]() $\eta $
-regular quad
$\eta $
-regular quad
![]() $(\mathcal {D},a,b,c,d)$
at scale
$(\mathcal {D},a,b,c,d)$
at scale
![]() $R\le L(p)$
,
$R\le L(p)$
,
 $$ \begin{align} R^2\Delta_p(R)+\sum_{\ell=R}^{L(p)}\ell \Delta_p(\ell)\Delta_p(R,\ell) \stackrel{<}{\scriptstyle{\frown}} \tfrac{\mathrm{d}}{\mathrm{ d}p}\phi_{p}[\mathcal{C}(\mathcal{D})] \stackrel{<}{\scriptstyle{\frown}} \sum_{\ell=1}^R \ell\Delta_p(\ell)+\sum_{\ell=R}^{L(p)}\ell \Delta_p(\ell)\Delta_p(R,\ell), \end{align} $$
$$ \begin{align} R^2\Delta_p(R)+\sum_{\ell=R}^{L(p)}\ell \Delta_p(\ell)\Delta_p(R,\ell) \stackrel{<}{\scriptstyle{\frown}} \tfrac{\mathrm{d}}{\mathrm{ d}p}\phi_{p}[\mathcal{C}(\mathcal{D})] \stackrel{<}{\scriptstyle{\frown}} \sum_{\ell=1}^R \ell\Delta_p(\ell)+\sum_{\ell=R}^{L(p)}\ell \Delta_p(\ell)\Delta_p(R,\ell), \end{align} $$
where the constants in
![]() $\stackrel{<}{\scriptstyle{\frown}}$
depend on
$\stackrel{<}{\scriptstyle{\frown}}$
depend on
![]() $\eta $
. Moreover, for
$\eta $
. Moreover, for
![]() $k=1$
or
$k=1$
or
![]() $k\ge 2$
even and any
$k\ge 2$
even and any
![]() $r \le R \le L(p)$
,
$r \le R \le L(p)$
,
 $$ \begin{align*} \big|\tfrac{\mathrm{d}}{\mathrm{d}p}\log\pi_k(p;r,R)]\big| \stackrel{<}{\scriptstyle{\frown}} \sum_{\ell=1}^R \ell\Delta_p(\ell)+\sum_{\ell=R}^{L(p)}\ell \Delta_p(\ell)\Delta_p(R,\ell), \end{align*} $$
$$ \begin{align*} \big|\tfrac{\mathrm{d}}{\mathrm{d}p}\log\pi_k(p;r,R)]\big| \stackrel{<}{\scriptstyle{\frown}} \sum_{\ell=1}^R \ell\Delta_p(\ell)+\sum_{\ell=R}^{L(p)}\ell \Delta_p(\ell)\Delta_p(R,\ell), \end{align*} $$
where the constants in
![]() $\stackrel{<}{\scriptstyle{\frown}}$
depend on k.
$\stackrel{<}{\scriptstyle{\frown}}$
depend on k.
After proving Proposition 1.8 in the next section (which states that
![]() $\Delta _p(r,R) \stackrel{>}{\scriptstyle{\frown}} (r/R)^{2-c}$
inside the critical window), we may use the quasi-multiplicativity of
$\Delta _p(r,R) \stackrel{>}{\scriptstyle{\frown}} (r/R)^{2-c}$
inside the critical window), we may use the quasi-multiplicativity of
![]() $\Delta _p$
to replace the first term
$\Delta _p$
to replace the first term
![]() $\sum _{\ell \le R}\ell \Delta _p(\ell )$
in the upper bounds above by
$\sum _{\ell \le R}\ell \Delta _p(\ell )$
in the upper bounds above by
![]() $R^2\Delta _p(R)$
, hence deducing an up-to-constant estimate on the derivative. This is stated in Corollary 7.1.
$R^2\Delta _p(R)$
, hence deducing an up-to-constant estimate on the derivative. This is stated in Corollary 7.1.
Remark 5.2. The formula given by equation (5.1) for the derivative of the crossing probability of
![]() $\mathcal {D}$
is significantly different than the one for percolation, since edges far from
$\mathcal {D}$
is significantly different than the one for percolation, since edges far from
![]() $\mathcal {D}$
– that correspond to the second term in the formula – may contribute substantially. Indeed, if we accept the asymptotic
$\mathcal {D}$
– that correspond to the second term in the formula – may contribute substantially. Indeed, if we accept the asymptotic
![]() $\Delta (r,R) \asymp (r/R)^{\iota }$
, and if
$\Delta (r,R) \asymp (r/R)^{\iota }$
, and if
![]() $\iota < 1$
, then the edges at distance
$\iota < 1$
, then the edges at distance
![]() $L(p)$
contribute most to equation (5.1); however, when
$L(p)$
contribute most to equation (5.1); however, when
![]() $\iota> 1$
, the derivative is governed by the contributions of edges close to
$\iota> 1$
, the derivative is governed by the contributions of edges close to
![]() $\mathcal {D}$
. See Section 8.2.4 for the consequences of these two types of behaviour.
$\mathcal {D}$
. See Section 8.2.4 for the consequences of these two types of behaviour.
The proof of Proposition 5.1 is based on the following lemma, which controls the influence of each edge on a crossing event. Below, we call
![]() $\Lambda _r(e)$
a pivotal box in
$\Lambda _r(e)$
a pivotal box in
![]() $\omega $
for the crossing event in
$\omega $
for the crossing event in
![]() $(\mathcal {D},a,b,c,d)$
if
$(\mathcal {D},a,b,c,d)$
if
![]() $\omega \cup \Lambda _{r}(e)$
contains a crossing of
$\omega \cup \Lambda _{r}(e)$
contains a crossing of
![]() $\mathcal {D}$
from
$\mathcal {D}$
from
![]() $(ab)$
to
$(ab)$
to
![]() $(cd)$
but
$(cd)$
but
![]() $\omega \smallsetminus \Lambda _r(e)$
does not; call this event
$\omega \smallsetminus \Lambda _r(e)$
does not; call this event
![]() $\mathrm {Piv}_{r,e}(\mathcal {D})$
. Here
$\mathrm {Piv}_{r,e}(\mathcal {D})$
. Here
![]() $\omega \cup \Lambda _{r}(e)$
and
$\omega \cup \Lambda _{r}(e)$
and
![]() $\omega \smallsetminus \Lambda _r(e)$
are the configurations obtained from
$\omega \smallsetminus \Lambda _r(e)$
are the configurations obtained from
![]() $\omega $
by opening and closing, respectively, all edges in
$\omega $
by opening and closing, respectively, all edges in
![]() $\Lambda _r(e)$
.
$\Lambda _r(e)$
.
Lemma 5.3. There exists
![]() $c> 0$
such that for any
$c> 0$
such that for any
![]() $\eta>0$
, the following holds. For
$\eta>0$
, the following holds. For
![]() $p \in (0,1)$
,
$p \in (0,1)$
,
![]() $R \le L(p)$
, every
$R \le L(p)$
, every
![]() $\eta $
-regular quad
$\eta $
-regular quad
![]() $(\mathcal {D},a,b,c,d)$
of size R and every edge e at a distance n from
$(\mathcal {D},a,b,c,d)$
of size R and every edge e at a distance n from
![]() $\partial \mathcal {D}$
,
$\partial \mathcal {D}$
,
 $$ \begin{align} \hphantom{\hspace{-72pt}}\Delta_p(R)\stackrel{<}{\scriptstyle{\frown}} \mathrm{Cov}_{p}[\omega_e;\mathcal{C}(\mathcal{D})] &\stackrel{<}{\scriptstyle{\frown}} \sum_{r = n/2}^{4R}\frac {\Delta_p(r)}r\phi_p[\mathrm{Piv}_{r,e}(\mathcal{D})] \qquad\qquad\quad\kern1.5pt\text{if } n \le 2R, \end{align} $$
$$ \begin{align} \hphantom{\hspace{-72pt}}\Delta_p(R)\stackrel{<}{\scriptstyle{\frown}} \mathrm{Cov}_{p}[\omega_e;\mathcal{C}(\mathcal{D})] &\stackrel{<}{\scriptstyle{\frown}} \sum_{r = n/2}^{4R}\frac {\Delta_p(r)}r\phi_p[\mathrm{Piv}_{r,e}(\mathcal{D})] \qquad\qquad\quad\kern1.5pt\text{if } n \le 2R, \end{align} $$
where the constants in
![]() $\asymp $
and
$\asymp $
and
![]() $\stackrel{<}{\scriptstyle{\frown}}$
depend on
$\stackrel{<}{\scriptstyle{\frown}}$
depend on
![]() $\eta $
.
$\eta $
.
For
![]() $k=1$
or
$k=1$
or
![]() $k\ge 2$
even, the same upper bounds hold for
$k\ge 2$
even, the same upper bounds hold for
![]() $|\mathrm {Cov}_{p}[\omega _e; A_k(r,R)]|/\phi _p[A_k(r,R)]$
instead of
$|\mathrm {Cov}_{p}[\omega _e; A_k(r,R)]|/\phi _p[A_k(r,R)]$
instead of
![]() $\mathrm {Cov}_{p}[\omega _e;\mathcal {C}(\mathcal {D})]$
, with n replaced by the distance from e to
$\mathrm {Cov}_{p}[\omega _e;\mathcal {C}(\mathcal {D})]$
, with n replaced by the distance from e to
![]() $\partial \mathrm {Ann}(r,R)$
and with constants that depend on k.
$\partial \mathrm {Ann}(r,R)$
and with constants that depend on k.
Before proving this lemma and explaining how it implies Theorem 1.6(i), we mention a few important remarks.
Remark 5.4. Due to the choice of
![]() $\mathcal {D}$
, all edges e inside
$\mathcal {D}$
, all edges e inside
![]() $\mathcal {D}$
are in case equation (5.2). By equation (RSW),
$\mathcal {D}$
are in case equation (5.2). By equation (RSW),
![]() $\phi _p[\mathrm {Piv}_{r,e}(\mathcal {D})]$
is uniformly bounded away from
$\phi _p[\mathrm {Piv}_{r,e}(\mathcal {D})]$
is uniformly bounded away from
![]() $0$
for all
$0$
for all
![]() $R \le r\le 2R$
. These terms of the sum account for a contribution of order at least
$R \le r\le 2R$
. These terms of the sum account for a contribution of order at least
![]() $\Delta _p(R)$
to the right-hand side of equation (5.2). When e is in the ‘bulk’ of
$\Delta _p(R)$
to the right-hand side of equation (5.2). When e is in the ‘bulk’ of
![]() $\mathcal {D}$
(that is, at a distance of order R from
$\mathcal {D}$
(that is, at a distance of order R from
![]() $\mathcal {D}^c$
), the lower and upper bounds in equation (5.2) are comparable.
$\mathcal {D}^c$
), the lower and upper bounds in equation (5.2) are comparable.
Remark 5.5. The same results hold (the proof below adapts readily) for covariances under a measure
![]() $\phi _{G}^{\xi }$
for any subgraph G of
$\phi _{G}^{\xi }$
for any subgraph G of
![]() $\mathbb {Z}^2$
that contains
$\mathbb {Z}^2$
that contains
![]() $\Lambda _{2R}$
, any boundary conditions
$\Lambda _{2R}$
, any boundary conditions
![]() $\xi $
and any edge e closer to
$\xi $
and any edge e closer to
![]() $\mathcal {D}$
than to
$\mathcal {D}$
than to
![]() $G^c$
. Similarly, it also applies to the measure on a torus of size at least
$G^c$
. Similarly, it also applies to the measure on a torus of size at least
![]() $2R$
.
$2R$
.
Remark 5.6. The proof of equation (5.3) can be readily adapted to get the following: for every p and
![]() $3r\le |x|\le L(p)$
,
$3r\le |x|\le L(p)$
,
where
![]() $(\mathcal {D},a,b,c,d)$
and
$(\mathcal {D},a,b,c,d)$
and
![]() $(\mathcal {D}',a',b',c',d')$
are two
$(\mathcal {D}',a',b',c',d')$
are two
![]() $\eta $
-regular quads of size r.
$\eta $
-regular quads of size r.
Remark 5.7. Interestingly, equation (5.2) enables us to deduce some sharp estimates for e near
![]() $\partial \mathcal {D}$
. For instance, in the case where
$\partial \mathcal {D}$
. For instance, in the case where
![]() $e\in \partial \mathcal {D}$
is at a distance
$e\in \partial \mathcal {D}$
is at a distance
![]() $\eta R$
of a change of direction of
$\eta R$
of a change of direction of
![]() $\partial \mathcal {D}$
, one may use that the probability of
$\partial \mathcal {D}$
, one may use that the probability of
![]() $\mathrm {Piv}_{r,e}(\mathcal {D})$
is of the order of the scale-to-scale three-arm event on the boundary: that is, of order
$\mathrm {Piv}_{r,e}(\mathcal {D})$
is of the order of the scale-to-scale three-arm event on the boundary: that is, of order
![]() $(r/R)^2$
. Then Proposition 1.8 implies that
$(r/R)^2$
. Then Proposition 1.8 implies that
![]() $\mathrm {Cov}_{p}[\omega _e;\mathcal {C}(\mathcal {D})] \asymp \Delta _p(R)$
. Note that this is quite different from the case of
$\mathrm {Cov}_{p}[\omega _e;\mathcal {C}(\mathcal {D})] \asymp \Delta _p(R)$
. Note that this is quite different from the case of
![]() $q=1$
, where the terms involved in the derivative are quite different for edges near
$q=1$
, where the terms involved in the derivative are quite different for edges near
![]() $\partial \mathcal {D}$
. Also note that we are not claiming that
$\partial \mathcal {D}$
. Also note that we are not claiming that
![]() $\mathrm {Cov}_{p}[\omega _e;\mathcal {C}(\mathcal {D})] $
is always of the order of
$\mathrm {Cov}_{p}[\omega _e;\mathcal {C}(\mathcal {D})] $
is always of the order of
![]() $\Delta _p(R)$
as e could be close to a corner or a wedge of the domain, in which case the estimate could break.
$\Delta _p(R)$
as e could be close to a corner or a wedge of the domain, in which case the estimate could break.
Theorem 1.6(i) is a particular case of Lemma 5.3.
Proof of Theorem 1.6(i)
To get the first estimate, apply equation (5.2), quasi-multiplicativity, and observe that the right-hand side is smaller than
![]() $\sum _{r = \eta R}^R\frac 1r\Delta _p(r) \stackrel{<}{\scriptstyle{\frown}} \Delta _p(R)$
. To get the second and third estimates, apply equations 5.3–5.4 and the quasi-multiplicativity of
$\sum _{r = \eta R}^R\frac 1r\Delta _p(r) \stackrel{<}{\scriptstyle{\frown}} \Delta _p(R)$
. To get the second and third estimates, apply equations 5.3–5.4 and the quasi-multiplicativity of
![]() $\Delta _p$
.
$\Delta _p$
.
Proof of Lemma 5.3
We will prove formulas for the crossing of a quad
![]() $(\mathcal {D},a,b,c,d)$
; the proof for arm events is similar and entails standard adaptations. Write
$(\mathcal {D},a,b,c,d)$
; the proof for arm events is similar and entails standard adaptations. Write
![]() $\mathcal {C}$
instead of
$\mathcal {C}$
instead of
![]() $\mathcal {C}(\mathcal {D})$
. Recall that
$\mathcal {C}(\mathcal {D})$
. Recall that
We will prove each of the equations separately, starting with the second.
Proof of equation (5.3)
Construct an increasing coupling
![]() $\mathbb {P}$
between
$\mathbb {P}$
between
![]() $\phi [\cdot \,|\,\omega _e = 0]$
and
$\phi [\cdot \,|\,\omega _e = 0]$
and
![]() $\phi [\cdot \,|\,\omega _e = 1]$
producing configurations
$\phi [\cdot \,|\,\omega _e = 1]$
producing configurations
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
as follows: the coupling contains three stages based on Theorem 4.1(ii), Lemma 3.13 and Theorem 4.9, respectively. We refer to Figure 12 for a picture.
$\omega '$
as follows: the coupling contains three stages based on Theorem 4.1(ii), Lemma 3.13 and Theorem 4.9, respectively. We refer to Figure 12 for a picture.
-
1. Apply the coupling inside
 $\Lambda _{n/4}(e)$
between
$\Lambda _{n/4}(e)$
between
 $\phi [\cdot \,|\,\omega _e = 0]$
and
$\phi [\cdot \,|\,\omega _e = 0]$
and
 $\phi [\cdot \,|\,\omega _e = 1]$
using the procedure of Theorem 4.1(ii), up to the associated stopping time, which we denote by
$\phi [\cdot \,|\,\omega _e = 1]$
using the procedure of Theorem 4.1(ii), up to the associated stopping time, which we denote by
 $\tau _1$
. If
$\tau _1$
. If
 $\tau _1 = \infty $
, continue the coupling using an arbitrary increasing coupling. Recall that when
$\tau _1 = \infty $
, continue the coupling using an arbitrary increasing coupling. Recall that when
 $\tau _1 < \infty $
,
$\tau _1 < \infty $
,
 $\mathcal {F}_{\tau _1}$
is a
$\mathcal {F}_{\tau _1}$
is a
 $1/2$
-well-separated outer flower domain on
$1/2$
-well-separated outer flower domain on
 $\Lambda _{n/4}$
and that
$\Lambda _{n/4}$
and that
 $\omega _{[\tau _1]}$
and
$\omega _{[\tau _1]}$
and
 $\omega ^{\prime }_{[\tau _1]}$
induce a boosting pair of boundary conditions on
$\omega ^{\prime }_{[\tau _1]}$
induce a boosting pair of boundary conditions on
 $\mathcal {F}_{\tau _1}$
.
$\mathcal {F}_{\tau _1}$
. -
2. Continue the coupling on
 $\Lambda _{n/2}^c$
between
$\Lambda _{n/2}^c$
between
 $\phi ^{\omega ^{\prime }_{[\tau _1]}}_{\mathcal {F}_{\tau _1}}$
and
$\phi ^{\omega ^{\prime }_{[\tau _1]}}_{\mathcal {F}_{\tau _1}}$
and
 $\phi ^{\omega _{[\tau _1]}}_{\mathcal {F}_{\tau _1}}$
using the procedure of Lemma 3.13, up to the associated stopping time, which we denote by
$\phi ^{\omega _{[\tau _1]}}_{\mathcal {F}_{\tau _1}}$
using the procedure of Lemma 3.13, up to the associated stopping time, which we denote by
 $\tau _2$
. If
$\tau _2$
. If
 $\tau _2 = \infty $
, continue the coupling using an arbitrary increasing coupling. Recall that when
$\tau _2 = \infty $
, continue the coupling using an arbitrary increasing coupling. Recall that when
 $\tau _2 < \infty $
,
$\tau _2 < \infty $
,
 $\mathcal {F}_{\tau _2}$
is a
$\mathcal {F}_{\tau _2}$
is a
 $1/2$
-well-separated inner flower domain on
$1/2$
-well-separated inner flower domain on
 $\Lambda _{n/2}$
and that
$\Lambda _{n/2}$
and that
 $\omega _{[\tau _2]}$
and
$\omega _{[\tau _2]}$
and
 $\omega ^{\prime }_{[\tau _2]}$
induce a boosting pair of boundary conditions on
$\omega ^{\prime }_{[\tau _2]}$
induce a boosting pair of boundary conditions on
 $\mathcal {F}_{\tau _2}$
.
$\mathcal {F}_{\tau _2}$
. -
3. Complete the coupling inside
 $\mathcal {F}_{\tau _2}$
using an arbitrary increasing coupling of
$\mathcal {F}_{\tau _2}$
using an arbitrary increasing coupling of
 $\phi ^{\omega ^{\prime }_{[\tau _2]}}_{\mathcal {F}_{\tau _2}}$
and
$\phi ^{\omega ^{\prime }_{[\tau _2]}}_{\mathcal {F}_{\tau _2}}$
and
 $\phi ^{\omega _{[\tau _2]}}_{\mathcal {F}_{\tau _2}}$
.
$\phi ^{\omega _{[\tau _2]}}_{\mathcal {F}_{\tau _2}}$
.

Figure 12 In blue, the edges discovered until
![]() $\tau _1$
. In red, the edges discovered between
$\tau _1$
. In red, the edges discovered between
![]() $\tau _1$
and
$\tau _1$
and
![]() $\tau _2$
. Finally, in green, the edges discovered afterwards. Note that the domain
$\tau _2$
. Finally, in green, the edges discovered afterwards. Note that the domain
![]() $\mathcal {D}$
is a priori much smaller than the box
$\mathcal {D}$
is a priori much smaller than the box
![]() $\Lambda _{n/2}$
.
$\Lambda _{n/2}$
.
For the upper bound, observe that since
![]() $\mathcal {D} \subset \Lambda _{n/2}$
and
$\mathcal {D} \subset \Lambda _{n/2}$
and
![]() $\Lambda _{n/2}(e)$
are disjoint, if
$\Lambda _{n/2}(e)$
are disjoint, if
![]() $\zeta $
and
$\zeta $
and
![]() $\zeta '$
are the boundary conditions induced on
$\zeta '$
are the boundary conditions induced on
![]() $\mathcal {F}_{\tau _1}$
, Theorem 4.9 gives
$\mathcal {F}_{\tau _1}$
, Theorem 4.9 gives
Finally,
![]() $\Delta _p(R,n/2)$
may be replaced by
$\Delta _p(R,n/2)$
may be replaced by
![]() $\Delta _p(R,n)$
due to equation (4.21). For the lower bound, Theorem 4.9 gives
$\Delta _p(R,n)$
due to equation (4.21). For the lower bound, Theorem 4.9 gives

The second term above is of constant order by Lemma 3.13. The first term is of order
![]() $\Delta _p(1,n/4)$
by Theorem 4.9. Since
$\Delta _p(1,n/4)$
by Theorem 4.9. Since
![]() $\Delta _p(1,n/4)\ge \Delta _p(n)$
and
$\Delta _p(1,n/4)\ge \Delta _p(n)$
and
![]() $\Delta _p(R,n/2)\ge \Delta _p(R,n)$
, we obtain the result.
$\Delta _p(R,n/2)\ge \Delta _p(R,n)$
, we obtain the result.
![]() $\diamond $
$\diamond $
Proof of equation (5.4)
We focus here on the case
![]() $p < p_c$
; when
$p < p_c$
; when
![]() $p> p_c$
, the proof is obtained by duality. Construct the following coupling
$p> p_c$
, the proof is obtained by duality. Construct the following coupling
![]() $\mathbb {P}$
between
$\mathbb {P}$
between
![]() $\phi _p[\cdot \,|\,\omega _e=0]$
and
$\phi _p[\cdot \,|\,\omega _e=0]$
and
![]() $\phi _p[\cdot \,|\,\omega _e=1]$
:
$\phi _p[\cdot \,|\,\omega _e=1]$
:
-
1. Use the coupling given by Theorem 4.1(ii) between
 $\phi _p[\cdot \,|\,\omega _e=0]$
and
$\phi _p[\cdot \,|\,\omega _e=0]$
and
 $\phi _p[\cdot \,|\,\omega _e=1]$
inside
$\phi _p[\cdot \,|\,\omega _e=1]$
inside
 $\Lambda _{L(p)}(e)$
; let
$\Lambda _{L(p)}(e)$
; let
 $\xi $
and
$\xi $
and
 $\xi '$
be the boundary conditions induced by the revealed configurations
$\xi '$
be the boundary conditions induced by the revealed configurations
 $\omega $
and
$\omega $
and
 $\omega '$
on the boundary of
$\omega '$
on the boundary of
 $\mathbb {Z}^2\smallsetminus \Lambda _{L(p)}(e)$
.
$\mathbb {Z}^2\smallsetminus \Lambda _{L(p)}(e)$
. -
2. Continue the coupling in
 $\mathbb {Z}^2\smallsetminus \Lambda _{L(p)}$
using the decision tree that explores the connected components of
$\mathbb {Z}^2\smallsetminus \Lambda _{L(p)}$
using the decision tree that explores the connected components of
 $\Lambda _{L(p)}(e)$
in
$\Lambda _{L(p)}(e)$
in
 $\omega '$
(see Example 2 of Section 2.3); let
$\omega '$
(see Example 2 of Section 2.3); let
 $\zeta ,\zeta '$
be the boundary conditions induced by the revealed regions of
$\zeta ,\zeta '$
be the boundary conditions induced by the revealed regions of
 $\omega $
and
$\omega $
and
 $\omega '$
on
$\omega '$
on
 $\partial \Lambda _{L(p)}$
.
$\partial \Lambda _{L(p)}$
. -
3. Use an arbitrary increasing coupling of
 $\phi _{\Lambda _{L(p)},p}^{\zeta }$
and
$\phi _{\Lambda _{L(p)},p}^{\zeta }$
and
 $\phi _{\Lambda _{L(p)},p}^{\zeta '}$
.
$\phi _{\Lambda _{L(p)},p}^{\zeta '}$
.
If
![]() $\xi = \xi '$
, then
$\xi = \xi '$
, then
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
are identical in the complement of
$\omega '$
are identical in the complement of
![]() $\Lambda _{L(p)}(e)$
. Moreover, as explained in Section 2.3, for
$\Lambda _{L(p)}(e)$
. Moreover, as explained in Section 2.3, for
![]() $\zeta $
to differ from
$\zeta $
to differ from
![]() $\zeta '$
,
$\zeta '$
,
![]() $\omega '$
must contain a connection between
$\omega '$
must contain a connection between
![]() $\Lambda _{L(p)}(e)$
and
$\Lambda _{L(p)}(e)$
and
![]() $\Lambda _{L(p)}$
. Thus, we find
$\Lambda _{L(p)}$
. Thus, we find

In the second inequality, we used the monotonicity of boundary conditions given by equation (CBC) and Theorem 4.9. Finally, due to the mixing property of Corollary 2.10 and Proposition 2.13, the second term of the last product is bounded above by
![]() $\exp [-cn/L(p)]$
for some positive constant c.
$\exp [-cn/L(p)]$
for some positive constant c.
Proof of equation (5.2)
For the lower bound, translate
![]() $\mathcal {D}$
and e such that
$\mathcal {D}$
and e such that
![]() $e\notin \Lambda _{\eta R/2}$
and
$e\notin \Lambda _{\eta R/2}$
and
![]() $\Lambda _{\eta R/2} \subset \mathcal {D}$
. Since
$\Lambda _{\eta R/2} \subset \mathcal {D}$
. Since
![]() $\mathcal {D}$
is assumed
$\mathcal {D}$
is assumed
![]() $\eta $
-regular, this is possible. We produce a coupling
$\eta $
-regular, this is possible. We produce a coupling
![]() $\mathbb {P}$
between
$\mathbb {P}$
between
![]() $\phi _p[\cdot \,|\,\omega _e=0]$
and
$\phi _p[\cdot \,|\,\omega _e=0]$
and
![]() $\phi _p[\cdot \,|\,\omega _e=1]$
as follows.
$\phi _p[\cdot \,|\,\omega _e=1]$
as follows.
-
1. Explore the double four-petal flower domain
 $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
in
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
in
 $\omega $
between
$\omega $
between
 $\Lambda _{\eta R/4}$
and
$\Lambda _{\eta R/4}$
and
 $\Lambda _{\eta R/8}$
; if no such double four-petal flower domain exists, reveal the rest of the configurations in arbitrary order.
$\Lambda _{\eta R/8}$
; if no such double four-petal flower domain exists, reveal the rest of the configurations in arbitrary order. -
2. Reveal
 $\omega $
and
$\omega $
and
 $\omega '$
inside
$\omega '$
inside
 $\mathcal {F}_{\mathrm {in}}$
.
$\mathcal {F}_{\mathrm {in}}$
. -
3. Reveal the configurations in
 $\mathcal {F}_{\mathrm {out}}$
.
$\mathcal {F}_{\mathrm {out}}$
.
Now, if
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
exists, the argument of equation (5.3) shows that
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
exists, the argument of equation (5.3) shows that
Indeed, e is at a distance comparable to R from
![]() $(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
; for details, see the proof of the point in equation (3.8) of Theorem 3.6. Note that this is simply a statement on the conditional probability of the connections between the petals
$(\mathcal {F}_{\mathrm {in}}, \mathcal {F}_{\mathrm {out}})$
; for details, see the proof of the point in equation (3.8) of Theorem 3.6. Note that this is simply a statement on the conditional probability of the connections between the petals
![]() $P_1$
and
$P_1$
and
![]() $P_3$
; we do not reveal the configurations
$P_3$
; we do not reveal the configurations
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
in
$\omega '$
in
![]() $\mathcal {F}_{\mathrm {out}}$
.
$\mathcal {F}_{\mathrm {out}}$
.
Then as in the proof of equation (3.8), the previous estimate gives that
Let H be the event that
![]() $P_1^{\mathrm {out}}$
and
$P_1^{\mathrm {out}}$
and
![]() $P_3^{\mathrm {out}}$
are connected in
$P_3^{\mathrm {out}}$
are connected in
![]() $\omega \cap \mathcal {F}_{\mathrm {out}} \cap \mathcal {D}$
to the arcs
$\omega \cap \mathcal {F}_{\mathrm {out}} \cap \mathcal {D}$
to the arcs
![]() $(ab)$
and
$(ab)$
and
![]() $(cd)$
, respectively, while
$(cd)$
, respectively, while
![]() $P_2^{\mathrm {out}}$
and
$P_2^{\mathrm {out}}$
and
![]() $P_4^{\mathrm {out}}$
are connected in
$P_4^{\mathrm {out}}$
are connected in
![]() $\omega ^* \cap \mathcal {F}_{\mathrm {out}} \cap \mathcal {D}$
to the arcs
$\omega ^* \cap \mathcal {F}_{\mathrm {out}} \cap \mathcal {D}$
to the arcs
![]() $(bc)$
and
$(bc)$
and
![]() $(da)$
, respectively. By equation (RSW),
$(da)$
, respectively. By equation (RSW),
Finally, when H occurs,
![]() $\mathcal {D}$
is crossed if and only if
$\mathcal {D}$
is crossed if and only if
![]() $P_1^{\mathrm {in}}$
and
$P_1^{\mathrm {in}}$
and
![]() $P_3^{\mathrm {in}}$
are connected inside
$P_3^{\mathrm {in}}$
are connected inside
![]() $\mathcal {F}_{\mathrm {in}}$
. As a consequence, the two displays above and Lemma 3.4 conclude that
$\mathcal {F}_{\mathrm {in}}$
. As a consequence, the two displays above and Lemma 3.4 conclude that

We turn to the upper bound. For
![]() $s \ge 1$
, let
$s \ge 1$
, let
![]() $\mathcal {P}_s := \mathrm {Piv}_{2^s,e}(\mathcal {D}) \smallsetminus \mathrm {Piv}_{2^{s-1},e}(\mathcal {D})$
. Also set
$\mathcal {P}_s := \mathrm {Piv}_{2^s,e}(\mathcal {D}) \smallsetminus \mathrm {Piv}_{2^{s-1},e}(\mathcal {D})$
. Also set
![]() $\mathcal {P}_0 := \mathrm {Piv}_{1,e}(\mathcal {D})$
. Observe that
$\mathcal {P}_0 := \mathrm {Piv}_{1,e}(\mathcal {D})$
. Observe that
![]() $\mathrm {Piv}_{2R,e}(\mathcal {D})$
occurs as such, and therefore the events
$\mathrm {Piv}_{2R,e}(\mathcal {D})$
occurs as such, and therefore the events
![]() $\mathcal {P}_s$
for
$\mathcal {P}_s$
for
![]() $s = 0,\dots , \lceil \log 2R \rceil $
partition the space. Thus
$s = 0,\dots , \lceil \log 2R \rceil $
partition the space. Thus
 $$ \begin{align} \mathrm{Cov}_{p}(\omega_e,\mathcal{C}) &= \sum_{s = 0}^{ \lceil \log 2R \rceil}(\phi [\omega_e | \mathcal{C} \cap \mathcal{P}_s]-\phi[\omega_e])\phi_p[\mathcal{C} \cap \mathcal{P}_s] \nonumber\\ &\stackrel{<}{\scriptstyle{\frown}} \sum_{s = 1}^{ \lceil \log 2R \rceil}(\phi_{\Lambda_{2^{s-1}}(e)}^1[\omega_e]-\phi_{\Lambda_{2^{s-1}}(e)}^0[\omega_e])\phi_p[\mathrm{Piv}_{2^s,e}(\mathcal{D})] \nonumber\\ &\stackrel{<}{\scriptstyle{\frown}} \sum_{r = 1}^{4R}\tfrac{1}r\Delta_p(r)\phi_p[\mathrm{Piv}_{r,e}(\mathcal{D})]. \end{align} $$
$$ \begin{align} \mathrm{Cov}_{p}(\omega_e,\mathcal{C}) &= \sum_{s = 0}^{ \lceil \log 2R \rceil}(\phi [\omega_e | \mathcal{C} \cap \mathcal{P}_s]-\phi[\omega_e])\phi_p[\mathcal{C} \cap \mathcal{P}_s] \nonumber\\ &\stackrel{<}{\scriptstyle{\frown}} \sum_{s = 1}^{ \lceil \log 2R \rceil}(\phi_{\Lambda_{2^{s-1}}(e)}^1[\omega_e]-\phi_{\Lambda_{2^{s-1}}(e)}^0[\omega_e])\phi_p[\mathrm{Piv}_{2^s,e}(\mathcal{D})] \nonumber\\ &\stackrel{<}{\scriptstyle{\frown}} \sum_{r = 1}^{4R}\tfrac{1}r\Delta_p(r)\phi_p[\mathrm{Piv}_{r,e}(\mathcal{D})]. \end{align} $$
In the first inequality, we use that for
![]() $s \geq 1$
,
$s \geq 1$
,
![]() $\mathcal {C} \cap \mathcal {P}_s$
is measurable in terms of the edges outside
$\mathcal {C} \cap \mathcal {P}_s$
is measurable in terms of the edges outside
![]() $\Lambda _{2^{s-1}}(e)$
, as well as equation (SMP) and the inclusion
$\Lambda _{2^{s-1}}(e)$
, as well as equation (SMP) and the inclusion
![]() $\mathcal {P}_s \subset \mathrm {Piv}_{2^s,e}(\mathcal {D})$
. The term
$\mathcal {P}_s \subset \mathrm {Piv}_{2^s,e}(\mathcal {D})$
. The term
![]() $s = 0$
of the first line is trivially bounded by
$s = 0$
of the first line is trivially bounded by
![]() $\phi _p[\mathrm {Piv}_{1,e}(\mathcal {D})]$
and may be absorbed by the term
$\phi _p[\mathrm {Piv}_{1,e}(\mathcal {D})]$
and may be absorbed by the term
![]() $s=1$
of the second line. The second inequality is a simple reindexing of the sum; it uses equation (4.21) and the monotonicity in r of the events
$s=1$
of the second line. The second inequality is a simple reindexing of the sum; it uses equation (4.21) and the monotonicity in r of the events
![]() $\mathrm {Piv}_{r,e}(\mathcal {D})$
.
$\mathrm {Piv}_{r,e}(\mathcal {D})$
.
Next, we eliminateFootnote
5
the terms for
![]() $1 \leq r < n/2$
from the last sum of equation (5.8). Notice that if
$1 \leq r < n/2$
from the last sum of equation (5.8). Notice that if
![]() $\mathrm {Piv}_{r,e}(\mathcal {D})$
occurs for
$\mathrm {Piv}_{r,e}(\mathcal {D})$
occurs for
![]() $r < n$
, then
$r < n$
, then
![]() $\mathrm {Piv}_{n,e}(\mathcal {D})$
also occurs, and in addition there exist four arms of alternating type between
$\mathrm {Piv}_{n,e}(\mathcal {D})$
also occurs, and in addition there exist four arms of alternating type between
![]() $\Lambda _r(e)$
and
$\Lambda _r(e)$
and
![]() $\partial \Lambda _n(e)$
. Due to equation (Mix) and the quasi-multiplicativity of the four-arm event,
$\partial \Lambda _n(e)$
. Due to equation (Mix) and the quasi-multiplicativity of the four-arm event,
Now, using equations (1.15) and (1.17), we find
 $$ \begin{align*} \sum_{r = 1}^n \tfrac{1}r\Delta_p(r)\phi_p[\mathrm{Piv}_{r,e}(\mathcal{D})] &\stackrel{<}{\scriptstyle{\frown}} \sum_{r = 1}^n \tfrac{1}r\Delta_p(r) \pi_4(p; r,n)\phi_p[\mathrm{ Piv}_{n,e}(\mathcal{D})]\\ &\!\stackrel{<}{\scriptstyle{\frown}} \Delta_p(n) \phi_p[\mathrm{Piv}_{n,e}(\mathcal{D})] \tfrac{1}{n^{\varepsilon}}\sum_{r = 1}^n \tfrac{1}{r^{1-\varepsilon}} \\ &\!\stackrel{<}{\scriptstyle{\frown}} \Delta_p(n) \phi_p[\mathrm{Piv}_{n,e}(\mathcal{D})] \stackrel{<}{\scriptstyle{\frown}} \sum_{r = n/2}^n \tfrac{1}r\Delta_p(r)\phi_p[\mathrm{ Piv}_{r,e}(\mathcal{D})]. \end{align*} $$
$$ \begin{align*} \sum_{r = 1}^n \tfrac{1}r\Delta_p(r)\phi_p[\mathrm{Piv}_{r,e}(\mathcal{D})] &\stackrel{<}{\scriptstyle{\frown}} \sum_{r = 1}^n \tfrac{1}r\Delta_p(r) \pi_4(p; r,n)\phi_p[\mathrm{ Piv}_{n,e}(\mathcal{D})]\\ &\!\stackrel{<}{\scriptstyle{\frown}} \Delta_p(n) \phi_p[\mathrm{Piv}_{n,e}(\mathcal{D})] \tfrac{1}{n^{\varepsilon}}\sum_{r = 1}^n \tfrac{1}{r^{1-\varepsilon}} \\ &\!\stackrel{<}{\scriptstyle{\frown}} \Delta_p(n) \phi_p[\mathrm{Piv}_{n,e}(\mathcal{D})] \stackrel{<}{\scriptstyle{\frown}} \sum_{r = n/2}^n \tfrac{1}r\Delta_p(r)\phi_p[\mathrm{ Piv}_{r,e}(\mathcal{D})]. \end{align*} $$
In conclusion, the sum in the last line of equation (5.8) may be restricted to
![]() $n/2 \leq r \leq 4R$
.
$n/2 \leq r \leq 4R$
.
Finally, we mention that all upper bounds also hold for
![]() $|\mathrm {Cov}_{p}[\omega _e; A_k(r,R)]|/\phi _p[A_k(r,R)]$
using the same proofs. Indeed, the fact that
$|\mathrm {Cov}_{p}[\omega _e; A_k(r,R)]|/\phi _p[A_k(r,R)]$
using the same proofs. Indeed, the fact that
![]() $\mathcal {C}$
is increasing was only used when proving the lower bound in equation (5.3) – see also Remark 5.8 below. Moreover, when bounding
$\mathcal {C}$
is increasing was only used when proving the lower bound in equation (5.3) – see also Remark 5.8 below. Moreover, when bounding
![]() $|\mathrm {Cov}_{p}[\omega _e; A_k(r,R)]|$
, it is standard that we obtain an additional multiplicative term
$|\mathrm {Cov}_{p}[\omega _e; A_k(r,R)]|$
, it is standard that we obtain an additional multiplicative term
![]() $\phi _p[A_k(r,R)]$
in the upper bound in each case equations 5.2–5.4.
$\phi _p[A_k(r,R)]$
in the upper bound in each case equations 5.2–5.4.
Remark 5.8. The upper bounds in equations (5.3) and (5.4) may be shown to apply to any event H instead of
![]() $\mathcal {C}(\mathcal {D})$
, as long as H depends only on the edges in
$\mathcal {C}(\mathcal {D})$
, as long as H depends only on the edges in
![]() $\Lambda _R$
. Indeed, for H increasing, the proof above applies mutatis mutandis. When H is not increasing, additional care needs to be taken when bounding
$\Lambda _R$
. Indeed, for H increasing, the proof above applies mutatis mutandis. When H is not increasing, additional care needs to be taken when bounding
![]() $|\phi [H \,|\, \omega _e = 1] - \phi [H \,|\, \omega _e = 0]|$
in equations (5.6) and (5.7). Notice, however, that in both equations, one may produce a coupling of
$|\phi [H \,|\, \omega _e = 1] - \phi [H \,|\, \omega _e = 0]|$
in equations (5.6) and (5.7). Notice, however, that in both equations, one may produce a coupling of
![]() $\phi [\cdot \,|\, \omega _e = 0]$
and
$\phi [\cdot \,|\, \omega _e = 0]$
and
![]() $\phi [\cdot \,|\, \omega _e = 1]$
that generates distinct configurations inside
$\phi [\cdot \,|\, \omega _e = 1]$
that generates distinct configurations inside
![]() $\Lambda _R$
with a probability bounded from above by the right-hand side of the respective equations. As a consequence, the terms on the right-hand side in equations (5.3) and (5.4) bound from above the distance in total variation between the restrictions of
$\Lambda _R$
with a probability bounded from above by the right-hand side of the respective equations. As a consequence, the terms on the right-hand side in equations (5.3) and (5.4) bound from above the distance in total variation between the restrictions of
![]() $\phi [\cdot \,|\, \omega _e = 1]$
and
$\phi [\cdot \,|\, \omega _e = 1]$
and
![]() $\phi [\cdot \,|\, \omega _e = 0]$
to
$\phi [\cdot \,|\, \omega _e = 0]$
to
![]() $\Lambda _R$
.
$\Lambda _R$
.
Proof of Proposition 5.1
We focus here on the expression for the crossing probability of a quad; the proof for the derivatives of probabilities of arm events is identical to that of the upper bound proved below.
Fix p and some
![]() $\eta $
-regular quad
$\eta $
-regular quad
![]() $(\mathcal {D},a,b,c,d)$
at scale
$(\mathcal {D},a,b,c,d)$
at scale
![]() $R\le L(p)$
. By grouping the contributions of different edges depending on their distance to the origin and the boundary of
$R\le L(p)$
. By grouping the contributions of different edges depending on their distance to the origin and the boundary of
![]() $\Lambda _R$
and using Lemma 5.3, we have
$\Lambda _R$
and using Lemma 5.3, we have
 $$ \begin{align*} \tfrac{\mathrm{d}}{\mathrm{d}p}\phi_{p}[\mathcal{C}(\mathcal{D})] &= \frac1{p(1-p)} \sum_{e} \mathrm{Cov}_p(\omega_e, \mathcal{C}(\mathcal{D})) \stackrel{>}{\scriptstyle{\frown}} R^2 \Delta_p(R) + \sum_{n =R}^{L(p)} n \Delta_p(n)\Delta_p(R,n), \end{align*} $$
$$ \begin{align*} \tfrac{\mathrm{d}}{\mathrm{d}p}\phi_{p}[\mathcal{C}(\mathcal{D})] &= \frac1{p(1-p)} \sum_{e} \mathrm{Cov}_p(\omega_e, \mathcal{C}(\mathcal{D})) \stackrel{>}{\scriptstyle{\frown}} R^2 \Delta_p(R) + \sum_{n =R}^{L(p)} n \Delta_p(n)\Delta_p(R,n), \end{align*} $$
since there are order
![]() $R^2$
edges in the case equation (5.2) and order n edges at a distance n from
$R^2$
edges in the case equation (5.2) and order n edges at a distance n from
![]() $\partial \mathcal {D}$
.
$\partial \mathcal {D}$
.
For the upper bound, we use the three upper bounds of Lemma 5.3. We split the edges into three categories: those at a distance less than
![]() $2R$
from
$2R$
from
![]() $\partial \mathcal {D}$
, those at a distance between
$\partial \mathcal {D}$
, those at a distance between
![]() $2R$
and
$2R$
and
![]() $2L(p)$
from
$2L(p)$
from
![]() $\partial \mathcal {D}$
and those at a distance larger than
$\partial \mathcal {D}$
and those at a distance larger than
![]() $2L(p)$
from
$2L(p)$
from
![]() $\partial \mathcal {D}$
.
$\partial \mathcal {D}$
.
For the two last categories, keeping in mind that there are
![]() $O(n)$
edges at a distance exactly
$O(n)$
edges at a distance exactly
![]() $n \geq 2R$
from
$n \geq 2R$
from
![]() $\partial \mathcal {D}$
, and applying equations (5.3) and (5.4), we find
$\partial \mathcal {D}$
, and applying equations (5.3) and (5.4), we find
 $$ \begin{align} \sum_{e:\,\mathrm{dist}(e, \partial \mathcal{D}) \geq 2R} \!\!\!\!\!\!\!\!\!\!\mathrm{Cov}_p(\omega_e, \mathcal{C}(\mathcal{D})) &\stackrel{<}{\scriptstyle{\frown}} \sum_{n= 2R}^{2L(p)} n \Delta_p(n)\Delta_p(R,n) +\!\!\!\!\sum_{n\geq 2L(p)}\!\!\!\! n \Delta_p(L(p))\Delta_p(R,L(p))e^{-cn/L(p)}\nonumber\\ &\!\stackrel{<}{\scriptstyle{\frown}} \sum_{n= 2R}^{2L(p)} n \Delta_p(n)\Delta_p(R,n) +L(p)^2 \Delta_p(L(p))\Delta_p(R,L(p)) \nonumber\\ & \!\stackrel{<}{\scriptstyle{\frown}} R^2 \Delta_p(R) + \sum_{n= R}^{L(p)} n \Delta_p(n)\Delta_p(R,n). \end{align} $$
$$ \begin{align} \sum_{e:\,\mathrm{dist}(e, \partial \mathcal{D}) \geq 2R} \!\!\!\!\!\!\!\!\!\!\mathrm{Cov}_p(\omega_e, \mathcal{C}(\mathcal{D})) &\stackrel{<}{\scriptstyle{\frown}} \sum_{n= 2R}^{2L(p)} n \Delta_p(n)\Delta_p(R,n) +\!\!\!\!\sum_{n\geq 2L(p)}\!\!\!\! n \Delta_p(L(p))\Delta_p(R,L(p))e^{-cn/L(p)}\nonumber\\ &\!\stackrel{<}{\scriptstyle{\frown}} \sum_{n= 2R}^{2L(p)} n \Delta_p(n)\Delta_p(R,n) +L(p)^2 \Delta_p(L(p))\Delta_p(R,L(p)) \nonumber\\ & \!\stackrel{<}{\scriptstyle{\frown}} R^2 \Delta_p(R) + \sum_{n= R}^{L(p)} n \Delta_p(n)\Delta_p(R,n). \end{align} $$
In the second inequality, we argue that due to the exponential factor, the first
![]() $L(p)$
summands account for a positive proportion on the entire second sum. The final inequality may be obtained by considering separately the cases
$L(p)$
summands account for a positive proportion on the entire second sum. The final inequality may be obtained by considering separately the cases
![]() $L(p)/2 \leq R \leq L(p)$
and
$L(p)/2 \leq R \leq L(p)$
and
![]() $R < L(p)/2$
. In the former, the second line is dominated entirely by the first term of the last line; in the latter, the second term of the last line dominates the whole expression.
$R < L(p)/2$
. In the former, the second line is dominated entirely by the first term of the last line; in the latter, the second term of the last line dominates the whole expression.
We turn to the edges in the first category: those close to
![]() $\partial \mathcal {D}$
. We refer to Figure 13 for an illustration. Fix
$\partial \mathcal {D}$
. We refer to Figure 13 for an illustration. Fix
![]() $n\le 2R$
. We start by studying the contribution to the derivative of the edges at a distance n of the arc
$n\le 2R$
. We start by studying the contribution to the derivative of the edges at a distance n of the arc
![]() $(ab)$
(the cases of the other arcs
$(ab)$
(the cases of the other arcs
![]() $(bc)$
,
$(bc)$
,
![]() $(cd)$
and
$(cd)$
and
![]() $(da)$
are treated similarly), and we precisely focus on the term on the right-hand side of equation (5.2) for these edges and corresponding to some fixed
$(da)$
are treated similarly), and we precisely focus on the term on the right-hand side of equation (5.2) for these edges and corresponding to some fixed
![]() $n/2 \leq r\leq 3R$
. Consider a family of vertices
$n/2 \leq r\leq 3R$
. Consider a family of vertices
![]() $a=x_0,\dots ,x_k$
found counterclockwise along
$a=x_0,\dots ,x_k$
found counterclockwise along
![]() $(ab)$
, with
$(ab)$
, with
![]() $\|x_i - x_{i-1}\|_{\infty } = r$
for
$\|x_i - x_{i-1}\|_{\infty } = r$
for
![]() $1 \le i \le k$
and with the last vertex
$1 \le i \le k$
and with the last vertex
![]() $x_k$
at a distance at most r of b (when r is large, k is equal to 0). Consider the event
$x_k$
at a distance at most r of b (when r is large, k is equal to 0). Consider the event
![]() $E_i$
that
$E_i$
that
![]() $(x_{i-4}x_{i-3})$
is dual-connected to
$(x_{i-4}x_{i-3})$
is dual-connected to
![]() $(da)$
and
$(da)$
and
![]() $(x_{i+3}x_{i+4})$
is connected to
$(x_{i+3}x_{i+4})$
is connected to
![]() $(cd)$
, with the convention that if
$(cd)$
, with the convention that if
![]() $i\le 4/\eta $
or
$i\le 4/\eta $
or
![]() $i\ge k-4/\eta $
, then
$i\ge k-4/\eta $
, then
![]() $E_i$
is the full event. We claim that for every
$E_i$
is the full event. We claim that for every
![]() $e\subset \Lambda _r(x_i)$
,
$e\subset \Lambda _r(x_i)$
,
Indeed, the inequality is trivial when
![]() $i\le 4/\eta $
or
$i\le 4/\eta $
or
![]() $i\ge k-4/\eta $
since E is the full event. For the remaining values of i (which exist only when
$i\ge k-4/\eta $
since E is the full event. For the remaining values of i (which exist only when
![]() $r\ll \eta R$
), observe that for
$r\ll \eta R$
), observe that for
![]() $\mathrm {Piv}_{r,e}(\mathcal {D})$
to occur,
$\mathrm {Piv}_{r,e}(\mathcal {D})$
to occur,
![]() $\Lambda _{2r}(x_i)$
needs to be connected by a primal path to
$\Lambda _{2r}(x_i)$
needs to be connected by a primal path to
![]() $(cd)$
and by dual paths to
$(cd)$
and by dual paths to
![]() $(bc)$
and
$(bc)$
and
![]() $(da)$
. In particular, the interface starting from d and delimiting the primal cluster of
$(da)$
. In particular, the interface starting from d and delimiting the primal cluster of
![]() $(cd)$
in
$(cd)$
in
![]() $\mathcal {D}$
necessarily hits
$\mathcal {D}$
necessarily hits
![]() $\Lambda _{2r}(x_i)$
before hitting the arc
$\Lambda _{2r}(x_i)$
before hitting the arc
![]() $(ab)$
. Let
$(ab)$
. Let
![]() $\Gamma $
be the section of this interface from d up to the first time it hits
$\Gamma $
be the section of this interface from d up to the first time it hits
![]() $\Lambda _{2r}(x_i)$
. Conditionally on
$\Lambda _{2r}(x_i)$
. Conditionally on
![]() $\Gamma $
, one may use equation (RSW) to construct a dual path connecting
$\Gamma $
, one may use equation (RSW) to construct a dual path connecting
![]() $\Gamma $
to
$\Gamma $
to
![]() $(x_{i-4}x_{i-3})$
and a primal path connecting
$(x_{i-4}x_{i-3})$
and a primal path connecting
![]() $\Gamma $
to
$\Gamma $
to
![]() $(x_{i+3}x_{i+4})$
with probability uniformly bounded away from zero. These paths, together with
$(x_{i+3}x_{i+4})$
with probability uniformly bounded away from zero. These paths, together with
![]() $\Gamma $
, induce the connections required by
$\Gamma $
, induce the connections required by
![]() $E_i$
.
$E_i$
.

Figure 13 A depiction of the points
![]() $x_0,\dots ,x_k$
(note that
$x_0,\dots ,x_k$
(note that
![]() $x_k$
is not necessarily equal to b). The occurrence of
$x_k$
is not necessarily equal to b). The occurrence of
![]() $\mathrm {Piv}_{r,e}(\mathcal {D})$
for some
$\mathrm {Piv}_{r,e}(\mathcal {D})$
for some
![]() $e \in \Lambda _r(x_i)$
induces the existence of the exploration path
$e \in \Lambda _r(x_i)$
induces the existence of the exploration path
![]() $\Gamma $
(in red). When orienting
$\Gamma $
(in red). When orienting
![]() $\Gamma $
in the direction of its exploration – that is, from d to
$\Gamma $
in the direction of its exploration – that is, from d to
![]() $\Lambda _{2r}(x_i)$
–
$\Lambda _{2r}(x_i)$
–
![]() $\Gamma $
has dual open edges on its right and primal ones on its left. Thus, conditionally on
$\Gamma $
has dual open edges on its right and primal ones on its left. Thus, conditionally on
![]() $\Gamma $
, the blue paths occur with uniformly positive probability and induce the occurrence of
$\Gamma $
, the blue paths occur with uniformly positive probability and induce the occurrence of
![]() $E_i$
.
$E_i$
.
Notice now that any edge at distance n from
![]() $(ab)$
is contained in at least one
$(ab)$
is contained in at least one
![]() $\Lambda _r(x_i)$
. Conversely there are
$\Lambda _r(x_i)$
. Conversely there are
![]() $O(r)$
vertices in each
$O(r)$
vertices in each
![]() $\Lambda _{r}(x_i)$
at a distance exactly n from
$\Lambda _{r}(x_i)$
at a distance exactly n from
![]() $(ab)$
. Thus, summing over the edges e at a distance n from
$(ab)$
. Thus, summing over the edges e at a distance n from
![]() $(ab)$
gives
$(ab)$
gives
 $$\begin{align*}\sum_{e:\mathrm{dist}(e,(ab))=n}\phi_p[\mathrm{ Piv}_{r,e}(\mathcal{D})]\stackrel{<}{\scriptstyle{\frown}} r \sum_{i=0}^k\phi_p[E_i]\stackrel{<}{\scriptstyle{\frown}} r, \end{align*}$$
$$\begin{align*}\sum_{e:\mathrm{dist}(e,(ab))=n}\phi_p[\mathrm{ Piv}_{r,e}(\mathcal{D})]\stackrel{<}{\scriptstyle{\frown}} r \sum_{i=0}^k\phi_p[E_i]\stackrel{<}{\scriptstyle{\frown}} r, \end{align*}$$
where the second inequality is due to the fact that at most
![]() $O(1)$
events
$O(1)$
events
![]() $E_i$
can occur simultaneously.
$E_i$
can occur simultaneously.
One may do the same with edges at a distance n of
![]() $(bc)$
,
$(bc)$
,
![]() $(cd)$
and
$(cd)$
and
![]() $(da)$
. Finally, summing the previous displayed equation over r and using equation (5.2), we find
$(da)$
. Finally, summing the previous displayed equation over r and using equation (5.2), we find
 $$ \begin{align*} \sum_{e:\mathrm{dist}(e,\partial \mathcal{D})\le 2R}\mathrm{Cov}_p(\omega_e,\mathcal{C}(\mathcal{D})) &\stackrel{<}{\scriptstyle{\frown}} \sum_{n=1}^{2R}\sum_{r=n/2}^{4R}\tfrac1r\Delta_p(r)\sum_{e:\mathrm{dist}(e,\partial \mathcal{D})=n}\phi_p[\mathrm{ Piv}_{r,e}(\mathcal{D})]\\ &\stackrel{<}{\scriptstyle{\frown}} \sum_{n=1}^{2R}\sum_{r=n/2}^{4R}\Delta_p(r) \stackrel{<}{\scriptstyle{\frown}} \sum_{r=1}^{R}r \Delta_p(r). \end{align*} $$
$$ \begin{align*} \sum_{e:\mathrm{dist}(e,\partial \mathcal{D})\le 2R}\mathrm{Cov}_p(\omega_e,\mathcal{C}(\mathcal{D})) &\stackrel{<}{\scriptstyle{\frown}} \sum_{n=1}^{2R}\sum_{r=n/2}^{4R}\tfrac1r\Delta_p(r)\sum_{e:\mathrm{dist}(e,\partial \mathcal{D})=n}\phi_p[\mathrm{ Piv}_{r,e}(\mathcal{D})]\\ &\stackrel{<}{\scriptstyle{\frown}} \sum_{n=1}^{2R}\sum_{r=n/2}^{4R}\Delta_p(r) \stackrel{<}{\scriptstyle{\frown}} \sum_{r=1}^{R}r \Delta_p(r). \end{align*} $$
The above combined with equation (5.9) implies the upper bound in equation (5.1).
5.2 Derivative for the mixing rate
Proposition 5.9. For every p and two edges e and f at a distance
![]() $R\le L(p)$
from each other,
$R\le L(p)$
from each other,
 $$ \begin{align} \Big|\tfrac{\mathrm{d}}{\mathrm{d}p}\log \mathrm{Cov}_p(\omega_e,\omega_f)\big| \stackrel{<}{\scriptstyle{\frown}} \sum_{\ell=1}^R\ell\Delta_p(\ell) + \sum_{\ell=R}^{L(p)} \ell \Delta_p(\ell)\Delta_p(R,\ell). \end{align} $$
$$ \begin{align} \Big|\tfrac{\mathrm{d}}{\mathrm{d}p}\log \mathrm{Cov}_p(\omega_e,\omega_f)\big| \stackrel{<}{\scriptstyle{\frown}} \sum_{\ell=1}^R\ell\Delta_p(\ell) + \sum_{\ell=R}^{L(p)} \ell \Delta_p(\ell)\Delta_p(R,\ell). \end{align} $$
Exactly as for crossing events, one may use the next section to replace
![]() $\sum _{\ell \le R}\ell \Delta _p(\ell )$
by
$\sum _{\ell \le R}\ell \Delta _p(\ell )$
by
![]() $R^2\Delta _p(R)$
; see Corollary 7.1 of Section 7.
$R^2\Delta _p(R)$
; see Corollary 7.1 of Section 7.
Remark 5.10. Since
![]() $\mathrm {Cov}_p(\omega _e,\omega _f)$
was shown in equation (5.3) to be comparable to
$\mathrm {Cov}_p(\omega _e,\omega _f)$
was shown in equation (5.3) to be comparable to
![]() $\Delta _p(R)^2$
, the above should be understood as a bound on the logarithmic derivative of
$\Delta _p(R)^2$
, the above should be understood as a bound on the logarithmic derivative of
![]() $\Delta _p(R)$
. Indeed, equation (5.10) combined with equation (5.3) yields
$\Delta _p(R)$
. Indeed, equation (5.10) combined with equation (5.3) yields
 $$ \begin{align} \Big|\log \frac{\Delta_p(R)}{\Delta_{p_c}(R)}\Big| \stackrel{<}{\scriptstyle{\frown}} \int_{p_c}^p \Big(\sum_{\ell=1}^R\ell\Delta_u(\ell)+ \sum_{\ell=R}^{L(u)} \ell \Delta_u(\ell)\Delta_u(R,\ell)\Big) \,du, \end{align} $$
$$ \begin{align} \Big|\log \frac{\Delta_p(R)}{\Delta_{p_c}(R)}\Big| \stackrel{<}{\scriptstyle{\frown}} \int_{p_c}^p \Big(\sum_{\ell=1}^R\ell\Delta_u(\ell)+ \sum_{\ell=R}^{L(u)} \ell \Delta_u(\ell)\Delta_u(R,\ell)\Big) \,du, \end{align} $$
for all p and
![]() $R \le L(p)$
. This inequality will be useful when R is of the same order as
$R \le L(p)$
. This inequality will be useful when R is of the same order as
![]() $L(p)$
, in which case the terms with
$L(p)$
, in which case the terms with
![]() $R\le \ell \le L(p)$
may be absorbed by the first sum on the right-hand side.
$R\le \ell \le L(p)$
may be absorbed by the first sum on the right-hand side.
Proof. Fix p, e and f as in the statement. Then
 $$ \begin{align} \tfrac{\mathrm{d}}{\mathrm{d}p} \mathrm{Cov}_p(\omega_e,\omega_f) &= \sum_{g \in \mathbb{E}} \phi_p[\omega_e \omega_f \omega_g ] - \phi_p[\omega_e \omega_f ]\phi_p[\omega_g] - \phi_p[\omega_f \omega_g ]\phi_p[\omega_e]\\&\quad - \phi_p[\omega_e \omega_g]\phi_p[\omega_f ] +2 \phi_p[\omega_e]\phi_p[\omega_f]\phi_p[\omega_g ].\nonumber \end{align} $$
$$ \begin{align} \tfrac{\mathrm{d}}{\mathrm{d}p} \mathrm{Cov}_p(\omega_e,\omega_f) &= \sum_{g \in \mathbb{E}} \phi_p[\omega_e \omega_f \omega_g ] - \phi_p[\omega_e \omega_f ]\phi_p[\omega_g] - \phi_p[\omega_f \omega_g ]\phi_p[\omega_e]\\&\quad - \phi_p[\omega_e \omega_g]\phi_p[\omega_f ] +2 \phi_p[\omega_e]\phi_p[\omega_f]\phi_p[\omega_g ].\nonumber \end{align} $$
We will bound separately the absolute value of each term in the sum above depending on the position of g. First, consider an edge
![]() $g \in \Lambda _{2R/3}(e)$
; the corresponding term in equation (5.12) may be written as
$g \in \Lambda _{2R/3}(e)$
; the corresponding term in equation (5.12) may be written as
Write
![]() $\ell $
for the distance between e and g, and set
$\ell $
for the distance between e and g, and set
![]() $G := \Lambda _{4\ell /3}(e)$
. Notice that f is outside of G at a distance of at least
$G := \Lambda _{4\ell /3}(e)$
. Notice that f is outside of G at a distance of at least
![]() $R/9$
from it. For any event A depending only on the edges in G, we have
$R/9$
from it. For any event A depending only on the edges in G, we have
 $$ \begin{align*} \phi_p[A] = \sum_{\xi} \phi_p[B_{\xi}] \phi_{G,p}^{\xi} [A] \quad \text{ and }\quad \phi_p[A \,|\,\omega_f] = \sum_{\xi} \phi_p[B_{\xi}\,|\,\omega_f] \phi_{G,p}^{\xi} [A], \end{align*} $$
$$ \begin{align*} \phi_p[A] = \sum_{\xi} \phi_p[B_{\xi}] \phi_{G,p}^{\xi} [A] \quad \text{ and }\quad \phi_p[A \,|\,\omega_f] = \sum_{\xi} \phi_p[B_{\xi}\,|\,\omega_f] \phi_{G,p}^{\xi} [A], \end{align*} $$
where the sum is over all boundary conditions
![]() $\xi $
imposed on G by the configuration outside of G, and
$\xi $
imposed on G by the configuration outside of G, and
![]() $B_{\xi }$
is the event that the boundary conditions induced on G are
$B_{\xi }$
is the event that the boundary conditions induced on G are
![]() $\xi $
. Thus, equation (5.13) may be written as
$\xi $
. Thus, equation (5.13) may be written as
 $$ \begin{align*} \phi_p[\omega_f]\sum_{\xi} (\phi_p[B_{\xi}\,|\,\omega_f] - \phi_p[B_{\xi}]) (\underbrace{\phi_{G,p}^{\xi}[\omega_e \omega_g] -\phi_{G,p}^{\xi}[\omega_g]\phi_p[\omega_e]- \phi_{G,p}^{\xi}[\omega_e] \phi_p[\omega_g] + \phi_p[\omega_e]\phi_p[\omega_g]}_{F(\xi)}). \end{align*} $$
$$ \begin{align*} \phi_p[\omega_f]\sum_{\xi} (\phi_p[B_{\xi}\,|\,\omega_f] - \phi_p[B_{\xi}]) (\underbrace{\phi_{G,p}^{\xi}[\omega_e \omega_g] -\phi_{G,p}^{\xi}[\omega_g]\phi_p[\omega_e]- \phi_{G,p}^{\xi}[\omega_e] \phi_p[\omega_g] + \phi_p[\omega_e]\phi_p[\omega_g]}_{F(\xi)}). \end{align*} $$
By adding and subtracting
![]() $\phi _{G,p}^{\xi }[\omega _e] \phi _{G,p}^{\xi }[\omega _g ]$
, we find
$\phi _{G,p}^{\xi }[\omega _e] \phi _{G,p}^{\xi }[\omega _g ]$
, we find
where
![]() $\mathrm {Cov}_{G}^{\xi }$
stands for the covariance under the measure
$\mathrm {Cov}_{G}^{\xi }$
stands for the covariance under the measure
![]() $\phi _{G,p}^{\xi }$
. Next, we apply Lemma 5.3 to
$\phi _{G,p}^{\xi }$
. Next, we apply Lemma 5.3 to
![]() $\phi _{G,p}^{\xi }$
instead of
$\phi _{G,p}^{\xi }$
instead of
![]() $\phi _p$
– notice that the choice of G ensures that both e and g are at a distance of order
$\phi _p$
– notice that the choice of G ensures that both e and g are at a distance of order
![]() $\ell $
from
$\ell $
from
![]() $\partial G$
, and the lemma does indeed apply as explained in Remark 5.5 – to obtain
$\partial G$
, and the lemma does indeed apply as explained in Remark 5.5 – to obtain
In addition, for any
![]() $\xi $
, Theorem 4.9 yields
$\xi $
, Theorem 4.9 yields
Then equation (5.13) may be bounded above by
 $$ \begin{align} \sum_{\xi} \|F\|_{\infty}\cdot |\phi_p[B_{\xi}|\omega_f] - \phi_p[B_{\xi}]| \stackrel{<}{\scriptstyle{\frown}} \Delta_p(R) \Delta_p(\ell, R)\Delta_p(\ell)^2 \asymp \Delta_p(\ell) \Delta_p(R)^2, \end{align} $$
$$ \begin{align} \sum_{\xi} \|F\|_{\infty}\cdot |\phi_p[B_{\xi}|\omega_f] - \phi_p[B_{\xi}]| \stackrel{<}{\scriptstyle{\frown}} \Delta_p(R) \Delta_p(\ell, R)\Delta_p(\ell)^2 \asymp \Delta_p(\ell) \Delta_p(R)^2, \end{align} $$
since the total variation distance between the restrictions of
![]() $\phi _p[\cdot \,|\omega _f]$
and
$\phi _p[\cdot \,|\omega _f]$
and
![]() $\phi _p$
to G is bounded by a universal multiple of
$\phi _p$
to G is bounded by a universal multiple of
![]() $\Delta _p(R) \Delta _p(\ell , R)$
, as shown in Lemma 5.3 (see also Remark 5.8). The second equivalence is given by the quasi-multiplicativity of
$\Delta _p(R) \Delta _p(\ell , R)$
, as shown in Lemma 5.3 (see also Remark 5.8). The second equivalence is given by the quasi-multiplicativity of
![]() $\Delta _p$
equation (1.15).
$\Delta _p$
equation (1.15).
Edges
![]() $g \in \Lambda _{2R/3}(f)$
have the same contribution to equation (5.13) due to symmetry. Finally, we consider edges g that are outside
$g \in \Lambda _{2R/3}(f)$
have the same contribution to equation (5.13) due to symmetry. Finally, we consider edges g that are outside
![]() $\Lambda _{2R/3}(e)\cup \Lambda _{2R/3}(f)$
; write
$\Lambda _{2R/3}(e)\cup \Lambda _{2R/3}(f)$
; write
![]() $\ell $
for the distance between g and e. Let G be the domain formed of the edges at a distance at least
$\ell $
for the distance between g and e. Let G be the domain formed of the edges at a distance at least
![]() $R/6$
from the segment uniting e and f; notice that g is at a distance at least
$R/6$
from the segment uniting e and f; notice that g is at a distance at least
![]() $R/6$
from G. Applying the same argument as in the first case, with the roles of
$R/6$
from G. Applying the same argument as in the first case, with the roles of
![]() $\omega _f$
and
$\omega _f$
and
![]() $\omega _g$
inverted, we find that the term corresponding to g in equation (5.12) is bounded by
$\omega _g$
inverted, we find that the term corresponding to g in equation (5.12) is bounded by
 $$ \begin{align} &\phi_p[\omega_g]\sum_{\xi} \big| \phi_p[\xi\,|\,\omega_g] - \phi_p[\xi]\big|\cdot\big|\mathrm{Cov}_{G,p}^{\xi}(\omega_e, \omega_f) + (\phi_{G,p}^{\xi}[\omega_e] -\phi_p[\omega_e])(\phi_{G,p}^{\xi}[\omega_f ] - \phi_p[\omega_f ] ) \big| \nonumber \\ &\qquad\qquad\stackrel{<}{\scriptstyle{\frown}} \Delta_p(\ell \wedge L(p) )\Delta_p(R,\ell \wedge L(p))e^{-c \ell/L(p)} \Delta_p(R)^2\nonumber\\ &\qquad\qquad\asymp \Delta_p(R)\Delta_p(\ell \wedge L(p) )^2 e^{-c \ell/L(p)}, \end{align} $$
$$ \begin{align} &\phi_p[\omega_g]\sum_{\xi} \big| \phi_p[\xi\,|\,\omega_g] - \phi_p[\xi]\big|\cdot\big|\mathrm{Cov}_{G,p}^{\xi}(\omega_e, \omega_f) + (\phi_{G,p}^{\xi}[\omega_e] -\phi_p[\omega_e])(\phi_{G,p}^{\xi}[\omega_f ] - \phi_p[\omega_f ] ) \big| \nonumber \\ &\qquad\qquad\stackrel{<}{\scriptstyle{\frown}} \Delta_p(\ell \wedge L(p) )\Delta_p(R,\ell \wedge L(p))e^{-c \ell/L(p)} \Delta_p(R)^2\nonumber\\ &\qquad\qquad\asymp \Delta_p(R)\Delta_p(\ell \wedge L(p) )^2 e^{-c \ell/L(p)}, \end{align} $$
where the sum on the left-hand side is over all the boundary conditions
![]() $\xi $
on G imposed by the configuration outside of G. Indeed, by Lemma 5.3, the total variation distance between the restrictions of
$\xi $
on G imposed by the configuration outside of G. Indeed, by Lemma 5.3, the total variation distance between the restrictions of
![]() $\phi [\cdot \,|\,\omega _g]$
and
$\phi [\cdot \,|\,\omega _g]$
and
![]() $\phi $
to G is bounded by a universal multiple of
$\phi $
to G is bounded by a universal multiple of
![]() $\Delta _p(\ell \wedge L(p) )\Delta _p(R,\ell \wedge L(p))e^{-c \ell /L(p)}$
, while each term in the second parenthesis of the left-hand side is bounded by multiples of
$\Delta _p(\ell \wedge L(p) )\Delta _p(R,\ell \wedge L(p))e^{-c \ell /L(p)}$
, while each term in the second parenthesis of the left-hand side is bounded by multiples of
![]() $\Delta _p(R)^2$
.
$\Delta _p(R)^2$
.
Summing now over g and using the triangular inequality and equations (5.14) and (5.15), we find
 $$ \begin{align*} \big|\tfrac{\mathrm{d}}{\mathrm{d}p} \mathrm{Cov}_p(\omega_e,\omega_f) \big| &\stackrel{<}{\scriptstyle{\frown}} \sum_{\ell =1}^{R/2} \ell \Delta_p(\ell) \Delta_p(R)^2 + \sum_{\ell>R/2} \ell \Delta_p(R)\Delta_p(\ell \wedge L(p) )^2 e^{-c \ell/L(p)}\\ &\stackrel{<}{\scriptstyle{\frown}} \Delta_p(R)^2 \Big(\sum_{\ell =1}^{R} \ell \Delta_p(\ell) + \sum_{\ell =R}^{L(p)} \ell \Delta_p(R,\ell)\Delta_p(\ell)\Big). \end{align*} $$
$$ \begin{align*} \big|\tfrac{\mathrm{d}}{\mathrm{d}p} \mathrm{Cov}_p(\omega_e,\omega_f) \big| &\stackrel{<}{\scriptstyle{\frown}} \sum_{\ell =1}^{R/2} \ell \Delta_p(\ell) \Delta_p(R)^2 + \sum_{\ell>R/2} \ell \Delta_p(R)\Delta_p(\ell \wedge L(p) )^2 e^{-c \ell/L(p)}\\ &\stackrel{<}{\scriptstyle{\frown}} \Delta_p(R)^2 \Big(\sum_{\ell =1}^{R} \ell \Delta_p(\ell) + \sum_{\ell =R}^{L(p)} \ell \Delta_p(R,\ell)\Delta_p(\ell)\Big). \end{align*} $$
The second inequality requires some basic algebra: we use the exponential factor to bound the contribution of terms with
![]() $\ell> L(p)$
by
$\ell> L(p)$
by
![]() $L(p)^2 \Delta _p(R)\Delta _p(L(p))^2$
; the quasi-multiplicativity given by equation (1.15) of
$L(p)^2 \Delta _p(R)\Delta _p(L(p))^2$
; the quasi-multiplicativity given by equation (1.15) of
![]() $\Delta _p$
as well as equations (4.14) and (4.21) allow us to bound the term above as well as the remaining sums over
$\Delta _p$
as well as equations (4.14) and (4.21) allow us to bound the term above as well as the remaining sums over
![]() $\ell \leq R/2$
and
$\ell \leq R/2$
and
![]() $R/2 < \ell \leq L(p)$
by the last line of the display. Finally, divide by
$R/2 < \ell \leq L(p)$
by the last line of the display. Finally, divide by
![]() $\mathrm {Cov}_p(\omega _e,\omega _f) \asymp \Delta _p(R)^2$
to obtain the desired result.
$\mathrm {Cov}_p(\omega _e,\omega _f) \asymp \Delta _p(R)^2$
to obtain the desired result.
6 Lower bound on
 $\Delta _p(r,R)$
: proof of Proposition 1.8
$\Delta _p(r,R)$
: proof of Proposition 1.8
In this section, we prove Proposition 1.8. The section will be divided in two as the case
![]() $1\le q<4$
is quite different from the case
$1\le q<4$
is quite different from the case
![]() $q=4$
.
$q=4$
.
6.1 Lower bound on
 $\Delta _p(r,R)$
for
$\Delta _p(r,R)$
for
 $1\le q<4$
$1\le q<4$
In this section, we assume that
![]() $1\le q<4$
. We will prove the following stronger statement.
$1\le q<4$
. We will prove the following stronger statement.
Proposition 6.1. Fix
![]() $1\le q<4$
. There exists
$1\le q<4$
. There exists
![]() $\delta =\delta (q)>0$
such that for
$\delta =\delta (q)>0$
such that for
![]() $p \in (0,1)$
and
$p \in (0,1)$
and
![]() $r\le R\le L(p)$
,
$r\le R\le L(p)$
,
This implies equation (1.20) since
![]() $\Delta _p(r,R)\ge \pi _4(p;r,R)$
by the observation at the beginning of Section 4.5 (one does not even require the polynomial improvement given by equation (1.17)). Let us mention that equation (6.1) is expected to fail for
$\Delta _p(r,R)\ge \pi _4(p;r,R)$
by the observation at the beginning of Section 4.5 (one does not even require the polynomial improvement given by equation (1.17)). Let us mention that equation (6.1) is expected to fail for
![]() $q=4$
, which explains why the case
$q=4$
, which explains why the case
![]() $q=4$
needs to be treated separately.
$q=4$
needs to be treated separately.
Proof. By symmetry, we only need to treat the case
![]() $p\ge p_c$
. The case
$p\ge p_c$
. The case
![]() $p=p_c$
was obtained in a recent paper [Reference Duminil-Copin, Manolescu and TassionDMT20, Proposition 6.8]. The argument extends readily to our setting.
$p=p_c$
was obtained in a recent paper [Reference Duminil-Copin, Manolescu and TassionDMT20, Proposition 6.8]. The argument extends readily to our setting.
Indeed, if E denotes the event that
![]() $\Lambda _{3R}$
contains both an open circuit and a dual open circuit surrounding
$\Lambda _{3R}$
contains both an open circuit and a dual open circuit surrounding
![]() $\Lambda _{2R}$
, with the open circuit being connected to
$\Lambda _{2R}$
, with the open circuit being connected to
![]() $\partial \Lambda _{4R}$
, then it is shown in [Reference Duminil-Copin, Manolescu and TassionDMT20] that
$\partial \Lambda _{4R}$
, then it is shown in [Reference Duminil-Copin, Manolescu and TassionDMT20] that
where the infimum is taken over all simply connected domains containing
![]() $\Lambda _{2R}$
and contained in
$\Lambda _{2R}$
and contained in
![]() $\Lambda _{3R}$
and
$\Lambda _{3R}$
and
![]() $\mathbf M_r(\mathcal {D},R)$
is an increasing random variable defined in [Reference Duminil-Copin, Manolescu and TassionDMT20, Section 1.5]. When
$\mathbf M_r(\mathcal {D},R)$
is an increasing random variable defined in [Reference Duminil-Copin, Manolescu and TassionDMT20, Section 1.5]. When
![]() $R \leq L(p)$
, equation (RSW) implies that
$R \leq L(p)$
, equation (RSW) implies that
![]() $\phi _{p}[E] \stackrel{>}{\scriptstyle{\frown}} 1$
. Moreover, since
$\phi _{p}[E] \stackrel{>}{\scriptstyle{\frown}} 1$
. Moreover, since
![]() $\mathbf M_r(\mathcal {D},R)$
is increasing,
$\mathbf M_r(\mathcal {D},R)$
is increasing,
for some universal
![]() $\delta _0> 0$
, where the last inequality is given by [Reference Duminil-Copin, Manolescu and TassionDMT20, Proposition 1.4]. Combining the above displays produces the desired bound.
$\delta _0> 0$
, where the last inequality is given by [Reference Duminil-Copin, Manolescu and TassionDMT20, Proposition 1.4]. Combining the above displays produces the desired bound.
Remark 6.2. The proof looks simple, but we wish to insist that the whole difficulty of the argument is contained in [Reference Duminil-Copin, Manolescu and TassionDMT20].
6.2 Lower bound on
 $\Delta _p(r,R)$
for
$\Delta _p(r,R)$
for
 $q=4$
$q=4$
The reasoning of the previous section does not apply for
![]() $q=4$
, as it is expected that
$q=4$
, as it is expected that
(see Remark 6.11). Nevertheless, this is not contradictory with the fact that
![]() $\Delta _p(r,R)\stackrel{>}{\scriptstyle{\frown}} (\tfrac rR)^{2-\delta }$
, as we know from Section 4.5 that
$\Delta _p(r,R)\stackrel{>}{\scriptstyle{\frown}} (\tfrac rR)^{2-\delta }$
, as we know from Section 4.5 that
![]() $\Delta _p(r,R)$
is polynomially larger than
$\Delta _p(r,R)$
is polynomially larger than
![]() $\pi _4(p;r,R)$
. Since we do not currently know how to prove that
$\pi _4(p;r,R)$
. Since we do not currently know how to prove that
![]() $\pi _4(p;r,R)\asymp (\tfrac rR)^2$
, we adopt a direct approach to prove Proposition 1.8 that does not involve the comparison to
$\pi _4(p;r,R)\asymp (\tfrac rR)^2$
, we adopt a direct approach to prove Proposition 1.8 that does not involve the comparison to
![]() $\pi _4(p;r,R)$
.
$\pi _4(p;r,R)$
.
Proof of Equation (1.20)
The lower bound on
![]() $\Delta _p(r,R)$
follows directly from the combination of the next two propositions, which, respectively, correspond to the required bound at
$\Delta _p(r,R)$
follows directly from the combination of the next two propositions, which, respectively, correspond to the required bound at
![]() $p_c$
and the stability of
$p_c$
and the stability of
![]() $\Delta _p$
below the characteristic length.
$\Delta _p$
below the characteristic length.
Proposition 6.3 (Lower bound at
 $p_c$
)
$p_c$
)
For
![]() $q=4$
, there exists
$q=4$
, there exists
![]() $\delta _0>0$
such that for every
$\delta _0>0$
such that for every
![]() $R\ge 2r>0$
,
$R\ge 2r>0$
,
Proposition 6.4 (Stability of
 $\Delta $
)
$\Delta $
)
For
![]() $q=4$
, every p and
$q=4$
, every p and
![]() $2\le r \le R\le L(p)$
,
$2\le r \le R\le L(p)$
,
The section is divided as follows. The proof makes use of the parafermionic observable introduced by Smirnov [Reference SmirnovSmi10]; we therefore start by recalling this notion. Then we prove each proposition in a separate section, in the order in which they are stated.
6.2.1 Parafermionic observable: a crash-course
Since the parafermionic observable is used only in this section, we give minimal details and refer to the literature: for instance, the review article [Reference Duminil-CopinDum17] and the research paper [Reference Duminil-Copin, Manolescu and TassionDMT20] (which implements reasoning very similar to the present, with similar notations). We also recommend that the reader look at Figure 14.

Figure 14 The primal and dual graphs in plain and dashed black lines. In bold (plain and dashed, respectively), the configurations
![]() $\omega $
and
$\omega $
and
![]() $\omega ^*$
. The graph
$\omega ^*$
. The graph
![]() $\Omega ^{\diamond }$
is in red, and the configuration
$\Omega ^{\diamond }$
is in red, and the configuration
![]() $\overline \omega $
is in blue. The path
$\overline \omega $
is in blue. The path
![]() $\gamma (\omega )$
is in bold blue. We also presented two examples of edges e and
$\gamma (\omega )$
is in bold blue. We also presented two examples of edges e and
![]() $e'$
, one for which the corresponding vertex of the primal graph has degree 3 and one for which it has degree 2.
$e'$
, one for which the corresponding vertex of the primal graph has degree 3 and one for which it has degree 2.
Parafermionic observables are usually defined in Dobrushin domains, but in the present study, we limit ourselves to situations where the wired arc is reduced to a single point and therefore the domain has free boundary conditions. We do, however, authorise the domains to be non-simply-connected.
Fix a finite connected subgraph
![]() $\Omega $
of
$\Omega $
of
![]() $\mathbb Z^2$
and a vertex
$\mathbb Z^2$
and a vertex
![]() $x\in \Omega $
with a neighbour
$x\in \Omega $
with a neighbour
![]() $x'$
in the infinite connected component of
$x'$
in the infinite connected component of
![]() $\mathbb Z^2\smallsetminus \Omega $
. Recall that
$\mathbb Z^2\smallsetminus \Omega $
. Recall that
![]() $\Omega ^{\diamond }$
is spanned by the edges of
$\Omega ^{\diamond }$
is spanned by the edges of
![]() $(\mathbb {Z}^2)^{\diamond }$
bordering the faces of
$(\mathbb {Z}^2)^{\diamond }$
bordering the faces of
![]() $(\mathbb {Z}^2)^{\diamond }$
that contain vertices of
$(\mathbb {Z}^2)^{\diamond }$
that contain vertices of
![]() $\Omega $
. As such, the vertices of
$\Omega $
. As such, the vertices of
![]() $\Omega ^{\diamond }$
have degree
$\Omega ^{\diamond }$
have degree
![]() $2$
or
$2$
or
![]() $4$
in
$4$
in
![]() $\Omega ^{\diamond }$
(here, one should be careful when looking at a vertex of
$\Omega ^{\diamond }$
(here, one should be careful when looking at a vertex of
![]() $\Omega ^{\diamond }$
that corresponds to an edge outside of
$\Omega ^{\diamond }$
that corresponds to an edge outside of
![]() $\Omega $
with both endpoints in
$\Omega $
with both endpoints in
![]() $\Omega $
: in this case, we think of this vertex as being split into two ‘prime ends’ of degree 2 in
$\Omega $
: in this case, we think of this vertex as being split into two ‘prime ends’ of degree 2 in
![]() $\Omega ^{\diamond }$
). Let
$\Omega ^{\diamond }$
). Let
![]() $e_x$
be the first edge of
$e_x$
be the first edge of
![]() $\Omega ^{\diamond }$
bordering the face of
$\Omega ^{\diamond }$
bordering the face of
![]() $(\mathbb {Z}^2)^{\diamond }$
containing x, when going around said face in clockwise order, starting from
$(\mathbb {Z}^2)^{\diamond }$
containing x, when going around said face in clockwise order, starting from
![]() $xx'$
.
$xx'$
.
For a configuration
![]() $\omega $
on
$\omega $
on
![]() $\Omega $
, let
$\Omega $
, let
![]() $\overline \omega $
be the loop configuration on
$\overline \omega $
be the loop configuration on
![]() $\Omega ^{\diamond }$
associated to
$\Omega ^{\diamond }$
associated to
![]() $\omega $
. In the loop configuration, the loop passing through
$\omega $
. In the loop configuration, the loop passing through
![]() $e_x$
is called an exploration path; it is denoted by
$e_x$
is called an exploration path; it is denoted by
![]() $\gamma =\gamma (\omega )$
and is oriented counterclockwise so as to have primal open edges on its left and dual-open edges on its right. For an edge
$\gamma =\gamma (\omega )$
and is oriented counterclockwise so as to have primal open edges on its left and dual-open edges on its right. For an edge
![]() $e \in \gamma $
, let
$e \in \gamma $
, let
![]() $\text {W}_{\gamma }(e,e_x)$
be the winding of
$\text {W}_{\gamma }(e,e_x)$
be the winding of
![]() $\gamma $
between e and
$\gamma $
between e and
![]() $e_x$
: that is, the number of left turns minus the number of right turns taken by
$e_x$
: that is, the number of left turns minus the number of right turns taken by
![]() $\gamma $
when going from e to
$\gamma $
when going from e to
![]() $e_x$
multiplied by
$e_x$
multiplied by
![]() $\pi /2$
.
$\pi /2$
.
Definition 6.5. For
![]() $(\Omega ,x)$
as above, the parafermionic observable
$(\Omega ,x)$
as above, the parafermionic observable
![]() $F=F_{\Omega ,x}$
is defined for any (medial) edge e of
$F=F_{\Omega ,x}$
is defined for any (medial) edge e of
![]() $\Omega ^{\diamond }$
by
$\Omega ^{\diamond }$
by
The parafermionic observable satisfies a very special property first observed in [Reference SmirnovSmi10] (see also [Reference Duminil-CopinDum17, Theorem 5.16] for a statement with a similar notation). For every vertex of
![]() $\Omega ^{\diamond }$
with four incident edges in
$\Omega ^{\diamond }$
with four incident edges in
![]() $\Omega ^{\diamond }$
,
$\Omega ^{\diamond }$
,
 $$ \begin{align} \sum_{i=1}^4 \eta(e_i) F(e_i) = F(e_1) - \mathrm{i}F(e_2) - F(e_3) + \mathrm{i}F(e_4) = 0, \end{align} $$
$$ \begin{align} \sum_{i=1}^4 \eta(e_i) F(e_i) = F(e_1) - \mathrm{i}F(e_2) - F(e_3) + \mathrm{i}F(e_4) = 0, \end{align} $$
where
![]() $e_1$
,
$e_1$
,
![]() $e_2$
,
$e_2$
,
![]() $e_3$
and
$e_3$
and
![]() $e_4$
are the four edges incident to v, indexed in clockwise order, and
$e_4$
are the four edges incident to v, indexed in clockwise order, and
![]() $\eta (e_i)$
is the complex number of norm one with the same direction as
$\eta (e_i)$
is the complex number of norm one with the same direction as
![]() $e_i$
and orientation from v towards the other endpoint of
$e_i$
and orientation from v towards the other endpoint of
![]() $e_i$
. Summing this relation over all vertices of
$e_i$
. Summing this relation over all vertices of
![]() $\Omega ^{\diamond }$
of degree 4, we obtain that
$\Omega ^{\diamond }$
of degree 4, we obtain that
where
![]() $\mathcal {C}$
is the set of medial-edges of
$\mathcal {C}$
is the set of medial-edges of
![]() $\Omega ^{\diamond }$
having exactly one endpoint of degree 2 in
$\Omega ^{\diamond }$
having exactly one endpoint of degree 2 in
![]() $\Omega ^{\diamond }$
, and
$\Omega ^{\diamond }$
, and
![]() $\eta (e)$
is the complex number of modulus one, collinear with the edge e and oriented towards the outside of
$\eta (e)$
is the complex number of modulus one, collinear with the edge e and oriented towards the outside of
![]() $\Omega $
.
$\Omega $
.
Remark 6.6. This relation should be understood as stating that the contour integral of the parafermionic observable along the boundary of
![]() $\Omega ^{\diamond }$
is
$\Omega ^{\diamond }$
is
![]() $0$
. While it is common to use the above in simply connected domains, we insist that equation (6.5) is valid for any
$0$
. While it is common to use the above in simply connected domains, we insist that equation (6.5) is valid for any
![]() $\Omega $
as above (it is important that x lies on the exterior face).
$\Omega $
as above (it is important that x lies on the exterior face).
For random-cluster models with general values of q between 1 and 4 and the loop
![]() $O(n)$
models, a similar property was used to obtain estimates for the two-point functions; see, for example, [Reference Duminil-Copin and SmirnovDS12, Reference Duminil-Copin, Sidoravicius and TassionDST17, Reference Duminil-Copin, Glazman, Peled and SpinkaDGPS17, Reference Duminil-Copin, Manolescu and TassionDMT20]. Here, we propose a new use for this property.
$O(n)$
models, a similar property was used to obtain estimates for the two-point functions; see, for example, [Reference Duminil-Copin and SmirnovDS12, Reference Duminil-Copin, Sidoravicius and TassionDST17, Reference Duminil-Copin, Glazman, Peled and SpinkaDGPS17, Reference Duminil-Copin, Manolescu and TassionDMT20]. Here, we propose a new use for this property.
For
![]() $q = 4$
, the complex phase of the observable (that is
$q = 4$
, the complex phase of the observable (that is
![]() $\mathrm {e}^{\mathrm {i}\mathrm {W}_{\gamma }(e,e_x)}$
) is invariant under addition of factors
$\mathrm {e}^{\mathrm {i}\mathrm {W}_{\gamma }(e,e_x)}$
) is invariant under addition of factors
![]() $2\pi $
to the winding. Therefore, it is (almost) determined by the orientation of e. Indeed, for any oriented edge e and any
$2\pi $
to the winding. Therefore, it is (almost) determined by the orientation of e. Indeed, for any oriented edge e and any
![]() $\omega $
such that
$\omega $
such that
![]() $\gamma $
passes through e,
$\gamma $
passes through e,
 $$ \begin{align} \eta(e)\mathrm{e}^{\mathrm{i}\mathrm{W}_{\gamma}(e,e_x)} =\begin{cases} +1 &\text{ if } \gamma \text{ is oriented like } e,\\ -1 &\text{ if } \gamma \text{ is oriented opposite to} e. \end{cases} \end{align} $$
$$ \begin{align} \eta(e)\mathrm{e}^{\mathrm{i}\mathrm{W}_{\gamma}(e,e_x)} =\begin{cases} +1 &\text{ if } \gamma \text{ is oriented like } e,\\ -1 &\text{ if } \gamma \text{ is oriented opposite to} e. \end{cases} \end{align} $$
Moreover, for
![]() $y \in \partial \Omega $
(exclude from this explanation the situation where y has exactly two opposite neighbours in
$y \in \partial \Omega $
(exclude from this explanation the situation where y has exactly two opposite neighbours in
![]() $\Omega $
), there exist two edges
$\Omega $
), there exist two edges
![]() $e,e' \in \mathcal {C}$
bordering the face of
$e,e' \in \mathcal {C}$
bordering the face of
![]() $(\mathbb {Z}^2)^{\diamond }$
containing y such that
$(\mathbb {Z}^2)^{\diamond }$
containing y such that
![]() $\gamma $
passes through e if and only if it passes through
$\gamma $
passes through e if and only if it passes through
![]() $e'$
; see Figure 14. When this happens and y is not equal to x, e and
$e'$
; see Figure 14. When this happens and y is not equal to x, e and
![]() $e'$
may be chosen such that
$e'$
may be chosen such that
![]() $\gamma $
always passes first through e towards the exterior of
$\gamma $
always passes first through e towards the exterior of
![]() $\Omega $
and then through
$\Omega $
and then through
![]() $e'$
towards the interior. Finally,
$e'$
towards the interior. Finally,
![]() $\gamma $
performs
$\gamma $
performs
![]() $4 - d_y$
positive
$4 - d_y$
positive
![]() $\pi /2$
turns between the passage through e and
$\pi /2$
turns between the passage through e and
![]() $e'$
, where
$e'$
, where
![]() $d_y$
is the degree of y inside
$d_y$
is the degree of y inside
![]() $\Omega $
. Thus,
$\Omega $
. Thus,
When
![]() $y=x$
, the two contributions to equation (6.5) of e and
$y=x$
, the two contributions to equation (6.5) of e and
![]() $e'$
are
$e'$
are
![]() $0$
and
$0$
and
![]() $3\pi /2$
, respectively. Inserting equations (6.6) and (6.7) into equation (6.5) yields
$3\pi /2$
, respectively. Inserting equations (6.6) and (6.7) into equation (6.5) yields
 $$ \begin{align} \sum_{\substack{y\in\partial\Omega\\y\ne x}}(4-d_y)\phi_{\Omega}^0[A(x,y)]=\tfrac{3\pi}2, \end{align} $$
$$ \begin{align} \sum_{\substack{y\in\partial\Omega\\y\ne x}}(4-d_y)\phi_{\Omega}^0[A(x,y)]=\tfrac{3\pi}2, \end{align} $$
where
![]() $A(x,y)$
is the event that
$A(x,y)$
is the event that
![]() $\gamma $
passes between y and its neighbour outside
$\gamma $
passes between y and its neighbour outside
![]() $\Omega $
. When y has a neighbour in the infinite component of
$\Omega $
. When y has a neighbour in the infinite component of
![]() $\Omega ^c$
, then
$\Omega ^c$
, then
![]() $A(x,y) = \{x \longleftrightarrow y\}$
; but since we do not ask
$A(x,y) = \{x \longleftrightarrow y\}$
; but since we do not ask
![]() $\Omega $
to be simply connected, this is not always the case for other y.
$\Omega $
to be simply connected, this is not always the case for other y.
A more sophisticated analysis also yields equation (6.8) when some
![]() $y \in \mathcal {C}$
have exactly two opposite neighbours in
$y \in \mathcal {C}$
have exactly two opposite neighbours in
![]() $\Omega $
.
$\Omega $
.
6.2.2 Lower bound on
 $\Delta _{p_c}(r,R)$
at
$\Delta _{p_c}(r,R)$
at
 $p_c$
: proof of Proposition 6.3
$p_c$
: proof of Proposition 6.3
The second inequality follows from equation (2.1); we therefore focus on the first one. By subtracting equation (6.8) for
![]() $\Omega =\Lambda _R$
and
$\Omega =\Lambda _R$
and
![]() $\Omega =\mathrm {Ann}(r,R)$
with
$\Omega =\mathrm {Ann}(r,R)$
with
![]() $x=(0,R)$
, we find
$x=(0,R)$
, we find
 $$ \begin{align} \sum_{y\in\partial\Lambda_R}(4-d_y)\big[\phi_{\Lambda_R}^0[A(x,y)]-\phi_{\mathrm{Ann}(r,R)}^0[A(x,y)]\big] =\sum_{y\in \partial\Lambda_r}(4-d_y)\phi_{\mathrm{Ann}(r,R)}^0[A(x,y)]. \end{align} $$
$$ \begin{align} \sum_{y\in\partial\Lambda_R}(4-d_y)\big[\phi_{\Lambda_R}^0[A(x,y)]-\phi_{\mathrm{Ann}(r,R)}^0[A(x,y)]\big] =\sum_{y\in \partial\Lambda_r}(4-d_y)\phi_{\mathrm{Ann}(r,R)}^0[A(x,y)]. \end{align} $$
We will now estimate the terms on the left- and right-hand sides of the above.
Remark 6.7. It is reasonable to expect that the left-hand side is of order
![]() $R \pi _1^+(R)^2\Delta _{p_c}(r,R)$
, while the right-hand side is of order
$R \pi _1^+(R)^2\Delta _{p_c}(r,R)$
, while the right-hand side is of order
![]() $r \pi _1^+(R)\pi _1^+(r)\pi _2(r,R)$
, which would produce the desired result. Nevertheless, we are not able to prove this due to boundary terms near corners of the inner box, which we cannot control. Instead, we will use a more sophisticated strategy. Let us mention that the conjectural scaling limit of the model suggests that
$r \pi _1^+(R)\pi _1^+(r)\pi _2(r,R)$
, which would produce the desired result. Nevertheless, we are not able to prove this due to boundary terms near corners of the inner box, which we cannot control. Instead, we will use a more sophisticated strategy. Let us mention that the conjectural scaling limit of the model suggests that
![]() $\pi _1^+(r,R)\asymp (r/R)$
and
$\pi _1^+(r,R)\asymp (r/R)$
and
![]() $\pi _2(r,R)\asymp \sqrt {r/R}$
, which would imply that
$\pi _2(r,R)\asymp \sqrt {r/R}$
, which would imply that
![]() $\Delta _{p_c}(r,R)\asymp \sqrt {r/R}$
.
$\Delta _{p_c}(r,R)\asymp \sqrt {r/R}$
.
We start with the right-hand side. For
![]() $y \in \partial \Lambda _r$
, the event
$y \in \partial \Lambda _r$
, the event
![]() $A(x,y)$
occurs if and only if x and y are connected in
$A(x,y)$
occurs if and only if x and y are connected in
![]() $\omega $
and
$\omega $
and
![]() $\Lambda _r$
and
$\Lambda _r$
and
![]() $\Lambda _R$
are connected by a path in
$\Lambda _R$
are connected by a path in
![]() $\omega ^*$
. Quasi-multiplicativity implies that
$\omega ^*$
. Quasi-multiplicativity implies that
 $$ \begin{align} \sum_{y\in \partial\Lambda_r}(4-d_y)\phi_{\mathrm{Ann}(r,R)}^0[A(x,y)] \asymp \pi_1^+(R)\pi_2(r,R)\sum_{k\le r/2}\phi_{\mathbb U}^0[(k,0)\longleftrightarrow \partial\Lambda_r], \end{align} $$
$$ \begin{align} \sum_{y\in \partial\Lambda_r}(4-d_y)\phi_{\mathrm{Ann}(r,R)}^0[A(x,y)] \asymp \pi_1^+(R)\pi_2(r,R)\sum_{k\le r/2}\phi_{\mathbb U}^0[(k,0)\longleftrightarrow \partial\Lambda_r], \end{align} $$
where
![]() $\mathbb U:=\{x\in \mathbb Z^2:x_1\le 0\text { or }x_2\le 0\}$
is the lower-left three-quarter plane.
$\mathbb U:=\{x\in \mathbb Z^2:x_1\le 0\text { or }x_2\le 0\}$
is the lower-left three-quarter plane.
We turn to the left-hand side. For
![]() $y\in \partial \Lambda _R$
,
$y\in \partial \Lambda _R$
,
![]() $A(x,y)$
corresponds to the event that x and y are connected. Also, the measure
$A(x,y)$
corresponds to the event that x and y are connected. Also, the measure
![]() $\phi _{\mathrm {Ann}(r,R)}^0$
may be viewed as the measure in
$\phi _{\mathrm {Ann}(r,R)}^0$
may be viewed as the measure in
![]() $\Lambda _R$
conditioned on the event
$\Lambda _R$
conditioned on the event
![]() $\{\Lambda _r \equiv 0\}$
that every edge with at least one endpoint in
$\{\Lambda _r \equiv 0\}$
that every edge with at least one endpoint in
![]() $\Lambda _{r-1}$
is closed. The previous study of
$\Lambda _{r-1}$
is closed. The previous study of
![]() $\Delta _{p_c}(r,R)$
thus implies that for any
$\Delta _{p_c}(r,R)$
thus implies that for any
![]() $r \le R/2$
,
$r \le R/2$
,
Indeed, consider the coupling constructed in Theorem 4.1(ii) between
![]() $\phi _{\Lambda _R}^0$
and
$\phi _{\Lambda _R}^0$
and
![]() $\phi _{\Lambda _R}^0[.\,|\, \Lambda _r\equiv 0]$
inside
$\phi _{\Lambda _R}^0[.\,|\, \Lambda _r\equiv 0]$
inside
![]() $\Lambda _{R/2}$
(see also Remark 4.3 for the application of the theorem to
$\Lambda _{R/2}$
(see also Remark 4.3 for the application of the theorem to
![]() $\phi _{\Lambda _R}^0$
rather than
$\phi _{\Lambda _R}^0$
rather than
![]() $\phi $
). To observe a difference for the event
$\phi $
). To observe a difference for the event
![]() $A(x,y)$
, it is necessary that the boundary conditions induced on
$A(x,y)$
, it is necessary that the boundary conditions induced on
![]() $\Lambda _{R/2}^c$
by the two configurations are distinct. Theorem 4.9 states that this occurs with a probability of order
$\Lambda _{R/2}^c$
by the two configurations are distinct. Theorem 4.9 states that this occurs with a probability of order
![]() $\Delta _{p_c}(r,R)$
. Finally, when the boundary conditions are indeed distinct, the difference of probabilities of
$\Delta _{p_c}(r,R)$
. Finally, when the boundary conditions are indeed distinct, the difference of probabilities of
![]() $A(x,y)$
is bounded from above by
$A(x,y)$
is bounded from above by
![]() $\phi _{\Lambda _R}^0[A(x,y)]-\phi _{\Lambda _R}^0[A(x,y)\,|\, \Lambda _{R/2}\equiv 0]$
.
$\phi _{\Lambda _R}^0[A(x,y)]-\phi _{\Lambda _R}^0[A(x,y)\,|\, \Lambda _{R/2}\equiv 0]$
.
Summing the above display, we deduce that
 $$ \begin{align} \sum_{y\in\partial\Lambda_R}(4-d_y)\big[ \phi_{\Lambda_R}^0[A(x,y)]-\phi_{\mathrm{ Ann}(r,R)}^0[A(x,y)]\big]\stackrel{<}{\scriptstyle{\frown}}\Delta_{p_c}(r,R) \Sigma_R, \end{align} $$
$$ \begin{align} \sum_{y\in\partial\Lambda_R}(4-d_y)\big[ \phi_{\Lambda_R}^0[A(x,y)]-\phi_{\mathrm{ Ann}(r,R)}^0[A(x,y)]\big]\stackrel{<}{\scriptstyle{\frown}}\Delta_{p_c}(r,R) \Sigma_R, \end{align} $$
where
 $$ \begin{align} \Sigma_R := \sum_{y\in\partial\Lambda_R}(4-d_y)\big[ \phi_{\Lambda_R}^0[A(x,y)]-\phi_{\Lambda_R}^0[A(x,y)\,|\, \Lambda_{R/2}\equiv 0]\big] \end{align} $$
$$ \begin{align} \Sigma_R := \sum_{y\in\partial\Lambda_R}(4-d_y)\big[ \phi_{\Lambda_R}^0[A(x,y)]-\phi_{\Lambda_R}^0[A(x,y)\,|\, \Lambda_{R/2}\equiv 0]\big] \end{align} $$
is a constant that depends on R only. Inserting equations (6.10) and (6.11) into equation (6.9) gives
for any
![]() $r \le R/2$
. Furthermore, equations (6.11) and (6.9) applied to
$r \le R/2$
. Furthermore, equations (6.11) and (6.9) applied to
![]() $r = R/2$
show that
$r = R/2$
show that
From the two displays above, we conclude that
 $$ \begin{align} \Delta_{p_c}(r,R) \stackrel{>}{\scriptstyle{\frown}} \pi_2(r,R)\, \frac{\sum_{k\le r/2}\phi_{\mathbb{U}}^0[(k,0)\longleftrightarrow \partial\Lambda_r]}{\sum_{k\le R/4}\phi_{\mathbb{U}}^0[(k,0)\longleftrightarrow \partial\Lambda_R]}\stackrel{>}{\scriptstyle{\frown}} \pi_2(r,R)(r/R). \end{align} $$
$$ \begin{align} \Delta_{p_c}(r,R) \stackrel{>}{\scriptstyle{\frown}} \pi_2(r,R)\, \frac{\sum_{k\le r/2}\phi_{\mathbb{U}}^0[(k,0)\longleftrightarrow \partial\Lambda_r]}{\sum_{k\le R/4}\phi_{\mathbb{U}}^0[(k,0)\longleftrightarrow \partial\Lambda_R]}\stackrel{>}{\scriptstyle{\frown}} \pi_2(r,R)(r/R). \end{align} $$
The inequality above is obtained by summing over
![]() $j = 0,\dots , R/r$
and
$j = 0,\dots , R/r$
and
![]() $k = 1,\dots , r/2$
the inequality below:
$k = 1,\dots , r/2$
the inequality below:
which is a direct consequence of the comparison between boundary conditions in equation (CBC).
![]() $\square $
$\square $
Remark 6.8. One can improve equation (6.2) when
![]() $r=1$
. Applying the left of equation (6.13) with
$r=1$
. Applying the left of equation (6.13) with
![]() $r=1$
, the comparison between boundary conditions in equations (CBC) and (2.1) implies that
$r=1$
, the comparison between boundary conditions in equations (CBC) and (2.1) implies that
 $$\begin{align*}\Delta_{p_c}(R)\stackrel{>}{\scriptstyle{\frown}} \frac{\pi_2(R)}{\sum_{k\le R/4}\phi_{\mathbb{U}}^0[(k,0)\longleftrightarrow \partial\Lambda_R]} \ge \frac{\pi_2(R)}{\tfrac14R\pi_1(3R/4)}\stackrel{>}{\scriptstyle{\frown}} \frac{\pi_2(R)}{R\pi_1(R)}\stackrel{>}{\scriptstyle{\frown}} \frac{R^{c-2}}{\pi_1(R)}. \end{align*}$$
$$\begin{align*}\Delta_{p_c}(R)\stackrel{>}{\scriptstyle{\frown}} \frac{\pi_2(R)}{\sum_{k\le R/4}\phi_{\mathbb{U}}^0[(k,0)\longleftrightarrow \partial\Lambda_R]} \ge \frac{\pi_2(R)}{\tfrac14R\pi_1(3R/4)}\stackrel{>}{\scriptstyle{\frown}} \frac{\pi_2(R)}{R\pi_1(R)}\stackrel{>}{\scriptstyle{\frown}} \frac{R^{c-2}}{\pi_1(R)}. \end{align*}$$
6.2.3 Stability of
 $\Delta _p(r,R)$
: proof of Proposition 6.4
$\Delta _p(r,R)$
: proof of Proposition 6.4
The proof is based on the following quantity. Call a subgraph
![]() $\Omega $
of
$\Omega $
of
![]() $\mathbb {Z}^2$
a topological R-annulus if it is of the form
$\mathbb {Z}^2$
a topological R-annulus if it is of the form
![]() $\Lambda _R \smallsetminus H$
with H a simply connected domain such that
$\Lambda _R \smallsetminus H$
with H a simply connected domain such that
![]() $\Lambda _{R/8}\subset H \subset \Lambda _{R/4}$
; see Figure 15. The boundary of
$\Lambda _{R/8}\subset H \subset \Lambda _{R/4}$
; see Figure 15. The boundary of
![]() $\Omega $
is split into
$\Omega $
is split into
![]() $\partial \Lambda _R$
and
$\partial \Lambda _R$
and
![]() $\partial _{\mathrm {in}}\Omega :=\partial \Omega \smallsetminus \partial \Lambda _R$
. Set
$\partial _{\mathrm {in}}\Omega :=\partial \Omega \smallsetminus \partial \Lambda _R$
. Set
 $$ \begin{align*} \mathbf N_{\Omega}(p):=\sum_{y\in \partial_{\mathrm{in}}\Omega}\phi_{\Omega,p}^0[y\longleftrightarrow \partial \Lambda_{R/2}]. \end{align*} $$
$$ \begin{align*} \mathbf N_{\Omega}(p):=\sum_{y\in \partial_{\mathrm{in}}\Omega}\phi_{\Omega,p}^0[y\longleftrightarrow \partial \Lambda_{R/2}]. \end{align*} $$
The first observation is the following lemma stating that for
![]() $q=4$
, the quantity
$q=4$
, the quantity
![]() $\mathbf N_{\Omega }(p)$
does not depend on the choice of the R-annulus
$\mathbf N_{\Omega }(p)$
does not depend on the choice of the R-annulus
![]() $\Omega $
or the choice of p such that
$\Omega $
or the choice of p such that
![]() $R\le L(p)$
.
$R\le L(p)$
.

Figure 15 In grey, the domain
![]() $\mathcal H$
(which is a topological R-annulus) carved by the event F (in blue). In red, the exploration path
$\mathcal H$
(which is a topological R-annulus) carved by the event F (in blue). In red, the exploration path
![]() $\gamma =\gamma (\omega )$
going around the boundary vertex x.
$\gamma =\gamma (\omega )$
going around the boundary vertex x.
Lemma 6.9. For every
![]() $p\ge p_c$
and
$p\ge p_c$
and
![]() $R \le L(p)$
,
$R \le L(p)$
,
where the infimum and supremum are taken over topological R-annuli.
Proof. We start by proving that
where
![]() $\Sigma _R$
was introduced in equation (6.12) in the previous section.
$\Sigma _R$
was introduced in equation (6.12) in the previous section.
Fix
![]() $\Omega $
a topological R-annulus, and set
$\Omega $
a topological R-annulus, and set
![]() $x := (0,R)$
. Then due to equation (2.1), for every
$x := (0,R)$
. Then due to equation (2.1), for every
![]() $y \in \partial _{\mathrm {in}}\Omega $
,
$y \in \partial _{\mathrm {in}}\Omega $
,
In particular, we have that
 $$ \begin{align} \mathbf N_{\Omega}(p_c) \asymp \frac{1}{ \pi_1^+(R)}\sum_{y \in \partial_{\mathrm{in}}\Omega}\phi_{\Omega,p_c}^0[A(x,y)]. \end{align} $$
$$ \begin{align} \mathbf N_{\Omega}(p_c) \asymp \frac{1}{ \pi_1^+(R)}\sum_{y \in \partial_{\mathrm{in}}\Omega}\phi_{\Omega,p_c}^0[A(x,y)]. \end{align} $$
Subtracting equation (6.8) for the domains
![]() $\Lambda _R$
and
$\Lambda _R$
and
![]() $\Omega $
, and following the proof of Proposition 6.3, we find that
$\Omega $
, and following the proof of Proposition 6.3, we find that
 $$ \begin{align*} \sum_{y \in \partial_{\mathrm{in}}\Omega}\phi_{\Omega,p_c}^0[A(x,y)]\asymp \Sigma_R, \end{align*} $$
$$ \begin{align*} \sum_{y \in \partial_{\mathrm{in}}\Omega}\phi_{\Omega,p_c}^0[A(x,y)]\asymp \Sigma_R, \end{align*} $$
which concludes the proof of equation (6.15).
We now prove that for every p and
![]() $R\le L(p)$
,
$R\le L(p)$
,
where the infimum and supremum are taken over topological R-annuli. Note that this inequality implies the result. Indeed, since
![]() $\mathbf N_{\Omega }(p)$
is increasing in p and
$\mathbf N_{\Omega }(p)$
is increasing in p and
![]() $\pi _4(p^*;R)=\pi _4(p;R)$
(by duality), the previous inequality implies that for
$\pi _4(p^*;R)=\pi _4(p;R)$
(by duality), the previous inequality implies that for
![]() $p\ge p_c$
and
$p\ge p_c$
and
![]() $R\le L(p)=L(p^*)$
,
$R\le L(p)=L(p^*)$
,
which combines with equation (6.15) to give the result. We now focus on the proof of equation (6.17). We proceed similarly to [Reference Duminil-Copin, Manolescu and TassionDMT20, Proposition 6.8], but from inside out.
Let F be the event that in
![]() $\mathrm {Ann}(R/8,R/4)$
, there exists an open circuit surrounding
$\mathrm {Ann}(R/8,R/4)$
, there exists an open circuit surrounding
![]() $\Lambda _{R/8}$
that is connected to
$\Lambda _{R/8}$
that is connected to
![]() $\Lambda _{R/8}$
, as well as a dual-open circuit, which is necessarily outside the open one; see Figure 15. If F occurs, let
$\Lambda _{R/8}$
, as well as a dual-open circuit, which is necessarily outside the open one; see Figure 15. If F occurs, let
![]() $\mathcal {H} = \mathcal {H}(\omega )$
be the graph formed of the union of all open clusters that intersect
$\mathcal {H} = \mathcal {H}(\omega )$
be the graph formed of the union of all open clusters that intersect
![]() $\Lambda _{R/8}$
, along with all finite components of
$\Lambda _{R/8}$
, along with all finite components of
![]() $\mathbb Z^2$
minus the said union. Then due to the definition of F,
$\mathbb Z^2$
minus the said union. Then due to the definition of F,
![]() $\Lambda _{R/8}\subset \mathcal {H} \subset \Lambda _{R/4}$
. Write
$\Lambda _{R/8}\subset \mathcal {H} \subset \Lambda _{R/4}$
. Write
![]() $\Omega (\omega ) := \Lambda _R\smallsetminus \mathcal {H}$
for the random topological R-annulus formed by removing
$\Omega (\omega ) := \Lambda _R\smallsetminus \mathcal {H}$
for the random topological R-annulus formed by removing
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
When the measure
![]() $\phi ^0_{\Lambda _R,p}$
is conditioned on
$\phi ^0_{\Lambda _R,p}$
is conditioned on
![]() $F\cap \{\Omega (\omega )=\Omega \}$
, its restriction to
$F\cap \{\Omega (\omega )=\Omega \}$
, its restriction to
![]() $\Omega $
is
$\Omega $
is
![]() $\phi ^0_{\Omega ,p}$
. Notice that if
$\phi ^0_{\Omega ,p}$
. Notice that if
![]() $y \in \partial _{\mathrm {in}} \Omega $
is connected to
$y \in \partial _{\mathrm {in}} \Omega $
is connected to
![]() $\partial \Lambda _{R/2}$
by an open path, then a four-arm event to distance
$\partial \Lambda _{R/2}$
by an open path, then a four-arm event to distance
![]() $R/8$
occurs around y. Thus, using the quasi-multiplicativity and equations (Mix) and (RSW) (to bound the probability of F from below), we find that
$R/8$
occurs around y. Thus, using the quasi-multiplicativity and equations (Mix) and (RSW) (to bound the probability of F from below), we find that
Conversely, the separation of arms for the four-arm event and equation (RSW) show that for each
![]() $y \in \mathrm {Ann}(5R/32, 7R/32)$
,
$y \in \mathrm {Ann}(5R/32, 7R/32)$
,
Summing over all y, we find
Remark 6.10. The previous proof shows as a byproduct that
![]() $\pi _4(p;R)\asymp \pi _4(R)$
for every
$\pi _4(p;R)\asymp \pi _4(R)$
for every
![]() $R\le L(p)$
. It is somehow surprising that the stability of
$R\le L(p)$
. It is somehow surprising that the stability of
![]() $\pi _4$
below the correlation length can be directly extracted from the parafermionic observable. Recall, however, that this is only valid for
$\pi _4$
below the correlation length can be directly extracted from the parafermionic observable. Recall, however, that this is only valid for
![]() $q = 4$
.
$q = 4$
.
Remark 6.11. The previous proof also implies that
![]() $R^2\pi _4(R)$
is of the order of
$R^2\pi _4(R)$
is of the order of
![]() $\mathbf N_{\Omega }(p_c)$
for every topological R-annulus
$\mathbf N_{\Omega }(p_c)$
for every topological R-annulus
![]() $\Omega $
. In particular, taking
$\Omega $
. In particular, taking
![]() $\Omega =\Lambda _{R/8}$
gives that
$\Omega =\Lambda _{R/8}$
gives that
The conjectural scaling limit of the model suggests that
![]() $\pi _1^+(R)\asymp R^{-1}$
, which would imply that
$\pi _1^+(R)\asymp R^{-1}$
, which would imply that
![]() $\pi _4(R)\asymp R^{-2}$
. We see that in this case, the fact that
$\pi _4(R)\asymp R^{-2}$
. We see that in this case, the fact that
![]() $\Delta _{p_c}(R)\gg \pi _4(R)$
is crucial for the bound in equation (6.2).
$\Delta _{p_c}(R)\gg \pi _4(R)$
is crucial for the bound in equation (6.2).
Proof of Proposition 6.4
We treat the case
![]() $p>p_c$
; the case
$p>p_c$
; the case
![]() $p<p_c$
can be done similarly. Fix
$p<p_c$
can be done similarly. Fix
![]() $r \leq R\le L(p)$
. The inequality in equation (5.11) implies that
$r \leq R\le L(p)$
. The inequality in equation (5.11) implies that
 $$ \begin{align*} \Big|\log \frac{\Delta_p(r,R)}{\Delta_{p_c}(r,R)}\Big| &\stackrel{<}{\scriptstyle{\frown}} \underbrace{\int_{p_c}^p \Big(\sum_{\ell=1}^R \ell\Delta_u(\ell)\Big)du}_{(A)} + \underbrace{\int_{p_c}^p \Big(\sum_{\ell=R}^{L(u)}\ell\Delta_u(\ell)\Delta_u(R,\ell)\Big) du}_{(B)}, \end{align*} $$
$$ \begin{align*} \Big|\log \frac{\Delta_p(r,R)}{\Delta_{p_c}(r,R)}\Big| &\stackrel{<}{\scriptstyle{\frown}} \underbrace{\int_{p_c}^p \Big(\sum_{\ell=1}^R \ell\Delta_u(\ell)\Big)du}_{(A)} + \underbrace{\int_{p_c}^p \Big(\sum_{\ell=R}^{L(u)}\ell\Delta_u(\ell)\Delta_u(R,\ell)\Big) du}_{(B)}, \end{align*} $$
and we need to prove that
![]() $(A)$
and
$(A)$
and
![]() $(B)$
are bounded by constants that are independent of r, R and
$(B)$
are bounded by constants that are independent of r, R and
![]() $p>p_c$
. The bound on
$p>p_c$
. The bound on
![]() $(B)$
is easy to obtain since equation (5.1) shows that
$(B)$
is easy to obtain since equation (5.1) shows that
![]() $(B) \stackrel{<}{\scriptstyle{\frown}} \phi _p[\mathcal {C}(\Lambda _R)] - \phi _{p_c}[\mathcal {C}(\Lambda _R)]\le 1$
. We therefore focus on
$(B) \stackrel{<}{\scriptstyle{\frown}} \phi _p[\mathcal {C}(\Lambda _R)] - \phi _{p_c}[\mathcal {C}(\Lambda _R)]\le 1$
. We therefore focus on
![]() $(A)$
.
$(A)$
.
Choose the topological R-annulus
![]() $\Omega $
minimising
$\Omega $
minimising
![]() $\mathbf N_{\Omega }(p)$
, and observe that by Lemma 6.9,
$\mathbf N_{\Omega }(p)$
, and observe that by Lemma 6.9,
![]() $\mathbf N_{\Omega }(p)\asymp \mathbf N_{\Omega }(p_c)$
. We claim that
$\mathbf N_{\Omega }(p)\asymp \mathbf N_{\Omega }(p_c)$
. We claim that
 $$ \begin{align} \tfrac{d}{d u} \log \mathbf N_{\Omega} (u) \stackrel{>}{\scriptstyle{\frown}}\sum_{\ell=1}^R \ell\Delta_u(\ell). \end{align} $$
$$ \begin{align} \tfrac{d}{d u} \log \mathbf N_{\Omega} (u) \stackrel{>}{\scriptstyle{\frown}}\sum_{\ell=1}^R \ell\Delta_u(\ell). \end{align} $$
Observe that equation (6.19) implies that
![]() $(A)\stackrel{<}{\scriptstyle{\frown}} \log \mathbf N_{\Omega }(p)-\log \mathbf N_{\Omega }(p_c)\stackrel{<}{\scriptstyle{\frown}}1$
, which concludes the proof of the proposition. Thus, we only need to prove equation (6.19), which we do next.
$(A)\stackrel{<}{\scriptstyle{\frown}} \log \mathbf N_{\Omega }(p)-\log \mathbf N_{\Omega }(p_c)\stackrel{<}{\scriptstyle{\frown}}1$
, which concludes the proof of the proposition. Thus, we only need to prove equation (6.19), which we do next.
Start by observing that
 $$ \begin{align} \tfrac{d}{d u} \log \mathbf N_{\Omega}(u) = \sum_{y\in \partial_{\mathrm{in}}\Omega}\tfrac{d}{d u} \phi_{\Omega,u}^0[y\longleftrightarrow \partial \Lambda_{R/2}] = \tfrac{1}{u(1-u)}\sum_{y\in \partial_{\mathrm{in}}\Omega}\,\sum_{e \in \Omega}\mathrm{Cov}[y\longleftrightarrow \partial \Lambda_{R/2},\omega_e ]. \end{align} $$
$$ \begin{align} \tfrac{d}{d u} \log \mathbf N_{\Omega}(u) = \sum_{y\in \partial_{\mathrm{in}}\Omega}\tfrac{d}{d u} \phi_{\Omega,u}^0[y\longleftrightarrow \partial \Lambda_{R/2}] = \tfrac{1}{u(1-u)}\sum_{y\in \partial_{\mathrm{in}}\Omega}\,\sum_{e \in \Omega}\mathrm{Cov}[y\longleftrightarrow \partial \Lambda_{R/2},\omega_e ]. \end{align} $$
Fix some
![]() $y \in \partial _{\mathrm {in}}\Omega $
, and set
$y \in \partial _{\mathrm {in}}\Omega $
, and set
![]() $N:=\lfloor \log _8 R\rfloor $
. Then there exist points
$N:=\lfloor \log _8 R\rfloor $
. Then there exist points
![]() $z_1,\dots , z_{N-2}$
in
$z_1,\dots , z_{N-2}$
in
![]() $\Omega $
such that for each k,
$\Omega $
such that for each k,
![]() $\Lambda _{8^k}(z_k) \subset \Omega $
but y is not connected to
$\Lambda _{8^k}(z_k) \subset \Omega $
but y is not connected to
![]() $\partial \Lambda _R$
in the subgraph
$\partial \Lambda _R$
in the subgraph
![]() $\Omega \smallsetminus \Lambda _{2 \cdot 8^k}(z_k)$
; the latter condition includes the situation where
$\Omega \smallsetminus \Lambda _{2 \cdot 8^k}(z_k)$
; the latter condition includes the situation where
![]() $y \in \Lambda _{2 \cdot 8^k}(z_k)$
. See Figure 16 and its caption for an explanation of this elementary fact. For
$y \in \Lambda _{2 \cdot 8^k}(z_k)$
. See Figure 16 and its caption for an explanation of this elementary fact. For
![]() $k < \ell $
, since
$k < \ell $
, since
![]() $\Lambda _{2 \cdot 8^k}(z_k)$
intersects the boundary of
$\Lambda _{2 \cdot 8^k}(z_k)$
intersects the boundary of
![]() $\Omega $
, but
$\Omega $
, but
![]() $\Lambda _{8^{\ell }}(z_{\ell }) \subset \Omega $
, we conclude that
$\Lambda _{8^{\ell }}(z_{\ell }) \subset \Omega $
, we conclude that
![]() $\Lambda _{8^k/2}(z_k)$
and
$\Lambda _{8^k/2}(z_k)$
and
![]() $\Lambda _{8^{\ell }/2}(z_{\ell })$
do not intersect. Thus, the boxes
$\Lambda _{8^{\ell }/2}(z_{\ell })$
do not intersect. Thus, the boxes
![]() $(\Lambda _{8^k/2}(z_k))_{k \le N-2}$
are pairwise disjoint.
$(\Lambda _{8^k/2}(z_k))_{k \le N-2}$
are pairwise disjoint.

Figure 16 By sliding the boxes along a given path one by one from the exterior towards y, one finds a first time that the twice larger box
![]() $\Lambda _{2\cdot 8^k}(z_k)$
disconnects y from the boundary. Note that by construction, the first time it stops cannot be quite the same for different k. In particular, the box
$\Lambda _{2\cdot 8^k}(z_k)$
disconnects y from the boundary. Note that by construction, the first time it stops cannot be quite the same for different k. In particular, the box
![]() $\Lambda _{8^k/2}(z_k)$
being at a distance
$\Lambda _{8^k/2}(z_k)$
being at a distance
![]() $8^k/2$
of the boundary of
$8^k/2$
of the boundary of
![]() $\Lambda _{8^k}(z_k)$
, it is also at such a distance of
$\Lambda _{8^k}(z_k)$
, it is also at such a distance of
![]() $\partial _{\mathrm {in}}\Omega $
. Since, on the contrary,
$\partial _{\mathrm {in}}\Omega $
. Since, on the contrary,
![]() $\Lambda _{8^{\ell }/2}(z_{\ell })$
is within a distance
$\Lambda _{8^{\ell }/2}(z_{\ell })$
is within a distance
![]() $8^{\ell }\times 3/2$
of it, we immediately deduce that the two boxes do not intersect as soon as
$8^{\ell }\times 3/2$
of it, we immediately deduce that the two boxes do not intersect as soon as
![]() $\ell <k$
.
$\ell <k$
.
Now, for any such k and
![]() $e \in \Lambda _{8^k/2}(z_k)$
, a similar argument as that used for the lower bound in equation (5.2) shows that
$e \in \Lambda _{8^k/2}(z_k)$
, a similar argument as that used for the lower bound in equation (5.2) shows that
Indeed, consider the coupling constructed in Theorem 4.1(ii) between
![]() $\phi _{\Omega ,u}^0[\,\cdot \,|\omega _e = 0]$
and
$\phi _{\Omega ,u}^0[\,\cdot \,|\omega _e = 0]$
and
![]() $\phi _{\Omega ,u}^0 [\,\cdot \,|\omega _e = 1]$
inside the box
$\phi _{\Omega ,u}^0 [\,\cdot \,|\omega _e = 1]$
inside the box
![]() $\Lambda _{8^k/4}(e)$
(see also Remark 4.3 for the application of the theorem to
$\Lambda _{8^k/4}(e)$
(see also Remark 4.3 for the application of the theorem to
![]() $\phi _{\Omega ,u}^0$
rather than
$\phi _{\Omega ,u}^0$
rather than
![]() $\phi $
). With a probability of order
$\phi $
). With a probability of order
![]() $\Delta _u(8^k)$
, we have
$\Delta _u(8^k)$
, we have
![]() $\tau < \infty $
and the boundary conditions induced on
$\tau < \infty $
and the boundary conditions induced on
![]() $\mathcal {F}_{\tau }$
by the two configurations form a boosting pair. When this occurs, by equation (RSW), the configuration inside
$\mathcal {F}_{\tau }$
by the two configurations form a boosting pair. When this occurs, by equation (RSW), the configuration inside
![]() $\mathcal {F}_{\tau }$
has a probability of at least
$\mathcal {F}_{\tau }$
has a probability of at least
to be such that the connection between y and
![]() $\partial \Lambda _{R/2}$
only occurs for the higher boundary condition.
$\partial \Lambda _{R/2}$
only occurs for the higher boundary condition.
Summing equation (6.21) over e and keeping in mind that all covariances in equation (6.20) are non-negative, we find
 $$ \begin{align*} \tfrac{d}{d u} \phi_{\Omega,u}^0[y\longleftrightarrow \partial \Lambda_{R/2}] &\stackrel{>}{\scriptstyle{\frown}} \sum_{k = 1}^{N -2}\sum_{e \in \Lambda_{8^k/2}(z_k)} \mathrm{Cov}[y\longleftrightarrow \partial \Lambda_{R/2},\omega_e ]\\ &\stackrel{>}{\scriptstyle{\frown}} \sum_{k = 1}^{N -2}8^{2k} \Delta_u(8^k)\phi_{\Omega,u}^0[y\longleftrightarrow \partial \Lambda_{R/2}]\\ &\stackrel{>}{\scriptstyle{\frown}} \Big(\sum_{\ell = 1}^{R}\ell \Delta_u(\ell)\Big)\phi_{\Omega,u}^0[y\longleftrightarrow \partial \Lambda_{R/2}]. \end{align*} $$
$$ \begin{align*} \tfrac{d}{d u} \phi_{\Omega,u}^0[y\longleftrightarrow \partial \Lambda_{R/2}] &\stackrel{>}{\scriptstyle{\frown}} \sum_{k = 1}^{N -2}\sum_{e \in \Lambda_{8^k/2}(z_k)} \mathrm{Cov}[y\longleftrightarrow \partial \Lambda_{R/2},\omega_e ]\\ &\stackrel{>}{\scriptstyle{\frown}} \sum_{k = 1}^{N -2}8^{2k} \Delta_u(8^k)\phi_{\Omega,u}^0[y\longleftrightarrow \partial \Lambda_{R/2}]\\ &\stackrel{>}{\scriptstyle{\frown}} \Big(\sum_{\ell = 1}^{R}\ell \Delta_u(\ell)\Big)\phi_{\Omega,u}^0[y\longleftrightarrow \partial \Lambda_{R/2}]. \end{align*} $$
For the last inequality, we used the fact that
![]() $\Delta _u(\ell ) \asymp \Delta _u(8^k)$
for any
$\Delta _u(\ell ) \asymp \Delta _u(8^k)$
for any
![]() $8^k\le \ell \le 8^{k+1}$
. Finally, summing over y, we find
$8^k\le \ell \le 8^{k+1}$
. Finally, summing over y, we find
 $$ \begin{align*} \tfrac{d}{d u} \mathbf N_{\Omega}(u) \stackrel{>}{\scriptstyle{\frown}} \mathbf N_{\Omega}(u)\sum_{\ell = 1}^{R}\ell \Delta_u(\ell), \end{align*} $$
$$ \begin{align*} \tfrac{d}{d u} \mathbf N_{\Omega}(u) \stackrel{>}{\scriptstyle{\frown}} \mathbf N_{\Omega}(u)\sum_{\ell = 1}^{R}\ell \Delta_u(\ell), \end{align*} $$
which concludes the proof of equation (6.19) and the whole proposition.
7 Proofs of the stability theorems
In this section, we prove stability results for crossing probabilities, arm events and
![]() $\Delta _p$
. First, observe that due to the previous section, Propositions 5.1 and 5.9 immediately lead to the following corollary.
$\Delta _p$
. First, observe that due to the previous section, Propositions 5.1 and 5.9 immediately lead to the following corollary.
Corollary 7.1.
-
(i) Fix
 $\eta>0$
. For every
$\eta>0$
. For every
 $p \in (0,1)$
and every
$p \in (0,1)$
and every
 $\eta $
-regular quad
$\eta $
-regular quad
 $(\mathcal {D},a,b,c,d)$
at scale
$(\mathcal {D},a,b,c,d)$
at scale
 $R\le L(p)$
, (7.1)
$R\le L(p)$
, (7.1) $$ \begin{align} \tfrac{\mathrm{d}}{\mathrm{d}p}\phi_{p}[\mathcal{C}(\mathcal{D})]\asymp R^2\Delta_p(R)+\sum_{\ell=R}^{L(p)}\ell \Delta_p(\ell)\Delta_p(R,\ell), \end{align} $$
$$ \begin{align} \tfrac{\mathrm{d}}{\mathrm{d}p}\phi_{p}[\mathcal{C}(\mathcal{D})]\asymp R^2\Delta_p(R)+\sum_{\ell=R}^{L(p)}\ell \Delta_p(\ell)\Delta_p(R,\ell), \end{align} $$
where the constants in
 $\asymp $
depend on
$\asymp $
depend on
 $\eta $
.
$\eta $
. -
(ii) For every
 $p \in (0,1)$
,
$p \in (0,1)$
,
 $k=1$
or
$k=1$
or
 $k\ge 2$
even and
$k\ge 2$
even and
 $r \le R \le L(p)$
, (7.2)
$r \le R \le L(p)$
, (7.2) $$ \begin{align} \big|\tfrac{\mathrm{d}}{\mathrm{d}p}\log\pi_k(p;r,R) \big|\stackrel{<}{\scriptstyle{\frown}} R^2\Delta_p(R)+\sum_{\ell=R}^{L(p)}\ell \Delta_p(\ell)\Delta_p(R,\ell), \end{align} $$
$$ \begin{align} \big|\tfrac{\mathrm{d}}{\mathrm{d}p}\log\pi_k(p;r,R) \big|\stackrel{<}{\scriptstyle{\frown}} R^2\Delta_p(R)+\sum_{\ell=R}^{L(p)}\ell \Delta_p(\ell)\Delta_p(R,\ell), \end{align} $$
where the constants in
 $\stackrel{<}{\scriptstyle{\frown}}$
depend on k.
$\stackrel{<}{\scriptstyle{\frown}}$
depend on k. -
(iii) For every
 $p \in (0,1)$
and two edges e and f at a distance
$p \in (0,1)$
and two edges e and f at a distance
 $R\le L(p)$
from each other, (7.3)
$R\le L(p)$
from each other, (7.3) $$ \begin{align} \big|\tfrac{\mathrm{d}}{\mathrm{d}p}\log \mathrm{Cov}_p(\omega_e,\omega_f)\big| \stackrel{<}{\scriptstyle{\frown}} R^2\Delta_p(R) + \sum_{\ell=R}^{L(p)} \ell \Delta_p(\ell)\Delta_p(R,\ell). \end{align} $$
$$ \begin{align} \big|\tfrac{\mathrm{d}}{\mathrm{d}p}\log \mathrm{Cov}_p(\omega_e,\omega_f)\big| \stackrel{<}{\scriptstyle{\frown}} R^2\Delta_p(R) + \sum_{\ell=R}^{L(p)} \ell \Delta_p(\ell)\Delta_p(R,\ell). \end{align} $$
Proof. By equations (1.20) and (1.15), for any
![]() $p \in (0,1)$
and
$p \in (0,1)$
and
![]() $R \leq L(p)$
,
$R \leq L(p)$
,
![]() $\sum _{\ell =1}^R \ell \Delta _p(\ell ) \stackrel{<}{\scriptstyle{\frown}} R^2\Delta _p(R)$
. Insert this into Propositions 5.1 and 5.9 to obtain the desired results.
$\sum _{\ell =1}^R \ell \Delta _p(\ell ) \stackrel{<}{\scriptstyle{\frown}} R^2\Delta _p(R)$
. Insert this into Propositions 5.1 and 5.9 to obtain the desired results.
We next prove the stability of crossing probabilities and arm event probabilities stated in Theorem 1.4.
Proof of Theorem 1.4
Fix
![]() $p \neq p_c$
. We prove equation (1.7); the stability for arm events can be deduced similarly. Fix some
$p \neq p_c$
. We prove equation (1.7); the stability for arm events can be deduced similarly. Fix some
![]() $\eta $
-regular discrete quad
$\eta $
-regular discrete quad
![]() $(\mathcal {D},a,b,c,d)$
at some scale
$(\mathcal {D},a,b,c,d)$
at some scale
![]() $R\ge 1$
. The inequality given by equation (1.7) is trivial when
$R\ge 1$
. The inequality given by equation (1.7) is trivial when
![]() $R> L(p)$
, and we focus on the case where
$R> L(p)$
, and we focus on the case where
![]() $R \le L(p)$
. Applying equation (7.1) to u between
$R \le L(p)$
. Applying equation (7.1) to u between
![]() $p_c$
and p, we find
$p_c$
and p, we find
 $$ \begin{align} \tfrac{\mathrm{d}}{\mathrm{d}u}\phi_{u}[\mathcal{C}(\mathcal{D})] & \asymp R^2\Delta_u(R)+\sum_{\ell=R}^{L(p)}\ell \Delta_u(\ell) \Delta_u(R, \ell) + \sum_{\ell=L(p)}^{L(u)}\ell \Delta_u(\ell)\Delta_u(R,\ell)\nonumber\\ &\stackrel{<}{\scriptstyle{\frown}} (\tfrac R{L(p)})^{\delta}\, \Big[L(p)^2\Delta_u(L(p)) + \sum_{\ell=L(p)}^{L(u)}\ell \Delta_u(\ell)\Delta_u(L(p),\ell)\Big], \end{align} $$
$$ \begin{align} \tfrac{\mathrm{d}}{\mathrm{d}u}\phi_{u}[\mathcal{C}(\mathcal{D})] & \asymp R^2\Delta_u(R)+\sum_{\ell=R}^{L(p)}\ell \Delta_u(\ell) \Delta_u(R, \ell) + \sum_{\ell=L(p)}^{L(u)}\ell \Delta_u(\ell)\Delta_u(R,\ell)\nonumber\\ &\stackrel{<}{\scriptstyle{\frown}} (\tfrac R{L(p)})^{\delta}\, \Big[L(p)^2\Delta_u(L(p)) + \sum_{\ell=L(p)}^{L(u)}\ell \Delta_u(\ell)\Delta_u(L(p),\ell)\Big], \end{align} $$
where the inequality is due to a simple computation based on the quasi-multiplicativity of
![]() $\Delta _p$
and equation (1.20). The terms for
$\Delta _p$
and equation (1.20). The terms for
![]() $\ell \geq L(p)$
are dominated by the corresponding sum in the second line.
$\ell \geq L(p)$
are dominated by the corresponding sum in the second line.
Corollary 7.1 applied to
![]() $\mathcal {C}(\Lambda _{L(p)})$
together with equation (7.4) imply that
$\mathcal {C}(\Lambda _{L(p)})$
together with equation (7.4) imply that
Integrate the above between
![]() $p_c$
and p to find
$p_c$
and p to find
Remark 7.2. One may also obtain the following improvement of equation (1.8) (similar to equation (1.7)):
where
![]() $\delta ,C> 0$
are universal constants depending only on q.
$\delta ,C> 0$
are universal constants depending only on q.
Furthermore, since Corollary 7.1 applies to logarithmic derivatives of certain arm event probabilities, (7.5) may also be shown for
![]() $\pi _k(p;R)$
(with
$\pi _k(p;R)$
(with
![]() $k=1$
or
$k=1$
or
![]() $k\ge 2$
even) and
$k\ge 2$
even) and
![]() $\pi _k^+(p;R)$
(for any
$\pi _k^+(p;R)$
(for any
![]() $k \geq 1$
), with C depending on k. Notice, however, that we do not claim to prove stability for probabilities of arm events in the half-plane with boundary conditions on the half-plane.
$k \geq 1$
), with C depending on k. Notice, however, that we do not claim to prove stability for probabilities of arm events in the half-plane with boundary conditions on the half-plane.
We now turn to the proof of the stability of
![]() $\Delta _p$
. Let us note that for
$\Delta _p$
. Let us note that for
![]() $q = 4$
, the stability of
$q = 4$
, the stability of
![]() $\Delta _p$
was also proved in Section 6.2, as a step towards equation (1.20).
$\Delta _p$
was also proved in Section 6.2, as a step towards equation (1.20).
Proof of Theorem 1.6(iii)
Fix
![]() $p \neq p_c$
,
$p \neq p_c$
,
![]() $R \le L(p)$
and two edges e and f at a distance R from each other. For u between p and
$R \le L(p)$
and two edges e and f at a distance R from each other. For u between p and
![]() $p_c$
, Corollary 7.1 gives
$p_c$
, Corollary 7.1 gives
 $$ \begin{align*} \Big|\tfrac{\mathrm{d}}{\mathrm{d}u}\log \mathrm{Cov}_u(\omega_e,\omega_f)\big| &\stackrel{<}{\scriptstyle{\frown}} R^2 \Delta_u(R)+\sum_{\ell=R}^{L(u)}\ell \Delta_u(\ell) \Delta_u(R,\ell) \stackrel{<}{\scriptstyle{\frown}} \tfrac{\mathrm{d}}{\mathrm{ d}u}\phi_u[\mathcal{C}(\Lambda_R)]. \end{align*} $$
$$ \begin{align*} \Big|\tfrac{\mathrm{d}}{\mathrm{d}u}\log \mathrm{Cov}_u(\omega_e,\omega_f)\big| &\stackrel{<}{\scriptstyle{\frown}} R^2 \Delta_u(R)+\sum_{\ell=R}^{L(u)}\ell \Delta_u(\ell) \Delta_u(R,\ell) \stackrel{<}{\scriptstyle{\frown}} \tfrac{\mathrm{d}}{\mathrm{ d}u}\phi_u[\mathcal{C}(\Lambda_R)]. \end{align*} $$
By integrating the above between
![]() $p_c$
and p, we find
$p_c$
and p, we find
 $$ \begin{align} \frac{\mathrm{Cov}_p(\omega_e,\omega_f)}{\mathrm{Cov}_{p_c}(\omega_e,\omega_f)} \asymp 1. \end{align} $$
$$ \begin{align} \frac{\mathrm{Cov}_p(\omega_e,\omega_f)}{\mathrm{Cov}_{p_c}(\omega_e,\omega_f)} \asymp 1. \end{align} $$
Now apply equation (5.3) to deduce that
Remark 7.3. It will not surprise the reader that the same type of improved stability as in equation (7.5) may be shown for the covariance. Getting the same result for
![]() $\Delta _p$
itself seems more difficult as we crucially rely on an up-to-constant relation between
$\Delta _p$
itself seems more difficult as we crucially rely on an up-to-constant relation between
![]() $\Delta _p$
and the covariance and that the derivative of
$\Delta _p$
and the covariance and that the derivative of
![]() $\Delta _p$
itself is less obvious.
$\Delta _p$
itself is less obvious.
8 Derivation of the scaling relations
This section is dedicated to proving the scaling relations (Theorems 1.9, 1.10 and 1.11). The proof of the near-critical scaling relations (Theorem 1.11) is based on the stability below the characteristic length (Theorem 1.4 and Theorem 1.6(iii)). With the latter results at our disposal, the proofs of the critical and near-critical scaling relations given by equations 1.22–1.27 are very close to those for Bernoulli percolation and contain no significant innovation. For this reason, we are voluntarily quick on these proofs, trying to merely recall the crucial ingredients.
The main novelties in this section are the independent proof of the scaling relation involving the magnetic field (Section 8.3) and the derivation of the scaling relation involving
![]() $\alpha $
.
$\alpha $
.
8.1 Scaling relations at criticality: proof of Theorem 1.9
In this section, we work with
![]() $p = p_c$
, and we drop it from the notation. We will prove a stronger result, which implies equation (1.22) when taking
$p = p_c$
, and we drop it from the notation. We will prove a stronger result, which implies equation (1.22) when taking
![]() $x\in \partial \Lambda _R$
.
$x\in \partial \Lambda _R$
.
Lemma 8.1. Fix
![]() $1\le q\le 4$
. For every
$1\le q\le 4$
. For every
![]() $R\ge 1$
and every
$R\ge 1$
and every
![]() $x\in \Lambda _R$
,
$x\in \Lambda _R$
,
Proof. The middle inequality is obvious. For the right one, observe that if
![]() $0$
and x are connected, then
$0$
and x are connected, then
![]() $0 \longleftrightarrow \partial \Lambda _r$
and
$0 \longleftrightarrow \partial \Lambda _r$
and
![]() $x\longleftrightarrow \partial \Lambda _r(x)$
, where
$x\longleftrightarrow \partial \Lambda _r(x)$
, where
![]() $r:=\lfloor |x|/C_{\mathrm {mix}}\rfloor $
. The invariance under translations of
$r:=\lfloor |x|/C_{\mathrm {mix}}\rfloor $
. The invariance under translations of
![]() $\phi _{p_c}$
, the mixing property given by equation (Mix) and the quasi-multiplicativity of the one-arm event in equation (2.3) give that
$\phi _{p_c}$
, the mixing property given by equation (Mix) and the quasi-multiplicativity of the one-arm event in equation (2.3) give that
We now prove the left inequality. The FKG inequality in equation (FKG) implies that
 $$ \begin{align*} \phi_{p_c}[0\stackrel{\Lambda_{2R}}{\longleftrightarrow} x, 0\longleftrightarrow \partial\Lambda_R] &\ge \phi_{p_c}[A_R,0\longleftrightarrow \partial\Lambda_{2R}, x\longleftrightarrow \partial\Lambda_{3R}(x)]\\ &\geq \phi_{p_c}[A_R]\pi_1(2R)\pi_1(3R)\\ &\stackrel{>}{\scriptstyle{\frown}} \pi_1(R)^2, \end{align*} $$
$$ \begin{align*} \phi_{p_c}[0\stackrel{\Lambda_{2R}}{\longleftrightarrow} x, 0\longleftrightarrow \partial\Lambda_R] &\ge \phi_{p_c}[A_R,0\longleftrightarrow \partial\Lambda_{2R}, x\longleftrightarrow \partial\Lambda_{3R}(x)]\\ &\geq \phi_{p_c}[A_R]\pi_1(2R)\pi_1(3R)\\ &\stackrel{>}{\scriptstyle{\frown}} \pi_1(R)^2, \end{align*} $$
Recall that
![]() $\mathsf {C}$
is the cluster of
$\mathsf {C}$
is the cluster of
![]() $0$
. Let
$0$
. Let
![]() $\mathrm {rad}(\mathsf {C}) := \max \{r:\mathsf {C} \text { intersects }\partial \Lambda _r \}$
be the radius of
$\mathrm {rad}(\mathsf {C}) := \max \{r:\mathsf {C} \text { intersects }\partial \Lambda _r \}$
be the radius of
![]() $\mathsf {C}$
.
$\mathsf {C}$
.
Lemma 8.2. For every
![]() $R \geq 1$
,
$R \geq 1$
,
Proof. Fix
![]() $n \geq 1$
. The inequality in the middle is the Cauchy-Schwarz inequality. For the first inequality, observe that equations (8.1) and (RSW′
) imply that
$n \geq 1$
. The inequality in the middle is the Cauchy-Schwarz inequality. For the first inequality, observe that equations (8.1) and (RSW′
) imply that

Divide the above by
![]() $\phi _{p_c}[R\le \mathrm {rad}(\mathsf {C})<4R]\le \pi _1(R)$
to obtain the first inequality in equation (8.2).
$\phi _{p_c}[R\le \mathrm {rad}(\mathsf {C})<4R]\le \pi _1(R)$
to obtain the first inequality in equation (8.2).
We turn to the last inequality of equation (8.2). We have

Fix
![]() $x,y \in \Lambda _{4R}$
, and assume first that
$x,y \in \Lambda _{4R}$
, and assume first that
![]() $|x|\le |y| \le |x-y|$
. Set
$|x|\le |y| \le |x-y|$
. Set
![]() $\ell := |x|$
and
$\ell := |x|$
and
![]() $k := |y|$
. Observe that the event on the right induces the following events, which are listed along with the order – up to constants – of their probabilities (which are obtained thanks to equation (2.3)):
$k := |y|$
. Observe that the event on the right induces the following events, which are listed along with the order – up to constants – of their probabilities (which are obtained thanks to equation (2.3)):
-
•
 $0 \longleftrightarrow \partial \Lambda _{\ell /C_{\mathrm {mix}} }$
– of probability of order
$0 \longleftrightarrow \partial \Lambda _{\ell /C_{\mathrm {mix}} }$
– of probability of order
 $\pi _1(\ell )$
;
$\pi _1(\ell )$
; -
•
 $x \longleftrightarrow \partial \Lambda _{\ell /C_{\mathrm {mix}} }(x)$
– of probability of order
$x \longleftrightarrow \partial \Lambda _{\ell /C_{\mathrm {mix}} }(x)$
– of probability of order
 $\pi _1(\ell )$
;
$\pi _1(\ell )$
; -
•
 $y \longleftrightarrow \partial \Lambda _{k/C_{\mathrm {mix}} }(y)$
– of probability of order
$y \longleftrightarrow \partial \Lambda _{k/C_{\mathrm {mix}} }(y)$
– of probability of order
 $\pi _1(k)$
;
$\pi _1(k)$
; -
•
 $\partial \Lambda _{\min \{\ell ,k \}} \longleftrightarrow \partial \Lambda _k$
– of probability of order
$\partial \Lambda _{\min \{\ell ,k \}} \longleftrightarrow \partial \Lambda _k$
– of probability of order
 $\pi _1(k)/\pi _1(\ell )$
;
$\pi _1(k)/\pi _1(\ell )$
; -
•
 $\partial \Lambda _{\min \{C_{\mathrm {mix}} k,R\}} \longleftrightarrow \partial \Lambda _{R}$
– of probability of order
$\partial \Lambda _{\min \{C_{\mathrm {mix}} k,R\}} \longleftrightarrow \partial \Lambda _{R}$
– of probability of order
 $\pi _1(R) /\pi _1(k)$
.
$\pi _1(R) /\pi _1(k)$
.
Several iterations of the mixing property in equations (Mix) and (2.3) imply that
Observe now that for
![]() $1 \le \ell \le k\le 4R$
, there are
$1 \le \ell \le k\le 4R$
, there are
![]() $8\ell $
vertices
$8\ell $
vertices
![]() $x \in \mathbb {Z}^2$
with
$x \in \mathbb {Z}^2$
with
![]() $|x| = \ell $
and
$|x| = \ell $
and
![]() $8k$
vertices y with
$8k$
vertices y with
![]() $|y| = k$
. Thus,
$|y| = k$
. Thus,
 $$ \begin{align*} \sum_{\substack{x,y\in \Lambda_{4R}\\ |x| \le |y| \le |x-y|}}\phi_{p_c}[0\longleftrightarrow x,0\longleftrightarrow y,0\longleftrightarrow \partial\Lambda_R] &\stackrel{<}{\scriptstyle{\frown}} \sum_{1 \le \ell \le k \le 4R} \ell\pi_1(\ell)k\pi_1(k)\pi_1(R) \stackrel{<}{\scriptstyle{\frown}} R^4\pi_1(R)^3, \end{align*} $$
$$ \begin{align*} \sum_{\substack{x,y\in \Lambda_{4R}\\ |x| \le |y| \le |x-y|}}\phi_{p_c}[0\longleftrightarrow x,0\longleftrightarrow y,0\longleftrightarrow \partial\Lambda_R] &\stackrel{<}{\scriptstyle{\frown}} \sum_{1 \le \ell \le k \le 4R} \ell\pi_1(\ell)k\pi_1(k)\pi_1(R) \stackrel{<}{\scriptstyle{\frown}} R^4\pi_1(R)^3, \end{align*} $$
where in the last line, we used that
 $$ \begin{align} \sum_{k=1}^Rk\pi_1(k)\stackrel{<}{\scriptstyle{\frown}} R^2\pi_1(R) \end{align} $$
$$ \begin{align} \sum_{k=1}^Rk\pi_1(k)\stackrel{<}{\scriptstyle{\frown}} R^2\pi_1(R) \end{align} $$
which is a consequence of equations (2.2) and (2.3). The same upper bound may be obtained for any of the other five possible orderings of
![]() $|x|, |y|, |x-y|$
. Overall, we conclude that
$|x|, |y|, |x-y|$
. Overall, we conclude that
which gives the result by dividing by
where in the last inequality, we used the mixing property in equations (Mix) and (RSW′ ).
Proof of Theorem 1.9
Lemma 8.1 applied with
![]() $R=2|x|$
and equation (2.3) directly imply equation (1.22). We turn to the proof of equation (1.23). Fix
$R=2|x|$
and equation (2.3) directly imply equation (1.22). We turn to the proof of equation (1.23). Fix
![]() $R \geq 1$
and
$R \geq 1$
and
![]() $r:=\varphi (R)$
. Let us start with the lower bound on
$r:=\varphi (R)$
. Let us start with the lower bound on
![]() $\phi _{p_c}[|\mathsf {C}| \geq R]$
. Let
$\phi _{p_c}[|\mathsf {C}| \geq R]$
. Let
![]() $c \in (0,1)$
be the constant appearing in the first bound
$c \in (0,1)$
be the constant appearing in the first bound
![]() $\stackrel{<}{\scriptstyle{\frown}}$
of equation (8.2). Then using the definition of
$\stackrel{<}{\scriptstyle{\frown}}$
of equation (8.2). Then using the definition of
![]() $\varphi $
, equation (8.2), the Paley–Zygmund inequality and equation (8.5), we find
$\varphi $
, equation (8.2), the Paley–Zygmund inequality and equation (8.5), we find
 $$ \begin{align*} \phi_{p_c}[|\mathsf{C}|\geq \tfrac{c}2R]&\ge \phi_{p_c}[|\mathsf{C}|\geq \tfrac{c}2 r^2\pi_1(r)]\\ &\ge \phi_{p_c}[|\mathsf{C}|\geq \tfrac{1}2\phi_{p_c}(|\mathsf{C}| \,|\,r\le \mathrm{rad}(\mathsf{C})< 4r)]\\ &\stackrel{>}{\scriptstyle{\frown}} \frac{\phi_{p_c}[|\mathsf{C}| \,|\,r\le \mathrm{rad}(\mathsf{ C})<4r]^2}{\phi_{p_c}[|\mathsf{C}|^2 \,|\, r\le \mathrm{rad}(\mathsf{C})<4r]}\,\phi_{p_c}[r\le \mathrm{ rad}(\mathsf{C})<4r]\\ &\stackrel{>}{\scriptstyle{\frown}}\phi_{p_c}[r\le \mathrm{rad}(\mathsf{C})<4r]\\ & \stackrel{>}{\scriptstyle{\frown}}\pi_1(r). \end{align*} $$
$$ \begin{align*} \phi_{p_c}[|\mathsf{C}|\geq \tfrac{c}2R]&\ge \phi_{p_c}[|\mathsf{C}|\geq \tfrac{c}2 r^2\pi_1(r)]\\ &\ge \phi_{p_c}[|\mathsf{C}|\geq \tfrac{1}2\phi_{p_c}(|\mathsf{C}| \,|\,r\le \mathrm{rad}(\mathsf{C})< 4r)]\\ &\stackrel{>}{\scriptstyle{\frown}} \frac{\phi_{p_c}[|\mathsf{C}| \,|\,r\le \mathrm{rad}(\mathsf{ C})<4r]^2}{\phi_{p_c}[|\mathsf{C}|^2 \,|\, r\le \mathrm{rad}(\mathsf{C})<4r]}\,\phi_{p_c}[r\le \mathrm{ rad}(\mathsf{C})<4r]\\ &\stackrel{>}{\scriptstyle{\frown}}\phi_{p_c}[r\le \mathrm{rad}(\mathsf{C})<4r]\\ & \stackrel{>}{\scriptstyle{\frown}}\pi_1(r). \end{align*} $$
This concludes the proof of the lower bound since equation (2.3) implies that
![]() $\phi ( \tfrac {c}2R) \asymp \phi (R) = r$
.
$\phi ( \tfrac {c}2R) \asymp \phi (R) = r$
.
We turn to the complementary upper bound. Using the Markov inequality in the third line and the definition of
![]() $\varphi $
and equation (8.1) in the fourth, we obtain that
$\varphi $
and equation (8.1) in the fourth, we obtain that
 $$ \begin{align*} \phi_{p_c}[|\mathsf{C}|\ge R] &= \phi_{p_c}[|\mathsf{C}|\ge R,\mathrm{rad}(\mathsf{C})> r] + \phi_{p_c}[|\mathsf{C}| \geq R,\mathrm{rad}(\mathsf{C})\le r]\\ &\le \pi_1(r)+\phi_{p_c}[|\mathsf{C} \cap \Lambda_r| \geq R] \\ &\le \pi_1(r)+\frac{1}{R}\sum_{u \in \Lambda_r}\phi_{p_c}[0 \longleftrightarrow u] \\ &\stackrel{<}{\scriptstyle{\frown}} \pi_1(r)+\frac{1}{r^2\pi_1(r)}\sum_{u \in \Lambda_r} \pi_1(|u|)^2\!\stackrel{<}{\scriptstyle{\frown}} \pi_1(r), \end{align*} $$
$$ \begin{align*} \phi_{p_c}[|\mathsf{C}|\ge R] &= \phi_{p_c}[|\mathsf{C}|\ge R,\mathrm{rad}(\mathsf{C})> r] + \phi_{p_c}[|\mathsf{C}| \geq R,\mathrm{rad}(\mathsf{C})\le r]\\ &\le \pi_1(r)+\phi_{p_c}[|\mathsf{C} \cap \Lambda_r| \geq R] \\ &\le \pi_1(r)+\frac{1}{R}\sum_{u \in \Lambda_r}\phi_{p_c}[0 \longleftrightarrow u] \\ &\stackrel{<}{\scriptstyle{\frown}} \pi_1(r)+\frac{1}{r^2\pi_1(r)}\sum_{u \in \Lambda_r} \pi_1(|u|)^2\!\stackrel{<}{\scriptstyle{\frown}} \pi_1(r), \end{align*} $$
where the last inequality follows from equation (2.2) via the following computation:
 $$ \begin{align*} \frac1k\sum_{k=1}^r \frac{k\pi_1(k)^2}{r\pi_1(r)^2} \stackrel{<}{\scriptstyle{\frown}} \frac{1}{r}\sum_{k=1}^r(k/r)^{1-2c}\stackrel{<}{\scriptstyle{\frown}} 1.\\[-45pt] \end{align*} $$
$$ \begin{align*} \frac1k\sum_{k=1}^r \frac{k\pi_1(k)^2}{r\pi_1(r)^2} \stackrel{<}{\scriptstyle{\frown}} \frac{1}{r}\sum_{k=1}^r(k/r)^{1-2c}\stackrel{<}{\scriptstyle{\frown}} 1.\\[-45pt] \end{align*} $$
8.2 Scaling relations in the near-critical regime: proof of Theorem 1.11
By Theorem 1.3 and equation (2.3), we have that
![]() $L(p)\asymp \xi (p)$
and
$L(p)\asymp \xi (p)$
and
![]() $\pi _1(L(p))\asymp \pi _1(\xi (p))$
, so we only need to show equations 1.25–1.28 with
$\pi _1(L(p))\asymp \pi _1(\xi (p))$
, so we only need to show equations 1.25–1.28 with
![]() $L(p)$
instead of
$L(p)$
instead of
![]() $\xi (p)$
.
$\xi (p)$
.
8.2.1 Proof of equation (1.25) (scaling relation between
 $\beta $
,
$\beta $
,
 $\nu $
and
$\nu $
and
 $\xi _1$
)
$\xi _1$
)
On the one hand, the stability below the characteristic length (Theorem 1.4) gives
On the other hand, the FKG inequality given by equations (FKG) and (RSW′ ) and Corollary 2.15 imply that
![]() $\square $
$\square $
8.2.2 Proof of equation (1.26) (scaling relation between
 $\gamma $
,
$\gamma $
,
 $\nu $
and
$\nu $
and
 $\xi _1$
)
$\xi _1$
)
We start with the case
![]() $p<p_c$
. Due to equations (Mix) and (RSW), Theorem 1.4 and Proposition 2.13, we have
$p<p_c$
. Due to equations (Mix) and (RSW), Theorem 1.4 and Proposition 2.13, we have
where
![]() $R:=\min \{|x|,L(p)\}$
and
$R:=\min \{|x|,L(p)\}$
and
![]() $c,C> 0$
are uniform constants. Summing equation (8.6) over
$c,C> 0$
are uniform constants. Summing equation (8.6) over
![]() $x\in \mathbb {Z}^2$
, we find
$x\in \mathbb {Z}^2$
, we find
 $$ \begin{align*} \sum_{R=1}^{L(p)} R\pi_1(R)^2 \stackrel{<}{\scriptstyle{\frown}} \chi(p) \stackrel{<}{\scriptstyle{\frown}} \sum_{R=1}^{L(p)} R\pi_1(R)^2 + \pi_1(L(p))^2 \!\!\sum_{R> L(p)} \!\! R \exp[-c\,R/L(p)]. \end{align*} $$
$$ \begin{align*} \sum_{R=1}^{L(p)} R\pi_1(R)^2 \stackrel{<}{\scriptstyle{\frown}} \chi(p) \stackrel{<}{\scriptstyle{\frown}} \sum_{R=1}^{L(p)} R\pi_1(R)^2 + \pi_1(L(p))^2 \!\!\sum_{R> L(p)} \!\! R \exp[-c\,R/L(p)]. \end{align*} $$
Due to the exponential factor, the second term on the right-hand side of the above is of order
![]() $L(p)^2\pi _1(L(p))^2$
. Finally, equation (1.26) follows from the observation that due to equations (2.2) and (2.3),
$L(p)^2\pi _1(L(p))^2$
. Finally, equation (1.26) follows from the observation that due to equations (2.2) and (2.3),
and from the equivalence in equation (1.6) between
![]() $L(p)$
and
$L(p)$
and
![]() $\xi (p)$
.
$\xi (p)$
.
We now turn to the case
![]() $p>p_c$
. The only additional difficulty comes from the fact that we need to force 0 and x not to be connected to infinity. For the lower bound, sum over every
$p>p_c$
. The only additional difficulty comes from the fact that we need to force 0 and x not to be connected to infinity. For the lower bound, sum over every
![]() $x\in \Lambda _{L(p)/2}$
the following inequality
$x\in \Lambda _{L(p)/2}$
the following inequality
where the first inequality is due to the spatial Markov property in equation (SMP), and the second inequality follows from equations (RSW) and ( p-MON) and an argument similar to Lemma 8.1.
We turn to the upper bound. Let
![]() $A_x^*$
be the event that there exists a circuit in
$A_x^*$
be the event that there exists a circuit in
![]() $\omega ^*$
surrounding 0 and x. By considering four translations and rotations of
$\omega ^*$
surrounding 0 and x. By considering four translations and rotations of
![]() $A_x^*$
and applying the FKG inequality, we find that
$A_x^*$
and applying the FKG inequality, we find that
for some constant
![]() $c> 0$
, due to Corollary 2.15. Applying the FKG inequality again, we have
$c> 0$
, due to Corollary 2.15. Applying the FKG inequality again, we have
 $$ \begin{align*} \phi_p[0\longleftrightarrow x,0\kern6pt\not\kern-6pt\longleftrightarrow\infty] &\le \phi_p[0\longleftrightarrow x]\phi_p[A_x^*]\\ &\stackrel{<}{\scriptstyle{\frown}} \pi_1(R)^2\exp(-c|x|/L(p)). \end{align*} $$
$$ \begin{align*} \phi_p[0\longleftrightarrow x,0\kern6pt\not\kern-6pt\longleftrightarrow\infty] &\le \phi_p[0\longleftrightarrow x]\phi_p[A_x^*]\\ &\stackrel{<}{\scriptstyle{\frown}} \pi_1(R)^2\exp(-c|x|/L(p)). \end{align*} $$
For the second inequality, we use equation (8.7) and bound the connection probability between
![]() $0$
and x by the argument of Lemma 8.1 together with Theorem 1.4. Summing this inequality over
$0$
and x by the argument of Lemma 8.1 together with Theorem 1.4. Summing this inequality over
![]() $x\in \mathbb {Z}^2$
gives the upper bound.
$x\in \mathbb {Z}^2$
gives the upper bound.
![]() $\square $
$\square $
8.2.3 Proof of equation (1.27) (scaling relation between
 $\iota $
and
$\iota $
and
 $\nu $
)
$\nu $
)
Assume
![]() $p> p_c$
; the case
$p> p_c$
; the case
![]() $p < p_c$
is identical. Write
$p < p_c$
is identical. Write
![]() $L = L(p)$
. Use Corollary 7.1 and integrate the derivative of
$L = L(p)$
. Use Corollary 7.1 and integrate the derivative of
![]() $g(p):=\phi _p[\mathcal {C}(\Lambda _{L})]$
between
$g(p):=\phi _p[\mathcal {C}(\Lambda _{L})]$
between
![]() $p_c$
and p to get
$p_c$
and p to get
 $$ \begin{align} \int_{p_c}^p L^2\Delta_{u}(L)du \stackrel{<}{\scriptstyle{\frown}} g(p)-g(p_c)\stackrel{<}{\scriptstyle{\frown}} 1. \end{align} $$
$$ \begin{align} \int_{p_c}^p L^2\Delta_{u}(L)du \stackrel{<}{\scriptstyle{\frown}} g(p)-g(p_c)\stackrel{<}{\scriptstyle{\frown}} 1. \end{align} $$
In the other direction, let
![]() $p_0 \in [p_c,p]$
be such that
$p_0 \in [p_c,p]$
be such that
![]() $L(p_0)=RL(p)$
for some
$L(p_0)=RL(p)$
for some
![]() $R> 1$
. Theorem 1.4 and the definition of
$R> 1$
. Theorem 1.4 and the definition of
![]() $L(p)$
imply that
$L(p)$
imply that
provided that R is large enough. For
![]() $u \in [p_0, p]$
, Corollary 7.1 together with the quasi-multiplicativity property Theorem 1.6(ii) imply
$u \in [p_0, p]$
, Corollary 7.1 together with the quasi-multiplicativity property Theorem 1.6(ii) imply
(Note that the constant in
![]() $\stackrel{<}{\scriptstyle{\frown}}$
depends on R.) Integrating the previous displayed equation between
$\stackrel{<}{\scriptstyle{\frown}}$
depends on R.) Integrating the previous displayed equation between
![]() $p_0$
and p and then using equation (8.9) gives
$p_0$
and p and then using equation (8.9) gives
 $$ \begin{align*} 1\stackrel{<}{\scriptstyle{\frown}} g(p)-g(p_0) \stackrel{<}{\scriptstyle{\frown}} \int_{p_0}^p L^2\Delta_{u}(L)du \le \int_{p_c}^p L^2\Delta_{u}(L)du. \end{align*} $$
$$ \begin{align*} 1\stackrel{<}{\scriptstyle{\frown}} g(p)-g(p_0) \stackrel{<}{\scriptstyle{\frown}} \int_{p_0}^p L^2\Delta_{u}(L)du \le \int_{p_c}^p L^2\Delta_{u}(L)du. \end{align*} $$
Together with equation (8.8), the previous displayed equation and the stability of
![]() $\Delta _u(L)$
given by Theorem 1.6(iii) show that
$\Delta _u(L)$
given by Theorem 1.6(iii) show that
 $$ \begin{align*} 1 \asymp \int_{p_c}^p L^2\Delta_{u}(L)du \asymp (p - p_c) L^2\Delta_{p_c}(L), \end{align*} $$
$$ \begin{align*} 1 \asymp \int_{p_c}^p L^2\Delta_{u}(L)du \asymp (p - p_c) L^2\Delta_{p_c}(L), \end{align*} $$
which concludes the proof.
![]() $\square $
$\square $
8.2.4 Proof of equation (1.28) (scaling relation between
 $\iota $
and
$\iota $
and
 $\alpha $
)
$\alpha $
)
A straightforward computation involving equation (1.9) shows that
 $$ \begin{align*} f''(p) = 2 \frac{\mathrm{d}}{\mathrm{d}p}\phi_p [\omega_e]=2\sum_{f}\mathrm{Cov}_p(\omega_e,\omega_f), \end{align*} $$
$$ \begin{align*} f''(p) = 2 \frac{\mathrm{d}}{\mathrm{d}p}\phi_p [\omega_e]=2\sum_{f}\mathrm{Cov}_p(\omega_e,\omega_f), \end{align*} $$
where e is a fixed edge of
![]() $\mathbb {Z}^2$
and the sum is over all edges f. By Lemma 5.3 applied to
$\mathbb {Z}^2$
and the sum is over all edges f. By Lemma 5.3 applied to
![]() $\mathcal {D}$
formed of the single edge e, we find (for the second equivalence, we use Theorem 1.6(iii))
$\mathcal {D}$
formed of the single edge e, we find (for the second equivalence, we use Theorem 1.6(iii))
where
![]() $\ell $
is the distance between e and f. Summing the displayed equation above over all edges f, we conclude that
$\ell $
is the distance between e and f. Summing the displayed equation above over all edges f, we conclude that
 $$ \begin{align*} f''(p) \asymp \sum_{\ell = 1}^{L(p)} \ell \Delta_{p_c}(\ell)^2, \end{align*} $$
$$ \begin{align*} f''(p) \asymp \sum_{\ell = 1}^{L(p)} \ell \Delta_{p_c}(\ell)^2, \end{align*} $$
as required.
![]() $\square $
$\square $
Remark 8.3. The above shows that if the phase transition is of second order (meaning that
![]() $f''(p)$
diverges as p tends to
$f''(p)$
diverges as p tends to
![]() $p_c$
), then
$p_c$
), then
![]() $\sum _{\ell }\ell \Delta _p(\ell )^2$
diverges, which, using the interpretation of crossing probabilities in terms of
$\sum _{\ell }\ell \Delta _p(\ell )^2$
diverges, which, using the interpretation of crossing probabilities in terms of
![]() $\Delta _p(\ell )$
, implies that the crossing probabilities of quads for the infinite-volume measure are not differentiable at
$\Delta _p(\ell )$
, implies that the crossing probabilities of quads for the infinite-volume measure are not differentiable at
![]() $p_c$
.
$p_c$
.
Remark 8.4. When
![]() $\sum _{\ell \geq 1}\ell \Delta (\ell )^2$
converges, the computation above simply proves that
$\sum _{\ell \geq 1}\ell \Delta (\ell )^2$
converges, the computation above simply proves that
![]() $f''(p)$
remains bounded uniformly in p. Nevertheless, it is easy to deduce by differentiating one more time that for
$f''(p)$
remains bounded uniformly in p. Nevertheless, it is easy to deduce by differentiating one more time that for
![]() $p\ne p_c$
(we drop p from the notation),
$p\ne p_c$
(we drop p from the notation),
 $$ \begin{align*} f'''(p) &\le \sum_{f,g}\phi[\omega_e\omega_f\omega_g]-\phi[\omega_e\omega_f]\phi[\omega_g]-\phi[\omega_f\omega_g]\phi[\omega_e]-\phi[\omega_e\omega_g]\phi[\omega_f]+2\phi[\omega_e]\phi[\omega_f]\phi[\omega_g]\\ &\stackrel{<}{\scriptstyle{\frown}} \sum_{\ell\le L(p)}\ell \Delta(\ell)\Delta(\ell',\ell)\sum_{\ell'\le\ell}\ell'\Delta(\ell')^2 \stackrel{<}{\scriptstyle{\frown}} L(p)^4\Delta(L(p))^3 \stackrel{<}{\scriptstyle{\frown}} \frac{1}{|p-p_c|^3L(p)^{2}}. \end{align*} $$
$$ \begin{align*} f'''(p) &\le \sum_{f,g}\phi[\omega_e\omega_f\omega_g]-\phi[\omega_e\omega_f]\phi[\omega_g]-\phi[\omega_f\omega_g]\phi[\omega_e]-\phi[\omega_e\omega_g]\phi[\omega_f]+2\phi[\omega_e]\phi[\omega_f]\phi[\omega_g]\\ &\stackrel{<}{\scriptstyle{\frown}} \sum_{\ell\le L(p)}\ell \Delta(\ell)\Delta(\ell',\ell)\sum_{\ell'\le\ell}\ell'\Delta(\ell')^2 \stackrel{<}{\scriptstyle{\frown}} L(p)^4\Delta(L(p))^3 \stackrel{<}{\scriptstyle{\frown}} \frac{1}{|p-p_c|^3L(p)^{2}}. \end{align*} $$
If one defines
![]() $\alpha $
in this framework by the formula
$\alpha $
in this framework by the formula
![]() $f'''(p)=|p-p_c|^{-\alpha -1-o(1)}$
, we deduce that
$f'''(p)=|p-p_c|^{-\alpha -1-o(1)}$
, we deduce that
![]() $\alpha \le 2-2\nu $
. The converse bound does not follow by the same computation since the summand on the first line is not of definite sign; at the time of writing, the matching lower bound on
$\alpha \le 2-2\nu $
. The converse bound does not follow by the same computation since the summand on the first line is not of definite sign; at the time of writing, the matching lower bound on
![]() $f'''(p)$
remains unproven.
$f'''(p)$
remains unproven.
8.3 Scaling relation with magnetic field: proof of Theorem 1.10
We insist again on the fact that this section is independent of the rest of the paper. Below, we work with the graph
![]() $\mathbb Z^2$
with the addition of the ghost vertex. We drop
$\mathbb Z^2$
with the addition of the ghost vertex. We drop
![]() $p_c$
and q but keep h in the notation except when it is equal to
$p_c$
and q but keep h in the notation except when it is equal to
![]() $0$
, in which case we omit it as well. We start with a lemma relating certain quantities at
$0$
, in which case we omit it as well. We start with a lemma relating certain quantities at
![]() $h=0$
with the corresponding quantities at
$h=0$
with the corresponding quantities at
![]() $h\ge 0$
.
$h\ge 0$
.
Set
![]() $\tilde \pi _1(h,R):=\phi _{\Lambda _R,h}^1[0\longleftrightarrow \partial \Lambda _R]$
, where connections need to occur in
$\tilde \pi _1(h,R):=\phi _{\Lambda _R,h}^1[0\longleftrightarrow \partial \Lambda _R]$
, where connections need to occur in
![]() $\mathbb {Z}^2$
. Additionally, let
$\mathbb {Z}^2$
. Additionally, let
![]() $A_R^*$
be the event that there exists a dual circuit in
$A_R^*$
be the event that there exists a dual circuit in
![]() $\mathrm {Ann}(R,2R)$
surrounding
$\mathrm {Ann}(R,2R)$
surrounding
![]() $\Lambda _R$
and
$\Lambda _R$
and
Finally, for
![]() $C> 1$
, define
$C> 1$
, define
Lemma 8.5. For any
![]() $C>1$
, there exists
$C>1$
, there exists
![]() $\varepsilon>0$
such that for every R,
$\varepsilon>0$
such that for every R,
Due to the definition of
![]() $h_c$
, crossing estimates as in equation (RSW) apply in the regime of
$h_c$
, crossing estimates as in equation (RSW) apply in the regime of
![]() $(r,h)$
with
$(r,h)$
with
![]() $r\le R$
and
$r\le R$
and
![]() $h\le h_c(R)$
. Indeed, the crossing probabilities in the primal model increase with h, which ensures the lower bounds. For the upper bounds, observe that
$h\le h_c(R)$
. Indeed, the crossing probabilities in the primal model increase with h, which ensures the lower bounds. For the upper bounds, observe that
![]() $\beta (h,r)$
involves the boundary conditions that render dual crossings least likely. (RSW) applied at
$\beta (h,r)$
involves the boundary conditions that render dual crossings least likely. (RSW) applied at
![]() $p_c$
combined with the definition of
$p_c$
combined with the definition of
![]() $h_c(R)$
implies the uniform positivity of
$h_c(R)$
implies the uniform positivity of
![]() $\beta (r,h)$
for
$\beta (r,h)$
for
![]() $r \leq R$
and
$r \leq R$
and
![]() $h \leq h_c(R)$
. The FKG inequality and the monotonicity of boundary conditions imply lower bounds for crossing probabilities in the dual model, as claimed.
$h \leq h_c(R)$
. The FKG inequality and the monotonicity of boundary conditions imply lower bounds for crossing probabilities in the dual model, as claimed.
As a consequence, a similar proof to that of Lemma 8.1 applies for all
![]() $r\le R$
and
$r\le R$
and
![]() $0\le h\le h_c(R)$
and yields
$0\le h\le h_c(R)$
and yields
 $$ \begin{align} \phi_{\mathrm{Ann}(r,2r),h}^1[y\longleftrightarrow \partial\Lambda_{2r}]&\stackrel{<}{\scriptstyle{\frown}} \pi_1(\mathrm{dist}(y,\partial \mathrm{ Ann}(r,2r))) && \text{ for } y \in \mathrm{Ann}(r,2r) \text{ and }\nonumber\\ \phi_{\Lambda_r,h}^1[0\longleftrightarrow y,0\longleftrightarrow \partial\Lambda_r]&\stackrel{<}{\scriptstyle{\frown}} \pi_1(r)\pi_1(\|y\| \wedge \mathrm{ dist}(y,\partial \Lambda_r)) &&\text{ for } y \in \Lambda_r, \end{align} $$
$$ \begin{align} \phi_{\mathrm{Ann}(r,2r),h}^1[y\longleftrightarrow \partial\Lambda_{2r}]&\stackrel{<}{\scriptstyle{\frown}} \pi_1(\mathrm{dist}(y,\partial \mathrm{ Ann}(r,2r))) && \text{ for } y \in \mathrm{Ann}(r,2r) \text{ and }\nonumber\\ \phi_{\Lambda_r,h}^1[0\longleftrightarrow y,0\longleftrightarrow \partial\Lambda_r]&\stackrel{<}{\scriptstyle{\frown}} \pi_1(r)\pi_1(\|y\| \wedge \mathrm{ dist}(y,\partial \Lambda_r)) &&\text{ for } y \in \Lambda_r, \end{align} $$
where the constants in
![]() $\stackrel{<}{\scriptstyle{\frown}}$
depend on C.
$\stackrel{<}{\scriptstyle{\frown}}$
depend on C.
Proof of Lemma 8.5
Fix
![]() $C> 1$
and
$C> 1$
and
![]() $r\le R$
. All constants in the signs
$r\le R$
. All constants in the signs
![]() $\stackrel{<}{\scriptstyle{\frown}}$
below are allowed to depend on C but not on r or R. The differential formula [Reference GrimmettGri06, Theorem 3.12] reads
$\stackrel{<}{\scriptstyle{\frown}}$
below are allowed to depend on C but not on r or R. The differential formula [Reference GrimmettGri06, Theorem 3.12] reads
 $$ \begin{align} \tfrac {d}{dh}\tilde\pi_1(h,r) = \tfrac{1}{1-e^{-h}}\sum_{y\in\Lambda_r}\phi_{\Lambda_r,h}^1[0\leftrightarrow \partial\Lambda_r,\omega_{y\mathfrak g}=1] -\phi_{\Lambda_r,h}^1[0\leftrightarrow \partial\Lambda_r]\phi_{\Lambda_r,h}^1[\omega_{y\mathfrak g}=1]. \end{align} $$
$$ \begin{align} \tfrac {d}{dh}\tilde\pi_1(h,r) = \tfrac{1}{1-e^{-h}}\sum_{y\in\Lambda_r}\phi_{\Lambda_r,h}^1[0\leftrightarrow \partial\Lambda_r,\omega_{y\mathfrak g}=1] -\phi_{\Lambda_r,h}^1[0\leftrightarrow \partial\Lambda_r]\phi_{\Lambda_r,h}^1[\omega_{y\mathfrak g}=1]. \end{align} $$
Let us analyse the right-hand side of the above. Recall that
![]() $\mathsf {C}$
is the cluster of the origin for the connectivity in
$\mathsf {C}$
is the cluster of the origin for the connectivity in
![]() $\mathbb {Z}^2$
. First, we show that the vertices
$\mathbb {Z}^2$
. First, we show that the vertices
![]() $y \notin \mathsf {C}$
have a negative contribution. Fix some
$y \notin \mathsf {C}$
have a negative contribution. Fix some
![]() $y \in \Lambda _r$
. For a set
$y \in \Lambda _r$
. For a set
![]() $\mathcal {C}\subset \Lambda _r$
containing
$\mathcal {C}\subset \Lambda _r$
containing
![]() $0$
and
$0$
and
![]() $y \notin \mathcal {C}$
,
$y \notin \mathcal {C}$
,

The first inequality is due to equations (SMP) and (CBC) since
![]() $\phi _{\Lambda _r,h}^1[ \cdot \,|\,\mathsf {C} = \mathcal {C}]$
is a random-cluster measure with free boundary conditions on
$\phi _{\Lambda _r,h}^1[ \cdot \,|\,\mathsf {C} = \mathcal {C}]$
is a random-cluster measure with free boundary conditions on
![]() $(\Lambda _r \smallsetminus \mathcal {C} ) \cup \{\mathfrak g\}$
and is stochastically dominated by the restriction of
$(\Lambda _r \smallsetminus \mathcal {C} ) \cup \{\mathfrak g\}$
and is stochastically dominated by the restriction of
![]() $\phi _{\Lambda _r,h}^1$
to
$\phi _{\Lambda _r,h}^1$
to
![]() $(\Lambda _r \smallsetminus \mathcal {C} ) \cup \{\mathfrak g\}$
.
$(\Lambda _r \smallsetminus \mathcal {C} ) \cup \{\mathfrak g\}$
.
Summing the above over every
![]() $\mathcal {C}\subset \Lambda _r$
, we find that
$\mathcal {C}\subset \Lambda _r$
, we find that
Plugging this inequality in equation (8.12) gives
 $$ \begin{align*} \tfrac {d}{dh}\tilde\pi_{1}(h,r) \le \tfrac{1}{1-e^{-h}} \sum_{y\in\Lambda_r}\phi_{\Lambda_r,h}^1[0\leftrightarrow y,0\leftrightarrow\partial\Lambda_r,\omega_{y\mathfrak g}=1] \le \sum_{y\in\Lambda_r}\phi_{\Lambda_r,h}^1[0\leftrightarrow y,0\leftrightarrow\partial\Lambda_r], \end{align*} $$
$$ \begin{align*} \tfrac {d}{dh}\tilde\pi_{1}(h,r) \le \tfrac{1}{1-e^{-h}} \sum_{y\in\Lambda_r}\phi_{\Lambda_r,h}^1[0\leftrightarrow y,0\leftrightarrow\partial\Lambda_r,\omega_{y\mathfrak g}=1] \le \sum_{y\in\Lambda_r}\phi_{\Lambda_r,h}^1[0\leftrightarrow y,0\leftrightarrow\partial\Lambda_r], \end{align*} $$
where the second inequality comes from equation (SMP), which implies that
Now, assuming that
![]() $h \le h_c(R)$
, equation (8.11) applies, and we conclude that
$h \le h_c(R)$
, equation (8.11) applies, and we conclude that
 $$ \begin{align*} \tfrac {d}{dh}\tilde\pi_1(h,r) \stackrel{<}{\scriptstyle{\frown}} \sum_{y \in \Lambda_r} \pi_1(r)\pi_1(\|y\|\wedge \mathrm{ dist}(y,\partial\Lambda_r)) \stackrel{<}{\scriptstyle{\frown}} r\pi_1(r)\sum_{k = 1}^{r/2} \pi_1(k) \stackrel{<}{\scriptstyle{\frown}} r^2\pi_1(r)^2. \end{align*} $$
$$ \begin{align*} \tfrac {d}{dh}\tilde\pi_1(h,r) \stackrel{<}{\scriptstyle{\frown}} \sum_{y \in \Lambda_r} \pi_1(r)\pi_1(\|y\|\wedge \mathrm{ dist}(y,\partial\Lambda_r)) \stackrel{<}{\scriptstyle{\frown}} r\pi_1(r)\sum_{k = 1}^{r/2} \pi_1(k) \stackrel{<}{\scriptstyle{\frown}} r^2\pi_1(r)^2. \end{align*} $$
The second inequality uses the fact that there are at most order r vertices at distance k from
![]() $0$
or
$0$
or
![]() $\partial \Lambda _r$
; the third one is a standard consequence of the polynomial decay of
$\partial \Lambda _r$
; the third one is a standard consequence of the polynomial decay of
![]() $\pi _1$
in equation (2.2) and its quasi-multiplicativity in equation (2.3). Keeping in mind that
$\pi _1$
in equation (2.2) and its quasi-multiplicativity in equation (2.3). Keeping in mind that
![]() $\pi _1(r) \le \tilde \pi _1(h,r)$
, the above implies
$\pi _1(r) \le \tilde \pi _1(h,r)$
, the above implies
A similar computation, where
![]() $\mathsf {C}$
is replaced by the cluster of
$\mathsf {C}$
is replaced by the cluster of
![]() $\partial \Lambda _{2r}$
, implies that
$\partial \Lambda _{2r}$
, implies that
 $$ \begin{align} -\tfrac {d}{dh} \log \beta(h,r) \stackrel{<}{\scriptstyle{\frown}} \sum_{y\in\mathrm{Ann}(r,2r)}\phi_{\mathrm{ Ann}(r,2r),h}^1[y\leftrightarrow\partial\mathrm{Ann}(r,2r)] \stackrel{<}{\scriptstyle{\frown}} r^2\pi_1(r). \end{align} $$
$$ \begin{align} -\tfrac {d}{dh} \log \beta(h,r) \stackrel{<}{\scriptstyle{\frown}} \sum_{y\in\mathrm{Ann}(r,2r)}\phi_{\mathrm{ Ann}(r,2r),h}^1[y\leftrightarrow\partial\mathrm{Ann}(r,2r)] \stackrel{<}{\scriptstyle{\frown}} r^2\pi_1(r). \end{align} $$
We are now in a position to conclude. Let
![]() $c_0$
be a constant larger than the constants involved in the inequalities
$c_0$
be a constant larger than the constants involved in the inequalities
![]() $\stackrel{<}{\scriptstyle{\frown}}$
in equations (8.13) and (8.14). Then for
$\stackrel{<}{\scriptstyle{\frown}}$
in equations (8.13) and (8.14). Then for
![]() $\varepsilon>0$
, integrate these two inequalities for h between
$\varepsilon>0$
, integrate these two inequalities for h between
![]() $0$
and
$0$
and
![]() $h' \le \min \{h_c(R),\varepsilon /(R^2\pi _1(R))\}$
. We find
$h' \le \min \{h_c(R),\varepsilon /(R^2\pi _1(R))\}$
. We find
 $$ \begin{align*} \left.\begin{array}{r} \log\tilde\pi_1(h',r) - \log\tilde\pi_1(r)\\ \log \beta(r) - \log \beta(h',r) \end{array}\right\} \le c_0h' r^2\pi_1(r) \le \varepsilon c_0. \end{align*} $$
$$ \begin{align*} \left.\begin{array}{r} \log\tilde\pi_1(h',r) - \log\tilde\pi_1(r)\\ \log \beta(r) - \log \beta(h',r) \end{array}\right\} \le c_0h' r^2\pi_1(r) \le \varepsilon c_0. \end{align*} $$
Now, for
![]() $\varepsilon < (\log C) /c_0$
, the above shows that
$\varepsilon < (\log C) /c_0$
, the above shows that
![]() $h' < h_c(R)$
, which implies equation (8.10).
$h' < h_c(R)$
, which implies equation (8.10).
Proof of Theorem 1.10
Fix
![]() $h>0$
. Again,
$h>0$
. Again,
![]() $\mathsf C$
is the cluster of the origin when considering connections in
$\mathsf C$
is the cluster of the origin when considering connections in
![]() $\mathbb Z^2$
only. We start with the lower bound. We have
$\mathbb Z^2$
only. We start with the lower bound. We have
where the fourth inequality is due to equation (1.23), the third to monotonicity in h equation (
h-MON) and the second to the fact that conditioned on
![]() $|\mathsf {C}| \geq 1/h$
, there is a positive probability for
$|\mathsf {C}| \geq 1/h$
, there is a positive probability for
![]() $0$
to be connected to
$0$
to be connected to
![]() $\mathfrak g$
. This last property can be easily deduced from the finite energy property, which states that every edge connecting
$\mathfrak g$
. This last property can be easily deduced from the finite energy property, which states that every edge connecting
![]() $\mathbb {Z}$
to
$\mathbb {Z}$
to
![]() $\mathfrak g$
has a probability larger than
$\mathfrak g$
has a probability larger than
![]() $(1-e^{-h})/(1+(q-1)e^{-h})$
and smaller than h of being open, regardless of the states of other edges.
$(1-e^{-h})/(1+(q-1)e^{-h})$
and smaller than h of being open, regardless of the states of other edges.
Let us now derive the upper bound. Let
![]() $\varepsilon $
be the quantity given by Lemma 8.5 for some fixed
$\varepsilon $
be the quantity given by Lemma 8.5 for some fixed
![]() $C> 1$
. Choose R to be the largest integer such that
$C> 1$
. Choose R to be the largest integer such that
![]() $h R^2\pi _1(R)\leq \varepsilon $
. Notice that this implies that
$h R^2\pi _1(R)\leq \varepsilon $
. Notice that this implies that
![]() $h\le h_c(R)$
. We deduce that
$h\le h_c(R)$
. We deduce that
 $$ \begin{align*} \phi_{h}[0 \longleftrightarrow\mathfrak g] &\le \pi_1(h,R)+\phi_h[0\longleftrightarrow\mathfrak g, \, 0\kern6pt\not\kern-6pt\longleftrightarrow \partial\Lambda_R]\\ &\le \pi_1(h,R)+\sum_{y\in \Lambda_R}\phi_h[0\longleftrightarrow y,\,\omega_{y\mathfrak g}=1]\\ &\le \pi_1(h,R)+ h \sum_{y\in \Lambda_R}\phi_h[0\longleftrightarrow y], \end{align*} $$
$$ \begin{align*} \phi_{h}[0 \longleftrightarrow\mathfrak g] &\le \pi_1(h,R)+\phi_h[0\longleftrightarrow\mathfrak g, \, 0\kern6pt\not\kern-6pt\longleftrightarrow \partial\Lambda_R]\\ &\le \pi_1(h,R)+\sum_{y\in \Lambda_R}\phi_h[0\longleftrightarrow y,\,\omega_{y\mathfrak g}=1]\\ &\le \pi_1(h,R)+ h \sum_{y\in \Lambda_R}\phi_h[0\longleftrightarrow y], \end{align*} $$
where the last inequality uses the finite energy property. Now,
![]() $h\le h_c(R)$
implies that
$h\le h_c(R)$
implies that
![]() $ \pi _1(h,R)\stackrel{<}{\scriptstyle{\frown}} \pi _1(R)$
and that similarly to Lemma 8.1,
$ \pi _1(h,R)\stackrel{<}{\scriptstyle{\frown}} \pi _1(R)$
and that similarly to Lemma 8.1,
![]() $\phi _h[0\longleftrightarrow y]\stackrel{<}{\scriptstyle{\frown}} \pi _1(|y|)^2$
. We deduce from the above that
$\phi _h[0\longleftrightarrow y]\stackrel{<}{\scriptstyle{\frown}} \pi _1(|y|)^2$
. We deduce from the above that
 $$ \begin{align*} \phi_{h}[0 \longleftrightarrow\mathfrak g] &\stackrel{<}{\scriptstyle{\frown}} \pi_1(R)+ h \sum_{y\in \Lambda_R} \pi_1(|y|)^2 \stackrel{<}{\scriptstyle{\frown}}\pi_1(R)+ hR^2\pi_1(R)^2 \stackrel{<}{\scriptstyle{\frown}}\pi_1(R), \end{align*} $$
$$ \begin{align*} \phi_{h}[0 \longleftrightarrow\mathfrak g] &\stackrel{<}{\scriptstyle{\frown}} \pi_1(R)+ h \sum_{y\in \Lambda_R} \pi_1(|y|)^2 \stackrel{<}{\scriptstyle{\frown}}\pi_1(R)+ hR^2\pi_1(R)^2 \stackrel{<}{\scriptstyle{\frown}}\pi_1(R), \end{align*} $$
where in the second inequality, we used a computation similar to equation (1.26). Recall the definition in equation (1.21) of
![]() $\varphi $
. Due to the quasi-multiplicativity of
$\varphi $
. Due to the quasi-multiplicativity of
![]() $\pi _1$
in equation (2.3), we have that
$\pi _1$
in equation (2.3), we have that
![]() $R=\varphi (\varepsilon /h) \stackrel{>}{\scriptstyle{\frown}} \varphi (1/h)$
. Applying equation (2.3) again, we find
$R=\varphi (\varepsilon /h) \stackrel{>}{\scriptstyle{\frown}} \varphi (1/h)$
. Applying equation (2.3) again, we find
which concludes the proof.
Acknowledgements
We thank Matthias Kloeckner, Christophe Garban, Alexander Glazman and the two anonymous referees for helpful comments on the manuscript, Matan Harel for useful discussions at an early stage of the project and Jeremy Dubout and Robin Pierre Kaufmann, who worked on parts of Sections 2.4 and 3 during their respective master’s theses with the two authors. Finally, we are extremely thankful to Vincent Tassion, whose discussions on this project have been very inspiring and absolutely crucial.
Conflict of Interest
The authors have no conflict of interest to declare.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding statement
The first author is supported by the ERC CriBLaM, the NCCR SwissMAP, the Simons Collaboration on localisation of waves, the Swiss NSF and an IDEX Chair from Paris-Saclay. The second author is supported by the NCCR SwissMAP and the Swiss NSF.