Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-16T15:52:44.269Z Has data issue: false hasContentIssue false
  • English
  • Français

Spikes and localised patterns for a novel Schnakenberg model in the semi-strong interaction regime

Part of: Parabolic equations and systems Physiological, cellular and medical topics Asymptotic theory Partial differential equations

Published online by Cambridge University Press:  25 January 2021

FAHAD AL SAADI ,
ALAN CHAMPNEYS Open the ORCID record for ALAN CHAMPNEYS [Opens in a new window] ,
CHUNYI GAI  and
THEODORE KOLOKOLNIKOV
FAHAD AL SAADI
Affiliation:
Department of Engineering Mathematics, University of Bristol, BristolBS8 1UB, UK, emails: a.r.champneys@bristol.ac.uk; fa17741@bristol.ac.uk Department of Systems Engineering, Military Technological College, Muscat, Oman
ALAN CHAMPNEYS
Affiliation:
Department of Engineering Mathematics, University of Bristol, BristolBS8 1UB, UK, emails: a.r.champneys@bristol.ac.uk; fa17741@bristol.ac.uk
CHUNYI GAI
Affiliation:
Department of Mathematics and Statistics, Dalhousie University, Halifax, Nova ScotiaB3H 4R2, Canada, emails: Chunyi.Gai@dal.ca; tkolokol@gmail.com
THEODORE KOLOKOLNIKOV
Affiliation:
Department of Mathematics and Statistics, Dalhousie University, Halifax, Nova ScotiaB3H 4R2, Canada, emails: Chunyi.Gai@dal.ca; tkolokol@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

An analysis is undertaken of the formation and stability of localised patterns in a 1D Schanckenberg model, with source terms in both the activator and inhibitor fields. The aim is to illustrate the connection between semi-strong asymptotic analysis and the theory of localised pattern formation within a pinning region created by a subcritical Turing bifurcation. A two-parameter bifurcation diagram of homogeneous, periodic and localised patterns is obtained numerically. A natural asymptotic scaling for semi-strong interaction theory is found where an activator source term 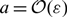\[a = O(\varepsilon )\] and the inhibitor source 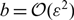\[b = O({\varepsilon ^2})\], with ε2 being the diffusion ratio. The theory predicts a fold of spike solutions leading to onset of localised patterns upon increase of b from zero. Non-local eigenvalue arguments show that both branches emanating from the fold are unstable, with the higher intensity branch becoming stable through a Hopf bifurcation as b increases beyond the 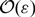\[O(\varepsilon )\] regime. All analytical results are found to agree with numerics. In particular, the asymptotic expression for the fold is found to be accurate beyond its region of validity, and its extension into the pinning region is found to form the low b boundary of the so-called homoclinic snaking region. Further numerical results point to both sub and supercritical Hopf bifurcation and novel spikeinsertion dynamics.

Keywords

reaction-diffusion systemspattern formationspikessnaking

MSC classification

Primary: 35B32: Bifurcation
Secondary: 35K57: Reaction-diffusion equations 92C15: Developmental biology, pattern formation 34E13: Multiple scale methods
Type
Papers
Information
European Journal of Applied Mathematics , Volume 33 , Issue 1 , February 2022 , pp. 133 - 152
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Al Saadi, F., Champneys, A. & Verschueren, N. (2020) Localised patterns and semi-strong interaction, a unifying framework for reaction-diffusion systems. Preprint. University of Bristol.Google Scholar
Beck, M., Knobloch, J., Lloyd, D., Sandstede, B. & Wagenknecht, T. (2009) Snakes, ladders, and isolas of localized patterns. SIAM J. Math. Anal. 41, 936–972.CrossRefGoogle Scholar
Benson, D., Sherratt, J. & Maini, P. (1993) Diffusion driven instability in inhomogeneous domain. Bull. Math. Biol. 55(2), 365–384.CrossRefGoogle Scholar
Breña–Medina, V. & Champneys, A. (2014) Subcritical Turing bifurcation and the morphogenesis of localized patterns. Phys. Rev. E 90, 032923.CrossRefGoogle ScholarPubMed
Burke, J. & Knobloch, E. (2006) Snakes and ladders: localized states in the Swift–Hohenberg equation. Physics Lett. A 360, 681–688.CrossRefGoogle Scholar
Doedel, E., Oldeman, B. et al. (2020) Auto-07p: continuation and bifurcation software for ordinary differential equations. https://github.com/auto-07p.Google Scholar
Doelman, A., Kaper, T. J. & Zegeling, P. A. (1997) Pattern formation in the one-dimensional gray-scott model. Nonlinearity 10(2), 523.CrossRefGoogle Scholar
Doelman, A. & Veerman, F. (2015) An explicit theory for pulses in two component, singularly perturbed, reaction–diffusion equations. J. Dyn. Differ. Equ. 27(3), 555–595.CrossRefGoogle Scholar
Gierer, A. & Meinhardt, H. (1972) A theory of biological pattern formation. Kybernetik 12(1), 30–39.CrossRefGoogle ScholarPubMed
Haragus, M. & Iooss, G. (2011) Local Bifurcations, Center Manifolds, and Normal Forms in Infinite-Dimensional Dynamical Systems, Springer, New York.CrossRefGoogle Scholar
Iron, D., Ward, M. & Wei, J. (2001) The stability of spike solutions to the one-dimensional gierer-meinhardt model. Physica D Nonlinear Phenomena 150(1), 25–62.CrossRefGoogle Scholar
Iron, D., Wei, J. & Winter, M. (2004) Stability analysis of turing patterns generated by the schnakenberg model. J. Math. Biol. 49(4), 358–390.CrossRefGoogle ScholarPubMed
Knobloch, E. (2015) Spatial localization in dissipative systems. Ann. Rev. Condens. Matter Phys. 6, 325–359.CrossRefGoogle Scholar
Knobloch, E. (2016) Localized structures and front propagation in systems with a conservation law. IMA J. Appl. Math. 81, 457–487.CrossRefGoogle Scholar
Kolokolnikov, T., Sun, W. & Ward, M. (2006) The stability of a stripe for the Gierer-Meinhardt model and the effect of saturation. SIAM J. Appl. Dyn. Sys. 5, 313–363.CrossRefGoogle Scholar
Kolokolnikov, T., Ward, M. J. & Wei, J. (2005) The existence and stability of spike equilibria in the one-dimensional gray–scott model: the low feed-rate regime. Stud. Appl. Math. 115(1), 21–71.CrossRefGoogle Scholar
Kolokolnikov, T. & Wei, J. (2018) Pattern formation in a reaction-diffusion system with space-dependent feed rate. SIAM Rev. 60(3), 626–645.CrossRefGoogle Scholar
Meron, E. (2015) Nonlinear Physics of Ecosystems, 3rd ed., CRC Press, USA.CrossRefGoogle Scholar
Muratov, C. & Osipov, V. V. (2000) Static spike autosolitons in the gray-scott model. J. Phys. A Math. General 33(48), 8893.CrossRefGoogle Scholar
Muratov, C. B. & Osipov, V. (2002) Stability of the static spike autosolitons in the gray–scott model. SIAM J. Appl. Math. 62(5), 1463–1487.CrossRefGoogle Scholar
Murray, J. (2002) Mathematical Biology II: Spatial Models and Biomedical Applications, 3rd ed., Springer-Verlag, New York.CrossRefGoogle Scholar
Pomeau, Y. (1986) Front motion, metastability and subcritical bifurcations in hydrodynamics. Physica D Nonlinear Phenomena 23, 3–11.CrossRefGoogle Scholar
Rademacher, J. (2013) First and second order semistrong interaction in reaction-diffusion systems. SIAM J. Appl. Dyn. Syst. 12, 175–203.CrossRefGoogle Scholar
Schnakenberg, J. (1979) Simple chemical reaction system with limit cycle behavior. Theor. Biol. 81(12), 389–400.CrossRefGoogle Scholar
Shaw, L. & Murry, J. (1990) Analysis of a model for complex skin pattern. SIAM J. Appl. Math. 50(2), 628–648.CrossRefGoogle Scholar
Siteur, K., Siero, E., Eppinga, M., Rademacher, J., Doelman, A. & Rietkerk, M. (2014) Beyond Turing: the response of patterned ecosystems to environmental change. Ecol. Complexity 20, 81–96.CrossRefGoogle Scholar
Swift, J. & Hohenberg, P. C. (1977) Hydrodynamic fluctuations at the convective instability. Phys. Rev. A 15, 319–328.CrossRefGoogle Scholar
Turing, A. M. (1952) The chemical basis of morphogenesis. Philos. Trans. R. Soc. London B Biol. Sci. 237, 37–72.Google Scholar
Verschueren, N. & Champneys, A. (2020) Dissecting the snake: from localized to patterns in isolated spikes in pattern formation systems. https://arxiv.org/abs/1809.07847.Google Scholar
Ward, M. & Wei, J. (2002) The existence and stability of asymmetric spike patterns for the Schnakenberg model. Stud. Appl. Math. 109, 229–264.CrossRefGoogle Scholar
Ward, M. & Wei, J. (2003) Hopf bifurcations and oscillatory instabilities of spike solutions for the one-dimensional gierer-meinhardt model. J. Nonlinear Sci. 13(2), 209–264.CrossRefGoogle Scholar
Wei, J. (1999) On single interior spike solutions of the gierer–meinhardt system: uniqueness and spectrum estimates. Eur. J. Appl. Math. 10(4), 353–378.CrossRefGoogle Scholar
Woods, P. & Champneys, A. (1999) Heteroclinic tangles and homoclinic snaking in the unfolding of a degenerate reversible Hamiltonian–Hopf bifurcation. Physica D Nonlinear Phenomena 129, 147–170.CrossRefGoogle Scholar
Zelnik, Y. R., Uecker, H., Feudel, U. & Meron, E. (2017) Desertification by front propagation? J. Theor. Biol. 418, 27–35.CrossRefGoogle ScholarPubMed