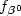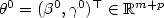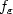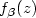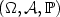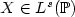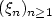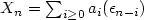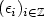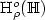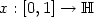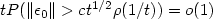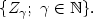Research Article
Asymptotic unbiased density estimators
-
- Published online by Cambridge University Press:
- 21 February 2009, pp. 1-14
-
- Article
- Export citation
Digital search trees and chaos game representation*
-
- Published online by Cambridge University Press:
- 21 February 2009, pp. 15-37
-
- Article
- Export citation
Number of hidden states and memory: a joint order estimation problem for Markov chains with Markov regime
-
- Published online by Cambridge University Press:
- 21 February 2009, pp. 38-50
-
- Article
- Export citation
Tail estimates for homogenization theorems in random media
-
- Published online by Cambridge University Press:
- 21 February 2009, pp. 51-69
-
- Article
- Export citation
Histogram selection in non Gaussian regression
-
- Published online by Cambridge University Press:
- 26 March 2009, pp. 70-86
-
- Article
- Export citation
Estimation of the hazard function in a semiparametric model with covariate measurement error
-
- Published online by Cambridge University Press:
- 26 March 2009, pp. 87-114
-
- Article
- Export citation
Linear prediction of long-range dependent time series
-
- Published online by Cambridge University Press:
- 26 March 2009, pp. 115-134
-
- Article
- Export citation
Plug-in estimators for higher-order transition densities in autoregression
-
- Published online by Cambridge University Press:
- 26 March 2009, pp. 135-151
-
- Article
- Export citation
Penalisations of multidimensional Brownian motion, VI
-
- Published online by Cambridge University Press:
- 11 June 2009, pp. 152-180
-
- Article
- Export citation
A comparison of automatic histogram constructions
-
- Published online by Cambridge University Press:
- 11 June 2009, pp. 181-196
-
- Article
- Export citation
Filtering the Wright-Fisher diffusion
-
- Published online by Cambridge University Press:
- 11 June 2009, pp. 197-217
-
- Article
- Export citation
Universal Ls-rate-optimality of Lr-optimal quantizers by dilatation and contraction
-
- Published online by Cambridge University Press:
- 12 June 2009, pp. 218-246
-
- Article
- Export citation
Enhanced Gaussian processes and applications
-
- Published online by Cambridge University Press:
- 04 July 2009, pp. 247-260
-
- Article
- Export citation
Hölderian invariance principle for Hilbertian linear processes
-
- Published online by Cambridge University Press:
- 04 July 2009, pp. 261-275
-
- Article
- Export citation
Estimation and tests in finite mixture models of nonparametric densities
-
- Published online by Cambridge University Press:
- 04 July 2009, pp. 276-282
-
- Article
- Export citation
Power of A Class of Goodness-of-Fit Tests I
-
- Published online by Cambridge University Press:
- 21 July 2009, pp. 283-300
-
- Article
- Export citation
The likelihood ratio test for general mixture models with or without structural parameter
-
- Published online by Cambridge University Press:
- 21 July 2009, pp. 301-327
-
- Article
- Export citation
On the number of word occurrences in a semi-Markov sequence of letters
-
- Published online by Cambridge University Press:
- 21 July 2009, pp. 328-342
-
- Article
- Export citation
Capacity bounds for the CDMA system and a neural network: a moderate deviations approach
-
- Published online by Cambridge University Press:
- 21 July 2009, pp. 343-362
-
- Article
- Export citation
Model selection for quantum homodyne tomography
-
- Published online by Cambridge University Press:
- 22 September 2009, pp. 363-399
-
- Article
- Export citation