Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-05-12T21:54:45.887Z Has data issue: false hasContentIssue false
  • English
  • Français

Tail estimates for homogenization theorems in random media

Published online by Cambridge University Press:  21 February 2009

Daniel Boivin
Daniel Boivin*
Affiliation:
Laboratoire de Mathématiques UMR 6205, Université de Bretagne Occidentale, 6, avenue Le Gorgeu, CS 93837, 29238 Brest Cedex 3, France; boivin@univ-brest.fr
Get access

Abstract

Consider a random environment in ${\mathbb Z}^d$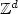 given by i.i.d. conductances. In this work, we obtain tail estimates for the fluctuations about the mean for the following characteristics of the environment: the effective conductance between opposite faces of a cube, the diffusion matrices of periodized environments and the spectral gap of the random walk in a finite cube.

Keywords

Periodic approximationrandom environmentsfluctuationseffective diffusion matrixeffective conductancenon-uniform ellipticity
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 13 , July 2009 , pp. 51 - 69
Copyright
© EDP Sciences, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

I. Benjamini and R. Rossignol, Submean variance bound for effective resistance on random electric networks. arXiv:math/0610393v4 [math.PR]
Boivin, D. and Depauw, J., Spectral homogenization of reversible random walks on ${\mathbb Z}^d$ in a random environment. Stochastic Process. Appl. 104 (2003) 29–56. CrossRef
Boivin, D. and Derriennic, Y., The ergodic theorem for additive cocycles of ${\mathbb Z}\sp d$ or ${\mathbb R}\sp d$ . Ergodic Theory Dynam. Syst. 11 (1991) 19–39. CrossRef
E. Bolthausen and A.S. Sznitman, Ten lectures on random media. DMV Seminar, Band 32, Birkhäuser (2002).
Bourgeat, A. and Piatnitski, A., Approximations of effective coefficients in stochastic homogenization. Ann. Inst. H. Poincaré Probab. Statist. 40 (2004) 153–165. CrossRef
Caputo, P. and Ioffe, D., Finite volume approximation of the effective diffusion matrix: the case of independent bond disorder. Ann. Inst. H. Poincaré Probab. Statist. 39 (2003) 505–525. CrossRef
F.R.K. Chung, Spectral graph theory. CBMS Regional Conference Series in Mathematics, 92. American Mathematical Society (1997).
E.B. Davies, Heat kernels and spectral theory. Cambridge Tracts in Mathematics, 92. Cambridge University Press (1989).
Delmotte, T., Inéalité de Harnack elliptique sur les graphes. Colloq. Math. 72 (1997) 19–37.
R. Durrett, Probability: Theory and Examples. Wadsworth & Brooks/Cole Statistics/Probability Series (1991).
Fontes, L.R.G. and Mathieu, P., On symmetric random walks with random conductances on ${\mathbb Z}^d$ . Probab. Theory Related Fields 134 (2006) 565–602. CrossRef
T. Funaki and H. Spohn, Motion by mean curvature from the Ginzburg-Landau $\nabla\phi$ interface model. Commun. Math. Phys. 185 (1997) 1–36.
G. Grimmett, Percolation. 2nd ed. Springer (1999).
E. Hebey, Nonlinear analysis on manifolds: Sobolev spaces and inequalities. Courant Lecture Notes Mathematics 5. American Mathematical Society (2000).
B.D. Hughes, Random walks and random environments. Vol. 2. Random environments. Oxford University Press (1996).
V.V. Jikov, S.M. Kozlov and O.A. Olejnik, Homogenization of differential operators and integral functionals. Springer-Verlag (1994).
Kesavan, S., Homogenization of elliptic eigenvalue problems I. Appl. Math. Optimization 5 (1979) 153–167. CrossRef
Kesten, H., On the speed of convergence in first-passage percolation. Ann. Appl. Probab. 3 (1993) 296–338. CrossRef
Kipnis, C. and Varadhan, S.R.S., Central limit theorem for additive functionals of reversible Markov processes and applications to simple exclusions. Comm. Math. Phys. 10 (1986) 1–19. CrossRef
Kozlov, S.M., The method of averaging and walks in inhomogeneous environments. Russ. Math. Surv. 40 (1985) 73–145. CrossRef
Kuennemann, R., The diffusion limit for reversible jump processes on $Z\sp m$ with ergodic random bond conductivities. Commun. Math. Phys. 90 (1983) 27–68. CrossRef
Owhadi, H., Approximation of the effective conductivity of ergodic media by periodization. Probab. Theory Related Fields 125 (2003) 225-258. CrossRef
Pardoux, E. and Veretennikov, A.Yu., On the Poisson equation and diffusion approximation. I. Ann. Probab. 29 (2001) 1061–1085.
Y. Peres, Probability on trees: An introductory climb. Lectures on probability theory and statistics. École d'été de Probabilités de Saint-Flour XXVII-1997, Springer. Lect. Notes Math. 1717 (1999) 193–280 .
L. Saloff-Coste, Lectures on finite Markov chains. Lectures on probability theory and statistics. École d'été de probabilités de Saint-Flour XXVI–1996, Springer. Lect. Notes Math. 1665 (1997) 301–413. CrossRef
Sidoravicius, V. and Sznitman, A.-S., Quenched invariance principles for walks on clusters of percolation or among random conductances. Probab. Theory Related Fields 129 (2004) 219–244. CrossRef
F. Spitzer, Principles of random walk. The University Series in Higher Mathematics. D. Van Nostrand Company (1964).
Wehr, J., A lower bound on the variance of conductance in random resistor networks. J. Statist. Phys. 86 (1997) 1359–1365. CrossRef
Yurinsky, V.V., Averaging of symmetric diffusion in random medium. Sib. Math. J. 2 (1986) 603–613.