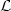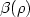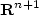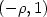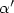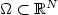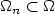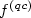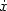Research Article
Aubry sets and the differentiability of the minimal average action in codimension one
-
- Published online by Cambridge University Press:
- 23 January 2009, pp. 1-48
-
- Article
- Export citation
Asymptotic behavior of nonlinear systems in varying domains with boundary conditions on varying sets
-
- Published online by Cambridge University Press:
- 23 January 2009, pp. 49-67
-
- Article
- Export citation
On the lower semicontinuous quasiconvex envelope for unbounded integrands (I)
-
- Published online by Cambridge University Press:
- 23 January 2009, pp. 68-101
-
- Article
- Export citation
Interior sphere property for level sets of the value function of an exit time problem
-
- Published online by Cambridge University Press:
- 23 January 2009, pp. 102-116
-
- Article
- Export citation
Nash equilibrium for a multiobjective control problem related to wastewater management
-
- Published online by Cambridge University Press:
- 23 January 2009, pp. 117-138
-
- Article
- Export citation
A variational approach to implicit ODEs and differential inclusions
-
- Published online by Cambridge University Press:
- 23 January 2009, pp. 139-148
-
- Article
- Export citation
Frictional contact of an anisotropic piezoelectric plate
-
- Published online by Cambridge University Press:
- 23 January 2009, pp. 149-172
-
- Article
- Export citation
Smooth optimal synthesis for infinite horizon variational problems
-
- Published online by Cambridge University Press:
- 23 January 2009, pp. 173-188
-
- Article
- Export citation
Control of constrained nonlinear uncertain discrete-time systems via robust controllable sets: a modal interval analysis approach
-
- Published online by Cambridge University Press:
- 23 January 2009, pp. 189-204
-
- Article
- Export citation
Direct design of robustly asymptotically stabilizing hybrid feedback
-
- Published online by Cambridge University Press:
- 23 January 2009, pp. 205-213
-
- Article
- Export citation
Minimizing movements for dislocation dynamics with a mean curvature term
-
- Published online by Cambridge University Press:
- 23 January 2009, pp. 214-244
-
- Article
- Export citation