Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hamdache, Kamel
and
Tilioua, Mouhcine
2004.
Interlayer Exchange Coupling for Ferromagnets through Spacers.
SIAM Journal on Applied Mathematics,
Vol. 64,
Issue. 3,
p.
1077.
ZORGATI, HAMDI
2005.
MODELING THIN CURVED FERROMAGNETIC FILMS.
Analysis and Applications,
Vol. 03,
Issue. 04,
p.
373.
Baía, Margarida
and
Zappale, Elvira
2007.
A note on the 3D–2D dimensional reduction of a micromagnetic thin film with nonhomogeneous profile.
Applicable Analysis,
Vol. 86,
Issue. 5,
p.
555.
Babadjian, Jean-François
and
Millot, Vincent
2009.
Homogenization of variational problems in manifold valued BV-spaces.
Calculus of Variations and Partial Differential Equations,
Vol. 36,
Issue. 1,
p.
7.
Mucci, Domenico
2009.
Relaxation of isotropic functionals with linear growth defined on manifold constrained Sobolev mappings.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 15,
Issue. 2,
p.
295.
Babadjian, Jean-François
and
Millot, Vincent
2010.
Homogenization of variational problems in manifold valued Sobolev spaces.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 16,
Issue. 4,
p.
833.
Gaudiello, Antonio
and
Hadiji, Rejeb
2010.
Junction of ferromagnetic thin films.
Calculus of Variations and Partial Differential Equations,
Vol. 39,
Issue. 3-4,
p.
593.
Hadda, Mohammed
Tilioua, Mouhcine
and
Lenci, Stefano
2012.
Thin Film Limits in Magnetoelastic Interactions.
Mathematical Problems in Engineering,
Vol. 2012,
Issue. 1,
De Maio, Umberto
Faella, Luisa
and
Soueid, Salwa
2014.
Quasy-stationary ferromagnetic thin films in degenerated cases.
Ricerche di Matematica,
Vol. 63,
Issue. S1,
p.
225.
Gaudiello, Antonio
and
Hadiji, Rejeb
2014.
Ferromagnetic thin multi-structures.
Journal of Differential Equations,
Vol. 257,
Issue. 5,
p.
1591.
Gaudiello, Antonio
and
Hamdache, Kamel
2015.
A reduced model for the polarization in a ferroelectric thin wire.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 22,
Issue. 6,
p.
1883.
Hadiji, Rejeb
and
Soueid, Salwa
2016.
Asymptotic analysis for two joined thin slanting ferromagnetic films.
Journal of Mathematical Analysis and Applications,
Vol. 434,
Issue. 2,
p.
1011.
Carbone, Luciano
Chacouche, Khaled
and
Gaudiello, Antonio
2018.
Fin junction of ferroelectric thin films.
Advances in Calculus of Variations,
Vol. 11,
Issue. 4,
p.
341.
Eleuteri, Michela
Prinari, Francesca
and
Zappale, Elvira
2024.
Asymptotic analysis of thin structures with point-dependent energy growth.
Mathematical Models and Methods in Applied Sciences,
Vol. 34,
Issue. 08,
p.
1401.
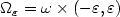 , $\omega\subset\mathbb R^2$
, $\omega\subset\mathbb R^2$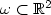 , whose
energy is given by
$$
{\cal E}_{\varepsilon}({\overline{m}})=\frac{1}{\varepsilon}
\int_{\Omega_{\varepsilon}}\left(W({\overline{m}},\nabla{\overline{m}})
+{\frac{1}{2}}\nabla {\overline{u}}\cdot {\overline{m}}\right)\,{\rm d}x
$$
, whose
energy is given by
$$
{\cal E}_{\varepsilon}({\overline{m}})=\frac{1}{\varepsilon}
\int_{\Omega_{\varepsilon}}\left(W({\overline{m}},\nabla{\overline{m}})
+{\frac{1}{2}}\nabla {\overline{u}}\cdot {\overline{m}}\right)\,{\rm d}x
$$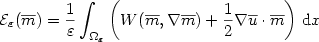 subject to
$$
\hbox{div}(-\nabla {\overline{u}}+{\overline{m}}\chi_{\Omega_\varepsilon})=0
\quad\hbox{ on }\mathbb R^3,
$$
subject to
$$
\hbox{div}(-\nabla {\overline{u}}+{\overline{m}}\chi_{\Omega_\varepsilon})=0
\quad\hbox{ on }\mathbb R^3,
$$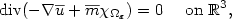 and to the constraint
$$
|\overline{m}|=1 \hbox{ on }\Omega_\varepsilon,
$$
and to the constraint
$$
|\overline{m}|=1 \hbox{ on }\Omega_\varepsilon,
$$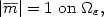 where W is any continuous function satisfying p-growth assumptions
with p> 1.
Partial results are also obtained in the case p=1, under
an additional assumption on W.
where W is any continuous function satisfying p-growth assumptions
with p> 1.
Partial results are also obtained in the case p=1, under
an additional assumption on W.




