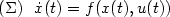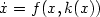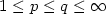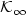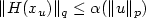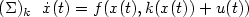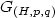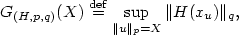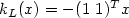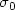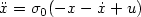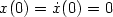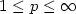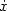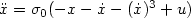Research Article
On the quasiconvex exposed points
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 1-19
-
- Article
- Export citation
Approximate Controllability of linear parabolic equations in perforated domains
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 21-38
-
- Article
- Export citation
Remarks on exact controllability for the Navier-Stokes equations
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 39-72
-
- Article
- Export citation
Relaxation of optimal control problems in Lp-SPACES
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 73-95
-
- Article
- Export citation
Contrôle par les coefficients dans le modèle elrod-adams
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 97-118
-
- Article
- Export citation
On the Geometry of Goursat Structures
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 119-181
-
- Article
- Export citation
Exact Boundary Controllability of a Hybrid System of elasticity by the HUM Method
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 183-199
-
- Article
- Export citation
On a model of rotating superfluids
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 201-238
-
- Article
- Export citation
Coplanar control of a satellite around the Earth
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 239-258
-
- Article
- Export citation
Simultaneous controllability in sharp time for two elastic strings
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 259-273
-
- Article
- Export citation
A Singular Perturbation Problem in Exact Controllability of the Maxwell System
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 275-289
-
- Article
- Export citation
On the Lp-stabilization of the double integrator subject to input saturation
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 291-331
-
- Article
- Export citation
Controllability of a slowly rotating Timoshenko beam
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 333-360
-
- Article
- Export citation
Stabilization of second order evolution equations by a class of unbounded feedbacks
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 361-386
-
- Article
- Export citation
Asymptotics of accessibility sets along an abnormal trajectory
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 387-414
-
- Article
- Export citation
Viscosity Solutions of the Bellman Equation for Exit Time Optimal Control Problems with Non-Lipschitz Dynamics
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 415-441
-
- Article
- Export citation
Comparison of active control techniques over a dihedral plane
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 443-466
-
- Article
- Export citation
Control problems for convection-diffusion equations with control localized on manifolds
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 467-488
-
- Article
- Export citation
3D-2D Asymptotic Analysis for Micromagnetic Thin Films
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 489-498
-
- Article
- Export citation
Local small time controllability and attainability of a set for nonlinear control system
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 499-516
-
- Article
- Export citation