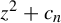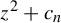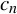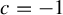1. Introduction
1.1. Background
In this paper, we discuss the concrete and interesting random holomorphic dynamical systems with parameters
![]() $c \in {\mathbb {C}}$
and
$c \in {\mathbb {C}}$
and
![]() $r \geq 0$
. More precisely, we will denote
$r \geq 0$
. More precisely, we will denote
![]() $f_{c}(z) = z^{2} + c$
throughout this paper and we consider random iterations of the form
$f_{c}(z) = z^{2} + c$
throughout this paper and we consider random iterations of the form
![]() ${f_{{c_{n}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}$
, where
${f_{{c_{n}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}$
, where
![]() $c_{n} (n=1, 2, \ldots )$
are complex-valued independent random variables that follow the uniform distribution on the closed disk
$c_{n} (n=1, 2, \ldots )$
are complex-valued independent random variables that follow the uniform distribution on the closed disk
![]() ${\bar {B}({c}, {r})} =\{c' \in \mathbb {C} \colon |c' - c| \leq r \}$
on the c-plane. The reader is referred to [Reference Sumi and Watanabe31, Remark 4.10]. See Setting 4.1 for the rigorous setting.
${\bar {B}({c}, {r})} =\{c' \in \mathbb {C} \colon |c' - c| \leq r \}$
on the c-plane. The reader is referred to [Reference Sumi and Watanabe31, Remark 4.10]. See Setting 4.1 for the rigorous setting.
The aim of this paper is twofold. First, we study the (dis)connectedness of random Julia sets and relate it to the bifurcation, and second, we investigate the bifurcation of our proposed random iterations and give quantitative estimates of bifurcation parameters.
In recent decades, there has been a rapid growth of studies on random dynamical systems. In deterministic autonomous dynamical systems, time-evolution rules are independent of time and homogeneous; however, they are dependent in random dynamical systems. Motivated by scientific demands, great efforts have been devoted to establishing fundamental results. For this field, refer to the textbook by Arnold [Reference Arnold1].
Fornæss and Sibony first studied random dynamical systems of complex analytic maps [Reference Fornæss and Sibony12]. They proved that small ‘random perturbations’ of a single map produce very stable dynamics on average. It is then natural to ask what happens when larger noise is added. This question is the central motivation of this paper.
Sumi expanded the results of Fornæss and Sibony by studying minimal sets and established foundations for the study of random holomorphic dynamical systems. He defined the mean stability, and showed that the set of mean stable systems is open and dense in the space of all random dynamical systems having mild conditions [Reference Sumi27]. We will quickly review this theory in §2.2. For details, see [Reference Sumi28, Reference Sumi29]. See also [Reference Sumi and Watanabe30, Reference Sumi and Watanabe31] for the author generalizing the setting from independent and identically distributed (i.i.d.) to non-i.i.d.
These previous studies motivate us to study the bifurcation of (i.i.d.) random quadratic dynamical systems induced by the uniform distribution on
![]() ${\bar {B}({c}, {r})} $
. More precisely, for a fixed parameter
${\bar {B}({c}, {r})} $
. More precisely, for a fixed parameter
![]() $c \in {\mathbb {C}}$
, we can define the bifurcation radius
$c \in {\mathbb {C}}$
, we can define the bifurcation radius
![]() ${\mathit {r}_{\mathrm {bif}}}(c)$
as the parameter satisfying that the random dynamical system is mean stable if and only if
${\mathit {r}_{\mathrm {bif}}}(c)$
as the parameter satisfying that the random dynamical system is mean stable if and only if
![]() $r \notin \{0, {\mathit {r}_{\mathrm {bif}}}(c)\}$
. Compare this with Theorem 2.16 and Definition 2.17.
$r \notin \{0, {\mathit {r}_{\mathrm {bif}}}(c)\}$
. Compare this with Theorem 2.16 and Definition 2.17.
The dynamical systems of quadratic polynomials
![]() $f_{c}(z) = z^{2} + c \ (c \in \mathbb {C})$
are extremely important for studying holomorphic dynamical systems. The celebrated Mandelbrot set is an iconic figure on the parameter plane, whose boundary is known as the deterministic bifurcation locus of quadratic polynomials. The Mandelbrot set
$f_{c}(z) = z^{2} + c \ (c \in \mathbb {C})$
are extremely important for studying holomorphic dynamical systems. The celebrated Mandelbrot set is an iconic figure on the parameter plane, whose boundary is known as the deterministic bifurcation locus of quadratic polynomials. The Mandelbrot set
![]() $\mathcal {M}$
is the set of all parameters whose critical orbit is bounded:
$\mathcal {M}$
is the set of all parameters whose critical orbit is bounded:
![]() $\mathcal {M} = \{ c \in \mathbb {C} \colon f_{c}^{\circ n}(0) \not \to \infty (n \to \infty ) \},$
where
$\mathcal {M} = \{ c \in \mathbb {C} \colon f_{c}^{\circ n}(0) \not \to \infty (n \to \infty ) \},$
where
![]() $f_{c}^{\circ n} = {f_{{c}} \circ \cdots \circ f_{{c}} \circ f_{{c}}}$
is the (autonomous) nth iterate of a map
$f_{c}^{\circ n} = {f_{{c}} \circ \cdots \circ f_{{c}} \circ f_{{c}}}$
is the (autonomous) nth iterate of a map
![]() $f_{c}$
. The condition
$f_{c}$
. The condition
![]() $ f_{c}^{\circ n}(0) \not \to \infty $
is equivalent to the Julia set of
$ f_{c}^{\circ n}(0) \not \to \infty $
is equivalent to the Julia set of
![]() $f_{c}$
being connected. See McMullen’s book [Reference McMullen19] and Milnor’s book [Reference Milnor21] for details.
$f_{c}$
being connected. See McMullen’s book [Reference McMullen19] and Milnor’s book [Reference Milnor21] for details.
Several authors have reported great studies on sample-wise dynamics for random iterations. For a fixed infinite sequence
![]() $(c_{n})_{n=1}^{\infty }$
, we consider the Julia set of compositions
$(c_{n})_{n=1}^{\infty }$
, we consider the Julia set of compositions
![]() ${f_{{c_{n}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}$
, which is called a non-autonomous Julia set or a random Julia set.
${f_{{c_{n}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}$
, which is called a non-autonomous Julia set or a random Julia set.
Brück, Büger, and Reitz investigated the (dis)connectedness of random Julia sets [Reference Brück, Büger and Reitz4]. They found interesting examples that illustrated the difficulty of random iteration compared with deterministic iteration and established several conditions relating the noise amplitude to the connectedness of random Julia sets. See Remark 3.2 and [Reference Brück and Büger3, Reference Büger5].
Brück, Büger, and Reitz showed that if center
![]() $c =0$
and radius
$c =0$
and radius
![]() $r \leq 1/4$
, then every random Julia set of
$r \leq 1/4$
, then every random Julia set of
![]() ${f_{{c_{n}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}$
is connected. Later in [Reference Lech and Zdunik17], Lech and Zdunik proved that if
${f_{{c_{n}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}$
is connected. Later in [Reference Lech and Zdunik17], Lech and Zdunik proved that if
![]() $c=0$
and
$c=0$
and
![]() $r>1/4$
, then almost every random Julia set is totally disconnected. For our viewpoint, this is equivalent to
$r>1/4$
, then almost every random Julia set is totally disconnected. For our viewpoint, this is equivalent to
![]() ${\mathit {r}_{\mathrm {bif}}}(0) =1/4.$
One motivation of this paper is to generalize this result for the cases where
${\mathit {r}_{\mathrm {bif}}}(0) =1/4.$
One motivation of this paper is to generalize this result for the cases where
![]() $c \neq 0$
.
$c \neq 0$
.
1.2. Main results
First, we consider a sufficient condition for the random Julia sets to be totally disconnected almost surely.
Main Result A. (Theorem 3.7)
In this statement, the distribution
![]() $\mu $
of
$\mu $
of
![]() $c_{n}$
needs not to be the uniform distribution on a disk. Under some assumption, if the critical point
$c_{n}$
needs not to be the uniform distribution on a disk. Under some assumption, if the critical point
![]() $0$
tends to
$0$
tends to
![]() $\infty $
with probability one, then the random Julia set
$\infty $
with probability one, then the random Julia set
![]() $J_{\omega }$
is totally disconnected almost surely.
$J_{\omega }$
is totally disconnected almost surely.
Second, we reveal the relationships between the bifurcation radius
![]() ${\mathit {r}_{\mathrm {bif}}}$
and the connectedness of random Julia sets. More precisely, the following holds.
${\mathit {r}_{\mathrm {bif}}}$
and the connectedness of random Julia sets. More precisely, the following holds.
Main Result B. (Theorem 4.6)
Suppose that the interior of
![]() $ {\bar {B}({c}, {r})} $
contains a superattracting parameter. Then the following four are equivalent.
$ {\bar {B}({c}, {r})} $
contains a superattracting parameter. Then the following four are equivalent.
-
(1) The inequality
 $r \leq {\mathit {r}_{\mathrm {bif}}} (c)$
holds.
$r \leq {\mathit {r}_{\mathrm {bif}}} (c)$
holds. -
(2) The random orbit of
 $z=0$
does not tend to
$z=0$
does not tend to
 $\infty $
surely.
$\infty $
surely. -
(3) The random Julia set is connected for every sample-path.
-
(4) The set of all total orbits of
 $z=0$
is bounded in
$z=0$
is bounded in
 ${\mathbb {C}}$
.
${\mathbb {C}}$
.
Also, the following four are equivalent.
-
(1′) The inequality
 $r> {\mathit {r}_{\mathrm {bif}}} (c)$
holds.
$r> {\mathit {r}_{\mathrm {bif}}} (c)$
holds. -
(2′) The random orbit of
 $z=0$
tends to
$z=0$
tends to
 $\infty $
almost surely.
$\infty $
almost surely. -
(3′) The random Julia set is totally disconnected almost surely.
-
(4′) The set of all total orbits of
 $z=0$
is not bounded in
$z=0$
is not bounded in
 ${\mathbb {C}}$
.
${\mathbb {C}}$
.
Furthermore, either the former or the latter is valid.
In particular, the following dichotomy holds.
Corollary 1.1. Let c be a superattracting parameter. If
![]() $r \leq {\mathit {r}_{\mathrm {bif}}} (c)$
, then every random Julia set is connected. If
$r \leq {\mathit {r}_{\mathrm {bif}}} (c)$
, then every random Julia set is connected. If
![]() $r> {\mathit {r}_{\mathrm {bif}}} (c)$
, then almost every random Julia set is totally disconnected.
$r> {\mathit {r}_{\mathrm {bif}}} (c)$
, then almost every random Julia set is totally disconnected.
Corollary 1.1 is a generalization of the fact that the autonomous Julia set of a single map
![]() $f_{c}$
is either connected or totally disconnected according to
$f_{c}$
is either connected or totally disconnected according to
![]() $c \in {\mathcal {M}}$
or not.
$c \in {\mathcal {M}}$
or not.
Next, we show some properties and present some quantitative estimates for the bifurcation radius as follows.
Main Result C. (Lemma 4.9, Theorems 4.10, 4.12, 4.14, 4.18, and Examples 4.21 and 4.23)
All the following hold.
-
(i) For every
 $c \in {\mathbb {C}}$
, we have
$c \in {\mathbb {C}}$
, we have
 ${\mathit {r}_{\mathrm {bif}}}(c) \leq \operatorname {\mathrm {dist}}(c, \partial\mathcal{M}).$
${\mathit {r}_{\mathrm {bif}}}(c) \leq \operatorname {\mathrm {dist}}(c, \partial\mathcal{M}).$
-
(ii) For every
 $c, c' \in {\mathbb {C}},$
we have
$c, c' \in {\mathbb {C}},$
we have
 $|\kern1.5pt{\mathit {r}_{\mathrm {bif}}}(c) - {\mathit {r}_{\mathrm {bif}}}(c')| \leq |c -c'|.$
$|\kern1.5pt{\mathit {r}_{\mathrm {bif}}}(c) - {\mathit {r}_{\mathrm {bif}}}(c')| \leq |c -c'|.$
-
(iii) If
 $0 \leq c \leq 1/4$
, then
$0 \leq c \leq 1/4$
, then
 ${\mathit {r}_{\mathrm {bif}}}(c) = 1/4 - c$
.
${\mathit {r}_{\mathrm {bif}}}(c) = 1/4 - c$
. -
(iv) If
 $-1/2 \leq c < 0$
, then
$-1/2 \leq c < 0$
, then
 ${\mathit {r}_{\mathrm {bif}}}(c) \leq 1/4 -c - c^{2}.$
${\mathit {r}_{\mathrm {bif}}}(c) \leq 1/4 -c - c^{2}.$
-
(v) We have
 $0.0386\cdots \leq {\mathit {r}_{\mathrm {bif}}}(-1) \leq 0.0399 \cdots $
.
$0.0386\cdots \leq {\mathit {r}_{\mathrm {bif}}}(-1) \leq 0.0399 \cdots $
. -
(vi) For the airplane parameter
 $\tilde {c_{3}} \approx -1.75487766$
, we have
$\tilde {c_{3}} \approx -1.75487766$
, we have
 ${\mathit {r}_{\mathrm {bif}}}(\tilde {c_{3}}) \leq 0.0021.$
${\mathit {r}_{\mathrm {bif}}}(\tilde {c_{3}}) \leq 0.0021.$
Here,
![]() $\operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
denotes the Euclidean distance from c to the boundary of the Mandelbrot set
$\operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
denotes the Euclidean distance from c to the boundary of the Mandelbrot set
![]() $\partial {\mathcal {M}}$
. Statement (iii) gives the examples of c satisfying equality
$\partial {\mathcal {M}}$
. Statement (iii) gives the examples of c satisfying equality
![]() ${\mathit {r}_{\mathrm {bif}}}(c) = \operatorname {\mathrm {dist}}(c, \partial\mathcal {M}).$
However, statements (iv), (v), and (vi) give the examples of c satisfying strict inequality
${\mathit {r}_{\mathrm {bif}}}(c) = \operatorname {\mathrm {dist}}(c, \partial\mathcal {M}).$
However, statements (iv), (v), and (vi) give the examples of c satisfying strict inequality
![]() ${\mathit {r}_{\mathrm {bif}}}(c) < \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
.
${\mathit {r}_{\mathrm {bif}}}(c) < \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
.
It is worth noting that for
![]() $c=-1$
or
$c=-1$
or
![]() $\tilde {c_{3}}$
, statements (v) and (vi) illustrate a large gap
$\tilde {c_{3}}$
, statements (v) and (vi) illustrate a large gap
![]() ${\mathit {r}_{\mathrm {bif}}}(c)\ll \operatorname {\mathrm {dist}}(c, \partial\mathcal {M}).$
Furthermore, we also have
${\mathit {r}_{\mathrm {bif}}}(c)\ll \operatorname {\mathrm {dist}}(c, \partial\mathcal {M}).$
Furthermore, we also have
![]() ${\mathit {r}_{\mathrm {bif}}}(c + \epsilon )\ll \operatorname {\mathrm {dist}}(c + \epsilon , \partial\mathcal {M})$
for a small
${\mathit {r}_{\mathrm {bif}}}(c + \epsilon )\ll \operatorname {\mathrm {dist}}(c + \epsilon , \partial\mathcal {M})$
for a small
![]() $\epsilon \in {\mathbb {C}}$
. The proofs of statements (v) and (vi) rely on parabolic implosion in a stochastic context. See Theorem 4.19.
$\epsilon \in {\mathbb {C}}$
. The proofs of statements (v) and (vi) rely on parabolic implosion in a stochastic context. See Theorem 4.19.
Combining statement (iv) with Corollary 1.1, we give a stronger result compared with the result by Lech and Zdunik. Compare Corollary 4.15 with Theorem 3.5. Moreover, we give a result for the case where c is far from
![]() $0$
.
$0$
.
Corollary 1.2. (Corollaries 4.15 and 4.25)
Almost every random Julia set is totally disconnected:
-
• if the central parameter
 $-1/4 \leq c < 0$
and the noise amplitude
$-1/4 \leq c < 0$
and the noise amplitude
 $r> 1/4 - c - c^{2};$
or
$r> 1/4 - c - c^{2};$
or -
• if the central parameter
 $c=-1 + \epsilon $
and the noise amplitude
$c=-1 + \epsilon $
and the noise amplitude
 $r> 0.0399 \cdots + |\epsilon | $
; or
$r> 0.0399 \cdots + |\epsilon | $
; or -
• if the central parameter
 $c = \tilde {c_{3}} + \epsilon $
and the noise amplitude
$c = \tilde {c_{3}} + \epsilon $
and the noise amplitude
 $r> 0.0021 + |\epsilon |.$
$r> 0.0021 + |\epsilon |.$
This corollary gives new examples which satisfy that the random Julia set is totally disconnected almost surely even if
![]() ${\bar {B}({c}, {r})} \subset \mathrm {int }{\,\mathcal {M}}$
.
${\bar {B}({c}, {r})} \subset \mathrm {int }{\,\mathcal {M}}$
.
In addition, Main Result B gives a quasiconformal conjugacy between Julia sets.
Main Result D. (Theorem 4.29 and Corollary 4.30)
Suppose that the interior of
![]() $ {\bar {B}({c}, {r})} $
contains a superattracting parameter
$ {\bar {B}({c}, {r})} $
contains a superattracting parameter
![]() $\tilde {c}$
and suppose
$\tilde {c}$
and suppose
![]() $r < {\mathit {r}_{\mathrm {bif}}} (c)$
. Then for every
$r < {\mathit {r}_{\mathrm {bif}}} (c)$
. Then for every
![]() $(c_{n})_{n=1}^{\infty }, (c^{\prime }_{n})_{n=1}^{\infty } \in {\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
, there exist
$(c_{n})_{n=1}^{\infty }, (c^{\prime }_{n})_{n=1}^{\infty } \in {\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
, there exist
![]() $K \geq 1$
and a sequence of maps
$K \geq 1$
and a sequence of maps
![]() $\{\varphi _{n}\}_{n \geq 0}$
such that
$\{\varphi _{n}\}_{n \geq 0}$
such that
![]() $\varphi _{n}$
maps the Julia sets of
$\varphi _{n}$
maps the Julia sets of
![]() $(c_{n})_{n=1}^{\infty }$
onto the Julia sets of
$(c_{n})_{n=1}^{\infty }$
onto the Julia sets of
![]() $(c^{\prime }_{n})_{n=1}^{\infty }\ K$
-quasiconformally and
$(c^{\prime }_{n})_{n=1}^{\infty }\ K$
-quasiconformally and
![]() $\varphi _{n+1}\circ f_{c_{n+1}}= f_{c^{\prime }_{n+1}} \circ \varphi _{n}$
on the iterated Julia set for every
$\varphi _{n+1}\circ f_{c_{n+1}}= f_{c^{\prime }_{n+1}} \circ \varphi _{n}$
on the iterated Julia set for every
![]() $n \geq 0$
. In particular, there exists a quasiconformal map
$n \geq 0$
. In particular, there exists a quasiconformal map
![]() $\varphi $
which maps the autonomous Julia set
$\varphi $
which maps the autonomous Julia set
![]() $J_{\tilde {c}}$
onto the non-autonomous Julia set.
$J_{\tilde {c}}$
onto the non-autonomous Julia set.
1.3. Structure of the paper
In §2, we discuss the elementary properties in the general form and define the bifurcation radius. Moreover, we quickly review Sumi’s theory on minimal sets and mean stability in §2.2. In §3, we establish some tools to decide connectedness and total disconnectedness. These are developed by Brück, Büger, and Reitz [Reference Brück, Büger and Reitz4], and Lech and Zdunik [Reference Lech and Zdunik17]. In addition, we show Main Result A relating bifurcation and connectedness. In §4, we prove Main Results B, C, and D. In §5, we discuss some open problems and generalization to other cases.
2. Preliminaries
In this section, we define the bifurcation radius and discuss the elementary properties required in subsequent sections. We consider minimal sets and mean stability, which appear in §2.2. They describe set-valued dynamics and we can apply them to quenched, or averaged, dynamics. The minimal sets provide the basis for our discussion and define the bifurcation radius, which is the main subject in this paper.
2.1. Setting and notation
In this section, we consider a slightly general setting.
Setting 2.1. Let
![]() $\mu $
be a Borel probability measure on the parameter plane
$\mu $
be a Borel probability measure on the parameter plane
![]() ${\mathbb {C}}$
with compact support. Denote the support by
${\mathbb {C}}$
with compact support. Denote the support by
![]() $\operatorname {\mathrm {supp}} \mu .$
We define the probability measure
$\operatorname {\mathrm {supp}} \mu .$
We define the probability measure
![]() $\mathbb {P}_{\mu }$
as the one-sided infinite product of
$\mathbb {P}_{\mu }$
as the one-sided infinite product of
![]() $\mu $
, which is supported on
$\mu $
, which is supported on
![]() $\Omega _{\mu } = \prod _{n = 1}^{\infty } \operatorname {\mathrm {supp}} \mu $
with the Borel
$\Omega _{\mu } = \prod _{n = 1}^{\infty } \operatorname {\mathrm {supp}} \mu $
with the Borel
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathfrak {B}_{\mu }$
.
$\mathfrak {B}_{\mu }$
.
The most simple and important example for
![]() $\mu $
is the normalized Lebesgue measure on
$\mu $
is the normalized Lebesgue measure on
![]() ${\bar {B}({c}, {r})} =\{c' \in \mathbb {C} \colon |c' - c| \leq r \}$
, which means the uniform distribution. Another example is the Dirac measure at c, which can be regarded as a deterministic dynamical system. We analyze these examples in §4.
${\bar {B}({c}, {r})} =\{c' \in \mathbb {C} \colon |c' - c| \leq r \}$
, which means the uniform distribution. Another example is the Dirac measure at c, which can be regarded as a deterministic dynamical system. We analyze these examples in §4.
Our random dynamical systems are the stochastic process perturbed by i.i.d. noise in a sense. One can generalize the setting to a non-i.i.d. setting, which we do not pursue here. For details, the reader is referred to [Reference Sumi and Watanabe30, Reference Sumi and Watanabe31].
Regarding noise, a natural consideration may be a distribution
![]() $\mu $
with unbounded support, say the Gaussian distribution. However, in unbounded cases, there are no planar attractors which we intend to investigate. Thus, we assume that
$\mu $
with unbounded support, say the Gaussian distribution. However, in unbounded cases, there are no planar attractors which we intend to investigate. Thus, we assume that
![]() $\operatorname {\mathrm {supp}} \mu $
is compact. See [Reference Büger5] for the detail and see also [Reference Comerford, Stankewitz and Sumi9] for more wild phenomena for the distributions with unbounded supports.
$\operatorname {\mathrm {supp}} \mu $
is compact. See [Reference Büger5] for the detail and see also [Reference Comerford, Stankewitz and Sumi9] for more wild phenomena for the distributions with unbounded supports.
The following is a well-known fact. See, for example, [Reference Durrett11, §6].
Lemma 2.2. Denote by
![]() $\sigma $
the natural left shift, that is,
$\sigma $
the natural left shift, that is,
![]() $\sigma \omega = (c_{2}, c_{3}, \ldots ) $
if
$\sigma \omega = (c_{2}, c_{3}, \ldots ) $
if
![]() $\omega = (c_{1}, c_{2}, \ldots )$
. Then
$\omega = (c_{1}, c_{2}, \ldots )$
. Then
![]() $\sigma \colon \Omega _{\mu } \to \Omega _{\mu }$
is a measure-preserving ergodic transformation with respect to
$\sigma \colon \Omega _{\mu } \to \Omega _{\mu }$
is a measure-preserving ergodic transformation with respect to
![]() $\mathbb {P}_{\mu }$
.
$\mathbb {P}_{\mu }$
.
We now define the Julia set for every noise realization
![]() $\omega $
.
$\omega $
.
Definition 2.3. For each
![]() $n \in {\mathbb {N}}$
and infinite sequence of parameters
$n \in {\mathbb {N}}$
and infinite sequence of parameters
![]() $\omega = (c_{n})_{n =1}^{\infty } \in {\mathbb {C}}^{{\mathbb {N}}}$
, we denote
$\omega = (c_{n})_{n =1}^{\infty } \in {\mathbb {C}}^{{\mathbb {N}}}$
, we denote
![]() ${{f}_{{\omega }}^{({n})}} := {f_{{c_{n}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}.$
${{f}_{{\omega }}^{({n})}} := {f_{{c_{n}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}.$
Definition 2.4. For each
![]() $\omega = (c_{n})_{n =1}^{\infty } \in {\mathbb {C}}^{{\mathbb {N}}}$
, we define the non-autonomous Julia set or the random Julia set of
$\omega = (c_{n})_{n =1}^{\infty } \in {\mathbb {C}}^{{\mathbb {N}}}$
, we define the non-autonomous Julia set or the random Julia set of
![]() $\omega $
by
$\omega $
by
If there exists
![]() $c_{0} \in {\mathbb {C}}$
such that
$c_{0} \in {\mathbb {C}}$
such that
![]() $c_{n} = c_{0}$
for every
$c_{n} = c_{0}$
for every
![]() $n \in {\mathbb {N}}$
, then for
$n \in {\mathbb {N}}$
, then for
![]() $\omega = (c_{n})_{n =1}^{\infty }$
, the non-autonomous Julia set
$\omega = (c_{n})_{n =1}^{\infty }$
, the non-autonomous Julia set
![]() $J_{\omega }$
is equal to the usual (autonomous) Julia set of
$J_{\omega }$
is equal to the usual (autonomous) Julia set of
![]() $f_{c_{0}}$
.
$f_{c_{0}}$
.
Analogously to the usual case, the non-autonomous Julia set is the common boundary of the basin at infinity and the filled Julia set defined as follows.
Definition 2.5. For each
![]() $\omega = (c_{n})_{n =1}^{\infty } \in {\mathbb {C}}^{{\mathbb {N}}}$
, we define the non-autonomous basin at infinity of
$\omega = (c_{n})_{n =1}^{\infty } \in {\mathbb {C}}^{{\mathbb {N}}}$
, we define the non-autonomous basin at infinity of
![]() $\omega $
by
$\omega $
by
![]() $A_{\omega } = \{ z \in {\widehat {\mathbb {C}}} \colon {{f}_{{\omega }}^{({n})}} (z) \to \infty \text { as } n\to \infty \}.$
We define the non-autonomous filled Julia set of
$A_{\omega } = \{ z \in {\widehat {\mathbb {C}}} \colon {{f}_{{\omega }}^{({n})}} (z) \to \infty \text { as } n\to \infty \}.$
We define the non-autonomous filled Julia set of
![]() $\omega $
by
$\omega $
by
![]() $K_{\omega } = {\widehat {\mathbb {C}}} \setminus\! A_{\omega }.$
$K_{\omega } = {\widehat {\mathbb {C}}} \setminus\! A_{\omega }.$
Here,
![]() ${\widehat {\mathbb {C}}} = {\mathbb {C}} \cup \{ \infty \}$
denotes the Riemann sphere, which is homeomorphic to the real two-dimensional sphere. We endow
${\widehat {\mathbb {C}}} = {\mathbb {C}} \cup \{ \infty \}$
denotes the Riemann sphere, which is homeomorphic to the real two-dimensional sphere. We endow
![]() ${\widehat {\mathbb {C}}}$
with the spherical metric d. A polynomial map
${\widehat {\mathbb {C}}}$
with the spherical metric d. A polynomial map
![]() $f \colon {\mathbb {C}} \to {\mathbb {C}}$
can be extended analytically to
$f \colon {\mathbb {C}} \to {\mathbb {C}}$
can be extended analytically to
![]() $f \colon {\widehat {\mathbb {C}}} \to {\widehat {\mathbb {C}}}$
by letting
$f \colon {\widehat {\mathbb {C}}} \to {\widehat {\mathbb {C}}}$
by letting
![]() $f(\infty ) = \infty .$
$f(\infty ) = \infty .$
For our convenience, we list the elementary properties of non-autonomous Julia sets, basins at infinity, and filled Julia sets. For
![]() $R> 0$
, we denote by
$R> 0$
, we denote by
![]() $D_{R}$
the open disk
$D_{R}$
the open disk
![]() $D_{R} = \{ z \in {\mathbb {C}} \colon |z| < R \}$
on the dynamical plane.
$D_{R} = \{ z \in {\mathbb {C}} \colon |z| < R \}$
on the dynamical plane.
Lemma 2.6. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() ${\mathbb {C}}$
with compact support. Then we have all the following.
${\mathbb {C}}$
with compact support. Then we have all the following.
-
(1) There exists
 $R> 0$
such that
$R> 0$
such that
 ${{f}_{{\omega }}^{({n})}} ({\widehat {\mathbb {C}}} \setminus\! D_{R}) \subset {\widehat {\mathbb {C}}} \setminus\! D_{2 R}$
for every
${{f}_{{\omega }}^{({n})}} ({\widehat {\mathbb {C}}} \setminus\! D_{R}) \subset {\widehat {\mathbb {C}}} \setminus\! D_{2 R}$
for every
 $n \in {\mathbb {N}}$
and
$n \in {\mathbb {N}}$
and
 $\omega \in \Omega _{\mu }$
.
$\omega \in \Omega _{\mu }$
. -
(2) Take
 $R> 0$
as above. The non-autonomous basin at infinity is then the union of the increasing sequence of the open subsets;
$R> 0$
as above. The non-autonomous basin at infinity is then the union of the increasing sequence of the open subsets;
 $A_{\omega } = \bigcup _{n=1}^{\infty } ({{f}_{{\omega }}^{({n})}})^{-1}({\widehat {\mathbb {C}}} \setminus\! \overline {D_{R}})$
for every
$A_{\omega } = \bigcup _{n=1}^{\infty } ({{f}_{{\omega }}^{({n})}})^{-1}({\widehat {\mathbb {C}}} \setminus\! \overline {D_{R}})$
for every
 $\omega \in \Omega _{\mu }$
. Hence,
$\omega \in \Omega _{\mu }$
. Hence,
 $A_{\omega }$
is an open neighborhood of
$A_{\omega }$
is an open neighborhood of
 $\infty $
. Conversely,
$\infty $
. Conversely,
 $K_{\omega } = \bigcap _{n=1}^{\infty } ({{f}_{{\omega }}^{({n})}})^{-1}(\overline {D_{R}})$
is a non-empty compact subset for every
$K_{\omega } = \bigcap _{n=1}^{\infty } ({{f}_{{\omega }}^{({n})}})^{-1}(\overline {D_{R}})$
is a non-empty compact subset for every
 $\omega \in \Omega _{\mu }$
.
$\omega \in \Omega _{\mu }$
. -
(3) For
 $\omega \in \Omega _{\mu }$
, we have
$\omega \in \Omega _{\mu }$
, we have
 $\partial A_{\omega } = J_{\omega } = \partial K_{\omega }$
.
$\partial A_{\omega } = J_{\omega } = \partial K_{\omega }$
. -
(4) For
 $\omega \in \Omega _{\mu }$
, we have
$\omega \in \Omega _{\mu }$
, we have
 $A_{\omega } = f_{c_{1}}^{-1}(A_{\sigma \omega })$
,
$A_{\omega } = f_{c_{1}}^{-1}(A_{\sigma \omega })$
,
 $K_{\omega } = f_{c_{1}}^{-1}(K_{\sigma \omega })$
, and
$K_{\omega } = f_{c_{1}}^{-1}(K_{\sigma \omega })$
, and
 $J_{\omega } = f_{c_{1}}^{-1}(J_{\sigma \omega })$
.
$J_{\omega } = f_{c_{1}}^{-1}(J_{\sigma \omega })$
.
For the proof, see [Reference Brück, Büger and Reitz4]. Note that the existence of such R is due to the compactness of
![]() $\operatorname {\mathrm {supp}} \mu .$
$\operatorname {\mathrm {supp}} \mu .$
2.2. Minimal sets, mean stability, and bifurcation
Consider the action of polynomial semigroups whose product is the composition of maps. Semigroup actions are related to random dynamical systems as set-valued dynamics. Here, we review the theory of polynomial semigroups, which enables us to define bifurcations.
Generally, one can consider rational semigroups, not polynomial. However, we focus on polynomial maps since we are interested in quadratic polynomials. The interested reader is referred to [Reference Hinkkanen and Martin15, Reference Stankewitz24].
We start with the definition of polynomial semigroups. Denote by
![]() ${\mathrm {Poly}}$
the space of all polynomials of degree two or more endowed with the topology of uniform convergence on
${\mathrm {Poly}}$
the space of all polynomials of degree two or more endowed with the topology of uniform convergence on
![]() ${\widehat {\mathbb {C}}}$
. We say that G is a polynomial semigroup if G is a non-empty subset of
${\widehat {\mathbb {C}}}$
. We say that G is a polynomial semigroup if G is a non-empty subset of
![]() ${\mathrm {Poly}}$
closed under mapping composition. Let
${\mathrm {Poly}}$
closed under mapping composition. Let
![]() $\Gamma $
be a subset of
$\Gamma $
be a subset of
![]() ${\mathrm {Poly}}$
. We say that G is generated by
${\mathrm {Poly}}$
. We say that G is generated by
![]() $\Gamma $
if for every
$\Gamma $
if for every
![]() $g \in G$
, there exist
$g \in G$
, there exist
![]() $n \in {\mathbb {N}}$
and
$n \in {\mathbb {N}}$
and
![]() $\gamma _{1}, \gamma _{2}, \ldots \gamma _{n} \in \Gamma $
such that
$\gamma _{1}, \gamma _{2}, \ldots \gamma _{n} \in \Gamma $
such that
![]() $g=\gamma _{n}\circ \cdots \circ \gamma _{2} \circ \gamma _{1}.$
$g=\gamma _{n}\circ \cdots \circ \gamma _{2} \circ \gamma _{1}.$
Definition 2.7. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() ${\mathbb {C}}$
with compact support. We define the polynomial semigroup
${\mathbb {C}}$
with compact support. We define the polynomial semigroup
![]() $G_{\mu }$
as the semigroup generated by the compact set
$G_{\mu }$
as the semigroup generated by the compact set
![]() $\Gamma = \{f_{c} \in {\mathrm {Poly}} \colon c \in \operatorname {\mathrm {supp}} \mu \}$
. Here
$\Gamma = \{f_{c} \in {\mathrm {Poly}} \colon c \in \operatorname {\mathrm {supp}} \mu \}$
. Here
![]() $f_{c}(z) = z^{2} + c$
is a quadratic polynomial, as we will assume throughout this paper.
$f_{c}(z) = z^{2} + c$
is a quadratic polynomial, as we will assume throughout this paper.
Note that the map
![]() ${\mathrm {Poly}} \times {\widehat {\mathbb {C}}} \ni (g, z) \mapsto g(z) \in {\widehat {\mathbb {C}}}$
is continuous. This implies that the map
${\mathrm {Poly}} \times {\widehat {\mathbb {C}}} \ni (g, z) \mapsto g(z) \in {\widehat {\mathbb {C}}}$
is continuous. This implies that the map
![]() $\Omega \times {\widehat {\mathbb {C}}} \ni (\omega , z) \mapsto {{f}_{{\omega }}^{({n})}}(z) \in {\widehat {\mathbb {C}}}$
is also continuous for every
$\Omega \times {\widehat {\mathbb {C}}} \ni (\omega , z) \mapsto {{f}_{{\omega }}^{({n})}}(z) \in {\widehat {\mathbb {C}}}$
is also continuous for every
![]() $n \in {\mathbb {N}}$
.
$n \in {\mathbb {N}}$
.
For every polynomial semigroup, we define the Julia set and Fatou set as follows. The following proposition connects the Julia set of polynomial semigroup and the random Julia sets. The idea of the proof can be found in [Reference Sumi25].
Definition 2.8. For a polynomial semigroup G, define the Julia set by
We call the complement
![]() $F(G)={\widehat {\mathbb {C}}} \setminus\! J(G)$
the Fatou set of G.
$F(G)={\widehat {\mathbb {C}}} \setminus\! J(G)$
the Fatou set of G.
Proposition 2.9. For a Borel probability measure
![]() $\mu $
on
$\mu $
on
![]() ${\mathbb {C}}$
with compact support, we have
${\mathbb {C}}$
with compact support, we have
![]() $J(G_{\mu }) = \overline {\bigcup _{\omega \in \Omega _{\mu }} J_{\omega }}$
.
$J(G_{\mu }) = \overline {\bigcup _{\omega \in \Omega _{\mu }} J_{\omega }}$
.
Next, we define minimal sets which play a crucial role in studying random holomorphic dynamical systems.
Definition 2.10. Let G be a polynomial semigroup. A subset
![]() $L' \subset {\widehat {\mathbb {C}}}$
is said to be forward invariant under G, or forward G-invariant, if
$L' \subset {\widehat {\mathbb {C}}}$
is said to be forward invariant under G, or forward G-invariant, if
![]() $g(L') \subset L'$
for every
$g(L') \subset L'$
for every
![]() $g \in G$
. A subset
$g \in G$
. A subset
![]() $L\subset {\widehat {\mathbb {C}}}$
is called a minimal set of G if L is a minimal element of the set of all forward G-invariant, non-empty, and compact subsets of
$L\subset {\widehat {\mathbb {C}}}$
is called a minimal set of G if L is a minimal element of the set of all forward G-invariant, non-empty, and compact subsets of
![]() ${\widehat {\mathbb {C}}}$
with respect to the inclusion relation
${\widehat {\mathbb {C}}}$
with respect to the inclusion relation
![]() $\subset $
.
$\subset $
.
We can easily show that a non-empty compact set
![]() $L\subset {\widehat {\mathbb {C}}}$
is minimal if and only if for every
$L\subset {\widehat {\mathbb {C}}}$
is minimal if and only if for every
![]() $z \in L$
, we have
$z \in L$
, we have
![]() $\overline {\bigcup _{g \in G}\{g(z)\}} = L$
.
$\overline {\bigcup _{g \in G}\{g(z)\}} = L$
.
Trivially, the singleton
![]() $\{\infty \}$
is a minimal set of G for every polynomial semigroup G. Thus, we are interested mainly in planar minimal sets as defined below.
$\{\infty \}$
is a minimal set of G for every polynomial semigroup G. Thus, we are interested mainly in planar minimal sets as defined below.
Definition 2.11. A subset
![]() $L \subset {\widehat {\mathbb {C}}}$
is said to be planar if
$L \subset {\widehat {\mathbb {C}}}$
is said to be planar if
![]() $\infty \notin L$
.
$\infty \notin L$
.
For example, if
![]() $\mu = \delta _{c}$
is the Dirac measure at c, then every periodic cycle of
$\mu = \delta _{c}$
is the Dirac measure at c, then every periodic cycle of
![]() $f_{c}$
is a minimal set of
$f_{c}$
is a minimal set of
![]() $G_{\delta _{c}}$
. Hence, there is an infinite number of planar minimal sets of
$G_{\delta _{c}}$
. Hence, there is an infinite number of planar minimal sets of
![]() $G_{\delta _{c}}$
for every
$G_{\delta _{c}}$
for every
![]() $c \in {\mathbb {C}}$
.
$c \in {\mathbb {C}}$
.
For the number of minimal sets, we have the following property.
Lemma 2.12. Let
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{2}$
be polynomial semigroups generated by
$G_{2}$
be polynomial semigroups generated by
![]() $\Gamma _{1}$
and
$\Gamma _{1}$
and
![]() $\Gamma _{2}$
, respectively. If
$\Gamma _{2}$
, respectively. If
![]() $\Gamma _{1} \subset \Gamma _{2}$
, then every minimal set
$\Gamma _{1} \subset \Gamma _{2}$
, then every minimal set
![]() $L_{2}$
of
$L_{2}$
of
![]() $G_{2}$
contains some minimal set
$G_{2}$
contains some minimal set
![]() $L_{1}$
of
$L_{1}$
of
![]() $G_{1}$
.
$G_{1}$
.
Proof. By definition, a minimal set
![]() $L_{2}$
of
$L_{2}$
of
![]() $G_{2}$
is forward invariant under
$G_{2}$
is forward invariant under
![]() $G_{2}$
. Since
$G_{2}$
. Since
![]() ${\Gamma _{1} \subset \Gamma _{2}}$
, the set
${\Gamma _{1} \subset \Gamma _{2}}$
, the set
![]() $L_{2}$
is forward invariant also under
$L_{2}$
is forward invariant also under
![]() $G_{1}$
. It follows from Zorn’s lemma that there exists a minimal set
$G_{1}$
. It follows from Zorn’s lemma that there exists a minimal set
![]() $L_{1}$
of
$L_{1}$
of
![]() $G_{1}$
such that
$G_{1}$
such that
![]() $L_{1} \subset L_{2}$
.
$L_{1} \subset L_{2}$
.
Definition 2.13. Let G be the polynomial semigroup generated by a subset
![]() $\Gamma $
of
$\Gamma $
of
![]() ${\mathrm {Poly}}$
. A minimal set
${\mathrm {Poly}}$
. A minimal set
![]() $L \subset {\widehat {\mathbb {C}}}$
of G is said to be attracting if there exist
$L \subset {\widehat {\mathbb {C}}}$
of G is said to be attracting if there exist
![]() $N \in {\mathbb {N}}$
and non-empty open subsets U and V of the Fatou set
$N \in {\mathbb {N}}$
and non-empty open subsets U and V of the Fatou set
![]() $F(G)$
such that the following two conditions hold.
$F(G)$
such that the following two conditions hold.
-
(i)
 $L \Subset V \Subset U \Subset F(G)$
.
$L \Subset V \Subset U \Subset F(G)$
. -
(ii) For every
 $f_{1}, f_{2}, \ldots , f_{N} \in \Gamma $
, we have
$f_{1}, f_{2}, \ldots , f_{N} \in \Gamma $
, we have
 ${f_{{N}} \circ \cdots \circ f_{{2}} \circ f_{{1}}}(U) \Subset V$
.
${f_{{N}} \circ \cdots \circ f_{{2}} \circ f_{{1}}}(U) \Subset V$
.
Here,
![]() $A \Subset B$
means that the closure
$A \Subset B$
means that the closure
![]() $\overline {A}$
is a relatively compact subset of B.
$\overline {A}$
is a relatively compact subset of B.
One can easily show that if the polynomial semigroup G is generated by a compact subset, then the minimal set
![]() $\{\infty \}$
is attracting. By using the hyperbolic metric, we have the following characterization of attracting minimal sets. For the proof, see [Reference Sumi28, Remark 3.5] or [Reference Sumi and Watanabe31, Lemma 2.8].
$\{\infty \}$
is attracting. By using the hyperbolic metric, we have the following characterization of attracting minimal sets. For the proof, see [Reference Sumi28, Remark 3.5] or [Reference Sumi and Watanabe31, Lemma 2.8].
Proposition 2.14. Let G be the polynomial semigroup generated by a compact subset
![]() $\Gamma $
of
$\Gamma $
of
![]() ${\mathrm {Poly}}$
. A minimal set
${\mathrm {Poly}}$
. A minimal set
![]() $L \subset F(G)$
of G is attracting if and only if the following holds. There exist
$L \subset F(G)$
of G is attracting if and only if the following holds. There exist
![]() $ N \in {\mathbb {N}}$
,
$ N \in {\mathbb {N}}$
,
![]() $0 < \alpha < 1$
,
$0 < \alpha < 1$
,
![]() $C> 0$
, and a neighborhood W of L such that for every
$C> 0$
, and a neighborhood W of L such that for every
![]() $k \in \mathbb {N}$
,
$k \in \mathbb {N}$
,
![]() $f_{1}, f_{2}, \ldots f_{k N} \in \Gamma $
, and
$f_{1}, f_{2}, \ldots f_{k N} \in \Gamma $
, and
![]() $z , z_{0} \in W$
, the spherical metric satisfies
$z , z_{0} \in W$
, the spherical metric satisfies
Now, we present the classification theorem, which states that every minimal set either is attracting, intersects the Julia set, or intersects some rotation domain. Compare the following theorem with the classification theorem for autonomous iteration of a single map. For the latter classical theorem, see [Reference Milnor21, Theorem 16.1] or [Reference Carleson and Gamelin6, Theorem IV.2.1].
Theorem 2.15. Let G be the polynomial semigroup generated by a compact subset
![]() $\Gamma $
of
$\Gamma $
of
![]() ${\mathrm {Poly}}$
. A minimal set
${\mathrm {Poly}}$
. A minimal set
![]() $L \subset {\widehat {\mathbb {C}}}$
of G is either one of the following three.
$L \subset {\widehat {\mathbb {C}}}$
of G is either one of the following three.
-
(i) L is attracting.
-
(ii)
 $L \cap J(G) \neq \emptyset $
.
$L \cap J(G) \neq \emptyset $
. -
(iii)
 $L \subset F(G)$
and there exist
$L \subset F(G)$
and there exist
 $g \in G$
and a connected component U of
$g \in G$
and a connected component U of
 $F(G)$
with
$F(G)$
with
 $L \cap U \neq \emptyset $
such that
$L \cap U \neq \emptyset $
such that
 $g(U) \subset U$
and U is a subset of a Siegel disk of autonomous iteration of g.
$g(U) \subset U$
and U is a subset of a Siegel disk of autonomous iteration of g.
For the proof, see [Reference Sumi28, Lemma 3.8]. The classification theorem leads to the following definitions. We say that a minimal set is J-touching if it is of type (ii) in Theorem 2.15. In addition, a minimal set is sub-rotative if it is of type (iii) in Theorem 2.15.
However, these two types of minimal sets are uncommon compared with the attracting minimal sets as stated by Theorem 2.16. Denote by
![]() $\mathcal {H}$
the set of all parameters
$\mathcal {H}$
the set of all parameters
![]() $c \in {\mathcal {M}}$
such that
$c \in {\mathcal {M}}$
such that
![]() $f_{c}$
is hyperbolic.
$f_{c}$
is hyperbolic.
Theorem 2.16. For every
![]() $c \in {\mathbb {C}}$
and
$c \in {\mathbb {C}}$
and
![]() $r> 0$
, define the polynomial semigroup
$r> 0$
, define the polynomial semigroup
![]() $G_{c, r}$
as the semigroup generated by
$G_{c, r}$
as the semigroup generated by
![]() $\{f_{c'} \in {\mathrm {Poly}} \colon |c' - c| \leq r\}$
. Here
$\{f_{c'} \in {\mathrm {Poly}} \colon |c' - c| \leq r\}$
. Here
![]() $f_{c}(z) = z^{2} + c$
. Then
$f_{c}(z) = z^{2} + c$
. Then
![]() $G_{c, r}$
has an attracting minimal set
$G_{c, r}$
has an attracting minimal set
![]() $\{\infty \}$
. Other than
$\{\infty \}$
. Other than
![]() $\{\infty \}$
, possible planar minimal sets are described as follows.
$\{\infty \}$
, possible planar minimal sets are described as follows.
-
• If
 $c\not \in \mathcal {H}$
, then
$c\not \in \mathcal {H}$
, then
 $G_{c, r}$
has no planar minimal sets for every
$G_{c, r}$
has no planar minimal sets for every
 $r> 0$
.
$r> 0$
. -
• If
 $c\in \mathcal {H}$
, then there exists
$c\in \mathcal {H}$
, then there exists
 ${\mathit {r}_{\mathrm {bif}}} (c)> 0$
such that the following hold.
${\mathit {r}_{\mathrm {bif}}} (c)> 0$
such that the following hold.-
– If
 $0 < r < {\mathit {r}_{\mathrm {bif}}} (c)$
, then
$0 < r < {\mathit {r}_{\mathrm {bif}}} (c)$
, then
 $G_{c, r}$
has exactly one planar minimal set and it is attracting.
$G_{c, r}$
has exactly one planar minimal set and it is attracting. -
– If
 $r = {\mathit {r}_{\mathrm {bif}}} (c)$
, then
$r = {\mathit {r}_{\mathrm {bif}}} (c)$
, then
 $G_{c, r}$
has exactly one planar minimal set and it is not attracting.
$G_{c, r}$
has exactly one planar minimal set and it is not attracting. -
– If
 ${\mathit {r}_{\mathrm {bif}}} (c) < r$
, then
${\mathit {r}_{\mathrm {bif}}} (c) < r$
, then
 $G_{c, r}$
has no planar minimal sets.
$G_{c, r}$
has no planar minimal sets.
-
Theorem 2.16 motivates us to define the bifurcation radius as follows. Note that our bifurcation occurs at most once because
![]() $f_{c}$
is of degree
$f_{c}$
is of degree
![]() $2,$
and in general, our bifurcation occurs at most
$2,$
and in general, our bifurcation occurs at most
![]() $d-1$
times if we work on polynomial maps of degree d.
$d-1$
times if we work on polynomial maps of degree d.
Definition 2.17. For every
![]() $c \in {\mathbb {C}}$
, we define the bifurcation radius
$c \in {\mathbb {C}}$
, we define the bifurcation radius
![]() ${\mathit {r}_{\mathrm {bif}}} (c) \geq 0$
according to the following cases. If
${\mathit {r}_{\mathrm {bif}}} (c) \geq 0$
according to the following cases. If
![]() $c \notin \mathcal {H}$
, we define
$c \notin \mathcal {H}$
, we define
![]() ${\mathit {r}_{\mathrm {bif}}} (c) = 0$
. If
${\mathit {r}_{\mathrm {bif}}} (c) = 0$
. If
![]() $c \in \mathcal {H}$
, we define the bifurcation radius
$c \in \mathcal {H}$
, we define the bifurcation radius
![]() ${\mathit {r}_{\mathrm {bif}}} (c)> 0$
as the unique
${\mathit {r}_{\mathrm {bif}}} (c)> 0$
as the unique
![]() $r>0$
such that
$r>0$
such that
![]() $G_{c, r}$
has the non-attracting planar minimal set.
$G_{c, r}$
has the non-attracting planar minimal set.
Equivalently, the bifurcation radius
![]() ${\mathit {r}_{\mathrm {bif}}} (c)$
is the maximum value for
${\mathit {r}_{\mathrm {bif}}} (c)$
is the maximum value for
![]() $r \geq 0$
such that
$r \geq 0$
such that
![]() $G_{c, r}$
has a planar minimal set, or equivalently, is the infimum value for
$G_{c, r}$
has a planar minimal set, or equivalently, is the infimum value for
![]() $r \geq 0$
such that
$r \geq 0$
such that
![]() $G_{c, r}$
has no planar minimal sets.
$G_{c, r}$
has no planar minimal sets.
The rest of this subsection is devoted to emphasizing the importance of deciding on the bifurcation parameters by presenting some interesting phenomena. See [Reference Sumi27, §3.6] for the details.
Definition 2.18. Let G be the polynomial semigroup generated by a compact subset
![]() $\Gamma $
of
$\Gamma $
of
![]() ${\mathrm {Poly}}$
. We say that G is mean stable if all the minimal sets of G are attracting.
${\mathrm {Poly}}$
. We say that G is mean stable if all the minimal sets of G are attracting.
By Theorem 2.16, for every
![]() $c \in {\mathbb {C}}$
and
$c \in {\mathbb {C}}$
and
![]() $r \geq 0,$
the polynomial semigroup
$r \geq 0,$
the polynomial semigroup
![]() $G_{c, r}$
is mean stable if and only if
$G_{c, r}$
is mean stable if and only if
![]() $r \notin \{0, {\mathit {r}_{\mathrm {bif}}}(c)\}.$
$r \notin \{0, {\mathit {r}_{\mathrm {bif}}}(c)\}.$
Before describing the dynamics of a mean stable system, we define the function representing the probability of random orbits tending to an attractor.
Definition 2.19. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() ${\mathbb {C}}$
with compact support. For every attracting minimal set L of
${\mathbb {C}}$
with compact support. For every attracting minimal set L of
![]() $G_{\mu }$
, we define the function
$G_{\mu }$
, we define the function
![]() ${T}_{L, \mu } \colon {\widehat {\mathbb {C}}} \to [0, 1]$
by
${T}_{L, \mu } \colon {\widehat {\mathbb {C}}} \to [0, 1]$
by
for every point
![]() $z \in {\widehat {\mathbb {C}}} $
, where
$z \in {\widehat {\mathbb {C}}} $
, where
![]() $d(w, L) = \min _{w' \in L} d(w, w')$
.
$d(w, L) = \min _{w' \in L} d(w, w')$
.
The following theorem reveals an interesting noise-induced order. That is, almost every orbit is attracted by some attracting minimal set and the probability
![]() $T_{L, \mu }(z)$
tending to the attractor L depends continuously on initial point z if the system is mean stable. For the details, see [Reference Sumi27, Theorem 3.15].
$T_{L, \mu }(z)$
tending to the attractor L depends continuously on initial point z if the system is mean stable. For the details, see [Reference Sumi27, Theorem 3.15].
Definition 2.20. For a polynomial semigroup G, define the kernel Julia set by
 $$ \begin{align*} J_{\mathrm{ker}}(G) = \bigcap_{g \in G} g^{-1}(J(G)). \end{align*} $$
$$ \begin{align*} J_{\mathrm{ker}}(G) = \bigcap_{g \in G} g^{-1}(J(G)). \end{align*} $$
Theorem 2.21. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() ${\mathbb {C}}$
with compact support. If
${\mathbb {C}}$
with compact support. If
![]() $J_{\mathrm {ker}}(G) = \emptyset $
, then
$J_{\mathrm {ker}}(G) = \emptyset $
, then
![]() $T_{\{\infty \}, \mu }$
is continuous on
$T_{\{\infty \}, \mu }$
is continuous on
![]() ${\widehat {\mathbb {C}}}$
. Moreover, the sum satisfies
${\widehat {\mathbb {C}}}$
. Moreover, the sum satisfies
![]() $\sum _{L} {T}_{L, \mu }(z) = 1$
for every
$\sum _{L} {T}_{L, \mu }(z) = 1$
for every
![]() $z \in {\widehat {\mathbb {C}}}$
where the sum runs over all attracting minimal sets L.
$z \in {\widehat {\mathbb {C}}}$
where the sum runs over all attracting minimal sets L.
The following gives a useful sufficient condition for
![]() $J_{\mathrm {ker}}(G) = \emptyset $
.
$J_{\mathrm {ker}}(G) = \emptyset $
.
Lemma 2.22. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() ${\mathbb {C}}$
with compact support. If
${\mathbb {C}}$
with compact support. If
![]() $\mathrm {int} (\operatorname {\mathrm {supp}} \mu ) \neq \emptyset $
, then
$\mathrm {int} (\operatorname {\mathrm {supp}} \mu ) \neq \emptyset $
, then
![]() $J_{\mathrm {ker}}(G_{\mu }) = \emptyset $
.
$J_{\mathrm {ker}}(G_{\mu }) = \emptyset $
.
See [Reference Sumi27, Lemma 5.34] for the proof. Notably, the continuity of
![]() ${T}_{L, \mu }$
in Theorem 2.21 does not occur in deterministic dynamical systems. Namely, if
${T}_{L, \mu }$
in Theorem 2.21 does not occur in deterministic dynamical systems. Namely, if
![]() $\mu $
is the Dirac measure at c, then the function
$\mu $
is the Dirac measure at c, then the function
![]() $T_{\{\infty \}, \mu }$
takes
$T_{\{\infty \}, \mu }$
takes
![]() $1$
on
$1$
on
![]() $A(f_{c})$
and
$A(f_{c})$
and
![]() $0$
on
$0$
on
![]() $K(f_{c})$
, where
$K(f_{c})$
, where
![]() $A(f_{c}) = A_{\omega }$
and
$A(f_{c}) = A_{\omega }$
and
![]() $K(f_{c}) = K_{\omega }$
for
$K(f_{c}) = K_{\omega }$
for
![]() $\omega = (c, c, \ldots )$
. Thus,
$\omega = (c, c, \ldots )$
. Thus,
![]() $T_{\{\infty \}, \mu }$
is discontinuous on the autonomous Julia set
$T_{\{\infty \}, \mu }$
is discontinuous on the autonomous Julia set
![]() $J(f_{c}) = J_{\omega }$
.
$J(f_{c}) = J_{\omega }$
.
Theorem 2.21 suggests that the dynamics of a mean stable system is similar to that of a hyperbolic map. In the latter case, every orbit on the Fatou set is contracted to an attracting cycle, while the complementary Julia set has zero areas.
The set of all hyperbolic rational maps is conjectured to be open and dense in the space of all rational maps. Even in the quadratic polynomial case, whether or not
![]() $\overline {\mathcal {H}} = {\,\mathcal {M}}$
remains unsolved. As is well known, this conjecture can be affirmatively solved if one proves that the boundary
$\overline {\mathcal {H}} = {\,\mathcal {M}}$
remains unsolved. As is well known, this conjecture can be affirmatively solved if one proves that the boundary
![]() $\partial {\mathcal {M}}$
is locally connected. Meanwhile, it is still open whether or not the boundary of the Mandelbrot set has a positive area, although Shishikura showed that it has the full Hausdorff dimension.
$\partial {\mathcal {M}}$
is locally connected. Meanwhile, it is still open whether or not the boundary of the Mandelbrot set has a positive area, although Shishikura showed that it has the full Hausdorff dimension.
Compared with the autonomous case, the following results show that we can solve random versions of the abovementioned conjectures. For the proof, see [Reference Sumi28, Reference Sumi and Watanabe31].
Theorem 2.23. For every
![]() $c \in {\mathbb {C}}$
and
$c \in {\mathbb {C}}$
and
![]() $r \geq 0$
, define the polynomial semigroup
$r \geq 0$
, define the polynomial semigroup
![]() $G_{c, r}$
as the semigroup generated by
$G_{c, r}$
as the semigroup generated by
![]() $\{f_{c'} \in {\mathrm {Poly}} \colon |c' - c| \leq r\}$
. Then we have all the following statements.
$\{f_{c'} \in {\mathrm {Poly}} \colon |c' - c| \leq r\}$
. Then we have all the following statements.
-
(i) The set
 $\{ (c, r) \in {\mathbb {C}} \times \ ${\mathbb {C}} \times \ $r \in [0, \infty )$
, the set
$r \in [0, \infty )$
, the set
 $\{c \in {\mathbb {C}} \colon G_{c, r} \text { is not mean stable} \}$
has zero two-dimensional Lebesgue measure.
$\{c \in {\mathbb {C}} \colon G_{c, r} \text { is not mean stable} \}$
has zero two-dimensional Lebesgue measure.
We also have the following tameness if noise is added.
Theorem 2.24. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() ${\mathbb {C}}$
with compact support. If
${\mathbb {C}}$
with compact support. If
![]() $J_{\mathrm {ker}}(G) = \emptyset $
, then the random Julia set
$J_{\mathrm {ker}}(G) = \emptyset $
, then the random Julia set
![]() $J_{\omega }$
has zero two-dimensional Lebesgue measure for
$J_{\omega }$
has zero two-dimensional Lebesgue measure for
![]() ${\mathbb {P}}_{\mu }$
-almost every
${\mathbb {P}}_{\mu }$
-almost every
![]() $\omega \in \Omega _{\mu }$
.
$\omega \in \Omega _{\mu }$
.
One may mistakenly consider that Theorem 2.24 is insignificant since it is difficult to construct autonomous Julia sets with positive areas. However, compared with the autonomous case, constructing the non-autonomous Julia set of positive areas is not very difficult. Jones et al found that there exists
![]() $\omega = (c_{n})_{n=1}^{\infty }$
with
$\omega = (c_{n})_{n=1}^{\infty }$
with
![]() $c_{n} \in \{0,\, 1/2,\, 1/4\}$
for all
$c_{n} \in \{0,\, 1/2,\, 1/4\}$
for all
![]() $n \in {\mathbb {N}}$
such that
$n \in {\mathbb {N}}$
such that
![]() $J_{\omega }$
has positive areas. They use the parabolic fixed point
$J_{\omega }$
has positive areas. They use the parabolic fixed point
![]() $1/2$
of the map
$1/2$
of the map
![]() $f_{1/4}.$
For the proof, see [Reference Comerford10, §5.2]. Developing the idea, Comerford proved the existence of measurable invariant sequences of line fields [Reference Comerford8].
$f_{1/4}.$
For the proof, see [Reference Comerford10, §5.2]. Developing the idea, Comerford proved the existence of measurable invariant sequences of line fields [Reference Comerford8].
As presented above, the dynamics of mean stable systems is similar to that of hyperbolic polynomial maps. However, they cause interesting phenomena that cannot occur in deterministic dynamical systems, e.g., continuity of
![]() $T_{L, \mu }$
, finiteness of the set of all minimal sets, etc. This motivates us to determine the bifurcation radius where the mean stability breaks.
$T_{L, \mu }$
, finiteness of the set of all minimal sets, etc. This motivates us to determine the bifurcation radius where the mean stability breaks.
3. Total disconnectedness
The systematic study of random iterations of the quadratic polynomial was done by Brück and Büger. In particular, Brück, Büger, and Reitz investigated the (dis)connectedness of the non-autonomous Julia sets in [Reference Brück, Büger and Reitz4]. Here, we present some conditions for the random Julia set to be connected or totally disconnected.
The following [Reference Brück, Büger and Reitz4, Theorem 1.1] shows that the critical orbits determine connectedness of Julia sets. Compared with the autonomous case, we need to modify the statement suitably.
Theorem 3.1. Let
![]() $\omega = (c_{n})_{n =1}^{\infty } \in {\mathbb {C}}^{{\mathbb {N}}}$
. Then the non-autonomous Julia set
$\omega = (c_{n})_{n =1}^{\infty } \in {\mathbb {C}}^{{\mathbb {N}}}$
. Then the non-autonomous Julia set
![]() $J_{\omega }$
is connected if and only if the orbit
$J_{\omega }$
is connected if and only if the orbit
![]() $\{ {{f}_{{\sigma ^{k}\omega }}^{({n})}} (0) \}_{n=1}^{\infty }$
is bounded in
$\{ {{f}_{{\sigma ^{k}\omega }}^{({n})}} (0) \}_{n=1}^{\infty }$
is bounded in
![]() ${\mathbb {C}}$
for every
${\mathbb {C}}$
for every
![]() $k \in {\mathbb {N}}$
.
$k \in {\mathbb {N}}$
.
Recall that if
![]() $\omega = (c_{n})_{n=1}^{\infty }$
, then
$\omega = (c_{n})_{n=1}^{\infty }$
, then
![]() ${{f}_{{\sigma ^{k}\omega }}^{({n})}} = {f_{{c_{k+n}}} \circ \cdots \circ f_{{c_{k+2}}} \circ f_{{c_{k+1}}}}$
by definition. We remark on the difficulty of the disconnected case compared with the autonomous case.
${{f}_{{\sigma ^{k}\omega }}^{({n})}} = {f_{{c_{k+n}}} \circ \cdots \circ f_{{c_{k+2}}} \circ f_{{c_{k+1}}}}$
by definition. We remark on the difficulty of the disconnected case compared with the autonomous case.
Remark 3.2. For an autonomous case, the Julia set of a quadratic polynomial is either connected or totally disconnected [Reference Milnor21, Problem 9-f]. However, for a non-autonomous case, we can construct a Julia set that has more than one but finitely many connected components. For instance, if
![]() $|c_{1}|> 1$
and
$|c_{1}|> 1$
and
![]() $c_{n} =0$
for every
$c_{n} =0$
for every
![]() $n \geq 2$
, then
$n \geq 2$
, then
![]() $J_{\omega } = f_{c_{1}}^{-1}(J_{\sigma \omega })$
has exactly two connected components where
$J_{\omega } = f_{c_{1}}^{-1}(J_{\sigma \omega })$
has exactly two connected components where
![]() $\omega = (c_{n})_{n=1}^{\infty }$
. Similarly, we can construct various non-autonomous Julia sets with finitely many connected components. Furthermore, there exists
$\omega = (c_{n})_{n=1}^{\infty }$
. Similarly, we can construct various non-autonomous Julia sets with finitely many connected components. Furthermore, there exists
![]() $\omega = (c_{n})_{n=1}^{\infty }$
such that
$\omega = (c_{n})_{n=1}^{\infty }$
such that
![]() $|c_{n}| < 2$
for every
$|c_{n}| < 2$
for every
![]() $n \in {\mathbb {N}}$
and
$n \in {\mathbb {N}}$
and
![]() ${{f}_{{\sigma ^{k}\omega }}^{({n})}}(0) \to \infty $
as
${{f}_{{\sigma ^{k}\omega }}^{({n})}}(0) \to \infty $
as
![]() $n \to \infty $
for every
$n \to \infty $
for every
![]() $k \in {\mathbb {N}}$
, but the filled Julia set
$k \in {\mathbb {N}}$
, but the filled Julia set
![]() $K_{\omega }$
contains a segment (see [Reference Brück, Büger and Reitz4, Example 4.4]). Thus, it is interesting to determine when the non-autonomous Julia set
$K_{\omega }$
contains a segment (see [Reference Brück, Büger and Reitz4, Example 4.4]). Thus, it is interesting to determine when the non-autonomous Julia set
![]() $J_{\omega }$
is connected, has finitely many connected components, is totally disconnected, and so on.
$J_{\omega }$
is connected, has finitely many connected components, is totally disconnected, and so on.
For the case when
![]() $\mu $
is the normalized Lebesgue measure on the disk
$\mu $
is the normalized Lebesgue measure on the disk
![]() ${\bar {B}({0}, {r})} $
, Brück, Büger, and Reitz showed that
${\bar {B}({0}, {r})} $
, Brück, Büger, and Reitz showed that
![]() $r = 1/4$
is the critical value where connectedness drastically changes as we see below. If
$r = 1/4$
is the critical value where connectedness drastically changes as we see below. If
![]() $r \leq 1/4,$
then the random Julia set
$r \leq 1/4,$
then the random Julia set
![]() $J_{\omega }$
is connected for every
$J_{\omega }$
is connected for every
![]() $\omega \in \Omega _{\mu }$
[Reference Brück, Büger and Reitz4, Remark 1.2]. Brück, Büger, and Reitz then questioned whether the random Julia set
$\omega \in \Omega _{\mu }$
[Reference Brück, Büger and Reitz4, Remark 1.2]. Brück, Büger, and Reitz then questioned whether the random Julia set
![]() $J_{\omega }$
is totally disconnected almost surely if
$J_{\omega }$
is totally disconnected almost surely if
![]() $r> 1/4$
.
$r> 1/4$
.
Lech and Zdunik [Reference Lech and Zdunik17] showed that it is true. We pay attention to their idea for a while.
Definition 3.3. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() ${\mathbb {C}}$
with compact support. Let
${\mathbb {C}}$
with compact support. Let
![]() $R> 0$
be a large number as in Lemma 2.6(1).
$R> 0$
be a large number as in Lemma 2.6(1).
For every
![]() $\omega \in \Omega _{\mu }$
, define the escape time
$\omega \in \Omega _{\mu }$
, define the escape time
![]() $k(z, \omega )$
of z from
$k(z, \omega )$
of z from
![]() $D_{R}$
by
$D_{R}$
by
 $$ \begin{align*} k(z, \omega) = \begin{cases} \min \{n \in {\mathbb{N}} \colon | {{f}_{{\omega}}^{({n})}} (z) |> R \} & \text{if } z \in A_{\omega}, \\ \infty & \text{if } z \in K_{\omega}. \end{cases} \end{align*} $$
$$ \begin{align*} k(z, \omega) = \begin{cases} \min \{n \in {\mathbb{N}} \colon | {{f}_{{\omega}}^{({n})}} (z) |> R \} & \text{if } z \in A_{\omega}, \\ \infty & \text{if } z \in K_{\omega}. \end{cases} \end{align*} $$
We say that the critical point
![]() $0$
is typically fast escaping if there exists
$0$
is typically fast escaping if there exists
![]() $\gamma> 0$
such that
$\gamma> 0$
such that
![]() ${\mathbb {P}}_{\mu }(\{\omega \in \Omega _{\mu } \colon k(0, \omega )> k\}) \leq e^{{-\gamma k}}$
for every
${\mathbb {P}}_{\mu }(\{\omega \in \Omega _{\mu } \colon k(0, \omega )> k\}) \leq e^{{-\gamma k}}$
for every
![]() $k \in {\mathbb {N}}$
.
$k \in {\mathbb {N}}$
.
Note that the escape time is related to the value of the Green function
where
![]() $\log _{+}a = \max \{a, \ 0\}$
for
$\log _{+}a = \max \{a, \ 0\}$
for
![]() $a \in {\mathbb {R}}$
. By [Reference Lech and Zdunik17, Proposition 8], there exists
$a \in {\mathbb {R}}$
. By [Reference Lech and Zdunik17, Proposition 8], there exists
![]() $C> 0$
such that for every
$C> 0$
such that for every
![]() $\omega \in \Omega _{\mu }$
and
$\omega \in \Omega _{\mu }$
and
![]() $z \in A_{\omega } \cap D_{R}$
, we have
$z \in A_{\omega } \cap D_{R}$
, we have
Hence, typical fast escaping can be defined using the Green functions. For details, see [Reference Lech and Zdunik17]. For other discussions on the Green function, see also [Reference Fornæss and Sibony12, Reference Jonsson16, Reference Sumi26].
The following theorem gives a sufficient condition of random Julia sets to be totally disconnected almost surely. For the proof, see [Reference Lech and Zdunik17, Theorem 11].
Theorem 3.4. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() ${\mathbb {C}}$
with compact support. If the critical point
${\mathbb {C}}$
with compact support. If the critical point
![]() $0$
is typically fast escaping, then the Julia set
$0$
is typically fast escaping, then the Julia set
![]() $J_{\omega }$
is totally disconnected for
$J_{\omega }$
is totally disconnected for
![]() ${\mathbb {P}}_{\mu }$
-almost every
${\mathbb {P}}_{\mu }$
-almost every
![]() $\omega \in \Omega _{\mu }$
.
$\omega \in \Omega _{\mu }$
.
Using the theorem above, the authors of [Reference Lech and Zdunik17] proved the following theorem.
Theorem 3.5. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() ${\mathbb {C}}$
with compact support. If
${\mathbb {C}}$
with compact support. If
![]() $\operatorname {\mathrm {supp}} \mu \supset {\bar {B}({0}, {1/4})}$
and
$\operatorname {\mathrm {supp}} \mu \supset {\bar {B}({0}, {1/4})}$
and
![]() $\operatorname {\mathrm {supp}} \mu \neq {\bar {B}({0}, {1/4})}$
, then the random Julia set
$\operatorname {\mathrm {supp}} \mu \neq {\bar {B}({0}, {1/4})}$
, then the random Julia set
![]() $J_{\omega }$
is totally disconnected for
$J_{\omega }$
is totally disconnected for
![]() ${\mathbb {P}}_{\mu }$
-almost every
${\mathbb {P}}_{\mu }$
-almost every
![]() $\omega \in \Omega _{\mu }$
.
$\omega \in \Omega _{\mu }$
.
Consider the case where
![]() $\mu $
is the normalized Lebesgue measure on the disk
$\mu $
is the normalized Lebesgue measure on the disk
![]() ${\bar {B}({c}, {r})} $
. From above, the connectedness changes at
${\bar {B}({c}, {r})} $
. From above, the connectedness changes at
![]() $r = 1/4$
if
$r = 1/4$
if
![]() $c = 0$
. Since the value
$c = 0$
. Since the value
![]() $1/4$
is the distance from
$1/4$
is the distance from
![]() $c = 0$
to the boundary of the Mandelbrot set, one may conjecture that the transition from connected to disconnected Julia sets equals the distance from c to the boundary of the Mandelbrot set for any
$c = 0$
to the boundary of the Mandelbrot set, one may conjecture that the transition from connected to disconnected Julia sets equals the distance from c to the boundary of the Mandelbrot set for any
![]() $c \in {\mathcal {M}}$
. However, Theorem 3.5 states that even if
$c \in {\mathcal {M}}$
. However, Theorem 3.5 states that even if
![]() $\operatorname {\mathrm {supp}} \mu $
is contained in the closure of the main cardioid of the Mandelbrot set, it can happen that the random Julia set
$\operatorname {\mathrm {supp}} \mu $
is contained in the closure of the main cardioid of the Mandelbrot set, it can happen that the random Julia set
![]() $J_{\omega }$
is totally disconnected almost surely.
$J_{\omega }$
is totally disconnected almost surely.
Before giving the sufficient condition of typical fast escaping, we show the following lemma.
Lemma 3.6. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() ${\mathbb {C}}$
with compact support. Define
${\mathbb {C}}$
with compact support. Define
![]() $E = \{z \in {\widehat {\mathbb {C}}} \colon {T}_{\{\infty \}, \mu }(z) = 1\}$
. If
$E = \{z \in {\widehat {\mathbb {C}}} \colon {T}_{\{\infty \}, \mu }(z) = 1\}$
. If
![]() $z \in E$
and
$z \in E$
and
![]() $k \in {\mathbb {N}}$
, then
$k \in {\mathbb {N}}$
, then
![]() ${{f}_{{\omega }}^{({k})}}(z) \in E$
for
${{f}_{{\omega }}^{({k})}}(z) \in E$
for
![]() ${\mathbb {P}}_{\mu }$
-almost every
${\mathbb {P}}_{\mu }$
-almost every
![]() $\omega \in \Omega _{\mu }.$
$\omega \in \Omega _{\mu }.$
Proof. Since
![]() ${\mathbb {P}}_{\mu }$
is the product of the probability measure
${\mathbb {P}}_{\mu }$
is the product of the probability measure
![]() $\mu $
, Fubini’s theorem implies
$\mu $
, Fubini’s theorem implies
 $$ \begin{align*} T_{\{\infty\}, \mu}(z) = \int_{{\bar{B}({c}, {r})} } T_{\{\infty\}, \mu}(f_{c_{1}} (z))\,\mathit{d} \mu (c_{1}) \end{align*} $$
$$ \begin{align*} T_{\{\infty\}, \mu}(z) = \int_{{\bar{B}({c}, {r})} } T_{\{\infty\}, \mu}(f_{c_{1}} (z))\,\mathit{d} \mu (c_{1}) \end{align*} $$
for every
![]() $z \in {\widehat {\mathbb {C}}}$
. By induction, we have
$z \in {\widehat {\mathbb {C}}}$
. By induction, we have
![]() $T_{\{\infty \}, \mu }(z) = \int _{\Omega } T_{\{\infty \}, \mu }({{f}_{{\omega }}^{({k})}}(z))\,\mathit{d}{\mathbb {P}}_{\mu } (\omega ).$
Thus, if
$T_{\{\infty \}, \mu }(z) = \int _{\Omega } T_{\{\infty \}, \mu }({{f}_{{\omega }}^{({k})}}(z))\,\mathit{d}{\mathbb {P}}_{\mu } (\omega ).$
Thus, if
![]() $T_{\{\infty \}, \mu }(z) = 1$
, then
$T_{\{\infty \}, \mu }(z) = 1$
, then
![]() $T_{\{\infty \}, \mu }({{f}_{{\omega }}^{({k})}} (z)) = 1$
with probability one.
$T_{\{\infty \}, \mu }({{f}_{{\omega }}^{({k})}} (z)) = 1$
with probability one.
The following is the new and original result that gives a sufficient condition for typical fast escaping.
Theorem 3.7. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() ${\mathbb {C}}$
with compact support. Suppose that
${\mathbb {C}}$
with compact support. Suppose that
![]() $T_{\{\infty \}, \mu }$
is continuous. If
$T_{\{\infty \}, \mu }$
is continuous. If
![]() $T_{\{\infty \}, \mu }(0) = 1,$
then the critical point
$T_{\{\infty \}, \mu }(0) = 1,$
then the critical point
![]() $0$
is typically fast escaping, and hence the random Julia set
$0$
is typically fast escaping, and hence the random Julia set
![]() $J_{\omega }$
is totally disconnected for
$J_{\omega }$
is totally disconnected for
![]() ${\mathbb {P}}_{\mu }$
-almost every
${\mathbb {P}}_{\mu }$
-almost every
![]() $\omega \in \Omega _{\mu }$
.
$\omega \in \Omega _{\mu }$
.
Proof. The latter statement is a consequence of Theorem 3.4. Thus, it suffices to show that the critical point
![]() $0$
is typically fast escaping. Let
$0$
is typically fast escaping. Let
![]() $R> 0$
be a large number as in Lemma 2.6(1). Set
$R> 0$
be a large number as in Lemma 2.6(1). Set
![]() $E = \{z \in {\widehat {\mathbb {C}}} \colon {T}_{\{\infty \}, \mu }(z) = 1\}$
, then E is compact since we assume that
$E = \{z \in {\widehat {\mathbb {C}}} \colon {T}_{\{\infty \}, \mu }(z) = 1\}$
, then E is compact since we assume that
![]() $T_{\{\infty \}, \mu }$
is continuous. (This is the only place where the assumption of continuity is used.)
$T_{\{\infty \}, \mu }$
is continuous. (This is the only place where the assumption of continuity is used.)
For every
![]() $z \in E$
, there exist
$z \in E$
, there exist
![]() $n_{z} \in {\mathbb {N}}$
and
$n_{z} \in {\mathbb {N}}$
and
![]() $c^{z}_{1}, c^{z}_{2}, \ldots c^{z}_{n_{z}} \in \operatorname {\mathrm {supp}} \mu $
such that
$c^{z}_{1}, c^{z}_{2}, \ldots c^{z}_{n_{z}} \in \operatorname {\mathrm {supp}} \mu $
such that
![]() $|f_{{c^{z}_{n_{z}}}} \circ \cdots \circ \ f_{{c^{z}_{2}}} \circ f_{{c^{z}_{1}}} (z)|> R$
. Since this map
$|f_{{c^{z}_{n_{z}}}} \circ \cdots \circ \ f_{{c^{z}_{2}}} \circ f_{{c^{z}_{1}}} (z)|> R$
. Since this map
![]() ${f_{{c^{z}_{n_{z}}}} \circ \cdots \circ f_{{c^{z}_{2}}} \circ f_{{c^{z}_{1}}}}$
is continuous, there exists an open neighborhood
${f_{{c^{z}_{n_{z}}}} \circ \cdots \circ f_{{c^{z}_{2}}} \circ f_{{c^{z}_{1}}}}$
is continuous, there exists an open neighborhood
![]() $O_{z}$
of z such that for every
$O_{z}$
of z such that for every
![]() $z' \in O_{z}$
, we have
$z' \in O_{z}$
, we have
![]() $|{f_{{c^{z}_{n_{z}}}} \circ \cdots \circ f_{{c^{z}_{2}}} \circ f_{{c^{z}_{1}}}} (z')|> R$
. We may and do assume that
$|{f_{{c^{z}_{n_{z}}}} \circ \cdots \circ f_{{c^{z}_{2}}} \circ f_{{c^{z}_{1}}}} (z')|> R$
. We may and do assume that
![]() $O_{z}$
is precompact.
$O_{z}$
is precompact.
We now consider the open covering
![]() $\{O_{z}\}_{z \in E}$
of E. Since E is compact, there exists a finite subcover. Namely, there exist
$\{O_{z}\}_{z \in E}$
of E. Since E is compact, there exists a finite subcover. Namely, there exist
![]() $\ell \in {\mathbb {N}}$
and
$\ell \in {\mathbb {N}}$
and
![]() $\ell $
open sets
$\ell $
open sets
![]() $O_{j}\ (j =1, \ldots , \ell )$
such that
$O_{j}\ (j =1, \ldots , \ell )$
such that
![]() $E \subset \bigcup _{j=1}^{\ell } O_{j}.$
Moreover, for each
$E \subset \bigcup _{j=1}^{\ell } O_{j}.$
Moreover, for each
![]() $j =1, \ldots , \ell $
, there exist
$j =1, \ldots , \ell $
, there exist
![]() $n_{j} \in {\mathbb {N}}$
and
$n_{j} \in {\mathbb {N}}$
and
![]() ${c^{j}_{1}, c^{j}_{2}, \ldots c^{j}_{n_{z}} \kern1.2pt{\in}\kern1.2pt \operatorname {\mathrm {supp}} \mu }$
such that for every
${c^{j}_{1}, c^{j}_{2}, \ldots c^{j}_{n_{z}} \kern1.2pt{\in}\kern1.2pt \operatorname {\mathrm {supp}} \mu }$
such that for every
![]() $z' \kern1.2pt{\in}\kern1.2pt O_{j}$
, we have
$z' \kern1.2pt{\in}\kern1.2pt O_{j}$
, we have
![]() ${|{f_{{c^{j}_{n_{j}}}} \kern-0.1pt\!\circ \cdots \circ f_{{c^{j}_{2}}} \kern-1.2pt{\circ}\kern-1.2pt f_{{c^{j}_{1}}}} (z')|\kern1.2pt{>}\kern1.2pt R\kern-0.1pt}$
. Let
${|{f_{{c^{j}_{n_{j}}}} \kern-0.1pt\!\circ \cdots \circ f_{{c^{j}_{2}}} \kern-1.2pt{\circ}\kern-1.2pt f_{{c^{j}_{1}}}} (z')|\kern1.2pt{>}\kern1.2pt R\kern-0.1pt}$
. Let
![]() ${N = \max _{j =1, \ldots , \ell } n_{j}}$
. By Lemma 2.6(1), we can assume that
${N = \max _{j =1, \ldots , \ell } n_{j}}$
. By Lemma 2.6(1), we can assume that
![]() $n_{j} = N$
for every
$n_{j} = N$
for every
![]() $j=1, \ldots , \ell $
. Since
$j=1, \ldots , \ell $
. Since
![]() ${\mathbb {C}} \ni c \mapsto f_{c} \in {\mathrm {Poly}}$
is continuous, for every
${\mathbb {C}} \ni c \mapsto f_{c} \in {\mathrm {Poly}}$
is continuous, for every
![]() $n =1, 2, \ldots , N$
, there exists an open neighborhood
$n =1, 2, \ldots , N$
, there exists an open neighborhood
![]() $U^{j}_{n}$
of
$U^{j}_{n}$
of
![]() $c^{j}_{n}$
such that for every
$c^{j}_{n}$
such that for every
![]() $c_{n} \in U^{j}_{n}$
and
$c_{n} \in U^{j}_{n}$
and
![]() $z' \in O_{j}$
, we have
$z' \in O_{j}$
, we have
![]() $|{f_{{c_{N}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}(z')|> R$
.
$|{f_{{c_{N}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}(z')|> R$
.
Define
![]() $\mathfrak {S}^{k}(z) = \{ \omega \in \Omega _{\mu } \colon |{{f}_{{\omega }}^{({k})}} (z) | \leq R \}$
for every
$\mathfrak {S}^{k}(z) = \{ \omega \in \Omega _{\mu } \colon |{{f}_{{\omega }}^{({k})}} (z) | \leq R \}$
for every
![]() $z \in {\widehat {\mathbb {C}}}$
. Then, by the construction above, we have
$z \in {\widehat {\mathbb {C}}}$
. Then, by the construction above, we have
![]() ${\mathbb {P}}_{\mu } (\Omega _{\mu } \setminus\! \mathfrak {S}^{N}(z)) \geq {\mathbb {P}}_{\mu } (\prod _{n=1}^{N} U^{j}_{n} \times \prod _{N+1}^{\infty } {\bar {B}({c}, {r})} )$
for every
${\mathbb {P}}_{\mu } (\Omega _{\mu } \setminus\! \mathfrak {S}^{N}(z)) \geq {\mathbb {P}}_{\mu } (\prod _{n=1}^{N} U^{j}_{n} \times \prod _{N+1}^{\infty } {\bar {B}({c}, {r})} )$
for every
![]() $j =1, \ldots , \ell $
and
$j =1, \ldots , \ell $
and
![]() $z \in O_{j}$
. Since
$z \in O_{j}$
. Since
![]() $c^{j}_{n} \in \operatorname {\mathrm {supp}} \mu $
and
$c^{j}_{n} \in \operatorname {\mathrm {supp}} \mu $
and
![]() $U^{j}_{n}$
is its open neighborhood, we have
$U^{j}_{n}$
is its open neighborhood, we have
![]() $\mu (U^{j}_{n})> 0$
for every
$\mu (U^{j}_{n})> 0$
for every
![]() $j =1, \ldots , \ell $
and
$j =1, \ldots , \ell $
and
![]() $n =1, 2, \ldots , N$
. Define
$n =1, 2, \ldots , N$
. Define
![]() $\alpha = \min _{j =1, \ldots , \ell } \prod _{n=1}^{N} \mu (U^{j}_{n})> 0.$
Then, for every
$\alpha = \min _{j =1, \ldots , \ell } \prod _{n=1}^{N} \mu (U^{j}_{n})> 0.$
Then, for every
![]() $z \in E$
, we have
$z \in E$
, we have
![]() ${\mathbb {P}}_{\mu } (\mathfrak {S}^{N}(z)) \leq 1-\alpha .$
${\mathbb {P}}_{\mu } (\mathfrak {S}^{N}(z)) \leq 1-\alpha .$
It follows from Fubini’s theorem that
 $$ \begin{align*} \mathbb{P}_{\mu} (\mathfrak{S}^{k + N}(z)) = \int_{\Omega_{\mu}} \mathbb{P}_{\mu} (\mathfrak{S}^{N}({{f}_{{\omega}}^{({k})}} (z)))\,\mathit{d} \mathbb{P}_{\mu}(\omega) \end{align*} $$
$$ \begin{align*} \mathbb{P}_{\mu} (\mathfrak{S}^{k + N}(z)) = \int_{\Omega_{\mu}} \mathbb{P}_{\mu} (\mathfrak{S}^{N}({{f}_{{\omega}}^{({k})}} (z)))\,\mathit{d} \mathbb{P}_{\mu}(\omega) \end{align*} $$
for every
![]() $k \in {\mathbb {N}}$
. If
$k \in {\mathbb {N}}$
. If
![]() $\omega \not \in \mathfrak {S}^{k}(z)$
, then
$\omega \not \in \mathfrak {S}^{k}(z)$
, then
![]() $\mathfrak {S}^{N}({{f}_{{\omega }}^{({k})}} (z)) = \emptyset $
by Lemma 2.6. Thus, the integral on the complement of
$\mathfrak {S}^{N}({{f}_{{\omega }}^{({k})}} (z)) = \emptyset $
by Lemma 2.6. Thus, the integral on the complement of
![]() $\mathfrak {S}^{k}(z)$
is zero;
$\mathfrak {S}^{k}(z)$
is zero;
![]() ${\mathbb {P}}_{\mu } (\mathfrak {S}^{k + N}(z)) = \int _{\mathfrak {S}^{k}(z)} {\mathbb {P}}_{\mu } (\mathfrak {S}^{N}({{f}_{{\omega }}^{({k})}} (z)))\,\mathit{d}{\mathbb {P}}_{\mu }(\omega )$
. By Lemma 3.6, we have
${\mathbb {P}}_{\mu } (\mathfrak {S}^{k + N}(z)) = \int _{\mathfrak {S}^{k}(z)} {\mathbb {P}}_{\mu } (\mathfrak {S}^{N}({{f}_{{\omega }}^{({k})}} (z)))\,\mathit{d}{\mathbb {P}}_{\mu }(\omega )$
. By Lemma 3.6, we have
![]() ${\mathbb {P}}_{\mu } (\mathfrak {S}^{k + N}(z)) \leq (1 - \alpha ) {\mathbb {P}}_{\mu } (\mathfrak {S}^{k}(z) ) $
if
${\mathbb {P}}_{\mu } (\mathfrak {S}^{k + N}(z)) \leq (1 - \alpha ) {\mathbb {P}}_{\mu } (\mathfrak {S}^{k}(z) ) $
if
![]() $z \in E$
.
$z \in E$
.
Repeating this, we have
![]() ${\mathbb {P}}_{\mu } ( \mathfrak {S}^{mN}(0)) \leq (1 - \alpha )^{m} $
for every
${\mathbb {P}}_{\mu } ( \mathfrak {S}^{mN}(0)) \leq (1 - \alpha )^{m} $
for every
![]() $m \in {\mathbb {N}}$
. Thus, we can find a constant
$m \in {\mathbb {N}}$
. Thus, we can find a constant
![]() $\gamma> 0$
such that
$\gamma> 0$
such that
for every
![]() $k \in {\mathbb {N}}$
. This completes the proof.
$k \in {\mathbb {N}}$
. This completes the proof.
Corollary 3.8. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() ${\mathbb {C}}$
whose support is compact and satisfies
${\mathbb {C}}$
whose support is compact and satisfies
![]() $\mathrm {int} (\operatorname {\mathrm {supp}} \mu ) \neq \emptyset $
. If
$\mathrm {int} (\operatorname {\mathrm {supp}} \mu ) \neq \emptyset $
. If
![]() $T_{\{\infty \}, \mu }(0) = 1,$
then the random Julia set
$T_{\{\infty \}, \mu }(0) = 1,$
then the random Julia set
![]() $J_{\omega }$
is totally disconnected for
$J_{\omega }$
is totally disconnected for
![]() ${\mathbb {P}}_{\mu }$
-almost every
${\mathbb {P}}_{\mu }$
-almost every
![]() $\omega \in \Omega _{\mu }$
.
$\omega \in \Omega _{\mu }$
.
Corollary 3.9. Let
![]() $\mu $
be a Borel probability measure on
$\mu $
be a Borel probability measure on
![]() ${\mathbb {C}}$
whose support is compact. If
${\mathbb {C}}$
whose support is compact. If
![]() $G_{\mu }$
has no planar minimal sets, then the random Julia set
$G_{\mu }$
has no planar minimal sets, then the random Julia set
![]() $J_{\omega }$
is totally disconnected for
$J_{\omega }$
is totally disconnected for
![]() ${\mathbb {P}}_{\mu }$
-almost every
${\mathbb {P}}_{\mu }$
-almost every
![]() $\omega \in \Omega _{\mu }$
.
$\omega \in \Omega _{\mu }$
.
Proof. Since
![]() $G_{\mu }$
has no planar minimal sets, the function satisfies
$G_{\mu }$
has no planar minimal sets, the function satisfies
![]() $T_{\{\infty \}, \mu } \equiv 1$
by Theorem 2.21. Since the constant function is continuous, Theorem 3.7 implies the conclusion.
$T_{\{\infty \}, \mu } \equiv 1$
by Theorem 2.21. Since the constant function is continuous, Theorem 3.7 implies the conclusion.
For instance, let
![]() $\mu = \delta _{0}/2 + \delta _{c}/2$
be the convex combination of the Dirac measures at
$\mu = \delta _{0}/2 + \delta _{c}/2$
be the convex combination of the Dirac measures at
![]() $0$
and c with
$0$
and c with
![]() $|c|> 1.$
If
$|c|> 1.$
If
![]() $|z|> 1$
, then
$|z|> 1$
, then
![]() ${{{f}}_{{0}}^{\circ {n}}} (z) \to \infty $
as
${{{f}}_{{0}}^{\circ {n}}} (z) \to \infty $
as
![]() $n \to \infty .$
If
$n \to \infty .$
If
![]() $|z| \leq 1$
, then
$|z| \leq 1$
, then
![]() $|f_{c}(z)| \geq -|z^{2}| + |c|> 1$
, and hence
$|f_{c}(z)| \geq -|z^{2}| + |c|> 1$
, and hence
![]() ${{{f}}_{{0}}^{\circ {n}}} \circ f_{c}(z) \to \infty $
as
${{{f}}_{{0}}^{\circ {n}}} \circ f_{c}(z) \to \infty $
as
![]() $n \to \infty .$
This shows that
$n \to \infty .$
This shows that
![]() $G_{\mu }$
has no planar minimal sets, which implies that the random Julia set is totally disconnected
$G_{\mu }$
has no planar minimal sets, which implies that the random Julia set is totally disconnected
![]() ${\mathbb {P}}_{\mu }$
-almost surely.
${\mathbb {P}}_{\mu }$
-almost surely.
In the next section, we apply Corollary 3.8 to the case where
![]() $\mu $
is the normalized Lebesgue measure on the disk
$\mu $
is the normalized Lebesgue measure on the disk
![]() ${\bar {B}({c}, {r})} $
.
${\bar {B}({c}, {r})} $
.
4. Main results on uniform noise process
Throughout this section, we consider the case where
![]() $\mu $
is the normalized Lebesgue measure on the disk
$\mu $
is the normalized Lebesgue measure on the disk
![]() ${\bar {B}({c}, {r})} $
as in Setting 4.1.
${\bar {B}({c}, {r})} $
as in Setting 4.1.
Setting 4.1. For fixed
![]() $c \in {\mathbb {C}}$
and
$c \in {\mathbb {C}}$
and
![]() $r \geq 0$
, we define the following Borel probability measure
$r \geq 0$
, we define the following Borel probability measure
![]() $\mu _{c, r}$
on
$\mu _{c, r}$
on
![]() ${\mathbb {C}}$
with compact support. If
${\mathbb {C}}$
with compact support. If
![]() $r> 0$
, define
$r> 0$
, define
![]() $\mu _{c, r}$
as the normalized Lebesgue measure on
$\mu _{c, r}$
as the normalized Lebesgue measure on
![]() ${\bar {B}({c}, {r})} =\{c' \in \mathbb {C} \colon |c' - c| \leq r \}$
. If
${\bar {B}({c}, {r})} =\{c' \in \mathbb {C} \colon |c' - c| \leq r \}$
. If
![]() $r = 0$
, define
$r = 0$
, define
![]() $\mu _{c, r}$
as the Dirac measure at c. We define the probability space
$\mu _{c, r}$
as the Dirac measure at c. We define the probability space
![]() $(\Omega _{c, r}, \ {\mathbb {P}}_{c, r}) = (\Omega _{\mu _{c, r}}, \ {\mathbb {P}}_{\mu _{c, r}})$
as in Setting 2.1. Namely, denote by
$(\Omega _{c, r}, \ {\mathbb {P}}_{c, r}) = (\Omega _{\mu _{c, r}}, \ {\mathbb {P}}_{\mu _{c, r}})$
as in Setting 2.1. Namely, denote by
![]() $\mathbb {P}_{c, r} $
the one-sided infinite product of
$\mathbb {P}_{c, r} $
the one-sided infinite product of
![]() $\mu _{c, r}$
supported on
$\mu _{c, r}$
supported on
![]() $\Omega _{c, r} = \prod _{n = 1}^{\infty } {\bar {B}({c}, {r})} $
with the Borel
$\Omega _{c, r} = \prod _{n = 1}^{\infty } {\bar {B}({c}, {r})} $
with the Borel
![]() $\sigma $
-algebra. In addition, let the polynomial semigroup
$\sigma $
-algebra. In addition, let the polynomial semigroup
![]() $G_{c, r}$
be defined by the semigroup generated by
$G_{c, r}$
be defined by the semigroup generated by
![]() $\{f_{c'} \in {\mathrm {Poly}} \colon c' \in {\bar {B}({c}, {r})} \}$
and define the function
$\{f_{c'} \in {\mathrm {Poly}} \colon c' \in {\bar {B}({c}, {r})} \}$
and define the function
![]() $T_{c, r} \colon {\widehat {\mathbb {C}}} \to ~[0, 1]$
, abusing notation, by
$T_{c, r} \colon {\widehat {\mathbb {C}}} \to ~[0, 1]$
, abusing notation, by
Remark 4.2. Setting 4.1 can be interpreted as an additive-noise stochastic process in the following way. Fix
![]() $c \in {\mathbb {C}}$
and
$c \in {\mathbb {C}}$
and
![]() $r \geq 0$
. On a probability space
$r \geq 0$
. On a probability space
![]() $(\Omega ,\ \mathfrak {B}, \ {\mathbb {P}})$
, take independent random variables
$(\Omega ,\ \mathfrak {B}, \ {\mathbb {P}})$
, take independent random variables
![]() $\nu _{n} \colon \Omega \to {\mathbb {C}}$
that follow the uniform distribution on
$\nu _{n} \colon \Omega \to {\mathbb {C}}$
that follow the uniform distribution on
![]() ${\bar {B}({0}, {r})} $
for all
${\bar {B}({0}, {r})} $
for all
![]() $n \in {\mathbb {N}}$
. Fix
$n \in {\mathbb {N}}$
. Fix
![]() $z_{0} \in {\mathbb {C}}$
and define the random variable
$z_{0} \in {\mathbb {C}}$
and define the random variable
![]() $Z_{0} \colon \Omega \to {\mathbb {C}}$
by a constant map with value
$Z_{0} \colon \Omega \to {\mathbb {C}}$
by a constant map with value
![]() $z_{0}$
. Define the
$z_{0}$
. Define the
![]() ${\mathbb {C}}$
-valued stochastic process
${\mathbb {C}}$
-valued stochastic process
![]() $\{Z_{n}\}_{n \geq 0}$
on
$\{Z_{n}\}_{n \geq 0}$
on
![]() $(\Omega ,\ \mathfrak {B}, \ {\mathbb {P}})$
, inductively by
$(\Omega ,\ \mathfrak {B}, \ {\mathbb {P}})$
, inductively by
![]() $Z_{n+1} =f_{c}(Z_{n}) + \nu _{n+1}$
for every
$Z_{n+1} =f_{c}(Z_{n}) + \nu _{n+1}$
for every
![]() $n \geq 0$
. Then the distribution of
$n \geq 0$
. Then the distribution of
![]() $Z_{n}$
are identical to that of the random variable
$Z_{n}$
are identical to that of the random variable
![]() ${{f}_{{\bullet }}^{({n})}}(z_{0}) \colon \Omega _{c,r} \to {\mathbb {C}}$
for every
${{f}_{{\bullet }}^{({n})}}(z_{0}) \colon \Omega _{c,r} \to {\mathbb {C}}$
for every
![]() $n \in {\mathbb {N}}$
, where
$n \in {\mathbb {N}}$
, where
![]() ${{f}_{{\bullet }}^{({n})}} (z_{0})$
is the map
${{f}_{{\bullet }}^{({n})}} (z_{0})$
is the map
![]() $\omega \mapsto {{f}_{{\omega }}^{({n})}} (z_{0}).$
This stochastic process describes the process driven by adding uniform noise independently to the deterministic dynamical systems of
$\omega \mapsto {{f}_{{\omega }}^{({n})}} (z_{0}).$
This stochastic process describes the process driven by adding uniform noise independently to the deterministic dynamical systems of
![]() $f_{c}$
with the initial value
$f_{c}$
with the initial value
![]() $z_{0}$
. Here, the parameter r describes the size of noise that satisfies
$z_{0}$
. Here, the parameter r describes the size of noise that satisfies
![]() $| \nu _{n} | \leq r$
almost surely for every
$| \nu _{n} | \leq r$
almost surely for every
![]() $n \in {\mathbb {N}}$
.
$n \in {\mathbb {N}}$
.
We investigate the bifurcation radius
![]() ${\mathit {r}_{\mathrm {bif}}}(c)$
defined in Definition 2.17. Our final goal is to determine
${\mathit {r}_{\mathrm {bif}}}(c)$
defined in Definition 2.17. Our final goal is to determine
![]() ${\mathit {r}_{\mathrm {bif}}}(c)$
and we provide some partial results in this paper.
${\mathit {r}_{\mathrm {bif}}}(c)$
and we provide some partial results in this paper.
4.1. Relation between bifurcation and connectedness
In this subsection, we reveal the relation between bifurcation and connectedness. We start the discussion with the following corollary.
Corollary 4.3. Suppose that
![]() $r> {\mathit {r}_{\mathrm {bif}}}(c)$
. Then the random Julia set
$r> {\mathit {r}_{\mathrm {bif}}}(c)$
. Then the random Julia set
![]() $J_{\omega }$
is totally disconnected for
$J_{\omega }$
is totally disconnected for
![]() ${\mathbb {P}}_{c, r}$
-almost every
${\mathbb {P}}_{c, r}$
-almost every
![]() $\omega $
.
$\omega $
.
Proof. If
![]() $r> {\mathit {r}_{\mathrm {bif}}}(c),$
then
$r> {\mathit {r}_{\mathrm {bif}}}(c),$
then
![]() $T_{c, r} \equiv 1$
by Theorems 2.16 and 2.21. It follows from Corollary 3.8 that the random Julia set
$T_{c, r} \equiv 1$
by Theorems 2.16 and 2.21. It follows from Corollary 3.8 that the random Julia set
![]() $J_{\omega }$
is totally disconnected almost surely.
$J_{\omega }$
is totally disconnected almost surely.
In the following, suppose that the interior of the support
![]() ${\bar {B}({c}, {r})} $
contains a superattracting parameter.
${\bar {B}({c}, {r})} $
contains a superattracting parameter.
Lemma 4.4. Suppose that the interior of
![]() $ {\bar {B}({c}, {r})} $
contains a superattracting parameter
$ {\bar {B}({c}, {r})} $
contains a superattracting parameter
![]() $\tilde {c}$
. If there exists
$\tilde {c}$
. If there exists
![]() $\omega \in \Omega _{c, r}$
such that
$\omega \in \Omega _{c, r}$
such that
![]() ${{f}_{{\omega }}^{({n})}} (0) \to \infty $
as
${{f}_{{\omega }}^{({n})}} (0) \to \infty $
as
![]() $n \to \infty $
, then
$n \to \infty $
, then
![]() $r> r_{\mathrm {bif}}(c)$
.
$r> r_{\mathrm {bif}}(c)$
.
Proof. We show that for every
![]() $z \in {\widehat {\mathbb {C}}}$
, there exist
$z \in {\widehat {\mathbb {C}}}$
, there exist
![]() $c_{1}, c_{2} , \ldots \in {\bar {B}({c}, {r})} $
such that
$c_{1}, c_{2} , \ldots \in {\bar {B}({c}, {r})} $
such that
![]() $f_{c_{n}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}} (z) \to \infty $
, which implies that
$f_{c_{n}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}} (z) \to \infty $
, which implies that
![]() $G_{c, r}$
has no planar minimal sets.
$G_{c, r}$
has no planar minimal sets.
The proof is divided into three cases. Denote by
![]() $K(f_{\tilde {c}})$
the autonomous filled Julia set of the superattracting map
$K(f_{\tilde {c}})$
the autonomous filled Julia set of the superattracting map
![]() $f_{\tilde {c}}.$
If
$f_{\tilde {c}}.$
If
![]() $z \not \in K(f_{\tilde {c}})$
, then
$z \not \in K(f_{\tilde {c}})$
, then
![]() $ f_{\tilde {c}}^{\circ n} (z) \to \infty $
by definition. If
$ f_{\tilde {c}}^{\circ n} (z) \to \infty $
by definition. If
![]() $z \in \partial K(f_{\tilde {c}})$
, then there exists
$z \in \partial K(f_{\tilde {c}})$
, then there exists
![]() $c_{1} \in {\bar {B}({c}, {r})} $
such that
$c_{1} \in {\bar {B}({c}, {r})} $
such that
![]() $f_{c_{1}}(z) \not \in K(f_{\tilde {c}})$
and hence
$f_{c_{1}}(z) \not \in K(f_{\tilde {c}})$
and hence
![]() $ f_{\tilde {c}}^{\circ n} \circ f_{c_{1}} (z) \to \infty $
. If
$ f_{\tilde {c}}^{\circ n} \circ f_{c_{1}} (z) \to \infty $
. If
![]() $z \in \mathrm {int }K(f_{\tilde {c}})$
, then by the no wandering domain theorem, the orbit
$z \in \mathrm {int }K(f_{\tilde {c}})$
, then by the no wandering domain theorem, the orbit
![]() $ f_{\tilde {c}}^{\circ n} (z) $
converges to the attracting cycle of
$ f_{\tilde {c}}^{\circ n} (z) $
converges to the attracting cycle of
![]() $0$
. By the assumption, we have
$0$
. By the assumption, we have
![]() $0 \in A_{\omega }.$
Since the non-autonomous basin
$0 \in A_{\omega }.$
Since the non-autonomous basin
![]() $A_{\omega }$
is open, there exists an open neighborhood D of
$A_{\omega }$
is open, there exists an open neighborhood D of
![]() $0$
such that for every
$0$
such that for every
![]() $z' \in D$
, we have
$z' \in D$
, we have
![]() ${{f}_{{\omega }}^{({n} )}} (z') \to \infty $
as
${{f}_{{\omega }}^{({n} )}} (z') \to \infty $
as
![]() $n \to \infty $
. Take
$n \to \infty $
. Take
![]() $N \in {\mathbb {N}}$
so that
$N \in {\mathbb {N}}$
so that
![]() $ f_{\tilde {c}}^{\circ N} (z) \in D$
, then
$ f_{\tilde {c}}^{\circ N} (z) \in D$
, then
![]() ${{f}_{{\omega }}^{({n})}} ( f_{\tilde {c}}^{\circ N} (z)) \to \infty $
as
${{f}_{{\omega }}^{({n})}} ( f_{\tilde {c}}^{\circ N} (z)) \to \infty $
as
![]() $n \to \infty $
. This completes the proof.
$n \to \infty $
. This completes the proof.
Lemma 4.5. Suppose that the interior of
![]() $ {\bar {B}({c}, {r})} $
contains a superattracting parameter
$ {\bar {B}({c}, {r})} $
contains a superattracting parameter
![]() $\tilde {c}$
. If
$\tilde {c}$
. If
![]() $L = \overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}$
is bounded in
$L = \overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}$
is bounded in
![]() ${\mathbb {C}}$
, then L is a planar minimal set of
${\mathbb {C}}$
, then L is a planar minimal set of
![]() $G_{c, r}$
.
$G_{c, r}$
.
Proof. Fix any
![]() $z \in L$
. First, we show
$z \in L$
. First, we show
![]() $\overline {\bigcup _{g \in G_{c, r}}\{g(z)\}} \subset L.$
By definition, there exists
$\overline {\bigcup _{g \in G_{c, r}}\{g(z)\}} \subset L.$
By definition, there exists
![]() $g_{n} \in G_{c, r}$
such that
$g_{n} \in G_{c, r}$
such that
![]() $g_{n}(0) \to z$
as
$g_{n}(0) \to z$
as
![]() $n \to \infty .$
Then, for every
$n \to \infty .$
Then, for every
![]() $g \in G_{c, r}$
, we have
$g \in G_{c, r}$
, we have
![]() $g \circ g_{n}(0) \to g(z)$
as
$g \circ g_{n}(0) \to g(z)$
as
![]() $n \to \infty .$
Since
$n \to \infty .$
Since
![]() $G_{c, r}$
is a semigroup, we have
$G_{c, r}$
is a semigroup, we have
![]() $g \circ g_{n} \in G_{c, r}$
. Thus, we have
$g \circ g_{n} \in G_{c, r}$
. Thus, we have
![]() $g(z) \in L,$
which implies
$g(z) \in L,$
which implies
![]() $\overline {\bigcup _{g \in G_{c, r}}\{g(z)\}} \subset L.$
Next, we show
$\overline {\bigcup _{g \in G_{c, r}}\{g(z)\}} \subset L.$
Next, we show
![]() $\overline {\bigcup _{g \in G_{c, r}}\{g(z)\}} \supset L.$
For every open set U which intersects L, take
$\overline {\bigcup _{g \in G_{c, r}}\{g(z)\}} \supset L.$
For every open set U which intersects L, take
![]() $g_{1} \in G_{c, r}$
such that
$g_{1} \in G_{c, r}$
such that
![]() $g_{1}(0) \in U.$
Since
$g_{1}(0) \in U.$
Since
![]() $g_{1}$
is continuous, there exists an open set
$g_{1}$
is continuous, there exists an open set
![]() $U_{0}$
such that
$U_{0}$
such that
![]() $0 \in U_{0}$
and
$0 \in U_{0}$
and
![]() $g_{1}(U_{0}) \subset U.$
Since
$g_{1}(U_{0}) \subset U.$
Since
![]() $\overline {\bigcup _{g \in G_{c, r}}\{g(z)\}} \subset L,$
the autonomous orbit
$\overline {\bigcup _{g \in G_{c, r}}\{g(z)\}} \subset L,$
the autonomous orbit
![]() $\{{{{f}}_{{\tilde {c}}}^{\circ {n}}} (z)\}_{n \in {\mathbb {N}}}$
is bounded, and hence
$\{{{{f}}_{{\tilde {c}}}^{\circ {n}}} (z)\}_{n \in {\mathbb {N}}}$
is bounded, and hence
![]() $z \in K(f_{\tilde {c}})$
. If
$z \in K(f_{\tilde {c}})$
. If
![]() $z \in \partial K(f_{\tilde {c}})$
, then there exists
$z \in \partial K(f_{\tilde {c}})$
, then there exists
![]() $c_{1} \in {\bar {B}({c}, {r})} $
such that
$c_{1} \in {\bar {B}({c}, {r})} $
such that
![]() $f_{c_{1}}(z) \not \in K(f_{\tilde {c}}),$
but this contradicts
$f_{c_{1}}(z) \not \in K(f_{\tilde {c}}),$
but this contradicts
![]() $\overline {\bigcup _{g \in G_{c, r}}\{g(z)\}} \subset L.$
Thus,
$\overline {\bigcup _{g \in G_{c, r}}\{g(z)\}} \subset L.$
Thus,
![]() $z \in \mathrm {int } K(f_{\tilde {c}})$
. It follows from the no wandering domain theorem that there exists
$z \in \mathrm {int } K(f_{\tilde {c}})$
. It follows from the no wandering domain theorem that there exists
![]() $N \in {\mathbb {N}}$
such that
$N \in {\mathbb {N}}$
such that
![]() ${{{f}}_{{\tilde {c}}}^{\circ {N}}} (z) \in U_{0}$
. Thus,
${{{f}}_{{\tilde {c}}}^{\circ {N}}} (z) \in U_{0}$
. Thus,
![]() $g_{1} \circ {{{f}}_{{\tilde {c}}}^{\circ {N}}} (z) \in U,$
which implies
$g_{1} \circ {{{f}}_{{\tilde {c}}}^{\circ {N}}} (z) \in U,$
which implies
![]() $\overline {\bigcup _{g \in G_{c, r}}\{g(z)\}} \supset L.$
This completes the proof.
$\overline {\bigcup _{g \in G_{c, r}}\{g(z)\}} \supset L.$
This completes the proof.
The following is the main theorem of this paper.
Theorem 4.6. Suppose that the interior of
![]() $ {\bar {B}({c}, {r})} $
contains a superattracting parameter
$ {\bar {B}({c}, {r})} $
contains a superattracting parameter
![]() $\tilde {c}$
. Then the following four are equivalent.
$\tilde {c}$
. Then the following four are equivalent.
-
(1) The inequality
 $r \leq {\mathit {r}_{\mathrm {bif}}} (c)$
holds.
$r \leq {\mathit {r}_{\mathrm {bif}}} (c)$
holds. -
(2) For every
 $\omega \in \Omega _{c, r}$
, the orbit
$\omega \in \Omega _{c, r}$
, the orbit
 $\{ {{f}_{{\omega }}^{({n})}} (0) \}_{n=1}^{\infty }$
is bounded; hence,
$\{ {{f}_{{\omega }}^{({n})}} (0) \}_{n=1}^{\infty }$
is bounded; hence,
 $T_{c, r}(0) = 0$
.
$T_{c, r}(0) = 0$
. -
(3) The random Julia set
 $J_{\omega }$
is connected for every
$J_{\omega }$
is connected for every
 $\omega \in \Omega _{c, r}$
.
$\omega \in \Omega _{c, r}$
. -
(4) The set
 $\overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}$
is a planar minimal set of
$\overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}$
is a planar minimal set of
 $G_{c, r}$
.
$G_{c, r}$
.
In contraposition to this, the following four are equivalent.
-
(1′) The inequality
 $r> {\mathit {r}_{\mathrm {bif}}} (c)$
holds.
$r> {\mathit {r}_{\mathrm {bif}}} (c)$
holds. -
(2′) For
 ${\mathbb {P}}_{c, r}$
-almost every
${\mathbb {P}}_{c, r}$
-almost every
 $\omega \in \Omega _{c, r}$
, the orbit
$\omega \in \Omega _{c, r}$
, the orbit
 ${{f}_{{\omega }}^{({n})}} (0) \to \infty \ (n \to \infty )$
:
${{f}_{{\omega }}^{({n})}} (0) \to \infty \ (n \to \infty )$
:
 $T_{c, r}(0) = 1$
.
$T_{c, r}(0) = 1$
. -
(3′) The random Julia set
 $J_{\omega }$
is totally disconnected for
$J_{\omega }$
is totally disconnected for
 ${\mathbb {P}}_{c, r}$
-almost every
${\mathbb {P}}_{c, r}$
-almost every
 $\omega \in \Omega _{c, r}$
.
$\omega \in \Omega _{c, r}$
. -
(4′) The set
 $\overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}$
is not bounded in
$\overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}$
is not bounded in
 ${\mathbb {C}}$
.
${\mathbb {C}}$
.
Furthermore, either the former or the latter is valid.
Proof. It is obvious that item
![]() $(1)$
or
$(1)$
or
![]() $(1')$
is valid. First, we show the equivalence of the four from items
$(1')$
is valid. First, we show the equivalence of the four from items
![]() $(1)$
to
$(1)$
to
![]() $(4).$
$(4).$
![]() $(1)\Rightarrow (2):$
If
$(1)\Rightarrow (2):$
If
![]() $r \leq {\mathit {r}_{\mathrm {bif}}} (c)$
, then
$r \leq {\mathit {r}_{\mathrm {bif}}} (c)$
, then
![]() ${{f}_{{\omega }}^{({n})}} (0) \not \to \infty $
as
${{f}_{{\omega }}^{({n})}} (0) \not \to \infty $
as
![]() $n \to \infty $
for every
$n \to \infty $
for every
![]() $\omega \in \Omega _{c, r}$
by Lemma 4.4. Hence,
$\omega \in \Omega _{c, r}$
by Lemma 4.4. Hence,
![]() $T_{c, r}(0) = 0$
.
$T_{c, r}(0) = 0$
.
![]() $(2)\Rightarrow (3):$
Take a large
$(2)\Rightarrow (3):$
Take a large
![]() $R> 0$
as in Lemma 2.6(1). Suppose that for every
$R> 0$
as in Lemma 2.6(1). Suppose that for every
![]() $\omega \in \Omega _{c, r}$
, we have
$\omega \in \Omega _{c, r}$
, we have
![]() $\{{{f}_{{\omega }}^{({n})}}(0) \}_{n=1}^{\infty }$
is bounded. Then
$\{{{f}_{{\omega }}^{({n})}}(0) \}_{n=1}^{\infty }$
is bounded. Then
![]() $|{{f}_{{\omega }}^{({n})}} (0)| < R$
for every
$|{{f}_{{\omega }}^{({n})}} (0)| < R$
for every
![]() $n\in {\mathbb {N}}$
. By Theorem 3.1, the random Julia set
$n\in {\mathbb {N}}$
. By Theorem 3.1, the random Julia set
![]() $J_{\omega }$
is connected for every
$J_{\omega }$
is connected for every
![]() $\omega \in \Omega _{c, r}$
.
$\omega \in \Omega _{c, r}$
.
![]() $(3)\Rightarrow (4):$
Suppose that the random Julia set
$(3)\Rightarrow (4):$
Suppose that the random Julia set
![]() $J_{\omega }$
is connected for every
$J_{\omega }$
is connected for every
![]() $\omega \in \Omega _{c, r}$
. For a large
$\omega \in \Omega _{c, r}$
. For a large
![]() $R> 0$
as in Lemma 2.6(1), it follows from Theorem 3.1 that
$R> 0$
as in Lemma 2.6(1), it follows from Theorem 3.1 that
![]() $|{{f}_{{\sigma ^{k}\omega }}^{({n})}} (0)| \leq R$
for every
$|{{f}_{{\sigma ^{k}\omega }}^{({n})}} (0)| \leq R$
for every
![]() $\omega \in \Omega _{c, r}$
,
$\omega \in \Omega _{c, r}$
,
![]() $n \in {\mathbb {N}}$
, and
$n \in {\mathbb {N}}$
, and
![]() $k \in {\mathbb {N}}$
. Thus, the set
$k \in {\mathbb {N}}$
. Thus, the set
![]() $L = \overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}$
is bounded in
$L = \overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}$
is bounded in
![]() ${\mathbb {C}}$
. By Lemma 4.5, the set L is a planar minimal set.
${\mathbb {C}}$
. By Lemma 4.5, the set L is a planar minimal set.
![]() $(4)\Rightarrow (1):$
This is trivial. See the latter part of Definition 2.17.
$(4)\Rightarrow (1):$
This is trivial. See the latter part of Definition 2.17.
The argument above completes the proof of the equivalence from items
![]() $(1)$
to
$(1)$
to
![]() $(4).$
Next, we show the equivalence of the four from items
$(4).$
Next, we show the equivalence of the four from items
![]() $(1')$
to
$(1')$
to
![]() $(4').$
$(4').$
![]() $(1')\Rightarrow (2'):$
If
$(1')\Rightarrow (2'):$
If
![]() $r> {\mathit {r}_{\mathrm {bif}}} (c)$
, then
$r> {\mathit {r}_{\mathrm {bif}}} (c)$
, then
![]() $G_{c, r}$
has no planar minimal sets by Theorem 2.16. It follows from Theorem 2.21 that
$G_{c, r}$
has no planar minimal sets by Theorem 2.16. It follows from Theorem 2.21 that
![]() $T_{c, r}(z) = 1$
for every
$T_{c, r}(z) = 1$
for every
![]() $z \in {\widehat {\mathbb {C}}}$
, and hence
$z \in {\widehat {\mathbb {C}}}$
, and hence
![]() $T_{c, r}(0) = 1$
.
$T_{c, r}(0) = 1$
.
![]() $(2')\Rightarrow (3'):$
Suppose
$(2')\Rightarrow (3'):$
Suppose
![]() $T_{c, r}(0) = 1$
. If
$T_{c, r}(0) = 1$
. If
![]() $r>0$
, then the random Julia set
$r>0$
, then the random Julia set
![]() $J_{\omega }$
is totally disconnected
$J_{\omega }$
is totally disconnected
![]() ${\mathbb {P}}_{c, r}$
-almost surely by Corollary 3.8. If
${\mathbb {P}}_{c, r}$
-almost surely by Corollary 3.8. If
![]() $r = 0,$
then it trivially follows that the autonomous Julia set is totally disconnected.
$r = 0,$
then it trivially follows that the autonomous Julia set is totally disconnected.
![]() $(3')\Rightarrow (4'):$
If item
$(3')\Rightarrow (4'):$
If item
![]() $(3')$
holds, then there exists
$(3')$
holds, then there exists
![]() $\omega \in \Omega _{c, r}$
such that the random Julia set
$\omega \in \Omega _{c, r}$
such that the random Julia set
![]() $J_{\omega }$
is disconnected. By Theorem 3.1, there exists
$J_{\omega }$
is disconnected. By Theorem 3.1, there exists
![]() $k \in {\mathbb {N}}$
such that
$k \in {\mathbb {N}}$
such that
![]() ${{f}_{{\sigma ^{k}\omega }}^{({n})}} (0) \to \infty $
as
${{f}_{{\sigma ^{k}\omega }}^{({n})}} (0) \to \infty $
as
![]() $n \to \infty .$
Since
$n \to \infty .$
Since
![]() ${{f}_{{\sigma ^{k}\omega }}^{({n})}} \in G_{c, r}$
, then
${{f}_{{\sigma ^{k}\omega }}^{({n})}} \in G_{c, r}$
, then
![]() $\overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}$
is unbounded.
$\overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}$
is unbounded.
![]() $(4')\Rightarrow (1'):$
Let
$(4')\Rightarrow (1'):$
Let
![]() $R> 0$
be large, as in Lemma 2.6(1). If
$R> 0$
be large, as in Lemma 2.6(1). If
![]() $\overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}$
is not bounded, then there exists
$\overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}$
is not bounded, then there exists
![]() $g \in G_{c, r}$
such that
$g \in G_{c, r}$
such that
![]() $|g(0)|> R.$
By definition of
$|g(0)|> R.$
By definition of
![]() $G_{c, r},$
there exist
$G_{c, r},$
there exist
![]() $N \in {\mathbb {N}}$
and
$N \in {\mathbb {N}}$
and
![]() $c_{1}, c_{2}, \ldots , c_{N} \in {\bar {B}({c}, {r})} $
such that
$c_{1}, c_{2}, \ldots , c_{N} \in {\bar {B}({c}, {r})} $
such that
![]() $g = {f_{{c_{N}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}.$
Letting
$g = {f_{{c_{N}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}.$
Letting
![]() $c_{n} = c$
for every
$c_{n} = c$
for every
![]() $n \geq N+1$
and
$n \geq N+1$
and
![]() $\omega = (c_{n})_{n=1}^{\infty }$
, we have
$\omega = (c_{n})_{n=1}^{\infty }$
, we have
![]() ${{f}_{{\omega }}^{({n})}} (0) \to \infty $
as
${{f}_{{\omega }}^{({n})}} (0) \to \infty $
as
![]() $n \to \infty $
by Lemma 2.6. It follows from Lemma 4.4 that
$n \to \infty $
by Lemma 2.6. It follows from Lemma 4.4 that
![]() $r> {\mathit {r}_{\mathrm {bif}}} (c)$
.
$r> {\mathit {r}_{\mathrm {bif}}} (c)$
.
Remark 4.7. The orbit
![]() $\{ {{f}_{{\omega }}^{({n})}} (0) \}_{n=1}^{\infty }$
is bounded for every
$\{ {{f}_{{\omega }}^{({n})}} (0) \}_{n=1}^{\infty }$
is bounded for every
![]() $\omega \in \Omega _{c, r}$
if and only if
$\omega \in \Omega _{c, r}$
if and only if
![]() $T_{c, r}(0) = 0$
.
$T_{c, r}(0) = 0$
.
Proof. It is obvious that the ‘only if’ part is true. Suppose
![]() $T_{c, r}(0) = 0$
and we show there does not exist
$T_{c, r}(0) = 0$
and we show there does not exist
![]() $\omega \in \Omega _{c, r}$
such that
$\omega \in \Omega _{c, r}$
such that
![]() ${{f}_{{\omega }}^{({n})}} (0) \to \infty $
as
${{f}_{{\omega }}^{({n})}} (0) \to \infty $
as
![]() $n \to \infty $
by contradiction. Take a large number
$n \to \infty $
by contradiction. Take a large number
![]() $R> 0$
as in Lemma 2.6(1). If there exists
$R> 0$
as in Lemma 2.6(1). If there exists
![]() $\omega = (c_{n})_{n \in {\mathbb {N}}} \in \Omega _{c, r}$
such that
$\omega = (c_{n})_{n \in {\mathbb {N}}} \in \Omega _{c, r}$
such that
![]() ${{f}_{{\omega }}^{({n})}}(0) \to \infty $
, then there exists
${{f}_{{\omega }}^{({n})}}(0) \to \infty $
, then there exists
![]() $N \in {\mathbb {N}}$
such that
$N \in {\mathbb {N}}$
such that
![]() $|{f_{{c_{N}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}} (0)|> R.$
Since
$|{f_{{c_{N}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}} (0)|> R.$
Since
![]() ${\mathbb {C}} \ni c \mapsto f_{c} \in {\mathrm {Poly}}$
is continuous, there exists an open neighborhood
${\mathbb {C}} \ni c \mapsto f_{c} \in {\mathrm {Poly}}$
is continuous, there exists an open neighborhood
![]() $U_{n}$
of
$U_{n}$
of
![]() $c_{n}$
for every
$c_{n}$
for every
![]() $n =1, 2, \ldots , N$
such that
$n =1, 2, \ldots , N$
such that
![]() $|{f_{{c^{\prime }_{N}}} \circ \cdots \circ f_{{c^{\prime }_{2}}} \circ f_{{c^{\prime }_{1}}}} (0)|> R$
for every
$|{f_{{c^{\prime }_{N}}} \circ \cdots \circ f_{{c^{\prime }_{2}}} \circ f_{{c^{\prime }_{1}}}} (0)|> R$
for every
![]() $c^{\prime }_{n} \in U_{n}$
(
$c^{\prime }_{n} \in U_{n}$
(
![]() $n =1, 2, \ldots , N$
). Moreover, we have
$n =1, 2, \ldots , N$
). Moreover, we have
![]() ${\mathbb {P}}_{c, r} ( \mathfrak {U} )> 0$
for
${\mathbb {P}}_{c, r} ( \mathfrak {U} )> 0$
for
![]() $ \mathfrak {U} = \prod _{n=1}^{N} U^{j}_{n} \times \prod _{N+1}^{\infty } {\bar {B}({c}, {r})} .$
However, for every
$ \mathfrak {U} = \prod _{n=1}^{N} U^{j}_{n} \times \prod _{N+1}^{\infty } {\bar {B}({c}, {r})} .$
However, for every
![]() $\omega ' \in \mathfrak {U}$
, it follows from Lemma 2.6 that
$\omega ' \in \mathfrak {U}$
, it follows from Lemma 2.6 that
![]() ${{f}_{{\omega '}}^{({n})}} (0) \to \infty $
as
${{f}_{{\omega '}}^{({n})}} (0) \to \infty $
as
![]() $n \to \infty $
, contradicting the assumption
$n \to \infty $
, contradicting the assumption
![]() $T_{c, r}(0) = 0$
. This shows that for every
$T_{c, r}(0) = 0$
. This shows that for every
![]() $\omega \in \Omega _{c, r}$
, we have
$\omega \in \Omega _{c, r}$
, we have
![]() $|{{f}_{{\omega }}^{({n})}} (0)| \leq R$
for every
$|{{f}_{{\omega }}^{({n})}} (0)| \leq R$
for every
![]() $n \in {\mathbb {N}}$
.
$n \in {\mathbb {N}}$
.
4.2. General properties
In this subsection, we give a trivial estimate of the bifurcation radius and show the continuity. The following is due to [Reference Brück, Büger and Reitz4].
Lemma 4.8. Suppose
![]() $r > 0$
. If
$r > 0$
. If
![]() ${\bar {B}({c}, {r})} \cap (\mathbb {C}\setminus\! {\,\mathcal {M}}) \neq \emptyset $
, then for every
${\bar {B}({c}, {r})} \cap (\mathbb {C}\setminus\! {\,\mathcal {M}}) \neq \emptyset $
, then for every
![]() $z \in {\mathbb {C}}$
, there exists
$z \in {\mathbb {C}}$
, there exists
![]() $\omega \in \Omega _{c, r}$
such that
$\omega \in \Omega _{c, r}$
such that
![]() ${{f}_{{\omega }}^{({n})}} (z) \to \infty $
as
${{f}_{{\omega }}^{({n})}} (z) \to \infty $
as
![]() $n \to \infty .$
$n \to \infty .$
Proof. Fix
![]() $c' \in {\bar {B}({c}, {r})} \setminus\! {\,\mathcal {M}}$
. Then the autonomous filled Julia set
$c' \in {\bar {B}({c}, {r})} \setminus\! {\,\mathcal {M}}$
. Then the autonomous filled Julia set
![]() $K(f_{c'})$
of
$K(f_{c'})$
of
![]() $f_{c'}$
has no interior point. Thus, if
$f_{c'}$
has no interior point. Thus, if
![]() $z \in K(f_{c'})$
, then there exists
$z \in K(f_{c'})$
, then there exists
![]() $c_{1} \in {\bar {B}({c}, {r})} $
such that
$c_{1} \in {\bar {B}({c}, {r})} $
such that
![]() $f_{c_{1}}(z) \notin K(f_{c'})$
. In this case, we have
$f_{c_{1}}(z) \notin K(f_{c'})$
. In this case, we have
![]() $f_{c'}^{\circ n} \circ f_{c_{1}}(z) \to \infty $
as
$f_{c'}^{\circ n} \circ f_{c_{1}}(z) \to \infty $
as
![]() $n \to \infty .$
Also, if
$n \to \infty .$
Also, if
![]() $z \notin K(f_{c'})$
, then by definition,
$z \notin K(f_{c'})$
, then by definition,
![]() $f_{c'}^{\circ n}(z) \to \infty $
as
$f_{c'}^{\circ n}(z) \to \infty $
as
![]() $n \to \infty .$
This completes the proof.
$n \to \infty .$
This completes the proof.
Denote by
![]() $\operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
the Euclidean distance from the point c to the compact set
$\operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
the Euclidean distance from the point c to the compact set
![]() $\partial\mathcal {M}$
.
$\partial\mathcal {M}$
.
Lemma 4.9. For every
![]() $c \in {\mathbb {C}}$
, we have
$c \in {\mathbb {C}}$
, we have
![]() ${\mathit {r}_{\mathrm {bif}}}(c) \leq \operatorname {\mathrm {dist}}(c, \partial\mathcal {M}).$
${\mathit {r}_{\mathrm {bif}}}(c) \leq \operatorname {\mathrm {dist}}(c, \partial\mathcal {M}).$
Proof. From Lemma 4.8, if
![]() $r> \operatorname {\mathrm {dist}}(c, \partial\mathcal {M}),$
then the polynomial semigroup
$r> \operatorname {\mathrm {dist}}(c, \partial\mathcal {M}),$
then the polynomial semigroup
![]() $G_{c, r}$
has no planar minimal sets. By Definition 2.17,
$G_{c, r}$
has no planar minimal sets. By Definition 2.17,
![]() ${\mathit {r}_{\mathrm {bif}}}(c)$
is the infimum value for
${\mathit {r}_{\mathrm {bif}}}(c)$
is the infimum value for
![]() $r \geq 0$
such that
$r \geq 0$
such that
![]() $G_{c, r}$
has no planar minimal sets. Hence,
$G_{c, r}$
has no planar minimal sets. Hence,
![]() ${\mathit {r}_{\mathrm {bif}}}(c) \leq \operatorname {\mathrm {dist}} (c, \partial\mathcal {M})$
.
${\mathit {r}_{\mathrm {bif}}}(c) \leq \operatorname {\mathrm {dist}} (c, \partial\mathcal {M})$
.
The following is a part of Main Result C.
Theorem 4.10. As a function, the bifurcation radius
![]() ${\mathit {r}_{\mathrm {bif}}} \colon \mathbb {C} \to [0, \infty )$
is
${\mathit {r}_{\mathrm {bif}}} \colon \mathbb {C} \to [0, \infty )$
is
![]() $1$
-Lipschitz. That is,
$1$
-Lipschitz. That is,
![]() $|\kern1.5pt{\mathit {r}_{\mathrm {bif}}}(c) - {\mathit {r}_{\mathrm {bif}}}(c')| \leq |c -c'|$
for every
$|\kern1.5pt{\mathit {r}_{\mathrm {bif}}}(c) - {\mathit {r}_{\mathrm {bif}}}(c')| \leq |c -c'|$
for every
![]() $c, c' \in {\mathbb {C}}$
.
$c, c' \in {\mathbb {C}}$
.
Proof. Fix
![]() $c, c' \in {\mathbb {C}}$
. Pick any
$c, c' \in {\mathbb {C}}$
. Pick any
![]() $r> | c -c' | $
and set
$r> | c -c' | $
and set
![]() $\epsilon = r - | c -c' |> 0$
. By definition, the polynomial semigroup
$\epsilon = r - | c -c' |> 0$
. By definition, the polynomial semigroup
![]() $G_{c, {\mathit {r}_{\mathrm {bif}}}(c)+\epsilon }$
has no planar minimal sets. Since
$G_{c, {\mathit {r}_{\mathrm {bif}}}(c)+\epsilon }$
has no planar minimal sets. Since
![]() ${\bar {B}({c}, {{\mathit {r}_{\mathrm {bif}}}(c) + \epsilon })} \subset {\bar {B}({c'}, {{\mathit {r}_{\mathrm {bif}}}(c)+r})}$
, it follows from Lemma 2.12 that also
${\bar {B}({c}, {{\mathit {r}_{\mathrm {bif}}}(c) + \epsilon })} \subset {\bar {B}({c'}, {{\mathit {r}_{\mathrm {bif}}}(c)+r})}$
, it follows from Lemma 2.12 that also
![]() $G_{c', {\mathit {r}_{\mathrm {bif}}}(c)+r}$
has no planar minimal sets. This implies that
$G_{c', {\mathit {r}_{\mathrm {bif}}}(c)+r}$
has no planar minimal sets. This implies that
![]() ${\mathit {r}_{\mathrm {bif}}}(c') \leq {\mathit {r}_{\mathrm {bif}}}(c)+r$
, and hence
${\mathit {r}_{\mathrm {bif}}}(c') \leq {\mathit {r}_{\mathrm {bif}}}(c)+r$
, and hence
![]() ${\mathit {r}_{\mathrm {bif}}}(c') - {\mathit {r}_{\mathrm {bif}}}(c) \leq | c -c' |.$
Exchanging c and
${\mathit {r}_{\mathrm {bif}}}(c') - {\mathit {r}_{\mathrm {bif}}}(c) \leq | c -c' |.$
Exchanging c and
![]() $c'$
with each other, we have also
$c'$
with each other, we have also
![]() ${\mathit {r}_{\mathrm {bif}}}(c) - {\mathit {r}_{\mathrm {bif}}}(c') \leq | c' -c |,$
which completes the proof.
${\mathit {r}_{\mathrm {bif}}}(c) - {\mathit {r}_{\mathrm {bif}}}(c') \leq | c' -c |,$
which completes the proof.
4.3. Inside the main cardioid
In this subsection, we present some estimates of
![]() ${\mathit {r}_{\mathrm {bif}}}(c)$
when c is in the main cardioid. Recall that the main cardioid is the set of all parameters
${\mathit {r}_{\mathrm {bif}}}(c)$
when c is in the main cardioid. Recall that the main cardioid is the set of all parameters
![]() ${c \in {\mathbb {C}}}$
for which there exists
${c \in {\mathbb {C}}}$
for which there exists
![]() $\unicode{x3bb} \in {\mathbb {C}}$
with
$\unicode{x3bb} \in {\mathbb {C}}$
with
![]() $|\unicode{x3bb} | < 1$
such that
$|\unicode{x3bb} | < 1$
such that
![]() $c = \unicode{x3bb} /2 -\unicode{x3bb} ^{2}/4,$
and its boundary is contained in
$c = \unicode{x3bb} /2 -\unicode{x3bb} ^{2}/4,$
and its boundary is contained in
![]() $\partial\mathcal {M}.$
$\partial\mathcal {M}.$
Corollary 4.11. If
![]() $ c = 0$
, then
$ c = 0$
, then
![]() ${\mathit {r}_{\mathrm {bif}}}(0) = 1/4$
.
${\mathit {r}_{\mathrm {bif}}}(0) = 1/4$
.
Proof. This is essentially due to [Reference Brück, Büger and Reitz4]. By Lemma 4.9, we have
![]() ${\mathit {r}_{\mathrm {bif}}}(0) \leq 1/4$
. A straight calculation shows that
${\mathit {r}_{\mathrm {bif}}}(0) \leq 1/4$
. A straight calculation shows that
![]() $\overline {D_{1/2}}$
is forward invariant under the polynomial semigroup
$\overline {D_{1/2}}$
is forward invariant under the polynomial semigroup
![]() $G_{0, 1/4}$
, and hence
$G_{0, 1/4}$
, and hence
![]() ${\mathit {r}_{\mathrm {bif}}}(0) \geq 1/4.$
${\mathit {r}_{\mathrm {bif}}}(0) \geq 1/4.$
We can easily verify that
![]() $\overline {D_{1/2}}$
is the planar minimal set of
$\overline {D_{1/2}}$
is the planar minimal set of
![]() $G_{0, 1/4}$
. Since the autonomous Julia set of
$G_{0, 1/4}$
. Since the autonomous Julia set of
![]() $f_{1/4}$
contains
$f_{1/4}$
contains
![]() $z = 1/2$
which is the parabolic fixed point of
$z = 1/2$
which is the parabolic fixed point of
![]() $f_{1/4},$
the Julia set of the semigroup satisfies
$f_{1/4},$
the Julia set of the semigroup satisfies
![]() $1/2 \in J(G_{0,1/4})$
by Proposition 2.9. Thus, the planar minimal set
$1/2 \in J(G_{0,1/4})$
by Proposition 2.9. Thus, the planar minimal set
![]() $\overline {D_{1/2}}$
of
$\overline {D_{1/2}}$
of
![]() $G_{0, 1/4}$
is J-touching at
$G_{0, 1/4}$
is J-touching at
![]() $z=1/2$
.
$z=1/2$
.
Corollary 4.11 shows that the equality in Lemma 4.9 may hold. Now, we show using Theorem 4.10 that we can determine the bifurcation radius if
![]() $0 \leq c \leq 1/4$
. The following is a part of Main Result C.
$0 \leq c \leq 1/4$
. The following is a part of Main Result C.
Theorem 4.12. If
![]() $0 \leq c \leq 1/4$
, then
$0 \leq c \leq 1/4$
, then
![]() ${\mathit {r}_{\mathrm {bif}}}(c) = 1/4 - c$
.
${\mathit {r}_{\mathrm {bif}}}(c) = 1/4 - c$
.
Proof. By Lemma 4.9, we have
![]() ${\mathit {r}_{\mathrm {bif}}}(c) \leq 1/4 - c$
if
${\mathit {r}_{\mathrm {bif}}}(c) \leq 1/4 - c$
if
![]() $0 \leq c \leq 1/4$
. If
$0 \leq c \leq 1/4$
. If
![]() $c' = 0$
, then
$c' = 0$
, then
![]() ${\mathit {r}_{\mathrm {bif}}}(c') = 1/4$
from Corollary 4.11. Thus, Theorem 4.10 yields that
${\mathit {r}_{\mathrm {bif}}}(c') = 1/4$
from Corollary 4.11. Thus, Theorem 4.10 yields that
![]() $|\kern1.5pt{\mathit {r}_{\mathrm {bif}}}(c) - 1/4| \leq c$
for
$|\kern1.5pt{\mathit {r}_{\mathrm {bif}}}(c) - 1/4| \leq c$
for
![]() $0 \leq c \leq 1/4$
, which completes the proof.
$0 \leq c \leq 1/4$
, which completes the proof.
We showed that
![]() ${\mathit {r}_{\mathrm {bif}}}(c) = \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
if
${\mathit {r}_{\mathrm {bif}}}(c) = \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
if
![]() $0 \leq c \leq 1/4$
. However, the author does not know whether there exists
$0 \leq c \leq 1/4$
. However, the author does not know whether there exists
![]() $c \in {\mathbb {C}}$
other than these, such that
$c \in {\mathbb {C}}$
other than these, such that
![]() $0 < {\mathit {r}_{\mathrm {bif}}}(c) = \operatorname {\mathrm {dist}}(c, \partial\mathcal {M}).$
For
$0 < {\mathit {r}_{\mathrm {bif}}}(c) = \operatorname {\mathrm {dist}}(c, \partial\mathcal {M}).$
For
![]() $c < 0$
, we will present some examples which satisfy
$c < 0$
, we will present some examples which satisfy
![]() ${\mathit {r}_{\mathrm {bif}}}(c) < \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
.
${\mathit {r}_{\mathrm {bif}}}(c) < \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
.
Lemma 4.13. For
![]() $c = 0$
and
$c = 0$
and
![]() $0 < r_{0} \leq 1/4$
, let
$0 < r_{0} \leq 1/4$
, let
![]() $\delta = (1 - \sqrt {1-4 r_{0}})/2$
. Then the following hold.
$\delta = (1 - \sqrt {1-4 r_{0}})/2$
. Then the following hold.
-
(i) The equality
 $\delta ^{2} + r_{0} = \delta $
holds. Thus, the point
$\delta ^{2} + r_{0} = \delta $
holds. Thus, the point
 $\delta $
is a fixed point of
$\delta $
is a fixed point of
 $f_{r_{0}}$
.
$f_{r_{0}}$
. -
(ii) The set
 $\overline {D_{\delta }}$
is the planar minimal set of
$\overline {D_{\delta }}$
is the planar minimal set of
 $G_{0, r_{0}}.$
$G_{0, r_{0}}.$
Proof. Statement (i) follows from the direct calculation. Now, we look at statement (ii). By statement (i), we have
![]() $f_{c_{1}}(\overline {D_{\delta }}) \subset \overline {D_{\delta }}$
for every
$f_{c_{1}}(\overline {D_{\delta }}) \subset \overline {D_{\delta }}$
for every
![]() $c_{1} \in {\bar {B}({0}, {r_{0}})}$
. Since
$c_{1} \in {\bar {B}({0}, {r_{0}})}$
. Since
![]() ${\bar {B}({0}, {r_{0}})}$
is symmetric under rotation, then the union
${\bar {B}({0}, {r_{0}})}$
is symmetric under rotation, then the union
![]() $\bigcup _{c_{1} \in {\bar {B}({0}, {r_{0}})}} \{f_{c_{1}}(0) \}$
is a round disk centered at the origin. By induction,
$\bigcup _{c_{1} \in {\bar {B}({0}, {r_{0}})}} \{f_{c_{1}}(0) \}$
is a round disk centered at the origin. By induction,
![]() $\bigcup _{c_{1}, c_{2}, \ldots , c_{n} \in {\bar {B}({0}, {r_{0}})}} \{{f_{{c_{n}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}(0) \}$
is a round disk centered at the origin for every
$\bigcup _{c_{1}, c_{2}, \ldots , c_{n} \in {\bar {B}({0}, {r_{0}})}} \{{f_{{c_{n}}} \circ \cdots \circ f_{{c_{2}}} \circ f_{{c_{1}}}}(0) \}$
is a round disk centered at the origin for every
![]() $n \in {\mathbb {N}}$
, and also
$n \in {\mathbb {N}}$
, and also
![]() $\overline {\bigcup _{g \in G_{0, r_{0}}}\{g(0)\}}$
is a closed round disk contained in
$\overline {\bigcup _{g \in G_{0, r_{0}}}\{g(0)\}}$
is a closed round disk contained in
![]() $\overline {D_{\delta }}$
. If
$\overline {D_{\delta }}$
. If
![]() $c_{n}=r_{0}$
for every
$c_{n}=r_{0}$
for every
![]() $n \in {\mathbb {N}}$
, then the autonomous iteration
$n \in {\mathbb {N}}$
, then the autonomous iteration
![]() ${{{f}}_{{r_{0}}}^{\circ {n}}}(0)$
converges to the fixed point
${{{f}}_{{r_{0}}}^{\circ {n}}}(0)$
converges to the fixed point
![]() $\delta $
of
$\delta $
of
![]() $f_{r_{0}}$
. This yields that
$f_{r_{0}}$
. This yields that
![]() $\overline {\bigcup _{g \in G_{0, r_{0}}}\{g(0)\}} = \overline {D_{\delta }}$
, and hence
$\overline {\bigcup _{g \in G_{0, r_{0}}}\{g(0)\}} = \overline {D_{\delta }}$
, and hence
![]() $\overline {D_{\delta }}$
is a minimal set of
$\overline {D_{\delta }}$
is a minimal set of
![]() $G_{0, r_{0}}$
.
$G_{0, r_{0}}$
.
The following is a part of Main Result C.
Theorem 4.14. Suppose that
![]() $0 \kern1.3pt{<}\kern1.3pt \epsilon \kern1.3pt{\leq}\kern1.3pt 1/2.$
For
$0 \kern1.3pt{<}\kern1.3pt \epsilon \kern1.3pt{\leq}\kern1.3pt 1/2.$
For
![]() $c\kern1.3pt{=}\kern1.3pt{-} \epsilon ,$
we have
$c\kern1.3pt{=}\kern1.3pt{-} \epsilon ,$
we have
![]() ${\mathit {r}_{\mathrm {bif}}}(-\epsilon ) \kern1.3pt{\leq}\kern1.3pt 1/4 \kern1.3pt{+} \epsilon \kern1.3pt{-}\kern1.3pt \epsilon ^{2}.$
${\mathit {r}_{\mathrm {bif}}}(-\epsilon ) \kern1.3pt{\leq}\kern1.3pt 1/4 \kern1.3pt{+} \epsilon \kern1.3pt{-}\kern1.3pt \epsilon ^{2}.$
Proof. Fix any
![]() $r> 1/4 + \epsilon - \epsilon ^{2}.$
We show that
$r> 1/4 + \epsilon - \epsilon ^{2}.$
We show that
![]() $G_{-{\epsilon }, r}$
has no planar minimal sets by contradiction, which implies
$G_{-{\epsilon }, r}$
has no planar minimal sets by contradiction, which implies
![]() ${\mathit {r}_{\mathrm {bif}}}(-\epsilon ) < r$
. Suppose that there exists a planar minimal set L of
${\mathit {r}_{\mathrm {bif}}}(-\epsilon ) < r$
. Suppose that there exists a planar minimal set L of
![]() $G_{-{\epsilon }, r}$
. Since
$G_{-{\epsilon }, r}$
. Since
![]() ${\bar {B}({-\epsilon }, {r})} \supset {\bar {B}({0}, {r- \epsilon })}$
, it follows from Lemma 2.12 that
${\bar {B}({-\epsilon }, {r})} \supset {\bar {B}({0}, {r- \epsilon })}$
, it follows from Lemma 2.12 that
![]() $G_{0, r-\epsilon }$
also has a planar minimal set. By Corollary 4.11, we have
$G_{0, r-\epsilon }$
also has a planar minimal set. By Corollary 4.11, we have
![]() $ r- \epsilon \leq 1/4$
. In addition, we assumed that
$ r- \epsilon \leq 1/4$
. In addition, we assumed that
![]() $r - \epsilon> 1/4 - \epsilon ^{2} \geq 0.$
By Lemmas 2.12 and 4.13(ii), we have
$r - \epsilon> 1/4 - \epsilon ^{2} \geq 0.$
By Lemmas 2.12 and 4.13(ii), we have
![]() $L \supset \overline {D_{\delta }}$
for
$L \supset \overline {D_{\delta }}$
for
![]() $\delta = (1 - \sqrt {1-4 (r - \epsilon ) })/2$
. Let
$\delta = (1 - \sqrt {1-4 (r - \epsilon ) })/2$
. Let
![]() $z_{0}= i \delta $
and
$z_{0}= i \delta $
and
![]() $c_{1} = -r - \epsilon $
, then
$c_{1} = -r - \epsilon $
, then
![]() $z_{0} \in L$
,
$z_{0} \in L$
,
![]() $c_{1} \in {\bar {B}({-\epsilon }, {r})}$
, and
$c_{1} \in {\bar {B}({-\epsilon }, {r})}$
, and
![]() $f_{c_{1}}(z_{0}) = - \delta ^{2} - r - \epsilon = - \delta - 2 \epsilon .$
Now, set
$f_{c_{1}}(z_{0}) = - \delta ^{2} - r - \epsilon = - \delta - 2 \epsilon .$
Now, set
![]() $R_{1} = (1 + \sqrt {1 - 4 (r - \epsilon ) })/2> 1/{2}$
, then
$R_{1} = (1 + \sqrt {1 - 4 (r - \epsilon ) })/2> 1/{2}$
, then
since
![]() $r> 1/4 + \epsilon - \epsilon ^{2}$
. Set
$r> 1/4 + \epsilon - \epsilon ^{2}$
. Set
![]() $z_{1} = f_{c_{1}}(z_{0})$
, then
$z_{1} = f_{c_{1}}(z_{0})$
, then
![]() $z_{1} < - R_{1}$
. Let
$z_{1} < - R_{1}$
. Let
![]() $c_{n}=r - \epsilon \in {\bar {B}({-\epsilon }, {r})}$
for every
$c_{n}=r - \epsilon \in {\bar {B}({-\epsilon }, {r})}$
for every
![]() $n \geq 2$
. Since
$n \geq 2$
. Since
![]() $z_{1} < - R_{1}$
, the direct calculation shows
$z_{1} < - R_{1}$
, the direct calculation shows
![]() $f_{c_{2}}(z_{1})> R_{1}^{2} + r - \epsilon = R_{1}.$
Set
$f_{c_{2}}(z_{1})> R_{1}^{2} + r - \epsilon = R_{1}.$
Set
![]() $z_{2} = f_{c_{2}}(z_{1})$
and
$z_{2} = f_{c_{2}}(z_{1})$
and
![]() $\alpha = z_{2} - R_{1}$
, then
$\alpha = z_{2} - R_{1}$
, then
![]() $z_{2} = R_{1} + \alpha $
and
$z_{2} = R_{1} + \alpha $
and
![]() $\alpha> 0$
. We can show by induction that
$\alpha> 0$
. We can show by induction that
![]() ${{{f}}_{{r - \epsilon }}^{\circ {n}}} (z_{2})> R_{1} + \alpha + n \alpha ^{2}$
for every
${{{f}}_{{r - \epsilon }}^{\circ {n}}} (z_{2})> R_{1} + \alpha + n \alpha ^{2}$
for every
![]() $n \in {\mathbb {N}}$
. Hence,
$n \in {\mathbb {N}}$
. Hence,
![]() ${{{f}}_{{r - \epsilon }}^{\circ {n}}} (z_{1})$
diverges to
${{{f}}_{{r - \epsilon }}^{\circ {n}}} (z_{1})$
diverges to
![]() $\infty $
as
$\infty $
as
![]() $n \to \infty $
. Thus, we have proved that there exist
$n \to \infty $
. Thus, we have proved that there exist
![]() $z_{0} \in L$
and
$z_{0} \in L$
and
![]() $\omega = (c_{n})_{n=1}^{\infty } \in \Omega _{-\epsilon , r}$
such that
$\omega = (c_{n})_{n=1}^{\infty } \in \Omega _{-\epsilon , r}$
such that
![]() ${{f}_{{\omega }}^{({n})}} (z_{0}) \to \infty $
as
${{f}_{{\omega }}^{({n})}} (z_{0}) \to \infty $
as
![]() ${n \to \infty }.$
This contradicts that L is planar and forward invariant under
${n \to \infty }.$
This contradicts that L is planar and forward invariant under
![]() $G_{-{\epsilon }, r}$
. This completes the proof since r is an arbitrary number that satisfies
$G_{-{\epsilon }, r}$
. This completes the proof since r is an arbitrary number that satisfies
![]() $r> 1/4 + \epsilon - \epsilon ^{2}.$
$r> 1/4 + \epsilon - \epsilon ^{2}.$
Note that we can show that
![]() $\operatorname {\mathrm {dist}} ( -\epsilon , \partial {\mathcal {M}} ) = 1/4 +\epsilon $
if
$\operatorname {\mathrm {dist}} ( -\epsilon , \partial {\mathcal {M}} ) = 1/4 +\epsilon $
if
![]() $0 < \epsilon \leq 1/4$
as follows. Assume
$0 < \epsilon \leq 1/4$
as follows. Assume
![]() $0 < \epsilon \leq 1/4$
, then
$0 < \epsilon \leq 1/4$
, then
![]() $\operatorname {\mathrm {dist}} ( -\epsilon , \partial {\mathcal {M}} ) \leq |-\epsilon - 1/4| = 1/4 +\epsilon $
since
$\operatorname {\mathrm {dist}} ( -\epsilon , \partial {\mathcal {M}} ) \leq |-\epsilon - 1/4| = 1/4 +\epsilon $
since
![]() $1/4 \in {\mathcal {M}}$
. Let
$1/4 \in {\mathcal {M}}$
. Let
![]() $C = \{ \unicode{x3bb} /2 -\unicode{x3bb} ^{2}/4 \colon \unicode{x3bb} = e^{i \theta }, \theta \in {\mathbb {R}} \}$
. Then
$C = \{ \unicode{x3bb} /2 -\unicode{x3bb} ^{2}/4 \colon \unicode{x3bb} = e^{i \theta }, \theta \in {\mathbb {R}} \}$
. Then
![]() $C \subset \partial {\mathcal {M}}$
and the domain bounded by C is contained in the interior of
$C \subset \partial {\mathcal {M}}$
and the domain bounded by C is contained in the interior of
![]() ${\mathcal {M}}$
, see [Reference Carleson and Gamelin6, Theorem VIII.1.3]. Since
${\mathcal {M}}$
, see [Reference Carleson and Gamelin6, Theorem VIII.1.3]. Since
 $$ \begin{align*} \bigg|-\frac{1}{4} - \frac{e^{i \theta}}{2} + \frac{e^{2i \theta}}{4}\bigg|^{2} &= \bigg(-\frac{1}{4} - \frac{e^{i \theta}}{2} + \frac{e^{2i \theta}}{4}\bigg) \bigg(-\frac{1}{4} - \frac{e^{-i \theta}}{2} + \frac{e^{-2i \theta}}{4}\bigg)\\ &= \frac{6 - (e^{2 i \theta} + e^{-2 i \theta})}{16} = \frac{6 - 2 \cos 2 \theta}{16}, \end{align*} $$
$$ \begin{align*} \bigg|-\frac{1}{4} - \frac{e^{i \theta}}{2} + \frac{e^{2i \theta}}{4}\bigg|^{2} &= \bigg(-\frac{1}{4} - \frac{e^{i \theta}}{2} + \frac{e^{2i \theta}}{4}\bigg) \bigg(-\frac{1}{4} - \frac{e^{-i \theta}}{2} + \frac{e^{-2i \theta}}{4}\bigg)\\ &= \frac{6 - (e^{2 i \theta} + e^{-2 i \theta})}{16} = \frac{6 - 2 \cos 2 \theta}{16}, \end{align*} $$
we have
![]() $\operatorname {\mathrm {dist}} (-1/4, \partial {\mathcal {M}}) = \min _{\theta \in {\mathbb {R}}}\sqrt {6 - 2 \cos 2 \theta }/4 = 1/2$
and the minimum is attained at
$\operatorname {\mathrm {dist}} (-1/4, \partial {\mathcal {M}}) = \min _{\theta \in {\mathbb {R}}}\sqrt {6 - 2 \cos 2 \theta }/4 = 1/2$
and the minimum is attained at
![]() $\theta = 0, \pi $
which correspond to
$\theta = 0, \pi $
which correspond to
![]() $c = 1/4, -3/4 \in {\,\mathcal {M}}$
, respectively. Since
$c = 1/4, -3/4 \in {\,\mathcal {M}}$
, respectively. Since
![]() $\mathrm {int} {\bar {B}({-\epsilon }, {1/4 +\epsilon })} \subset \mathrm {int} {\bar {B}({-1/4}, {1/2})} \subset \mathrm {int} {\,\mathcal {M}}$
, we have
$\mathrm {int} {\bar {B}({-\epsilon }, {1/4 +\epsilon })} \subset \mathrm {int} {\bar {B}({-1/4}, {1/2})} \subset \mathrm {int} {\,\mathcal {M}}$
, we have
![]() $\operatorname {\mathrm {dist}} ( -\epsilon , \partial {\mathcal {M}} ) \geq 1/4 +\epsilon .$
Therefore, Theorem 4.14 reveals that strict inequality
$\operatorname {\mathrm {dist}} ( -\epsilon , \partial {\mathcal {M}} ) \geq 1/4 +\epsilon .$
Therefore, Theorem 4.14 reveals that strict inequality
![]() ${\mathit {r}_{\mathrm {bif}}}(c) < \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
holds if
${\mathit {r}_{\mathrm {bif}}}(c) < \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
holds if
![]() $-1/4 \leq c < 0$
.
$-1/4 \leq c < 0$
.
Combining the theorem above with Corollary 4.3, we have a little better result than Theorem 3.5.
Corollary 4.15. Suppose that
![]() $0 < \epsilon \leq 1/2.$
If
$0 < \epsilon \leq 1/2.$
If
![]() $c=- \epsilon $
and
$c=- \epsilon $
and
![]() $r> 1/4 + \epsilon - \epsilon ^{2}$
, then the random Julia set
$r> 1/4 + \epsilon - \epsilon ^{2}$
, then the random Julia set
![]() $J_{\omega }$
is totally disconnected for
$J_{\omega }$
is totally disconnected for
![]() ${\mathbb {P}}_{-\epsilon , r}$
-almost every
${\mathbb {P}}_{-\epsilon , r}$
-almost every
![]() $\omega \in \Omega _{-\epsilon , r}$
.
$\omega \in \Omega _{-\epsilon , r}$
.
This shows that the random Julia set
![]() $J_{\omega }$
is totally disconnected for almost every
$J_{\omega }$
is totally disconnected for almost every
![]() $\omega $
even if
$\omega $
even if
![]() ${\bar {B}({c}, {r})} \subset \mathrm {int} {\,\mathcal {M}}$
and
${\bar {B}({c}, {r})} \subset \mathrm {int} {\,\mathcal {M}}$
and
![]() ${\bar {B}({c}, {r})} \not \supset {\bar {B}({0}, {1/4})}$
. This is stronger than Theorem 3.5 proved by Lech and Zdunik.
${\bar {B}({c}, {r})} \not \supset {\bar {B}({0}, {1/4})}$
. This is stronger than Theorem 3.5 proved by Lech and Zdunik.
4.4. Outside the main cardioid
Recall that a parameter
![]() $\tilde {c}$
is said to be superattracting if there exists
$\tilde {c}$
is said to be superattracting if there exists
![]() $p \in {\mathbb {N}}$
such that
$p \in {\mathbb {N}}$
such that
![]() ${{{f}}_{{\tilde {c}}}^{\circ {p}}} (0) = 0$
. For example,
${{{f}}_{{\tilde {c}}}^{\circ {p}}} (0) = 0$
. For example,
![]() $\tilde {c} = 0$
and
$\tilde {c} = 0$
and
![]() $-1$
are superattracting parameters with
$-1$
are superattracting parameters with
![]() $p = 1$
and
$p = 1$
and
![]() $2$
, respectively. In this subsection, we show the non-trivial estimates of
$2$
, respectively. In this subsection, we show the non-trivial estimates of
![]() ${\mathit {r}_{\mathrm {bif}}}(-1)$
.
${\mathit {r}_{\mathrm {bif}}}(-1)$
.
Lemma 4.16. Let
![]() $c=-1$
,
$c=-1$
,
![]() $r \geq 0$
, and
$r \geq 0$
, and
![]() $\delta \geq 0$
. Denote
$\delta \geq 0$
. Denote
![]() $\overline {{D}}_{\delta } = \{z \in \mathbb {C} \colon |z| \leq \delta \}$
. Then
$\overline {{D}}_{\delta } = \{z \in \mathbb {C} \colon |z| \leq \delta \}$
. Then
![]() $f_{c_{2}} \circ f_{c_{1}}(\overline {{D}}_{\delta }) \subset \overline {{D}}_{\delta }$
for every
$f_{c_{2}} \circ f_{c_{1}}(\overline {{D}}_{\delta }) \subset \overline {{D}}_{\delta }$
for every
![]() $c_{1}, \ c_{2} \in {\bar {B}({-1}, {r})}$
if and only if
$c_{1}, \ c_{2} \in {\bar {B}({-1}, {r})}$
if and only if
Proof. Assume that
![]() $f_{c_{2}} \circ f_{c_{1}}(\overline {{D}}_{\delta }) \subset \overline {{D}}_{\delta }$
for every
$f_{c_{2}} \circ f_{c_{1}}(\overline {{D}}_{\delta }) \subset \overline {{D}}_{\delta }$
for every
![]() $c_{1}, \ c_{2} \in {\bar {B}({-1}, {r})}$
. For
$c_{1}, \ c_{2} \in {\bar {B}({-1}, {r})}$
. For
![]() $z = i \delta $
,
$z = i \delta $
,
![]() $c_{1} = -1 -r$
, and
$c_{1} = -1 -r$
, and
![]() $c_{2} = -1 +r$
, we have
$c_{2} = -1 +r$
, we have
![]() $f_{c_{1}}(z) = - \delta ^{2} -1-r$
and
$f_{c_{1}}(z) = - \delta ^{2} -1-r$
and
![]() $f_{c_{2}} \circ f_{c_{1}}(z) = \delta ^{4} +2(1+r)\delta ^{2} + r^{2} + 3r.$
Hence, inequality (1) holds.
$f_{c_{2}} \circ f_{c_{1}}(z) = \delta ^{4} +2(1+r)\delta ^{2} + r^{2} + 3r.$
Hence, inequality (1) holds.
Conversely, assume that inequality (1) holds. If
![]() $z \in \overline {{D}}_{\delta }$
and
$z \in \overline {{D}}_{\delta }$
and
![]() $c_{1} \in {\bar {B}({-1}, {r})}$
, then
$c_{1} \in {\bar {B}({-1}, {r})}$
, then
![]() $|f_{c_{1}}(z) +1| \leq |z|^{2} + |c_{1}+1| \leq \delta ^{2} + r$
. In addition, if
$|f_{c_{1}}(z) +1| \leq |z|^{2} + |c_{1}+1| \leq \delta ^{2} + r$
. In addition, if
![]() $|z_{1} + 1| \leq \delta ^{2} + r$
and
$|z_{1} + 1| \leq \delta ^{2} + r$
and
![]() $c_{2} \in {\bar {B}({-1}, {r})}$
, then
$c_{2} \in {\bar {B}({-1}, {r})}$
, then
 $$ \begin{align*} |f_{c_{2}}(z_{1})| &= |(z_{1} + 1)^{2} -2 z_{1} -2 + 1 + c_{2}| \\ &\leq |z_{1} +1|^{2} + 2|z_{1} + 1| + | 1 + c_{2} | \leq \delta^{4}+2(1+r)\delta^{2} + r^{2} + 3r. \end{align*} $$
$$ \begin{align*} |f_{c_{2}}(z_{1})| &= |(z_{1} + 1)^{2} -2 z_{1} -2 + 1 + c_{2}| \\ &\leq |z_{1} +1|^{2} + 2|z_{1} + 1| + | 1 + c_{2} | \leq \delta^{4}+2(1+r)\delta^{2} + r^{2} + 3r. \end{align*} $$
Thus, if inequality (1) holds, then
![]() $f_{c_{2}} \circ f_{c_{1}}(\overline {{D}}_{\delta }) \subset \overline {{D}}_{\delta }$
for every
$f_{c_{2}} \circ f_{c_{1}}(\overline {{D}}_{\delta }) \subset \overline {{D}}_{\delta }$
for every
![]() $c_{1}, \ c_{2} \in {\bar {B}({-1}, {r})}$
.
$c_{1}, \ c_{2} \in {\bar {B}({-1}, {r})}$
.
Lemma 4.17. Denote by
![]() $\delta _{\mathrm \max } = 0.453\cdots $
the (positive real) root of
$\delta _{\mathrm \max } = 0.453\cdots $
the (positive real) root of
![]() $\delta ^{3} + 2\delta -1$
. Define the function
$\delta ^{3} + 2\delta -1$
. Define the function
![]() $\rho \colon [0, \delta _{\mathrm \max }] \to {\mathbb {R}}$
by
$\rho \colon [0, \delta _{\mathrm \max }] \to {\mathbb {R}}$
by
Then, for every
![]() $\delta \in [0, \delta _{\mathrm \max }] $
, we have
$\delta \in [0, \delta _{\mathrm \max }] $
, we have
![]() $\delta ^{4}+2(1+\rho (\delta ) )\delta ^{2} + \rho (\delta ) ^{2} + 3\rho (\delta ) = \delta $
and
$\delta ^{4}+2(1+\rho (\delta ) )\delta ^{2} + \rho (\delta ) ^{2} + 3\rho (\delta ) = \delta $
and
![]() $\rho (\delta ) \geq 0.$
$\rho (\delta ) \geq 0.$
Proof. The former part
![]() $\delta ^{4}+2(1+\rho (\delta ) )\delta ^{2} + \rho (\delta ) ^{2} + 3\rho (\delta ) = \delta $
follows from a straight calculation. We show
$\delta ^{4}+2(1+\rho (\delta ) )\delta ^{2} + \rho (\delta ) ^{2} + 3\rho (\delta ) = \delta $
follows from a straight calculation. We show
![]() $\rho (\delta ) \geq 0.$
A simple calculation shows that
$\rho (\delta ) \geq 0.$
A simple calculation shows that
 $$ \begin{align*} 2 \rho (\delta) = \frac{- ({2 \delta^{2} + 3})^{2} + 4 \delta^{2} + 4\delta +9}{(2 \delta^{2} + 3) + \sqrt{4 \delta^{2} + 4\delta +9}} = \frac{- 4 \delta (\delta^{3} + 2\delta-1)}{(2 \delta^{2} + 3) + \sqrt{4 \delta^{2} + 4\delta +9}}. \end{align*} $$
$$ \begin{align*} 2 \rho (\delta) = \frac{- ({2 \delta^{2} + 3})^{2} + 4 \delta^{2} + 4\delta +9}{(2 \delta^{2} + 3) + \sqrt{4 \delta^{2} + 4\delta +9}} = \frac{- 4 \delta (\delta^{3} + 2\delta-1)}{(2 \delta^{2} + 3) + \sqrt{4 \delta^{2} + 4\delta +9}}. \end{align*} $$
Define
![]() $\tilde {\rho }(\delta ) = \delta ^{3} + 2\delta -1,$
then
$\tilde {\rho }(\delta ) = \delta ^{3} + 2\delta -1,$
then
![]() $\tilde {\rho }(0) = -1 <0$
and
$\tilde {\rho }(0) = -1 <0$
and
![]() $\tilde {\rho }'(\delta ) = 3 \delta ^{2} + 2> 0$
. Thus,
$\tilde {\rho }'(\delta ) = 3 \delta ^{2} + 2> 0$
. Thus,
![]() ${\rho (\delta ) \geq 0}$
for every
${\rho (\delta ) \geq 0}$
for every
![]() $\delta \in [0, \delta _{\mathrm \max }] $
.
$\delta \in [0, \delta _{\mathrm \max }] $
.
We now give the lower bound of
![]() ${\mathit {r}_{\mathrm {bif}}}(-1),$
which is one of the main results of this paper.
${\mathit {r}_{\mathrm {bif}}}(-1),$
which is one of the main results of this paper.
Theorem 4.18. Let
![]() $\rho $
be defined as in Lemma 4.17. Then
$\rho $
be defined as in Lemma 4.17. Then
![]() $\rho $
takes the maximum value
$\rho $
takes the maximum value
![]() $r_{\mathrm \max } = 0.0386\cdots $
, and hence
$r_{\mathrm \max } = 0.0386\cdots $
, and hence
![]() $r_{\mathrm \max } \leq r_{\mathrm {bif}}(-1)$
.
$r_{\mathrm \max } \leq r_{\mathrm {bif}}(-1)$
.
Proof. We have that the derivative
![]() $\rho '(\delta ) = -2 \delta +(2 \delta + 1)/\sqrt {4 \delta ^{2} + 4 \delta + 9}.$
Thus,
$\rho '(\delta ) = -2 \delta +(2 \delta + 1)/\sqrt {4 \delta ^{2} + 4 \delta + 9}.$
Thus,
![]() $\rho '(\delta ) = 0$
if and only if
$\rho '(\delta ) = 0$
if and only if
![]() $16 \delta ^4 + 16 \delta ^3 + 32\delta ^2 - 4 \delta - 1 = 0$
. Let
$16 \delta ^4 + 16 \delta ^3 + 32\delta ^2 - 4 \delta - 1 = 0$
. Let
![]() $\delta ^{*} = 0.229\cdots $
be the unique positive root of this quartic equation. Then,
$\delta ^{*} = 0.229\cdots $
be the unique positive root of this quartic equation. Then,
![]() $\rho (\delta )$
takes the maximum value at
$\rho (\delta )$
takes the maximum value at
![]() $\delta = \delta ^{*}$
. A numerical computation shows that the maximum value
$\delta = \delta ^{*}$
. A numerical computation shows that the maximum value
![]() $r_{\mathrm \max }$
is approximately
$r_{\mathrm \max }$
is approximately
![]() $0.0386\cdots $
.
$0.0386\cdots $
.
By Lemmas 4.16 and 4.17, for every
![]() $\delta \in [0, \delta _{\mathrm \max }] $
, the set
$\delta \in [0, \delta _{\mathrm \max }] $
, the set
![]() $\overline {{D}}_{\delta } $
gives a forward invariant set under the polynomial semigroup
$\overline {{D}}_{\delta } $
gives a forward invariant set under the polynomial semigroup
![]() $G_{-1, \rho (\delta )}$
. Thus, we have
$G_{-1, \rho (\delta )}$
. Thus, we have
![]() $\rho (\delta ) \leq r_{\mathrm {bif}}(-1)$
. In particular,
$\rho (\delta ) \leq r_{\mathrm {bif}}(-1)$
. In particular,
![]() $r_{\mathrm \max } = \rho (\delta ^{*}) \leq r_{\mathrm {bif}}(-1)$
. This completes the proof.
$r_{\mathrm \max } = \rho (\delta ^{*}) \leq r_{\mathrm {bif}}(-1)$
. This completes the proof.
Next, we consider the upper bound of
![]() ${\mathit {r}_{\mathrm {bif}}}(-1).$
The following theorem gives upper bounds, whose proof suggests a kind of parabolic implosion in the stochastic sense.
${\mathit {r}_{\mathrm {bif}}}(-1).$
The following theorem gives upper bounds, whose proof suggests a kind of parabolic implosion in the stochastic sense.
Theorem 4.19. Suppose that
![]() $ {\bar {B}({c}, {r_{0}})}$
contains a superattracting parameter
$ {\bar {B}({c}, {r_{0}})}$
contains a superattracting parameter
![]() $\tilde {c}$
. If there exist
$\tilde {c}$
. If there exist
![]() $N \in {\mathbb {N}}$
and
$N \in {\mathbb {N}}$
and
![]() $c_{1}, c_{2} \ldots , c_{N} \in {\bar {B}({c}, {r_{0}})}$
such that
$c_{1}, c_{2} \ldots , c_{N} \in {\bar {B}({c}, {r_{0}})}$
such that
![]() $f_{c_{N}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}$
has a parabolic periodic point, then
$f_{c_{N}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}$
has a parabolic periodic point, then
![]() $r_{\mathrm {bif}}(c) \leq r_{0}$
.
$r_{\mathrm {bif}}(c) \leq r_{0}$
.
Proof. Fix
![]() $r> r_{0}$
and apply Lemma 4.4. Set
$r> r_{0}$
and apply Lemma 4.4. Set
![]() $g = f_{c_{N}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}$
and let
$g = f_{c_{N}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}$
and let
![]() $z^{*}$
denote the parabolic periodic point of g. Then there exists
$z^{*}$
denote the parabolic periodic point of g. Then there exists
![]() $p\in {\mathbb {N}}$
such that
$p\in {\mathbb {N}}$
such that
![]() ${{{g}}^{\circ {p}}} (z^{*}) = z^{*}$
, and the multiplier of
${{{g}}^{\circ {p}}} (z^{*}) = z^{*}$
, and the multiplier of
![]() ${{{g}}^{\circ {p}}}$
at
${{{g}}^{\circ {p}}}$
at
![]() $z^{*}$
is
$z^{*}$
is
![]() $1.$
Thus, there exists a critical point
$1.$
Thus, there exists a critical point
![]() $z_{0}$
of g such that
$z_{0}$
of g such that
![]() ${{{g}}^{\circ {np}}}(z_{0}) \to z^{*}$
as
${{{g}}^{\circ {np}}}(z_{0}) \to z^{*}$
as
![]() $n \to \infty .$
Since
$n \to \infty .$
Since
![]() $g = f_{c_{N}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}$
, there exists
$g = f_{c_{N}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}$
, there exists
![]() $0 \leq k \leq N-1$
such that
$0 \leq k \leq N-1$
such that
![]() $f_{c_{k}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}} (z_{0}) = 0$
by the chain rule. Here, if
$f_{c_{k}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}} (z_{0}) = 0$
by the chain rule. Here, if
![]() $k =0 $
, then we define
$k =0 $
, then we define
![]() $f_{c_{k}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}$
to be the identity map. In any case, we have
$f_{c_{k}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}$
to be the identity map. In any case, we have
![]() ${{{g}}^{\circ {np-1}}} \circ {f_{{c_{N}}} \circ \cdots \circ f_{{c_{k+2}}} \circ f_{{c_{k+1}}}} (0) \to z^{*}$
as
${{{g}}^{\circ {np-1}}} \circ {f_{{c_{N}}} \circ \cdots \circ f_{{c_{k+2}}} \circ f_{{c_{k+1}}}} (0) \to z^{*}$
as
![]() $n \to \infty .$
Now, let
$n \to \infty .$
Now, let
![]() $\epsilon = r - r_{0}> 0$
, then there exists
$\epsilon = r - r_{0}> 0$
, then there exists
![]() $n_{0} \in {\mathbb {N}}$
such that
$n_{0} \in {\mathbb {N}}$
such that
![]() $n_{0} \geq 2$
and
$n_{0} \geq 2$
and
Set
![]() $w = {{{g}}^{\circ {n_{0}p-1}}} \circ {f_{{c_{N}}} \circ \cdots \circ f_{{c_{k+2}}} \circ f_{{c_{k+1}}}} (0)$
. Since the parabolic periodic point
$w = {{{g}}^{\circ {n_{0}p-1}}} \circ {f_{{c_{N}}} \circ \cdots \circ f_{{c_{k+2}}} \circ f_{{c_{k+1}}}} (0)$
. Since the parabolic periodic point
![]() $z^{*}$
belongs to the autonomous Julia set
$z^{*}$
belongs to the autonomous Julia set
![]() $J(g)$
of g and the Julia set is the boundary of the basin at infinity, perturbation of
$J(g)$
of g and the Julia set is the boundary of the basin at infinity, perturbation of
![]() $c_{N}$
allows us to find a random orbit which escapes to the basin at infinity. Namely, there exists
$c_{N}$
allows us to find a random orbit which escapes to the basin at infinity. Namely, there exists
![]() $c' \in {\bar {B}({c_{N}}, {\epsilon })}$
such that
$c' \in {\bar {B}({c_{N}}, {\epsilon })}$
such that
where
![]() $A(g)$
denotes the basin at infinity for the autonomous iteration of g. Note that
$A(g)$
denotes the basin at infinity for the autonomous iteration of g. Note that
![]() ${c' \in {\bar {B}({c}, {r})}} $
since
${c' \in {\bar {B}({c}, {r})}} $
since
![]() $c_{N} \in {\bar {B}({c}, {r_{0}})}$
and
$c_{N} \in {\bar {B}({c}, {r_{0}})}$
and
![]() $\epsilon = r - r_{0}$
. By definition, we have
$\epsilon = r - r_{0}$
. By definition, we have
![]() ${{{g}}^{\circ {n}}} (w') \to \infty $
as
${{{g}}^{\circ {n}}} (w') \to \infty $
as
![]() $n \to \infty $
. Thus, Lemma 4.4 gives that
$n \to \infty $
. Thus, Lemma 4.4 gives that
![]() ${\mathit {r}_{\mathrm {bif}}}(c) < r.$
This completes the proof since r is an arbitrary number that satisfies
${\mathit {r}_{\mathrm {bif}}}(c) < r.$
This completes the proof since r is an arbitrary number that satisfies
![]() $r>r_{0}.$
$r>r_{0}.$
Theorem 4.19 gives an alternative proof of
![]() ${\mathit {r}_{\mathrm {bif}}}(0) \leq 1/4$
since
${\mathit {r}_{\mathrm {bif}}}(0) \leq 1/4$
since
![]() $f_{1/4}$
has a parabolic fixed point at
$f_{1/4}$
has a parabolic fixed point at
![]() $z =1/2$
.
$z =1/2$
.
The following gives an algorithm to find an upper bound of the bifurcation radius.
Theorem 4.20. Suppose c is a superattracting parameter. Fix
![]() $N \in {\mathbb {N}}$
and
$N \in {\mathbb {N}}$
and
![]() $k \in {\mathbb {N}}$
, and let
$k \in {\mathbb {N}}$
, and let
![]() $p_{i} \in \{0, 1, \ldots , k-1\} $
for each
$p_{i} \in \{0, 1, \ldots , k-1\} $
for each
![]() $i =1, 2, \ldots , N.$
Define
$i =1, 2, \ldots , N.$
Define
![]() $\zeta _{k} = e^{2 \pi i/k}$
and
$\zeta _{k} = e^{2 \pi i/k}$
and
![]() $c_{i} = c + \rho \zeta _{k}^{p_{i}},$
where
$c_{i} = c + \rho \zeta _{k}^{p_{i}},$
where
![]() $\rho $
is a complex variable. Let
$\rho $
is a complex variable. Let
![]() $\Delta (\rho )$
be the discriminant of the algebraic equation
$\Delta (\rho )$
be the discriminant of the algebraic equation
![]() $f_{c_{N}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}(z) - z =0$
in the variable z, which is a polynomial in the variable
$f_{c_{N}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}(z) - z =0$
in the variable z, which is a polynomial in the variable
![]() $\rho $
. If
$\rho $
. If
![]() $\Delta (\rho _{0}) = 0$
for some
$\Delta (\rho _{0}) = 0$
for some
![]() $\rho _{0},$
then
$\rho _{0},$
then
![]() $r_{\mathrm {bif}}(c) \leq |\rho _{0}|.$
$r_{\mathrm {bif}}(c) \leq |\rho _{0}|.$
Proof. Under the assumptions, if
![]() $\rho = \rho _{0},$
then
$\rho = \rho _{0},$
then
![]() $f_{c_{N}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}(z) - z =0$
has a multiple root. This implies that the map
$f_{c_{N}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}(z) - z =0$
has a multiple root. This implies that the map
![]() $f_{c_{N}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}$
has a parabolic fixed point with multiplier
$f_{c_{N}} \circ \cdots \circ f_{c_{2}} \circ f_{c_{1}}$
has a parabolic fixed point with multiplier
![]() $1.$
Since
$1.$
Since
![]() $c_{1}, c_{2} \ldots , c_{N} \in {\bar {B}({c}, {r_{0}})}$
with
$c_{1}, c_{2} \ldots , c_{N} \in {\bar {B}({c}, {r_{0}})}$
with
![]() $r_{0} = |\rho _{0}|,$
we have
$r_{0} = |\rho _{0}|,$
we have
![]() $r_{\mathrm {bif}}(c) \leq r_{0}$
by Theorem 4.19.
$r_{\mathrm {bif}}(c) \leq r_{0}$
by Theorem 4.19.
We now give upper bounds of
![]() ${\mathit {r}_{\mathrm {bif}}}(-1)$
.
${\mathit {r}_{\mathrm {bif}}}(-1)$
.
Example 4.21. Suppose
![]() $c=-1.$
Let
$c=-1.$
Let
![]() $N = 4$
,
$N = 4$
,
![]() $k =6,$
and
$k =6,$
and
![]() $(p_{1}, p_{2}, p_{3}, p_{4}) = (1, 2, 5,4 ).$
Then numerical calculation shows the following result. The discriminant
$(p_{1}, p_{2}, p_{3}, p_{4}) = (1, 2, 5,4 ).$
Then numerical calculation shows the following result. The discriminant
![]() $\Delta (\rho )$
of
$\Delta (\rho )$
of
![]() $f_{c_{4}} \circ f_{c_{3}} \circ f_{c_{2}} \circ f_{c_{1}}(z) -z $
vanishes at
$f_{c_{4}} \circ f_{c_{3}} \circ f_{c_{2}} \circ f_{c_{1}}(z) -z $
vanishes at
![]() $\rho _{0} \approx 0.0399 \cdots $
, and hence
$\rho _{0} \approx 0.0399 \cdots $
, and hence
![]() ${\mathit {r}_{\mathrm {bif}}}(-1) \leq 0.0399 \cdots $
.
${\mathit {r}_{\mathrm {bif}}}(-1) \leq 0.0399 \cdots $
.
We have some comments on the upper bounds of
![]() ${\mathit {r}_{\mathrm {bif}}}(-1).$
${\mathit {r}_{\mathrm {bif}}}(-1).$
Remark 4.22. In Example 4.21, the numerical errors should be treated carefully because the discriminant of the equation
![]() $f_{c_{4}} \circ f_{c_{3}} \circ f_{c_{2}} \circ f_{c_{1}}(z) - z =0$
with respect to z is a polynomial
$f_{c_{4}} \circ f_{c_{3}} \circ f_{c_{2}} \circ f_{c_{1}}(z) - z =0$
with respect to z is a polynomial
![]() $\Delta ({\rho })$
of degree
$\Delta ({\rho })$
of degree
![]() $32$
, and each coefficient is a very large number in absolute value, that is, of the order of approximately
$32$
, and each coefficient is a very large number in absolute value, that is, of the order of approximately
![]() $10^{19}$
–
$10^{19}$
–
![]() $10^{26}$
. The author used validated numerics to estimate
$10^{26}$
. The author used validated numerics to estimate
![]() $\rho _{0}$
, which showed
$\rho _{0}$
, which showed
![]() ${\mathit {r}_{\mathrm {bif}}}(-1) \leq |\rho _{0}| \leq 0.0399217$
. Since validated numerics gives values including mathematically strict error evaluation, this value
${\mathit {r}_{\mathrm {bif}}}(-1) \leq |\rho _{0}| \leq 0.0399217$
. Since validated numerics gives values including mathematically strict error evaluation, this value
![]() $0.0399217$
is a rigorous upper bound of
$0.0399217$
is a rigorous upper bound of
![]() ${\mathit {r}_{\mathrm {bif}}}(-1).$
For more details on validated numerics, see [Reference Petković and Petković22], for example.
${\mathit {r}_{\mathrm {bif}}}(-1).$
For more details on validated numerics, see [Reference Petković and Petković22], for example.
Note also that all the
![]() $6^{4}$
candidates
$6^{4}$
candidates
![]() $(p_{1}, p_{2}, p_{3}, p_{4}) \in \{0, 1, 2, 3, 4, 5\}^{4}$
were (non-rigorously) verified. That is, for every
$(p_{1}, p_{2}, p_{3}, p_{4}) \in \{0, 1, 2, 3, 4, 5\}^{4}$
were (non-rigorously) verified. That is, for every
![]() $(p_{1}, p_{2}, p_{3}, p_{4}) \in \{0, 1, 2, 3, 4, 5\}^{4}$
, the discriminant
$(p_{1}, p_{2}, p_{3}, p_{4}) \in \{0, 1, 2, 3, 4, 5\}^{4}$
, the discriminant
![]() $\Delta ({\rho })$
of the equation
$\Delta ({\rho })$
of the equation
![]() $f_{c_{4}} \circ f_{c_{3}} \circ f_{c_{2}} \circ f_{c_{1}}(z) - z =0$
was computed using
$f_{c_{4}} \circ f_{c_{3}} \circ f_{c_{2}} \circ f_{c_{1}}(z) - z =0$
was computed using
![]() $c_{1}, \ldots , c_{4}$
as in Theorem 4.20, and we numerically computed the roots of
$c_{1}, \ldots , c_{4}$
as in Theorem 4.20, and we numerically computed the roots of
![]() $\Delta ({\rho })$
. This computation shows that
$\Delta ({\rho })$
. This computation shows that
![]() $24$
candidates
$24$
candidates
![]() $(p_{1}, p_{2}, p_{3}, p_{4})$
including
$(p_{1}, p_{2}, p_{3}, p_{4})$
including
![]() $(1, 2, 5,4 )$
attain the same minimum absolute value
$(1, 2, 5,4 )$
attain the same minimum absolute value
![]() $|\rho _{0}| \approx 0.0399 \cdots $
. Also, the author replaced
$|\rho _{0}| \approx 0.0399 \cdots $
. Also, the author replaced
![]() $\zeta _{6}$
by
$\zeta _{6}$
by
![]() $\zeta _{4} = e^{2 \pi i/4} = i$
, and computed the roots of
$\zeta _{4} = e^{2 \pi i/4} = i$
, and computed the roots of
![]() $\Delta ({\rho })$
in the same manner, which gave less sharp estimates.
$\Delta ({\rho })$
in the same manner, which gave less sharp estimates.
We now give the upper bound for another parameter.
Example 4.23. Suppose
![]() $\tilde {c_{3}} \approx -1.75487766$
is the airplane parameter such that
$\tilde {c_{3}} \approx -1.75487766$
is the airplane parameter such that
![]() $\tilde {c_{3}}$
is a real number and
$\tilde {c_{3}}$
is a real number and
![]() $f_{\tilde {c_{3}}}$
has a superattracting periodic point with period
$f_{\tilde {c_{3}}}$
has a superattracting periodic point with period
![]() $3$
. Let
$3$
. Let
![]() $N = 3$
,
$N = 3$
,
![]() $k =6,$
and
$k =6,$
and
![]() $(p_{1}, p_{2}, p_{3}) = (0, 3, 0).$
Then a similar numerical computation shows that
$(p_{1}, p_{2}, p_{3}) = (0, 3, 0).$
Then a similar numerical computation shows that
![]() ${\mathit {r}_{\mathrm {bif}}}(\tilde {c_{3}}) \leq 0.0021.$
${\mathit {r}_{\mathrm {bif}}}(\tilde {c_{3}}) \leq 0.0021.$
Remark 4.24. Recall that we can calculate the connected component W of
![]() $\mathrm {int} \,\mathcal {M}$
which contains
$\mathrm {int} \,\mathcal {M}$
which contains
![]() $-1$
. The component W is the open disk with center
$-1$
. The component W is the open disk with center
![]() $-1$
and radius
$-1$
and radius
![]() $1/4,$
thus
$1/4,$
thus
![]() $\operatorname {\mathrm {dist}} (-1, \partial {\mathcal {M}}) = 1/4.$
For
$\operatorname {\mathrm {dist}} (-1, \partial {\mathcal {M}}) = 1/4.$
For
![]() $c=-1$
, we have
$c=-1$
, we have
![]() ${\mathit {r}_{\mathrm {bif}}}(-1) \ll \operatorname {\mathrm {dist}} (-1, \partial {\mathcal {M}})$
by the example above. Similarly,
${\mathit {r}_{\mathrm {bif}}}(-1) \ll \operatorname {\mathrm {dist}} (-1, \partial {\mathcal {M}})$
by the example above. Similarly,
![]() ${\mathit {r}_{\mathrm {bif}}}(\tilde {c_{3}}) \ll \operatorname {\mathrm {dist}} (\tilde {c_{3}}, \partial {\mathcal {M}})$
since
${\mathit {r}_{\mathrm {bif}}}(\tilde {c_{3}}) \ll \operatorname {\mathrm {dist}} (\tilde {c_{3}}, \partial {\mathcal {M}})$
since
![]() $ \operatorname {\mathrm {dist}}(\tilde {c_{3}}, \partial {\mathcal {M}}) \approx 0.00487766$
for the airplane parameter
$ \operatorname {\mathrm {dist}}(\tilde {c_{3}}, \partial {\mathcal {M}}) \approx 0.00487766$
for the airplane parameter
![]() $\tilde {c_{3}}$
. See [Reference Giarrusso and Fisher13] for the explicit parameterization of period-
$\tilde {c_{3}}$
. See [Reference Giarrusso and Fisher13] for the explicit parameterization of period-
![]() $3$
hyperbolic components. This strict inequality is in contrast with the equality
$3$
hyperbolic components. This strict inequality is in contrast with the equality
![]() ${\mathit {r}_{\mathrm {bif}}}(0) = \operatorname {\mathrm {dist}}(0, \partial {\mathcal {M}})$
.
${\mathit {r}_{\mathrm {bif}}}(0) = \operatorname {\mathrm {dist}}(0, \partial {\mathcal {M}})$
.
Corollary 4.25. Almost every random Julia set is totally disconnected:
-
• if the central parameter
 $c=-1+ \epsilon $
and the noise amplitude
$c=-1+ \epsilon $
and the noise amplitude
 $r> 0.0399 \cdots + |\epsilon |$
; or
$r> 0.0399 \cdots + |\epsilon |$
; or -
• if the central parameter
 $c =\tilde {c_{3}} + \epsilon $
and the noise amplitude
$c =\tilde {c_{3}} + \epsilon $
and the noise amplitude
 $r> 0.0021 + |\epsilon |.$
$r> 0.0021 + |\epsilon |.$
Proof. By Theorem 4.6,
![]() ${\mathbb {P}}_{c, r}$
-almost every random Julia set is totally disconnected if
${\mathbb {P}}_{c, r}$
-almost every random Julia set is totally disconnected if
![]() ${r> {\mathit {r}_{\mathrm {bif}}}(c).}$
In addition, we have
${r> {\mathit {r}_{\mathrm {bif}}}(c).}$
In addition, we have
![]() ${\mathit {r}_{\mathrm {bif}}}(c + \epsilon ) \leq {\mathit {r}_{\mathrm {bif}}}(c) + |\epsilon |$
for every
${\mathit {r}_{\mathrm {bif}}}(c + \epsilon ) \leq {\mathit {r}_{\mathrm {bif}}}(c) + |\epsilon |$
for every
![]() $\epsilon \in {\mathbb {C}}$
by Theorem 4.10. Thus, the conclusion follows from Examples 4.21 and 4.23.
$\epsilon \in {\mathbb {C}}$
by Theorem 4.10. Thus, the conclusion follows from Examples 4.21 and 4.23.
4.5. Application to quasiconformal conjugacy
By combining Theorem 4.6 and the theory of non-autonomous holomorphic motions by Comerford, we can deduce that non-autonomous Julia sets are quasiconformally conjugate to the autonomous Julia set. In this subsection, we see an overview of this conjugacy. For a more detailed meaning, the reader is referred to [Reference Comerford7].
For
![]() $\omega = (c_{1}, c_{2}, \ldots ) \in {\mathbb {C}}^{{\mathbb {N}}},$
we denote
$\omega = (c_{1}, c_{2}, \ldots ) \in {\mathbb {C}}^{{\mathbb {N}}},$
we denote
![]() $\sigma ^{m}\omega = (c_{m+1}, c_{m+2}, \ldots )$
for every
$\sigma ^{m}\omega = (c_{m+1}, c_{m+2}, \ldots )$
for every
![]() $m \geq 0.$
$m \geq 0.$
Definition 4.26. Let
![]() $\delta> 0$
and let
$\delta> 0$
and let
![]() $\omega \in {\mathbb {C}}^{{\mathbb {N}}}$
be a bounded sequence of parameters. We say that
$\omega \in {\mathbb {C}}^{{\mathbb {N}}}$
be a bounded sequence of parameters. We say that
![]() $\omega $
has post-critical distance
$\omega $
has post-critical distance
![]() $\geq \delta $
if
$\geq \delta $
if
Here,
![]() ${{f}_{{\omega }}^{({0})}}$
is understood as the identity map for every
${{f}_{{\omega }}^{({0})}}$
is understood as the identity map for every
![]() $\omega $
.
$\omega $
.
The sequence
![]() $\omega $
has post-critical distance
$\omega $
has post-critical distance
![]() $\geq \delta $
for some
$\geq \delta $
for some
![]() $\delta> 0$
if and only if non-autonomous dynamics is uniformly expanding (hyperbolic) if and only if non-autonomous dynamics is uniformly contractive at critical points. See [Reference Comerford7, Theorem 3.3] for the details.
$\delta> 0$
if and only if non-autonomous dynamics is uniformly expanding (hyperbolic) if and only if non-autonomous dynamics is uniformly contractive at critical points. See [Reference Comerford7, Theorem 3.3] for the details.
We next define hyperbolic components by analogy with the deterministic case. Denote
![]() $\ell ^{\infty }({\mathbb {C}}) = \{ \omega = (c_{n})_{n=1}^{\infty } \colon \sup _{n}|c_{n}| < \infty \}.$
$\ell ^{\infty }({\mathbb {C}}) = \{ \omega = (c_{n})_{n=1}^{\infty } \colon \sup _{n}|c_{n}| < \infty \}.$
Definition 4.27. Every connected component of
is called a hyperbolic component.
After formulating the concepts above, Comerford proved the following theorem [Reference Comerford7, Theorem 6.1].
Theorem 4.28. Suppose that
![]() $\omega = (c_{n})_{n=1}^{\infty }$
and
$\omega = (c_{n})_{n=1}^{\infty }$
and
![]() $\omega ' = (c^{\prime }_{n})_{n=1}^{\infty }$
lie in the same hyperbolic component. Then there exist
$\omega ' = (c^{\prime }_{n})_{n=1}^{\infty }$
lie in the same hyperbolic component. Then there exist
![]() $K \geq 1$
and a sequence of maps
$K \geq 1$
and a sequence of maps
![]() $\{\varphi _{n}\}_{n \geq 0}$
such that
$\{\varphi _{n}\}_{n \geq 0}$
such that
![]() $\varphi _{n}$
maps
$\varphi _{n}$
maps
![]() $J_{\sigma ^{n} \omega }$
onto
$J_{\sigma ^{n} \omega }$
onto
![]() $J_{\sigma ^{n} \omega '}\ K$
-quasiconformally and
$J_{\sigma ^{n} \omega '}\ K$
-quasiconformally and
![]() $\varphi _{n+1}\circ f_{c_{n+1}}= f_{c^{\prime }_{n+1}} \circ \varphi _{n}$
on
$\varphi _{n+1}\circ f_{c_{n+1}}= f_{c^{\prime }_{n+1}} \circ \varphi _{n}$
on
![]() $J_{\sigma ^{n} \omega }$
for every
$J_{\sigma ^{n} \omega }$
for every
![]() $n \geq 0$
.
$n \geq 0$
.
We say that
![]() $\omega $
and
$\omega $
and
![]() $\omega '$
are quasiconformally conjugate on their iterated Julia sets if such a sequence
$\omega '$
are quasiconformally conjugate on their iterated Julia sets if such a sequence
![]() $\{\varphi _{n}\}_{n \geq 0}$
exists.
$\{\varphi _{n}\}_{n \geq 0}$
exists.
More precisely, the sequence
![]() $\{\varphi _{n}\}_{n \geq 0}$
is bi-equicontinuous, as defined in [Reference Comerford7, §4]. Using the theorem above, we show the new results.
$\{\varphi _{n}\}_{n \geq 0}$
is bi-equicontinuous, as defined in [Reference Comerford7, §4]. Using the theorem above, we show the new results.
Theorem 4.29. Suppose that the interior of
![]() $ {\bar {B}({c}, {r})} $
contains a superattracting parameter
$ {\bar {B}({c}, {r})} $
contains a superattracting parameter
![]() $\tilde {c}$
and suppose
$\tilde {c}$
and suppose
![]() $r < {\mathit {r}_{\mathrm {bif}}} (c)$
. Then every two
$r < {\mathit {r}_{\mathrm {bif}}} (c)$
. Then every two
![]() $\omega , \omega ' \in {\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
are quasiconformally conjugate on their iterated Julia sets.
$\omega , \omega ' \in {\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
are quasiconformally conjugate on their iterated Julia sets.
Proof. By Definition 2.17 and Theorem 4.6, the polynomial semigroup
![]() $G_{c, r}$
has the planar attracting minimal set
$G_{c, r}$
has the planar attracting minimal set
![]() $L = \overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}.$
Define
$L = \overline {\bigcup _{g \in G_{c, r}}\{g(0)\}}.$
Define
![]() $\delta = \operatorname {\mathrm {dist}} (L, J(G_{c,r})),$
which is strictly positive by Definition 2.13 of attracting minimal sets. For every
$\delta = \operatorname {\mathrm {dist}} (L, J(G_{c,r})),$
which is strictly positive by Definition 2.13 of attracting minimal sets. For every
![]() $\omega \in {\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
,
$\omega \in {\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
,
![]() $m \geq 0$
, and
$m \geq 0$
, and
![]() $n\geq m$
, we have
$n\geq m$
, we have
![]() ${{f}_{{\sigma ^{m} \omega }}^{({n - m})}} (0) \in L$
since
${{f}_{{\sigma ^{m} \omega }}^{({n - m})}} (0) \in L$
since
![]() ${{f}_{{\sigma ^{m} \omega }}^{({n - m})}} \in G_{c, r}$
. Also,
${{f}_{{\sigma ^{m} \omega }}^{({n - m})}} \in G_{c, r}$
. Also,
![]() $J_{\sigma ^{m} \omega } \subset J(G_{c,r})$
by Proposition 2.9. Therefore,
$J_{\sigma ^{m} \omega } \subset J(G_{c,r})$
by Proposition 2.9. Therefore,
![]() $\omega $
has post-critical distance
$\omega $
has post-critical distance
![]() $\geq \delta $
with uniform
$\geq \delta $
with uniform
![]() $\delta> 0.$
Since the
$\delta> 0.$
Since the
![]() $\ell ^{\infty }$
-ball
$\ell ^{\infty }$
-ball
![]() ${\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
is connected, the ball
${\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
is connected, the ball
![]() ${\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
is contained in a hyperbolic component. Thus, every two
${\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
is contained in a hyperbolic component. Thus, every two
![]() $\omega , \omega ' \in {\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
are quasiconformally conjugate on their iterated Julia sets by Theorem 4.28.
$\omega , \omega ' \in {\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
are quasiconformally conjugate on their iterated Julia sets by Theorem 4.28.
More precisely, we can show by using [Reference Comerford7, Theorem 1.3] that the maximal dilatation K of the quasiconformal conjugacy
![]() $\{\varphi _{n}\}_{n \geq 0}$
depends on c and r but not on
$\{\varphi _{n}\}_{n \geq 0}$
depends on c and r but not on
![]() $\omega $
nor
$\omega $
nor
![]() $\omega '.$
This is because the
$\omega '.$
This is because the
![]() $\delta $
in the proof is independent of
$\delta $
in the proof is independent of
![]() $\omega $
. In addition, we can show that the maximal dilatation K tends to
$\omega $
. In addition, we can show that the maximal dilatation K tends to
![]() $1$
as r tends to
$1$
as r tends to
![]() $0$
.
$0$
.
Lastly, we give the following corollary.
Corollary 4.30. Suppose that the interior of
![]() $ {\bar {B}({c}, {r})} $
contains a superattracting parameter
$ {\bar {B}({c}, {r})} $
contains a superattracting parameter
![]() $\tilde {c}$
. Denote the autonomous Julia set by
$\tilde {c}$
. Denote the autonomous Julia set by
![]() $J_{\tilde {c}} = J_{\tilde {\omega }}$
where
$J_{\tilde {c}} = J_{\tilde {\omega }}$
where
![]() $\tilde {\omega } = (\tilde {c}, \tilde {c}, \ldots ).$
If
$\tilde {\omega } = (\tilde {c}, \tilde {c}, \ldots ).$
If
![]() $r < {\mathit {r}_{\mathrm {bif}}} (c)$
, then for every
$r < {\mathit {r}_{\mathrm {bif}}} (c)$
, then for every
![]() $\omega \in {\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
, there exists a map
$\omega \in {\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
, there exists a map
![]() $\varphi $
that maps
$\varphi $
that maps
![]() $J_{\tilde {c}}$
onto the non-autonomous Julia set
$J_{\tilde {c}}$
onto the non-autonomous Julia set
![]() $J_{\omega }$
quasiconformally. If
$J_{\omega }$
quasiconformally. If
![]() $r> {\mathit {r}_{\mathrm {bif}}} (c),$
then for
$r> {\mathit {r}_{\mathrm {bif}}} (c),$
then for
![]() ${\mathbb {P}}_{c, r}$
-almost every
${\mathbb {P}}_{c, r}$
-almost every
![]() $\omega $
, the autonomous Julia set
$\omega $
, the autonomous Julia set
![]() $J_{\tilde {c}}$
is not homeomorphic to the non-autonomous Julia set
$J_{\tilde {c}}$
is not homeomorphic to the non-autonomous Julia set
![]() $J_{\omega }.$
$J_{\omega }.$
Proof. First suppose
![]() $r < {\mathit {r}_{\mathrm {bif}}} (c)$
. By Theorem 4.29, there exists a quasiconformal conjugacy
$r < {\mathit {r}_{\mathrm {bif}}} (c)$
. By Theorem 4.29, there exists a quasiconformal conjugacy
![]() $\{\varphi _{n}\}_{n \geq 0}$
between
$\{\varphi _{n}\}_{n \geq 0}$
between
![]() $\tilde {\omega }$
and
$\tilde {\omega }$
and
![]() $\omega $
for every
$\omega $
for every
![]() $\omega \in {\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
. By definition, the map
$\omega \in {\bar {B}({c}, {r})} ^{{\mathbb {N}}}$
. By definition, the map
![]() $\varphi _{0}$
quasiconformally maps
$\varphi _{0}$
quasiconformally maps
![]() $J_{\tilde {c}}$
onto
$J_{\tilde {c}}$
onto
![]() $J_{\omega }.$
Next suppose
$J_{\omega }.$
Next suppose
![]() $r> {\mathit {r}_{\mathrm {bif}}} (c)$
. Then by Theorem 4.6, the non-autonomous Julia set
$r> {\mathit {r}_{\mathrm {bif}}} (c)$
. Then by Theorem 4.6, the non-autonomous Julia set
![]() $J_{\omega }$
is totally disconnected almost surely. Since the autonomous Julia set
$J_{\omega }$
is totally disconnected almost surely. Since the autonomous Julia set
![]() $J_{\tilde {c}}$
of superattracting parameter
$J_{\tilde {c}}$
of superattracting parameter
![]() $\tilde {c}$
is connected, these
$\tilde {c}$
is connected, these
![]() $J_{\tilde {c}}$
and
$J_{\tilde {c}}$
and
![]() $J_{\omega }$
cannot be homeomorphic each other.
$J_{\omega }$
cannot be homeomorphic each other.
5. Conclusive discussions
In this section, we discuss three perspectives, namely, open problems, other problems about geometric measure theory, and application to the general settings.
5.1. Open problems
We give the examples of c satisfying the equality
![]() ${\mathit {r}_{\mathrm {bif}}}(c) = \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
and the examples of c satisfying the strict inequality
${\mathit {r}_{\mathrm {bif}}}(c) = \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
and the examples of c satisfying the strict inequality
![]() ${\mathit {r}_{\mathrm {bif}}}(c) < \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
. The author conjectures that the former ones are uncommon. More precisely, the author considers the answer to the following question is yes.
${\mathit {r}_{\mathrm {bif}}}(c) < \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
. The author conjectures that the former ones are uncommon. More precisely, the author considers the answer to the following question is yes.
Question 5.1. If c does not belong to the main cardioid, then does
![]() ${\mathit {r}_{\mathrm {bif}}}(c) < \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
hold? If
${\mathit {r}_{\mathrm {bif}}}(c) < \operatorname {\mathrm {dist}}(c, \partial\mathcal {M})$
hold? If
![]() $c \notin [0, 1/4],$
then does it hold?
$c \notin [0, 1/4],$
then does it hold?
We numerically estimated
![]() $0.0386\cdots \leq {\mathit {r}_{\mathrm {bif}}}(-1) \leq 0.0399 \cdots $
. However, the actual value remains unknown. More generally, for every superattracting parameter
$0.0386\cdots \leq {\mathit {r}_{\mathrm {bif}}}(-1) \leq 0.0399 \cdots $
. However, the actual value remains unknown. More generally, for every superattracting parameter
![]() $\tilde {c}$
, it is interesting to determine the bifurcation radius.
$\tilde {c}$
, it is interesting to determine the bifurcation radius.
Question 5.2. What is the exact value of
![]() ${\mathit {r}_{\mathrm {bif}}}(\tilde {c})$
for a superattracting parameter
${\mathit {r}_{\mathrm {bif}}}(\tilde {c})$
for a superattracting parameter
![]() $\tilde {c}$
? How does it relate to other dynamical quantities?
$\tilde {c}$
? How does it relate to other dynamical quantities?
In addition, it would be meaningful to investigate their asymptotic behavior.
Question 5.3. Let
![]() $\tilde {c}_{p}$
be a superattracting parameter with period p for every
$\tilde {c}_{p}$
be a superattracting parameter with period p for every
![]() $p \in {\mathbb {N}}$
. How does
$p \in {\mathbb {N}}$
. How does
![]() ${\mathit {r}_{\mathrm {bif}}}(\tilde {c}_{p})$
decrease as
${\mathit {r}_{\mathrm {bif}}}(\tilde {c}_{p})$
decrease as
![]() $p \to \infty $
?
$p \to \infty $
?
Our strategy to estimate
![]() ${\mathit {r}_{\mathrm {bif}}}(-1)$
from above is to find multiple roots of some algebraic equation. This raises the following question.
${\mathit {r}_{\mathrm {bif}}}(-1)$
from above is to find multiple roots of some algebraic equation. This raises the following question.
Question 5.4. For every superattracting parameter
![]() $\tilde {c}$
, is the bifurcation radius
$\tilde {c}$
, is the bifurcation radius
![]() ${\mathit {r}_{\mathrm {bif}}}(\tilde {c})$
an algebraic number?
${\mathit {r}_{\mathrm {bif}}}(\tilde {c})$
an algebraic number?
At least, if
![]() $\tilde {c} = 0,$
then
$\tilde {c} = 0,$
then
![]() ${\mathit {r}_{\mathrm {bif}}}(0) = 1/4$
is algebraic and is related to the parabolic parameter
${\mathit {r}_{\mathrm {bif}}}(0) = 1/4$
is algebraic and is related to the parabolic parameter
![]() $c =1/4$
.
$c =1/4$
.
We are interested also in parameters which are not superattracting. Recall that Theorem 4.6 is concerned with the case where
![]() ${\bar {B}({c}, {r})} $
contains superattracting parameters.
${\bar {B}({c}, {r})} $
contains superattracting parameters.
Question 5.5. Can we generalize Theorem 4.6 when
![]() ${\bar {B}({c}, {r})}$
does not contain superattracting parameters?
${\bar {B}({c}, {r})}$
does not contain superattracting parameters?
Question 5.6. How does
![]() ${\mathit {r}_{\mathrm {bif}}}(c)$
decrease as
${\mathit {r}_{\mathrm {bif}}}(c)$
decrease as
![]() $c \to \partial {\mathcal {M}}$
? For example, within
$c \to \partial {\mathcal {M}}$
? For example, within
![]() $\epsilon> 0$
, how does
$\epsilon> 0$
, how does
![]() ${\mathit {r}_{\mathrm {bif}}}(-3/4 + \epsilon )$
decrease as
${\mathit {r}_{\mathrm {bif}}}(-3/4 + \epsilon )$
decrease as
![]() $\epsilon \to 0$
?
$\epsilon \to 0$
?
5.2. Other problems about geometric measure theory
One can consider the Hausdorff dimensions and other geometric properties of random Julia sets. For instance, the uniform perfectness and the Johnness was investigated. See [Reference Sumi26, Theorems 1.6 and 1.12].
Regarding dimensions, the following facts are known. Suppose
![]() $c=0$
and
$c=0$
and
![]() $0 < r < 1/4$
, and let
$0 < r < 1/4$
, and let
![]() $({\mathbb {P}}_{0, r}, \Omega _{0, r})$
as in Setting 4.1. Denote by
$({\mathbb {P}}_{0, r}, \Omega _{0, r})$
as in Setting 4.1. Denote by
![]() $\mathrm {HD} (J)$
the Hausdorff dimension of a set
$\mathrm {HD} (J)$
the Hausdorff dimension of a set
![]() $J.$
Then, there exists
$J.$
Then, there exists
![]() $1 < d_{0, r} <2$
such that
$1 < d_{0, r} <2$
such that
![]() $\mathrm {HD}( J_{\omega }) = d_{0, r}$
for
$\mathrm {HD}( J_{\omega }) = d_{0, r}$
for
![]() ${\mathbb {P}}_{0, r}$
-almost every
${\mathbb {P}}_{0, r}$
-almost every
![]() $\omega \in \Omega _{0, r}.$
See [Reference Mayer, Skorulski and Urbański18, Theorems 8.8 and 8.10] by Mayer, Skorulski, and Urbański. In addition, denote by
$\omega \in \Omega _{0, r}.$
See [Reference Mayer, Skorulski and Urbański18, Theorems 8.8 and 8.10] by Mayer, Skorulski, and Urbański. In addition, denote by
![]() $\mathcal {H}^{d}$
the d-dimensional Hausdorff measure and by
$\mathcal {H}^{d}$
the d-dimensional Hausdorff measure and by
![]() $\mathcal {P}^{d}$
the d-dimensional Packing measure, then
$\mathcal {P}^{d}$
the d-dimensional Packing measure, then
![]() $\mathcal {H}^{d_{0, r}} ( J_{\omega }) = 0$
and
$\mathcal {H}^{d_{0, r}} ( J_{\omega }) = 0$
and
![]() $\mathcal {P}^{d_{0, r}} ( J_{\omega }) = \infty $
for
$\mathcal {P}^{d_{0, r}} ( J_{\omega }) = \infty $
for
![]() ${\mathbb {P}}_{0, r}$
-almost every
${\mathbb {P}}_{0, r}$
-almost every
![]() $\omega \in \Omega _{0, r}.$
See [Reference Mayer, Skorulski and Urbański18, Theorem 8.16]. Note that this is different from the deterministic case, and hence almost every
$\omega \in \Omega _{0, r}.$
See [Reference Mayer, Skorulski and Urbański18, Theorem 8.16]. Note that this is different from the deterministic case, and hence almost every
![]() $J_{\omega }$
is not bi-Lipschitz equivalent to any autonomous hyperbolic Julia sets.
$J_{\omega }$
is not bi-Lipschitz equivalent to any autonomous hyperbolic Julia sets.
Sumi kindly taught me that for every
![]() $c \in {\mathbb {C}}$
and
$c \in {\mathbb {C}}$
and
![]() $r>0$
, there exists a constant
$r>0$
, there exists a constant
![]() $d_{c, r}$
such that
$d_{c, r}$
such that
![]() $\mathrm {HD}( J_{\omega }) = d_{c, r}$
for
$\mathrm {HD}( J_{\omega }) = d_{c, r}$
for
![]() ${\mathbb {P}}_{c, r}$
-almost every
${\mathbb {P}}_{c, r}$
-almost every
![]() $\omega \in \Omega _{c, r}$
. Rugh showed that the dimension
$\omega \in \Omega _{c, r}$
. Rugh showed that the dimension
![]() $d_{c, r}$
depends real-analytically on
$d_{c, r}$
depends real-analytically on
![]() $\mathrm {Re} (c)$
,
$\mathrm {Re} (c)$
,
![]() $\mathrm {Im} (c)$
, and r within
$\mathrm {Im} (c)$
, and r within
![]() $|c| + r <1/4$
. See [Reference Rugh23] for the exact statements. This is the motivation for the following question.
$|c| + r <1/4$
. See [Reference Rugh23] for the exact statements. This is the motivation for the following question.
Question 5.7. How does the typical dimension
![]() $d_{c, r}$
depend on c and r?
$d_{c, r}$
depend on c and r?
For other geometric properties, Brück showed that the random Julia set
![]() $J_{\omega }$
is a quasi-circle for every
$J_{\omega }$
is a quasi-circle for every
![]() $\omega \in \Omega _{0, r}$
if
$\omega \in \Omega _{0, r}$
if
![]() $r < 1/4.$
See [Reference Brück2, Corollary 4.5].
$r < 1/4.$
See [Reference Brück2, Corollary 4.5].
Theorem 4.29 generalizes this result. However, the following questions are open.
Question 5.8. Suppose
![]() $r> {\mathit {r}_{\mathrm {bif}}}(c).$
Then for
$r> {\mathit {r}_{\mathrm {bif}}}(c).$
Then for
![]() ${\mathbb {P}}_{c,r} \times {\mathbb {P}}_{c,r}$
-almost every
${\mathbb {P}}_{c,r} \times {\mathbb {P}}_{c,r}$
-almost every
![]() $(\omega , \omega ')$
, are the Julia sets
$(\omega , \omega ')$
, are the Julia sets
![]() $J_{\omega }$
and
$J_{\omega }$
and
![]() $J_{\omega '}$
quasiconformally equivalent? Note that almost every Julia set is homeomorphic to the (usual) Cantor set.
$J_{\omega '}$
quasiconformally equivalent? Note that almost every Julia set is homeomorphic to the (usual) Cantor set.
Question 5.9. If
![]() $r = {\mathit {r}_{\mathrm {bif}}}(c),$
then is almost every random Julia set
$r = {\mathit {r}_{\mathrm {bif}}}(c),$
then is almost every random Julia set
![]() $J_{\omega }$
quasiconformally equivalent to the autonomous Julia set?
$J_{\omega }$
quasiconformally equivalent to the autonomous Julia set?
In this paper, we considered the measure-theoretic aspect of the typicality problem. For the topological aspect, see [Reference Gong, Qiu and Li14], for example.
5.3. Application to general settings
We mainly considered random dynamical systems induced by uniform noise on disks as in Setting 4.1. However, random dynamical systems induced by any distribution
![]() $\mu $
with compact support can be considered. Even for Setting 2.1, we can apply the numerical estimates given in §4. More precisely, the following hold.
$\mu $
with compact support can be considered. Even for Setting 2.1, we can apply the numerical estimates given in §4. More precisely, the following hold.
Theorem 5.10. Let
![]() $\mu $
be a Borel probability measure on the parameter plane
$\mu $
be a Borel probability measure on the parameter plane
![]() ${\mathbb {C}}$
with compact support and let
${\mathbb {C}}$
with compact support and let
![]() $({\mathbb {P}}_{\mu }, \Omega _{\mu })$
be defined as in Setting 2.1. If there exists
$({\mathbb {P}}_{\mu }, \Omega _{\mu })$
be defined as in Setting 2.1. If there exists
![]() $c \in {\mathbb {C}}$
such that
$c \in {\mathbb {C}}$
such that
![]() $\operatorname {\mathrm {supp}} \mu \subset {\bar {B}({c}, {{\mathit {r}_{\mathrm {bif}}}(c)})}$
, then the polynomial semigroup
$\operatorname {\mathrm {supp}} \mu \subset {\bar {B}({c}, {{\mathit {r}_{\mathrm {bif}}}(c)})}$
, then the polynomial semigroup
![]() $G_{\mu }$
has a planar minimal set. If there exists
$G_{\mu }$
has a planar minimal set. If there exists
![]() $c \in {\mathbb {C}}$
such that
$c \in {\mathbb {C}}$
such that
![]() $\mathrm {int} (\operatorname {\mathrm {supp}} \mu ) \supset {\bar {B}({c}, {{\mathit {r}_{\mathrm {bif}}}(c)})}$
, then the random Julia set
$\mathrm {int} (\operatorname {\mathrm {supp}} \mu ) \supset {\bar {B}({c}, {{\mathit {r}_{\mathrm {bif}}}(c)})}$
, then the random Julia set
![]() $J_{\omega }$
is totally disconnected for
$J_{\omega }$
is totally disconnected for
![]() ${\mathbb {P}}_{\mu }$
-almost every
${\mathbb {P}}_{\mu }$
-almost every
![]() $\omega \in \Omega _{\mu }$
.
$\omega \in \Omega _{\mu }$
.
Proof. Suppose that there exists
![]() $c \in {\mathbb {C}}$
such that
$c \in {\mathbb {C}}$
such that
![]() $\operatorname {\mathrm {supp}} \mu \subset {\bar {B}({c}, {{\mathit {r}_{\mathrm {bif}}}(c)})}$
. By definition, the polynomial semigroup
$\operatorname {\mathrm {supp}} \mu \subset {\bar {B}({c}, {{\mathit {r}_{\mathrm {bif}}}(c)})}$
. By definition, the polynomial semigroup
![]() $G_{c, {\mathit {r}_{\mathrm {bif}}}(c)}$
has a planar minimal set. Thus, Lemma 2.12 gives that
$G_{c, {\mathit {r}_{\mathrm {bif}}}(c)}$
has a planar minimal set. Thus, Lemma 2.12 gives that
![]() $G_{\mu }$
also has a planar minimal set.
$G_{\mu }$
also has a planar minimal set.
Similarly, if there exists
![]() $c \in {\mathbb {C}}$
such that
$c \in {\mathbb {C}}$
such that
![]() $\mathrm {int} (\operatorname {\mathrm {supp}} \mu ) \supset {\bar {B}({c}, {{\mathit {r}_{\mathrm {bif}}}(c)})}$
, then
$\mathrm {int} (\operatorname {\mathrm {supp}} \mu ) \supset {\bar {B}({c}, {{\mathit {r}_{\mathrm {bif}}}(c)})}$
, then
![]() $G_{\mu }$
does not have any planar minimal sets. Thus,
$G_{\mu }$
does not have any planar minimal sets. Thus,
![]() $G_{\mu }$
is mean stable, and
$G_{\mu }$
is mean stable, and
![]() $T_{\{\infty \}, \mu }$
is identically equal to
$T_{\{\infty \}, \mu }$
is identically equal to
![]() $1$
by Theorem 2.21. Combining this with Theorem 3.7, we have that the random Julia set
$1$
by Theorem 2.21. Combining this with Theorem 3.7, we have that the random Julia set
![]() $J_{\omega }$
is totally disconnected for
$J_{\omega }$
is totally disconnected for
![]() ${\mathbb {P}}_{\mu }$
-almost every
${\mathbb {P}}_{\mu }$
-almost every
![]() $\omega \in \Omega _{\mu }$
.
$\omega \in \Omega _{\mu }$
.
Example 5.11. Let
![]() $\mu _{s}$
be the normalized Lebesgue measure on
$\mu _{s}$
be the normalized Lebesgue measure on
![]() ${\mathbb {C}}$
with
${\mathbb {C}}$
with
![]() $\operatorname {\mathrm {supp}} \mu _{s} =\{c \in {\mathbb {C}} \colon |\mathrm {Re} \ c| \leq s, |\mathrm {Im}\ c| \leq s\}$
for
$\operatorname {\mathrm {supp}} \mu _{s} =\{c \in {\mathbb {C}} \colon |\mathrm {Re} \ c| \leq s, |\mathrm {Im}\ c| \leq s\}$
for
![]() $s \geq 0$
. Then there exists
$s \geq 0$
. Then there exists
![]() $s^{*}> 0$
such that
$s^{*}> 0$
such that
![]() $G_{\mu _{s}}$
is mean stable if and only if
$G_{\mu _{s}}$
is mean stable if and only if
![]() $s \notin \{0, s^{*}\}.$
Theorem 5.10 and Corollary 4.11 imply
$s \notin \{0, s^{*}\}.$
Theorem 5.10 and Corollary 4.11 imply
![]() $(4 \sqrt 2)^{-1} \leq s^{*} \leq 4^{-1}.$
$(4 \sqrt 2)^{-1} \leq s^{*} \leq 4^{-1}.$
Generally, we may apply our results to non-quadratic cases. Since ‘the Mandelbrot set is universal’ [Reference McMullen and Lei20], the structure of the quadratic family exists for any non-trivial family. Thus, our quadratic results apply to random dynamical systems of any non-trivial family. In this case, it is difficult to obtain quantitative estimates of bifurcation parameters.
Acknowledgments
The author thanks Hiroki Sumi for detailed comments and valuable discussions. The author thanks Isaia Nisoli for the instruction to use validated numerics. The manuscript has been edited for English language by a professional native proofreader at Xtra, Inc. This work was supported by the Research Institute for Mathematical Sciences, an International Joint Usage/Research Center located in Kyoto University. This work is supported by JSPS Grant-in-Aid for Research Activity Start-up Grant Number JP 21K20323 and Grant-in-Aid for Early-Career Scientists Grant Number JP 23K13000.