Article contents
On minimal self-joinings in topological dynamics
Published online by Cambridge University Press: 19 September 2008
Abstract
If X is a compact metric space and T a homeomorphism of X we say (X, T) has almost minimal power joinings (AMPJ) if there is a dense GδX* in X such that for each finite set k, x∈(X*)k and l:k → ℤ−{0}, the orbit closure cl {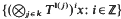 } is a product of off-diagonals (POOD) on Xk. By an offdiagonal on Xk′, k′k we mean a set of the form (⊗,j∈k′Tm(j))Δ, Δ the diagonal in Xk′, m:k′→ℤ any function, and by a POOD on Xk we mean that k is split into subsets k′, on each Xk′ we put an off-diagonal and then we take the product of these.
} is a product of off-diagonals (POOD) on Xk. By an offdiagonal on Xk′, k′k we mean a set of the form (⊗,j∈k′Tm(j))Δ, Δ the diagonal in Xk′, m:k′→ℤ any function, and by a POOD on Xk we mean that k is split into subsets k′, on each Xk′ we put an off-diagonal and then we take the product of these.
We show that examples of AMPJ exist and that this definition leads to a theory completely analogous to Rudolph's theory of minimal self-joinings in ergodic theory. In particular if (X, T) has AMPJ the automorphism group of T is {Tn}, T has only almost 1-1 factors (other than the trivial one) and the automorphism group and factors of ⊕i ∊ kT, k finite or countably infinite, can be very explicitly described. We also discuss ℝ-actions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1987
References
REFERENCES
- 11
- Cited by




