Research Article
The ordering on permutations induced by continuous maps of the real line
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 155-160
-
- Article
-
- You have access
- Export citation
The algebraic-geometric AKNS potentials
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 1-24
-
- Article
-
- You have access
- Export citation
Periodic attractors as a result of diffusion
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 319-335
-
- Article
-
- You have access
- Export citation
An ergodic theorem for iterated maps
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 481-488
-
- Article
-
- You have access
- Export citation
Finitely presented dynamical systems
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 489-507
-
- Article
-
- You have access
- Export citation
Orbit types for maps of the interval
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 161-164
-
- Article
-
- You have access
- Export citation
Topological dynamics and ergodic theory
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 25-47
-
- Article
-
- You have access
- Export citation
Weakly mixing PET
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 337-349
-
- Article
-
- You have access
- Export citation
Dynamics of Markov chains and stable manifolds for random diffeomorphisms
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 351-374
-
- Article
-
- You have access
- Export citation
A counter-example to a C2 closing lemma
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 509-530
-
- Article
-
- You have access
- Export citation
Periodic orbits for dissipative twist maps
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 165-173
-
- Article
-
- You have access
- Export citation
Semi-rigidity of horocycle flows over compact surfaces of variable negative curvature
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 49-72
-
- Article
-
- You have access
- Export citation
On ergodic actions whose self-joinings are graphs
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 531-557
-
- Article
-
- You have access
- Export citation
Time-like geodesic flows on Lorentz manifolds
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 175-192
-
- Article
-
- You have access
- Export citation
Generic 3-parameter families of vector fields on the plane, unfolding a singularity with nilpotent linear part. The cusp case of codimension 3
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 375-413
-
- Article
-
- You have access
- Export citation
An extension of Ratner's rigidity theorem to n-dimensional hyperbolic space
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 73-92
-
- Article
-
- You have access
- Export citation
Recurrence without uniform recurrence
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 559-566
-
- Article
-
- You have access
- Export citation
A refinement of the Conley index and an application to the stability of hyperbolic invariant sets
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 93-103
-
- Article
-
- You have access
- Export citation
Eventually positive matrices with rational eigenvectors†
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 193-196
-
- Article
-
- You have access
- Export citation
Diffeomorphisms on surfaces with a finite number of moduli
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 415-462
-
- Article
-
- You have access
- Export citation

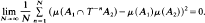

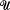 of
of 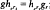 such a flow exists, leaves μ invariant, and is unique up to constant scaling of the parameter (Margulis). We show that any measure-theoretic conjugacy: (
such a flow exists, leaves μ invariant, and is unique up to constant scaling of the parameter (Margulis). We show that any measure-theoretic conjugacy: (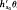 θ, where θ is a homeomorphic conjugacy:
θ, where θ is a homeomorphic conjugacy: 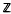 -action with minimal self-joinings are disjoint.
-action with minimal self-joinings are disjoint.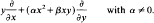
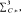 consisting of germs of cusp type whose 4-jet is
consisting of germs of cusp type whose 4-jet is 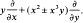
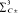 transversally in (0, 0) is fibre-
transversally in (0, 0) is fibre-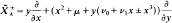
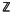 )-conjugate to a matrix all sufficiently large powers of which have strictly positive entries. We show that when the ‘large’ eigenvectors are commensurable and satisfy the obvious necessary conditions, then
)-conjugate to a matrix all sufficiently large powers of which have strictly positive entries. We show that when the ‘large’ eigenvectors are commensurable and satisfy the obvious necessary conditions, then