Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-27T13:02:18.938Z Has data issue: false hasContentIssue false
  • English
  • Français

A mechanism for ejecting a horseshoe from a partially hyperbolic chain recurrence class

Part of: Local and nonlocal bifurcation theory Topological dynamics Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  03 November 2023

CHRISTIAN BONATTI  and
KATSUTOSHI SHINOHARA
CHRISTIAN BONATTI
Affiliation:
Institut de Mathématiques de Bourgogne CNRS – URM 5584, Université de Bourgogne, Dijon 21004, France (e-mail: christian.bonatti@u-bourgogne.fr)
KATSUTOSHI SHINOHARA*
Affiliation:
Graduate School of Business Administration, Hitotsubashi University, 2-1 Naka, Kunitachi, Tokyo 186-8601, Japan
*
e-mail: ka.shinohara@r.hit-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a 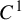$C^1$-perturbation technique for ejecting an a priori given finite set of periodic points preserving a given finite set of homo/heteroclinic intersections from a chain recurrence class of a periodic point. The technique is first stated under a simpler setting called a Markov iterated function system, a two-dimensional iterated function system in which the compositions are chosen in a Markovian way. Then we apply the result to the setting of three-dimensional partially hyperbolic diffeomorphisms.

Keywords

iterated function systemswild diffeomorphismchain recurrence classC1-generic diffeomorphisms

MSC classification

Primary: 37B25: Lyapunov functions and stability; attractors, repellers
Secondary: 37D30: Partially hyperbolic systems and dominated splittings 37G35: Attractors and their bifurcations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 63
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bonatti, C. and Crovisier, S.. Récurrence et généricité. Invent. Math. 158(1) (2004), 33–104.CrossRefGoogle Scholar
Bonatti, C., Crovisier, S., Díaz, L. J. and Gourmelon, N.. Internal perturbations of homoclinic classes: non-domination, cycles, and self-replication. Ergod. Th. & Dynam. Sys. 33(3) (2013), 739–776.CrossRefGoogle Scholar
Bonatti, C. and Díaz, L. J.. On maximal transitive sets of generic diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 96 (2002), 171–197.CrossRefGoogle Scholar
Bonatti, C. and Díaz, L. J.. Connexions hétéroclines et généricité d’une infinité de puits ou de sources. Ann. Sci. Éc. Norm. Supér. (4) 32 (1999), 135–150.CrossRefGoogle Scholar
Bonatti, C. and Díaz, L. J.. Robust heterodimensional cycles and ${C}^1$ -generic dynamics. J. Inst. Math. Jussieu 7(3) (2008), 469–525.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. J. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity. A Global Geometric and Probabilistic Perspective (Encyclopaedia of Mathematical Sciences, 102, Mathematical Physics, III). Springer-Verlag, Berlin, 2005.Google Scholar
Bonatti, C.. Towards a global view of dynamical systems, for the ${C}^1$ -topology. Ergod. Th. & Dynam. Sys. 31(4) (2011), 959–993.CrossRefGoogle Scholar
Bonatti, C. and Shinohara, K.. Flexible periodic points. Ergod. Th. & Dynam. Sys. 35(5) (2015), 1394–1422.CrossRefGoogle Scholar
Bonatti, C. and Shinohara, K.. Volume hyperbolicity and Wildness. Ergod. Th. & Dynam. Sys. 38(3) (2018), 886–920.CrossRefGoogle Scholar
Bonatti, C. and Shinohara, K.. Aperiodic chain recurrence classes of ${C}^1$ -generic diffeomorphisms. Preprint, 2022, arXiv:2209.13249.Google Scholar
Crovisier, S.. Periodic orbits and chain recurrent sets of ${C}^1$ -diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 104 (2006), 87–141.CrossRefGoogle Scholar
Gourmelon, N.. A Franks’ lemma that preserves invariant manifolds. Ergod. Th. & Dynam. Sys. 36(4) (2016), 1167–1203.CrossRefGoogle Scholar
Leslie, J. A.. On a differential structure for the group of diffeomorphisms. Topology 6(2) (1967), 263–271.CrossRefGoogle Scholar
Wang, X.. Hyperbolicity versus weak periodic orbits inside homoclinic classes. Ergod. Th. & Dynam. Sys. 38(6) (2018), 2345–2400.CrossRefGoogle Scholar