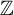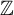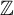1. Introduction
On the surface it would seem that there is a fundamental incompatibility between the concepts of entropy and orbit equivalence. On the one hand, Ornstein and Weiss proved, building on a seminal theorem of Dye in the integer case, that any two free ergodic probability-measure-preserving (p.m.p) actions of a countably infinite amenable group are orbit equivalent, so that any asymptotic information about the dynamics or the group that is not a mere corollary to ergodicity or amenability can be completely obliterated [Reference Dye7, Reference Ornstein and Weiss20, Reference Ornstein and Weiss21]. On the other hand, it is precisely for amenable groups that the original Kolmogorov–Sinai form of entropy based on the asymptotic averaging of Shannon entropies is most naturally and generally defined, and in that setting a rich theory has developed whose highlights include the classification of Bernoulli actions up to measure conjugacy by their entropy, first established by Ornstein for the integers and then by Ornstein and Weiss for all countably infinite amenable groups [Reference Ornstein18, Reference Ornstein and Weiss20, Reference Ornstein and Weiss21].
It turns out, however, that there is a certain combinatorial robustness with which entropy registers the higher-order statistics of set intersections, permitting a degree of reshuffling in the way that orbits are parameterized. Indeed, this became manifest in the Ornstein theory of Bernoulli actions and in related research on Kakutani equivalence [Reference del Junco and Rudolph5, Reference Katok13, Reference Ornstein, Rudolph and Weiss19], as well as in the work of Vershik on actions of locally finite groups [Reference Vershik24, Reference Vershik25]. Ultimately these threads were united in the abstract theory of Kammeyer and Rudolph which describes, for actions of a fixed countable amenable group, how entropy may or may not be preserved under orbit equivalences subject to various conditions, and how entropy can serve as a complete invariant, up to some restricted notion of orbit equivalence, within certain classes of actions [Reference Kammeyer and Rudolph11, Reference Kammeyer and Rudolph12, Reference Rudolph23].
More recently, taking a rather different geometric perspective not based on the combinatorial shuffling of orbit segments, and inspired by growing interest in integrable notions of equivalence in the study of measure rigidity, Austin proved that if G and H are any two finitely generated amenable groups and
![]() $G\curvearrowright (X,\mu )$
and
$G\curvearrowright (X,\mu )$
and
![]() $H\curvearrowright (Y,\nu )$
are free p.m.p. actions that are integrably orbit equivalent (that is, there is an orbit equivalence between them whose cocycles, when restricted to each group element and composed with a fixed word-length metric, give integrable functions), then the actions have the same entropy [Reference Austin1]. Curiously, a separate argument was required to handle the virtually cyclic case (one based, in fact, on Kakutani equivalence), while the proof in the not-virtually-cyclic case actually shows that the equality of entropies still holds if one instead assumes the weaker relation of Shannon orbit equivalence, in which the cocycle partitions associated to the orbit equivalence are assumed to have finite Shannon entropy. In [Reference Kerr and Li16], this entropy invariance under Shannon orbit equivalence was verified to hold more generally when G and H are any countable amenable groups that are neither virtually cyclic nor locally finite. The non-local-finiteness assumption is necessary here, as a theorem of Vershik shows that any two non-trivial Bernoulli actions of a countably infinite locally finite group are boundedly orbit equivalent [Reference Vershik24, Reference Vershik25] (see the discussion in the introduction to [Reference Kerr and Li16]). However, it remained an open question whether the non-virtual-cyclicity condition can be dropped, and, in particular, whether a Shannon orbit equivalence between free p.m.p.
$H\curvearrowright (Y,\nu )$
are free p.m.p. actions that are integrably orbit equivalent (that is, there is an orbit equivalence between them whose cocycles, when restricted to each group element and composed with a fixed word-length metric, give integrable functions), then the actions have the same entropy [Reference Austin1]. Curiously, a separate argument was required to handle the virtually cyclic case (one based, in fact, on Kakutani equivalence), while the proof in the not-virtually-cyclic case actually shows that the equality of entropies still holds if one instead assumes the weaker relation of Shannon orbit equivalence, in which the cocycle partitions associated to the orbit equivalence are assumed to have finite Shannon entropy. In [Reference Kerr and Li16], this entropy invariance under Shannon orbit equivalence was verified to hold more generally when G and H are any countable amenable groups that are neither virtually cyclic nor locally finite. The non-local-finiteness assumption is necessary here, as a theorem of Vershik shows that any two non-trivial Bernoulli actions of a countably infinite locally finite group are boundedly orbit equivalent [Reference Vershik24, Reference Vershik25] (see the discussion in the introduction to [Reference Kerr and Li16]). However, it remained an open question whether the non-virtual-cyclicity condition can be dropped, and, in particular, whether a Shannon orbit equivalence between free p.m.p.
![]() ${\mathbb Z}$
-actions preserves entropy. Carderi et al observed in [Reference Carderi, Joseph, Le Maître and Tessera4] that, for free p.m.p.
${\mathbb Z}$
-actions preserves entropy. Carderi et al observed in [Reference Carderi, Joseph, Le Maître and Tessera4] that, for free p.m.p.
![]() ${\mathbb Z}$
-actions, finiteness of entropy is preserved by Shannon orbit equivalence. The first goal of the present paper is to establish the following.
${\mathbb Z}$
-actions, finiteness of entropy is preserved by Shannon orbit equivalence. The first goal of the present paper is to establish the following.
Theorem A. Let G and H be finitely generated virtually Abelian groups. Let
![]() $G\stackrel {\alpha }{\curvearrowright } (X,\mu )$
and
$G\stackrel {\alpha }{\curvearrowright } (X,\mu )$
and
![]() $H\stackrel {\beta }{\curvearrowright } (Y,\nu )$
be free p.m.p. actions that are Shannon orbit equivalent. Then
$H\stackrel {\beta }{\curvearrowright } (Y,\nu )$
be free p.m.p. actions that are Shannon orbit equivalent. Then
![]() $h(\alpha ) = h(\beta )$
.
$h(\alpha ) = h(\beta )$
.
The proofs of entropy invariance for Shannon orbit equivalence in [Reference Austin1, Reference Kerr and Li16] rely on the existence of sparse but coarsely dense trees inside Følner sets, which requires the group to have superlinear growth and thereby rules out virtual cyclicity. The entropy already registers along these trees when it is computed at a fine enough resolution, while the exponential complexity of the cocycles, relative to the size of the ambient Følner set, is small when restricted to the tree, so that one can effectively assume that the cocycle values along the tree are constant and thus transfer the entropy growth over to the second action. This already yields Theorem A in the case when neither G nor H is virtually cyclic, and it also yields an entropy inequality if one of G and H is not virtually cyclic. For finite acting groups, the entropy is equal to the Shannon entropy of the space divided by the cardinality of the group and hence is preserved under any orbit equivalence. The problem thus reduces to establishing the entropy inequality
![]() $h(\alpha ) \leq h(\beta )$
when G is infinite and virtually cyclic. As in [Reference Austin1, Reference Kerr and Li16], the strategy is to iteratively apply the cocycle identity in order to bound the cocycle complexity across sparse but coarsely dense subsets of Følner subsets of G, except that now these subsets must be highly separated (e.g., in the case of
$h(\alpha ) \leq h(\beta )$
when G is infinite and virtually cyclic. As in [Reference Austin1, Reference Kerr and Li16], the strategy is to iteratively apply the cocycle identity in order to bound the cocycle complexity across sparse but coarsely dense subsets of Følner subsets of G, except that now these subsets must be highly separated (e.g., in the case of
![]() ${\mathbb Z}$
, sparse sets of points of roughly uniform distribution inside large intervals), so that we can no longer argue in a geometric way entirely within G. To compensate for this, we employ the algebraic structure of H as a finitely generated virtually Abelian group in tandem with the ‘almost linear’ structure of G as a virtually cyclic group. Unlike in [Reference Kerr and Li16], where no restrictions are imposed on H beyond amenability or soficity, the hypotheses on H of virtual Abelianness and finite generation are now required to secure the desired small exponential complexity (see Lemmas 3.2 and 3.3). Another novelty of our argument is the use of the Jewett–Krieger theorem, which, for the purpose of obtaining lower bounds, allows us to express dynamical entropy by means of the cardinality of certain partitions instead of their Shannon entropy.
${\mathbb Z}$
, sparse sets of points of roughly uniform distribution inside large intervals), so that we can no longer argue in a geometric way entirely within G. To compensate for this, we employ the algebraic structure of H as a finitely generated virtually Abelian group in tandem with the ‘almost linear’ structure of G as a virtually cyclic group. Unlike in [Reference Kerr and Li16], where no restrictions are imposed on H beyond amenability or soficity, the hypotheses on H of virtual Abelianness and finite generation are now required to secure the desired small exponential complexity (see Lemmas 3.2 and 3.3). Another novelty of our argument is the use of the Jewett–Krieger theorem, which, for the purpose of obtaining lower bounds, allows us to express dynamical entropy by means of the cardinality of certain partitions instead of their Shannon entropy.
We do not know whether the statement of Theorem A holds when G and H are not-locally-finite countably infinite amenable groups and one of them is assumed to be virtually Abelian and finitely generated (although one does get an entropy inequality by [Reference Kerr and Li16]). In the proof of Austin’s result, the virtually cyclic case can be dealt with separately since, by a result of Bowen [Reference Austin2], if two free p.m.p. actions of finite generated groups are integrably orbit equivalent, then the groups have the same growth, so that either both groups are virtually cyclic or neither is. This conclusion no longer holds for Shannon orbit equivalence, as illustrated in Remark 4.1. Nevertheless, by concentrating our attention on single groups (that is, the case
![]() $G=H$
) we can use Theorem A as follows to resolve the remaining case, within the amenable context, of Shannon orbit equivalence rigidity for Bernoulli actions.
$G=H$
) we can use Theorem A as follows to resolve the remaining case, within the amenable context, of Shannon orbit equivalence rigidity for Bernoulli actions.
By work of Ornstein and Weiss [Reference Ornstein and Weiss21] (generalizing Ornstein’s isomorphism theorem for
![]() $G={\mathbb Z}$
[Reference Ornstein18]), two Bernoulli actions of a given countably infinite amenable group G are measure conjugate if and only if they have the same entropy. As observed in [Reference Kerr and Li16], this combines with the results of Austin and Kerr–Li mentioned above to show that if G is a countably infinite amenable group that is neither virtually cyclic nor locally finite, then two Bernoulli actions of G are Shannon orbit equivalent if and only if they are measure conjugate. If G is countably infinite and locally finite, then this conclusion fails in a rather dramatic way, as we saw above. In view of the Ornstein–Weiss entropy classification of Bernoulli actions, Theorem A now completes the picture for countably infinite amenable groups by covering the remaining virtually cyclic case, so that we can assert the following.
$G={\mathbb Z}$
[Reference Ornstein18]), two Bernoulli actions of a given countably infinite amenable group G are measure conjugate if and only if they have the same entropy. As observed in [Reference Kerr and Li16], this combines with the results of Austin and Kerr–Li mentioned above to show that if G is a countably infinite amenable group that is neither virtually cyclic nor locally finite, then two Bernoulli actions of G are Shannon orbit equivalent if and only if they are measure conjugate. If G is countably infinite and locally finite, then this conclusion fails in a rather dramatic way, as we saw above. In view of the Ornstein–Weiss entropy classification of Bernoulli actions, Theorem A now completes the picture for countably infinite amenable groups by covering the remaining virtually cyclic case, so that we can assert the following.
Theorem B. Two Bernoulli actions of a countable amenable group that is not locally finite are Shannon orbit equivalent if and only if they are measure conjugate.
By a theorem of Belinskaya [Reference Belinskaya3], two aperiodic ergodic p.m.p. transformations are integrably orbit equivalent if and only if they are flip conjugate (which means that they are either measure conjugate or one is measure conjugate to the inverse of the other). Recently Carderi et al showed that, for ergodic p.m.p. transformations, Shannon orbit equivalence is strictly weaker than flip conjugacy [Reference Carderi, Joseph, Le Maître and Tessera4], and so together these results illustrate that Theorem A is not merely a formal strengthening of the analogous assertion for integrable orbit equivalence from [Reference Austin1]. What Carderi et al demonstrate is that if T is any aperiodic ergodic p.m.p. transformation such that
![]() $T^n$
is ergodic for some
$T^n$
is ergodic for some
![]() $n\geq 2$
, then there is another ergodic p.m.p. transformation to which T is Shannon orbit equivalent (in fact, orbit equivalent in a certain stronger quantitative sense) but not flip conjugate.
$n\geq 2$
, then there is another ergodic p.m.p. transformation to which T is Shannon orbit equivalent (in fact, orbit equivalent in a certain stronger quantitative sense) but not flip conjugate.
In the second part of the paper, we further analyze this gap between Shannon and integrable orbit equivalence by establishing the following theorem in the odometer context. Recall that, by a theorem of Halmos and von Neumann [Reference Halmos and von Neumann9], discrete spectrum p.m.p. transformations are determined up to measure conjugacy by their eigenvalues with multiplicity, and even up to flip conjugacy since the eigenvalues form a group. This applies, in particular, to odometers, where the eigenvalues are all roots of unity. In this case, the eigenvalue information is encoded by a supernatural number
![]() $\prod _p p^{k_p}$
, where p ranges over the primes and each
$\prod _p p^{k_p}$
, where p ranges over the primes and each
![]() $k_p$
belongs to
$k_p$
belongs to
![]() $\{ 0,1,2,\ldots , \infty \}$
(see §4). The universal odometer is defined by the condition that
$\{ 0,1,2,\ldots , \infty \}$
(see §4). The universal odometer is defined by the condition that
![]() $k_p = \infty $
for each p.
$k_p = \infty $
for each p.
Theorem C. Every
![]() ${\mathbb Z}$
-odometer is Shannon orbit equivalent to the universal
${\mathbb Z}$
-odometer is Shannon orbit equivalent to the universal
![]() ${\mathbb Z}$
-odometer.
${\mathbb Z}$
-odometer.
Theorem C provides us with an example of an uncountable family of ergodic p.m.p. transformations such that no two of them are integrably orbit equivalent, although one of them is Shannon orbit equivalent to all of the others. We point out that it is unknown whether Shannon orbit equivalence is a transitive relation, and so we are not claiming that
![]() ${\mathbb Z}$
-odometers are all Shannon orbit equivalent to each other, which seems to be a much more difficult problem.
${\mathbb Z}$
-odometers are all Shannon orbit equivalent to each other, which seems to be a much more difficult problem.
Our proof of Theorem C should be compared with the proof of the theorem of Dye which asserts that any two aperiodic ergodic p.m.p. actions on standard probability spaces are orbit equivalent (see [Reference Katznelson and Weiss14] or [Reference Kerr and Li15, §4.9]). What is special in our case is that the Rokhlin towers are canonically given to us in a nested way by the odometer structure, so that we have a certain combinatorial rigidity that allows us to scramble information across orbits with some uniform quantitative control. However, we do not see how to implement the required amount of control by simply following the recursive procedure used to establish Dye’s theorem in [Reference Katznelson and Weiss14, Reference Kerr and Li15], and so we have developed a more intricate doubly recursive construction that will do the job.
The proofs of Theorems A and C will be carried out in §§3 and 4, respectively, after we set up some notation and terminology in §2.
2. Preliminaries
Partitions of measure spaces are always assumed to be measurable, and we always ignore sets of measure zero in a partition, so that when we speak of the cardinality of a partition we mean the cardinality of the collection of its non-null members. If
![]() ${\mathscr P}$
is a partition and F is a finite subset of a group acting on the space, then we write
${\mathscr P}$
is a partition and F is a finite subset of a group acting on the space, then we write
![]() ${\mathscr P}^F$
for the join
${\mathscr P}^F$
for the join
![]() $\bigvee _{g\in F} g^{-1} {\mathscr P}$
.
$\bigvee _{g\in F} g^{-1} {\mathscr P}$
.
Let
![]() $G\curvearrowright (X,\mu )$
and
$G\curvearrowright (X,\mu )$
and
![]() $H\curvearrowright (Y,\nu )$
be free p.m.p. actions of countable groups. The actions are orbit equivalent if there is a measure isomorphism
$H\curvearrowright (Y,\nu )$
be free p.m.p. actions of countable groups. The actions are orbit equivalent if there is a measure isomorphism
![]() $\varphi $
from a G-invariant conull set
$\varphi $
from a G-invariant conull set
![]() $X_0 \subseteq X$
to an H-invariant conull set
$X_0 \subseteq X$
to an H-invariant conull set
![]() $Y_0 \subseteq Y$
such that
$Y_0 \subseteq Y$
such that
![]() $\varphi (Gx) = H\varphi (x)$
for all
$\varphi (Gx) = H\varphi (x)$
for all
![]() $x\in X_0$
. Such a map
$x\in X_0$
. Such a map
![]() $\varphi $
is called an orbit equivalence, and associated to it are cocycles
$\varphi $
is called an orbit equivalence, and associated to it are cocycles
![]() $\kappa : G\times X \to ~H$
and
$\kappa : G\times X \to ~H$
and
![]() $\unicode{x3bb} : H\times Y\to G$
defined almost everywhere (a.e.) by
$\unicode{x3bb} : H\times Y\to G$
defined almost everywhere (a.e.) by
![]() $\kappa (g,x)\varphi (x) = \varphi (gx)$
and
$\kappa (g,x)\varphi (x) = \varphi (gx)$
and
![]() $\unicode{x3bb} (s,y) \varphi ^{-1} (y) = \varphi ^{-1} (sy)$
, with freeness guaranteeing a.e. uniqueness. They satisfy the cocycle identities
$\unicode{x3bb} (s,y) \varphi ^{-1} (y) = \varphi ^{-1} (sy)$
, with freeness guaranteeing a.e. uniqueness. They satisfy the cocycle identities
![]() $\kappa (gh,x) = \kappa (g,hx) \kappa (h,x)$
and
$\kappa (gh,x) = \kappa (g,hx) \kappa (h,x)$
and
![]() $\unicode{x3bb} (st,y) = \unicode{x3bb} (s,ty) \unicode{x3bb} (t,y)$
. From the cocycle
$\unicode{x3bb} (st,y) = \unicode{x3bb} (s,ty) \unicode{x3bb} (t,y)$
. From the cocycle
![]() $\kappa $
, we obtain, for every
$\kappa $
, we obtain, for every
![]() $g\in G$
, a countable partition
$g\in G$
, a countable partition
![]() $\{ X_{g,s} : s\in H \}$
of X, where
$\{ X_{g,s} : s\in H \}$
of X, where
![]() $X_{g,s} = \{ x\in X : \kappa (g,x) = s \}$
. The cocycle
$X_{g,s} = \{ x\in X : \kappa (g,x) = s \}$
. The cocycle
![]() $\unicode{x3bb} $
similarly yields a partition
$\unicode{x3bb} $
similarly yields a partition
![]() $\{ Y_{s,g} : g\in G \}$
of Y for every
$\{ Y_{s,g} : g\in G \}$
of Y for every
![]() $s\in H$
. We refer to these partitions as the cocycle partitions associated to
$s\in H$
. We refer to these partitions as the cocycle partitions associated to
![]() $\kappa $
and
$\kappa $
and
![]() $\unicode{x3bb} $
.
$\unicode{x3bb} $
.
The Shannon entropy of a countable partition
![]() ${\mathscr P}$
of a probability space
${\mathscr P}$
of a probability space
![]() $(X,\mu )$
is defined by
$(X,\mu )$
is defined by
![]() $H({\mathscr P} ) = \sum _{A\in {\mathscr P}} -\mu (A) \log \mu (A)$
and its conditional version with respect to a second countable partition
$H({\mathscr P} ) = \sum _{A\in {\mathscr P}} -\mu (A) \log \mu (A)$
and its conditional version with respect to a second countable partition
![]() ${\mathscr Q}$
by
${\mathscr Q}$
by
![]() $H({\mathscr P} |{\mathscr Q} ) = \sum _{B\in {\mathscr Q}} \sum _{A\in {\mathscr P}} -\mu (A\cap B) \log [\mu (A\cap B)/\mu (B)]$
. We also employ the notation
$H({\mathscr P} |{\mathscr Q} ) = \sum _{B\in {\mathscr Q}} \sum _{A\in {\mathscr P}} -\mu (A\cap B) \log [\mu (A\cap B)/\mu (B)]$
. We also employ the notation
![]() $H({\mathscr P} )$
, using the same formula, when
$H({\mathscr P} )$
, using the same formula, when
![]() ${\mathscr P}$
is any countable disjoint collection of measurable subsets of X. In §4, we use the fact that if
${\mathscr P}$
is any countable disjoint collection of measurable subsets of X. In §4, we use the fact that if
![]() ${\mathscr P}$
is a countable partition of X and
${\mathscr P}$
is a countable partition of X and
![]() $\{ B_i \}_{i\in I}$
is a countable collection of measurable subsets of X with
$\{ B_i \}_{i\in I}$
is a countable collection of measurable subsets of X with
![]() $\bigcup _{i\in I} B_i = X$
, then
$\bigcup _{i\in I} B_i = X$
, then
![]() $H({\mathscr P} ) \leq \sum _{i\in I} H({\mathscr P}_{B_i} )$
, where
$H({\mathscr P} ) \leq \sum _{i\in I} H({\mathscr P}_{B_i} )$
, where
![]() ${\mathscr P}_{B_i}$
denotes the restriction of
${\mathscr P}_{B_i}$
denotes the restriction of
![]() ${\mathscr P}$
to
${\mathscr P}$
to
![]() $B_i$
, that is, the partition
$B_i$
, that is, the partition
![]() $\{ A\cap B_i : A\in {\mathscr P} \}$
of
$\{ A\cap B_i : A\in {\mathscr P} \}$
of
![]() $B_i$
. This is a consequence of the observation that, for all disjoint measurable sets
$B_i$
. This is a consequence of the observation that, for all disjoint measurable sets
![]() $A,B\subseteq X$
, one has
$A,B\subseteq X$
, one has
![]() $H(\{ A\sqcup B \}) \leq H(\{ A,B \}) = H(\{ A \}) + H(\{ B \})$
. In §3, we use standard facts about Shannon entropy that can be found, for example, in [Reference Kerr and Li15, §§9.1 and 9.2].
$H(\{ A\sqcup B \}) \leq H(\{ A,B \}) = H(\{ A \}) + H(\{ B \})$
. In §3, we use standard facts about Shannon entropy that can be found, for example, in [Reference Kerr and Li15, §§9.1 and 9.2].
Returning to the orbit equivalence scenario from above, if the cocycle partitions associated to
![]() $\kappa $
all have finite Shannon entropy, then we say that
$\kappa $
all have finite Shannon entropy, then we say that
![]() $\kappa $
is Shannon, and if both
$\kappa $
is Shannon, and if both
![]() $\kappa $
and
$\kappa $
and
![]() $\unicode{x3bb} $
are Shannon, then we refer to
$\unicode{x3bb} $
are Shannon, then we refer to
![]() $\varphi $
as a Shannon orbit equivalence. When such a
$\varphi $
as a Shannon orbit equivalence. When such a
![]() $\varphi $
exists, we say that the actions
$\varphi $
exists, we say that the actions
![]() $G\curvearrowright (X,\mu )$
and
$G\curvearrowright (X,\mu )$
and
![]() $H\curvearrowright (Y,\nu )$
are Shannon orbit equivalent. Note that, by the cocycle identities and the subadditivity of Shannon entropy with respect to joins, the partitions
$H\curvearrowright (Y,\nu )$
are Shannon orbit equivalent. Note that, by the cocycle identities and the subadditivity of Shannon entropy with respect to joins, the partitions
![]() $\{ X_{g,s} : s\in H \}$
for
$\{ X_{g,s} : s\in H \}$
for
![]() $g\in G$
all have finite Shannon entropy as soon as we know that the ones for g belonging to some generating set do.
$g\in G$
all have finite Shannon entropy as soon as we know that the ones for g belonging to some generating set do.
In the case when G and H are finitely generated and are equipped with word-length metrics
![]() $|\!\cdot \! |_G$
and
$|\!\cdot \! |_G$
and
![]() $|\!\cdot \! |_H$
, we can ask whether the integrals
$|\!\cdot \! |_H$
, we can ask whether the integrals
![]() $\int _X |\kappa (g,x)|_H \, d\mu $
and
$\int _X |\kappa (g,x)|_H \, d\mu $
and
![]() $\int _Y |\unicode{x3bb} (s,x)|_G \, d\nu $
are finite for all
$\int _Y |\unicode{x3bb} (s,x)|_G \, d\nu $
are finite for all
![]() $g\in G$
and
$g\in G$
and
![]() $s\in H$
, in which case we say that
$s\in H$
, in which case we say that
![]() $\varphi $
is an integrable orbit equivalence (this does not depend on the choice of word-length metrics). The actions are integrably orbit equivalent if such a
$\varphi $
is an integrable orbit equivalence (this does not depend on the choice of word-length metrics). The actions are integrably orbit equivalent if such a
![]() $\varphi $
exists. A theorem of Belinskaya says that two aperiodic ergodic p.m.p.
$\varphi $
exists. A theorem of Belinskaya says that two aperiodic ergodic p.m.p.
![]() ${\mathbb Z}$
-actions are integrably orbit equivalent if and only if they are flip conjugate, that is, measure conjugate up to an automorphism of
${\mathbb Z}$
-actions are integrably orbit equivalent if and only if they are flip conjugate, that is, measure conjugate up to an automorphism of
![]() ${\mathbb Z}$
[Reference Belinskaya3] (see the appendix in [Reference Carderi, Joseph, Le Maître and Tessera4] for a short proof). However, for
${\mathbb Z}$
[Reference Belinskaya3] (see the appendix in [Reference Carderi, Joseph, Le Maître and Tessera4] for a short proof). However, for
![]() ${\mathbb Z}^2$
-actions, even bounded orbit equivalence (in which the cocycles have finite image when restricted to each group element) is considerably weaker than measure conjugacy modulo a group automorphism [Reference Fieldsteel and Friedman8]. By [Reference Austin1, Lemma 2.1], integrable orbit equivalence implies Shannon orbit equivalence.
${\mathbb Z}^2$
-actions, even bounded orbit equivalence (in which the cocycles have finite image when restricted to each group element) is considerably weaker than measure conjugacy modulo a group automorphism [Reference Fieldsteel and Friedman8]. By [Reference Austin1, Lemma 2.1], integrable orbit equivalence implies Shannon orbit equivalence.
Suppose that G is amenable and let
![]() $\{ F_n \}$
be a Følner sequence for G, that is, a sequence of non-empty finite subsets of G satisfying
$\{ F_n \}$
be a Følner sequence for G, that is, a sequence of non-empty finite subsets of G satisfying
![]() $\lim _{n\to \infty } |gF_n \Delta F_n |/|F_n| = 0$
for all
$\lim _{n\to \infty } |gF_n \Delta F_n |/|F_n| = 0$
for all
![]() $g\in G$
. The entropy of a finite partition
$g\in G$
. The entropy of a finite partition
![]() ${\mathscr P}$
under the action
${\mathscr P}$
under the action
![]() $G\stackrel {\alpha }{\curvearrowright } (X,\mu )$
is defined by
$G\stackrel {\alpha }{\curvearrowright } (X,\mu )$
is defined by
which is a limit that always exists and is equal to
where F ranges over all non-empty finite subsets of G (see [Reference Kerr and Li15]). The entropy of the action is then defined by
where
![]() ${\mathscr P}$
ranges over all finite partitions of X. For more details, see [Reference Kerr and Li15, Ch. 9].
${\mathscr P}$
ranges over all finite partitions of X. For more details, see [Reference Kerr and Li15, Ch. 9].
3. Entropy and Shannon orbit equivalence
Given two finite subsets F and K of a group G and a
![]() $\delta> 0$
, we say that F is
$\delta> 0$
, we say that F is
![]() $(K,\delta )$
-invariant if
$(K,\delta )$
-invariant if
![]() $| \{ t\in F : Kt \subseteq F \} | \geq (1-\delta ) |F|$
.
$| \{ t\in F : Kt \subseteq F \} | \geq (1-\delta ) |F|$
.
Lemma 3.1. Let G and H be countable amenable groups. Let
![]() $G\stackrel {\alpha }{\curvearrowright } (X,\mu )$
and
$G\stackrel {\alpha }{\curvearrowright } (X,\mu )$
and
![]() ${H\stackrel {\beta }{\curvearrowright } (Y,\nu )}$
be free p.m.p. actions that are orbit equivalent and let
${H\stackrel {\beta }{\curvearrowright } (Y,\nu )}$
be free p.m.p. actions that are orbit equivalent and let
![]() $\kappa : G\times X\to H$
and
$\kappa : G\times X\to H$
and
![]() $\unicode{x3bb} : H\times Y\to G$
be the associated cocycles. Let
$\unicode{x3bb} : H\times Y\to G$
be the associated cocycles. Let
![]() $\{ F_n \}$
be a Følner sequence for G. Let L be a finite subset of H and let
$\{ F_n \}$
be a Følner sequence for G. Let L be a finite subset of H and let
![]() $\delta> 0$
. Then, for every sufficiently large
$\delta> 0$
. Then, for every sufficiently large
![]() $n\in {\mathbb N}$
, there is a set
$n\in {\mathbb N}$
, there is a set
![]() $X_n\subseteq X$
with
$X_n\subseteq X$
with
![]() $\mu (X_n)\geq 1-\delta $
such that the sets
$\mu (X_n)\geq 1-\delta $
such that the sets
![]() $\kappa (F_n ,x)$
for
$\kappa (F_n ,x)$
for
![]() $x\in X_n$
are
$x\in X_n$
are
![]() $(L,\delta )$
-invariant.
$(L,\delta )$
-invariant.
Proof. By conjugating
![]() $\beta $
by an orbit equivalence, we may assume that both actions are on
$\beta $
by an orbit equivalence, we may assume that both actions are on
![]() $(X,\mu )$
and that the identity map on X is an orbit equivalence between
$(X,\mu )$
and that the identity map on X is an orbit equivalence between
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. Take a set
$\beta $
. Take a set
![]() $V \subseteq X$
such that
$V \subseteq X$
such that
![]() $\mu (V) \geq 1-\delta ^2 /2$
and
$\mu (V) \geq 1-\delta ^2 /2$
and
![]() $\unicode{x3bb} (L,V)$
is finite. For every
$\unicode{x3bb} (L,V)$
is finite. For every
![]() $n\in {\mathbb N}$
,
$n\in {\mathbb N}$
,
 $$ \begin{align*} \int_X \frac{1}{|F_n|} \sum_{t\in F_n} 1_{\alpha_{t^{-1}} (X\setminus V)} \, d\mu = \frac{1}{|F_n|} \sum_{t\in F_n} \int_X 1_{\alpha_{t^{-1}} (X\setminus V)} \, d\mu = \mu (X\setminus V) \leq \frac{\delta^2}{2} \end{align*} $$
$$ \begin{align*} \int_X \frac{1}{|F_n|} \sum_{t\in F_n} 1_{\alpha_{t^{-1}} (X\setminus V)} \, d\mu = \frac{1}{|F_n|} \sum_{t\in F_n} \int_X 1_{\alpha_{t^{-1}} (X\setminus V)} \, d\mu = \mu (X\setminus V) \leq \frac{\delta^2}{2} \end{align*} $$
so that there exists an
![]() $X_n\subseteq X$
with
$X_n\subseteq X$
with
![]() $\mu (X_n) \geq 1-\delta $
such that
$\mu (X_n) \geq 1-\delta $
such that
![]() $|F_n|^{-1} \sum _{t\in F_n} 1_{\alpha _{t^{-1}} (X\setminus V)}$
is bounded above by
$|F_n|^{-1} \sum _{t\in F_n} 1_{\alpha _{t^{-1}} (X\setminus V)}$
is bounded above by
![]() $\delta /2$
on
$\delta /2$
on
![]() $X_n$
, that is,
$X_n$
, that is,
![]() $|\{ t\in F_n : \alpha _t x \in V \} | \geq (1-\delta /2)|F_n |$
for all
$|\{ t\in F_n : \alpha _t x \in V \} | \geq (1-\delta /2)|F_n |$
for all
![]() $x\in X_n$
. Now suppose that n is large enough so that
$x\in X_n$
. Now suppose that n is large enough so that
![]() $F_n$
is
$F_n$
is
![]() $(\unicode{x3bb} (L,V),\delta /2)$
-invariant. Let
$(\unicode{x3bb} (L,V),\delta /2)$
-invariant. Let
![]() $x\in X_n$
. For every
$x\in X_n$
. For every
![]() $h\in L$
and
$h\in L$
and
![]() $t\in G$
,
$t\in G$
,
and so in the case when
![]() $\alpha _t x\in V$
, we get
$\alpha _t x\in V$
, we get
![]() $\beta _{L\kappa (t,x)} x\subseteq \alpha _{\unicode{x3bb} (L,V)t} x$
. Let
$\beta _{L\kappa (t,x)} x\subseteq \alpha _{\unicode{x3bb} (L,V)t} x$
. Let
![]() $F_n'$
be the set of all
$F_n'$
be the set of all
![]() $t\in F_n$
such that
$t\in F_n$
such that
![]() $\alpha _t x \in V$
. Then
$\alpha _t x \in V$
. Then
![]() $|F_n' | \geq (1-\delta /2)|F_n|$
, and so
$|F_n' | \geq (1-\delta /2)|F_n|$
, and so
 $$ \begin{align*} | \{ h\in \kappa (F_n',x) : Lh\subseteq \kappa (F_n,x) \} | &\geq | \{ t\in F_n' : \unicode{x3bb} (L,V)t\subseteq F_n \} | \\ &\geq | \{ t\in F_n : \unicode{x3bb} (L,V)t\subseteq F_n \} | - |F_n\setminus F_n' |\\ &\geq (1-\delta /2)|F_n| - (\delta /2)|F_n| \\ &= (1-\delta )|\kappa (F_n,x)| , \end{align*} $$
$$ \begin{align*} | \{ h\in \kappa (F_n',x) : Lh\subseteq \kappa (F_n,x) \} | &\geq | \{ t\in F_n' : \unicode{x3bb} (L,V)t\subseteq F_n \} | \\ &\geq | \{ t\in F_n : \unicode{x3bb} (L,V)t\subseteq F_n \} | - |F_n\setminus F_n' |\\ &\geq (1-\delta /2)|F_n| - (\delta /2)|F_n| \\ &= (1-\delta )|\kappa (F_n,x)| , \end{align*} $$
that is,
![]() $\kappa (F_n,x)$
is
$\kappa (F_n,x)$
is
![]() $(L,\delta )$
-invariant.
$(L,\delta )$
-invariant.
Lemma 3.2. Let G be a finitely generated virtually Abelian group, equipped with a word metric. Let
![]() $r,n\in {\mathbb N}$
. Let
$r,n\in {\mathbb N}$
. Let
![]() $\Omega _0 \subseteq \{ 1,\ldots , n \}$
and set
$\Omega _0 \subseteq \{ 1,\ldots , n \}$
and set
![]() $\Omega _1 = \{ 1,\ldots ,n \} \setminus \Omega _0$
. For every
$\Omega _1 = \{ 1,\ldots ,n \} \setminus \Omega _0$
. For every
![]() ${i\in \Omega _0}$
let
${i\in \Omega _0}$
let
![]() $b_i$
be a fixed element of G. Then the number of elements of G of the form
$b_i$
be a fixed element of G. Then the number of elements of G of the form
![]() $b_1 \cdots b_n$
, where
$b_1 \cdots b_n$
, where
![]() $b_i$
is an element of the r-ball around
$b_i$
is an element of the r-ball around
![]() $e_G$
for every
$e_G$
for every
![]() $i\in \Omega _1$
, is at most
$i\in \Omega _1$
, is at most
![]() $e^{c_1 |\Omega _0|} c_2 (rn)^k$
, where k is the order of polynomial growth of G and
$e^{c_1 |\Omega _0|} c_2 (rn)^k$
, where k is the order of polynomial growth of G and
![]() $c_1 , c_2>0$
are constants that do not depend on r, n or the elements
$c_1 , c_2>0$
are constants that do not depend on r, n or the elements
![]() $b_i$
for
$b_i$
for
![]() $i\in \Omega _0$
.
$i\in \Omega _0$
.
Proof. By hypothesis, G has an Abelian subgroup A of finite index, which we may assume to be normal by replacing it with the intersection of all of its conjugates, which is again of finite index. Since finite-index subgroups of finitely generated groups are also finitely generated, the subgroup A is finitely generated. Fix a finite symmetric generating set S for A, and choose a set
![]() $\{ g_1 , \ldots , g_l \}$
of representatives for the cosets of A with
$\{ g_1 , \ldots , g_l \}$
of representatives for the cosets of A with
![]() $g_1 = e_G$
. Set
$g_1 = e_G$
. Set
![]() $F = \{ g_2 , \ldots , g_l , g_2^{-1} , \ldots , g_l^{-1} \}$
. Since any two word metrics on G are bi-Lipschitz equivalent, we may assume that the given word metric is with respect to the symmetric generating set
$F = \{ g_2 , \ldots , g_l , g_2^{-1} , \ldots , g_l^{-1} \}$
. Since any two word metrics on G are bi-Lipschitz equivalent, we may assume that the given word metric is with respect to the symmetric generating set
![]() $S \cup F$
. Write
$S \cup F$
. Write
![]() $B(m)$
for the ball of radius m around
$B(m)$
for the ball of radius m around
![]() $e_G$
. Since G has polynomial growth of order k, there exists a
$e_G$
. Since G has polynomial growth of order k, there exists a
![]() $C>0$
such that
$C>0$
such that
![]() $|B(m)| \leq Cm^k$
for every
$|B(m)| \leq Cm^k$
for every
![]() $m\in {\mathbb N}$
. Since A has finite index in G, the set of all automorphisms of A of the form
$m\in {\mathbb N}$
. Since A has finite index in G, the set of all automorphisms of A of the form
![]() $a\mapsto gag^{-1}$
for some
$a\mapsto gag^{-1}$
for some
![]() $g\in G$
is finite, and so there is a finite set
$g\in G$
is finite, and so there is a finite set
![]() $E\subseteq G$
such that each of these automorphisms has the form
$E\subseteq G$
such that each of these automorphisms has the form
![]() $a\mapsto gag^{-1}$
for some
$a\mapsto gag^{-1}$
for some
![]() $g\in E$
. Set
$g\in E$
. Set
![]() $K = \{ e_G \} \cup \bigcup _{g\in E} g(S\cup F)g^{-1}$
, which is a finite subset of G, so that there exists a
$K = \{ e_G \} \cup \bigcup _{g\in E} g(S\cup F)g^{-1}$
, which is a finite subset of G, so that there exists a
![]() $d\in {\mathbb N}$
for which
$d\in {\mathbb N}$
for which
![]() $K\subseteq B(d)$
.
$K\subseteq B(d)$
.
Suppose we are given
![]() $b_i \in B(r)$
for
$b_i \in B(r)$
for
![]() $i\in \Omega _1$
. For each
$i\in \Omega _1$
. For each
![]() $i=1,\ldots ,n$
, we can write
$i=1,\ldots ,n$
, we can write
![]() ${b_i = a_i g_{l_i}}$
for some
${b_i = a_i g_{l_i}}$
for some
![]() $a_i \in A$
and
$a_i \in A$
and
![]() $1\leq l_i \leq l$
. Using that elements of A commute, and writing
$1\leq l_i \leq l$
. Using that elements of A commute, and writing
![]() $h_i = g_{l_1} \cdots g_{l_{i-1}}$
for
$h_i = g_{l_1} \cdots g_{l_{i-1}}$
for
![]() $1 < i\leq n$
and
$1 < i\leq n$
and
![]() $h_1 = e_G$
,
$h_1 = e_G$
,
 $$ \begin{align*} b_1 \cdots b_n &= a_1 g_{l_1} \cdots a_n g_{l_n} \\ &= \bigg( \prod_{i=1}^n h_i a_i h_i^{-1} \bigg) g_{l_1} \cdots g_{l_n} \\ &= \bigg( \prod_{i\in\Omega_0} h_i a_i h_i^{-1} \bigg) \bigg( \prod_{i\in\Omega_1} h_i a_i h_i^{-1} \bigg) g_{l_1} \cdots g_{l_n}. \end{align*} $$
$$ \begin{align*} b_1 \cdots b_n &= a_1 g_{l_1} \cdots a_n g_{l_n} \\ &= \bigg( \prod_{i=1}^n h_i a_i h_i^{-1} \bigg) g_{l_1} \cdots g_{l_n} \\ &= \bigg( \prod_{i\in\Omega_0} h_i a_i h_i^{-1} \bigg) \bigg( \prod_{i\in\Omega_1} h_i a_i h_i^{-1} \bigg) g_{l_1} \cdots g_{l_n}. \end{align*} $$
Since
![]() $a_i$
is fixed for every
$a_i$
is fixed for every
![]() $i\in \Omega _0$
, there are at most
$i\in \Omega _0$
, there are at most
![]() $|E|^{|\Omega _0 |}$
possibilities for
$|E|^{|\Omega _0 |}$
possibilities for
![]() $\prod _{i\in \Omega _0} h_i a_i h_i^{-1}$
. Now, for every
$\prod _{i\in \Omega _0} h_i a_i h_i^{-1}$
. Now, for every
![]() $a\in B(r+1) \cap A$
and
$a\in B(r+1) \cap A$
and
![]() $h\in G$
, the element
$h\in G$
, the element
![]() $hah^{-1}$
is equal to
$hah^{-1}$
is equal to
![]() $gag^{-1}$
for some
$gag^{-1}$
for some
![]() $g\in E$
and thus belongs to
$g\in E$
and thus belongs to
![]() $K^{r+1}$
, which is contained in
$K^{r+1}$
, which is contained in
![]() $B((r+1)d)$
. Since, for every
$B((r+1)d)$
. Since, for every
![]() $i\in \Omega _1$
, we have
$i\in \Omega _1$
, we have
![]() $a_i = b_i g_{l_i}^{-1} \in B(r+1)$
, it follows that
$a_i = b_i g_{l_i}^{-1} \in B(r+1)$
, it follows that
![]() $\prod _{i\in \Omega _1} h_i a_i h_i^{-1}\in B((r+1)d |\Omega _1 |) \subseteq B ((r+1)d n)$
, and so the product
$\prod _{i\in \Omega _1} h_i a_i h_i^{-1}\in B((r+1)d |\Omega _1 |) \subseteq B ((r+1)d n)$
, and so the product
![]() $(\prod _{i\in \Omega _1} h_i a_i h_i^{-1} )g_{l_1} \cdots g_{l_n}$
lies in
$(\prod _{i\in \Omega _1} h_i a_i h_i^{-1} )g_{l_1} \cdots g_{l_n}$
lies in
![]() ${B((r+1)d +1)n)}$
, which has cardinality at most
${B((r+1)d +1)n)}$
, which has cardinality at most
![]() $C((r+1)d +1)n)^k$
. Therefore, the total number of possibilities for
$C((r+1)d +1)n)^k$
. Therefore, the total number of possibilities for
![]() $b_1 \cdots b_n$
is bounded above by
$b_1 \cdots b_n$
is bounded above by
![]() $|E|^{|\Omega _0 |}C((r+1)d +1)n)^k$
. We can thus take
$|E|^{|\Omega _0 |}C((r+1)d +1)n)^k$
. We can thus take
![]() $c_1 = \log |E|$
and
$c_1 = \log |E|$
and
![]() $c_2 = C(3d)^k$
.
$c_2 = C(3d)^k$
.
Let G be an infinite virtually cyclic group and let H be a countably infinite group. Let
![]() $G\overset {\alpha }\curvearrowright (X, \mu )$
and
$G\overset {\alpha }\curvearrowright (X, \mu )$
and
![]() $H\overset {\beta }\curvearrowright (X, \mu )$
be free ergodic p.m.p. actions such that the identity map on X is an orbit equivalence between the actions and the cocycle
$H\overset {\beta }\curvearrowright (X, \mu )$
be free ergodic p.m.p. actions such that the identity map on X is an orbit equivalence between the actions and the cocycle
![]() $\kappa : G\times X\rightarrow H$
is Shannon. For each
$\kappa : G\times X\rightarrow H$
is Shannon. For each
![]() $g\in G$
, denote by
$g\in G$
, denote by
![]() ${\mathscr Q}_g$
the countable partition of X consisting of the sets
${\mathscr Q}_g$
the countable partition of X consisting of the sets
![]() $\{x\in X: \kappa (g, x)=h\}$
for
$\{x\in X: \kappa (g, x)=h\}$
for
![]() $h\in H$
. Let
$h\in H$
. Let
![]() $a\in G$
be such that
$a\in G$
be such that
![]() $\langle a\rangle $
is a finite-index normal subgroup of G. Such an element always exists since the intersection of the conjugates of any finite-index cyclic subgroup of G is a normal cyclic subgroup of finite index. For all
$\langle a\rangle $
is a finite-index normal subgroup of G. Such an element always exists since the intersection of the conjugates of any finite-index cyclic subgroup of G is a normal cyclic subgroup of finite index. For all
![]() $n, m\in {\mathbb N}$
, the join
$n, m\in {\mathbb N}$
, the join
![]() $\bigvee _{j=0}^{n-1}a^{-jm}{\mathscr Q}_{a^m}$
refines
$\bigvee _{j=0}^{n-1}a^{-jm}{\mathscr Q}_{a^m}$
refines
![]() ${\mathscr Q}_{a^{nm}}$
, and so
${\mathscr Q}_{a^{nm}}$
, and so
 $$ \begin{align*} \frac{1}{|G: \langle a^m\rangle|}H({\mathscr Q}_{a^m})\ge \frac{1}{|G: \langle a^{nm}\rangle|} H\bigg(\bigvee_{j=0}^{n-1}a^{-jm}{\mathscr Q}_{a^m}\bigg)\ge \frac{1}{|G: \langle a^{nm}\rangle|}H({\mathscr Q}_{a^{nm}}). \end{align*} $$
$$ \begin{align*} \frac{1}{|G: \langle a^m\rangle|}H({\mathscr Q}_{a^m})\ge \frac{1}{|G: \langle a^{nm}\rangle|} H\bigg(\bigvee_{j=0}^{n-1}a^{-jm}{\mathscr Q}_{a^m}\bigg)\ge \frac{1}{|G: \langle a^{nm}\rangle|}H({\mathscr Q}_{a^{nm}}). \end{align*} $$
Since
![]() ${\mathscr Q}_{a^{-m}}=a^m{\mathscr Q}_{a^m}$
, one also has
${\mathscr Q}_{a^{-m}}=a^m{\mathscr Q}_{a^m}$
, one also has
Since any two finite-index subgroups of an infinite group have non-trivial intersection, it follows that
![]() $\inf _{m\in {\mathbb N}}({1}/{|G: \langle a^m\rangle |})H({\mathscr Q}_{a^m})$
is equal to the infimum of
$\inf _{m\in {\mathbb N}}({1}/{|G: \langle a^m\rangle |})H({\mathscr Q}_{a^m})$
is equal to the infimum of
![]() $({1}/{|G: \langle g\rangle |})H({\mathscr Q}_g)$
over all generators g of finite-index normal subgroups of G and hence is a numerical invariant of the orbit equivalence between
$({1}/{|G: \langle g\rangle |})H({\mathscr Q}_g)$
over all generators g of finite-index normal subgroups of G and hence is a numerical invariant of the orbit equivalence between
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. We denote this quantity by
$\beta $
. We denote this quantity by
![]() $h(\kappa )$
.
$h(\kappa )$
.
Lemma 3.3. If, in the above setting, H is virtually Abelian and finitely generated, then
![]() $h(\kappa )=0$
.
$h(\kappa )=0$
.
Proof. Take an
![]() $a\in G$
that generates a finite-index normal subgroup. Then we have
$a\in G$
that generates a finite-index normal subgroup. Then we have
![]() ${h(\kappa )=\inf _{n\in {\mathbb N}}({1}/{|G:\langle a\rangle |n})H({\mathscr Q}_{a^n})}$
. Choose a set R of coset representatives for
${h(\kappa )=\inf _{n\in {\mathbb N}}({1}/{|G:\langle a\rangle |n})H({\mathscr Q}_{a^n})}$
. Choose a set R of coset representatives for
![]() $\langle a\rangle $
with
$\langle a\rangle $
with
![]() $e_G\in R$
. For each
$e_G\in R$
. For each
![]() $n\in {\mathbb N}$
, put
$n\in {\mathbb N}$
, put
![]() $I_n=\{e_G, a, \ldots , a^{n-1}\}$
and
$I_n=\{e_G, a, \ldots , a^{n-1}\}$
and
![]() $F_n=I_nR$
. Let
$F_n=I_nR$
. Let
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Take a finite subset
![]() ${\mathscr Q}_a'$
of
${\mathscr Q}_a'$
of
![]() ${\mathscr Q}_a$
such that setting
${\mathscr Q}_a$
such that setting
![]() $C=X\setminus \bigcup {\mathscr Q}_a'$
and
$C=X\setminus \bigcup {\mathscr Q}_a'$
and
![]() ${\mathscr D} = ({\mathscr Q}_a\setminus {\mathscr Q}_a')\cup \{X\setminus C\}$
one has
${\mathscr D} = ({\mathscr Q}_a\setminus {\mathscr Q}_a')\cup \{X\setminus C\}$
one has
![]() $\mu (C)<\varepsilon /(2|R|)$
and
$\mu (C)<\varepsilon /(2|R|)$
and
![]() $H({\mathscr D})<\varepsilon $
. Set
$H({\mathscr D})<\varepsilon $
. Set
![]() ${\mathscr C}=\{C, X\setminus C\}$
.
${\mathscr C}=\{C, X\setminus C\}$
.
Note that each member of
![]() ${\mathscr D}$
is the union of at most
${\mathscr D}$
is the union of at most
![]() $|{\mathscr Q}_a'|$
many members of
$|{\mathscr Q}_a'|$
many members of
![]() ${\mathscr Q}_a$
. Let
${\mathscr Q}_a$
. Let
![]() $n\in {\mathbb N}$
and let D be a non-null member of
$n\in {\mathbb N}$
and let D be a non-null member of
![]() ${\mathscr D}^{I_n}$
. Then D is the union of at most
${\mathscr D}^{I_n}$
. Then D is the union of at most
![]() $|{\mathscr Q}_a'|^n$
many members of
$|{\mathscr Q}_a'|^n$
many members of
![]() ${\mathscr Q}_a^{I_n}$
. Thus,
${\mathscr Q}_a^{I_n}$
. Thus,
 $$ \begin{align} \sum_{B\in {\mathscr Q}_a^{I_n}, \,B\subseteq D}-\frac{\mu(B)}{\mu(D)}\log \frac{\mu(B)}{\mu(D)}\le \log |{\mathscr Q}_a'|^n. \end{align} $$
$$ \begin{align} \sum_{B\in {\mathscr Q}_a^{I_n}, \,B\subseteq D}-\frac{\mu(B)}{\mu(D)}\log \frac{\mu(B)}{\mu(D)}\le \log |{\mathscr Q}_a'|^n. \end{align} $$
Take
![]() $0<\delta <\varepsilon $
such that
$0<\delta <\varepsilon $
such that
![]() $\delta \log |{\mathscr Q}_a'|<\varepsilon $
. By the mean ergodic theorem, when
$\delta \log |{\mathscr Q}_a'|<\varepsilon $
. By the mean ergodic theorem, when
![]() $n\in {\mathbb N}$
is sufficiently large there is a collection
$n\in {\mathbb N}$
is sufficiently large there is a collection
![]() ${\mathscr C}_n\subseteq {\mathscr C}^{F_n}$
such that
${\mathscr C}_n\subseteq {\mathscr C}^{F_n}$
such that
![]() $\mu (\bigcup {\mathscr C}_n)>1-\delta $
and, for each
$\mu (\bigcup {\mathscr C}_n)>1-\delta $
and, for each
![]() $A\in {\mathscr C}_n$
, one has
$A\in {\mathscr C}_n$
, one has
![]() $({1}/{|F_n|})\sum _{g\in F_n}1_C(gx)\le \mu (C)+\varepsilon /(2|R|)$
for all
$({1}/{|F_n|})\sum _{g\in F_n}1_C(gx)\le \mu (C)+\varepsilon /(2|R|)$
for all
![]() $x\in A$
. Denote by
$x\in A$
. Denote by
![]() ${\mathscr C}_n'$
the set of all
${\mathscr C}_n'$
the set of all
![]() $B\in {\mathscr C}^{I_n}$
containing some non-null
$B\in {\mathscr C}^{I_n}$
containing some non-null
![]() $A\in {\mathscr C}_n$
. Then
$A\in {\mathscr C}_n$
. Then
![]() $\mu (\bigcup {\mathscr C}_n')\ge \mu (\bigcup {\mathscr C}_n)\ge 1-\delta $
. For each
$\mu (\bigcup {\mathscr C}_n')\ge \mu (\bigcup {\mathscr C}_n)\ge 1-\delta $
. For each
![]() $B\in {\mathscr C}_n'$
and
$B\in {\mathscr C}_n'$
and
![]() $x\in B$
, taking an
$x\in B$
, taking an
![]() $A\in {\mathscr C}_n$
with
$A\in {\mathscr C}_n$
with
![]() $A\subseteq B$
and a
$A\subseteq B$
and a
![]() $y\in A$
,
$y\in A$
,
 $$ \begin{align} \frac{1}{|I_n|}\sum_{g\in I_n}1_C(gx) &=\frac{1}{|I_n|}\sum_{g\in I_n}1_C(gy)\notag \\ &\le \frac{1}{|I_n|}\sum_{g\in F_n}1_C(gy)\notag\\ &=\frac{|R|}{|F_n|}\sum_{g\in F_n}1_C(gy)\notag \\&\le |R|\bigg(\mu(C)+\frac{\varepsilon}{2|R|}\bigg)\notag \\ &\le \varepsilon. \end{align} $$
$$ \begin{align} \frac{1}{|I_n|}\sum_{g\in I_n}1_C(gx) &=\frac{1}{|I_n|}\sum_{g\in I_n}1_C(gy)\notag \\ &\le \frac{1}{|I_n|}\sum_{g\in F_n}1_C(gy)\notag\\ &=\frac{|R|}{|F_n|}\sum_{g\in F_n}1_C(gy)\notag \\&\le |R|\bigg(\mu(C)+\frac{\varepsilon}{2|R|}\bigg)\notag \\ &\le \varepsilon. \end{align} $$
Denote by
![]() ${\mathscr D}_n'$
the collection of members of
${\mathscr D}_n'$
the collection of members of
![]() ${\mathscr D}^{I_n}$
contained in some member of
${\mathscr D}^{I_n}$
contained in some member of
![]() ${\mathscr C}_n'$
. Then
${\mathscr C}_n'$
. Then
![]() $\mu (\bigcup {\mathscr D}_n')=\mu (\bigcup {\mathscr C}_n')>1-\delta $
; therefore, using (1),
$\mu (\bigcup {\mathscr D}_n')=\mu (\bigcup {\mathscr C}_n')>1-\delta $
; therefore, using (1),
 $$ \begin{align} \sum_{D\in {\mathscr D}^{I_n}\setminus {\mathscr D}_n'}\,\sum_{B\in {\mathscr Q}_a^{I_n},\, B\subseteq D}-\mu(D)\cdot \frac{\mu(B)}{\mu(D)}\log \frac{\mu(B)}{\mu(D)} &\le \sum_{D\in {\mathscr D}^{I_n}\setminus {\mathscr D}_n'}\mu(D)\log |{\mathscr Q}_a'|^n \notag\\ &\le n\delta \log |{\mathscr Q}_a'| \notag\\ &<n\varepsilon. \end{align} $$
$$ \begin{align} \sum_{D\in {\mathscr D}^{I_n}\setminus {\mathscr D}_n'}\,\sum_{B\in {\mathscr Q}_a^{I_n},\, B\subseteq D}-\mu(D)\cdot \frac{\mu(B)}{\mu(D)}\log \frac{\mu(B)}{\mu(D)} &\le \sum_{D\in {\mathscr D}^{I_n}\setminus {\mathscr D}_n'}\mu(D)\log |{\mathscr Q}_a'|^n \notag\\ &\le n\delta \log |{\mathscr Q}_a'| \notag\\ &<n\varepsilon. \end{align} $$
Write k for the order of polynomial growth of H and let
![]() $r\in {\mathbb N}$
be such that the set
$r\in {\mathbb N}$
be such that the set
![]() $\{ \kappa (a,x) : x\in \bigcup {\mathscr Q}_a' \}$
is contained in the r-ball around
$\{ \kappa (a,x) : x\in \bigcup {\mathscr Q}_a' \}$
is contained in the r-ball around
![]() $e_H$
with respect to some fixed word metric on H. Then, by Lemma 3.2, there are
$e_H$
with respect to some fixed word metric on H. Then, by Lemma 3.2, there are
![]() $c_1 , c_2> 0$
not depending on n such that every
$c_1 , c_2> 0$
not depending on n such that every
![]() $D\in {\mathscr D}_n'$
intersects at most
$D\in {\mathscr D}_n'$
intersects at most
![]() $e^{c_1 |\Omega _D|}c_2 (rn)^k$
many members of
$e^{c_1 |\Omega _D|}c_2 (rn)^k$
many members of
![]() ${\mathscr Q}_{a^n}$
, where
${\mathscr Q}_{a^n}$
, where
![]() $\Omega _D=\{g\in I_n: gx\in C\}$
for
$\Omega _D=\{g\in I_n: gx\in C\}$
for
![]() $x\in D$
, and, for such a D, we have
$x\in D$
, and, for such a D, we have
![]() $|\Omega _D|\le \varepsilon n$
by (2); hence,
$|\Omega _D|\le \varepsilon n$
by (2); hence,
 $$ \begin{align} \sum_{B\in {\mathscr Q}_{a^n}\vee {\mathscr D}^{I_n},\, B\subseteq D}-\frac{\mu(B)}{\mu(D)}\log \frac{\mu(B)}{\mu(D)} \le \log (e^{\varepsilon c_1 n} c_2 (rn)^k ). \end{align} $$
$$ \begin{align} \sum_{B\in {\mathscr Q}_{a^n}\vee {\mathscr D}^{I_n},\, B\subseteq D}-\frac{\mu(B)}{\mu(D)}\log \frac{\mu(B)}{\mu(D)} \le \log (e^{\varepsilon c_1 n} c_2 (rn)^k ). \end{align} $$
Denote by
![]() ${\mathscr P}_n$
the partition of X consisting of the members of
${\mathscr P}_n$
the partition of X consisting of the members of
![]() ${\mathscr Q}_a^{I_n}$
contained in
${\mathscr Q}_a^{I_n}$
contained in
![]() ${\bigcup ({\mathscr D}^{I_n}\setminus {\mathscr D}_n')}$
along with the members of
${\bigcup ({\mathscr D}^{I_n}\setminus {\mathscr D}_n')}$
along with the members of
![]() ${\mathscr Q}_{a^n}\vee {\mathscr D}^{I_n}$
contained in
${\mathscr Q}_{a^n}\vee {\mathscr D}^{I_n}$
contained in
![]() $\bigcup {\mathscr D}_n'$
. Then
$\bigcup {\mathscr D}_n'$
. Then
![]() ${\mathscr P}_n$
refines both
${\mathscr P}_n$
refines both
![]() ${\mathscr Q}_{a^n}$
and
${\mathscr Q}_{a^n}$
and
![]() ${\mathscr D}^{I_n}$
, and since
${\mathscr D}^{I_n}$
, and since
![]() $H({\mathscr D}^{I_n} ) \leq |I_n| H({\mathscr D} ) < n\varepsilon $
, we therefore obtain, using (3) and (4),
$H({\mathscr D}^{I_n} ) \leq |I_n| H({\mathscr D} ) < n\varepsilon $
, we therefore obtain, using (3) and (4),
 $$ \begin{align*} H({\mathscr Q}_{a^n})&\le H({\mathscr P}_n)\\ &= H({\mathscr D}^{I_n})+H({\mathscr P}_n|{\mathscr D}^{I_n})\\ &\le n\varepsilon+\sum_{D\in {\mathscr D}^{I_n}\setminus {\mathscr D}_n'}\,\sum_{B\in {\mathscr Q}_a^{I_n},\, B\subseteq D}-\mu(D)\cdot \frac{\mu(B)}{\mu(D)}\log \frac{\mu(B)}{\mu(D)}\\ &\quad +\sum_{D\in {\mathscr D}_n'}\,\sum_{B\in {\mathscr Q}_{a^n}\vee {\mathscr D}^{I_n},\, B\subseteq D}-\mu(D)\cdot \frac{\mu(B)}{\mu(D)}\log \frac{\mu(B)}{\mu(D)}\\ &\le n\varepsilon+n\varepsilon+\sum_{D\in {\mathscr D}_n'}\mu(D)\log (e^{\varepsilon c_1 n} c_2 (rn)^k )\\ &\le n\varepsilon (2+c_1 )+\log (c_2 (rn)^k). \end{align*} $$
$$ \begin{align*} H({\mathscr Q}_{a^n})&\le H({\mathscr P}_n)\\ &= H({\mathscr D}^{I_n})+H({\mathscr P}_n|{\mathscr D}^{I_n})\\ &\le n\varepsilon+\sum_{D\in {\mathscr D}^{I_n}\setminus {\mathscr D}_n'}\,\sum_{B\in {\mathscr Q}_a^{I_n},\, B\subseteq D}-\mu(D)\cdot \frac{\mu(B)}{\mu(D)}\log \frac{\mu(B)}{\mu(D)}\\ &\quad +\sum_{D\in {\mathscr D}_n'}\,\sum_{B\in {\mathscr Q}_{a^n}\vee {\mathscr D}^{I_n},\, B\subseteq D}-\mu(D)\cdot \frac{\mu(B)}{\mu(D)}\log \frac{\mu(B)}{\mu(D)}\\ &\le n\varepsilon+n\varepsilon+\sum_{D\in {\mathscr D}_n'}\mu(D)\log (e^{\varepsilon c_1 n} c_2 (rn)^k )\\ &\le n\varepsilon (2+c_1 )+\log (c_2 (rn)^k). \end{align*} $$
As none of r,
![]() $c_1$
,
$c_1$
,
![]() $c_2$
and k depend on n, this yields
$c_2$
and k depend on n, this yields
Letting
![]() $\varepsilon \to 0$
, we obtain
$\varepsilon \to 0$
, we obtain
![]() $h(\kappa )=0$
.
$h(\kappa )=0$
.
Question 3.4. Is there any way to extend the definition of
![]() $h(\kappa )$
to other amenable groups G?
$h(\kappa )$
to other amenable groups G?
Let
![]() $G\stackrel {\alpha }{\curvearrowright } (X,\mu )$
be a free ergodic p.m.p. action of a countably infinite amenable group. A finite partition
$G\stackrel {\alpha }{\curvearrowright } (X,\mu )$
be a free ergodic p.m.p. action of a countably infinite amenable group. A finite partition
![]() ${\mathscr P}$
of X is said to be
${\mathscr P}$
of X is said to be
![]() $\alpha $
-uniform if the convergence in the pointwise ergodic theorem applied to each of the indicator functions of members of
$\alpha $
-uniform if the convergence in the pointwise ergodic theorem applied to each of the indicator functions of members of
![]() ${\mathscr P}$
is uniform off of a null set, that is, one obtains a uniquely ergodic subshift action of G by using
${\mathscr P}$
is uniform off of a null set, that is, one obtains a uniquely ergodic subshift action of G by using
![]() ${\mathscr P}$
in the obvious way to define a G-equivariant map into the shift over G with symbol set
${\mathscr P}$
in the obvious way to define a G-equivariant map into the shift over G with symbol set
![]() ${\mathscr P}$
and then taking the closure of the image of some G-invariant conull subset of X. In this topological model, the unique invariant Borel probability measure defines a p.m.p. action that is measure conjugate to the quotient of
${\mathscr P}$
and then taking the closure of the image of some G-invariant conull subset of X. In this topological model, the unique invariant Borel probability measure defines a p.m.p. action that is measure conjugate to the quotient of
![]() $\alpha $
determined by the invariant sub-
$\alpha $
determined by the invariant sub-
![]() $\sigma $
-algebra generated by
$\sigma $
-algebra generated by
![]() ${\mathscr P}$
, and
${\mathscr P}$
, and
![]() ${\mathscr P}$
becomes, modulo null sets, a clopen generating partition. We can then apply the variational principle and generator theorems to conclude that the measure entropy
${\mathscr P}$
becomes, modulo null sets, a clopen generating partition. We can then apply the variational principle and generator theorems to conclude that the measure entropy
![]() $h(\alpha ,{\mathscr P} )$
is equal to the topological entropy of
$h(\alpha ,{\mathscr P} )$
is equal to the topological entropy of
![]() ${\mathscr P}$
as a clopen partition, which can be expressed as
${\mathscr P}$
as a clopen partition, which can be expressed as
![]() $\lim _{n\to \infty } ({1}/{|F_n |}) \log |{\mathscr P}^{F_n} |$
for any Følner sequence
$\lim _{n\to \infty } ({1}/{|F_n |}) \log |{\mathscr P}^{F_n} |$
for any Følner sequence
![]() $\{ F_n \}$
for G.
$\{ F_n \}$
for G.
Lemma 3.5. Let G be an infinite virtually cyclic group and let H be a countably infinite amenable group. Let
![]() $G\stackrel {\alpha }{\curvearrowright } (X,\mu )$
and
$G\stackrel {\alpha }{\curvearrowright } (X,\mu )$
and
![]() $H\stackrel {\beta }{\curvearrowright } (X,\mu )$
be free ergodic p.m.p. actions such that the identity map on X is an orbit equivalence for which the cocycle
$H\stackrel {\beta }{\curvearrowright } (X,\mu )$
be free ergodic p.m.p. actions such that the identity map on X is an orbit equivalence for which the cocycle
![]() $\kappa : G\times X\to H$
is Shannon. Then
$\kappa : G\times X\to H$
is Shannon. Then
Proof. Take an
![]() $a\in G$
that generates a finite-index normal subgroup of G. It suffices to show that
$a\in G$
that generates a finite-index normal subgroup of G. It suffices to show that
![]() $h(\beta )+({1}/{|G: \langle a\rangle |})H({\mathscr Q}_a)\ge h(\alpha )$
. By the Jewett–Krieger theorem [Reference Jewett10, Reference Krieger17, Reference Rosenthal22, Reference Weiss26], every finite partition of X can be approximated arbitrarily well in the Rokhlin metric
$h(\beta )+({1}/{|G: \langle a\rangle |})H({\mathscr Q}_a)\ge h(\alpha )$
. By the Jewett–Krieger theorem [Reference Jewett10, Reference Krieger17, Reference Rosenthal22, Reference Weiss26], every finite partition of X can be approximated arbitrarily well in the Rokhlin metric
![]() $d({\mathscr P} , {\mathscr Q} ) = H({\mathscr P} | {\mathscr Q} ) + H({\mathscr Q} | {\mathscr P} )$
by
$d({\mathscr P} , {\mathscr Q} ) = H({\mathscr P} | {\mathscr Q} ) + H({\mathscr Q} | {\mathscr P} )$
by
![]() $\beta $
-uniform finite partitions. Since the function
$\beta $
-uniform finite partitions. Since the function
![]() ${\mathscr Q} \mapsto h(\alpha , {\mathscr Q} )$
on finite partitions is continuous with respect to this metric, it is therefore enough to show, given a
${\mathscr Q} \mapsto h(\alpha , {\mathscr Q} )$
on finite partitions is continuous with respect to this metric, it is therefore enough to show, given a
![]() $\beta $
-uniform partition
$\beta $
-uniform partition
![]() ${\mathscr P}$
, that
${\mathscr P}$
, that
![]() $h(\beta )+({1}/{|G: \langle a\rangle |})H({\mathscr Q}_a)\ge h(\alpha , {\mathscr P})$
.
$h(\beta )+({1}/{|G: \langle a\rangle |})H({\mathscr Q}_a)\ge h(\alpha , {\mathscr P})$
.
Choose a set R of coset representatives for
![]() $\langle a\rangle $
with
$\langle a\rangle $
with
![]() $e_G\in R$
. For each
$e_G\in R$
. For each
![]() $n\in {\mathbb N}$
, set
$n\in {\mathbb N}$
, set
![]() ${I_n=\{e_G, a, \ldots , a^{n-1}\}}$
and
${I_n=\{e_G, a, \ldots , a^{n-1}\}}$
and
![]() $F_n=RI_n$
.
$F_n=RI_n$
.
Let
![]() $0<\varepsilon <1/8$
. Since
$0<\varepsilon <1/8$
. Since
![]() ${\mathscr P}$
is
${\mathscr P}$
is
![]() $\beta $
-uniform, so is
$\beta $
-uniform, so is
![]() ${\mathscr P}^R$
. Thus, there are some non-empty finite set
${\mathscr P}^R$
. Thus, there are some non-empty finite set
![]() $K\subseteq H$
and
$K\subseteq H$
and
![]() $\delta>0$
such that, for any non-empty
$\delta>0$
such that, for any non-empty
![]() $(K, \delta )$
-invariant finite set
$(K, \delta )$
-invariant finite set
![]() $L\subseteq H$
, one has
$L\subseteq H$
, one has
![]() $h(\beta , {\mathscr P}^R)+\varepsilon \ge ({1}/{|L|})\log |{\mathscr P}^{RL}|$
(recall our convention that we do not count null sets when taking the cardinality of a partition).
$h(\beta , {\mathscr P}^R)+\varepsilon \ge ({1}/{|L|})\log |{\mathscr P}^{RL}|$
(recall our convention that we do not count null sets when taking the cardinality of a partition).
For each
![]() $n\in {\mathbb N}$
,
$n\in {\mathbb N}$
,
and
so that
For each non-null
![]() $C\in {\mathscr Q}_a^{I_n}$
,
$C\in {\mathscr Q}_a^{I_n}$
,
 $$ \begin{align} \sum_{B\in {\mathscr P}^{F_n}\vee{\mathscr Q}_a^{I_n},\, B\subseteq C}-\frac{\mu(B)}{\mu(C)}\log \frac{\mu(B)}{\mu(C)}\le \log |{\mathscr P}|^{|F_n|}=|F_n|\log |{\mathscr P}|. \end{align} $$
$$ \begin{align} \sum_{B\in {\mathscr P}^{F_n}\vee{\mathscr Q}_a^{I_n},\, B\subseteq C}-\frac{\mu(B)}{\mu(C)}\log \frac{\mu(B)}{\mu(C)}\le \log |{\mathscr P}|^{|F_n|}=|F_n|\log |{\mathscr P}|. \end{align} $$
By Lemma 3.1, when
![]() $n\in {\mathbb N}$
is sufficiently large, there is an
$n\in {\mathbb N}$
is sufficiently large, there is an
![]() $X_n\subseteq X$
such that
$X_n\subseteq X$
such that
![]() ${\mu (X_n)>1-\varepsilon }$
and, for each
${\mu (X_n)>1-\varepsilon }$
and, for each
![]() $x\in X_n$
, the set
$x\in X_n$
, the set
![]() $\kappa (F_n, x)$
is
$\kappa (F_n, x)$
is
![]() $(K, \delta )$
-invariant. Denote by
$(K, \delta )$
-invariant. Denote by
![]() ${\mathscr C}_n$
the collection of all
${\mathscr C}_n$
the collection of all
![]() $C\in {\mathscr Q}_a^{I_n}$
satisfying
$C\in {\mathscr Q}_a^{I_n}$
satisfying
![]() $\mu (C\cap X_n)>0$
. Then
$\mu (C\cap X_n)>0$
. Then
![]() ${\bigcup ({\mathscr Q}_a^{I_n}\setminus {\mathscr C}_n)\le \mu (X\setminus X_n)<\varepsilon }$
. Using (6), we obtain
${\bigcup ({\mathscr Q}_a^{I_n}\setminus {\mathscr C}_n)\le \mu (X\setminus X_n)<\varepsilon }$
. Using (6), we obtain

and hence, combining with (5),

It follows that there is some
![]() $C\in {\mathscr C}_n$
such that
$C\in {\mathscr C}_n$
such that
 $$ \begin{align*} \sum_{B\in {\mathscr P}^{F_n}\vee{\mathscr Q}_a^{I_n},\, B\subseteq C}-\frac{\mu(B)}{\mu(C)}\log \frac{\mu(B)}{\mu(C)}\ge |F_n|h(\alpha, {\mathscr P})-|I_n|H({\mathscr Q}_a)-\varepsilon |F_n|\log |{\mathscr P}|. \end{align*} $$
$$ \begin{align*} \sum_{B\in {\mathscr P}^{F_n}\vee{\mathscr Q}_a^{I_n},\, B\subseteq C}-\frac{\mu(B)}{\mu(C)}\log \frac{\mu(B)}{\mu(C)}\ge |F_n|h(\alpha, {\mathscr P})-|I_n|H({\mathscr Q}_a)-\varepsilon |F_n|\log |{\mathscr P}|. \end{align*} $$
Denoting by
![]() ${\mathscr S}_n$
the set of all
${\mathscr S}_n$
the set of all
![]() $A\in {\mathscr P}^{F_n}$
satisfying
$A\in {\mathscr P}^{F_n}$
satisfying
![]() $\mu (A\cap C)>0$
, we then have
$\mu (A\cap C)>0$
, we then have
 $$ \begin{align} \log |{\mathscr S}_n| &\ge \sum_{B\in {\mathscr P}^{F_n}\vee{\mathscr Q}_a^{I_n},\, B\subseteq C}-\frac{\mu(B)}{\mu(C)}\log \frac{\mu(B)}{\mu(C)} \notag\\ &\ge |F_n|h(\alpha, {\mathscr P})-|I_n|H({\mathscr Q}_a)-\varepsilon |F_n|\log |{\mathscr P}|. \end{align} $$
$$ \begin{align} \log |{\mathscr S}_n| &\ge \sum_{B\in {\mathscr P}^{F_n}\vee{\mathscr Q}_a^{I_n},\, B\subseteq C}-\frac{\mu(B)}{\mu(C)}\log \frac{\mu(B)}{\mu(C)} \notag\\ &\ge |F_n|h(\alpha, {\mathscr P})-|I_n|H({\mathscr Q}_a)-\varepsilon |F_n|\log |{\mathscr P}|. \end{align} $$
For each
![]() $a^k\in I_n$
, note that
$a^k\in I_n$
, note that
is the same for all
![]() ${x\in C}$
. Thus, the map
${x\in C}$
. Thus, the map
![]() $g\mapsto \kappa (g, x)$
from
$g\mapsto \kappa (g, x)$
from
![]() $I_n$
to H is the same for all
$I_n$
to H is the same for all
![]() ${x\in C}$
. Denote the image of this map by
${x\in C}$
. Denote the image of this map by
![]() $L_0$
. Choose an
$L_0$
. Choose an
![]() $x_0\in X_n\cap C$
and put
$x_0\in X_n\cap C$
and put
![]() ${L=\kappa (F_n, x_0)}$
. Then L is
${L=\kappa (F_n, x_0)}$
. Then L is
![]() $(K, \delta )$
-invariant and
$(K, \delta )$
-invariant and
![]() $L\supseteq L_0$
.
$L\supseteq L_0$
.
For each
![]() $A\in {\mathscr S}_n$
, one has
$A\in {\mathscr S}_n$
, one has
![]() $A\cap C=B_A\cap C$
for a unique
$A\cap C=B_A\cap C$
for a unique
![]() $B_A\in {\mathscr P}^{RL_0}$
. Thus,
$B_A\in {\mathscr P}^{RL_0}$
. Thus,
and hence, using (7) and the fact that
![]() $|L| = |F_n | = |R| |I_n|$
,
$|L| = |F_n | = |R| |I_n|$
,
 $$ \begin{align*} h(\beta)\ge h(\beta, {\mathscr P}^R) &\ge \frac{1}{|L|}\log |{\mathscr P}^{RL}|-\varepsilon \\ &\ge \frac{1}{|L|}\log |{\mathscr S}_n|-\varepsilon \\ &\ge h(\alpha, {\mathscr P})-\frac{1}{|R|}H({\mathscr Q}_a)-\varepsilon \log |{\mathscr P}|-\varepsilon. \end{align*} $$
$$ \begin{align*} h(\beta)\ge h(\beta, {\mathscr P}^R) &\ge \frac{1}{|L|}\log |{\mathscr P}^{RL}|-\varepsilon \\ &\ge \frac{1}{|L|}\log |{\mathscr S}_n|-\varepsilon \\ &\ge h(\alpha, {\mathscr P})-\frac{1}{|R|}H({\mathscr Q}_a)-\varepsilon \log |{\mathscr P}|-\varepsilon. \end{align*} $$
Letting
![]() $\varepsilon \to 0$
yields
$\varepsilon \to 0$
yields
![]() $h(\beta )\ge h(\alpha , {\mathscr P})-({1}/{|R|})H({\mathscr Q}_a)=h(\alpha , {\mathscr P})-({1}/{|G: \langle a\rangle |}) H({\mathscr Q}_a)$
.
$h(\beta )\ge h(\alpha , {\mathscr P})-({1}/{|R|})H({\mathscr Q}_a)=h(\alpha , {\mathscr P})-({1}/{|G: \langle a\rangle |}) H({\mathscr Q}_a)$
.
Proof of Theorem A
We may assume, by conjugating
![]() $\beta $
by a Shannon orbit equivalence, that
$\beta $
by a Shannon orbit equivalence, that
![]() $(Y,\nu ) = (X,\mu )$
and that the identity map on X is a Shannon orbit equivalence between the two actions. We may also assume that the actions are ergodic in view of the ergodic decomposition and the entropy integral formula with respect to this decomposition. Furthermore, we may assume that G and H are infinite, for the entropy of a p.m.p. action of a finite group is equal to the Shannon entropy of the space (that is, the supremum of the Shannon entropies of all finite partitions of the space, which is a quantity preserved under measure isomorphism) divided by the cardinality of the group.
$(Y,\nu ) = (X,\mu )$
and that the identity map on X is a Shannon orbit equivalence between the two actions. We may also assume that the actions are ergodic in view of the ergodic decomposition and the entropy integral formula with respect to this decomposition. Furthermore, we may assume that G and H are infinite, for the entropy of a p.m.p. action of a finite group is equal to the Shannon entropy of the space (that is, the supremum of the Shannon entropies of all finite partitions of the space, which is a quantity preserved under measure isomorphism) divided by the cardinality of the group.
If neither G nor H is virtually cyclic, then
![]() $h(\alpha ) = h(\beta )$
by Theorem 4.1 and Proposition 3.28 of [Reference Kerr and Li16]. If both G and H are virtually cyclic, then
$h(\alpha ) = h(\beta )$
by Theorem 4.1 and Proposition 3.28 of [Reference Kerr and Li16]. If both G and H are virtually cyclic, then
![]() $h(\alpha ) = h(\beta )$
by Lemmas 3.3 and 3.5. If only one of G and H is virtually cyclic, say G without loss of generality, then
$h(\alpha ) = h(\beta )$
by Lemmas 3.3 and 3.5. If only one of G and H is virtually cyclic, say G without loss of generality, then
![]() ${h(\alpha ) \geq h(\beta )}$
by Theorem 4.1 and Proposition 3.28 of [Reference Kerr and Li16], while
${h(\alpha ) \geq h(\beta )}$
by Theorem 4.1 and Proposition 3.28 of [Reference Kerr and Li16], while
![]() $h(\alpha ) \leq h(\beta )$
by Lemmas 3.3 and 3.5, so that we again obtain
$h(\alpha ) \leq h(\beta )$
by Lemmas 3.3 and 3.5, so that we again obtain
![]() $h(\alpha ) = h(\beta )$
.
$h(\alpha ) = h(\beta )$
.
4. Odometers
A supernatural number is a formal product of the form
![]() $\prod _p p^{k_p}$
, where p ranges over the primes and each
$\prod _p p^{k_p}$
, where p ranges over the primes and each
![]() $k_p$
belongs to
$k_p$
belongs to
![]() $\{ 0,1,2,\ldots , \infty \}$
. Let
$\{ 0,1,2,\ldots , \infty \}$
. Let
![]() $q = \prod _p p^{k_p}$
be a supernatural number having infinitely many prime factors counted with multiplicity (that is, there are infinitely many non-zero
$q = \prod _p p^{k_p}$
be a supernatural number having infinitely many prime factors counted with multiplicity (that is, there are infinitely many non-zero
![]() $k_p$
or at least one
$k_p$
or at least one
![]() $k_p$
is
$k_p$
is
![]() $\infty $
). Take a sequence
$\infty $
). Take a sequence
![]() $\{ n_j \}$
of natural numbers such that the prime p occurs exactly
$\{ n_j \}$
of natural numbers such that the prime p occurs exactly
![]() $k_p$
times among the prime factorizations of the
$k_p$
times among the prime factorizations of the
![]() $n_j$
and form the inverse limit of the cyclic groups
$n_j$
and form the inverse limit of the cyclic groups
![]() ${\mathbb Z} / (n_1 \cdots n_j ){\mathbb Z}$
with connecting maps that reduce mod
${\mathbb Z} / (n_1 \cdots n_j ){\mathbb Z}$
with connecting maps that reduce mod
![]() $n_1 \cdots n_j$
. The group
$n_1 \cdots n_j$
. The group
![]() ${\mathbb Z}$
acts by translation on the inverse limit in a continuous and uniquely ergodic way. We call the resulting ergodic p.m.p. action the q-odometer. One can also construct this action by taking the product
${\mathbb Z}$
acts by translation on the inverse limit in a continuous and uniquely ergodic way. We call the resulting ergodic p.m.p. action the q-odometer. One can also construct this action by taking the product
![]() ${\prod _{j=1}^\infty \{ 0,1,\ldots , n_j -1 \}}$
equipped with the product of uniform probability measures and letting the canonical generator of
${\prod _{j=1}^\infty \{ 0,1,\ldots , n_j -1 \}}$
equipped with the product of uniform probability measures and letting the canonical generator of
![]() ${\mathbb Z}$
act by addition by
${\mathbb Z}$
act by addition by
![]() $(1,0,0,\ldots )$
with carry over to the right, with the maximal element
$(1,0,0,\ldots )$
with carry over to the right, with the maximal element
![]() $(n_j - 1)_{j=1}^\infty $
being sent to the minimal one
$(n_j - 1)_{j=1}^\infty $
being sent to the minimal one
![]() $(0,0,0,\ldots )$
(from the ergodic-theoretic viewpoint, this special orbit can be ignored). In either case, the specific choice of the numbers
$(0,0,0,\ldots )$
(from the ergodic-theoretic viewpoint, this special orbit can be ignored). In either case, the specific choice of the numbers
![]() $n_j$
does not matter up to either topological or measure conjugacy, so there is no ambiguity in the terminology. In general, we refer to these p.m.p. actions as odometers, or
$n_j$
does not matter up to either topological or measure conjugacy, so there is no ambiguity in the terminology. In general, we refer to these p.m.p. actions as odometers, or
![]() ${\mathbb Z}$
-odometers if we wish to explicitly distinguish them from actions of other residually finite groups that can be similarly constructed as inverse limits of finite quotients.
${\mathbb Z}$
-odometers if we wish to explicitly distinguish them from actions of other residually finite groups that can be similarly constructed as inverse limits of finite quotients.
In the case when
![]() $k_p = \infty $
for every p, we speak of the universal odometer.
$k_p = \infty $
for every p, we speak of the universal odometer.
Odometers have discrete spectrum and hence, by the Halmos–von Neumann theorem, are classified up to measure conjugacy by their eigenvalues with multiplicity. For the above q-odometer, these eigenvalues (apart from
![]() $1$
) are obtained by collecting together over all primes p the pth roots of unity counted with multiplicity
$1$
) are obtained by collecting together over all primes p the pth roots of unity counted with multiplicity
![]() $k_p$
. In particular, supernatural numbers with infinitely many prime factors (counting multiplicity) form a complete invariant for odometers up to measure conjugacy (and even flip conjugacy, since the eigenvalues form a group).
$k_p$
. In particular, supernatural numbers with infinitely many prime factors (counting multiplicity) form a complete invariant for odometers up to measure conjugacy (and even flip conjugacy, since the eigenvalues form a group).
In preparation for the proof of Theorem C, we set up some notation and terminology. Let
![]() $(X,\mu )$
be a probability space and let
$(X,\mu )$
be a probability space and let
![]() $T:X\to X$
be an aperiodic measure-preserving transformation. Let S be a partial transformation of X (that is, a bimeasurable bijection from one measurable subset of X to another) such that, for every x in its domain, the image
$T:X\to X$
be an aperiodic measure-preserving transformation. Let S be a partial transformation of X (that is, a bimeasurable bijection from one measurable subset of X to another) such that, for every x in its domain, the image
![]() $Sx$
is contained in the T-orbit of x. Set
$Sx$
is contained in the T-orbit of x. Set
which is a partition of the domain of S. We will make use of the Shannon entropy
![]() $H({\mathscr P}_{S,T})$
of such disjoint collections. Note that if two partial transformations
$H({\mathscr P}_{S,T})$
of such disjoint collections. Note that if two partial transformations
![]() $S_1$
and
$S_1$
and
![]() $S_2$
agree on the intersection of their domains, then their common extension S satisfies
$S_2$
agree on the intersection of their domains, then their common extension S satisfies
![]() $H({\mathscr P}_{S,T} ) \leq H({\mathscr P}_{S_1,T} ) + H({\mathscr P}_{S_2,T} )$
.
$H({\mathscr P}_{S,T} ) \leq H({\mathscr P}_{S_1,T} ) + H({\mathscr P}_{S_2,T} )$
.
By a ladder for T we mean a pair
![]() $(\{ C_i \}_{i=0}^{n-1} , S)$
, where
$(\{ C_i \}_{i=0}^{n-1} , S)$
, where
![]() $C_1 , \ldots , C_{n-1}$
are pairwise disjoint measurable subsets of X (the rungs of the ladder) and S is a measure isomorphism from
$C_1 , \ldots , C_{n-1}$
are pairwise disjoint measurable subsets of X (the rungs of the ladder) and S is a measure isomorphism from
![]() $C_0 \sqcup \cdots \sqcup C_{n-2}$
to
$C_0 \sqcup \cdots \sqcup C_{n-2}$
to
![]() $C_1 \sqcup \cdots \sqcup C_{n-1}$
such that
$C_1 \sqcup \cdots \sqcup C_{n-1}$
such that
![]() $SC_i = C_{i+1}$
for every
$SC_i = C_{i+1}$
for every
![]() ${i=0,\ldots , n-2}$
and, for every
${i=0,\ldots , n-2}$
and, for every
![]() $x\in C_0 \sqcup \cdots \sqcup C_{n-2}$
, the point
$x\in C_0 \sqcup \cdots \sqcup C_{n-2}$
, the point
![]() $Sx$
is contained in the T-orbit of x. By a tower for T we mean a pair
$Sx$
is contained in the T-orbit of x. By a tower for T we mean a pair
![]() $(B,n)$
, where B is a measurable subset of X,
$(B,n)$
, where B is a measurable subset of X,
![]() $n\in {\mathbb N}$
, and the sets
$n\in {\mathbb N}$
, and the sets
![]() $B , T^{-1} B , T^{-2} B ,\ldots , T^{-(n-1)} B$
(the levels of the tower) are pairwise disjoint. A tower is, in effect, a special kind of ladder, but the terminological distinction is useful in the proof below.
$B , T^{-1} B , T^{-2} B ,\ldots , T^{-(n-1)} B$
(the levels of the tower) are pairwise disjoint. A tower is, in effect, a special kind of ladder, but the terminological distinction is useful in the proof below.
We now proceed to establish Theorem C, which says that every
![]() ${\mathbb Z}$
-odometer is Shannon orbit equivalent to the universal
${\mathbb Z}$
-odometer is Shannon orbit equivalent to the universal
![]() ${\mathbb Z}$
-odometer.
${\mathbb Z}$
-odometer.
Proof of Theorem C
Let q be a supernatural number with infinitely many prime factors counting multiplicity and let us show that the q-odometer and the universal odometer are Shannon orbit equivalent. Let T be the q-odometer acting on the space
![]() $(X,\mu )$
, for which we give a concrete realization below. Take a sequence
$(X,\mu )$
, for which we give a concrete realization below. Take a sequence
![]() $\{ p_n \}$
of prime numbers in which every prime appears infinitely often. Take a sequence
$\{ p_n \}$
of prime numbers in which every prime appears infinitely often. Take a sequence
![]() $a_1 , a_2 , \ldots $
of integers greater than
$a_1 , a_2 , \ldots $
of integers greater than
![]() $1$
, to be further specified. Take another sequence
$1$
, to be further specified. Take another sequence
![]() $1 = d_0 < d_1 < d_2 \ldots $
of integers, to be further specified, such that the successive quotients
$1 = d_0 < d_1 < d_2 \ldots $
of integers, to be further specified, such that the successive quotients
![]() $d_n / d_{n-1}$
for
$d_n / d_{n-1}$
for
![]() $n\geq 1$
are integers greater than
$n\geq 1$
are integers greater than
![]() $2$
and, counting multiplicity, the prime factors appearing among these quotients are the same as those appearing in q. For
$2$
and, counting multiplicity, the prime factors appearing among these quotients are the same as those appearing in q. For
![]() $n\geq 1$
, set
$n\geq 1$
, set
![]() $w_n = \prod _{i=1}^n a_i$
and
$w_n = \prod _{i=1}^n a_i$
and
![]() $v_n = \sum _{i=1}^n w_i$
. The numbers
$v_n = \sum _{i=1}^n w_i$
. The numbers
![]() $a_n$
and
$a_n$
and
![]() $d_n$
play a role in the recursive construction that we carry out below and will be specified once we complete the description of the construction. For each
$d_n$
play a role in the recursive construction that we carry out below and will be specified once we complete the description of the construction. For each
![]() $n\geq 1$
, the ratio
$n\geq 1$
, the ratio
![]() $w_n / d_n$
will be between
$w_n / d_n$
will be between
![]() $\frac 12$
and
$\frac 12$
and
![]() $1$
and will tend to
$1$
and will tend to
![]() $1$
as
$1$
as
![]() $n\to \infty $
. The construction will produce a transformation S of X that is measure conjugate to the universal odometer.
$n\to \infty $
. The construction will produce a transformation S of X that is measure conjugate to the universal odometer.
We may regard X as the product
![]() $\prod _{n=1}^\infty \{ 0,1,\ldots , {d_n}/{d_{n-1}} -1 \}$
and
$\prod _{n=1}^\infty \{ 0,1,\ldots , {d_n}/{d_{n-1}} -1 \}$
and
![]() $\mu $
as the product of uniform probability measures, with T acting by addition by
$\mu $
as the product of uniform probability measures, with T acting by addition by
![]() $(1,0,0,\ldots )$
with carry over to the right. Then, for each
$(1,0,0,\ldots )$
with carry over to the right. Then, for each
![]() $m\in {\mathbb N}$
, we have a canonical tower decomposition
$m\in {\mathbb N}$
, we have a canonical tower decomposition
![]() ${X = \bigsqcup _{k=0}^{d_m - 1} T^{-k} B_m}$
, where the base
${X = \bigsqcup _{k=0}^{d_m - 1} T^{-k} B_m}$
, where the base
![]() $B_m$
is the set of all
$B_m$
is the set of all
![]() $(x_n )_n \in \prod _{n=1}^\infty \{ 0,1,\ldots , {d_n}/{d_{n-1}} - 1 \}$
such that
$(x_n )_n \in \prod _{n=1}^\infty \{ 0,1,\ldots , {d_n}/{d_{n-1}} - 1 \}$
such that
![]() $x_n = 0$
for
$x_n = 0$
for
![]() $n=1,\ldots , m$
. We refer to this tower as the
$n=1,\ldots , m$
. We refer to this tower as the
![]() $B_m$
tower.
$B_m$
tower.
By a double recursion over
![]() $n\in {\mathbb N}$
(on the outside) and
$n\in {\mathbb N}$
(on the outside) and
![]() $m\geq n$
(on the inside, for a fixed n), we construct an array of ladders
$m\geq n$
(on the inside, for a fixed n), we construct an array of ladders
![]() ${\mathscr L}_{n,m} = ( \{ C_{n,m,i} \}_{i=0}^{a_n-1} , S_{n,m} )$
for T. For a fixed n the ladders
${\mathscr L}_{n,m} = ( \{ C_{n,m,i} \}_{i=0}^{a_n-1} , S_{n,m} )$
for T. For a fixed n the ladders
![]() ${\mathscr L}_{n,m}$
for
${\mathscr L}_{n,m}$
for
![]() $m\geq n$
are pairwise disjoint. The construction is such that:
$m\geq n$
are pairwise disjoint. The construction is such that:
-
(i) for all
 $n\leq l \leq m$
and
$n\leq l \leq m$
and
 $0\leq i\leq a_n-1$
, each level in the
$0\leq i\leq a_n-1$
, each level in the
 $B_m$
tower is either contained in
$B_m$
tower is either contained in
 $C_{n,l,i}$
or disjoint from it; and
$C_{n,l,i}$
or disjoint from it; and -
(ii) for all
 $m\geq n>1$
, one has
$m\geq n>1$
, one has
 $\bigsqcup _{i=0}^{a_n - 1} C_{n,m,i} \subseteq \bigsqcup _{l=n-1}^m C_{n-1,l,0}$
(that is, the ladder
$\bigsqcup _{i=0}^{a_n - 1} C_{n,m,i} \subseteq \bigsqcup _{l=n-1}^m C_{n-1,l,0}$
(that is, the ladder
 ${\mathscr L}_{n,m}$
is contained in the union of the bases of the ladders
${\mathscr L}_{n,m}$
is contained in the union of the bases of the ladders
 ${\mathscr L}_{n-1,l}$
for
${\mathscr L}_{n-1,l}$
for
 ${l=n-1,\ldots , m}$
).
${l=n-1,\ldots , m}$
).
Now, let
![]() $m \geq n \geq 1$
and suppose that we have completed the stages of the outer recursion from
$m \geq n \geq 1$
and suppose that we have completed the stages of the outer recursion from
![]() $1$
to
$1$
to
![]() $n-1$
(unless we are in the base case
$n-1$
(unless we are in the base case
![]() $n=1$
) and of the inner recursion from n to
$n=1$
) and of the inner recursion from n to
![]() $m-1$
(unless we are in the base case
$m-1$
(unless we are in the base case
![]() $m=n$
). We break into three cases.
$m=n$
). We break into three cases.
(I) Case
![]() $m=n=1$
. Here we define:
$m=n=1$
. Here we define:
-
•
 $C_{1,1,i} = T^{-i} B_1$
for
$C_{1,1,i} = T^{-i} B_1$
for
 $i=0,\ldots , a_1 -1$
; and
$i=0,\ldots , a_1 -1$
; and -
•
 $S_{1,1} = T^{-1}$
on
$S_{1,1} = T^{-1}$
on
 $\bigsqcup _{i=0}^{a_1 - 2} C_{1,1,i}$
.
$\bigsqcup _{i=0}^{a_1 - 2} C_{1,1,i}$
.
The ladder
![]() ${\mathscr L}_{1,1}$
is then defined to be
${\mathscr L}_{1,1}$
is then defined to be
![]() $( \{ C_{1,1,i} \}_{i=0}^{a_1-1} , S_{1,1} )$
.
$( \{ C_{1,1,i} \}_{i=0}^{a_1-1} , S_{1,1} )$
.
(II) Case
![]() $m=n>1$
. By the recursive hypothesis (i), for
$m=n>1$
. By the recursive hypothesis (i), for
![]() $l=n-1,n$
, each level of the
$l=n-1,n$
, each level of the
![]() $B_n$
tower is either contained in
$B_n$
tower is either contained in
![]() $C_{n-1,l,0}$
or disjoint from it. Let
$C_{n-1,l,0}$
or disjoint from it. Let
![]() $r_{n,n} \in {\mathbb N}$
and
$r_{n,n} \in {\mathbb N}$
and
![]() $0\leq s(n,n,0) < s(n,n,1) < \cdots < s(n,n,r_{n,n} ) < d_n$
be such that the levels of the
$0\leq s(n,n,0) < s(n,n,1) < \cdots < s(n,n,r_{n,n} ) < d_n$
be such that the levels of the
![]() $B_n$
tower contained in the set
$B_n$
tower contained in the set
are precisely
![]() $T^{-s(n,n,0)} B_n , T^{-s(n,n,1)} B_n , \ldots , T^{-s(n,n,r_{n,n}-1)} B_n$
(the duplication of n in the notation is for consistency with case III below). We define:
$T^{-s(n,n,0)} B_n , T^{-s(n,n,1)} B_n , \ldots , T^{-s(n,n,r_{n,n}-1)} B_n$
(the duplication of n in the notation is for consistency with case III below). We define:
-
•
 $C_{n,n,i} = T^{-s(n,n,i)} B_n$
for every
$C_{n,n,i} = T^{-s(n,n,i)} B_n$
for every
 $i=0,\ldots , a_n-1$
; and
$i=0,\ldots , a_n-1$
; and -
•
 $S_{n,n} = T^{-s(n,n,i+1) + s(n,n,i)}$
on
$S_{n,n} = T^{-s(n,n,i+1) + s(n,n,i)}$
on
 $T^{-s(n,n,i)} B_n$
for every
$T^{-s(n,n,i)} B_n$
for every
 $i=0,\ldots , a_n -2$
.
$i=0,\ldots , a_n -2$
.
The ladder
![]() ${\mathscr L}_{n,n}$
is then defined to be
${\mathscr L}_{n,n}$
is then defined to be
![]() $(\{ C_{n,n,i} \}_{i=0}^{a_n-1} , S_{n,n} )$
.
$(\{ C_{n,n,i} \}_{i=0}^{a_n-1} , S_{n,n} )$
.
(III) Case
![]() $m>n$
. If
$m>n$
. If
![]() $n=1$
, we write
$n=1$
, we write
![]() $W_{n,m}$
for the set
$W_{n,m}$
for the set
![]() $X\setminus \bigsqcup _{l=1}^{m-1} \bigsqcup _{i=0}^{a_1-1} C_{1,l,i}$
, whereas if
$X\setminus \bigsqcup _{l=1}^{m-1} \bigsqcup _{i=0}^{a_1-1} C_{1,l,i}$
, whereas if
![]() $n>1$
, we write
$n>1$
, we write
![]() $W_{n,m}$
for the set
$W_{n,m}$
for the set
 $$ \begin{align*} \bigg(\bigsqcup_{l=n-1}^m C_{n-1,l,0} \bigg) \setminus \bigg(\bigsqcup_{l=n}^{m-1} \bigsqcup_{i=0}^{a_n - 1} C_{n,l,i} \bigg). \end{align*} $$
$$ \begin{align*} \bigg(\bigsqcup_{l=n-1}^m C_{n-1,l,0} \bigg) \setminus \bigg(\bigsqcup_{l=n}^{m-1} \bigsqcup_{i=0}^{a_n - 1} C_{n,l,i} \bigg). \end{align*} $$
By the recursive hypothesis (i), each level of the
![]() $B_m$
tower is either contained in
$B_m$
tower is either contained in
![]() $W_{n,m}$
or disjoint from it. Let
$W_{n,m}$
or disjoint from it. Let
![]() ${0\leq s(n,m,0) < s(n,m,1) < \cdots < s(n,m,r_{n,m}) < d_m}$
be such that the levels of the
${0\leq s(n,m,0) < s(n,m,1) < \cdots < s(n,m,r_{n,m}) < d_m}$
be such that the levels of the
![]() $B_m$
tower contained in
$B_m$
tower contained in
![]() $W_{n,m}$
are precisely
$W_{n,m}$
are precisely
![]() $T^{-s(n,m,0)} B_m , T^{-s(n,m,1)} B_m , \ldots , T^{-s(n,m,r_{n,m})} B_m$
. Set
$T^{-s(n,m,0)} B_m , T^{-s(n,m,1)} B_m , \ldots , T^{-s(n,m,r_{n,m})} B_m$
. Set
![]() $t_{n,m}$
to be the largest positive integer such that
$t_{n,m}$
to be the largest positive integer such that
For each
![]() $j=0,\ldots , t_{n,m} -1$
, define:
$j=0,\ldots , t_{n,m} -1$
, define:
-
•
 $C_{n,m,i}^{(j)} = T^{-s(n,m,a_n j+i)} B_m$
for every
$C_{n,m,i}^{(j)} = T^{-s(n,m,a_n j+i)} B_m$
for every
 $i=0,\ldots , a_n-1$
; and
$i=0,\ldots , a_n-1$
; and -
•
 $S_{n,m}^{(j)} = T^{-s(n,m,a_n j+i+1) + s(n,m,a_n j+i)}$
on
$S_{n,m}^{(j)} = T^{-s(n,m,a_n j+i+1) + s(n,m,a_n j+i)}$
on
 $T^{-s(n,m,a_n j+i)} B_m$
for every
$T^{-s(n,m,a_n j+i)} B_m$
for every
 ${i=0,\ldots , a_n -2}$
.
${i=0,\ldots , a_n -2}$
.
Then
![]() ${\mathscr L}_{n,m}^{(j)} := ( \{ C_{n,m,i}^{(j)} \}_{i=0}^{a_n-1} , S_{n,m}^{(j)} )$
for
${\mathscr L}_{n,m}^{(j)} := ( \{ C_{n,m,i}^{(j)} \}_{i=0}^{a_n-1} , S_{n,m}^{(j)} )$
for
![]() $j=0,\ldots , t_{n,m} -1$
are ladders for T, and they are pairwise disjoint. We combine them to create a single ladder
$j=0,\ldots , t_{n,m} -1$
are ladders for T, and they are pairwise disjoint. We combine them to create a single ladder
![]() ${\mathscr L}_{n,m} := (\{ C_{n,m,i} \}_{i=0}^{a_n-1} , S_{n,m} )$
by setting
${\mathscr L}_{n,m} := (\{ C_{n,m,i} \}_{i=0}^{a_n-1} , S_{n,m} )$
by setting
![]() $C_{n,m,i} = \bigsqcup _{j=0}^{t_{n,m}-1} C_{n,m,i}^{(j)}$
and defining
$C_{n,m,i} = \bigsqcup _{j=0}^{t_{n,m}-1} C_{n,m,i}^{(j)}$
and defining
![]() $S_{n,m}$
to coincide with
$S_{n,m}$
to coincide with
![]() $S_{n,m}^{(j)}$
on
$S_{n,m}^{(j)}$
on
![]() $\bigsqcup _{i=0}^{a_n - 2} C_{n,m,i}^{(j)}$
for every
$\bigsqcup _{i=0}^{a_n - 2} C_{n,m,i}^{(j)}$
for every
![]() $j=0,\ldots , t_{n,m} - 1$
. This completes the construction. Note that (i) and (ii) are satisfied for n and m.
$j=0,\ldots , t_{n,m} - 1$
. This completes the construction. Note that (i) and (ii) are satisfied for n and m.
For convenience, we extend the notation
![]() $t_{n,m}$
from case (III) by setting
$t_{n,m}$
from case (III) by setting
![]() $t_{n,n} = 1$
for every
$t_{n,n} = 1$
for every
![]() $n\geq 1$
.
$n\geq 1$
.
For each
![]() $j = 0,\ldots , t_{n,m} - 1$
, we define the spread of the ladder
$j = 0,\ldots , t_{n,m} - 1$
, we define the spread of the ladder
![]() ${\mathscr L}_{n,m}^{(j)}$
to be the maximum of the positive integers
${\mathscr L}_{n,m}^{(j)}$
to be the maximum of the positive integers
![]() $s(n,m,a_n j + i+1) - s(n,m,a_n j + i)$
over all
$s(n,m,a_n j + i+1) - s(n,m,a_n j + i)$
over all
![]() ${i=0,\ldots , a_n -2}$
(this is the maximum distance, in terms of levels in the
${i=0,\ldots , a_n -2}$
(this is the maximum distance, in terms of levels in the
![]() $B_m$
tower, between the rungs of the ladder). By construction, one sees that, when
$B_m$
tower, between the rungs of the ladder). By construction, one sees that, when
![]() $m> n$
, the spreads of the ladders
$m> n$
, the spreads of the ladders
![]() ${\mathscr L}_{n,m}^{(j)}$
for
${\mathscr L}_{n,m}^{(j)}$
for
![]() $j=0,\ldots , , t_{n,m} -1$
are bounded above by
$j=0,\ldots , , t_{n,m} -1$
are bounded above by
![]() $d_{m-1}$
(for this, it is important that there is always at least one unused level left over at the top of the tower when building the ladders
$d_{m-1}$
(for this, it is important that there is always at least one unused level left over at the top of the tower when building the ladders
![]() ${\mathscr L}_{n,m}$
, so that the spread of the ladders at the next stage
${\mathscr L}_{n,m}$
, so that the spread of the ladders at the next stage
![]() $m+1$
for a fixed n is at most
$m+1$
for a fixed n is at most
![]() $d_m$
, and this is guaranteed by (8)).
$d_m$
, and this is guaranteed by (8)).
Let
![]() $n\in {\mathbb N}$
. For each
$n\in {\mathbb N}$
. For each
![]() $i=0,\ldots , a_n - 1$
, set
$i=0,\ldots , a_n - 1$
, set
![]() $C_{n,i} = \bigsqcup _{m=n}^\infty C_{n,m,i}$
and define
$C_{n,i} = \bigsqcup _{m=n}^\infty C_{n,m,i}$
and define
![]() $S_n$
on
$S_n$
on
![]() $\bigsqcup _{m=n}^\infty \operatorname {\mathrm {dom}} (S_{n,m} )$
by setting
$\bigsqcup _{m=n}^\infty \operatorname {\mathrm {dom}} (S_{n,m} )$
by setting
![]() $S_n = S_{n,m}$
on
$S_n = S_{n,m}$
on
![]() $\operatorname {\mathrm {dom}} (S_{n,m} )$
for every
$\operatorname {\mathrm {dom}} (S_{n,m} )$
for every
![]() $m\geq n$
. Then
$m\geq n$
. Then
![]() ${{\mathscr L}_n := (\{ C_{n,i} \}_{i=0}^{a_n -1} , S_n )}$
is a ladder for T.
${{\mathscr L}_n := (\{ C_{n,i} \}_{i=0}^{a_n -1} , S_n )}$
is a ladder for T.
We use the ladders
![]() ${\mathscr L}_{n,m}$
to build the transformation S as follows. For
${\mathscr L}_{n,m}$
to build the transformation S as follows. For
![]() $m\geq n\geq 1$
, set
$m\geq n\geq 1$
, set
 $$ \begin{align*} D_{n,m} = S_1^{a_1 - 1} S_2^{a_2 - 1} \cdots S_{n-1}^{a_{n-1} - 1} \bigg(\bigsqcup_{i=0}^{a_n-2} C_{n,m,i} \bigg). \end{align*} $$
$$ \begin{align*} D_{n,m} = S_1^{a_1 - 1} S_2^{a_2 - 1} \cdots S_{n-1}^{a_{n-1} - 1} \bigg(\bigsqcup_{i=0}^{a_n-2} C_{n,m,i} \bigg). \end{align*} $$
The sets
![]() $D_{n,m}$
are pairwise disjoint and their union has measure one. We then define S so that on
$D_{n,m}$
are pairwise disjoint and their union has measure one. We then define S so that on
![]() $D_{n,m}$
it is given by
$D_{n,m}$
it is given by
Up to measure conjugacy, this yields an odometer: for each n, the union of the sets
![]() $D_{n,m}$
over
$D_{n,m}$
over
![]() $m\geq n$
represents the set of points whose coordinates in the odometer from
$m\geq n$
represents the set of points whose coordinates in the odometer from
![]() $1$
to
$1$
to
![]() $n-1$
are maximum but whose coordinate at n is not maximum, so that S produces a roll-over of the first
$n-1$
are maximum but whose coordinate at n is not maximum, so that S produces a roll-over of the first
![]() $n-1$
coordinates, increments the nth coordinate by
$n-1$
coordinates, increments the nth coordinate by
![]() $1$
, and does not change any other coordinates.
$1$
, and does not change any other coordinates.
We assume
![]() $d_n$
to be taken large enough to guarantee that
$d_n$
to be taken large enough to guarantee that
![]() $r_{n,n} \geq p_n$
(or
$r_{n,n} \geq p_n$
(or
![]() $d_1 \geq p_1$
in the case
$d_1 \geq p_1$
in the case
![]() $n=1$
). Then the largest multiple of
$n=1$
). Then the largest multiple of
![]() $p_n$
no greater than
$p_n$
no greater than
![]() $r_{n,n}$
(or
$r_{n,n}$
(or
![]() $d_1 - 1$
in the case
$d_1 - 1$
in the case
![]() $n=1$
) is non-zero, and we declare
$n=1$
) is non-zero, and we declare
![]() $a_n$
to be this multiple (we still need to further specify
$a_n$
to be this multiple (we still need to further specify
![]() $d_n$
below, but the way in which
$d_n$
below, but the way in which
![]() $a_n$
depends on
$a_n$
depends on
![]() $d_n$
is not affected by this). This will ensure that S is the universal odometer. In the course of what follows, we specify how large the numbers
$d_n$
is not affected by this). This will ensure that S is the universal odometer. In the course of what follows, we specify how large the numbers
![]() $d_n$
should be chosen so as to obtain a Shannon orbit equivalence.
$d_n$
should be chosen so as to obtain a Shannon orbit equivalence.
For
![]() $m\geq n\geq 1$
, define
$m\geq n\geq 1$
, define
![]() $R_{n,m}$
to be the restriction of
$R_{n,m}$
to be the restriction of
![]() $S_n$
to
$S_n$
to
![]() $\bigsqcup _{l=n}^m \operatorname {\mathrm {dom}} (S_{n,l} )$
. For
$\bigsqcup _{l=n}^m \operatorname {\mathrm {dom}} (S_{n,l} )$
. For
![]() $n\in {\mathbb N}$
and
$n\in {\mathbb N}$
and
![]() $A\subseteq \bigsqcup _{l=n}^m C_{n,l,0}$
, write
$A\subseteq \bigsqcup _{l=n}^m C_{n,l,0}$
, write
![]() $\bar {R}_{n,m} A$
for the set
$\bar {R}_{n,m} A$
for the set
![]() $\bigsqcup _{i=0}^{a_n-1} R_{n,m}^i A$
(that is, the saturation of A within the ladders
$\bigsqcup _{i=0}^{a_n-1} R_{n,m}^i A$
(that is, the saturation of A within the ladders
![]() ${\mathscr L}_{n,l}$
for
${\mathscr L}_{n,l}$
for
![]() $l=n,\ldots , m$
), and for
$l=n,\ldots , m$
), and for
![]() $m\geq n$
, set
$m\geq n$
, set
![]() $A_{n,m} = \bigsqcup _{l=n}^m C_{n,l,0}$
and
$A_{n,m} = \bigsqcup _{l=n}^m C_{n,l,0}$
and
 $$ \begin{align*} E_{n,m} = \bar{R}_{1,m} \bar{R}_{2,m} \cdots \bar{R}_{n,m} A_{n,m} = \bigsqcup_{i=0}^{a_1 \cdots a_n -1} S^i A_{n,m}. \end{align*} $$
$$ \begin{align*} E_{n,m} = \bar{R}_{1,m} \bar{R}_{2,m} \cdots \bar{R}_{n,m} A_{n,m} = \bigsqcup_{i=0}^{a_1 \cdots a_n -1} S^i A_{n,m}. \end{align*} $$
Note that
![]() $E_{n,m} \subseteq E_{n,m'}$
when
$E_{n,m} \subseteq E_{n,m'}$
when
![]() $m'> m$
,
$m'> m$
,
![]() $E_{n,m} \supseteq E_{n',m}$
when
$E_{n,m} \supseteq E_{n',m}$
when
![]() $n'> n$
and
$n'> n$
and
![]() $E_{n,n} \subseteq E_{n-1,n}$
when
$E_{n,n} \subseteq E_{n-1,n}$
when
![]() $n> 1$
. Also, for each
$n> 1$
. Also, for each
![]() $n\geq 1$
, the increasing union
$n\geq 1$
, the increasing union
![]() $\bigcup _{m=n}^\infty E_{n,m}$
has measure one.
$\bigcup _{m=n}^\infty E_{n,m}$
has measure one.
By choosing the numbers
![]() $d_n$
to be large enough in succession, we can arrange for the following additional conditions to hold. First, if for
$d_n$
to be large enough in succession, we can arrange for the following additional conditions to hold. First, if for
![]() $n\geq 1$
we set
$n\geq 1$
we set
then we may assume that
![]() $\lim _{n\to \infty } \beta _n = 0$
and
$\lim _{n\to \infty } \beta _n = 0$
and
 $$ \begin{align} \sum_{n=1}^\infty \beta_n \log \frac{9w_n^2 d_n}{\beta_n} < \infty. \end{align} $$
$$ \begin{align} \sum_{n=1}^\infty \beta_n \log \frac{9w_n^2 d_n}{\beta_n} < \infty. \end{align} $$
Write
![]() $\theta _{n,m} = (1+w_{n-1} ) d_{m-1}$
. For
$\theta _{n,m} = (1+w_{n-1} ) d_{m-1}$
. For
![]() $n\geq 3$
, the ratio
$n\geq 3$
, the ratio
![]() $w_{n-1} / d_{n-1}$
is at least
$w_{n-1} / d_{n-1}$
is at least
![]() $1 - (v_{n-2} + p_{n-1} w_{n-2} )/d_{n-1}$
(see (16)) and thus can be assumed to be no smaller than
$1 - (v_{n-2} + p_{n-1} w_{n-2} )/d_{n-1}$
(see (16)) and thus can be assumed to be no smaller than
![]() $\frac 12$
, so that, for
$\frac 12$
, so that, for
![]() $n \geq 2$
, we can make the quantity
$n \geq 2$
, we can make the quantity
![]() $({1}/{w_{n-1}}) \log d_{n-1}$
small enough to ensure that
$({1}/{w_{n-1}}) \log d_{n-1}$
small enough to ensure that
 $$ \begin{align} -\frac{1}{w_{n-1}} \log \bigg(\frac{1}{w_{n-1}} \cdot \frac{1}{\theta_{n,n}} \bigg) < \frac{1}{2^{n+2}}. \end{align} $$
$$ \begin{align} -\frac{1}{w_{n-1}} \log \bigg(\frac{1}{w_{n-1}} \cdot \frac{1}{\theta_{n,n}} \bigg) < \frac{1}{2^{n+2}}. \end{align} $$
Moreover, we may assume, for
![]() $n\geq 2$
, that
$n\geq 2$
, that
 $$ \begin{align} -\frac{v_{n-1} + p_n w_{n-1}}{d_n} \log \bigg( \frac{v_{n-1} + p_n w_{n-1}}{d_n} \cdot \frac{1}{\theta_{n,n+1}} \bigg) < \frac{1}{2^{n+2}} , \end{align} $$
$$ \begin{align} -\frac{v_{n-1} + p_n w_{n-1}}{d_n} \log \bigg( \frac{v_{n-1} + p_n w_{n-1}}{d_n} \cdot \frac{1}{\theta_{n,n+1}} \bigg) < \frac{1}{2^{n+2}} , \end{align} $$
and also, for every
![]() $m \geq 4$
and
$m \geq 4$
and
![]() $p=1,\ldots , m-2$
, that
$p=1,\ldots , m-2$
, that
 $$ \begin{gather*} -\frac{v_p}{d_{m-1}} \log \bigg( \frac{v_p}{d_{m-1}} \cdot \frac{1}{\theta_{p,m}} \bigg) < \frac{1}{2^{m+1}} , \end{gather*} $$
$$ \begin{gather*} -\frac{v_p}{d_{m-1}} \log \bigg( \frac{v_p}{d_{m-1}} \cdot \frac{1}{\theta_{p,m}} \bigg) < \frac{1}{2^{m+1}} , \end{gather*} $$
which implies that, for all
![]() $n\geq 2$
,
$n\geq 2$
,
 $$ \begin{align} \sum_{m=n+2}^\infty -\frac{v_n}{d_{m-1}} \log \bigg( \frac{v_n}{d_{m-1}} \cdot \frac{1}{\theta_{n,m}} \bigg) \leq \sum_{m=n+2}^\infty \frac{1}{2^{m+1}} \leq \frac{1}{2^{n+1}}. \end{align} $$
$$ \begin{align} \sum_{m=n+2}^\infty -\frac{v_n}{d_{m-1}} \log \bigg( \frac{v_n}{d_{m-1}} \cdot \frac{1}{\theta_{n,m}} \bigg) \leq \sum_{m=n+2}^\infty \frac{1}{2^{m+1}} \leq \frac{1}{2^{n+1}}. \end{align} $$
Finally, we may also assume that
 $$ \begin{align} \sum_{m=2}^\infty -\frac{a_1}{d_m} \log \frac{a_1}{d_m^2} < \infty. \end{align} $$
$$ \begin{align} \sum_{m=2}^\infty -\frac{a_1}{d_m} \log \frac{a_1}{d_m^2} < \infty. \end{align} $$
Let
![]() $n\geq 1$
. Define
$n\geq 1$
. Define
![]() $K_n$
to be the union of the tower levels
$K_n$
to be the union of the tower levels
![]() $T^{-i} B_n$
with
$T^{-i} B_n$
with
![]() $0 < i \leq d_n - 1$
such that both
$0 < i \leq d_n - 1$
such that both
![]() $T^{-i}B_n$
and
$T^{-i}B_n$
and
![]() $T^{-(i-1)}B_n$
are contained in
$T^{-(i-1)}B_n$
are contained in
![]() $E_{n, n}$
, that is, the set of all
$E_{n, n}$
, that is, the set of all
![]() ${x\in E_{n,n} \setminus B_n}$
such that
${x\in E_{n,n} \setminus B_n}$
such that
![]() $Tx \in E_{n,n}$
. Given an
$Tx \in E_{n,n}$
. Given an
![]() $x\in K_n$
, we wish to show that
$x\in K_n$
, we wish to show that
![]() $Tx$
can be expressed as
$Tx$
can be expressed as
![]() $S^k x$
for some k within certain bounds. Since both x and
$S^k x$
for some k within certain bounds. Since both x and
![]() $Tx$
belong to
$Tx$
belong to
![]() $E_{n,n}$
, by construction there exist a
$E_{n,n}$
, by construction there exist a
![]() $y\in X$
in some rung of the ladder
$y\in X$
in some rung of the ladder
![]() ${\mathscr L}_{n,n}$
and a
${\mathscr L}_{n,n}$
and a
![]() $k_0 \geq 0$
with
$k_0 \geq 0$
with
![]() $k_0 \leq w_{n-1} -1$
such that
$k_0 \leq w_{n-1} -1$
such that
![]() $x = S^{k_0} y$
, as well as a
$x = S^{k_0} y$
, as well as a
![]() $z\in X$
in some rung of the ladder
$z\in X$
in some rung of the ladder
![]() ${\mathscr L}_{n,n}$
and a
${\mathscr L}_{n,n}$
and a
![]() $k_1 \geq 0$
with
$k_1 \geq 0$
with
![]() $k_1 \leq w_{n-1} -1$
such that
$k_1 \leq w_{n-1} -1$
such that
![]() $Tx = S^{k_1} z$
. Since
$Tx = S^{k_1} z$
. Since
![]() $x=S_1^{l_1}S_2^{l_2} \cdots S_{n-1}^{l_{n-1}}y$
for some
$x=S_1^{l_1}S_2^{l_2} \cdots S_{n-1}^{l_{n-1}}y$
for some
![]() $l_1,\ldots , l_{n-1}$
satisfying
$l_1,\ldots , l_{n-1}$
satisfying
![]() $0\le l_j\le a_j-1$
for all j, and for all
$0\le l_j\le a_j-1$
for all j, and for all
![]() $1\leq p\leq l$
the spreads of the ladders
$1\leq p\leq l$
the spreads of the ladders
![]() ${\mathscr L}_{p,l}^{(j)}$
for
${\mathscr L}_{p,l}^{(j)}$
for
![]() $j=0,\ldots , t_{p,l} - 1$
are bounded above by
$j=0,\ldots , t_{p,l} - 1$
are bounded above by
![]() $d_{l-1}$
, the jump in levels within the
$d_{l-1}$
, the jump in levels within the
![]() $B_n$
tower in going from y to x is at most
$B_n$
tower in going from y to x is at most
![]() $(a_1 + \cdots + a_{n-1} )d_{n-1}$
. Similarly, the jump in levels within the
$(a_1 + \cdots + a_{n-1} )d_{n-1}$
. Similarly, the jump in levels within the
![]() $B_n$
tower in going from z to
$B_n$
tower in going from z to
![]() $Tx$
is at most
$Tx$
is at most
![]() $(a_1 + \cdots + a_{n-1} ) d_{n-1}$
. Thus, the jump in levels within the
$(a_1 + \cdots + a_{n-1} ) d_{n-1}$
. Thus, the jump in levels within the
![]() $B_n$
tower in going from y to z is at most
$B_n$
tower in going from y to z is at most
![]() $2w_{n-1} d_{n-1} + 1$
. Since y and z both lie in rungs of the ladder
$2w_{n-1} d_{n-1} + 1$
. Since y and z both lie in rungs of the ladder
![]() ${\mathscr L}_{n,n}$
, it follows that we have
${\mathscr L}_{n,n}$
, it follows that we have
![]() $y = S_n^j z$
for some j satisfying
$y = S_n^j z$
for some j satisfying
![]() $|j| \leq 2w_{n-1} d_{n-1} + 1$
(this will typically be a very crude bound, governed by the extreme scenario in which each level of the
$|j| \leq 2w_{n-1} d_{n-1} + 1$
(this will typically be a very crude bound, governed by the extreme scenario in which each level of the
![]() $B_n$
tower between those containing y and z is a rung of the ladder
$B_n$
tower between those containing y and z is a rung of the ladder
![]() ${\mathscr L}_{n,n}^{(0)}$
), which implies that
${\mathscr L}_{n,n}^{(0)}$
), which implies that
![]() $y = S^{k_2} z$
for some
$y = S^{k_2} z$
for some
![]() $k_2$
satisfying
$k_2$
satisfying
Putting things together, we conclude that
![]() $Tx = S^k x$
, where k satisfies
$Tx = S^k x$
, where k satisfies
Next, observe that, for
![]() $n\geq 2$
,
$n\geq 2$
,
 $$ \begin{align} \mu (X\setminus E_{n,n} ) &\leq \sum_{j=1}^{n-1} \frac{(r_{j,n} - a_j t_{j,n} + 1)w_{j-1}}{d_n} + \frac{(r_{n,n} - a_n + 1)w_{n-1}}{d_n} \notag\\ &\leq \sum_{j=1}^{n-1} \frac{a_j w_{j-1}}{d_n} + \frac{p_n w_{n-1}}{d_n} \notag\\ &= \frac{v_{n-1} + p_n w_{n-1}}{d_n}. \end{align} $$
$$ \begin{align} \mu (X\setminus E_{n,n} ) &\leq \sum_{j=1}^{n-1} \frac{(r_{j,n} - a_j t_{j,n} + 1)w_{j-1}}{d_n} + \frac{(r_{n,n} - a_n + 1)w_{n-1}}{d_n} \notag\\ &\leq \sum_{j=1}^{n-1} \frac{a_j w_{j-1}}{d_n} + \frac{p_n w_{n-1}}{d_n} \notag\\ &= \frac{v_{n-1} + p_n w_{n-1}}{d_n}. \end{align} $$
Since
![]() $K_n$
can be obtained from
$K_n$
can be obtained from
![]() $E_{n,n} \setminus B_n$
by removing
$E_{n,n} \setminus B_n$
by removing
![]() $T^{-1} (X\setminus E_{n,n} )$
, we thereby obtain, recalling the definition of
$T^{-1} (X\setminus E_{n,n} )$
, we thereby obtain, recalling the definition of
![]() $\beta _n$
from (9),
$\beta _n$
from (9),
Since
![]() $\beta _n \to 0$
, this shows that
$\beta _n \to 0$
, this shows that
![]() $\mu (K_n ) \to 1$
. Thus, S generates the same equivalence relation as T modulo a null set. For
$\mu (K_n ) \to 1$
. Thus, S generates the same equivalence relation as T modulo a null set. For
![]() $n>1$
, setting
$n>1$
, setting
![]() $K_n' = K_n \setminus K_{n-1}$
and using (17),
$K_n' = K_n \setminus K_{n-1}$
and using (17),
The cocycle partition
![]() ${\mathscr P}_{T,S}$
of T with respect to S, using the fact that a uniform partition of a measurable set maximizes the entropy among all partitions of the set with a given cardinality, and writing
${\mathscr P}_{T,S}$
of T with respect to S, using the fact that a uniform partition of a measurable set maximizes the entropy among all partitions of the set with a given cardinality, and writing
![]() $\unicode{x3bb} _{n-1} = 2\cdot 4w_{n-1}^2 d_{n-1} + 1$
for brevity, then satisfies
$\unicode{x3bb} _{n-1} = 2\cdot 4w_{n-1}^2 d_{n-1} + 1$
for brevity, then satisfies

Finally, we show that
![]() $H({\mathscr P}_{S,T} )$
is also finite. For
$H({\mathscr P}_{S,T} )$
is also finite. For
![]() $n\geq 1$
, set
$n\geq 1$
, set
![]() $D_n = \bigsqcup _{m=n}^\infty D_{n,m}$
. Notice that, for
$D_n = \bigsqcup _{m=n}^\infty D_{n,m}$
. Notice that, for
![]() $m-1\geq n\geq 1$
, we have
$m-1\geq n\geq 1$
, we have
![]() $D_{n,m} \subseteq X\setminus E_{n,m-1}$
, and so, in the case
$D_{n,m} \subseteq X\setminus E_{n,m-1}$
, and so, in the case
![]() $m-1> n \geq 1$
, we obtain
$m-1> n \geq 1$
, we obtain
Suppose that
![]() $m> n=1$
. Then, for every
$m> n=1$
. Then, for every
![]() $x\in D_{1,m}$
, we have
$x\in D_{1,m}$
, we have
![]() $Sx = T^{-k} x$
for some
$Sx = T^{-k} x$
for some
![]() ${1 \leq k \leq d_{m-1}}$
(since the distance between successive rungs in each
${1 \leq k \leq d_{m-1}}$
(since the distance between successive rungs in each
![]() ${\mathscr L}_{1,m}^{(j)}$
is at most
${\mathscr L}_{1,m}^{(j)}$
is at most
![]() $d_{m-1}$
). Using, as before, the fact that a uniform partition of a measurable set maximizes the entropy among all partitions of the set with a given cardinality, and also using the fact that
$d_{m-1}$
). Using, as before, the fact that a uniform partition of a measurable set maximizes the entropy among all partitions of the set with a given cardinality, and also using the fact that
![]() ${\mathscr P}_{S|_{D_{1,1}},T}$
and
${\mathscr P}_{S|_{D_{1,1}},T}$
and
![]() ${\mathscr P}_{S|_{D_{1,2}},T}$
are finite collections, we obtain
${\mathscr P}_{S|_{D_{1,2}},T}$
are finite collections, we obtain
 $$ \begin{align*} H({\mathscr P}_{S|_{D_1} ,T} ) &\leq \sum_{m=1}^\infty H({\mathscr P}_{S|_{D_{1,m}} ,T} ) \\ &\leq H({\mathscr P}_{S|_{D_{1,1}} ,T} ) + H({\mathscr P}_{S|_{D_{1,2}} ,T} ) + \sum_{m=3}^\infty d_{m-1} \bigg( -\frac{\mu (D_{1,m})}{d_{m-1}} \log \frac{\mu (D_{1,m})}{d_{m-1}} \bigg) \\ &\stackrel{({19})}{\leq} H({\mathscr P}_{S|_{D_{1,1}} ,T} ) + H({\mathscr P}_{S|_{D_{1,2}} ,T} ) + \sum_{m=3}^\infty -\frac{a_1}{d_{m-1}} \log \bigg( \frac{a_1}{d_{m-1}}\cdot\frac{1}{d_{m-1}} \bigg) \\ &\stackrel{({14})}{<} \infty. \end{align*} $$
$$ \begin{align*} H({\mathscr P}_{S|_{D_1} ,T} ) &\leq \sum_{m=1}^\infty H({\mathscr P}_{S|_{D_{1,m}} ,T} ) \\ &\leq H({\mathscr P}_{S|_{D_{1,1}} ,T} ) + H({\mathscr P}_{S|_{D_{1,2}} ,T} ) + \sum_{m=3}^\infty d_{m-1} \bigg( -\frac{\mu (D_{1,m})}{d_{m-1}} \log \frac{\mu (D_{1,m})}{d_{m-1}} \bigg) \\ &\stackrel{({19})}{\leq} H({\mathscr P}_{S|_{D_{1,1}} ,T} ) + H({\mathscr P}_{S|_{D_{1,2}} ,T} ) + \sum_{m=3}^\infty -\frac{a_1}{d_{m-1}} \log \bigg( \frac{a_1}{d_{m-1}}\cdot\frac{1}{d_{m-1}} \bigg) \\ &\stackrel{({14})}{<} \infty. \end{align*} $$
Now suppose that
![]() $m\geq n>1$
. By definition,
$m\geq n>1$
. By definition,
![]() $S = S_{n,m} S_{n-1}^{-a_{n-1} + 1} \cdots S_1^{-a_1 + 1}$
on
$S = S_{n,m} S_{n-1}^{-a_{n-1} + 1} \cdots S_1^{-a_1 + 1}$
on
![]() $D_{n,m}$
. On
$D_{n,m}$
. On
![]() $\operatorname {\mathrm {dom}} (S_{n,m} ) = \bigsqcup _{i=0}^{a_{n-1} - 2} C_{n,m,i}$
, we have
$\operatorname {\mathrm {dom}} (S_{n,m} ) = \bigsqcup _{i=0}^{a_{n-1} - 2} C_{n,m,i}$
, we have
![]() $S_{n,m} x = T^{-k} x$
for some
$S_{n,m} x = T^{-k} x$
for some
![]() $0\leq k \leq d_{m-1}$
. On the other hand, for each
$0\leq k \leq d_{m-1}$
. On the other hand, for each
![]() $1\leq p \leq n-1$
, on
$1\leq p \leq n-1$
, on
![]() $\operatorname {\mathrm {dom}} (S_{p,m} )$
, we have
$\operatorname {\mathrm {dom}} (S_{p,m} )$
, we have
![]() $S_p^{-a_p + 1} = T^k$
for some
$S_p^{-a_p + 1} = T^k$
for some
![]() $0 \leq k \leq a_p d_{m-1}$
(using the bound
$0 \leq k \leq a_p d_{m-1}$
(using the bound
![]() $d_{m-1}$
on the spreads of the ladders
$d_{m-1}$
on the spreads of the ladders
![]() ${\mathscr L}_{p,m}^{(j)}$
). Therefore, on
${\mathscr L}_{p,m}^{(j)}$
). Therefore, on
![]() $D_{n,m}$
, we have
$D_{n,m}$
, we have
![]() $S = T^k$
for some non-zero k with
$S = T^k$
for some non-zero k with
![]() $-d_{m-1} \leq k \leq w_{n-1} d_{m-1}$
, and there are at most
$-d_{m-1} \leq k \leq w_{n-1} d_{m-1}$
, and there are at most
![]() $(1+w_{n-1} ) d_{m-1}$
possibilities for this k. Again using the fact that a uniform partition of a measurable set maximizes the entropy among all partitions of the set with a given cardinality, and writing
$(1+w_{n-1} ) d_{m-1}$
possibilities for this k. Again using the fact that a uniform partition of a measurable set maximizes the entropy among all partitions of the set with a given cardinality, and writing
![]() $\theta _{n,m} = (1+w_{n-1} ) d_{m-1}$
as before, it follows that
$\theta _{n,m} = (1+w_{n-1} ) d_{m-1}$
as before, it follows that
 $$ \begin{align*} H({\mathscr P}_{S|_{D_n} ,T} ) &\leq \sum_{m=n}^\infty H({\mathscr P}_{S|_{D_{n,m}} ,T} ) \\ &\leq \theta_{n,n} \bigg( -\frac{\mu (D_{n,n} )}{\theta_{n,n}} \log \frac{\mu (D_{n,n} )}{\theta_{n,n}} \bigg) \\&\quad + \theta_{n,n+1} \bigg( -\frac{\mu (D_{n,n+1} )}{\theta_{n,n+1}} \log \frac{\mu (D_{n,n+1} )}{\theta_{n,n+1}} \bigg) \\ &\quad + \sum_{m=n+2}^\infty \theta_{n,m} \bigg( -\frac{\mu (D_{n,m} )}{\theta_{n,m}} \log \frac{\mu (D_{n,m} )}{\theta_{n,m}} \bigg) \\ &\stackrel{({19})}{\leq} -\frac{1}{w_{n-1}} \log \bigg(\frac{1}{w_{n-1}} \cdot \frac{1}{\theta_{n,n}} \bigg) \\ &\quad - \frac{v_{n-1} + p_n w_{n-1}}{d_n} \log \bigg( \frac{v_{n-1} + p_n w_{n-1}}{d_n} \cdot \frac{1}{\theta_{n,n+1}} \bigg) \\ &\quad + \sum_{m=n+2}^\infty -\frac{v_n}{d_{m-1}} \log \bigg( \frac{v_n}{d_{m-1}} \cdot \frac{1}{\theta_{n,m}} \bigg) \\ &\stackrel{({11},{12},{13})}{\leq} \frac{1}{2^{n+2}} + \frac{1}{2^{n+2}} + \frac{1}{2^{n+1}} = \frac{1}{2^n}. \end{align*} $$
$$ \begin{align*} H({\mathscr P}_{S|_{D_n} ,T} ) &\leq \sum_{m=n}^\infty H({\mathscr P}_{S|_{D_{n,m}} ,T} ) \\ &\leq \theta_{n,n} \bigg( -\frac{\mu (D_{n,n} )}{\theta_{n,n}} \log \frac{\mu (D_{n,n} )}{\theta_{n,n}} \bigg) \\&\quad + \theta_{n,n+1} \bigg( -\frac{\mu (D_{n,n+1} )}{\theta_{n,n+1}} \log \frac{\mu (D_{n,n+1} )}{\theta_{n,n+1}} \bigg) \\ &\quad + \sum_{m=n+2}^\infty \theta_{n,m} \bigg( -\frac{\mu (D_{n,m} )}{\theta_{n,m}} \log \frac{\mu (D_{n,m} )}{\theta_{n,m}} \bigg) \\ &\stackrel{({19})}{\leq} -\frac{1}{w_{n-1}} \log \bigg(\frac{1}{w_{n-1}} \cdot \frac{1}{\theta_{n,n}} \bigg) \\ &\quad - \frac{v_{n-1} + p_n w_{n-1}}{d_n} \log \bigg( \frac{v_{n-1} + p_n w_{n-1}}{d_n} \cdot \frac{1}{\theta_{n,n+1}} \bigg) \\ &\quad + \sum_{m=n+2}^\infty -\frac{v_n}{d_{m-1}} \log \bigg( \frac{v_n}{d_{m-1}} \cdot \frac{1}{\theta_{n,m}} \bigg) \\ &\stackrel{({11},{12},{13})}{\leq} \frac{1}{2^{n+2}} + \frac{1}{2^{n+2}} + \frac{1}{2^{n+1}} = \frac{1}{2^n}. \end{align*} $$
We then have
 $$ \begin{align*} H({\mathscr P}_{S,T} ) \leq \sum_{n=1}^\infty H({\mathscr P}_{S|_{D_n} ,T} ) < H({\mathscr P}_{S|_{D_1} ,T} ) + \sum_{n=2}^\infty \frac{1}{2^n} < \infty. \\[-50pt]\end{align*} $$
$$ \begin{align*} H({\mathscr P}_{S,T} ) \leq \sum_{n=1}^\infty H({\mathscr P}_{S|_{D_n} ,T} ) < H({\mathscr P}_{S|_{D_1} ,T} ) + \sum_{n=2}^\infty \frac{1}{2^n} < \infty. \\[-50pt]\end{align*} $$
Remark 4.1. If one is permitted to use two different acting groups, then one can show much more easily that certain actions that are known not to be integrably orbit equivalent are, in fact, Shannon orbit equivalent. This phenomenon was observed in [Reference Delabie, Koivisto, Le Maître and Tessera6] in the context of measure equivalence for groups. Consider, for example, the odometer
![]() ${\mathbb Z}$
-action on
${\mathbb Z}$
-action on
![]() $\{ 0,1,2,3 \}^{\mathbb N}$
and the action of
$\{ 0,1,2,3 \}^{\mathbb N}$
and the action of
![]() ${\mathbb Z}^2$
on
${\mathbb Z}^2$
on
![]() $\{ 0,1 \}^{\mathbb N} \times \{ 0,1 \}^{\mathbb N} = (\{ 0,1 \} \times \{ 0,1 \} )^{\mathbb N}$
implemented on the canonical generators by
$\{ 0,1 \}^{\mathbb N} \times \{ 0,1 \}^{\mathbb N} = (\{ 0,1 \} \times \{ 0,1 \} )^{\mathbb N}$
implemented on the canonical generators by
![]() $T\times \mathrm {id}$
and
$T\times \mathrm {id}$
and
![]() $\mathrm {id}\times T$
, where T denotes the odometer transformation of
$\mathrm {id}\times T$
, where T denotes the odometer transformation of
![]() $\{ 0,1\}^{\mathbb N}$
. Let
$\{ 0,1\}^{\mathbb N}$
. Let
![]() $\sigma : \{ 0,1 \} \times \{ 0,1 \} \to \{0,1,2,3 \}$
be the bijection given by
$\sigma : \{ 0,1 \} \times \{ 0,1 \} \to \{0,1,2,3 \}$
be the bijection given by
![]() $0\mapsto (0,0)$
,
$0\mapsto (0,0)$
,
![]() $1\mapsto (0,1)$
,
$1\mapsto (0,1)$
,
![]() $2\mapsto (1,0)$
and
$2\mapsto (1,0)$
and
![]() $3\mapsto (1,1)$
, and define the homeomorphism
$3\mapsto (1,1)$
, and define the homeomorphism
![]() ${\Phi : (\{ 0,1 \} \times \{ 0,1 \} )^{\mathbb N} \to \{ 0,1,2,3 \}^{\mathbb N}}$
by
${\Phi : (\{ 0,1 \} \times \{ 0,1 \} )^{\mathbb N} \to \{ 0,1,2,3 \}^{\mathbb N}}$
by
![]() $(a_n , b_n )_n \mapsto (\sigma (a_n ,b_n ))_n$
. Then
$(a_n , b_n )_n \mapsto (\sigma (a_n ,b_n ))_n$
. Then
![]() $\Phi $
is an orbit equivalence, and the cocycle partition
$\Phi $
is an orbit equivalence, and the cocycle partition
![]() ${\mathscr P}$
associated to the generator of
${\mathscr P}$
associated to the generator of
![]() ${\mathbb Z}$
is a coarsening of the partition
${\mathbb Z}$
is a coarsening of the partition
![]() ${\mathscr Q}$
of
${\mathscr Q}$
of
![]() $\{ 0,1,2,3 \}^{\mathbb N}$
consisting of sets of the form
$\{ 0,1,2,3 \}^{\mathbb N}$
consisting of sets of the form
![]() $\prod _n A_n$
, where, for some N, one has
$\prod _n A_n$
, where, for some N, one has
![]() $A_n = \{ 3 \}$
for
$A_n = \{ 3 \}$
for
![]() $n=1,\ldots , N$
,
$n=1,\ldots , N$
,
![]() $A_{N+1} = \{ j \}$
for some
$A_{N+1} = \{ j \}$
for some
![]() $j\in \{ 0,1,2 \}$
and
$j\in \{ 0,1,2 \}$
and
![]() ${A_n = \{ 0,1,2,3 \}}$
for
${A_n = \{ 0,1,2,3 \}}$
for
![]() $n\geq N+2$
. The Shannon entropy of
$n\geq N+2$
. The Shannon entropy of
![]() ${\mathscr Q}$
is
${\mathscr Q}$
is
![]() ${\sum _{n=1}^\infty -3\cdot 4^{-n} \log 4^{-n} < \infty }$
, so that
${\sum _{n=1}^\infty -3\cdot 4^{-n} \log 4^{-n} < \infty }$
, so that
![]() ${\mathscr P}$
has finite Shannon entropy. The cocycle partitions associated to the canonical generators of
${\mathscr P}$
has finite Shannon entropy. The cocycle partitions associated to the canonical generators of
![]() ${\mathbb Z}^2$
can similarly be seen to have finite Shannon entropy, and so the two actions are Shannon orbit equivalent. On the other hand, a result of Bowen [Reference Austin2] shows that if two free p.m.p. actions of finite generated groups are integrably orbit equivalent, then the groups must have the same growth, which is not the case for
${\mathbb Z}^2$
can similarly be seen to have finite Shannon entropy, and so the two actions are Shannon orbit equivalent. On the other hand, a result of Bowen [Reference Austin2] shows that if two free p.m.p. actions of finite generated groups are integrably orbit equivalent, then the groups must have the same growth, which is not the case for
![]() ${\mathbb Z}$
and
${\mathbb Z}$
and
![]() ${\mathbb Z}^2$
.
${\mathbb Z}^2$
.
Acknowledgements
The first author was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy EXC 2044-390685587, Mathematics Münster: Dynamics–Geometry–Structure, and by the SFB 1442 of the DFG. The second author was supported by NSF grant DMS-1900746.