Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-27T12:24:51.305Z Has data issue: false hasContentIssue false
  • English
  • Français

Conditional intermediate entropy and Birkhoff average properties of hyperbolic flows

Part of: Dynamical systems with hyperbolic behavior Ergodic theory Smooth dynamical systems: general theory Topological dynamics

Published online by Cambridge University Press:  14 November 2023

XIAOBO HOU Open the ORCID record for XIAOBO HOU [Opens in a new window]  and
XUETING TIAN
XIAOBO HOU
Affiliation:
School of Mathematical Science, Fudan University, Shanghai 200433, PR China (e-mail: 20110180003@fudan.edu.cn)
XUETING TIAN*
Affiliation:
School of Mathematical Science, Fudan University, Shanghai 200433, PR China (e-mail: 20110180003@fudan.edu.cn)
*
e-mail: xuetingtian@fudan.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Katok [Lyapunov exponents, entropy and periodic points of diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173] conjectured that every 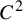$C^{2}$ diffeomorphism f on a Riemannian manifold has the intermediate entropy property, that is, for any constant 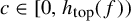$c \in [0, h_{\mathrm {top}}(f))$, there exists an ergodic measure 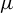$\mu $ of f satisfying 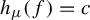$h_{\mu }(f)=c$. In this paper, we obtain a conditional intermediate metric entropy property and two conditional intermediate Birkhoff average properties for basic sets of flows that characterize the refined roles of ergodic measures in the invariant ones. In this process, we establish a ‘multi-horseshoe’ entropy-dense property and use it to get the goal combined with conditional variational principles. We also obtain the same result for singular hyperbolic attractors.

Keywords

hyperbolic setssingular hyperbolic attractormetric entropyhorseshoesymbolic dynamics

MSC classification

Primary: 37A25: Ergodicity, mixing, rates of mixing 37C10: Vector fields, flows, ordinary differential equations
Secondary: 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.) 37C70: Attractors and repellers, topological structure 37B10: Symbolic dynamics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 32
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramov, L. M.. On the entropy of a flow. Doklady Akademii Nauk SSSR 128 (1959), 873–875.Google Scholar
Araújo, V. and Pacifico, M. J.. Three-Dimensional Flows (A Series of Modern Surveys in Mathematics, 53). Springer-Verlag, Berlin, 2010.10.1007/978-3-642-11414-4CrossRefGoogle Scholar
Barreira, L. and Doutor, P.. Almost additive multi-fractal analysis. J. Math. Pures Appl. (9) 92 (2009), 1–17.10.1016/j.matpur.2009.04.006CrossRefGoogle Scholar
Barreira, L. and Holanda, C.. Equilibrium and Gibbs measures for flows. Pure Appl. Funct. Anal. 6 (2021), 37–56.Google Scholar
Barreira, L. and Holanda, C.. Almost additive multifractal analysis for flows. Nonlinearity 34 (2021), 4283–4314.10.1088/1361-6544/abf8f9CrossRefGoogle Scholar
Barreira, L. and Saussol, B.. Multifractal analysis of hyperbolic flows. Comm. Math. Phys. 214 (2000), 339–371.10.1007/s002200000268CrossRefGoogle Scholar
Bowen, R.. Periodic orbits for hyperbolic flows. Amer. J. Math. 94 (1972), 1–30.10.2307/2373590CrossRefGoogle Scholar
Bowen, R.. Symbolic dynamics for hyperbolic flows. Amer. J. Math. 95 (1973), 429–460.10.2307/2373793CrossRefGoogle Scholar
Bowen, R.. Some systems with unique equilibrium states. Math. Syst. Theory 8 ( 3 ) (1974/75), 193–202.10.1007/BF01762666CrossRefGoogle Scholar
Burguet, D.. Topological and almost Borel universality for systems with the weak specification property. Ergod. Th. & Dynam. Sys. 40 (2020), 2098–2115.10.1017/etds.2019.7CrossRefGoogle Scholar
Climenhaga, V., Topological pressure of simultaneous level sets. Nonlinearity. 26 ( 1 ) (2013), 241–268.10.1088/0951-7715/26/1/241CrossRefGoogle Scholar
Crovisier, S. and Yang, D., Robust transitivity of singular hyperbolic attractors. Math. Z. 298 (2021), 469–488.10.1007/s00209-020-02618-1CrossRefGoogle Scholar
Cuneo, N., Additive, almost additive and asymptotically additive potential sequences are equivalent. Commun. Math. Phys. 377 (2020), 2579–2595.10.1007/s00220-020-03780-7CrossRefGoogle Scholar
Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic Theory on the Compact Space (Lecture Notes in Mathematics, 527). Springer, Berlin, 2010.Google Scholar
Dong, Y., Hou, X. and Tian, X.. Multi-horseshoe dense property and intermediate entropy property of ergodic measures with same level. Preprint, 2022, arXiv:2207.02403.Google Scholar
Feng, D. and Huang, W.. Lyapunov spectrum of asymptotically sub-additive potentials. Commun. Math. Phys. 297(1) (2010), 1–43.10.1007/s00220-010-1031-xCrossRefGoogle Scholar
Guan, L., Sun, P. and Wu, W.. Measures of intermediate entropies and homogeneous dynamics. Nonlinearity 9 (2017), 3349–3361.10.1088/1361-6544/aa8040CrossRefGoogle Scholar
Guckenheimer, J.. A strange, strange attractor. The Hopf Bifurcation Theorems and its Applications (Applied Mathematical Series, 19). Eds. Marsden, J. E. and McCracken, M.. Springer-Verlag, Berlin, 1976, pp. 368–381.10.1007/978-1-4612-6374-6_25CrossRefGoogle Scholar
Guckenheimer, J. and Williams, R. F.. Structural stability of Lorenz attractors. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 59–72.10.1007/BF02684769CrossRefGoogle Scholar
Holanda, C.. Asymptotically additive families of functions and a physical equivalence problem for flows. Preprint, 2023, arXiv:2210.05926.Google Scholar
Huang, W., Xu, L. and Xu, S.. Ergodic measures of intermediate entropy for affine transformations of nilmanifolds. Electron. Res. Arch. 29 (2021), 2819–2827.10.3934/era.2021015CrossRefGoogle Scholar
Katok, A.. Lyapunov exponents, entropy and periodic points of diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.10.1007/BF02684777CrossRefGoogle Scholar
Konieczny, J., Kupsa, M. and Kwietniak, D.. Arcwise connectedness of the set of ergodic measures of hereditary shifts. Proc. Amer. Math. Soc. 146 (2018), 3425–3438.10.1090/proc/14029CrossRefGoogle Scholar
Li, J. and Oprocha, P.. Properties of invariant measures in dynamical systems with the shadowing property. Ergod. Th. & Dynam. Sys. 38 (2018), 2257–2294.10.1017/etds.2016.125CrossRefGoogle Scholar
Li, M., Gan, S. and Wen, L.. Robustly transitive singular sets via approach of extended linear Poincaré flow. Discrete Contin. Dyn. Syst. 13 (2005), 239–269.10.3934/dcds.2005.13.239CrossRefGoogle Scholar
Li, M., Shi, Y., Wang, S. and Wang, X.. Measures of intermediate entropies for star vector fields. Israel J. Math. 240 (2020), 791–819.10.1007/s11856-020-2080-2CrossRefGoogle Scholar
Lin, W. and Tian, X.. Ergodic optimization restricted on certain subsets of invariant measures. J. Math. Anal. Appl. 530 (2024), 127709.10.1016/j.jmaa.2023.127709CrossRefGoogle Scholar
Metzger, R. and Morales, C. A.. On sectional-hyperbolic systems. Ergod. Th. & Dynam. Sys. 28 (2008), 1587–1597.10.1017/S0143385707000995CrossRefGoogle Scholar
Morales, C. A., Pacifico, M. J. and Pujals, E.. Robust transitive singular sets for 3-flows are partially hyperbolic attractors or repellers. Ann. of Math. (2) 160 (2004), 1–58.Google Scholar
Pacifico, M. J., Yang, F. and Yang, J.. Entropy theory for sectional hyperbolic flows. Ann. Inst. H. Poincaré Anal. Non Linéaire 38 (2021), 1001–1030.10.1016/j.anihpc.2020.10.001CrossRefGoogle Scholar
Parry, W. and Pollicott, M.. Zeta Functions and the Periodic Orbit Structure of Hyperbolic Dynamics (Asteŕisque, 187–188). Société Mathématique de France, France, 1990.Google Scholar
Quas, A. and Soo, T.. Ergodic universality of some topological dynamical systems. Trans. Amer. Math. Soc. 368 (2016), 4137–4170.10.1090/tran/6489CrossRefGoogle Scholar
Shi, Y., Tian, X., Varandas, P. and Wang, X.. On multifractal analysis and large deviations of singular-hyperbolic attractors. Nonlinearity. 36 (2023), 5216–5251.10.1088/1361-6544/ace491CrossRefGoogle Scholar
Shi, Y., Tian, X. and Wang, X.. The space of ergodic measures for Lorenz attractors. Preprint, 2022, arXiv:2006.08193.Google Scholar
Sun, P.. Ergodic measures of intermediate entropies for dynamical systems with approximate product property. Preprint, 2022, arXiv:1906.09862.Google Scholar
Tian, X., Wang, S. and Wang, X.. Intermediate Lyapunov exponents for systems with periodic orbit gluing property. Discrete Contin. Dyn. Syst. 39(2) (2019), 1019–1032.10.3934/dcds.2019042CrossRefGoogle Scholar
Ures, R.. Intrinsic ergodicity of partially hyperbolic diffeomorphisms with a hyperbolic linear part. Proc. Amer. Math. Soc. 140 (2012), 1973–1985.10.1090/S0002-9939-2011-11040-2CrossRefGoogle Scholar
Walters, P.. On the pseudo-orbit tracing property and its relationship to stability. The Structure of Attractors in Dynamical Systems (Fargo, ND, 1977) (Lecture notes in mathematics, 668). Eds. Markley, N. G., Martin, J. C. and Perrizo, W.. Springer, Berlin, 1978, 231–244.10.1007/BFb0101795CrossRefGoogle Scholar
Williams, R. F.. The structure of Lorenz attractors. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 73–99.10.1007/BF02684770CrossRefGoogle Scholar