Article contents
Continuity of Hausdorff dimension across generic dynamical Lagrange and Markov spectra II
Published online by Cambridge University Press: 22 April 2021
Abstract
Let
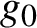 $g_0$
be a smooth pinched negatively curved Riemannian metric on a complete surface N, and let
$g_0$
be a smooth pinched negatively curved Riemannian metric on a complete surface N, and let
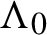 $\Lambda _0$
be a basic hyperbolic set of the geodesic flow of
$\Lambda _0$
be a basic hyperbolic set of the geodesic flow of
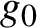 $g_0$
with Hausdorff dimension strictly smaller than two. Given a small smooth perturbation g of
$g_0$
with Hausdorff dimension strictly smaller than two. Given a small smooth perturbation g of
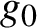 $g_0$
and a smooth real-valued function f on the unit tangent bundle to N with respect to g, let
$g_0$
and a smooth real-valued function f on the unit tangent bundle to N with respect to g, let
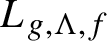 $L_{g,\Lambda ,f}$
(respectively
$L_{g,\Lambda ,f}$
(respectively
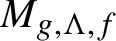 $M_{g,\Lambda ,f}$
) be the Lagrange (respectively Markov) spectrum of asymptotic highest (respectively highest) values of f along the geodesics in the hyperbolic continuation
$M_{g,\Lambda ,f}$
) be the Lagrange (respectively Markov) spectrum of asymptotic highest (respectively highest) values of f along the geodesics in the hyperbolic continuation
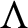 $\Lambda $
of
$\Lambda $
of
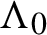 $\Lambda _0$
. We prove that for generic choices of g and f, the Hausdorff dimensions of the sets
$\Lambda _0$
. We prove that for generic choices of g and f, the Hausdorff dimensions of the sets
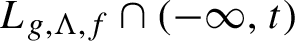 $L_{g,\Lambda , f}\cap (-\infty , t)$
vary continuously with
$L_{g,\Lambda , f}\cap (-\infty , t)$
vary continuously with
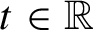 $t\in \mathbb {R}$
and, moreover,
$t\in \mathbb {R}$
and, moreover,
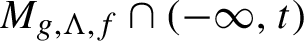 $M_{g,\Lambda , f}\cap (-\infty , t)$
has the same Hausdorff dimension as
$M_{g,\Lambda , f}\cap (-\infty , t)$
has the same Hausdorff dimension as
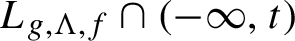 $L_{g,\Lambda , f}\cap (-\infty , t)$
for all
$L_{g,\Lambda , f}\cap (-\infty , t)$
for all
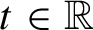 $t\in \mathbb {R}$
.
$t\in \mathbb {R}$
.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 2
- Cited by





