Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-25T21:18:32.470Z Has data issue: false hasContentIssue false
  • English
  • Français

Weil–Châtelet divisible elements in Tate–Shafarevich groups I: The Bashmakov problem for elliptic curves over $ \mathbb{Q} $

Part of: Arithmetic algebraic geometry

Published online by Cambridge University Press:  26 February 2013

Mirela Çiperiani  and
Jakob Stix
Mirela Çiperiani
Affiliation:
Department of Mathematics, The University of Texas at Austin, 1 University Station, C1200 Austin, Texas 78712, USA email mirela@math.utexas.edu
Jakob Stix
Affiliation:
Mathematisches Institut, Universität Heidelberg, Im Neuenheimer Feld 288, 69120 Heidelberg, Germany email stix@mathi.uni-heidelberg.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For an abelian variety 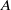$A$ over a number field 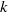$k$ we discuss the maximal divisible subgroup of 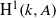${\mathrm{H} }^{1} (k, A)$ and its intersection with the subgroup Ш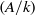$(A/ k)$. The results are most complete for elliptic curves over 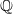$ \mathbb{Q} $.

Keywords

elliptic curveabelian varietySelmer groupWeil–Châtelet groupTate–Shafarevich group

MSC classification

Secondary: 11G05: Elliptic curves over global fields 11G10: Abelian varieties of dimension $> 1$
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 5 , May 2013 , pp. 729 - 753
Copyright
© The Author(s) 2013 

References

Anderson, G. and Ihara, Y., Pro-$\ell $ branched coverings of ${ \mathbb{P} }^{1} $ and higher circular $\ell $-units, Ann. of Math. (2) 128 (1988), 271–293.Google Scholar
Bashmakov, M. I., On the divisibility of principal homogeneous spaces over Abelian varieties, Izv. Akad. Nauk SSSR Ser. Mat. 28 (1964), 661–664.Google Scholar
Bashmakov, M. I., The cohomology of abelian varieties over a number field, Russian Math. Surveys 27 (1972), 25–70 (English translation).Google Scholar
Cassels, J. W. S., Arithmetic on curves of genus 1. III. The Tate–Shafarevich and Selmer groups, Proc. Lond. Math. Soc. (3) 12 (1962), 259–296.Google Scholar
Cassels, J. W. S., Lectures on elliptic curves, London Mathematical Society Student Texts, vol. 24 (Cambridge University Press, Cambridge, 1991).Google Scholar
Çiperiani, M. and Stix, J., Weil–Châtelet divisible elements in Tate–Shafarevich groups II: on a question of Cassels, Preprint (2012).Google Scholar
Çiperiani, M. and Wiles, A., Solvable points on genus one curves, Duke Math. J. 142 (2008), 381–464.Google Scholar
Friedberg, S. and Hoffstein, J., Nonvanishing theorems for automorphic $L$-functions on $\mathrm{GL} (2)$, Ann. of Math. (2) 142 (1995), 385–423.Google Scholar
Harari, D. and Szamuely, T., Galois sections for abelianized fundamental groups, with an Appendix by E. V. Flynn, Math. Ann. 344 (2009), 779–800.Google Scholar
Jannsen, U., Continuous étale cohomology, Math. Ann. 280 (1988), 207–245.Google Scholar
Jones, N., Almost all elliptic curves are Serre curves, Trans. Amer. Math. Soc. 362 (2010), 1547–1570.Google Scholar
Kolyvagin, V. A., Euler systems, in The Grothendieck Festschrift, vol. II, Progress in Mathematics, vol. 87 (Birkhauser Boston, Boston, MA, 1990), 435–483.Google Scholar
Mazur, B., Modular curves and the Eisenstein ideal, Publ. Math. Inst. Hautes Études Sci. 47 (1978), 33–186.CrossRefGoogle Scholar
Mazur, B., On the passage from local to global in number theory, Bull. Amer. Math. Soc. 29 (1993), 14–50.Google Scholar
Milne, J. S., Arithmetic duality theorems, Perspectives in Mathematics, vol. 1 (Academic Press, Inc, Boston, MA, 1986).Google Scholar
Neumann, O., $p$-closed algebraic number fields with bounded ramification, Izv. Akad. Nauk SSSR Ser. Mat. 39 (1975), 259–271, 471.Google Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of number fields, Grundlehren der Mathematischen Wissenschaften, vol. 323, second edition (Springer, 2008).Google Scholar
Poonen, B. and Stoll, M., The Cassels-Tate pairing on polarized abelian varieties, Ann. of Math. (2) 150 (1999), 1109–1149.CrossRefGoogle Scholar
Ribet, K., Images of semistable Galois representations, Pacific J. Math. 181 (1997), 277–297.Google Scholar
Serre, J.-P., Propriétés Galoisiennes des points d’ordre fini des courbes elliptiques, Invent. Math. 15 (1972), 259–331.CrossRefGoogle Scholar
Serre, J.-P., Points rationnels des courbes modulaires ${X}_{0} (N)$ [d’après Barry Mazur], in Séminaire Bourbaki (1977/78), exposé 511, Lecture Notes in Mathematics, vol. 710 (Springer, Berlin, 1979), 89–100.Google Scholar
Shafarevich, I. R., Extensions with given ramification points (in Russian), Publ. Math. Inst. Hautes Études Sci. 18 (1963), 71–95; translated in Amer. Math. Soc. Transl. 59 (1966), 128–149.Google Scholar
Stix, J., The Brauer–Manin obstruction for sections of the fundamental group, J. Pure Appl. Algebra 215 (2011), 1371–1397.Google Scholar
Stix, J., Rational points and arithmetic of fundamental groups: evidence for the section conjecture, Springer Lecture Notes in Mathematics, vol. 2054 (Springer, 2013).Google Scholar
Zink, Th., Étale cohomology and duality in number fields, Appendix 2 in Haberland, K., Galois cohomology of algebraic number fields (VEB Deutscher Verlag der Wissenschaften, 1978).Google Scholar
Zywina, D., Elliptic curves with maximal Galois action on their torsion points, Bull. Lond. Math. Soc. 42 (2010), 811–826.Google Scholar