No CrossRef data available.
Article contents
There are at most finitely many singular moduli that are S-units
Part of:
Arithmetic algebraic geometry
Arithmetic and non-Archimedean dynamical systems
Diophantine approximation, transcendental number theory
Discontinuous groups and automorphic forms
Published online by Cambridge University Press: 05 March 2024
Abstract
We show that for every finite set of prime numbers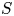 
$S$, there are at most finitely many singular moduli that are 
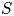$S$-units. The key new ingredient is that for every prime number 
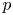$p$, singular moduli are 
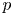$p$-adically disperse. We prove analogous results for the Weber modular functions, the 
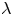$\lambda$-invariants and the McKay–Thompson series associated with the elements of the monster group. Finally, we also obtain that a modular function that specializes to infinitely many algebraic units at quadratic imaginary numbers must be a weak modular unit.
- Type
- Research Article
- Information
- Copyright
- © 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
Bilu, Y., Habegger, P. and Kühne, L., No singular modulus is a unit, Int. Math. Res. Not. IMRN 2020 (2020), 10005–10041.10.1093/imrn/rny274CrossRefGoogle Scholar
Bombieri, E. and Gubler, W., Heights in Diophantine geometry, New Mathematical Monographs, vol. 4 (Cambridge University Press, Cambridge, 2006).Google Scholar
Borcherds, R. E., Monstrous moonshine and monstrous Lie superalgebras, Invent. Math. 109 (1992), 405–444.10.1007/BF01232032CrossRefGoogle Scholar
Campagna, F., On singular moduli that are 
$S$-units, Manuscripta Math. 166 (2021), 73–90.10.1007/s00229-020-01230-1CrossRefGoogle Scholar
$S$-units, Manuscripta Math. 166 (2021), 73–90.10.1007/s00229-020-01230-1CrossRefGoogle ScholarCharles, F., Exceptional isogenies between reductions of pairs of elliptic curves, Duke Math. J. 167 (2018), 2039–2072.10.1215/00127094-2018-0011CrossRefGoogle Scholar
Chen, I. and Yui, N., Singular values of Thompson series, in Groups, difference sets, and the Monster (Columbus, OH, 1993), Ohio State University Mathematical Research Institute Publications, vol. 4 (de Gruyter, Berlin, 1996), 255–326.10.1515/9783110893106.255CrossRefGoogle Scholar
Clozel, L. and Ullmo, E., Équidistribution des points de Hecke, in Contributions to automorphic forms, geometry, and number theory (Johns Hopkins University Press, Baltimore, MD, 2004), 193–254.Google Scholar
Coleman, R. and McMurdy, K., Fake CM and the stable model of $X_0(Np^3)$, Doc. Math. Extra Vol. (2006), 261–300.Google Scholar
$X_0(Np^3)$, Doc. Math. Extra Vol. (2006), 261–300.Google ScholarColmez, P., Sur la hauteur de Faltings des variétés abéliennes à multiplication complexe, Compos. Math. 111 (1998), 359–368.10.1023/A:1000390105495CrossRefGoogle Scholar
Conway, J. H. and Norton, S. P., Monstrous moonshine, Bull. Lond. Math. Soc. 11 (1979), 308–339.10.1112/blms/11.3.308CrossRefGoogle Scholar
David, S. and Hirata-Kohno, N., Linear forms in elliptic logarithms, J. Reine Angew. Math. 628 (2009), 37–89.Google Scholar
Diamond, F. and Im, J., Modular forms and modular curves, in Seminar on Fermat's Last Theorem (Toronto, ON, 1993–1994), CMS Conference Proceedings, vol. 17 (American Mathematical Society, Providence, RI, 1995), 39–133.Google Scholar
Drinfel'd, V. G., Two theorems on modular curves, Funkcional. Anal. i Priložen. 7 (1973), 83–84.Google Scholar
Duke, W., Hyperbolic distribution problems and half-integral weight Maass forms, Invent. Math. 92 (1988), 73–90.10.1007/BF01393993CrossRefGoogle Scholar
Enge, A. and Sutherland, A. V., Class invariants by the CRT method, in Algorithmic number theory, Lecture Notes in Computer Science, vol. 6197 (Springer, Berlin, 2010), 142–156.10.1007/978-3-642-14518-6_14CrossRefGoogle Scholar
Fröhlich, A., Formal groups, Lecture Notes in Mathematics, vol. 74 (Springer, Berlin–New York, 1968).10.1007/BFb0074373CrossRefGoogle Scholar
Gross, B. H., On canonical and quasicanonical liftings, Invent. Math. 84 (1986), 321–326.10.1007/BF01388810CrossRefGoogle Scholar
Gross, B. H. and Zagier, D. B., On singular moduli, J. Reine Angew. Math. 355 (1985), 191–220.Google Scholar
Habegger, P., Singular moduli that are algebraic units, Algebra Number Theory 9 (2015), 1515–1524.10.2140/ant.2015.9.1515CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York–Heidelberg, 1977).10.1007/978-1-4757-3849-0CrossRefGoogle Scholar
Herrero, S., Menares, R. and Rivera-Letelier, J., $p$-adic distribution of CM points and Hecke orbits I: Convergence towards the Gauss point, Algebra Number Theory 14 (2020), 1239–1290.10.2140/ant.2020.14.1239CrossRefGoogle Scholar
$p$-adic distribution of CM points and Hecke orbits I: Convergence towards the Gauss point, Algebra Number Theory 14 (2020), 1239–1290.10.2140/ant.2020.14.1239CrossRefGoogle ScholarHerrero, S., Menares, R. and Rivera-Letelier, J., $p$-Adic distribution of CM points and Hecke orbits. II: Linnik equidistribution on the supersingular locus, Preprint (2021), arXiv:2102.04865.Google Scholar
$p$-Adic distribution of CM points and Hecke orbits. II: Linnik equidistribution on the supersingular locus, Preprint (2021), arXiv:2102.04865.Google ScholarHopkins, M. J. and Gross, B. H., Equivariant vector bundles on the Lubin-Tate moduli space, in Topology and representation theory (Evanston, IL, 1992), Contemporary Mathematics, vol. 158 (American Mathematical Society, Providence, RI, 1994), 23–88.10.1090/conm/158/01453CrossRefGoogle Scholar
Katz, N. M., p-adic properties of modular schemes and modular forms, Lecture Notes in Mathematics, vol. 350 (Springer, Berlin--New York, 1973), 69–190.Google Scholar
Kubert, D. S. and Lang, S., Modular units, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 244 (Springer, New York–Berlin, 1981).10.1007/978-1-4757-1741-9CrossRefGoogle Scholar
Lang, S., Elliptic functions, second edition, Graduate Texts in Mathematics, vol. 112 (Springer, New York, 1987), with an appendix by J. Tate.10.1007/978-1-4612-4752-4CrossRefGoogle Scholar
Li, Y., Singular units and isogenies between CM elliptic curves, Compos. Math. 157 (2021), 1022–1035.10.1112/S0010437X21007077CrossRefGoogle Scholar
Lubin, J., Serre, J.-P. and Tate, J., Elliptic curves and formal groups, in Seminar at Woods Hole Institute on algebraic geometry (1964), https://web.ma.utexas.edu/users/voloch/LST/lst.pdf.Google Scholar
McMurdy, K. and Coleman, R., Stable reduction of $X_0(p^3)$, Algebra Number Theory 4 (2010), 357–431, with an appendix by Everett W. Howe.10.2140/ant.2010.4.357CrossRefGoogle Scholar
$X_0(p^3)$, Algebra Number Theory 4 (2010), 357–431, with an appendix by Everett W. Howe.10.2140/ant.2010.4.357CrossRefGoogle ScholarSchertz, R., Die singulären Werte der Weberschen Funktionen $\mathfrak {f}$, $\mathfrak {f}_{1}$, $\mathfrak {f}_{2}$, $\gamma _{2}$, $\gamma _{3}$, J. Reine Angew. Math. 286 (1976), 46–74.Google Scholar
$\mathfrak {f}$, 
$\mathfrak {f}_{1}$, 
$\mathfrak {f}_{2}$, 
$\gamma _{2}$, 
$\gamma _{3}$, J. Reine Angew. Math. 286 (1976), 46–74.Google ScholarShimura, G., Introduction to the arithmetic theory of automorphic functions (Kanô Memorial Lectures, vol. 1), Publications of the Mathematical Society of Japan, vol. 11 (Princeton University Press, Princeton, NJ; Iwanami Shoten, Tokyo, 1971).Google Scholar
Siegel, C., Über die Classenzahl quadratischer Zahlkörper, Acta Arith. 1 (1935), 83–86.10.4064/aa-1-1-83-86CrossRefGoogle Scholar
Silverman, J. H., The arithmetic of elliptic curves, second edition, Graduate Texts in Mathematics, vol. 106 (Springer, Dordrecht, 2009).10.1007/978-0-387-09494-6CrossRefGoogle Scholar
Sutherland, A., Norms of singular moduli for $|D| \le 2000$, https://math.mit.edu/~drew/NormsOfSingularModuli2000.pdf.Google Scholar
$|D| \le 2000$, https://math.mit.edu/~drew/NormsOfSingularModuli2000.pdf.Google ScholarYang, T. and Yin, H., Some non-congruence subgroups and the associated modular curves, J. Number Theory 161 (2016), 17–48.10.1016/j.jnt.2015.04.002CrossRefGoogle Scholar
Yang, T., Yin, H. and Yu, P., The lambda invariants at CM points, Int. Math. Res. Not. IMRN 2021 (2021), 5542–5603.10.1093/imrn/rnz230CrossRefGoogle Scholar
Yui, N. and Zagier, D., On the singular values of Weber modular functions, Math. Comp. 66 (1997), 1645–1662.10.1090/S0025-5718-97-00854-5CrossRefGoogle Scholar