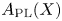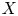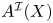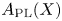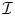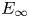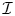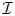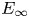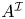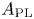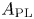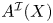1. Introduction
Determining the homotopy type of a topological space is a difficult task in general. One possibility of simplifying the problem is to aim for algebraic models of spaces, so that the study of homotopy types reduces to an algebraic question. If one is interested in the homotopy type of a rational nilpotent space of finite type, then this is possible, and the Sullivan cochain algebra is such an algebraic model: the algebra of rational singular cochains of a space, ![]() $C(X;\mathbb {Q})$, is quasi-isomorphic to the commutative differential graded algebra (cdga)
$C(X;\mathbb {Q})$, is quasi-isomorphic to the commutative differential graded algebra (cdga) ![]() $A_{\mathrm {PL}}(X)$ of polynomial forms on
$A_{\mathrm {PL}}(X)$ of polynomial forms on ![]() $X$, which is a very powerful tool in rational homotopy theory [Reference Bousfield and GugenheimBG76, Reference SullivanSul77]. The functor
$X$, which is a very powerful tool in rational homotopy theory [Reference Bousfield and GugenheimBG76, Reference SullivanSul77]. The functor ![]() $A_{\mathrm {PL}}$ has a contravariant adjoint, called the Sullivan realization in [Reference Félix, Halperin and ThomasFHT01, § 17]. With the help of this adjoint pair of functors one can determine the homotopy type of rational nilpotent spaces of finite type (see [Reference Bousfield and GugenheimBG76, Chapter 9], or [Reference HessHes07, Theorem 1.25] for the simply connected case).
$A_{\mathrm {PL}}$ has a contravariant adjoint, called the Sullivan realization in [Reference Félix, Halperin and ThomasFHT01, § 17]. With the help of this adjoint pair of functors one can determine the homotopy type of rational nilpotent spaces of finite type (see [Reference Bousfield and GugenheimBG76, Chapter 9], or [Reference HessHes07, Theorem 1.25] for the simply connected case).
For a general commutative ring ![]() $k$ the cochains
$k$ the cochains ![]() $C(X;k)$ on a space
$C(X;k)$ on a space ![]() $X$ with values in
$X$ with values in ![]() $k$ form a differential graded algebra whose cohomology is the singular cohomology
$k$ form a differential graded algebra whose cohomology is the singular cohomology ![]() $H^{*}(X;k)$ of
$H^{*}(X;k)$ of ![]() $X$. The multiplication of
$X$. The multiplication of ![]() $C(X;k)$ induces the cup product on
$C(X;k)$ induces the cup product on ![]() $H^{*}(X;k)$. However, for general
$H^{*}(X;k)$. However, for general ![]() $k$, there is no cdga which is quasi-isomorphic to
$k$, there is no cdga which is quasi-isomorphic to ![]() $C(X;k)$, for example because the Steenrod operations witness the non-commutativity of
$C(X;k)$, for example because the Steenrod operations witness the non-commutativity of ![]() $C(X;\mathbb {F}_p)$. So it seems that we cannot hope for a strictly commutative model for the cochains of a space that determines the homotopy type. However,
$C(X;\mathbb {F}_p)$. So it seems that we cannot hope for a strictly commutative model for the cochains of a space that determines the homotopy type. However, ![]() $C(X;k)$ is always commutative up to coherent homotopy. This can be encoded using the language of operads [Reference MayMay72]: the multiplication of
$C(X;k)$ is always commutative up to coherent homotopy. This can be encoded using the language of operads [Reference MayMay72]: the multiplication of ![]() $C(X;k)$ extends to the action of an
$C(X;k)$ extends to the action of an ![]() $E_{\infty }$ operad in chain complexes turning
$E_{\infty }$ operad in chain complexes turning ![]() $C(X;k)$ into an
$C(X;k)$ into an ![]() $E_{\infty }$ dga.
$E_{\infty }$ dga.
This gives rise to an algebraic model for the homotopy type of a space by a result of Mandell. He shows that the cochain functor ![]() $C(-;\mathbb {Z})$ to
$C(-;\mathbb {Z})$ to ![]() $E_{\infty }$ dgas classifies nilpotent spaces of finite type up to weak equivalence [Reference MandellMan06, Main Theorem]. But here, the algebraic model consists of the cochain algebra together with its
$E_{\infty }$ dgas classifies nilpotent spaces of finite type up to weak equivalence [Reference MandellMan06, Main Theorem]. But here, the algebraic model consists of the cochain algebra together with its ![]() $E_\infty$-algebra structure, so this algebraic model is rather involved.
$E_\infty$-algebra structure, so this algebraic model is rather involved.
One can describe homotopy coherent commutative multiplications on chain complexes using diagram categories instead of operads. Let ![]() $\mathcal {I}$ be the category with objects the finite sets
$\mathcal {I}$ be the category with objects the finite sets ![]() ${\mathbf {m}}= \{1\,\ldots , m\}, m\geq 0$, with the convention that
${\mathbf {m}}= \{1\,\ldots , m\}, m\geq 0$, with the convention that ![]() ${\mathbf {0}}$ is the empty set. Morphisms in
${\mathbf {0}}$ is the empty set. Morphisms in ![]() $\mathcal {I}$ are the injections. Concatenation in
$\mathcal {I}$ are the injections. Concatenation in ![]() $\mathcal {I}$ and the tensor product of chain complexes of
$\mathcal {I}$ and the tensor product of chain complexes of ![]() $k$-modules give rise to a symmetric monoidal product
$k$-modules give rise to a symmetric monoidal product ![]() $\boxtimes$ on the category
$\boxtimes$ on the category ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ of
$\mathrm {Ch}^{\mathcal {I}}_k$ of ![]() $\mathcal {I}$-diagrams in
$\mathcal {I}$-diagrams in ![]() $\mathrm {Ch}_k$. A commutative
$\mathrm {Ch}_k$. A commutative ![]() $\mathcal {I}$-dga is a commutative monoid in
$\mathcal {I}$-dga is a commutative monoid in ![]() $(\mathrm {Ch}^{\mathcal {I}}_k,\boxtimes )$ or, equivalently, a lax symmetric monoidal functor
$(\mathrm {Ch}^{\mathcal {I}}_k,\boxtimes )$ or, equivalently, a lax symmetric monoidal functor ![]() $\mathcal {I} \to \mathrm {Ch}_k$. Equipped with suitable model structures, the category of commutative
$\mathcal {I} \to \mathrm {Ch}_k$. Equipped with suitable model structures, the category of commutative ![]() $\mathcal {I}$-dgas,
$\mathcal {I}$-dgas, ![]() $\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$, is Quillen equivalent to the category of
$\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$, is Quillen equivalent to the category of ![]() $E_{\infty }$ dgas [Reference Richter and ShipleyRS17, § 9]. This is analogous to the situation in spaces, where commutative monoids in
$E_{\infty }$ dgas [Reference Richter and ShipleyRS17, § 9]. This is analogous to the situation in spaces, where commutative monoids in ![]() $\mathcal {I}$-diagrams of spaces are equivalent to
$\mathcal {I}$-diagrams of spaces are equivalent to ![]() $E_{\infty }$ spaces [Reference Sagave and SchlichtkrullSS12, § 3].
$E_{\infty }$ spaces [Reference Sagave and SchlichtkrullSS12, § 3].
Chasing the ![]() $E_{\infty }$ dga of cochains
$E_{\infty }$ dga of cochains ![]() $C(X;k)$ on a space
$C(X;k)$ on a space ![]() $X$ through the chain of Quillen equivalences relating
$X$ through the chain of Quillen equivalences relating ![]() $E_{\infty }$ dgas and commutative
$E_{\infty }$ dgas and commutative ![]() $\mathcal {I}$-dgas shows that
$\mathcal {I}$-dgas shows that ![]() $C(X;k)$ can be represented by a commutative
$C(X;k)$ can be represented by a commutative ![]() $\mathcal {I}$-dga. The purpose of this paper is to construct a direct point-set level model
$\mathcal {I}$-dga. The purpose of this paper is to construct a direct point-set level model ![]() $A^{\mathcal {I}}(X)$ for the quasi-isomorphism type of commutative
$A^{\mathcal {I}}(X)$ for the quasi-isomorphism type of commutative ![]() $\mathcal {I}$-dgas determined by
$\mathcal {I}$-dgas determined by ![]() $C(X;k)$ that should be viewed as an integral generalization of
$C(X;k)$ that should be viewed as an integral generalization of ![]() $A_{\mathrm {PL}}(X)$. Despite the fact that
$A_{\mathrm {PL}}(X)$. Despite the fact that ![]() $A_{\mathrm {PL}}(X)$ was introduced more than 40 years ago and has been widely studied, it appears that a direct integral counterpart was neither known nor expected to exist.
$A_{\mathrm {PL}}(X)$ was introduced more than 40 years ago and has been widely studied, it appears that a direct integral counterpart was neither known nor expected to exist.
If ![]() $E$ is a commutative
$E$ is a commutative ![]() $\mathcal {I}$-dga, then its Bousfield–Kan homotopy colimit
$\mathcal {I}$-dga, then its Bousfield–Kan homotopy colimit ![]() $E_{h\mathcal {I}}$ has a canonical action of the Barratt–Eccles operad, which is an
$E_{h\mathcal {I}}$ has a canonical action of the Barratt–Eccles operad, which is an ![]() $E_{\infty }$ operad built from the symmetric groups. The commutative
$E_{\infty }$ operad built from the symmetric groups. The commutative ![]() $\mathcal {I}$-dga
$\mathcal {I}$-dga ![]() $A^{\mathcal {I}}(X)$ thus gives rise to an
$A^{\mathcal {I}}(X)$ thus gives rise to an ![]() $E_{\infty }$ dga
$E_{\infty }$ dga ![]() $A^{\mathcal {I}}(X)_{h\mathcal {I}}$ which can be compared to the usual cochains without referring to model structures.
$A^{\mathcal {I}}(X)_{h\mathcal {I}}$ which can be compared to the usual cochains without referring to model structures.
Theorem 1.1 The contravariant functors ![]() $X \mapsto A^{\mathcal {I}}(X)_{h\mathcal {I}}$ and
$X \mapsto A^{\mathcal {I}}(X)_{h\mathcal {I}}$ and ![]() $X \mapsto C(X;k)$ from simplicial sets to
$X \mapsto C(X;k)$ from simplicial sets to ![]() $E_{\infty }$ dgas are naturally quasi-isomorphic.
$E_{\infty }$ dgas are naturally quasi-isomorphic.
We prove the theorem using Mandell's uniqueness result for cochain theories [Reference MandellMan02, Main Theorem].
Since our definition of ![]() $A^{\mathcal {I}}$ does not rely on the existing constructions of
$A^{\mathcal {I}}$ does not rely on the existing constructions of ![]() $E_{\infty }$ structures on cochains, the theorem implies that our approach provides an alternative model of the
$E_{\infty }$ structures on cochains, the theorem implies that our approach provides an alternative model of the ![]() $E_{\infty }$ dga
$E_{\infty }$ dga ![]() $C(X;k)$, namely
$C(X;k)$, namely ![]() $A^{\mathcal {I}}(X)_{h\mathcal {I}}$ with its canonical action of the Barratt-Eccles operad. If
$A^{\mathcal {I}}(X)_{h\mathcal {I}}$ with its canonical action of the Barratt-Eccles operad. If ![]() $k$ is a field of characteristic
$k$ is a field of characteristic ![]() $0$, then there is a natural quasi-isomorphism
$0$, then there is a natural quasi-isomorphism ![]() $A^{\mathcal {I}}(X)_{h\mathcal {I}} \to A_{\mathrm {PL}}(X)$ relating our approach to the classical polynomial forms (see Theorem 5.9).
$A^{\mathcal {I}}(X)_{h\mathcal {I}} \to A_{\mathrm {PL}}(X)$ relating our approach to the classical polynomial forms (see Theorem 5.9).
The passage through commutative ![]() $\mathcal {I}$-dgas has the advantage that it provides a rather simple
$\mathcal {I}$-dgas has the advantage that it provides a rather simple ![]() $E_{\infty }$ model
$E_{\infty }$ model ![]() $A^{\mathcal {I}}(X)_{h\mathcal {I}}$ for the cochain algebra of a space
$A^{\mathcal {I}}(X)_{h\mathcal {I}}$ for the cochain algebra of a space ![]() $X$. In contrast, the existing constructions of
$X$. In contrast, the existing constructions of ![]() $E_{\infty }$ structures on the standard model for the cochain algebra are involved: based on work of Hinich and Schechtman [Reference Hinich and SchechtmanHS87], Mandell [Reference MandellMan02, § 5] lifts the action of the acyclic Eilenberg–Zilber operad to the action of an actual
$E_{\infty }$ structures on the standard model for the cochain algebra are involved: based on work of Hinich and Schechtman [Reference Hinich and SchechtmanHS87], Mandell [Reference MandellMan02, § 5] lifts the action of the acyclic Eilenberg–Zilber operad to the action of an actual ![]() $E_{\infty }$ operad. McClure and Smith generalize Steenrod's cup-
$E_{\infty }$ operad. McClure and Smith generalize Steenrod's cup-![]() $i$-products to multivariable operations that give the cochains of a space the structure of an
$i$-products to multivariable operations that give the cochains of a space the structure of an ![]() $E_\infty$-algebra via the action of the surjection operad [Reference McClure and SmithMS03]. Berger and Fresse [Reference Berger and FresseBF04] use elaborate combinatorial arguments to define an action of the Barratt–Eccles operad that extends the action of the surjection operad. Another approach to capture the commutativity of
$E_\infty$-algebra via the action of the surjection operad [Reference McClure and SmithMS03]. Berger and Fresse [Reference Berger and FresseBF04] use elaborate combinatorial arguments to define an action of the Barratt–Eccles operad that extends the action of the surjection operad. Another approach to capture the commutativity of ![]() $C(X;k)$ has been pursued by Karoubi [Reference KaroubiKar09] who introduces a notion of quasi-commutative dgas that is based on a certain reduced tensor product, constructs a quasi-commutative model for the cochains, and uses Mandell's results to relate it to ordinary cochains.
$C(X;k)$ has been pursued by Karoubi [Reference KaroubiKar09] who introduces a notion of quasi-commutative dgas that is based on a certain reduced tensor product, constructs a quasi-commutative model for the cochains, and uses Mandell's results to relate it to ordinary cochains.
Since it is often easier to work with strictly commutative objects rather than ![]() $E_{\infty }$ objects, we also expect that the commutative
$E_{\infty }$ objects, we also expect that the commutative ![]() $\mathcal {I}$-dga
$\mathcal {I}$-dga ![]() $A^{\mathcal {I}}(X)$ will be a useful replacement of the
$A^{\mathcal {I}}(X)$ will be a useful replacement of the ![]() $E_{\infty }$ dga
$E_{\infty }$ dga ![]() $C(X;k)$ in applications. For instance, iterated bar constructions for
$C(X;k)$ in applications. For instance, iterated bar constructions for ![]() $E_\infty$ algebras as developed in [Reference FresseFre11] are rather involved whereas iterated bar construction for commutative monoids are straightforward. Commutative
$E_\infty$ algebras as developed in [Reference FresseFre11] are rather involved whereas iterated bar construction for commutative monoids are straightforward. Commutative ![]() $\mathcal {I}$-dgas are tensored over simplicial sets whereas enrichments for
$\mathcal {I}$-dgas are tensored over simplicial sets whereas enrichments for ![]() $E_\infty$ monoids are more complicated because the coproduct is not just the underlying monoidal product. This allows for constructions such as higher-order Hochschild homology [Reference PirashviliPir00] for commutative
$E_\infty$ monoids are more complicated because the coproduct is not just the underlying monoidal product. This allows for constructions such as higher-order Hochschild homology [Reference PirashviliPir00] for commutative ![]() $\mathcal {I}$-dgas.
$\mathcal {I}$-dgas.
Writing ![]() $A^{\mathcal {I}}(X;\mathbb {Z})$ for
$A^{\mathcal {I}}(X;\mathbb {Z})$ for ![]() $A^{\mathcal {I}}(X)$ when working over
$A^{\mathcal {I}}(X)$ when working over ![]() $k = \mathbb {Z}$, Theorem 1.1 leads to the following reformulation of the main theorem of Mandell [Reference MandellMan06] that highlights the usefulness of
$k = \mathbb {Z}$, Theorem 1.1 leads to the following reformulation of the main theorem of Mandell [Reference MandellMan06] that highlights the usefulness of ![]() $A^{\mathcal {I}}$.
$A^{\mathcal {I}}$.
Theorem 1.2 Two finite type nilpotent spaces ![]() $X$ and
$X$ and ![]() $Y$ are weakly equivalent if and only if
$Y$ are weakly equivalent if and only if ![]() $A^{\mathcal {I}}(X;\mathbb {Z})$ and
$A^{\mathcal {I}}(X;\mathbb {Z})$ and ![]() $A^{\mathcal {I}}(Y;\mathbb {Z})$ are weakly equivalent in
$A^{\mathcal {I}}(Y;\mathbb {Z})$ are weakly equivalent in ![]() $\mathrm {Ch}^{\mathcal {I}}_{\mathbb {Z}}[\mathcal {C}]$.
$\mathrm {Ch}^{\mathcal {I}}_{\mathbb {Z}}[\mathcal {C}]$.
1.3 Outline of the construction
Our chain complexes are homologically graded so that cochains are concentrated in non-positive degrees. We model spaces by simplicial sets and consider the singular complex of a topological space if necessary.
The functor ![]() $A_{\mathrm {PL}}\colon \mathrm {sSet}^{{{\mathrm {op}}}} \to \mathrm {cdga}_{\mathbb {Q}}$ of polynomial forms used in rational homotopy theory (see e.g. [Reference Bousfield and GugenheimBG76, § 1]) motivates our definition of
$A_{\mathrm {PL}}\colon \mathrm {sSet}^{{{\mathrm {op}}}} \to \mathrm {cdga}_{\mathbb {Q}}$ of polynomial forms used in rational homotopy theory (see e.g. [Reference Bousfield and GugenheimBG76, § 1]) motivates our definition of ![]() $A^{\mathcal {I}}$. We recall that
$A^{\mathcal {I}}$. We recall that ![]() $A_{\mathrm {PL}}$ arises by Kan extending the functor
$A_{\mathrm {PL}}$ arises by Kan extending the functor ![]() $A_{\mathrm {PL},\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {cdga}_{\mathbb {Q}}$ sending
$A_{\mathrm {PL},\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {cdga}_{\mathbb {Q}}$ sending ![]() $[p]$ in
$[p]$ in ![]() $\Delta$ to the algebra of polynomial differential forms
$\Delta$ to the algebra of polynomial differential forms
Here ![]() $\Lambda$ is the free graded commutative algebra over
$\Lambda$ is the free graded commutative algebra over ![]() $\mathbb {Q}$, the generators
$\mathbb {Q}$, the generators ![]() $t_i$ have degree
$t_i$ have degree ![]() $0$, and the
$0$, and the ![]() $dt_i$ have degree
$dt_i$ have degree ![]() $-1$ (in our homological grading). Setting
$-1$ (in our homological grading). Setting ![]() $d(t_i) = dt_i$ extends to a differential that turns
$d(t_i) = dt_i$ extends to a differential that turns ![]() $A_{\mathrm {PL},q}$ into a commutative dga, and addition of the
$A_{\mathrm {PL},q}$ into a commutative dga, and addition of the ![]() $t_i$ and insertion of
$t_i$ and insertion of ![]() $0$ define the simplicial structure of
$0$ define the simplicial structure of ![]() $A_{\mathrm {PL},\bullet }$.
$A_{\mathrm {PL},\bullet }$.
The topological standard ![]() $p$-simplex can be written as
$p$-simplex can be written as
and as
Setting ![]() $x_i = t_0 + \cdots + t_{i-1}$ for
$x_i = t_0 + \cdots + t_{i-1}$ for ![]() $1 \leq i \leq p$ yields an isomorphism
$1 \leq i \leq p$ yields an isomorphism
and this simple but crucial trick gives rise to the following reformulation: let ![]() $\mathbb {C} D^{0}$ be the free commutative
$\mathbb {C} D^{0}$ be the free commutative ![]() $\mathbb {Q}$-dga on the chain complex
$\mathbb {Q}$-dga on the chain complex ![]() $D^{0}$ with
$D^{0}$ with ![]() $(D^{0})_i=0$ if
$(D^{0})_i=0$ if ![]() $i\neq 0,-1$ and
$i\neq 0,-1$ and ![]() $d_0\colon (D^{0})_0 \to (D^{0})_{-1}$ being
$d_0\colon (D^{0})_0 \to (D^{0})_{-1}$ being ![]() $\mathrm {id}_{\mathbb {Q}}$. Moreover, let
$\mathrm {id}_{\mathbb {Q}}$. Moreover, let ![]() $S^{0}$ in
$S^{0}$ in ![]() $\mathrm {Ch}_{\mathbb {Q}}$ be the monoidal unit, i.e., the chain complex with a copy of
$\mathrm {Ch}_{\mathbb {Q}}$ be the monoidal unit, i.e., the chain complex with a copy of ![]() $\mathbb {Q}$ concentrated in degree
$\mathbb {Q}$ concentrated in degree ![]() $0$. Sending
$0$. Sending ![]() $1 \in (\mathbb {C} D^{0})_0$ to either
$1 \in (\mathbb {C} D^{0})_0$ to either ![]() $0$ or
$0$ or ![]() $1$ in
$1$ in ![]() $\mathbb {Q}$ defines two commutative
$\mathbb {Q}$ defines two commutative ![]() $\mathbb {C} D^{0}$-algebra structures on
$\mathbb {C} D^{0}$-algebra structures on ![]() $S^{0}$ that we denote by
$S^{0}$ that we denote by ![]() $S^{0}_0$ and
$S^{0}_0$ and ![]() $S^{0}_1$. We argue in § 5.8 that the simplicial
$S^{0}_1$. We argue in § 5.8 that the simplicial ![]() $\mathbb {Q}$-cdga
$\mathbb {Q}$-cdga ![]() $A_{\mathrm {PL},\bullet }$ is isomorphic to the two-sided bar construction
$A_{\mathrm {PL},\bullet }$ is isomorphic to the two-sided bar construction
whose face maps are provided by the algebra structures on ![]() $S^{0}_1$ and
$S^{0}_1$ and ![]() $S^{0}_0$ and the multiplication of
$S^{0}_0$ and the multiplication of ![]() $\mathbb {C} D^{0}$, and whose degeneracy maps are induced by the unit of
$\mathbb {C} D^{0}$, and whose degeneracy maps are induced by the unit of ![]() $\mathbb {C} D^{0}$.
$\mathbb {C} D^{0}$.
While polynomial differential forms appear to have no obvious counterpart in commutative ![]() $\mathcal {I}$-dgas, their description in terms of a two-sided bar construction easily generalizes to commutative
$\mathcal {I}$-dgas, their description in terms of a two-sided bar construction easily generalizes to commutative ![]() $\mathcal {I}$-dgas over an arbitrary commutative ground ring
$\mathcal {I}$-dgas over an arbitrary commutative ground ring ![]() $k$. For this we consider the left adjoint
$k$. For this we consider the left adjoint
 \[ \mathbb{C} F_{{\mathbf{1}}}^{\mathcal{I}} \colon \mathrm{Ch}_k \to \mathrm{Ch}^{\mathcal{I}}_k[\mathcal{C}], \qquad A\mapsto \biggl({\mathbf{m}}\mapsto \bigoplus_{s \geq 0} \biggl(\biggl(\bigoplus_{\mathcal{I}({\mathbf{1}}^{\sqcup s},{\mathbf{m}})} A^{\otimes s}\biggr)\bigg / \Sigma_s\biggr)\biggr) \]
\[ \mathbb{C} F_{{\mathbf{1}}}^{\mathcal{I}} \colon \mathrm{Ch}_k \to \mathrm{Ch}^{\mathcal{I}}_k[\mathcal{C}], \qquad A\mapsto \biggl({\mathbf{m}}\mapsto \bigoplus_{s \geq 0} \biggl(\biggl(\bigoplus_{\mathcal{I}({\mathbf{1}}^{\sqcup s},{\mathbf{m}})} A^{\otimes s}\biggr)\bigg / \Sigma_s\biggr)\biggr) \]
to the evaluation of a commutative ![]() $\mathcal {I}$-dga at the object
$\mathcal {I}$-dga at the object ![]() ${\mathbf {1}}$ in
${\mathbf {1}}$ in ![]() $\mathcal {I}$ and recall that the unit
$\mathcal {I}$ and recall that the unit ![]() $U^{\mathcal {I}}$ in
$U^{\mathcal {I}}$ in ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ is the constant
$\mathrm {Ch}^{\mathcal {I}}_k$ is the constant ![]() $\mathcal {I}$-diagram on the unit
$\mathcal {I}$-diagram on the unit ![]() $S^{0}$ in
$S^{0}$ in ![]() $\mathrm {Ch}_k$. As above, we form
$\mathrm {Ch}_k$. As above, we form ![]() $\mathbb {C} F_{{\mathbf {1}}}^{\mathcal {I}} D^{0}$, observe that
$\mathbb {C} F_{{\mathbf {1}}}^{\mathcal {I}} D^{0}$, observe that ![]() $U^{\mathcal {I}}$ gives rise to two commutative
$U^{\mathcal {I}}$ gives rise to two commutative ![]() $\mathbb {C} F_{{\mathbf {1}}}^{\mathcal {I}} D^{0}$ algebras
$\mathbb {C} F_{{\mathbf {1}}}^{\mathcal {I}} D^{0}$ algebras ![]() $U^{\mathcal {I}}_0$ and
$U^{\mathcal {I}}_0$ and ![]() $U^{\mathcal {I}}_1$, and define
$U^{\mathcal {I}}_1$, and define ![]() $A^{\mathcal {I}}_{\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ to be the two-sided bar construction
$A^{\mathcal {I}}_{\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ to be the two-sided bar construction
At this point it is central to work with strictly commutative objects since the multiplication map of an ![]() $E_{\infty }$ object is typically not an
$E_{\infty }$ object is typically not an ![]() $E_{\infty }$ map. It is also important to use
$E_{\infty }$ map. It is also important to use ![]() ${\mathbf {1}}$ rather than
${\mathbf {1}}$ rather than ![]() ${\mathbf {0}}$ in the above left adjoint since this ensures that
${\mathbf {0}}$ in the above left adjoint since this ensures that ![]() $A^{\mathcal {I}}_p({\mathbf {m}})$ is contractible. This is related to J. Smith's insight that one has to use positive model structures for commutative symmetric ring spectra. Using that
$A^{\mathcal {I}}_p({\mathbf {m}})$ is contractible. This is related to J. Smith's insight that one has to use positive model structures for commutative symmetric ring spectra. Using that ![]() $\boxtimes$ is the coproduct in commutative
$\boxtimes$ is the coproduct in commutative ![]() $\mathcal {I}$-dgas, we get an isomorphism
$\mathcal {I}$-dgas, we get an isomorphism
identifying the simplicial degree ![]() $p$ part of
$p$ part of ![]() $A^{\mathcal {I}}_\bullet$ with a free commutative
$A^{\mathcal {I}}_\bullet$ with a free commutative ![]() $\mathcal {I}$-dga on
$\mathcal {I}$-dga on ![]() $p$ generators. We also describe the simplicial structure maps of
$p$ generators. We also describe the simplicial structure maps of ![]() $A^{\mathcal {I}}_\bullet$ in terms of these generators (see § 3.4).
$A^{\mathcal {I}}_\bullet$ in terms of these generators (see § 3.4).
Via Kan extension and restriction along the canonical functor ![]() $\Delta ^{{{\mathrm {op}}}} \to \mathrm {sSet}^{{{\mathrm {op}}}}$, this
$\Delta ^{{{\mathrm {op}}}} \to \mathrm {sSet}^{{{\mathrm {op}}}}$, this ![]() $A^{\mathcal {I}}_{\bullet }$ gives rise to functors
$A^{\mathcal {I}}_{\bullet }$ gives rise to functors ![]() $A^{\mathcal {I}} \colon \mathrm {sSet}^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ and
$A^{\mathcal {I}} \colon \mathrm {sSet}^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ and ![]() $\langle -\rangle _\mathcal {I} \colon \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]^{{{\mathrm {op}}}} \to \mathrm {sSet}$ (see Definition 3.6). More explicitly, the evaluation of
$\langle -\rangle _\mathcal {I} \colon \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]^{{{\mathrm {op}}}} \to \mathrm {sSet}$ (see Definition 3.6). More explicitly, the evaluation of ![]() $A^{\mathcal {I}}(X)$ at
$A^{\mathcal {I}}(X)$ at ![]() $\mathcal {I}$-degree
$\mathcal {I}$-degree ![]() ${\mathbf {m}}$ and chain complex level
${\mathbf {m}}$ and chain complex level ![]() $q$ is the
$q$ is the ![]() $k$-module of simplicial set morphisms
$k$-module of simplicial set morphisms ![]() $\mathrm {sSet}(X,A^{\mathcal {I}}_{\bullet }({\mathbf {m}})_q)$. For every
$\mathrm {sSet}(X,A^{\mathcal {I}}_{\bullet }({\mathbf {m}})_q)$. For every ![]() $E$ in
$E$ in ![]() $\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$, we set
$\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$, we set ![]() $\langle E\rangle _\mathcal {I} = \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}](E, A^{\mathcal {I}}_\bullet )$. The functors
$\langle E\rangle _\mathcal {I} = \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}](E, A^{\mathcal {I}}_\bullet )$. The functors ![]() $A^{\mathcal {I}}$ and
$A^{\mathcal {I}}$ and ![]() $\langle -\rangle _\mathcal {I}$ are contravariant right adjoint in the sense that there are natural isomorphisms
$\langle -\rangle _\mathcal {I}$ are contravariant right adjoint in the sense that there are natural isomorphisms ![]() $\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}](E, A^{\mathcal {I}}(X))\cong \mathrm {sSet}(X, \langle E \rangle _\mathcal {I})$. They are integral analogues of the functor of polynomial forms and of the Sullivan realization functor.
$\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}](E, A^{\mathcal {I}}(X))\cong \mathrm {sSet}(X, \langle E \rangle _\mathcal {I})$. They are integral analogues of the functor of polynomial forms and of the Sullivan realization functor.
1.4 Homotopical analysis of  $A^{\mathcal {I}}$
$A^{\mathcal {I}}$
We equip simplicial sets with the standard model structure and the category of commutative ![]() $\mathcal {I}$-dgas
$\mathcal {I}$-dgas ![]() $\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ with the descending
$\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ with the descending ![]() $\mathcal {I}$-model structure making it Quillen equivalent to
$\mathcal {I}$-model structure making it Quillen equivalent to ![]() $E_{\infty }$ dgas (see § 4 for details).
$E_{\infty }$ dgas (see § 4 for details).
Theorem 1.5 Both ![]() $A^{\mathcal {I}}$ and
$A^{\mathcal {I}}$ and ![]() $\langle -\rangle _\mathcal {I}$ send cofibrations to fibrations and acyclic cofibrations to acyclic fibrations. They induce functors on the corresponding homotopy categories
$\langle -\rangle _\mathcal {I}$ send cofibrations to fibrations and acyclic cofibrations to acyclic fibrations. They induce functors on the corresponding homotopy categories ![]() $\mathbb {R}\langle - \rangle _\mathcal {I} \colon \mathrm {Ho}(\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}])^{{{\mathrm {op}}}}\to \mathrm {Ho}(\mathrm {sSet})$ and
$\mathbb {R}\langle - \rangle _\mathcal {I} \colon \mathrm {Ho}(\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}])^{{{\mathrm {op}}}}\to \mathrm {Ho}(\mathrm {sSet})$ and ![]() $\mathbb {R}A^{\mathcal {I}}\colon \mathrm {Ho}(\mathrm {sSet})^{{{\mathrm {op}}}}\to \mathrm {Ho}(\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}])$ that are related by a natural isomorphism
$\mathbb {R}A^{\mathcal {I}}\colon \mathrm {Ho}(\mathrm {sSet})^{{{\mathrm {op}}}}\to \mathrm {Ho}(\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}])$ that are related by a natural isomorphism
Here, ![]() $\mathbb {R}(-)$ indicates that we right-derive the functors on
$\mathbb {R}(-)$ indicates that we right-derive the functors on ![]() $(\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}])^{{{\mathrm {op}}}}$ and
$(\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}])^{{{\mathrm {op}}}}$ and ![]() $\mathrm {sSet}^{{{\mathrm {op}}}}$. So no fibrant replacement is necessary before applying
$\mathrm {sSet}^{{{\mathrm {op}}}}$. So no fibrant replacement is necessary before applying ![]() $A^{\mathcal {I}}$ since all simplicial sets are cofibrant, while a cofibrant replacement in
$A^{\mathcal {I}}$ since all simplicial sets are cofibrant, while a cofibrant replacement in ![]() $\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ is necessary to derive
$\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ is necessary to derive ![]() $\langle - \rangle _{\mathcal {I}}$.
$\langle - \rangle _{\mathcal {I}}$.
A similar result for ![]() $A_{\mathrm {PL}}\colon \mathrm {sSet}^{{{\mathrm {op}}}} \to \mathrm {cdga}_{\mathbb {Q}}$ has been established by Bousfield and Gugenheim [Reference Bousfield and GugenheimBG76, § 8]. Mandell [Reference MandellMan02, § 4] constructed an analogous adjunction between simplicial sets and
$A_{\mathrm {PL}}\colon \mathrm {sSet}^{{{\mathrm {op}}}} \to \mathrm {cdga}_{\mathbb {Q}}$ has been established by Bousfield and Gugenheim [Reference Bousfield and GugenheimBG76, § 8]. Mandell [Reference MandellMan02, § 4] constructed an analogous adjunction between simplicial sets and ![]() $E_{\infty }$ dgas using the
$E_{\infty }$ dgas using the ![]() $E_{\infty }$ structure on cochains as input. The functor of homotopy categories
$E_{\infty }$ structure on cochains as input. The functor of homotopy categories ![]() $\mathbb {R}A^{\mathcal {I}}$ fails to be full for the same reason as its counterpart studied by Mandell (see the discussion after [Reference MandellMan06, Theorem 0.2]). One of the referees of this paper raised the interesting question whether there exists a modification of our diagrammatic approach that remedies this shortcoming.
$\mathbb {R}A^{\mathcal {I}}$ fails to be full for the same reason as its counterpart studied by Mandell (see the discussion after [Reference MandellMan06, Theorem 0.2]). One of the referees of this paper raised the interesting question whether there exists a modification of our diagrammatic approach that remedies this shortcoming.
Since all simplicial sets are cofibrant, the statement of Theorem 1.5 implies that each ![]() $A^{\mathcal {I}}(X)$ is descending
$A^{\mathcal {I}}(X)$ is descending ![]() $\mathcal {I}$-fibrant. Writing
$\mathcal {I}$-fibrant. Writing ![]() $\mathcal {I}_{+}$ for the full subcategory of
$\mathcal {I}_{+}$ for the full subcategory of ![]() $\mathcal {I}$ on objects
$\mathcal {I}$ on objects ![]() ${\mathbf {m}}$ with
${\mathbf {m}}$ with ![]() $|{\mathbf {m}}|\geq 1$, this means that for each morphism
$|{\mathbf {m}}|\geq 1$, this means that for each morphism ![]() ${\mathbf {m}} \to {\mathbf {n}}$ in
${\mathbf {m}} \to {\mathbf {n}}$ in ![]() $\mathcal {I}_+$ and each
$\mathcal {I}_+$ and each ![]() $q \geq -|{\mathbf {m}}|$, the induced map
$q \geq -|{\mathbf {m}}|$, the induced map ![]() $H_q(A^{\mathcal {I}}(X)({\mathbf {m}})) \to H_q(A^{\mathcal {I}}(X)({\mathbf {n}}))$ is an isomorphism. Hence each chain complex
$H_q(A^{\mathcal {I}}(X)({\mathbf {m}})) \to H_q(A^{\mathcal {I}}(X)({\mathbf {n}}))$ is an isomorphism. Hence each chain complex ![]() $A^{\mathcal {I}}(X)({\mathbf {m}})$ with
$A^{\mathcal {I}}(X)({\mathbf {m}})$ with ![]() ${\mathbf {m}}$ in
${\mathbf {m}}$ in ![]() $\mathcal {I}_+$ captures the cohomology groups of
$\mathcal {I}_+$ captures the cohomology groups of ![]() $X$ up to degree
$X$ up to degree ![]() $|{\mathbf {m}}|$. This is the maximal information to be expected from
$|{\mathbf {m}}|$. This is the maximal information to be expected from ![]() $A^{\mathcal {I}}(X)({\mathbf {m}})$ as it is a chain complex concentrated in degrees between
$A^{\mathcal {I}}(X)({\mathbf {m}})$ as it is a chain complex concentrated in degrees between ![]() $0$ and
$0$ and ![]() $-|{\mathbf {m}}|$. Since the descending
$-|{\mathbf {m}}|$. Since the descending ![]() $\mathcal {I}$-model structure is the left Bousfield localization of a descending level model structure, it also follows that weak homotopy equivalences
$\mathcal {I}$-model structure is the left Bousfield localization of a descending level model structure, it also follows that weak homotopy equivalences ![]() $X \to Y$ induce isomorphisms
$X \to Y$ induce isomorphisms ![]() $H_q(A^{\mathcal {I}}(Y)({\mathbf {m}})) \to H_q(A^{\mathcal {I}}(X)({\mathbf {m}}))$ if
$H_q(A^{\mathcal {I}}(Y)({\mathbf {m}})) \to H_q(A^{\mathcal {I}}(X)({\mathbf {m}}))$ if ![]() ${\mathbf {m}}$ is in
${\mathbf {m}}$ is in ![]() $\mathcal {I}_+$ and
$\mathcal {I}_+$ and ![]() $q \geq -|{\mathbf {m}}|$.
$q \geq -|{\mathbf {m}}|$.
Analogous to the corresponding statement about ![]() $A_{\mathrm {PL}}$, the proof of the theorem is based on the observation that the simplicial sets
$A_{\mathrm {PL}}$, the proof of the theorem is based on the observation that the simplicial sets ![]() $A^{\mathcal {I}}_{\bullet }({\mathbf {m}})_q$ are contractible for a fixed
$A^{\mathcal {I}}_{\bullet }({\mathbf {m}})_q$ are contractible for a fixed ![]() ${\mathbf {m}}$ in
${\mathbf {m}}$ in ![]() $\mathcal {I}_+$ and a fixed chain level
$\mathcal {I}_+$ and a fixed chain level ![]() $q$ with
$q$ with ![]() $0 \geq q \geq -|{\mathbf {m}}|$.
$0 \geq q \geq -|{\mathbf {m}}|$.
Remark 1.6 After a first version of the present manuscript was made available, the authors learned from Dan Petersen that he recently found another construction of a commutative ![]() $\mathcal {I}$-dga that models the cochain algebra of a space [Reference PetersenPet20]. His approach applies to locally contractible topological spaces, uses sheaf cohomology, and has applications in the study of configuration spaces.
$\mathcal {I}$-dga that models the cochain algebra of a space [Reference PetersenPet20]. His approach applies to locally contractible topological spaces, uses sheaf cohomology, and has applications in the study of configuration spaces.
1.7 Notation and conventions
Throughout the paper, ![]() $k$ denotes a commutative ring with unit, and
$k$ denotes a commutative ring with unit, and ![]() $\mathrm {Ch}_k$ denotes the category of unbounded homologically graded chain complexes of
$\mathrm {Ch}_k$ denotes the category of unbounded homologically graded chain complexes of ![]() $k$-modules. For
$k$-modules. For ![]() $q\in \mathbb {Z}$, we as usual write
$q\in \mathbb {Z}$, we as usual write ![]() $S^{q}$ for the chain complex with
$S^{q}$ for the chain complex with ![]() $k$ concentrated in degree
$k$ concentrated in degree ![]() $q$, and
$q$, and ![]() $D^{q}$ for the chain complex with
$D^{q}$ for the chain complex with ![]() $(D^{q})_i=k$ if
$(D^{q})_i=k$ if ![]() $i\in \{q,q-1\}$, with
$i\in \{q,q-1\}$, with ![]() $(D^{q})_i=0$ for all other
$(D^{q})_i=0$ for all other ![]() $i$, and with
$i$, and with ![]() $d_q = \mathrm {id}_k$.
$d_q = \mathrm {id}_k$.
1.8 Organization
In § 2 we study homotopy colimits of commutative ![]() $\mathcal {I}$-dgas. Section 3 provides the construction of the functor
$\mathcal {I}$-dgas. Section 3 provides the construction of the functor ![]() $A^{\mathcal {I}}$. We review model structures on
$A^{\mathcal {I}}$. We review model structures on ![]() $\mathcal {I}$-chain complexes and commutative
$\mathcal {I}$-chain complexes and commutative ![]() $\mathcal {I}$-dgas in § 4. In § 5 we establish the homotopical properties of
$\mathcal {I}$-dgas in § 4. In § 5 we establish the homotopical properties of ![]() $A^{\mathcal {I}}$, prove a comparison to the usual cochains disregarding multiplicative structures, and prove Theorem 1.5. In the final § 6, we prove the
$A^{\mathcal {I}}$, prove a comparison to the usual cochains disregarding multiplicative structures, and prove Theorem 1.5. In the final § 6, we prove the ![]() $E_{\infty }$ comparison from Theorem 1.1 as Theorem 6.2 and explain how to derive Theorem 1.2.
$E_{\infty }$ comparison from Theorem 1.1 as Theorem 6.2 and explain how to derive Theorem 1.2.
2. Homotopy colimits of  $\mathcal {I}$-chain complexes
$\mathcal {I}$-chain complexes
Let ![]() $\mathcal {I}$ be the category with objects the finite sets
$\mathcal {I}$ be the category with objects the finite sets ![]() ${\mathbf {m}}=\{1,\ldots ,m\}$ for
${\mathbf {m}}=\{1,\ldots ,m\}$ for ![]() $m\geq 0$ and with morphisms the injective maps. In this section we study multiplicative properties of the homotopy colimit functor for
$m\geq 0$ and with morphisms the injective maps. In this section we study multiplicative properties of the homotopy colimit functor for ![]() $\mathcal {I}$-diagrams of chain complexes.
$\mathcal {I}$-diagrams of chain complexes.
Definition 2.1 An ![]() $\mathcal {I}$-chain complex is a functor
$\mathcal {I}$-chain complex is a functor ![]() $\mathcal {I} \to \mathrm {Ch}_k$, and
$\mathcal {I} \to \mathrm {Ch}_k$, and ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ denotes the resulting functor category.
$\mathrm {Ch}^{\mathcal {I}}_k$ denotes the resulting functor category.
For each ![]() ${\mathbf {m}}$ in
${\mathbf {m}}$ in ![]() $\mathcal {I}$ there is an adjunction
$\mathcal {I}$ there is an adjunction ![]() $F^{\mathcal {I}}_{{\mathbf {m}}}\colon \mathrm {Ch}_k \rightleftarrows \mathrm {Ch}^{\mathcal {I}}_k \colon \mathrm {Ev}_{{\mathbf {m}}}$ with right adjoint the evaluation functor
$F^{\mathcal {I}}_{{\mathbf {m}}}\colon \mathrm {Ch}_k \rightleftarrows \mathrm {Ch}^{\mathcal {I}}_k \colon \mathrm {Ev}_{{\mathbf {m}}}$ with right adjoint the evaluation functor ![]() $\mathrm {Ev}_{{\mathbf {m}}}(P) = P({\mathbf {m}})$ and left adjoint
$\mathrm {Ev}_{{\mathbf {m}}}(P) = P({\mathbf {m}})$ and left adjoint
The functor ![]() $F^{\mathcal {I}}_{{\mathbf {0}}}$ is isomorphic to the constant functor since
$F^{\mathcal {I}}_{{\mathbf {0}}}$ is isomorphic to the constant functor since ![]() ${\mathbf {0}}$ is initial in
${\mathbf {0}}$ is initial in ![]() $\mathcal {I}$.
$\mathcal {I}$.
2.2 Homotopy colimits
Our next aim is to define Bousfield–Kan style homotopy colimits for ![]() $\mathcal {I}$-diagrams of chain complexes. For the subsequent multiplicative analysis, we fix notation and conventions about bicomplexes.
$\mathcal {I}$-diagrams of chain complexes. For the subsequent multiplicative analysis, we fix notation and conventions about bicomplexes.
Definition 2.3 Let ![]() $\mathrm {Ch}_k(\mathrm {Ch}_k)$ be the category of chain complexes in
$\mathrm {Ch}_k(\mathrm {Ch}_k)$ be the category of chain complexes in ![]() $\mathrm {Ch}_k$. Its objects are
$\mathrm {Ch}_k$. Its objects are ![]() $\mathbb {Z} \times \mathbb {Z}$-graded
$\mathbb {Z} \times \mathbb {Z}$-graded ![]() $k$-modules
$k$-modules ![]() $(Y_{p,q})_{p,q \in \mathbb {Z}}$ with
$(Y_{p,q})_{p,q \in \mathbb {Z}}$ with ![]() $k$-linear horizontal differentials,
$k$-linear horizontal differentials, ![]() $d_h \colon Y_{p,q} \rightarrow Y_{p-1,q}$, and
$d_h \colon Y_{p,q} \rightarrow Y_{p-1,q}$, and ![]() $k$-linear vertical differentials,
$k$-linear vertical differentials, ![]() $d_v \colon Y_{p,q} \rightarrow Y_{p,q-1}$, such that
$d_v \colon Y_{p,q} \rightarrow Y_{p,q-1}$, such that
A morphism ![]() $g \colon Y \rightarrow Z$ in
$g \colon Y \rightarrow Z$ in ![]() $\mathrm {Ch}_k(\mathrm {Ch}_k)$ is a family
$\mathrm {Ch}_k(\mathrm {Ch}_k)$ is a family ![]() $(g_{p,q} \colon Y_{p,q} \rightarrow Z_{p,q})_{p,q \in \mathbb {Z} \times \mathbb {Z}}$ of
$(g_{p,q} \colon Y_{p,q} \rightarrow Z_{p,q})_{p,q \in \mathbb {Z} \times \mathbb {Z}}$ of ![]() $k$-linear maps that commute with the horizontal and vertical differentials, i.e.,
$k$-linear maps that commute with the horizontal and vertical differentials, i.e.,
for all ![]() $p,q \in \mathbb {Z}$.
$p,q \in \mathbb {Z}$.
Since we require horizontal and vertical differentials to commute, an additional sign is needed to form the total complex.
Definition 2.4 Let ![]() $Y$ be an object in
$Y$ be an object in ![]() $\mathrm {Ch}_k(\mathrm {Ch}_k)$. Its associated total complex
$\mathrm {Ch}_k(\mathrm {Ch}_k)$. Its associated total complex ![]() $\operatorname {Tot}(Y)$ is the chain complex with
$\operatorname {Tot}(Y)$ is the chain complex with ![]() $\operatorname {Tot}(Y)_n = \bigoplus _{p+q=n} Y_{p,q}$ in chain degree
$\operatorname {Tot}(Y)_n = \bigoplus _{p+q=n} Y_{p,q}$ in chain degree ![]() $n \in \mathbb {Z}$ and with differential
$n \in \mathbb {Z}$ and with differential ![]() $d_{\operatorname {Tot}}(y) = d_h(y) + (-1)^{p}d_v(y)$ for every homogeneous
$d_{\operatorname {Tot}}(y) = d_h(y) + (-1)^{p}d_v(y)$ for every homogeneous ![]() $y \in Y_{p,q}$.
$y \in Y_{p,q}$.
Let ![]() $\mathrm {sCh}_k$ be the category of simplicial objects in
$\mathrm {sCh}_k$ be the category of simplicial objects in ![]() $\mathrm {Ch}_k$.
$\mathrm {Ch}_k$.
Definition 2.5 For ![]() $A \in \mathrm {sCh}_k$ we denote by
$A \in \mathrm {sCh}_k$ we denote by ![]() $C_*(A)$ the chain complex in chain complexes with
$C_*(A)$ the chain complex in chain complexes with ![]() $(C_*(A))_{p,q} = A_{p,q}$. We define the horizontal differential on
$(C_*(A))_{p,q} = A_{p,q}$. We define the horizontal differential on ![]() $C_*(A)$,
$C_*(A)$, ![]() $d_h\colon A_{p,q} \rightarrow A_{p-1,q}$, as
$d_h\colon A_{p,q} \rightarrow A_{p-1,q}$, as
 \[ d_h = \sum_{i=0}^{p} (-1)^{i} d_i \]
\[ d_h = \sum_{i=0}^{p} (-1)^{i} d_i \]
where the ![]() $d_i$ are the simplicial face maps of
$d_i$ are the simplicial face maps of ![]() $A$. The vertical differential on
$A$. The vertical differential on ![]() $C_*(A)$ is given by the differential
$C_*(A)$ is given by the differential ![]() $d^{A}$ on
$d^{A}$ on ![]() $A$.
$A$.
As the ![]() $d_i$ commute with
$d_i$ commute with ![]() $d^{A}$, this gives indeed a chain complex in chain complexes whose horizontal part is concentrated in non-negative degrees.
$d^{A}$, this gives indeed a chain complex in chain complexes whose horizontal part is concentrated in non-negative degrees.
Construction Let ![]() $P\colon \mathcal {I} \to \mathrm {Ch}_k$ be an
$P\colon \mathcal {I} \to \mathrm {Ch}_k$ be an ![]() $\mathcal {I}$-chain complex. The simplicial replacement of
$\mathcal {I}$-chain complex. The simplicial replacement of ![]() $P$ is the simplicial chain complex
$P$ is the simplicial chain complex ![]() $\operatorname {srep}(P) \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch_k}$ given in simplicial degree
$\operatorname {srep}(P) \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch_k}$ given in simplicial degree ![]() $[p]$ by
$[p]$ by
 \[ \operatorname{srep}(P)[p] = \bigoplus_{({{\mathbf{n}_0}} \xleftarrow{\alpha_1} \cdots \xleftarrow{\alpha_p} {{\mathbf{n}_p}}) \in N(\mathcal{I})_p} P({{\mathbf{n}_p}}). \]
\[ \operatorname{srep}(P)[p] = \bigoplus_{({{\mathbf{n}_0}} \xleftarrow{\alpha_1} \cdots \xleftarrow{\alpha_p} {{\mathbf{n}_p}}) \in N(\mathcal{I})_p} P({{\mathbf{n}_p}}). \]
The last face map sends the copy of ![]() $P({{\mathbf{n}_p}})$ indexed by
$P({{\mathbf{n}_p}})$ indexed by ![]() $(\alpha _1,\ldots , \alpha _p)$ via
$(\alpha _1,\ldots , \alpha _p)$ via ![]() $P(\alpha _p)$ to the copy of
$P(\alpha _p)$ to the copy of ![]() $P({{\mathbf{n}_{p-1}}})$ indexed by
$P({{\mathbf{n}_{p-1}}})$ indexed by ![]() $(\alpha _1,\ldots ,\alpha _{p-1})$. The other face and degeneracy maps are induced by the identity on
$(\alpha _1,\ldots ,\alpha _{p-1})$. The other face and degeneracy maps are induced by the identity on ![]() $P({{\mathbf{n}_p}})$ and corresponding simplicial structure maps of the nerve
$P({{\mathbf{n}_p}})$ and corresponding simplicial structure maps of the nerve ![]() $\mathcal {N}(\mathcal {I})$ of
$\mathcal {N}(\mathcal {I})$ of ![]() $\mathcal {I}$.
$\mathcal {I}$.
The homotopy colimit functor ![]() $(-)_{h\mathcal {I}}\colon \mathrm {Ch}^{\mathcal {I}}_k \to \mathrm {Ch}_k$ is defined by
$(-)_{h\mathcal {I}}\colon \mathrm {Ch}^{\mathcal {I}}_k \to \mathrm {Ch}_k$ is defined by
A bicomplex spectral sequence argument shows that ![]() $P_{h\mathcal {I}} \to Q_{h\mathcal {I}}$ is a quasi-isomorphism if each
$P_{h\mathcal {I}} \to Q_{h\mathcal {I}}$ is a quasi-isomorphism if each ![]() $P({\mathbf {m}}) \to Q({\mathbf {m}})$ is a quasi-isomorphism. There is a canonical map
$P({\mathbf {m}}) \to Q({\mathbf {m}})$ is a quasi-isomorphism. There is a canonical map ![]() $P_{h\mathcal {I}} \to \operatorname {colim}_{\mathcal {I}}P$, and one can show by cell induction that it is a quasi-isomorphism if
$P_{h\mathcal {I}} \to \operatorname {colim}_{\mathcal {I}}P$, and one can show by cell induction that it is a quasi-isomorphism if ![]() $P$ is cofibrant in the projective level model structure on
$P$ is cofibrant in the projective level model structure on ![]() $\mathrm {Ch}^{\mathcal {I}}_k$. Together this shows that
$\mathrm {Ch}^{\mathcal {I}}_k$. Together this shows that ![]() $P_{h\mathcal {I}}$ is a model for the homotopy colimit of
$P_{h\mathcal {I}}$ is a model for the homotopy colimit of ![]() $P$. A more elaborate argument that shows that
$P$. A more elaborate argument that shows that ![]() $P_{h\mathcal {I}}$ is a corrected homotopy colimit can be found in [Reference Rodríguez GonzálezRG14]. A version of the above homotopy colimit for functors with values in modules can be found in [Reference Davis and LückDL98, Definition 3.13].
$P_{h\mathcal {I}}$ is a corrected homotopy colimit can be found in [Reference Rodríguez GonzálezRG14]. A version of the above homotopy colimit for functors with values in modules can be found in [Reference Davis and LückDL98, Definition 3.13].
2.7 Commutative  $\mathcal {I}$-dgas
$\mathcal {I}$-dgas
The ordered concatenation of ordered sets ![]() ${\mathbf {m}}\sqcup {\mathbf {n}} = {\mathbf {m+n}}$ equips
${\mathbf {m}}\sqcup {\mathbf {n}} = {\mathbf {m+n}}$ equips ![]() $\mathcal {I}$ with a symmetric strict monoidal structure that has
$\mathcal {I}$ with a symmetric strict monoidal structure that has ![]() ${\mathbf {0}}$ as a strict unit and the block permutations as symmetry isomorphisms. If
${\mathbf {0}}$ as a strict unit and the block permutations as symmetry isomorphisms. If ![]() $P,Q \colon \mathcal {I}\to \mathrm {Ch}_k$ are
$P,Q \colon \mathcal {I}\to \mathrm {Ch}_k$ are ![]() $\mathcal {I}$-chain complexes, then the left Kan extension of
$\mathcal {I}$-chain complexes, then the left Kan extension of
along ![]() $\sqcup \colon \mathcal {I} \times \mathcal {I} \to \mathcal {I}$ provides an
$\sqcup \colon \mathcal {I} \times \mathcal {I} \to \mathcal {I}$ provides an ![]() $\mathcal {I}$-chain complex
$\mathcal {I}$-chain complex ![]() $P\boxtimes Q$. This defines a symmetric monoidal product
$P\boxtimes Q$. This defines a symmetric monoidal product ![]() $\boxtimes$ on
$\boxtimes$ on ![]() $\mathrm {Ch}^{\mathcal {I}}_k$, the Day convolution product, with unit the constant
$\mathrm {Ch}^{\mathcal {I}}_k$, the Day convolution product, with unit the constant ![]() $\mathcal {I}$-diagram
$\mathcal {I}$-diagram ![]() $U^{\mathcal {I}}= F_\mathbf{0}^{\mathcal {I}}(S^{0})$.
$U^{\mathcal {I}}= F_\mathbf{0}^{\mathcal {I}}(S^{0})$.
Definition 2.8 A commutative ![]() $\mathcal {I}$-dga is a commutative monoid in
$\mathcal {I}$-dga is a commutative monoid in ![]() $(\mathrm {Ch}^{\mathcal {I}}_k, \boxtimes , U^{\mathcal {I}})$, i.e., a lax symmetric monoidal functor
$(\mathrm {Ch}^{\mathcal {I}}_k, \boxtimes , U^{\mathcal {I}})$, i.e., a lax symmetric monoidal functor ![]() $(\mathcal {I}, \sqcup , {\mathbf {0}}) \to (\mathrm {Ch}_k, \otimes , S^{0})$. The resulting category of commutative
$(\mathcal {I}, \sqcup , {\mathbf {0}}) \to (\mathrm {Ch}_k, \otimes , S^{0})$. The resulting category of commutative ![]() $\mathcal {I}$-dgas is denoted by
$\mathcal {I}$-dgas is denoted by ![]() $\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$.
$\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$.
We write ![]() $\mathbb {C}\colon \mathrm {Ch}^{\mathcal {I}}_k \rightleftarrows \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}] \colon U$ for the adjunction with right adjoint the forgetful functor and left adjoint the free functor
$\mathbb {C}\colon \mathrm {Ch}^{\mathcal {I}}_k \rightleftarrows \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}] \colon U$ for the adjunction with right adjoint the forgetful functor and left adjoint the free functor ![]() $\mathbb {C}$ given by
$\mathbb {C}$ given by
The definition of ![]() $\boxtimes$ as a left Kan extension implies the existence of a natural isomorphism
$\boxtimes$ as a left Kan extension implies the existence of a natural isomorphism ![]() $F_{{{\mathbf{n}_1}}}^{\mathcal {I}}(A^{1}) \boxtimes F_{{{\mathbf{n}_2}}}^{\mathcal {I}}(A^{2}) \cong F_{{{\mathbf{n}_1\sqcup \mathbf{n}_2}}}^{\mathcal {I}}(A^{1}\otimes A^{2})$. This shows that in the case
$F_{{{\mathbf{n}_1}}}^{\mathcal {I}}(A^{1}) \boxtimes F_{{{\mathbf{n}_2}}}^{\mathcal {I}}(A^{2}) \cong F_{{{\mathbf{n}_1\sqcup \mathbf{n}_2}}}^{\mathcal {I}}(A^{1}\otimes A^{2})$. This shows that in the case ![]() $P = F_{{\mathbf {1}}}^{\mathcal {I}}(A)$, we have an isomorphism
$P = F_{{\mathbf {1}}}^{\mathcal {I}}(A)$, we have an isomorphism ![]() $F_{{\mathbf {1}}}^{\mathcal {I}}(A)^{\boxtimes s} \cong F_{{\mathbf {1}}^{\sqcup s}}^{\mathcal {I}}(A^{\otimes s})$ of
$F_{{\mathbf {1}}}^{\mathcal {I}}(A)^{\boxtimes s} \cong F_{{\mathbf {1}}^{\sqcup s}}^{\mathcal {I}}(A^{\otimes s})$ of ![]() $\Sigma _s$-equivariant objects where
$\Sigma _s$-equivariant objects where ![]() $\Sigma _s$ acts on the target by permuting both the
$\Sigma _s$ acts on the target by permuting both the ![]() $\otimes$-powers of
$\otimes$-powers of ![]() $A$ and the index set of the sum. The commutative
$A$ and the index set of the sum. The commutative ![]() $\mathcal {I}$-dga
$\mathcal {I}$-dga ![]() $\mathbb {C}(F_{{\mathbf {1}}}^{\mathcal {I}}(A))$ will be of particular importance for us, and we note that the above implies
$\mathbb {C}(F_{{\mathbf {1}}}^{\mathcal {I}}(A))$ will be of particular importance for us, and we note that the above implies
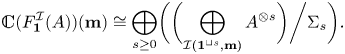 \begin{equation} \mathbb{C}(F_{{\mathbf{1}}}^{\mathcal{I}}(A))({\mathbf{m}}) \cong \bigoplus_{s \geq 0} \biggl(\biggl(\bigoplus_{\mathcal{I}({\mathbf{1}}^{\sqcup s},{\mathbf{m}})} A^{\otimes s}\biggl)\bigg / \Sigma_s\biggl). \end{equation}
\begin{equation} \mathbb{C}(F_{{\mathbf{1}}}^{\mathcal{I}}(A))({\mathbf{m}}) \cong \bigoplus_{s \geq 0} \biggl(\biggl(\bigoplus_{\mathcal{I}({\mathbf{1}}^{\sqcup s},{\mathbf{m}})} A^{\otimes s}\biggl)\bigg / \Sigma_s\biggl). \end{equation}2.9 Homotopy colimits of commutative  $\mathcal {I}$-dgas
$\mathcal {I}$-dgas
We will now construct an operad action on the homotopy colimit of a commutative ![]() $\mathcal {I}$-dga. Our construction involves a symmetric monoidal structure on simplicial chain complexes.
$\mathcal {I}$-dga. Our construction involves a symmetric monoidal structure on simplicial chain complexes.
Definition 2.10 Let ![]() $A$ and
$A$ and ![]() $B$ be two simplicial chain complexes. Their tensor product
$B$ be two simplicial chain complexes. Their tensor product ![]() $A \hat {\otimes } B$ is the simplicial chain complex with
$A \hat {\otimes } B$ is the simplicial chain complex with
in simplicial degree ![]() $p$ and chain degree
$p$ and chain degree ![]() $n$. The simplicial structure maps act coordinatewise and the differential
$n$. The simplicial structure maps act coordinatewise and the differential ![]() $d^{\hat {\otimes }}$ is
$d^{\hat {\otimes }}$ is
for ![]() $a \otimes b \in A_{p,\ell } \otimes B_{p, m}$. The symmetry isomorphism
$a \otimes b \in A_{p,\ell } \otimes B_{p, m}$. The symmetry isomorphism ![]() $c \colon A \hat {\otimes } B \rightarrow B \hat {\otimes } A$ sends a homogeneous element
$c \colon A \hat {\otimes } B \rightarrow B \hat {\otimes } A$ sends a homogeneous element ![]() $a \otimes b$ as above to
$a \otimes b$ as above to ![]() $(-1)^{\ell \cdot m} b \otimes a$.
$(-1)^{\ell \cdot m} b \otimes a$.
We denote by ![]() $\widetilde {\Sigma }_s$ the translation category of the symmetric group
$\widetilde {\Sigma }_s$ the translation category of the symmetric group ![]() $\Sigma _s$. Its objects are elements
$\Sigma _s$. Its objects are elements ![]() $\sigma \in \Sigma _s$ and
$\sigma \in \Sigma _s$ and ![]() $\tau \in \Sigma _s$ is the unique morphism from
$\tau \in \Sigma _s$ is the unique morphism from ![]() $\sigma$ to
$\sigma$ to ![]() $\tau \circ \sigma$ in
$\tau \circ \sigma$ in ![]() $\widetilde {\Sigma }_s$. Since there is exactly one morphism between each pair of objects, we get a functor
$\widetilde {\Sigma }_s$. Since there is exactly one morphism between each pair of objects, we get a functor
by specifying that ![]() $(\sigma \; \tau _1,\ldots , \tau _s)$ is sent to the composite
$(\sigma \; \tau _1,\ldots , \tau _s)$ is sent to the composite
of the block permutation ![]() $\sigma (j_1,\ldots ,j_s) \colon {{\mathbf{j}_1}}\sqcup \cdots \sqcup {{\mathbf{j}_s}} \to {{\mathbf{j}_{\sigma ^{-1}(1)}}} \sqcup \cdots \sqcup {{\mathbf{j}_{\sigma ^{-1}(s)}}}$ induced by
$\sigma (j_1,\ldots ,j_s) \colon {{\mathbf{j}_1}}\sqcup \cdots \sqcup {{\mathbf{j}_s}} \to {{\mathbf{j}_{\sigma ^{-1}(1)}}} \sqcup \cdots \sqcup {{\mathbf{j}_{\sigma ^{-1}(s)}}}$ induced by ![]() $\sigma$ and the concatenation of the
$\sigma$ and the concatenation of the ![]() $\tau _{\sigma ^{-1}(j)}$ (see [Reference MayMay74, § 4] and [Reference Cohen, Lada and MayCLM76, Correction 34 on p. 490]).
$\tau _{\sigma ^{-1}(j)}$ (see [Reference MayMay74, § 4] and [Reference Cohen, Lada and MayCLM76, Correction 34 on p. 490]).
The action (2.4) is associative, unital, and symmetric. It turns the collection of categories ![]() $(\widetilde {\Sigma }_n)_{n\geq 0}$ into an operad
$(\widetilde {\Sigma }_n)_{n\geq 0}$ into an operad ![]() $\widetilde {\Sigma }$ in the category
$\widetilde {\Sigma }$ in the category ![]() $\mathrm {cat}$ of small categories. For the next definition, we use that the nerve functor
$\mathrm {cat}$ of small categories. For the next definition, we use that the nerve functor ![]() $\mathcal {N}\colon \mathrm {cat} \to \mathrm {sSet}$ and the
$\mathcal {N}\colon \mathrm {cat} \to \mathrm {sSet}$ and the ![]() $k$-linearization
$k$-linearization ![]() $k\{-\}\colon \mathrm {sSet} \to \mathrm {sMod}_k$ are strong symmetric monoidal and that the associated chain complex functor
$k\{-\}\colon \mathrm {sSet} \to \mathrm {sMod}_k$ are strong symmetric monoidal and that the associated chain complex functor ![]() $C_*\colon \mathrm {sMod}_k \to \mathrm {Ch}_k$ is lax symmetric monoidal (compare Proposition 2.16 below).
$C_*\colon \mathrm {sMod}_k \to \mathrm {Ch}_k$ is lax symmetric monoidal (compare Proposition 2.16 below).
Definition 2.11 The Barratt–Eccles operad is the ![]() $E_{\infty }$ operad
$E_{\infty }$ operad ![]() $\mathcal {E}$ in
$\mathcal {E}$ in ![]() $\mathrm {Ch}_k$ with
$\mathrm {Ch}_k$ with ![]() $\mathcal {E}_n = C_*(k\{\mathcal {N}(\widetilde {\Sigma }_n)\})$ and operad structure induced by the functor (2.4).
$\mathcal {E}_n = C_*(k\{\mathcal {N}(\widetilde {\Sigma }_n)\})$ and operad structure induced by the functor (2.4).
The commutativity operad ![]() $\mathcal {C}$ in
$\mathcal {C}$ in ![]() $\mathrm {Ch}_k$ is the operad with
$\mathrm {Ch}_k$ is the operad with ![]() $\mathcal {C}_n = S^{0}$ concentrated in chain complex level
$\mathcal {C}_n = S^{0}$ concentrated in chain complex level ![]() $0$. The operad
$0$. The operad ![]() $\mathcal {E}$ admits a canonical operad map
$\mathcal {E}$ admits a canonical operad map ![]() $\mathcal {E} \to \mathcal {C}$ which is a quasi-isomorphism in each level. Moreover,
$\mathcal {E} \to \mathcal {C}$ which is a quasi-isomorphism in each level. Moreover, ![]() $\mathcal {E}_n$ is a free
$\mathcal {E}_n$ is a free ![]() $k[\Sigma _n]$-module for each
$k[\Sigma _n]$-module for each ![]() $n$. Thus
$n$. Thus ![]() $\mathcal {E}$ is an
$\mathcal {E}$ is an ![]() $E_{\infty }$ operad in
$E_{\infty }$ operad in ![]() $\mathrm {Ch}_k$ in the terminology of [Reference MandellMan02, Definition 4.1].
$\mathrm {Ch}_k$ in the terminology of [Reference MandellMan02, Definition 4.1].
Applying the nerve to ![]() $\widetilde {\Sigma }$ defines an operad in
$\widetilde {\Sigma }$ defines an operad in ![]() $\mathrm {sSet}$ that is more commonly referred to as the Barratt–Eccles operad. It is well known that the latter operad acts on the nerve of a permutative category [Reference MayMay74, Theorem 4.9]. The next lemma recalls the underlying action of
$\mathrm {sSet}$ that is more commonly referred to as the Barratt–Eccles operad. It is well known that the latter operad acts on the nerve of a permutative category [Reference MayMay74, Theorem 4.9]. The next lemma recalls the underlying action of ![]() $\widetilde {\Sigma }$ for the permutative category
$\widetilde {\Sigma }$ for the permutative category ![]() $\mathcal {I}$.
$\mathcal {I}$.
Lemma 2.12 The operad ![]() $\widetilde {\Sigma }$ in
$\widetilde {\Sigma }$ in ![]() $\mathrm {cat}$ acts on
$\mathrm {cat}$ acts on ![]() $\mathcal {I}$. On objects
$\mathcal {I}$. On objects ![]() $\sigma$ in
$\sigma$ in ![]() $\widetilde {\Sigma }_n$ and
$\widetilde {\Sigma }_n$ and ![]() ${\mathbf {m}_i}$ in
${\mathbf {m}_i}$ in ![]() $\mathcal {I}$, the action is given by
$\mathcal {I}$, the action is given by ![]() $(\sigma \; {{\mathbf{m}_1}}, \ldots , {{\mathbf{m}_n}}) \mapsto {{\mathbf{m}_{\sigma ^{-1}(1)}}} \sqcup \cdots \sqcup {{\mathbf{m}_{\sigma ^{-1}(n)}}}$.
$(\sigma \; {{\mathbf{m}_1}}, \ldots , {{\mathbf{m}_n}}) \mapsto {{\mathbf{m}_{\sigma ^{-1}(1)}}} \sqcup \cdots \sqcup {{\mathbf{m}_{\sigma ^{-1}(n)}}}$.
Proof. This is a special case of [Reference MayMay74, Lemmas 4.3 and 4.4]. Functoriality in morphisms of ![]() $\widetilde {\Sigma }_n$ uses the symmetry isomorphism of
$\widetilde {\Sigma }_n$ uses the symmetry isomorphism of ![]() $\mathcal {I}$ while the functoriality in
$\mathcal {I}$ while the functoriality in ![]() $\mathcal {I}$ is the evident one.
$\mathcal {I}$ is the evident one.
The next result is our main motivation for considering the Barratt–Eccles operad. It is analogous to the result about ![]() $\mathcal {I}$-diagrams in spaces established in [Reference SchlichtkrullSch09, Proposition 6.5].
$\mathcal {I}$-diagrams in spaces established in [Reference SchlichtkrullSch09, Proposition 6.5].
Theorem 2.13 For every commutative ![]() $\mathcal {I}$-dga
$\mathcal {I}$-dga ![]() $E$, the chain complex
$E$, the chain complex ![]() $E_{h\mathcal {I}}$ has a natural action of the Barratt–Eccles operad
$E_{h\mathcal {I}}$ has a natural action of the Barratt–Eccles operad ![]() $\mathcal {E}$.
$\mathcal {E}$.
Proof. We can view the simplicial ![]() $k$-module
$k$-module ![]() $k\{\mathcal {N}(\widetilde {\Sigma }_n)\}$ as a simplicial chain complex concentrated in chain degree
$k\{\mathcal {N}(\widetilde {\Sigma }_n)\}$ as a simplicial chain complex concentrated in chain degree ![]() $0$. The operad structure of
$0$. The operad structure of ![]() $\widetilde {\Sigma }$ turns these simplicial
$\widetilde {\Sigma }$ turns these simplicial ![]() $k$-modules into an operad in
$k$-modules into an operad in ![]() $\mathrm {sMod}_k$ and in
$\mathrm {sMod}_k$ and in ![]() $s\mathrm {Ch}_k$. We construct an action
$s\mathrm {Ch}_k$. We construct an action
It is enough to specify the action of a ![]() $q$-simplex
$q$-simplex ![]() $\sigma _0 \xleftarrow {\tau _1} \sigma _1 \leftarrow \ldots \xleftarrow {\tau _q} \sigma _q$ in
$\sigma _0 \xleftarrow {\tau _1} \sigma _1 \leftarrow \ldots \xleftarrow {\tau _q} \sigma _q$ in ![]() $\mathcal {N}(\widetilde {\Sigma }_s)$ on a collection of elements
$\mathcal {N}(\widetilde {\Sigma }_s)$ on a collection of elements ![]() $(\alpha ^{i}_1, \ldots , \alpha ^{i}_q; x^{i})$ in
$(\alpha ^{i}_1, \ldots , \alpha ^{i}_q; x^{i})$ in ![]() $\operatorname {srep}(E)[q]_{p_i}$ where
$\operatorname {srep}(E)[q]_{p_i}$ where ![]() $\alpha ^{i}_j \colon {\mathbf{n}^{i}_j} \to {\mathbf{n}^{i}_{j-1}}$ is a map in
$\alpha ^{i}_j \colon {\mathbf{n}^{i}_j} \to {\mathbf{n}^{i}_{j-1}}$ is a map in ![]() $\mathcal {I}$ and
$\mathcal {I}$ and ![]() $x^{i}$ is an element in
$x^{i}$ is an element in ![]() $E({{\mathbf{n}}^{i}_q})_{p_i}$. On the indices
$E({{\mathbf{n}}^{i}_q})_{p_i}$. On the indices ![]() $(\alpha ^{i}_1, \ldots , \alpha ^{i}_q)$ for the sums in the simplicial replacement, we use the action of
$(\alpha ^{i}_1, \ldots , \alpha ^{i}_q)$ for the sums in the simplicial replacement, we use the action of ![]() $(\tau _1,\ldots , \tau _q)$ provided by the previous lemma. As element in
$(\tau _1,\ldots , \tau _q)$ provided by the previous lemma. As element in ![]() $E({\mathbf{n}_q^{\sigma _q^{-1}(1)}} \sqcup \cdots \sqcup {\mathbf{n}_q^{\sigma _q^{-1}(s)}})_{p_1+\cdots + p_s}$ we take the product
$E({\mathbf{n}_q^{\sigma _q^{-1}(1)}} \sqcup \cdots \sqcup {\mathbf{n}_q^{\sigma _q^{-1}(s)}})_{p_1+\cdots + p_s}$ we take the product ![]() $x^{\sigma _q^{-1}(1)}\cdots x^{\sigma _q^{-1}(s)}$. Since
$x^{\sigma _q^{-1}(1)}\cdots x^{\sigma _q^{-1}(s)}$. Since ![]() $E$ is commutative, this does indeed define an operad action in
$E$ is commutative, this does indeed define an operad action in ![]() $\mathrm {sCh}_k$. By Propositions 2.16 and 2.17 below, the composite
$\mathrm {sCh}_k$. By Propositions 2.16 and 2.17 below, the composite ![]() $\operatorname {Tot} C_*$ is lax symmetric monoidal. Hence it follows that
$\operatorname {Tot} C_*$ is lax symmetric monoidal. Hence it follows that ![]() $\mathcal {E}$ acts on
$\mathcal {E}$ acts on ![]() $E_{h\mathcal {I}}$.
$E_{h\mathcal {I}}$.
2.14 Monoidality of  $C_*$ and
$C_*$ and  $\operatorname {Tot}$
$\operatorname {Tot}$
It remains to verify the monoidal properties of ![]() $C_*$ and
$C_*$ and ![]() $\operatorname {Tot}$ that were used in the proof of Theorem 2.13.
$\operatorname {Tot}$ that were used in the proof of Theorem 2.13.
Definition 2.15 Let ![]() $Y$ and
$Y$ and ![]() $Z$ be two objects in
$Z$ be two objects in ![]() $\mathrm {Ch}_k(\mathrm {Ch}_k)$. Their tensor product is
$\mathrm {Ch}_k(\mathrm {Ch}_k)$. Their tensor product is ![]() $Y \otimes Z$ is the object in
$Y \otimes Z$ is the object in ![]() $\mathrm {Ch}_k(\mathrm {Ch}_k)$ with
$\mathrm {Ch}_k(\mathrm {Ch}_k)$ with
and differentials ![]() $d_h^{\otimes }(y \otimes z) = d_h(y) \otimes z + (-1)^{a_1}y \otimes d_h(z)$ and
$d_h^{\otimes }(y \otimes z) = d_h(y) \otimes z + (-1)^{a_1}y \otimes d_h(z)$ and ![]() $d_v^{\otimes }(y \otimes z) = {d_v(y) \otimes z} + (-1)^{b_1} y \otimes d_v(z)$. The symmetry isomorphism
$d_v^{\otimes }(y \otimes z) = {d_v(y) \otimes z} + (-1)^{b_1} y \otimes d_v(z)$. The symmetry isomorphism ![]() $\tau \colon Y \otimes Z \rightarrow Z \otimes Y$ sends a homogeneous element
$\tau \colon Y \otimes Z \rightarrow Z \otimes Y$ sends a homogeneous element ![]() $y \otimes z \in Y_{a_1,b_1} \otimes Z_{a_2,b_2}$ to
$y \otimes z \in Y_{a_1,b_1} \otimes Z_{a_2,b_2}$ to ![]() $(-1)^{a_1a_2 +b_1b_2} z \otimes y$.
$(-1)^{a_1a_2 +b_1b_2} z \otimes y$.
Proposition 2.16 The functor ![]() $C_* \colon \mathrm {sCh}_k \rightarrow {\mathrm {Ch}_k}(\mathrm {Ch}_k)$ is lax symmetric monoidal.
$C_* \colon \mathrm {sCh}_k \rightarrow {\mathrm {Ch}_k}(\mathrm {Ch}_k)$ is lax symmetric monoidal.
Proof. As in [Reference Mac LaneMac63, Theorem VIII.8.8] we denote ![]() $(p,q)$-shuffles as two disjoint subsets
$(p,q)$-shuffles as two disjoint subsets ![]() $\mu _1 < \cdots < \mu _p$ and
$\mu _1 < \cdots < \mu _p$ and ![]() $\nu _1 < \cdots < \nu _q$ of
$\nu _1 < \cdots < \nu _q$ of ![]() $\{0,\ldots , p+q-1\}$. For simplicial chain complexes
$\{0,\ldots , p+q-1\}$. For simplicial chain complexes ![]() $A$ and
$A$ and ![]() $B$ we define maps
$B$ we define maps
that turn ![]() $C_*$ into a lax symmetric monoidal functor: if
$C_*$ into a lax symmetric monoidal functor: if ![]() $a \otimes b$ is a homogeneous element in
$a \otimes b$ is a homogeneous element in ![]() $A_{r_1,r_2} \otimes B_{s_1,s_2}$ we set
$A_{r_1,r_2} \otimes B_{s_1,s_2}$ we set
Here, the sum runs over all ![]() $(r_1,s_1)$-shuffles
$(r_1,s_1)$-shuffles ![]() $(\mu , \nu )$ and
$(\mu , \nu )$ and ![]() $\text {sgn}(\mu ,\nu )$ denotes the signum of the associated permutation.
$\text {sgn}(\mu ,\nu )$ denotes the signum of the associated permutation.
As the simplicial structure maps of ![]() $A$ and
$A$ and ![]() $B$ commute with
$B$ commute with ![]() $d^{A}$ and
$d^{A}$ and ![]() $d^{B}$, it follows that
$d^{B}$, it follows that ![]() $\operatorname {sh}$ commutes with the vertical differential. The proof that the horizontal differential is compatible with
$\operatorname {sh}$ commutes with the vertical differential. The proof that the horizontal differential is compatible with ![]() $\operatorname {sh}$ is the same as for
$\operatorname {sh}$ is the same as for ![]() $\operatorname {sh}$ in the context of simplicial modules.
$\operatorname {sh}$ in the context of simplicial modules.
It remains to show that ![]() $\operatorname {sh}$ turns
$\operatorname {sh}$ turns ![]() $C_*$ into a lax symmetric monoidal functor, i.e., we have to show that
$C_*$ into a lax symmetric monoidal functor, i.e., we have to show that
for any homogeneous element ![]() $a \otimes b \in A_{r_1,r_2} \otimes B_{s_1,s_2}$. As
$a \otimes b \in A_{r_1,r_2} \otimes B_{s_1,s_2}$. As ![]() $\tau (a \otimes b) = (-1)^{r_1s_1+r_2s_2} b \otimes a$, the right-hand side of equation (2.5) is
$\tau (a \otimes b) = (-1)^{r_1s_1+r_2s_2} b \otimes a$, the right-hand side of equation (2.5) is
with ![]() $(\xi ,\zeta )$ being
$(\xi ,\zeta )$ being ![]() $(s_1,r_1)$-shuffles, whereas the left-hand side of the equation gives
$(s_1,r_1)$-shuffles, whereas the left-hand side of the equation gives
because ![]() $\tau$ introduces the sign
$\tau$ introduces the sign ![]() $(-1)^{r_2s_2}$. Precomposing with the permutation that exchanges the blocks
$(-1)^{r_2s_2}$. Precomposing with the permutation that exchanges the blocks ![]() $0 < \cdots < r_1-1$ and
$0 < \cdots < r_1-1$ and ![]() $r_1 < \cdots < r_1+s_1 -1$ gives a bijection between the summation indices and introduces the sign
$r_1 < \cdots < r_1+s_1 -1$ gives a bijection between the summation indices and introduces the sign ![]() $(-1)^{r_1s_1}$. Hence the two sides agree.
$(-1)^{r_1s_1}$. Hence the two sides agree.
Proposition 2.17 The functor ![]() $\operatorname {Tot}$ is strong symmetric monoidal.
$\operatorname {Tot}$ is strong symmetric monoidal.
Proof. Spelling out what ![]() $\operatorname {Tot}(Y) \otimes \operatorname {Tot}(Z)$ is in degree
$\operatorname {Tot}(Y) \otimes \operatorname {Tot}(Z)$ is in degree ![]() $n$ we obtain
$n$ we obtain
and we send a homogeneous element ![]() $y \otimes z \in Y_{r_1,r_2} \otimes Z_{s_1,s_2}$ to the element
$y \otimes z \in Y_{r_1,r_2} \otimes Z_{s_1,s_2}$ to the element
This gives isomorphisms
that are associative. It is clear that ![]() $\operatorname {Tot}$ respects the unit up to isomorphism.
$\operatorname {Tot}$ respects the unit up to isomorphism.
The maps ![]() $\varphi _{Y,Z}$ are compatible with the differential. Let
$\varphi _{Y,Z}$ are compatible with the differential. Let ![]() $y \otimes z$ be a homogeneous element in
$y \otimes z$ be a homogeneous element in ![]() $Y_{r_1,r_2} \otimes Z_{s_1,s_2}$. The composition
$Y_{r_1,r_2} \otimes Z_{s_1,s_2}$. The composition ![]() $d_{\operatorname {Tot}} \circ \varphi$ applied to
$d_{\operatorname {Tot}} \circ \varphi$ applied to ![]() $y \otimes z$ gives
$y \otimes z$ gives
 \begin{align*} d_{\operatorname{Tot}} \circ \varphi(y \otimes z) &= (-1)^{r_2s_1}d_h^{\otimes}(y \otimes z) + (-1)^{r_2s_1}(-1)^{r_1+s_1}d_v^{\otimes}(y \otimes z) \\ &= (-1)^{r_2s_1}d_h(y) \otimes z + (-1)^{r_2s_1+r_1} y \otimes d_h(z) \\ &\quad + (-1)^{r_2s_1+r_1+s_1}d_v(y) \otimes z + (-1)^{r_2s_1+r_1+s_1+r_2} y\otimes d_v(z). \end{align*}
\begin{align*} d_{\operatorname{Tot}} \circ \varphi(y \otimes z) &= (-1)^{r_2s_1}d_h^{\otimes}(y \otimes z) + (-1)^{r_2s_1}(-1)^{r_1+s_1}d_v^{\otimes}(y \otimes z) \\ &= (-1)^{r_2s_1}d_h(y) \otimes z + (-1)^{r_2s_1+r_1} y \otimes d_h(z) \\ &\quad + (-1)^{r_2s_1+r_1+s_1}d_v(y) \otimes z + (-1)^{r_2s_1+r_1+s_1+r_2} y\otimes d_v(z). \end{align*}
First applying the differential to ![]() $y \otimes z$ and then
$y \otimes z$ and then ![]() $\varphi$ yields
$\varphi$ yields
 \begin{align*} & \varphi(d_{\operatorname{Tot}}(y) \otimes z + (-1)^{r_1+r_2}y \otimes d_{\operatorname{Tot}}(z)) \\ &\quad = \varphi(d_h(y) \otimes z + (-1)^{r_1}d_v(y) \otimes z + (-1)^{r_1+r_2}y \otimes d_h(z) + (-1)^{r_1+r_2+s_1} y \otimes d_v(z)) \\ &\quad = (-1)^{r_2s_1}d_h(y) \otimes z + (-1)^{r_1+(r_2-1)s_1}d_v(y) \otimes z + (-1)^{r_1+r_2+r_2(s_1-1)}y \otimes d_h(z)\\ &\qquad + (-1)^{r_1+r_2+s_1+r_2s_1} y \otimes d_v(z), \end{align*}
\begin{align*} & \varphi(d_{\operatorname{Tot}}(y) \otimes z + (-1)^{r_1+r_2}y \otimes d_{\operatorname{Tot}}(z)) \\ &\quad = \varphi(d_h(y) \otimes z + (-1)^{r_1}d_v(y) \otimes z + (-1)^{r_1+r_2}y \otimes d_h(z) + (-1)^{r_1+r_2+s_1} y \otimes d_v(z)) \\ &\quad = (-1)^{r_2s_1}d_h(y) \otimes z + (-1)^{r_1+(r_2-1)s_1}d_v(y) \otimes z + (-1)^{r_1+r_2+r_2(s_1-1)}y \otimes d_h(z)\\ &\qquad + (-1)^{r_1+r_2+s_1+r_2s_1} y \otimes d_v(z), \end{align*}and thus both terms agree.
We denote the symmetry isomorphism in the category of chain complexes by ![]() $\chi$. Then
$\chi$. Then
and this is equal to
Remark 2.18 One can also consider a symmetric monoidal structure on ![]() $\mathrm {Ch}_k(\mathrm {Ch}_k)$ with the same underlying tensor product but with symmetry isomorphism
$\mathrm {Ch}_k(\mathrm {Ch}_k)$ with the same underlying tensor product but with symmetry isomorphism
for homogeneous elements ![]() $y \otimes z \in Y_{r_1,r_2} \otimes Z_{s_1,s_2}$. Then one can take
$y \otimes z \in Y_{r_1,r_2} \otimes Z_{s_1,s_2}$. Then one can take ![]() $\varphi$ in Proposition 2.17 to be the identity. However, this symmetry isomorphism is not compatible with the shuffle transformation from the proof of Proposition 2.16.
$\varphi$ in Proposition 2.17 to be the identity. However, this symmetry isomorphism is not compatible with the shuffle transformation from the proof of Proposition 2.16.
Remark 2.19 For a simplicial chain complex ![]() $A$ one can also consider a normalized object
$A$ one can also consider a normalized object ![]() $N(A) \in \mathrm {Ch}_k(\mathrm {Ch}_k)$ where one divides out by the subobject generated by degenerate elements. As the simplicial structure maps commute with the differential of
$N(A) \in \mathrm {Ch}_k(\mathrm {Ch}_k)$ where one divides out by the subobject generated by degenerate elements. As the simplicial structure maps commute with the differential of ![]() $A$, this is well defined, and the proof of Proposition 2.16 can be adapted as in [Reference Mac LaneMac63, Corollary VIII.8.9] to show that the functor
$A$, this is well defined, and the proof of Proposition 2.16 can be adapted as in [Reference Mac LaneMac63, Corollary VIII.8.9] to show that the functor ![]() $N\colon \mathrm {sCh}_k \rightarrow \mathrm {Ch}_k(\mathrm {Ch}_k)$ is also lax symmetric monoidal. Consequently, one can also use
$N\colon \mathrm {sCh}_k \rightarrow \mathrm {Ch}_k(\mathrm {Ch}_k)$ is also lax symmetric monoidal. Consequently, one can also use ![]() $N$ instead of
$N$ instead of ![]() $C_*$ in the definition of the Barratt–Eccles operad
$C_*$ in the definition of the Barratt–Eccles operad ![]() $\mathcal {E}$ and the homotopy colimit
$\mathcal {E}$ and the homotopy colimit ![]() $P_{h\mathcal {I}}$ so that Theorem 2.13 remains valid.
$P_{h\mathcal {I}}$ so that Theorem 2.13 remains valid.
3. Cochain functors with values in  $\mathcal {I}$-chain complexes
$\mathcal {I}$-chain complexes
In this section we construct the functor ![]() $A^{\mathcal {I}}$ discussed in the introduction and a version of the ordinary cochains with values in
$A^{\mathcal {I}}$ discussed in the introduction and a version of the ordinary cochains with values in ![]() $\mathcal {I}$-chain complexes.
$\mathcal {I}$-chain complexes.
3.1 Adjunctions induced by simplicial objects
We briefly recall an ubiquitous construction principle for adjunctions that we will later apply to simplicial objects in the categories of commutative ![]() $\mathcal {I}$-dgas and
$\mathcal {I}$-dgas and ![]() $\mathcal {I}$-chain complexes in order to define the commutative
$\mathcal {I}$-chain complexes in order to define the commutative ![]() $\mathcal {I}$-dga of polynomial forms on a simplicial set and an integral version of the Sullivan realization functor (see Definition 3.6).
$\mathcal {I}$-dga of polynomial forms on a simplicial set and an integral version of the Sullivan realization functor (see Definition 3.6).
Construction Let ![]() $D_{\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathcal {D}$ be a simplicial object in a complete category
$D_{\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathcal {D}$ be a simplicial object in a complete category ![]() $\mathcal {D}$. Passing to opposite categories,
$\mathcal {D}$. Passing to opposite categories, ![]() $D_{\bullet }$ gives rise to a functor
$D_{\bullet }$ gives rise to a functor ![]() $\widetilde {D}^{\bullet } \colon \Delta \to \mathcal {D}^{{{\mathrm {op}}}}$. Since
$\widetilde {D}^{\bullet } \colon \Delta \to \mathcal {D}^{{{\mathrm {op}}}}$. Since ![]() $\mathcal {D}$ is complete,
$\mathcal {D}$ is complete, ![]() $\mathcal {D}^{{{\mathrm {op}}}}$ is cocomplete. Hence restriction and left Kan extension along
$\mathcal {D}^{{{\mathrm {op}}}}$ is cocomplete. Hence restriction and left Kan extension along ![]() $\Delta \to \mathrm {sSet}, [p]\mapsto \Delta ^{p}$ define an adjunction
$\Delta \to \mathrm {sSet}, [p]\mapsto \Delta ^{p}$ define an adjunction
Writing ![]() $D \colon \mathrm {sSet}^{{{\mathrm {op}}}} \to \mathcal {D}$ for the opposite of
$D \colon \mathrm {sSet}^{{{\mathrm {op}}}} \to \mathcal {D}$ for the opposite of ![]() $\widetilde {D}$, this implies that for a simplicial set
$\widetilde {D}$, this implies that for a simplicial set ![]() $X$ and an object
$X$ and an object ![]() $E$ of
$E$ of ![]() $\mathcal {D}$, we have a natural isomorphism
$\mathcal {D}$, we have a natural isomorphism
exhibiting ![]() $D$ and
$D$ and ![]() $K_D$ as contravariant right adjoint functors. Unraveling definitions, the contravariant functors
$K_D$ as contravariant right adjoint functors. Unraveling definitions, the contravariant functors ![]() $K_D$ and
$K_D$ and ![]() $D$ are given by
$D$ are given by ![]() $K_D(E)_\bullet = \mathcal {D}(E,D_\bullet )$ and
$K_D(E)_\bullet = \mathcal {D}(E,D_\bullet )$ and ![]() $D(X) = \lim _{\Delta ^{p} \to X} D_p$ where the limit is taken over the category of elements of
$D(X) = \lim _{\Delta ^{p} \to X} D_p$ where the limit is taken over the category of elements of ![]() $X$. In the special case
$X$. In the special case ![]() $\mathcal {D} = \mathrm {Set}$, writing
$\mathcal {D} = \mathrm {Set}$, writing ![]() $X$ as a colimit of representable functors indexed over its category of elements provides a natural bijection
$X$ as a colimit of representable functors indexed over its category of elements provides a natural bijection ![]() $D(X) \cong \mathrm {sSet}(X,D)$.
$D(X) \cong \mathrm {sSet}(X,D)$.
The functor ![]() $D$ extends the original functor
$D$ extends the original functor ![]() $D_{\bullet }$ in that there is a natural isomorphism
$D_{\bullet }$ in that there is a natural isomorphism ![]() $D_{\bullet } \cong D(\Delta ^{\bullet })$. The construction is also functorial in
$D_{\bullet } \cong D(\Delta ^{\bullet })$. The construction is also functorial in ![]() $D_{\bullet }$, i.e., a natural transformation
$D_{\bullet }$, i.e., a natural transformation ![]() $D_{\bullet } \to D'_{\bullet }$ of functors
$D_{\bullet } \to D'_{\bullet }$ of functors ![]() $\Delta ^{{{\mathrm {op}}}}\to \mathcal {D}$ induces a natural transformation
$\Delta ^{{{\mathrm {op}}}}\to \mathcal {D}$ induces a natural transformation ![]() $D \to D'$ of functors
$D \to D'$ of functors ![]() $\mathrm {sSet}^{{{\mathrm {op}}}} \to \mathcal {D}$.
$\mathrm {sSet}^{{{\mathrm {op}}}} \to \mathcal {D}$.
We note an immediate consequence of having the adjunction ![]() $(\widetilde D, K_D)$.
$(\widetilde D, K_D)$.
Lemma 3.3 The functor ![]() $D$ takes colimits in
$D$ takes colimits in ![]() $\mathrm {sSet}$ to limits in
$\mathrm {sSet}$ to limits in ![]() $\mathcal {D}$, and
$\mathcal {D}$, and ![]() $K_D$ takes colimits in
$K_D$ takes colimits in ![]() $\mathcal {D}$ to limits in
$\mathcal {D}$ to limits in ![]() $\mathrm {sSet}$.
$\mathrm {sSet}$.
When ![]() $D_{\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ is a simplicial object in commutative
$D_{\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ is a simplicial object in commutative ![]() $\mathcal {I}$-dgas, we may apply Construction 3.2 both to
$\mathcal {I}$-dgas, we may apply Construction 3.2 both to ![]() $D_{\bullet }$ and to its composite
$D_{\bullet }$ and to its composite ![]() $D'_{\bullet } = UD_{\bullet }$ with the forgetful functor
$D'_{\bullet } = UD_{\bullet }$ with the forgetful functor ![]() $U\colon \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}] \to \mathrm {Ch}^{\mathcal {I}}_k$. Since the extensions of
$U\colon \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}] \to \mathrm {Ch}^{\mathcal {I}}_k$. Since the extensions of ![]() $D_{\bullet }$ and
$D_{\bullet }$ and ![]() $D'_{\bullet }$ to functors on
$D'_{\bullet }$ to functors on ![]() $\mathrm {sSet}$ are defined by limit constructions and
$\mathrm {sSet}$ are defined by limit constructions and ![]() $U$ commutes with limits, we have a natural isomorphism
$U$ commutes with limits, we have a natural isomorphism ![]() $U(D(X)) \cong D'(X)$ for a simplicial set
$U(D(X)) \cong D'(X)$ for a simplicial set ![]() $X$. The adjoints
$X$. The adjoints ![]() $K_{D}$ and
$K_{D}$ and ![]() $K_{D'}$ are related by a natural isomorphism
$K_{D'}$ are related by a natural isomorphism ![]() $K_{D'} \cong K_{D}\circ \mathbb {C} \colon (\mathrm {Ch}^{\mathcal {I}}_k)^{{{\mathrm {op}}}} \to \mathrm {sSet}$. An analogous remark applies to simplicial objects of algebras in
$K_{D'} \cong K_{D}\circ \mathbb {C} \colon (\mathrm {Ch}^{\mathcal {I}}_k)^{{{\mathrm {op}}}} \to \mathrm {sSet}$. An analogous remark applies to simplicial objects of algebras in ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ over a more general operad than the commutativity operad.
$\mathrm {Ch}^{\mathcal {I}}_k$ over a more general operad than the commutativity operad.
For ![]() $D_{\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$, the fact that
$D_{\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$, the fact that ![]() $\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}] \to \mathrm {Set}$,
$\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}] \to \mathrm {Set}$, ![]() $E\mapsto E({\mathbf {m}})_q$ commutes with limits implies that the underlying set of
$E\mapsto E({\mathbf {m}})_q$ commutes with limits implies that the underlying set of ![]() $D(X)({\mathbf {m}})_q$ is
$D(X)({\mathbf {m}})_q$ is ![]() $\mathrm {sSet}(X,D_{\bullet }({\mathbf {m}})_q)$. The pointwise
$\mathrm {sSet}(X,D_{\bullet }({\mathbf {m}})_q)$. The pointwise ![]() $k$-module structure, differentials and multiplications on these sets give rise to the commutative
$k$-module structure, differentials and multiplications on these sets give rise to the commutative ![]() $\mathcal {I}$-dga structure on
$\mathcal {I}$-dga structure on ![]() $D(X)$.
$D(X)$.
3.4 The commutative  $\mathcal {I}$-dga version of polynomial forms
$\mathcal {I}$-dga version of polynomial forms
Composing the left adjoints in the adjunctions ![]() $(F_{{\mathbf {1}}}^{\mathcal {I}},\mathrm {Ev_{{\mathbf {1}}}})$ and
$(F_{{\mathbf {1}}}^{\mathcal {I}},\mathrm {Ev_{{\mathbf {1}}}})$ and ![]() $(\mathbb {C},U)$ introduced in (2.1) and (2.2) provides a left adjoint
$(\mathbb {C},U)$ introduced in (2.1) and (2.2) provides a left adjoint ![]() $\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}} \colon \mathrm {Ch}_k \to \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ made explicit in (2.3). We are particularly interested in the commutative
$\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}} \colon \mathrm {Ch}_k \to \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ made explicit in (2.3). We are particularly interested in the commutative ![]() $\mathcal {I}$-dga
$\mathcal {I}$-dga ![]() $\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0})$. For an element
$\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0})$. For an element ![]() $i \in k$, the
$i \in k$, the ![]() $k$-module map
$k$-module map ![]() $(D^{0})_0 = k \to k = \mathrm {Ev}_1(U^{\mathcal {I}})_0$ determined by
$(D^{0})_0 = k \to k = \mathrm {Ev}_1(U^{\mathcal {I}})_0$ determined by ![]() $1\mapsto i$ gives rise to a map
$1\mapsto i$ gives rise to a map ![]() $\varepsilon _i \colon \mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0}) \to U^{\mathcal {I}}$. We write
$\varepsilon _i \colon \mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0}) \to U^{\mathcal {I}}$. We write ![]() $U^{\mathcal {I}}_0$ and
$U^{\mathcal {I}}_0$ and ![]() $U^{\mathcal {I}}_1$ for the two commutative
$U^{\mathcal {I}}_1$ for the two commutative ![]() $\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0})$-algebras resulting from the elements
$\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0})$-algebras resulting from the elements ![]() $0,1 \in k$.
$0,1 \in k$.
Definition 3.5 We let ![]() $A^{\mathcal {I}}_{\bullet }\colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ be the simplicial commutative
$A^{\mathcal {I}}_{\bullet }\colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ be the simplicial commutative ![]() $\mathcal {I}$-dga given by the two-sided bar construction
$\mathcal {I}$-dga given by the two-sided bar construction
As with the space-level version (see e.g. [Reference MayMay72]), the outer face maps are provided by the module structures of ![]() $U^{\mathcal {I}}_0$ and
$U^{\mathcal {I}}_0$ and ![]() $U^{\mathcal {I}}_1$ resulting from the above algebra structures, the inner face maps come from the multiplication of
$U^{\mathcal {I}}_1$ resulting from the above algebra structures, the inner face maps come from the multiplication of ![]() $\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0})$, and the degeneracy maps are induced by its unit.
$\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0})$, and the degeneracy maps are induced by its unit.
To make this simplicial object more explicit, we write ![]() $D^{0}_r$ for the chain complex with copies of
$D^{0}_r$ for the chain complex with copies of ![]() $k$ on generators
$k$ on generators ![]() $r$ in degree
$r$ in degree ![]() $0$ and on
$0$ and on ![]() $dr$ in degree
$dr$ in degree ![]() $-1$ and
$-1$ and ![]() $0$ elsewhere. Its non-zero differential is
$0$ elsewhere. Its non-zero differential is ![]() $d(a\cdot r) = a\cdot dr$. Since
$d(a\cdot r) = a\cdot dr$. Since ![]() $\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}$ is left adjoint and
$\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}$ is left adjoint and ![]() $U^{\mathcal {I}}$ is the unit for
$U^{\mathcal {I}}$ is the unit for ![]() $\boxtimes$, commuting
$\boxtimes$, commuting ![]() $\mathbb {C} F_1^{\mathcal {I}}$ with coproducts provides an isomorphism of commutative
$\mathbb {C} F_1^{\mathcal {I}}$ with coproducts provides an isomorphism of commutative ![]() $\mathcal {I}$-dgas
$\mathcal {I}$-dgas
where the generators ![]() $r_1(p), \ldots , r_p(p)$ correspond to the
$r_1(p), \ldots , r_p(p)$ correspond to the ![]() $p$ copies of
$p$ copies of ![]() $\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0})$. By adjunction, maps
$\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0})$. By adjunction, maps ![]() $f \colon \mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0}_{r_1(p)} \oplus \cdots \oplus D^{0}_{r_p(p)}) \to E$ in
$f \colon \mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0}_{r_1(p)} \oplus \cdots \oplus D^{0}_{r_p(p)}) \to E$ in ![]() $\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ correspond to families of elements
$\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ correspond to families of elements ![]() $f(r_1(p)), \ldots , f(r_p(p)) \in E(\mathbf {1})_0$.
$f(r_1(p)), \ldots , f(r_p(p)) \in E(\mathbf {1})_0$.
We now set ![]() $r_0(p) = 0$ and define
$r_0(p) = 0$ and define ![]() $r_{p+1}(p)$ to be the image of
$r_{p+1}(p)$ to be the image of ![]() $1$ under the map
$1$ under the map
induced by the unit. With this notation, the simplicial structure maps of the two-sided bar construction (3.2) are determined by requiring
 \begin{equation} d_i(r_j(p)) = \begin{cases} r_j(p-1) & \text{if } j \leq i ,\\ r_{j-1}(p-1) & \text{if } j> i, \end{cases}\quad s_i(r_j(p)) = \begin{cases} r_j(p+1) & \text{if } j \leq i , \\ r_{j+1}(p+1) & \text{if } j > i. \end{cases} \end{equation}
\begin{equation} d_i(r_j(p)) = \begin{cases} r_j(p-1) & \text{if } j \leq i ,\\ r_{j-1}(p-1) & \text{if } j> i, \end{cases}\quad s_i(r_j(p)) = \begin{cases} r_j(p+1) & \text{if } j \leq i , \\ r_{j+1}(p+1) & \text{if } j > i. \end{cases} \end{equation}Applying Construction 3.2, we obtain the following pair of adjoint functors.
Definition 3.6
(i) The commutative
 $\mathcal {I}$-dga of polynomial forms on a simplicial set
$\mathcal {I}$-dga of polynomial forms on a simplicial set  $X$,
$X$,  $A^{\mathcal {I}}(X)$, is defined as
This defines a functor
$A^{\mathcal {I}}(X)$, is defined as
This defines a functor \[ A^{\mathcal{I}}(X) = \mathrm{sSet}(X, A^{\mathcal{I}}_\bullet). \]
\[ A^{\mathcal{I}}(X) = \mathrm{sSet}(X, A^{\mathcal{I}}_\bullet). \] $A^{\mathcal {I}} \colon \mathrm {sSet}^{{{\mathrm {op}}}} \rightarrow \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$.
$A^{\mathcal {I}} \colon \mathrm {sSet}^{{{\mathrm {op}}}} \rightarrow \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$.(ii) Its adjoint functor
 $\langle -\rangle _\mathcal {I} \colon \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]^{{{\mathrm {op}}}}\rightarrow \mathrm {sSet}$ sends a commutative
$\langle -\rangle _\mathcal {I} \colon \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]^{{{\mathrm {op}}}}\rightarrow \mathrm {sSet}$ sends a commutative  $\mathcal {I}$-dga
$\mathcal {I}$-dga  $E$ to
The simplicial set
$E$ to
The simplicial set \[ \langle E\rangle_\mathcal{I} = \mathrm{Ch}^{\mathcal{I}}_k[\mathcal{C}](E, A^{\mathcal{I}}_\bullet). \]
\[ \langle E\rangle_\mathcal{I} = \mathrm{Ch}^{\mathcal{I}}_k[\mathcal{C}](E, A^{\mathcal{I}}_\bullet). \] $\langle E\rangle _\mathcal {I}$ is the Sullivan realization of
$\langle E\rangle _\mathcal {I}$ is the Sullivan realization of  $E$.
$E$.
For a simplicial ![]() $k$-module
$k$-module ![]() $Z \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Mod}_k$, extra degeneracies are a family of
$Z \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Mod}_k$, extra degeneracies are a family of ![]() $k$-linear maps
$k$-linear maps ![]() $s_{p+1}\colon Z_p \to Z_{p+1}$ satisfying:
$s_{p+1}\colon Z_p \to Z_{p+1}$ satisfying: ![]() $d_{p+1} s_{p+1} = {{\mathrm {id}}}_{Z_p}$ if
$d_{p+1} s_{p+1} = {{\mathrm {id}}}_{Z_p}$ if ![]() $p \geq 0$;
$p \geq 0$; ![]() $d_i s_{p+1} = s_p d_i \colon Z_p \to Z_p$ if
$d_i s_{p+1} = s_p d_i \colon Z_p \to Z_p$ if ![]() $p\geq 1$ and
$p\geq 1$ and ![]() $0\leq i \leq p$; and
$0\leq i \leq p$; and ![]() $0 = d_0 s_1 \colon Z_0 \to Z_0$. The presence of extra degeneracies implies that
$0 = d_0 s_1 \colon Z_0 \to Z_0$. The presence of extra degeneracies implies that ![]() $Z$ is contractible to
$Z$ is contractible to ![]() $0$ (in the sense that
$0$ (in the sense that ![]() $Z \to 0$ is a weak equivalence in
$Z \to 0$ is a weak equivalence in ![]() $\mathrm {sMod}_k$) since the maps
$\mathrm {sMod}_k$) since the maps ![]() $(-1)^{p+1} s_{p+1}$ define a contracting homotopy for the chain complex
$(-1)^{p+1} s_{p+1}$ define a contracting homotopy for the chain complex ![]() $C_*(Z)$.
$C_*(Z)$.
The following lemma is the technical backbone for our homotopical analysis of the prolongation ![]() $A^{\mathcal {I}}$ of
$A^{\mathcal {I}}$ of ![]() $A^{\mathcal {I}}_{\bullet }$ in § 5. It is analogous to [Reference Bousfield and GugenheimBG76, Proposition 1.1].
$A^{\mathcal {I}}_{\bullet }$ in § 5. It is analogous to [Reference Bousfield and GugenheimBG76, Proposition 1.1].
Lemma 3.7 Let ![]() ${\mathbf {m}}$ be an object of
${\mathbf {m}}$ be an object of ![]() $\mathcal {I}$ with
$\mathcal {I}$ with ![]() $m = |{\mathbf {m}}|\geq 1$. Then for all integers
$m = |{\mathbf {m}}|\geq 1$. Then for all integers ![]() $q$ satisfying
$q$ satisfying ![]() $0 \geq q > -m$, the simplicial
$0 \geq q > -m$, the simplicial ![]() $k$-module
$k$-module ![]() $A^{\mathcal {I}}_\bullet ({\mathbf {m}})_q$ is contractible to
$A^{\mathcal {I}}_\bullet ({\mathbf {m}})_q$ is contractible to ![]() $0$.
$0$.
Remark 3.8 The statement of the lemma does not hold for general ![]() ${\mathbf {m}}$ and
${\mathbf {m}}$ and ![]() $q$. The easiest case is
$q$. The easiest case is ![]() ${\mathbf {m}} = {\mathbf {0}}$ and
${\mathbf {m}} = {\mathbf {0}}$ and ![]() $q=0$ where
$q=0$ where ![]() $A^{\mathcal {I}}_\bullet ({\mathbf {0}})_0$ is the constant simplicial object on
$A^{\mathcal {I}}_\bullet ({\mathbf {0}})_0$ is the constant simplicial object on ![]() $k$, which is not contractible. One can also show that
$k$, which is not contractible. One can also show that ![]() $\pi _1(A^{\mathcal {I}}_\bullet ({\mathbf {1}})_{-1})$ is non-trivial.
$\pi _1(A^{\mathcal {I}}_\bullet ({\mathbf {1}})_{-1})$ is non-trivial.
Proof of Lemma 3.7 Let ![]() $A$ be a chain complex. The canonical bijection
$A$ be a chain complex. The canonical bijection
induces natural isomorphisms
 \begin{equation} \mathbb{C}(F_{{\mathbf{1}}}^{\mathcal{I}}(A))({\mathbf{m}}) = \bigoplus_{s\geq 0}\biggl(\bigoplus_{\mathcal{I}({\mathbf{1}}^{\sqcup s},{\mathbf{m}})} A^{\otimes s}/\Sigma_s\biggr) \xrightarrow{\cong} \bigoplus_{T \subseteq {\mathbf{m}}} A^{\otimes T}\xrightarrow{\cong} (A \oplus S^{0})^{\otimes m}. \end{equation}
\begin{equation} \mathbb{C}(F_{{\mathbf{1}}}^{\mathcal{I}}(A))({\mathbf{m}}) = \bigoplus_{s\geq 0}\biggl(\bigoplus_{\mathcal{I}({\mathbf{1}}^{\sqcup s},{\mathbf{m}})} A^{\otimes s}/\Sigma_s\biggr) \xrightarrow{\cong} \bigoplus_{T \subseteq {\mathbf{m}}} A^{\otimes T}\xrightarrow{\cong} (A \oplus S^{0})^{\otimes m}. \end{equation}
Here the last isomorphism sends the tensor power indexed by ![]() $T$ to an iterated tensor product of copies of
$T$ to an iterated tensor product of copies of ![]() $A$ and
$A$ and ![]() $S^{0}$ with copies of
$S^{0}$ with copies of ![]() $A$ placed at the entries indexed by
$A$ placed at the entries indexed by ![]() $T$.
$T$.
The isomorphism (3.4) specializes to an isomorphism
where we now write ![]() $r_{p+1}(p)$ for the generator of
$r_{p+1}(p)$ for the generator of ![]() $(S^{0})_0$. Under this identification, the simplicial structure maps of
$(S^{0})_0$. Under this identification, the simplicial structure maps of ![]() $[p] \mapsto A^{\mathcal {I}}_p({\mathbf {m}})_q$ are again determined by (3.3).
$[p] \mapsto A^{\mathcal {I}}_p({\mathbf {m}})_q$ are again determined by (3.3).
As a first step, we now notice that ![]() $A^{\mathcal {I}}_{\bullet } ({\mathbf {1}})_0$ is contractible since
$A^{\mathcal {I}}_{\bullet } ({\mathbf {1}})_0$ is contractible since ![]() $s_{p+1}(r_j(p)) = r_{j}(p+1)$ defines extra degeneracies for this simplicial object. For the case of a general
$s_{p+1}(r_j(p)) = r_{j}(p+1)$ defines extra degeneracies for this simplicial object. For the case of a general ![]() ${\mathbf {m}}$ and
${\mathbf {m}}$ and ![]() $0\geq q > -m$, we notice that the above isomorphisms induce an isomorphism of simplicial objects
$0\geq q > -m$, we notice that the above isomorphisms induce an isomorphism of simplicial objects
 \[ A^{\mathcal{I}}_p({\mathbf{m}})_q \cong \bigoplus_{\substack{q_1+ \cdots + q_m = q\\ q_i = 0, -1} } A^{\mathcal{I}}_p({\mathbf{1}})_{q_1} \otimes \dots \otimes A^{\mathcal{I}}_p({\mathbf{1}})_{q_m}. \]
\[ A^{\mathcal{I}}_p({\mathbf{m}})_q \cong \bigoplus_{\substack{q_1+ \cdots + q_m = q\\ q_i = 0, -1} } A^{\mathcal{I}}_p({\mathbf{1}})_{q_1} \otimes \dots \otimes A^{\mathcal{I}}_p({\mathbf{1}})_{q_m}. \]
Since ![]() $q > -m$, each summand has at least one tensor factor that is of chain complex degree
$q > -m$, each summand has at least one tensor factor that is of chain complex degree ![]() $0$ and thus contractible by the previous step. Since the shuffle map is a chain homotopy equivalence [Reference Mac LaneMac63, Theorem VIII.8.1], it follows that each summand and thus the whole sum is contractible.
$0$ and thus contractible by the previous step. Since the shuffle map is a chain homotopy equivalence [Reference Mac LaneMac63, Theorem VIII.8.1], it follows that each summand and thus the whole sum is contractible.
3.9 Ordinary cochains
Let ![]() $C(X;k)$ be the cochains with values in
$C(X;k)$ be the cochains with values in ![]() $k$ on the simplicial set
$k$ on the simplicial set ![]() $X$, viewed as a homologically graded chain complex concentrated in non-positive degrees. (At this point, we disregard its cup product structure.) So for
$X$, viewed as a homologically graded chain complex concentrated in non-positive degrees. (At this point, we disregard its cup product structure.) So for ![]() $q \geq 0$, we have
$q \geq 0$, we have ![]() $C(X;k)_{-q} = \mathrm {Set}(X_q,k)$ with the pointwise
$C(X;k)_{-q} = \mathrm {Set}(X_q,k)$ with the pointwise ![]() $k$-module structure and differential induced by the face maps of
$k$-module structure and differential induced by the face maps of ![]() $X$. The cochains on the standard
$X$. The cochains on the standard ![]() $n$-simplices assemble to a functor
$n$-simplices assemble to a functor ![]() $C_{\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}_k, [p] \mapsto C(\Delta ^{p};k)$. The following lemma is well known (see e.g. [Reference Félix, Halperin and ThomasFHT01, Lemmas 10.11 and 10.12(ii)]).
$C_{\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}_k, [p] \mapsto C(\Delta ^{p};k)$. The following lemma is well known (see e.g. [Reference Félix, Halperin and ThomasFHT01, Lemmas 10.11 and 10.12(ii)]).
Lemma 3.10
(i) The extension of
 $C_{\bullet }$ to a functor
$C_{\bullet }$ to a functor  $\mathrm {sSet}^{{{\mathrm {op}}}}\to \mathrm {Ch}_k$ resulting from Construction 3.2 is naturally isomorphic to
$\mathrm {sSet}^{{{\mathrm {op}}}}\to \mathrm {Ch}_k$ resulting from Construction 3.2 is naturally isomorphic to  $C(-;k)$.
$C(-;k)$.(ii) For all
 $q \in \mathbb {Z}$, the simplicial
$q \in \mathbb {Z}$, the simplicial  $k$-module
$k$-module  $C_{\bullet ,q} = C(\Delta ^{\bullet };k)_q$ is contractible to
$C_{\bullet ,q} = C(\Delta ^{\bullet };k)_q$ is contractible to  $0$.
$0$.
Proof. For (i), we note that the description of the extension as ![]() $\lim _{\Delta ^{p} \to X} C(\Delta ^{p};k)$ implies that there is a natural map from
$\lim _{\Delta ^{p} \to X} C(\Delta ^{p};k)$ implies that there is a natural map from ![]() $C(X;k)$. Writing
$C(X;k)$. Writing ![]() $X$ as a colimit of representable functors over its category of elements, the evaluation of this map at
$X$ as a colimit of representable functors over its category of elements, the evaluation of this map at ![]() $q$ is a bijection since taking maps into
$q$ is a bijection since taking maps into ![]() $k$ turns colimits into limits.
$k$ turns colimits into limits.
For (ii), we only need to consider the case ![]() $q \leq 0$, set
$q \leq 0$, set ![]() $n = -q$ and define
$n = -q$ and define
on ![]() $f \colon (\Delta ^{p})_n \to k$ as follows: We set
$f \colon (\Delta ^{p})_n \to k$ as follows: We set ![]() $s_{p+1}(f) \colon (\Delta ^{p+1})_n \to k$ to be
$s_{p+1}(f) \colon (\Delta ^{p+1})_n \to k$ to be ![]() $0$ on all
$0$ on all ![]() $n$-simplices not in the image of
$n$-simplices not in the image of ![]() $d^{p+1}\colon \Delta ^{p} \to \Delta ^{p+1}$ and require that
$d^{p+1}\colon \Delta ^{p} \to \Delta ^{p+1}$ and require that ![]() $s_{p+1}(f)$ restricts to
$s_{p+1}(f)$ restricts to ![]() $f$ on the last face. Identifying
$f$ on the last face. Identifying ![]() $\Delta ^{p+1}_n$ with
$\Delta ^{p+1}_n$ with ![]() $\Delta ([n],[p+1])$, this means that
$\Delta ([n],[p+1])$, this means that ![]() $s_{p+1}(f)(d^{p+1}\alpha ') = f(\alpha ')$ and
$s_{p+1}(f)(d^{p+1}\alpha ') = f(\alpha ')$ and ![]() $s_{p+1}(f)(\alpha) = 0$ if
$s_{p+1}(f)(\alpha) = 0$ if ![]() $p+1 \in \alpha ([n])$. Then for
$p+1 \in \alpha ([n])$. Then for ![]() $\beta \colon [n] \to [p]$, the equation
$\beta \colon [n] \to [p]$, the equation ![]() $d_{p+1}(s_{p+1}(f))(\beta ) = \beta$ holds by definition, and
$d_{p+1}(s_{p+1}(f))(\beta ) = \beta$ holds by definition, and ![]() $d_0s_1 = 0$ in simplicial degree
$d_0s_1 = 0$ in simplicial degree ![]() $0$ is also immediate. Now assume
$0$ is also immediate. Now assume ![]() $p\geq 1$. If
$p\geq 1$. If ![]() $\beta$ has
$\beta$ has ![]() $p$ in its image, then
$p$ in its image, then ![]() $d_is_{p+1}(f)(\beta ) = 0 = s_pd_i(f)(\beta )$. Otherwise, we must have
$d_is_{p+1}(f)(\beta ) = 0 = s_pd_i(f)(\beta )$. Otherwise, we must have ![]() $\beta = d^{p} \beta '$ and thus
$\beta = d^{p} \beta '$ and thus
 \begin{align*} d_i s_{p+1}(f)(d^{p} \beta') &= s_{p+1}(f)(d^{i}d^{p} \beta') = s_{p+1}(f)(d^{p+1}d^{i} \beta') \\ &= f(d^{i} \beta') = (d_if)(\beta') = s_p d_i(f)(d^{p}\beta'). \end{align*}
\begin{align*} d_i s_{p+1}(f)(d^{p} \beta') &= s_{p+1}(f)(d^{i}d^{p} \beta') = s_{p+1}(f)(d^{p+1}d^{i} \beta') \\ &= f(d^{i} \beta') = (d_if)(\beta') = s_p d_i(f)(d^{p}\beta'). \end{align*} For later use, we lift ![]() $C_{\bullet }$ to
$C_{\bullet }$ to ![]() $\mathcal {I}$-chain complexes by defining
$\mathcal {I}$-chain complexes by defining
Corollary 3.11
(i) The extension
 $C^{\mathcal {I}}$ of
$C^{\mathcal {I}}$ of  $C^{\mathcal {I}}_{\bullet }$ to a functor
$C^{\mathcal {I}}_{\bullet }$ to a functor  $\mathrm {sSet}^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k$ resulting from Construction 3.2 is naturally isomorphic to
$\mathrm {sSet}^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k$ resulting from Construction 3.2 is naturally isomorphic to  $X \mapsto F^{\mathcal {I}}_{{\mathbf {0}}}C(X; k)$.
$X \mapsto F^{\mathcal {I}}_{{\mathbf {0}}}C(X; k)$.(ii) For all
 $q \in \mathbb {Z}$ and
$q \in \mathbb {Z}$ and  ${\mathbf {m}}$ in
${\mathbf {m}}$ in  $\mathcal {I}$, the simplicial
$\mathcal {I}$, the simplicial  $k$-module
$k$-module  $C^{\mathcal {I}}_\bullet ({\mathbf {m}})_q = F_{{\mathbf {0}}}^{\mathcal {I}}(C(\Delta ^{\bullet };k)_q)$ is contractible to
$C^{\mathcal {I}}_\bullet ({\mathbf {m}})_q = F_{{\mathbf {0}}}^{\mathcal {I}}(C(\Delta ^{\bullet };k)_q)$ is contractible to  $0$.
$0$.
4. Homotopy theory of  $\mathcal {I}$-chain complexes and commutative
$\mathcal {I}$-chain complexes and commutative  $\mathcal {I}$-dgas
$\mathcal {I}$-dgas
In this section we review and set up results about model category structures on ![]() $\mathcal {I}$-chain complexes and commutative
$\mathcal {I}$-chain complexes and commutative ![]() $\mathcal {I}$-dgas. Much of this is motivated by (and analogous to) the corresponding results for space valued functors developed in [Reference Sagave and SchlichtkrullSS12, § 3].
$\mathcal {I}$-dgas. Much of this is motivated by (and analogous to) the corresponding results for space valued functors developed in [Reference Sagave and SchlichtkrullSS12, § 3].
We continue to consider the category of unbounded chain complexes ![]() $\mathrm {Ch}_k$ and equip it with the projective model structure whose weak equivalences are the quasi-isomorphisms and whose fibrations are the level-wise surjections [Reference HoveyHov99, Theorem 2.3.11]. It has the inclusions
$\mathrm {Ch}_k$ and equip it with the projective model structure whose weak equivalences are the quasi-isomorphisms and whose fibrations are the level-wise surjections [Reference HoveyHov99, Theorem 2.3.11]. It has the inclusions ![]() $S^{q-1}\hookrightarrow D^{q}$ as generating cofibrations and the maps
$S^{q-1}\hookrightarrow D^{q}$ as generating cofibrations and the maps ![]() $0 \to D^{q}$ as generating acyclic cofibrations. We will also need the following variant of this model structure.
$0 \to D^{q}$ as generating acyclic cofibrations. We will also need the following variant of this model structure.
Proposition 4.1 Let ![]() $s$ be an integer. Then
$s$ be an integer. Then ![]() $\mathrm {Ch}_k$ admits an
$\mathrm {Ch}_k$ admits an ![]() $s$-truncated model structure where a map
$s$-truncated model structure where a map ![]() $f \colon A \to B$ is a weak equivalence if
$f \colon A \to B$ is a weak equivalence if ![]() $H_q(f)\colon H_q(A) \to H_q(B)$ is an isomorphism for all
$H_q(f)\colon H_q(A) \to H_q(B)$ is an isomorphism for all ![]() $q \geq s$ and a fibration if
$q \geq s$ and a fibration if ![]() $f_q\colon A_q \to B_q$ is an epimorphism for all
$f_q\colon A_q \to B_q$ is an epimorphism for all ![]() $q > s$. The
$q > s$. The ![]() $s$-truncated model structure is combinatorial and right proper.
$s$-truncated model structure is combinatorial and right proper.
Proof. By shifting it is enough to consider the case ![]() $s =0$. The smart truncation
$s =0$. The smart truncation
to non-negatively graded chain complexes is right adjoint to the functor that adds copies of ![]() $0$ in negative degrees. The desired model structure arises by applying [Reference HirschhornHir03, Theorem 11.3.2] to this adjunction and the standard projective model structure on
$0$ in negative degrees. The desired model structure arises by applying [Reference HirschhornHir03, Theorem 11.3.2] to this adjunction and the standard projective model structure on ![]() $\mathrm {Ch}_k^{\geq 0}$ [Reference Dwyer and SpalińskiDS95, § 7]. The assumptions of the theorem are trivially satisfied. The resulting model structure is combinatorial since
$\mathrm {Ch}_k^{\geq 0}$ [Reference Dwyer and SpalińskiDS95, § 7]. The assumptions of the theorem are trivially satisfied. The resulting model structure is combinatorial since ![]() $\mathrm {Ch}_k$ is, and right proper because all objects are fibrant.
$\mathrm {Ch}_k$ is, and right proper because all objects are fibrant.
Remark 4.2 Since the usual long exact sequence argument is not applicable, we do not know if the ![]() $s$-truncated model structure is left proper. We do not investigate this further since it is not relevant for our applications.
$s$-truncated model structure is left proper. We do not investigate this further since it is not relevant for our applications.
4.3 Level model structures
We call an object ![]() ${\mathbf {m}}$ of
${\mathbf {m}}$ of ![]() $\mathcal {I}$ positive if
$\mathcal {I}$ positive if ![]() $|{\mathbf {m}}|\geq 1$ and write
$|{\mathbf {m}}|\geq 1$ and write ![]() $\mathcal {I}_+$ for the full subcategory of positive objects in
$\mathcal {I}_+$ for the full subcategory of positive objects in ![]() $\mathcal {I}$. To ease notation, we write
$\mathcal {I}$. To ease notation, we write ![]() $m$ for the cardinality of
$m$ for the cardinality of ![]() ${\mathbf {m}} = \{1,\ldots ,m\}$.
${\mathbf {m}} = \{1,\ldots ,m\}$.
A map ![]() $f\colon P \to Q$ in
$f\colon P \to Q$ in ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ is an absolute level equivalence (respectively absolute level fibration) if
$\mathrm {Ch}^{\mathcal {I}}_k$ is an absolute level equivalence (respectively absolute level fibration) if ![]() $f({\mathbf {m}})$ is a quasi-isomorphism (respectively a fibration) in
$f({\mathbf {m}})$ is a quasi-isomorphism (respectively a fibration) in ![]() $\mathrm {Ch}_k$ for all
$\mathrm {Ch}_k$ for all ![]() ${\mathbf {m}}$ in
${\mathbf {m}}$ in ![]() $\mathcal {I}$. A map
$\mathcal {I}$. A map ![]() $f\colon P \to Q$ in
$f\colon P \to Q$ in ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ is a descending level equivalence (respectively descending level fibration) if for all
$\mathrm {Ch}^{\mathcal {I}}_k$ is a descending level equivalence (respectively descending level fibration) if for all ![]() ${\mathbf {m}}$ in
${\mathbf {m}}$ in ![]() $\mathcal {I}_+$, the map
$\mathcal {I}_+$, the map ![]() $f({\mathbf {m}})$ is a weak equivalence (respectively fibration) in the
$f({\mathbf {m}})$ is a weak equivalence (respectively fibration) in the ![]() $-m$-truncated model structure on
$-m$-truncated model structure on ![]() $\mathrm {Ch}_k$.
$\mathrm {Ch}_k$.
Proposition 4.4 These maps define an absolute level and a descending level model structure on ![]() $\mathrm {Ch}^{\mathcal {I}}_k$. Both model structures are combinatorial and right proper, and the absolute level model structure is in addition left proper.
$\mathrm {Ch}^{\mathcal {I}}_k$. Both model structures are combinatorial and right proper, and the absolute level model structure is in addition left proper.
Proof. For integers ![]() $s \leq t$, the identity functor is a left Quillen functor from the
$s \leq t$, the identity functor is a left Quillen functor from the ![]() $t$-truncated model structure to the
$t$-truncated model structure to the ![]() $s$-truncated model structure since
$s$-truncated model structure since ![]() $s$-truncated weak equivalences (respectively fibrations) are
$s$-truncated weak equivalences (respectively fibrations) are ![]() $t$-truncated weak equivalences (respectively fibrations). To obtain the descending level model structure, we can therefore apply [Reference Hebestreit, Sagave and SchlichtkrullHSS20, Proposition 3.10] to the constant functor
$t$-truncated weak equivalences (respectively fibrations). To obtain the descending level model structure, we can therefore apply [Reference Hebestreit, Sagave and SchlichtkrullHSS20, Proposition 3.10] to the constant functor ![]() $\mathcal {C}\colon \mathcal {I} \to \mathrm {Cat}$ with value
$\mathcal {C}\colon \mathcal {I} \to \mathrm {Cat}$ with value ![]() $\mathrm {Ch}_k$ where
$\mathrm {Ch}_k$ where ![]() $\mathcal {C}({\mathbf {m}})$ is equipped with the
$\mathcal {C}({\mathbf {m}})$ is equipped with the ![]() $-m$-truncated model structure. The absolute level model structure arises by considering the same functor where
$-m$-truncated model structure. The absolute level model structure arises by considering the same functor where ![]() $\mathcal {C}({\mathbf {m}})$ carries the standard projective model structure for all
$\mathcal {C}({\mathbf {m}})$ carries the standard projective model structure for all ![]() ${\mathbf {m}}$.
${\mathbf {m}}$.
The cofibrations in the absolute level model structure are the retracts of relative cell complexes built out of cells of the form ![]() $F^{\mathcal {I}}_{{\mathbf {m}}}(S^{q-1} \hookrightarrow D^{q})$ with
$F^{\mathcal {I}}_{{\mathbf {m}}}(S^{q-1} \hookrightarrow D^{q})$ with ![]() ${\mathbf {m}}$ in
${\mathbf {m}}$ in ![]() $\mathcal {I}$ and
$\mathcal {I}$ and ![]() $q \in \mathbb {Z}$. Here
$q \in \mathbb {Z}$. Here ![]() $F^{\mathcal {I}}_{{\mathbf {m}}}$ is the free functor defined in (2.1). For the descending level model structure, it follows from the proof of the previous proposition that one may use
$F^{\mathcal {I}}_{{\mathbf {m}}}$ is the free functor defined in (2.1). For the descending level model structure, it follows from the proof of the previous proposition that one may use
as the set of generating cofibrations and
as the set of generating acyclic cofibrations.
4.5  $\mathcal {I}$-model structures
$\mathcal {I}$-model structures
We now again use the homotopy colimit ![]() $P_{h\mathcal {I}}$ from Construction 2.6. A map
$P_{h\mathcal {I}}$ from Construction 2.6. A map ![]() $P \to Q$ in
$P \to Q$ in ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ is an
$\mathrm {Ch}^{\mathcal {I}}_k$ is an ![]() $\mathcal {I}$-equivalence if it induces a quasi-isomorphism
$\mathcal {I}$-equivalence if it induces a quasi-isomorphism ![]() $P_{h\mathcal {I}} \to Q_{h\mathcal {I}}$. An
$P_{h\mathcal {I}} \to Q_{h\mathcal {I}}$. An ![]() $\mathcal {I}$-chain complex
$\mathcal {I}$-chain complex ![]() $P$ is absolute
$P$ is absolute ![]() $\mathcal {I}$-fibrant if
$\mathcal {I}$-fibrant if ![]() $\alpha _*\colon P({\mathbf {m}}) \to P({\mathbf {n}})$ is a quasi-isomorphism for all
$\alpha _*\colon P({\mathbf {m}}) \to P({\mathbf {n}})$ is a quasi-isomorphism for all ![]() $\alpha \colon {\mathbf {m}} \to {\mathbf {n}}$ in
$\alpha \colon {\mathbf {m}} \to {\mathbf {n}}$ in ![]() $\mathcal {I}$. It is descending
$\mathcal {I}$. It is descending ![]() $\mathcal {I}$-fibrant if for all
$\mathcal {I}$-fibrant if for all ![]() $\alpha \colon {\mathbf {m}} \to {\mathbf {n}}$ in
$\alpha \colon {\mathbf {m}} \to {\mathbf {n}}$ in ![]() $\mathcal {I}_+$, the map
$\mathcal {I}_+$, the map ![]() $\alpha _*\colon P({\mathbf {m}}) \to P({\mathbf {n}})$ is a weak equivalence in the
$\alpha _*\colon P({\mathbf {m}}) \to P({\mathbf {n}})$ is a weak equivalence in the ![]() $-m$-truncated model structure, that is, if for all
$-m$-truncated model structure, that is, if for all ![]() $q\geq -m$, the map
$q\geq -m$, the map ![]() $H_q(\alpha _*)\colon H_q(P({\mathbf {m}})) \to H_q(P({\mathbf {n}}))$ is an isomorphism.
$H_q(\alpha _*)\colon H_q(P({\mathbf {m}})) \to H_q(P({\mathbf {n}}))$ is an isomorphism.
The next lemma will be needed to identify the ![]() $\mathcal {I}$-equivalences as part of a descending model structure.
$\mathcal {I}$-equivalences as part of a descending model structure.
Lemma 4.6 A map ![]() $P \to Q$ between descending
$P \to Q$ between descending ![]() $\mathcal {I}$-fibrant objects in
$\mathcal {I}$-fibrant objects in ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ is an
$\mathrm {Ch}^{\mathcal {I}}_k$ is an ![]() $\mathcal {I}$-equivalence if and only if it is a descending level equivalence.
$\mathcal {I}$-equivalence if and only if it is a descending level equivalence.
Proof. For each positive ![]() ${\mathbf {m}}$ we consider the following commutative diagram.
${\mathbf {m}}$ we consider the following commutative diagram.

The right hand horizontal maps are induced by the inclusion ![]() $\mathcal {I}_{\geq m} \to \mathcal {I}$ of the full subcategory of objects of cardinality at least
$\mathcal {I}_{\geq m} \to \mathcal {I}$ of the full subcategory of objects of cardinality at least ![]() $m$. Since this inclusion is homotopy cofinal (compare [Reference Sagave and SchlichtkrullSS12, Corollary 5.9]), they are quasi-isomorphisms. The left hand horizontal maps are induced by the inclusion of the object
$m$. Since this inclusion is homotopy cofinal (compare [Reference Sagave and SchlichtkrullSS12, Corollary 5.9]), they are quasi-isomorphisms. The left hand horizontal maps are induced by the inclusion of the object ![]() ${\mathbf {m}}$ in
${\mathbf {m}}$ in ![]() $\mathcal {I}_{\geq m}$. They are
$\mathcal {I}_{\geq m}$. They are ![]() $-m$-truncated equivalences by [Reference DuggerDug01, Proposition 5.4] because the restrictions of
$-m$-truncated equivalences by [Reference DuggerDug01, Proposition 5.4] because the restrictions of ![]() $P$ and
$P$ and ![]() $Q$ to
$Q$ to ![]() $\mathcal {I}_{\geq m}$ are diagrams of
$\mathcal {I}_{\geq m}$ are diagrams of ![]() $-m$-truncated equivalences. The claim then follows by two-out-of-three and the fact that a map is a quasi-isomorphism if and only if it is an
$-m$-truncated equivalences. The claim then follows by two-out-of-three and the fact that a map is a quasi-isomorphism if and only if it is an ![]() $s$-truncated equivalence for all
$s$-truncated equivalence for all ![]() $s<0$.
$s<0$.
Using this lemma, we can build the desired model structures.
Proposition 4.7 The absolute (respectively descending) level model structure on ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ admits a left Bousfield localization with fibrant objects the absolute (respectively descending)
$\mathrm {Ch}^{\mathcal {I}}_k$ admits a left Bousfield localization with fibrant objects the absolute (respectively descending) ![]() $\mathcal {I}$-fibrant objects. The weak equivalences in these two model structures coincide, and they are given by the
$\mathcal {I}$-fibrant objects. The weak equivalences in these two model structures coincide, and they are given by the ![]() $\mathcal {I}$-equivalences. Both model structures are left proper and combinatorial.
$\mathcal {I}$-equivalences. Both model structures are left proper and combinatorial.
Proof. For the absolute case, we apply [Reference DuggerDug01, Theorem 5.2]. Since the weak equivalences in the latter case are the maps that induce weak equivalences on the corrected homotopy colimits, they coincide with the ![]() $\mathcal {I}$-equivalences. The resulting model structure is left proper and combinatorial since these properties are preserved by left Bousfield localization.
$\mathcal {I}$-equivalences. The resulting model structure is left proper and combinatorial since these properties are preserved by left Bousfield localization.
Let ![]() $\mathcal {N}$ be the subcategory of
$\mathcal {N}$ be the subcategory of ![]() $\mathcal {I}$ given by the subset inclusions and let
$\mathcal {I}$ given by the subset inclusions and let ![]() $P$ be an
$P$ be an ![]() $\mathcal {I}$-chain complex. Since the homotopy colimit over
$\mathcal {I}$-chain complex. Since the homotopy colimit over ![]() $\mathcal {N}$ is equivalent to the colimit of a suitable cofibrant replacement of the underlying
$\mathcal {N}$ is equivalent to the colimit of a suitable cofibrant replacement of the underlying ![]() $\mathcal {N}$-diagram, there is a natural isomorphism
$\mathcal {N}$-diagram, there is a natural isomorphism ![]() $\operatorname {colim}_{{\mathbf {m}}\in \mathcal {N}} H_q(P({\mathbf {m}})) \cong H_q(\operatorname {hocolim}_{{\mathbf {m}} \in \mathcal {N}}P({\mathbf {m}}))$. Hence any descending level equivalence
$\operatorname {colim}_{{\mathbf {m}}\in \mathcal {N}} H_q(P({\mathbf {m}})) \cong H_q(\operatorname {hocolim}_{{\mathbf {m}} \in \mathcal {N}}P({\mathbf {m}}))$. Hence any descending level equivalence ![]() $P \to Q$ induces a quasi-isomorphism
$P \to Q$ induces a quasi-isomorphism ![]() $\operatorname {hocolim}_{\mathcal {N}}P \to \operatorname {hocolim}_{\mathcal {N}}Q$ and thus an
$\operatorname {hocolim}_{\mathcal {N}}P \to \operatorname {hocolim}_{\mathcal {N}}Q$ and thus an ![]() $\mathcal {I}$-equivalence by [Reference ShipleyShi00, Proposition 2.2.9]. So the weak equivalences of the descending level model structure are contained in those of the absolute
$\mathcal {I}$-equivalence by [Reference ShipleyShi00, Proposition 2.2.9]. So the weak equivalences of the descending level model structure are contained in those of the absolute ![]() $\mathcal {I}$-model structure, and the same is by definition true for the cofibrations. We can thus apply [Reference ColeCol06, Theorem 2.1] to obtain a model structure that has the weak equivalences and cofibrations of the second model structure to be constructed. Using Lemma 4.6, an object
$\mathcal {I}$-model structure, and the same is by definition true for the cofibrations. We can thus apply [Reference ColeCol06, Theorem 2.1] to obtain a model structure that has the weak equivalences and cofibrations of the second model structure to be constructed. Using Lemma 4.6, an object ![]() $P$ is descending
$P$ is descending ![]() $\mathcal {I}$-fibrant if and only if every absolute
$\mathcal {I}$-fibrant if and only if every absolute ![]() $\mathcal {I}$-fibrant replacement
$\mathcal {I}$-fibrant replacement ![]() $P \to P'$ is a descending level equivalence. Hence the dual of [Reference ColeCol06, Proposition 3.6] shows that the fibrant objects of the second model structure are the descending
$P \to P'$ is a descending level equivalence. Hence the dual of [Reference ColeCol06, Proposition 3.6] shows that the fibrant objects of the second model structure are the descending ![]() $\mathcal {I}$-fibrant objects. The model structure is combinatorial by [Reference BarwickBar10, Lemma 4.6 and Proposition 2.2] and left proper since the absolute
$\mathcal {I}$-fibrant objects. The model structure is combinatorial by [Reference BarwickBar10, Lemma 4.6 and Proposition 2.2] and left proper since the absolute ![]() $\mathcal {I}$-model structure is.
$\mathcal {I}$-model structure is.
We call these two model structures the absolute and descending ![]() $\mathcal {I}$-model structures on
$\mathcal {I}$-model structures on ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ and their fibrations absolute and descending
$\mathrm {Ch}^{\mathcal {I}}_k$ and their fibrations absolute and descending ![]() $\mathcal {I}$-fibrations.
$\mathcal {I}$-fibrations.
Remark 4.8 Analogous to [Reference Sagave and SchlichtkrullSS12, Proposition 6.16], ![]() $\mathcal {I}$-model structures on chain complexes can be constructed without relying on an abstract existence theorem for left Bousfield localizations. This has been done by Joachimi [Reference JoachimiJoa11] in the absolute case, and we expect that similar arguments apply in the descending case. The advantage of the direct approach is that it provides an explicit characterization of the
$\mathcal {I}$-model structures on chain complexes can be constructed without relying on an abstract existence theorem for left Bousfield localizations. This has been done by Joachimi [Reference JoachimiJoa11] in the absolute case, and we expect that similar arguments apply in the descending case. The advantage of the direct approach is that it provides an explicit characterization of the ![]() $\mathcal {I}$-fibrations by a homotopy pullback condition like in [Reference Sagave and SchlichtkrullSS12, Proposition 3.2].
$\mathcal {I}$-fibrations by a homotopy pullback condition like in [Reference Sagave and SchlichtkrullSS12, Proposition 3.2].
Corollary 4.9 A map between descending ![]() $\mathcal {I}$-fibrant objects is a descending level fibration if and only if it is a descending
$\mathcal {I}$-fibrant objects is a descending level fibration if and only if it is a descending ![]() $\mathcal {I}$-fibration.
$\mathcal {I}$-fibration.
Proof. This follows from [Reference HirschhornHir03, Proposition 3.3.16].
The following useful consequence of Lemma 4.6 was already used in the proof of Proposition 4.7.
Corollary 4.10 If ![]() $P$ is descending
$P$ is descending ![]() $\mathcal {I}$-fibrant in
$\mathcal {I}$-fibrant in ![]() $\mathrm {Ch}^{\mathcal {I}}_k$, then a fibrant replacement
$\mathrm {Ch}^{\mathcal {I}}_k$, then a fibrant replacement ![]() $P \to P'$ in the absolute
$P \to P'$ in the absolute ![]() $\mathcal {I}$-model structure is a descending level equivalence.
$\mathcal {I}$-model structure is a descending level equivalence.
We also note that the homology groups of ![]() $P_{h\mathcal {I}}$ can be read off from a fibrant object
$P_{h\mathcal {I}}$ can be read off from a fibrant object ![]() $P$ in the following way.
$P$ in the following way.
Lemma 4.11 If ![]() $P$ is absolute
$P$ is absolute ![]() $\mathcal {I}$-fibrant in
$\mathcal {I}$-fibrant in ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ and
$\mathrm {Ch}^{\mathcal {I}}_k$ and ![]() ${\mathbf {m}}$ is any object in
${\mathbf {m}}$ is any object in ![]() $\mathcal {I}$, then the canonical map
$\mathcal {I}$, then the canonical map ![]() $P({\mathbf {m}}) \to P_{h\mathcal {I}}$ is a quasi-isomorphism. If
$P({\mathbf {m}}) \to P_{h\mathcal {I}}$ is a quasi-isomorphism. If ![]() $P$ is only descending
$P$ is only descending ![]() $\mathcal {I}$-fibrant, then the induced map
$\mathcal {I}$-fibrant, then the induced map ![]() $H_q(P({\mathbf {m}})) \to H_q(P_{h\mathcal {I}})$ is an isomorphism when
$H_q(P({\mathbf {m}})) \to H_q(P_{h\mathcal {I}})$ is an isomorphism when ![]() ${\mathbf {m}}$ is positive and
${\mathbf {m}}$ is positive and ![]() $q\geq -m$.
$q\geq -m$.
Proof. The absolute case follows from [Reference DuggerDug01, Proposition 5.4] since ![]() $\mathcal {I}$ has contractible classifying space. With Corollary 4.10, the claim for
$\mathcal {I}$ has contractible classifying space. With Corollary 4.10, the claim for ![]() $P$ descending
$P$ descending ![]() $\mathcal {I}$-fibrant follows from the absolute case.
$\mathcal {I}$-fibrant follows from the absolute case.
As another consequence of [Reference DuggerDug01, Theorem 5.2], we note that the adjunction ![]() $\operatorname {colim}_{\mathcal {I}} \colon \mathrm {Ch}^{\mathcal {I}}_k \rightleftarrows \mathrm {Ch}_k \colon \mathrm {const}_{\mathcal {I}}$ is a Quillen equivalence when
$\operatorname {colim}_{\mathcal {I}} \colon \mathrm {Ch}^{\mathcal {I}}_k \rightleftarrows \mathrm {Ch}_k \colon \mathrm {const}_{\mathcal {I}}$ is a Quillen equivalence when ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ is equipped with the absolute or descending
$\mathrm {Ch}^{\mathcal {I}}_k$ is equipped with the absolute or descending ![]() $\mathcal {I}$-model structure. In particular, the composite of
$\mathcal {I}$-model structure. In particular, the composite of
is always a quasi-isomorphism, and each ![]() $P$ in
$P$ in ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ is related by a zig-zag of
$\mathrm {Ch}^{\mathcal {I}}_k$ is related by a zig-zag of ![]() $\mathcal {I}$-equivalences
$\mathcal {I}$-equivalences
to a constant ![]() $\mathcal {I}$-diagram
$\mathcal {I}$-diagram ![]() $\operatorname {colim}_{\mathcal {I}} (P)^{\mathrm {cof}}$ where
$\operatorname {colim}_{\mathcal {I}} (P)^{\mathrm {cof}}$ where ![]() $P^{\mathrm {cof}} \to P$ is a cofibrant replacement.
$P^{\mathrm {cof}} \to P$ is a cofibrant replacement.
We record the following lemma for later use.
Lemma 4.12 If ![]() $(P_{j})_{j \in J}$ is a family of
$(P_{j})_{j \in J}$ is a family of ![]() $\mathcal {I}$-chain complexes, then the canonical map
$\mathcal {I}$-chain complexes, then the canonical map
 \[ \bigg(\prod_{j \in J} P_{j} \bigg)_{h\mathcal{I}} \to \prod_{j \in J} (P_{j})_{h\mathcal{I}} \]
\[ \bigg(\prod_{j \in J} P_{j} \bigg)_{h\mathcal{I}} \to \prod_{j \in J} (P_{j})_{h\mathcal{I}} \]
is a quasi-isomorphism provided that all the ![]() $P_{j}$ are descending
$P_{j}$ are descending ![]() $\mathcal {I}$-fibrant.
$\mathcal {I}$-fibrant.
Proof. Arbitrary products of weak equivalences between fibrant objects in a model category are weak equivalences. Therefore, using that (4.2) is a zig-zag of ![]() $\mathcal {I}$-equivalences between descending
$\mathcal {I}$-equivalences between descending ![]() $\mathcal {I}$-fibrant objects under our assumptions allows us to assume that each
$\mathcal {I}$-fibrant objects under our assumptions allows us to assume that each ![]() $P_{j}$ is of the form
$P_{j}$ is of the form ![]() $\operatorname {const}_{\mathcal {I}} A_{j}$. Forming the adjoint of the isomorphism
$\operatorname {const}_{\mathcal {I}} A_{j}$. Forming the adjoint of the isomorphism ![]() $\prod _{j \in J}\operatorname {const}_{\mathcal {I}} A_{j} \xrightarrow {\cong } \operatorname {const}_{\mathcal {I}} (\prod _{j \in J} A_{j})$ under the Quillen equivalence
$\prod _{j \in J}\operatorname {const}_{\mathcal {I}} A_{j} \xrightarrow {\cong } \operatorname {const}_{\mathcal {I}} (\prod _{j \in J} A_{j})$ under the Quillen equivalence ![]() $(\operatorname {colim}_{\mathcal {I}},\mathrm {const}_{\mathcal {I}})$ shows that the composite in
$(\operatorname {colim}_{\mathcal {I}},\mathrm {const}_{\mathcal {I}})$ shows that the composite in
 \[ \bigg(\prod_{j \in J}\operatorname{const}_{\mathcal{I}} A_{j}\bigg)_{h\mathcal{I}} \to \prod_{j \in J} (\operatorname{const}_{\mathcal{I}}A_{j})_{h\mathcal{I}} \xrightarrow{\sim} \prod_{j \in J}A_{j} \]
\[ \bigg(\prod_{j \in J}\operatorname{const}_{\mathcal{I}} A_{j}\bigg)_{h\mathcal{I}} \to \prod_{j \in J} (\operatorname{const}_{\mathcal{I}}A_{j})_{h\mathcal{I}} \xrightarrow{\sim} \prod_{j \in J}A_{j} \]is a quasi-isomorphism. Since the second map is a product of quasi-isomorphisms, the claim follows by two-out-of-three.
4.13 Commutative  $\mathcal {I}$-dgas
$\mathcal {I}$-dgas
Although essentially only our formulation of Theorem 1.5 depends on the existence of a lifted model structure on ![]() $\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$, the following result is the main motivation for working with commutative
$\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$, the following result is the main motivation for working with commutative ![]() $\mathcal {I}$-dgas.
$\mathcal {I}$-dgas.
Theorem 4.14 The category ![]() $\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ admits a descending
$\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ admits a descending ![]() $\mathcal {I}$-model structure where a map is a weak equivalence (or fibration) if the underlying map in the descending
$\mathcal {I}$-model structure where a map is a weak equivalence (or fibration) if the underlying map in the descending ![]() $\mathcal {I}$-model structure on
$\mathcal {I}$-model structure on ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ is. With this model structure,
$\mathrm {Ch}^{\mathcal {I}}_k$ is. With this model structure, ![]() $\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ is Quillen equivalent to the category of
$\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ is Quillen equivalent to the category of ![]() $E_{\infty }$ dgas and to the category of commutative
$E_{\infty }$ dgas and to the category of commutative ![]() $Hk$-algebra spectra.
$Hk$-algebra spectra.
Proof. The identification of ![]() $\mathcal {I}$-diagrams with generalized symmetric spectra (see [Reference Richter and ShipleyRS17, Proposition 9.1] or [Reference Pavlov and ScholbachPS19, § 3.2]) and [Reference Pavlov and ScholbachPS19, Propositions 3.2.2 and 3.3.1] imply that
$\mathcal {I}$-diagrams with generalized symmetric spectra (see [Reference Richter and ShipleyRS17, Proposition 9.1] or [Reference Pavlov and ScholbachPS19, § 3.2]) and [Reference Pavlov and ScholbachPS19, Propositions 3.2.2 and 3.3.1] imply that ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ admits a positive
$\mathrm {Ch}^{\mathcal {I}}_k$ admits a positive ![]() $\mathcal {I}$-model structure with weak equivalences the
$\mathcal {I}$-model structure with weak equivalences the ![]() $\mathcal {I}$-equivalences. This model structure has more cofibrations than the descending
$\mathcal {I}$-equivalences. This model structure has more cofibrations than the descending ![]() $\mathcal {I}$-model structure and less cofibrations than the absolute
$\mathcal {I}$-model structure and less cofibrations than the absolute ![]() $\mathcal {I}$-model structure. The positive
$\mathcal {I}$-model structure. The positive ![]() $\mathcal {I}$-model structure lifts to
$\mathcal {I}$-model structure lifts to ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ by [Reference Pavlov and ScholbachPS19, Theorem 4.1], and the resulting model category is Quillen equivalent to commutative
$\mathrm {Ch}^{\mathcal {I}}_k$ by [Reference Pavlov and ScholbachPS19, Theorem 4.1], and the resulting model category is Quillen equivalent to commutative ![]() $Hk$-algebra spectra and to
$Hk$-algebra spectra and to ![]() $E_{\infty }$ dgas [Reference Richter and ShipleyRS17, Theorem 9.5, Corollary 8.3].
$E_{\infty }$ dgas [Reference Richter and ShipleyRS17, Theorem 9.5, Corollary 8.3].
The descending ![]() $\mathcal {I}$-model structure on
$\mathcal {I}$-model structure on ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ is left proper, combinatorial, and has less cofibrations than the positive one. Hence the existence of the descending
$\mathrm {Ch}^{\mathcal {I}}_k$ is left proper, combinatorial, and has less cofibrations than the positive one. Hence the existence of the descending ![]() $\mathcal {I}$-model structure on
$\mathcal {I}$-model structure on ![]() $\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ and the Quillen equivalence to the positive
$\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ and the Quillen equivalence to the positive ![]() $\mathcal {I}$-model structure immediately follow from [Reference HirschhornHir03, Theorem 11.3.2].
$\mathcal {I}$-model structure immediately follow from [Reference HirschhornHir03, Theorem 11.3.2].
The equivalence of homotopy categories resulting from this theorem is actually induced by the homotopy colimit over ![]() $\mathcal {I}$ with the
$\mathcal {I}$ with the ![]() $\mathcal {E}$-action from Theorem 2.13.
$\mathcal {E}$-action from Theorem 2.13.
Proposition 4.15 The functor ![]() $(-)_{h\mathcal {I}} \colon \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}] \to \mathrm {Ch}_k[\mathcal {E}]$ induces an equivalence of categories
$(-)_{h\mathcal {I}} \colon \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}] \to \mathrm {Ch}_k[\mathcal {E}]$ induces an equivalence of categories ![]() $\mathrm {Ho}(\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]) \to \mathrm {Ho}(\mathrm {Ch}_k[\mathcal {E}])$.
$\mathrm {Ho}(\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]) \to \mathrm {Ho}(\mathrm {Ch}_k[\mathcal {E}])$.
Proof. An ![]() $\mathcal {I}$-chain complex
$\mathcal {I}$-chain complex ![]() $X$ admits a bar resolution
$X$ admits a bar resolution ![]() $\overline {X} \to X$ defined by
$\overline {X} \to X$ defined by ![]() $\overline {X}({\mathbf {n}}) = \operatorname {hocolim}_{\mathcal {I}\downarrow {\mathbf {n}}}(X \circ \pi )$ where
$\overline {X}({\mathbf {n}}) = \operatorname {hocolim}_{\mathcal {I}\downarrow {\mathbf {n}}}(X \circ \pi )$ where ![]() $\pi \colon \mathcal {I}\downarrow {\mathbf {n}} \to \mathcal {I}$ is the canonical projection from the overcategory forgetting the augmentation to
$\pi \colon \mathcal {I}\downarrow {\mathbf {n}} \to \mathcal {I}$ is the canonical projection from the overcategory forgetting the augmentation to ![]() ${\mathbf {n}}$. The inclusion of the terminal object in
${\mathbf {n}}$. The inclusion of the terminal object in ![]() $\mathcal {I}\downarrow {\mathbf {n}}$ induces a map
$\mathcal {I}\downarrow {\mathbf {n}}$ induces a map ![]() $\overline {X} \to X$ which is a level equivalence by a homotopy cofinality argument. The bar resolution has the property
$\overline {X} \to X$ which is a level equivalence by a homotopy cofinality argument. The bar resolution has the property ![]() $\operatorname {colim}_{\mathcal {I}} \overline {X} \cong X_{h\mathcal {I}}$. When
$\operatorname {colim}_{\mathcal {I}} \overline {X} \cong X_{h\mathcal {I}}$. When ![]() $M$ is an
$M$ is an ![]() $\mathcal {E}$-algebra in
$\mathcal {E}$-algebra in ![]() $\mathrm {Ch}^{\mathcal {I}}_k$, then
$\mathrm {Ch}^{\mathcal {I}}_k$, then ![]() $\overline {M}$ inherits an
$\overline {M}$ inherits an ![]() $\mathcal {E}$-algebra structure with diagonal
$\mathcal {E}$-algebra structure with diagonal ![]() $\mathcal {E}$-action (compare Theorem 2.13 and the analogous space-level statement in [Reference SchlichtkrullSch09, Lemma 6.7]). When
$\mathcal {E}$-action (compare Theorem 2.13 and the analogous space-level statement in [Reference SchlichtkrullSch09, Lemma 6.7]). When ![]() $M$ is a commutative
$M$ is a commutative ![]() $\mathcal {I}$-dga, then the
$\mathcal {I}$-dga, then the ![]() $\mathcal {E}$-algebra structure on
$\mathcal {E}$-algebra structure on ![]() $\operatorname {colim}_{\mathcal {I}}(\overline {M})$ resulting from this observation and the strong monoidality of
$\operatorname {colim}_{\mathcal {I}}(\overline {M})$ resulting from this observation and the strong monoidality of ![]() $\operatorname {colim}_{\mathcal {I}}$ coincides with the one on
$\operatorname {colim}_{\mathcal {I}}$ coincides with the one on ![]() $M_{h\mathcal {I}}$ provided by Theorem 2.13. We also note that if
$M_{h\mathcal {I}}$ provided by Theorem 2.13. We also note that if ![]() $X$ is a cofibrant
$X$ is a cofibrant ![]() $\mathcal {I}$-chain complex, then the map
$\mathcal {I}$-chain complex, then the map ![]() $\operatorname {colim}_{\mathcal {I}}\overline {X} \to \operatorname {colim}_{\mathcal {I}}X$ is a quasi-isomorphism. This can be checked directly on free
$\operatorname {colim}_{\mathcal {I}}\overline {X} \to \operatorname {colim}_{\mathcal {I}}X$ is a quasi-isomorphism. This can be checked directly on free ![]() $\mathcal {I}$-chain complexes, and the general case follows because both sides preserve colimits and send generating cofibrations to levelwise injections.
$\mathcal {I}$-chain complexes, and the general case follows because both sides preserve colimits and send generating cofibrations to levelwise injections.
To prove the proposition, we note that the chain of Quillen equivalences from Theorem 4.14 sends a commutative ![]() $\mathcal {I}$-dga
$\mathcal {I}$-dga ![]() $M$ to
$M$ to ![]() $\operatorname {colim}_{\mathcal {I}}M^{\mathrm {cof}}$, the colimit over
$\operatorname {colim}_{\mathcal {I}}M^{\mathrm {cof}}$, the colimit over ![]() $\mathcal {I}$ of a cofibrant replacement of
$\mathcal {I}$ of a cofibrant replacement of ![]() $M$ in
$M$ in ![]() $\mathrm {Ch}_k^{\mathcal {I}}[\mathcal {E}]$. This colimit is related to
$\mathrm {Ch}_k^{\mathcal {I}}[\mathcal {E}]$. This colimit is related to ![]() $M_{h\mathcal {I}}$ by a natural zig-zag of
$M_{h\mathcal {I}}$ by a natural zig-zag of ![]() $\mathcal {E}$-algebra maps
$\mathcal {E}$-algebra maps
where the first map is a quasi-isomorphism since the cofibrant replacement is an ![]() $\mathcal {I}$-equivalence and the last map is a quasi-isomorphism by the above discussion since
$\mathcal {I}$-equivalence and the last map is a quasi-isomorphism by the above discussion since ![]() $M^{\mathrm {cof}}$ is a cofibrant
$M^{\mathrm {cof}}$ is a cofibrant ![]() $\mathcal {I}$-chain complex by [Reference Pavlov and ScholbachPS19, Theorem 4.4].
$\mathcal {I}$-chain complex by [Reference Pavlov and ScholbachPS19, Theorem 4.4].
For later use we note that the commutative ![]() $\mathcal {I}$-dga
$\mathcal {I}$-dga ![]() $\mathbb {C} F_{{\mathbf {1}}}^{\mathcal {I}}(A)$ from (2.3) has the following homotopical feature.
$\mathbb {C} F_{{\mathbf {1}}}^{\mathcal {I}}(A)$ from (2.3) has the following homotopical feature.
Lemma 4.16 Let ![]() $A$ be a cofibrant acyclic chain complex. Then each
$A$ be a cofibrant acyclic chain complex. Then each ![]() $(\mathbb {C} F_{{\mathbf {1}}}^{\mathcal {I}}(A))({\mathbf {m}})$ is cofibrant in
$(\mathbb {C} F_{{\mathbf {1}}}^{\mathcal {I}}(A))({\mathbf {m}})$ is cofibrant in ![]() $\mathrm {Ch}_k$, and the unit
$\mathrm {Ch}_k$, and the unit ![]() $U^{\mathcal {I}} \to {C} F_{\mathbf {1}}^{\mathcal {I}}(A)$ is an absolute level equivalence.
$U^{\mathcal {I}} \to {C} F_{\mathbf {1}}^{\mathcal {I}}(A)$ is an absolute level equivalence.
Proof. This is an immediate consequence of the isomorphism (3.4).
5. Comparison of cochain functors
We now define a simplicial ![]() $\mathcal {I}$-chain complex
$\mathcal {I}$-chain complex ![]() $B^{\mathcal {I}}_{\bullet }$ by setting
$B^{\mathcal {I}}_{\bullet }$ by setting ![]() $B^{\mathcal {I}}_p = A^{\mathcal {I}}_p \boxtimes C^{\mathcal {I}}_p$ in simplicial level
$B^{\mathcal {I}}_p = A^{\mathcal {I}}_p \boxtimes C^{\mathcal {I}}_p$ in simplicial level ![]() $p$ and using the
$p$ and using the ![]() $\boxtimes$-products of the simplicial structure maps of
$\boxtimes$-products of the simplicial structure maps of ![]() $A^{\mathcal {I}}$ and
$A^{\mathcal {I}}$ and ![]() $C^{\mathcal {I}}$ as simplicial structure maps for
$C^{\mathcal {I}}$ as simplicial structure maps for ![]() $B^{\mathcal {I}}_{\bullet }$. There is a natural isomorphism
$B^{\mathcal {I}}_{\bullet }$. There is a natural isomorphism
that results from the definition of ![]() $\boxtimes$ as a left Kan extension.
$\boxtimes$ as a left Kan extension.
The unit maps ![]() $U^{\mathcal {I}} \to C^{\mathcal {I}}$ and
$U^{\mathcal {I}} \to C^{\mathcal {I}}$ and ![]() $U^{\mathcal {I}} \to A^{\mathcal {I}}$ induce a chain
$U^{\mathcal {I}} \to A^{\mathcal {I}}$ induce a chain
of maps of simplicial objects in ![]() $\mathrm {Ch}^{\mathcal {I}}_k$. By Construction 3.2, this chain gives rise to a chain of natural transformations
$\mathrm {Ch}^{\mathcal {I}}_k$. By Construction 3.2, this chain gives rise to a chain of natural transformations ![]() $A^{\mathcal {I}} \to B^{\mathcal {I}} \leftarrow C^{\mathcal {I}}$ of functors
$A^{\mathcal {I}} \to B^{\mathcal {I}} \leftarrow C^{\mathcal {I}}$ of functors ![]() $(\mathrm {sSet})^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k$.
$(\mathrm {sSet})^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k$.
Theorem 5.1 For every simplicial set ![]() $X$, the maps
$X$, the maps ![]() $A^{\mathcal {I}}(X) \to B^{\mathcal {I}}(X) \leftarrow C^{\mathcal {I}}(X)$ are descending level equivalences between descending
$A^{\mathcal {I}}(X) \to B^{\mathcal {I}}(X) \leftarrow C^{\mathcal {I}}(X)$ are descending level equivalences between descending ![]() $\mathcal {I}$-fibrant objects.
$\mathcal {I}$-fibrant objects.
We prove the theorem at the end of the section. The definition of ![]() $B^{\mathcal {I}}$ and our strategy of proof are motivated by the corresponding rational result in [Reference Félix, Halperin and ThomasFHT01, § 10].
$B^{\mathcal {I}}$ and our strategy of proof are motivated by the corresponding rational result in [Reference Félix, Halperin and ThomasFHT01, § 10].
Corollary 5.2 If ![]() $X \to Y$ is a weak homotopy equivalence of simplicial sets, then
$X \to Y$ is a weak homotopy equivalence of simplicial sets, then ![]() $A^{\mathcal {I}}(Y) \to A^{\mathcal {I}}(X)$ is a descending level equivalence between descending
$A^{\mathcal {I}}(Y) \to A^{\mathcal {I}}(X)$ is a descending level equivalence between descending ![]() $\mathcal {I}$-fibrant objects.
$\mathcal {I}$-fibrant objects.
Proof. The map ![]() $C^{\mathcal {I}}(Y) \to C^{\mathcal {I}}(X)$ is an
$C^{\mathcal {I}}(Y) \to C^{\mathcal {I}}(X)$ is an ![]() $\mathcal {I}$-equivalence since
$\mathcal {I}$-equivalence since ![]() $C(Y) \to C(X)$ is a quasi-isomorphism of chain complexes by the homotopy invariance of singular homology. By the theorem, the claim about
$C(Y) \to C(X)$ is a quasi-isomorphism of chain complexes by the homotopy invariance of singular homology. By the theorem, the claim about ![]() $A^{\mathcal {I}}(Y) \to A^{\mathcal {I}}(X)$ follows.
$A^{\mathcal {I}}(Y) \to A^{\mathcal {I}}(X)$ follows.
Combining Theorem 5.1 with Lemma 4.11 does in particular imply that for positive objects ![]() ${\mathbf {m}}$, the chain complex
${\mathbf {m}}$, the chain complex ![]() $A^{\mathcal {I}}(X)({\mathbf {m}})$ captures the cohomology groups of
$A^{\mathcal {I}}(X)({\mathbf {m}})$ captures the cohomology groups of ![]() $X$ in degrees between
$X$ in degrees between ![]() $0$ and
$0$ and ![]() $|{\mathbf {m}}|$. It should not be surprising that there is a functor from spaces to chain complexes concentrated in degrees between
$|{\mathbf {m}}|$. It should not be surprising that there is a functor from spaces to chain complexes concentrated in degrees between ![]() $0$ and
$0$ and ![]() $- |{\mathbf {m}}|$ which has this property: if one applies the smart truncation
$- |{\mathbf {m}}|$ which has this property: if one applies the smart truncation ![]() $\tau _{\geq -m}$ degreewise to the simplicial object
$\tau _{\geq -m}$ degreewise to the simplicial object ![]() $[p] \mapsto A_{\mathrm {PL},p}$ and applies Construction 2.6 to the resulting simplicial object
$[p] \mapsto A_{\mathrm {PL},p}$ and applies Construction 2.6 to the resulting simplicial object ![]() $\tau _{\geq -m}A_{\mathrm {PL},\bullet }$, one gets back
$\tau _{\geq -m}A_{\mathrm {PL},\bullet }$, one gets back ![]() $\tau _{\geq -m}A_{\mathrm {PL}}$ since
$\tau _{\geq -m}A_{\mathrm {PL}}$ since ![]() $\tau _{\geq -m}$ is right adjoint. In view of this, the chain complexes
$\tau _{\geq -m}$ is right adjoint. In view of this, the chain complexes ![]() $A^{\mathcal {I}}(X)({\mathbf {m}})$ are analogous to truncations of
$A^{\mathcal {I}}(X)({\mathbf {m}})$ are analogous to truncations of ![]() $A_{\mathrm {PL}}(X)$.
$A_{\mathrm {PL}}(X)$.
Lemma 5.3 The maps in (5.2) are absolute level equivalences between absolute ![]() $\mathcal {I}$-fibrant objects when evaluated in simplicial degree
$\mathcal {I}$-fibrant objects when evaluated in simplicial degree ![]() $p$.
$p$.
Proof. Let ![]() ${\mathbf {m}}$ be an object in
${\mathbf {m}}$ be an object in ![]() $\mathcal {I}$. By Lemma 4.16 the map
$\mathcal {I}$. By Lemma 4.16 the map ![]() $S^{0} = U^{\mathcal {I}}({\mathbf {m}}) \to A^{\mathcal {I}}_p({\mathbf {m}})$ is a quasi-isomorphism between cofibrant and fibrant objects and thus even a chain homotopy equivalence. The map
$S^{0} = U^{\mathcal {I}}({\mathbf {m}}) \to A^{\mathcal {I}}_p({\mathbf {m}})$ is a quasi-isomorphism between cofibrant and fibrant objects and thus even a chain homotopy equivalence. The map ![]() $S^{0} \to C(\Delta ^{p}) = C_{p}$ is a quasi-isomorphism by the known computation of
$S^{0} \to C(\Delta ^{p}) = C_{p}$ is a quasi-isomorphism by the known computation of ![]() $H^{*}(\Delta ^{p};k)$. Applying
$H^{*}(\Delta ^{p};k)$. Applying ![]() $F^{\mathcal {I}}_{{\mathbf {0}}}$, it provides an absolute level equivalence
$F^{\mathcal {I}}_{{\mathbf {0}}}$, it provides an absolute level equivalence ![]() $U^{\mathcal {I}} \to C^{\mathcal {I}}_p$. By (5.1), we can decompose
$U^{\mathcal {I}} \to C^{\mathcal {I}}_p$. By (5.1), we can decompose ![]() $U^{\mathcal {I}}({\mathbf {m}}) \to B^{\mathcal {I}}_p({\mathbf {m}})$ as
$U^{\mathcal {I}}({\mathbf {m}}) \to B^{\mathcal {I}}_p({\mathbf {m}})$ as
We already showed that the first map is a quasi-isomorphism. The last one is a quasi-isomorphism since ![]() $-\otimes C_p$ preserves chain homotopy equivalences. The
$-\otimes C_p$ preserves chain homotopy equivalences. The ![]() $\mathcal {I}$-chain complexes
$\mathcal {I}$-chain complexes ![]() $A^{\mathcal {I}}_p$,
$A^{\mathcal {I}}_p$, ![]() $B^{\mathcal {I}}_p$, and
$B^{\mathcal {I}}_p$, and ![]() $C^{\mathcal {I}}_p$ are absolute
$C^{\mathcal {I}}_p$ are absolute ![]() $\mathcal {I}$-fibrant for each
$\mathcal {I}$-fibrant for each ![]() $p\geq 0$ since they are absolute level equivalent to
$p\geq 0$ since they are absolute level equivalent to ![]() $U^{\mathcal {I}}$ and
$U^{\mathcal {I}}$ and ![]() $U^{\mathcal {I}} = \operatorname {const}_{\mathcal {I}}S^{0}$ is absolute
$U^{\mathcal {I}} = \operatorname {const}_{\mathcal {I}}S^{0}$ is absolute ![]() $\mathcal {I}$-fibrant.
$\mathcal {I}$-fibrant.
Lemma 5.4 For all ![]() ${q \in \mathbb {Z}}$ and all positive objects
${q \in \mathbb {Z}}$ and all positive objects ![]() ${\mathbf {m}}$ in
${\mathbf {m}}$ in ![]() $\mathcal {I}$, the simplicial
$\mathcal {I}$, the simplicial ![]() $k$-module
$k$-module ![]() $B^{\mathcal {I}}_{\bullet }({\mathbf {m}})_q$ is contractible to
$B^{\mathcal {I}}_{\bullet }({\mathbf {m}})_q$ is contractible to ![]() $0$.
$0$.
Proof. From (5.1) we get an isomorphism ![]() $B^{\mathcal {I}}_{\bullet }({\mathbf {m}})_q \cong \bigoplus _{r+s=q} A^{\mathcal {I}}_{\bullet }({\mathbf {m}})_{r}\otimes C_{\bullet ,s}$ of simplicial
$B^{\mathcal {I}}_{\bullet }({\mathbf {m}})_q \cong \bigoplus _{r+s=q} A^{\mathcal {I}}_{\bullet }({\mathbf {m}})_{r}\otimes C_{\bullet ,s}$ of simplicial ![]() $k$-modules. Since
$k$-modules. Since ![]() $C_{\bullet , s}$ is contractible for every
$C_{\bullet , s}$ is contractible for every ![]() $s$ by Lemma 3.10(ii), so are the tensor products and thus also the sum.
$s$ by Lemma 3.10(ii), so are the tensor products and thus also the sum.
Lemma 5.5 Let ![]() $D_{\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k$ be a simplicial object in
$D_{\bullet } \colon \Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k$ be a simplicial object in ![]() $\mathcal {I}$-chain complexes such that for all positive objects
$\mathcal {I}$-chain complexes such that for all positive objects ![]() ${\mathbf {m}}$ in
${\mathbf {m}}$ in ![]() $\mathcal {I}$ and all integers
$\mathcal {I}$ and all integers ![]() $q$ with
$q$ with ![]() $q > -|{\mathbf {m}}|$, the simplicial
$q > -|{\mathbf {m}}|$, the simplicial ![]() $k$-module
$k$-module ![]() $D_{\bullet }({\mathbf {m}})_q$ is contractible to
$D_{\bullet }({\mathbf {m}})_q$ is contractible to ![]() $0$. Then for all
$0$. Then for all ![]() $p \geq 0$, the boundary inclusion
$p \geq 0$, the boundary inclusion ![]() $\partial \Delta ^{p} \to \Delta ^{p}$ induces a descending level fibration
$\partial \Delta ^{p} \to \Delta ^{p}$ induces a descending level fibration ![]() $D( \Delta ^{p}) \to D(\partial \Delta ^{p})$.
$D( \Delta ^{p}) \to D(\partial \Delta ^{p})$.
Proof. A map in ![]() $\mathrm {Ch}^{\mathcal {I}}_k$ is a descending level fibration if and only if it has the right lifting property against the maps
$\mathrm {Ch}^{\mathcal {I}}_k$ is a descending level fibration if and only if it has the right lifting property against the maps ![]() $(U \to V) = F^{\mathcal {I}}_{{\mathbf {m}}}(0 \to D^{q})$ with
$(U \to V) = F^{\mathcal {I}}_{{\mathbf {m}}}(0 \to D^{q})$ with ![]() ${\mathbf {m}}$ positive and
${\mathbf {m}}$ positive and ![]() $q > - |{\mathbf {m}}|$. By the adjunction (3.1), the lifting property for
$q > - |{\mathbf {m}}|$. By the adjunction (3.1), the lifting property for ![]() $U\to V$ and
$U\to V$ and ![]() $D(\Delta ^{p}) \to D(\partial \Delta ^{p})$ is equivalent to the lifting property for
$D(\Delta ^{p}) \to D(\partial \Delta ^{p})$ is equivalent to the lifting property for ![]() $\partial \Delta ^{p} \to \Delta ^{p}$ and
$\partial \Delta ^{p} \to \Delta ^{p}$ and ![]() $K_D(V) \to K_D(U)$. Inspecting the definition of
$K_D(V) \to K_D(U)$. Inspecting the definition of ![]() $K_D$, it follows that asking the latter lifting property for all
$K_D$, it follows that asking the latter lifting property for all ![]() $p\geq 0$ is equivalent to asking the map of simplicial sets
$p\geq 0$ is equivalent to asking the map of simplicial sets ![]() $\mathrm {Ch}^{\mathcal {I}}_k(V,D_{\bullet }) \to \mathrm {Ch}^{\mathcal {I}}_k(U,D_{\bullet })$ to be an acyclic Kan fibration. Since
$\mathrm {Ch}^{\mathcal {I}}_k(V,D_{\bullet }) \to \mathrm {Ch}^{\mathcal {I}}_k(U,D_{\bullet })$ to be an acyclic Kan fibration. Since ![]() $(F^{\mathcal {I}}_{{\mathbf {m}}}, \mathrm {Ev}_{{\mathbf {m}}})$ is an adjunction and since morphisms in
$(F^{\mathcal {I}}_{{\mathbf {m}}}, \mathrm {Ev}_{{\mathbf {m}}})$ is an adjunction and since morphisms in ![]() $\mathrm {Ch}_k$ out of
$\mathrm {Ch}_k$ out of ![]() $D^{q}$ correspond to level
$D^{q}$ correspond to level ![]() $q$ elements, the assumption that
$q$ elements, the assumption that ![]() $U \to V$ is
$U \to V$ is ![]() $F^{\mathcal {I}}_{{\mathbf {m}}}(0 \to D^{q})$ implies that
$F^{\mathcal {I}}_{{\mathbf {m}}}(0 \to D^{q})$ implies that ![]() $\mathrm {Ch}^{\mathcal {I}}_k(V,D_{\bullet }) \to \mathrm {Ch}^{\mathcal {I}}_k(U,D_{\bullet })$ is isomorphic to
$\mathrm {Ch}^{\mathcal {I}}_k(V,D_{\bullet }) \to \mathrm {Ch}^{\mathcal {I}}_k(U,D_{\bullet })$ is isomorphic to ![]() $D_{\bullet }({\mathbf {m}})_q \to 0$. The source of this map is contractible by assumption and a Kan complex because it is the underlying simplicial set of a simplicial
$D_{\bullet }({\mathbf {m}})_q \to 0$. The source of this map is contractible by assumption and a Kan complex because it is the underlying simplicial set of a simplicial ![]() $k$-module. Hence
$k$-module. Hence ![]() $D_{\bullet }({\mathbf {m}})_q \to 0$ is an acyclic Kan fibration.
$D_{\bullet }({\mathbf {m}})_q \to 0$ is an acyclic Kan fibration.
Remark 5.6 When ![]() $D_{\bullet }({\mathbf {m}})_q$ is not contractible,
$D_{\bullet }({\mathbf {m}})_q$ is not contractible, ![]() $D(\Delta ^{p})_q \to D(\partial \Delta ^{p})_q$ fails to be surjective. In view of Remark 3.8, this shows for example that
$D(\Delta ^{p})_q \to D(\partial \Delta ^{p})_q$ fails to be surjective. In view of Remark 3.8, this shows for example that ![]() $A^{\mathcal {I}}(\Delta ^{p}) \to A^{\mathcal {I}}(\partial \Delta ^{p})$ is not an absolute level fibration.
$A^{\mathcal {I}}(\Delta ^{p}) \to A^{\mathcal {I}}(\partial \Delta ^{p})$ is not an absolute level fibration.
Proposition 5.7 Let ![]() $D_{\bullet } \to D'_{\bullet }$ be a natural transformation of functors
$D_{\bullet } \to D'_{\bullet }$ be a natural transformation of functors ![]() ${\Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k}$. Suppose that for all
${\Delta ^{{{\mathrm {op}}}} \to \mathrm {Ch}^{\mathcal {I}}_k}$. Suppose that for all ![]() $p \geq 0$, the map
$p \geq 0$, the map ![]() $D_p \to D'_p$ is an absolute level equivalence between absolute
$D_p \to D'_p$ is an absolute level equivalence between absolute ![]() $\mathcal {I}$-fibrant objects and that for all positive objects
$\mathcal {I}$-fibrant objects and that for all positive objects ![]() ${\mathbf {m}}$ and all
${\mathbf {m}}$ and all ![]() $q > -|{\mathbf {m}}|$, the simplicial
$q > -|{\mathbf {m}}|$, the simplicial ![]() $k$-modules
$k$-modules ![]() $D_{\bullet }({\mathbf {m}})_q$ and
$D_{\bullet }({\mathbf {m}})_q$ and ![]() $D'_{\bullet }({\mathbf {m}})_q$ are contractible. Then for every simplicial set
$D'_{\bullet }({\mathbf {m}})_q$ are contractible. Then for every simplicial set ![]() $X$, the map
$X$, the map ![]() $D(X) \to D'(X)$ is a descending level equivalence between descending
$D(X) \to D'(X)$ is a descending level equivalence between descending ![]() $\mathcal {I}$-fibrant objects.
$\mathcal {I}$-fibrant objects.
Proof. As usual, this is proved by cell induction. Let us first assume that for all ![]() $p \geq 0$, the map
$p \geq 0$, the map ![]() $D(\partial \Delta ^{p}) \to D'(\partial \Delta ^{p})$ is a descending level equivalence between descending
$D(\partial \Delta ^{p}) \to D'(\partial \Delta ^{p})$ is a descending level equivalence between descending ![]() $\mathcal {I}$-fibrant objects. Any simplicial set
$\mathcal {I}$-fibrant objects. Any simplicial set ![]() $X$ can be written as a cell complex
$X$ can be written as a cell complex ![]() $X = \operatorname {colim}_{\lambda < \kappa }X_{\lambda }$ built from attaching cells of the form
$X = \operatorname {colim}_{\lambda < \kappa }X_{\lambda }$ built from attaching cells of the form ![]() $\partial \Delta ^{p} \to \Delta ^{p}$. The functor
$\partial \Delta ^{p} \to \Delta ^{p}$. The functor ![]() $D$ takes the inclusion
$D$ takes the inclusion ![]() $\partial \Delta ^{p} \to \Delta ^{p}$ to a descending level fibration by Lemma 5.5. Since we assume that
$\partial \Delta ^{p} \to \Delta ^{p}$ to a descending level fibration by Lemma 5.5. Since we assume that ![]() $D(\partial \Delta ^{p})$ and
$D(\partial \Delta ^{p})$ and ![]() $D_p \cong D(\Delta ^{p})$ are descending
$D_p \cong D(\Delta ^{p})$ are descending ![]() $\mathcal {I}$-fibrant, it follows from Corollary 4.9 that
$\mathcal {I}$-fibrant, it follows from Corollary 4.9 that ![]() $D(\Delta ^{p}) \to D(\partial \Delta ^{p})$ is a descending
$D(\Delta ^{p}) \to D(\partial \Delta ^{p})$ is a descending ![]() $\mathcal {I}$-fibration. The same holds for
$\mathcal {I}$-fibration. The same holds for ![]() $D'$. Since both
$D'$. Since both ![]() $D$ and
$D$ and ![]() $D'$ take colimits to limits by Lemma 3.3, the coglueing lemma in the descending level model structure and the fact that base change preserves
$D'$ take colimits to limits by Lemma 3.3, the coglueing lemma in the descending level model structure and the fact that base change preserves ![]() $\mathcal {I}$-fibrations shows that
$\mathcal {I}$-fibrations shows that ![]() $D(X) \to D'(X)$ arises as a limit of pointwise descending level equivalences between inverse systems of descending
$D(X) \to D'(X)$ arises as a limit of pointwise descending level equivalences between inverse systems of descending ![]() $\mathcal {I}$-fibrations. Hence it is a descending level equivalence between descending
$\mathcal {I}$-fibrations. Hence it is a descending level equivalence between descending ![]() $\mathcal {I}$-fibrant objects.
$\mathcal {I}$-fibrant objects.
Since ![]() $\partial \Delta ^{p}$ only has non-degenerate simplices in dimensions strictly less than
$\partial \Delta ^{p}$ only has non-degenerate simplices in dimensions strictly less than ![]() $p$, an analogous induction over the dimension of
$p$, an analogous induction over the dimension of ![]() $\partial \Delta ^{p}$ shows the remaining claim about
$\partial \Delta ^{p}$ shows the remaining claim about ![]() $D(\partial \Delta ^{p}) \to D'(\partial \Delta ^{p})$.
$D(\partial \Delta ^{p}) \to D'(\partial \Delta ^{p})$.
Proof of Theorem 5.1 Combining Lemma 3.7, Corollary 3.11(ii), Lemmas 5.4, and 5.3, the two maps ![]() $A^{\mathcal {I}} \to B^{\mathcal {I}}$ and
$A^{\mathcal {I}} \to B^{\mathcal {I}}$ and ![]() $C^{\mathcal {I}} \to B^{\mathcal {I}}$ satisfy the hypotheses of Proposition 5.7.
$C^{\mathcal {I}} \to B^{\mathcal {I}}$ satisfy the hypotheses of Proposition 5.7.
We can now also prove Theorem 1.5 from the introduction.
Proof of Theorem 1.5 The adjunction ![]() $(A^{\mathcal {I}}, \langle -\rangle _\mathcal {I})$ arises from
$(A^{\mathcal {I}}, \langle -\rangle _\mathcal {I})$ arises from ![]() $A^{\mathcal {I}}_{\bullet }$ by applying Construction 3.2. Lemmas 3.7 and 5.5 show that
$A^{\mathcal {I}}_{\bullet }$ by applying Construction 3.2. Lemmas 3.7 and 5.5 show that ![]() $A^{\mathcal {I}}$ sends cofibrations to descending level fibrations and thus to descending
$A^{\mathcal {I}}$ sends cofibrations to descending level fibrations and thus to descending ![]() $\mathcal {I}$-fibrations. Corollary 5.2 implies that
$\mathcal {I}$-fibrations. Corollary 5.2 implies that ![]() $A^{\mathcal {I}}$ sends weak homotopy equivalences to descending level equivalences and thus to
$A^{\mathcal {I}}$ sends weak homotopy equivalences to descending level equivalences and thus to ![]() $\mathcal {I}$-equivalences. The rest is an immediate consequence of the self-duality of model structures with respect to the passage to opposite categories and the adjunction isomorphisms (3.1).
$\mathcal {I}$-equivalences. The rest is an immediate consequence of the self-duality of model structures with respect to the passage to opposite categories and the adjunction isomorphisms (3.1).
5.8 The relation to polynomial forms
In order to relate ![]() $A^{\mathcal {I}}$ to the functor
$A^{\mathcal {I}}$ to the functor ![]() $A_{\mathrm {PL}}$ used in rational homotopy theory, we first identify the functor
$A_{\mathrm {PL}}$ used in rational homotopy theory, we first identify the functor ![]() $A_{\mathrm {PL},\bullet }$ described in (1.3) as a two-sided bar construction. Arguing as in § 3.4 and using the notation
$A_{\mathrm {PL},\bullet }$ described in (1.3) as a two-sided bar construction. Arguing as in § 3.4 and using the notation ![]() $D^{0}_r$ introduced there, we get an isomorphism
$D^{0}_r$ introduced there, we get an isomorphism
where ![]() $\mathbb {C}$ denotes the free commutative dga on a chain complex. The assignments
$\mathbb {C}$ denotes the free commutative dga on a chain complex. The assignments
define inverse isomorphisms between ![]() $B_{p}(S^{0},\mathbb {C} D^{0}, S^{0})$ and
$B_{p}(S^{0},\mathbb {C} D^{0}, S^{0})$ and ![]() $A_{\mathrm {PL},p}$, and these isomorphisms are compatible with the structure maps described in § 1.3.
$A_{\mathrm {PL},p}$, and these isomorphisms are compatible with the structure maps described in § 1.3.
By adjunction, the canonical map ![]() $D^{0} \to (\operatorname {const}_{\mathcal {I}} \mathbb {C} D^{0})({\mathbf {1}})$ induces a map of commutative
$D^{0} \to (\operatorname {const}_{\mathcal {I}} \mathbb {C} D^{0})({\mathbf {1}})$ induces a map of commutative ![]() $\mathcal {I}$-dgas
$\mathcal {I}$-dgas ![]() $\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0}) \to \operatorname {const}_{\mathcal {I}} \mathbb {C} D^{0}$. Using the above description of
$\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0}) \to \operatorname {const}_{\mathcal {I}} \mathbb {C} D^{0}$. Using the above description of ![]() $A_{\mathrm {PL},\bullet }$ as a two-sided bar construction, this map in turn induces a map
$A_{\mathrm {PL},\bullet }$ as a two-sided bar construction, this map in turn induces a map ![]() $A^{\mathcal {I}}_{\bullet } \to \operatorname {const}_{\mathcal {I}}A_{\mathrm {PL},\bullet }$ in
$A^{\mathcal {I}}_{\bullet } \to \operatorname {const}_{\mathcal {I}}A_{\mathrm {PL},\bullet }$ in ![]() $\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ and thus a natural map
$\mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}]$ and thus a natural map ![]() $A^{\mathcal {I}}(X) \to \operatorname {const}_{\mathcal {I}} A_{\mathrm {PL}}(X)$ on the extensions to simplicial sets.
$A^{\mathcal {I}}(X) \to \operatorname {const}_{\mathcal {I}} A_{\mathrm {PL}}(X)$ on the extensions to simplicial sets.
Theorem 5.9 Let ![]() $k$ be a field of characteristic
$k$ be a field of characteristic ![]() $0$. Then
$0$. Then ![]() $A^{\mathcal {I}}(X) \to \operatorname {const}_{\mathcal {I}} A_{\mathrm {PL}}(X)$ is a descending level equivalence. It induces a quasi-isomorphism
$A^{\mathcal {I}}(X) \to \operatorname {const}_{\mathcal {I}} A_{\mathrm {PL}}(X)$ is a descending level equivalence. It induces a quasi-isomorphism ![]() $A^{\mathcal {I}}(X)_{h\mathcal {I}} \to A_{\mathrm {PL}}(X)$ that is an
$A^{\mathcal {I}}(X)_{h\mathcal {I}} \to A_{\mathrm {PL}}(X)$ that is an ![]() $\mathcal {E}$-algebra map if we view the cdga
$\mathcal {E}$-algebra map if we view the cdga ![]() $A_{\mathrm {PL}}(X)$ as an
$A_{\mathrm {PL}}(X)$ as an ![]() $\mathcal {E}$-algebra by restricting along the canonical operad map from
$\mathcal {E}$-algebra by restricting along the canonical operad map from ![]() $\mathcal {E}$ to the commutativity operad.
$\mathcal {E}$ to the commutativity operad.
Proof. In characteristic zero the homology groups of ![]() $(D^{0})^{\otimes n}/\Sigma _n$ are isomorphic to the coinvariants
$(D^{0})^{\otimes n}/\Sigma _n$ are isomorphic to the coinvariants ![]() $H_*(D^{0})^{\otimes n}/\Sigma _n$ and the latter term is trivial for
$H_*(D^{0})^{\otimes n}/\Sigma _n$ and the latter term is trivial for ![]() $n \geq 1$ because
$n \geq 1$ because ![]() $D^{0}$ is acyclic. Therefore
$D^{0}$ is acyclic. Therefore ![]() $\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0}) \to \operatorname {const}_{\mathcal {I}} \mathbb {C} D^{0}$ is an absolute level equivalence. The claim about general
$\mathbb {C} F^{\mathcal {I}}_{{\mathbf {1}}}(D^{0}) \to \operatorname {const}_{\mathcal {I}} \mathbb {C} D^{0}$ is an absolute level equivalence. The claim about general ![]() $X$ follows from Proposition 5.7 and the contractibility property of
$X$ follows from Proposition 5.7 and the contractibility property of ![]() $A_{\mathrm {PL},\bullet }$ established in [Reference Bousfield and GugenheimBG76, Proposition 1.1]. Applying
$A_{\mathrm {PL},\bullet }$ established in [Reference Bousfield and GugenheimBG76, Proposition 1.1]. Applying ![]() $(-)_{h\mathcal {I}}$ to this descending level equivalence and composing with the natural quasi-isomorphism (4.1) gives the quasi-isomorphism
$(-)_{h\mathcal {I}}$ to this descending level equivalence and composing with the natural quasi-isomorphism (4.1) gives the quasi-isomorphism ![]() $A^{\mathcal {I}}(X)_{h\mathcal {I}} \to A_{\mathrm {PL}}(X)$. To see that it is an
$A^{\mathcal {I}}(X)_{h\mathcal {I}} \to A_{\mathrm {PL}}(X)$. To see that it is an ![]() $\mathcal {E}$-algebra map, we note that it follows from the definitions that (4.1) is an
$\mathcal {E}$-algebra map, we note that it follows from the definitions that (4.1) is an ![]() $\mathcal {E}$-algebra map when evaluated on a cdga.
$\mathcal {E}$-algebra map when evaluated on a cdga.
6. Comparison of  $E_{\infty }$ structures
$E_{\infty }$ structures
Let ![]() $\mathcal {E}$ be the Barratt–Eccles operad introduced in Definition 2.11. We now define
$\mathcal {E}$ be the Barratt–Eccles operad introduced in Definition 2.11. We now define ![]() $A\colon \mathrm {sSet}^{{\mathrm {op}}} \to \mathrm {Ch}_k[\mathcal {E}]$ to be the composite
$A\colon \mathrm {sSet}^{{\mathrm {op}}} \to \mathrm {Ch}_k[\mathcal {E}]$ to be the composite ![]() $A = (A^{\mathcal {I}})_{h\mathcal {I}}$ of the functor
$A = (A^{\mathcal {I}})_{h\mathcal {I}}$ of the functor ![]() $A^{\mathcal {I}}$ from the previous section and the functor
$A^{\mathcal {I}}$ from the previous section and the functor ![]() $(-)_{h\mathcal {I}}\colon \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}] \to \mathrm {Ch}_k[\mathcal {E}]$ resulting from Theorem 2.13. The following proposition shows that
$(-)_{h\mathcal {I}}\colon \mathrm {Ch}^{\mathcal {I}}_k[\mathcal {C}] \to \mathrm {Ch}_k[\mathcal {E}]$ resulting from Theorem 2.13. The following proposition shows that ![]() $A$ is a cochain theory in the sense of [Reference MandellMan02].
$A$ is a cochain theory in the sense of [Reference MandellMan02].
Proposition 6.1 The functor ![]() $A\colon \mathrm {sSet}^{{\mathrm {op}}} \to \mathrm {Ch}_k[\mathcal {E}]$ has the following properties.
$A\colon \mathrm {sSet}^{{\mathrm {op}}} \to \mathrm {Ch}_k[\mathcal {E}]$ has the following properties.
(i) It sends weak equivalence of simplicial sets to quasi-isomorphisms.
(ii) For a sub-simplicial set
 $Y \subseteq X$, the induced map from
$Y \subseteq X$, the induced map from  $\mathrm {hofib}{(A(X/Y) \to A(*))}$ to
$\mathrm {hofib}{(A(X/Y) \to A(*))}$ to  $\mathrm {hofib}(A(X) \to A(Y))$ is a quasi-isomorphism.
$\mathrm {hofib}(A(X) \to A(Y))$ is a quasi-isomorphism.(iii) For a family
 $(X_{j})_{j \in J}$ of simplicial sets indexed by a set
$(X_{j})_{j \in J}$ of simplicial sets indexed by a set  $J$, the canonical map
$J$, the canonical map  $A(\coprod _{j \in J} X_{j}) \to \prod _{j \in J} A(X_{j})$ is a quasi-isomorphism.
$A(\coprod _{j \in J} X_{j}) \to \prod _{j \in J} A(X_{j})$ is a quasi-isomorphism.(iv) It satisfies
 $H_0(A(*))\cong k$ and
$H_0(A(*))\cong k$ and  $H_n(A(*)) \cong 0$ if
$H_n(A(*)) \cong 0$ if  $n\neq 0$.
$n\neq 0$.
Proof. Part (i) follows from Corollary 5.2, part (iv) is an immediate consequence of Theorem 5.1, and part (iii) follows from Lemma 4.12 because ![]() $A^{\mathcal {I}}$ takes coproducts in
$A^{\mathcal {I}}$ takes coproducts in ![]() $\mathrm {sSet}$ to products of fibrant objects in
$\mathrm {sSet}$ to products of fibrant objects in ![]() $\mathrm {Ch}^{\mathcal {I}}_k$.
$\mathrm {Ch}^{\mathcal {I}}_k$.
For part (ii), we view ![]() $X/Y$ as the pushout of
$X/Y$ as the pushout of ![]() $* \leftarrow Y \to X$. The functor
$* \leftarrow Y \to X$. The functor ![]() $A^{\mathcal {I}}$ sends this pushout to a pullback diagram displayed as the front face in the following cube.
$A^{\mathcal {I}}$ sends this pushout to a pullback diagram displayed as the front face in the following cube.

Here the vertical maps on the front are descending level fibrations between descending ![]() $\mathcal {I}$-fibrant objects by Theorem 1.5. The bottom face is obtained by applying a fibrant replacement in the absolute
$\mathcal {I}$-fibrant objects by Theorem 1.5. The bottom face is obtained by applying a fibrant replacement in the absolute ![]() $\mathcal {I}$-model structure to the map
$\mathcal {I}$-model structure to the map ![]() $A^{\mathcal {I}}(*) \to A^{\mathcal {I}}(Y)$, and the inwards pointing arrows on the bottom are descending level equivalences by Corollary 4.10. The right hand face is obtained by factoring
$A^{\mathcal {I}}(*) \to A^{\mathcal {I}}(Y)$, and the inwards pointing arrows on the bottom are descending level equivalences by Corollary 4.10. The right hand face is obtained by factoring ![]() $A^{\mathcal {I}}(X) \to A^{\mathcal {I}}(Y)'$ as an acyclic cofibration
$A^{\mathcal {I}}(X) \to A^{\mathcal {I}}(Y)'$ as an acyclic cofibration ![]() $A^{\mathcal {I}}(X) \to A^{\mathcal {I}}(X)'$ followed by a fibration
$A^{\mathcal {I}}(X) \to A^{\mathcal {I}}(X)'$ followed by a fibration ![]() $A^{\mathcal {I}}(X)' \to A^{\mathcal {I}}(Y)'$ in the absolute
$A^{\mathcal {I}}(X)' \to A^{\mathcal {I}}(Y)'$ in the absolute ![]() $\mathcal {I}$-model structure. Then
$\mathcal {I}$-model structure. Then ![]() $A^{\mathcal {I}}(X) \to A^{\mathcal {I}}(X)'$ is also a descending level equivalence by Corollary 4.10. The last term
$A^{\mathcal {I}}(X) \to A^{\mathcal {I}}(X)'$ is also a descending level equivalence by Corollary 4.10. The last term ![]() $A^{\mathcal {I}}(X/Y)'$ is obtained by requiring the back face to be a pullback. Right properness of the descending level model structure implies that
$A^{\mathcal {I}}(X/Y)'$ is obtained by requiring the back face to be a pullback. Right properness of the descending level model structure implies that ![]() $A^{\mathcal {I}}(X/Y) \to A^{\mathcal {I}}(X/Y)'$ is a descending level equivalence. It then follows from Lemma 4.11 that the square obtained by applying
$A^{\mathcal {I}}(X/Y) \to A^{\mathcal {I}}(X/Y)'$ is a descending level equivalence. It then follows from Lemma 4.11 that the square obtained by applying ![]() $(-)_{h\mathcal {I}}$ to the front face is quasi-isomorphic to the square obtained by evaluating the back face at the object
$(-)_{h\mathcal {I}}$ to the front face is quasi-isomorphic to the square obtained by evaluating the back face at the object ![]() ${\mathbf {0}}$. The latter square is homotopy cartesian by construction.
${\mathbf {0}}$. The latter square is homotopy cartesian by construction.
Let ![]() $\mathcal {E}^{\mathrm {cof}}$ be a cofibrant
$\mathcal {E}^{\mathrm {cof}}$ be a cofibrant ![]() $E_{\infty }$ operad in the sense of [Reference MandellMan02, Definition 4.2]. Then there exists an operad map
$E_{\infty }$ operad in the sense of [Reference MandellMan02, Definition 4.2]. Then there exists an operad map ![]() $\mathcal {E}^{\mathrm {cof}} \to \mathcal {E}$ to the Barratt–Eccles operad [Reference MandellMan02, Lemma 4.5], and by restricting along
$\mathcal {E}^{\mathrm {cof}} \to \mathcal {E}$ to the Barratt–Eccles operad [Reference MandellMan02, Lemma 4.5], and by restricting along ![]() $\mathcal {E}^{\mathrm {cof}} \to \mathcal {E}$ we may view
$\mathcal {E}^{\mathrm {cof}} \to \mathcal {E}$ we may view ![]() $A$ as a functor to
$A$ as a functor to ![]() $\mathcal {E}^{\mathrm {cof}}$-algebras. On the other hand, the cosimplicial normalization functor for the category
$\mathcal {E}^{\mathrm {cof}}$-algebras. On the other hand, the cosimplicial normalization functor for the category ![]() $\mathrm {Ch}_k[\mathcal {E}^{\mathrm {cof}}]$ provided by [Reference MandellMan02, Theorem 5.8] allows one to lift the ordinary cochain functor
$\mathrm {Ch}_k[\mathcal {E}^{\mathrm {cof}}]$ provided by [Reference MandellMan02, Theorem 5.8] allows one to lift the ordinary cochain functor ![]() $C\colon \mathrm {sSet}^{{\mathrm {op}}} \to \mathrm {Ch}_k$ to a functor with values in
$C\colon \mathrm {sSet}^{{\mathrm {op}}} \to \mathrm {Ch}_k$ to a functor with values in ![]() $\mathrm {Ch}_k[\mathcal {E}^{\mathrm {cof}}]$ (compare [Reference MandellMan02, § 1]). We are now in a situation where [Reference MandellMan02, Main Theorem] applies.
$\mathrm {Ch}_k[\mathcal {E}^{\mathrm {cof}}]$ (compare [Reference MandellMan02, § 1]). We are now in a situation where [Reference MandellMan02, Main Theorem] applies.
Theorem 6.2 The functor ![]() $A \colon \mathrm {sSet}^{{\mathrm {op}}} \to \mathrm {Ch}_k[\mathcal {E}^{\mathrm {cof}}]$ is naturally quasi-isomorphic to the singular cochain functor
$A \colon \mathrm {sSet}^{{\mathrm {op}}} \to \mathrm {Ch}_k[\mathcal {E}^{\mathrm {cof}}]$ is naturally quasi-isomorphic to the singular cochain functor ![]() $C \colon \mathrm {sSet}^{{\mathrm {op}}} \to \mathrm {Ch}_k[\mathcal {E}^{\mathrm {cof}}]$.
$C \colon \mathrm {sSet}^{{\mathrm {op}}} \to \mathrm {Ch}_k[\mathcal {E}^{\mathrm {cof}}]$.
Remark 6.3 It is well known how to express the cup-![]() $i$ products on the singular cohomology of spaces using the Barratt-Eccles operad, see for instance [Reference Berger and FresseBF04, Theorem 2.1.1]. This way the
$i$ products on the singular cohomology of spaces using the Barratt-Eccles operad, see for instance [Reference Berger and FresseBF04, Theorem 2.1.1]. This way the ![]() $\mathcal {E}$-algebra structure on
$\mathcal {E}$-algebra structure on ![]() $A(X) = A^{\mathcal {I}}(X)_{h\mathcal {I}}$ gives rise to cup-
$A(X) = A^{\mathcal {I}}(X)_{h\mathcal {I}}$ gives rise to cup-![]() $i$ products, and the previous theorem shows that they are equivalent to the usual cup-
$i$ products, and the previous theorem shows that they are equivalent to the usual cup-![]() $i$ products on the cochain algebra.
$i$ products on the cochain algebra.
Theorem 6.2 also allows us to express Mandell's theorem [Reference MandellMan06] using ![]() $A^{\mathcal {I}}$.
$A^{\mathcal {I}}$.
Proof of Theorem 1.2 Let ![]() $X$ and
$X$ and ![]() $Y$ be two finite type nilpotent spaces. By Proposition 4.15, the commutative
$Y$ be two finite type nilpotent spaces. By Proposition 4.15, the commutative ![]() $\mathcal {I}$-dgas
$\mathcal {I}$-dgas ![]() $A^{\mathcal {I}}(X;\mathbb {Z})$ and
$A^{\mathcal {I}}(X;\mathbb {Z})$ and ![]() $A^{\mathcal {I}}(Y;\mathbb {Z})$ are
$A^{\mathcal {I}}(Y;\mathbb {Z})$ are ![]() $\mathcal {I}$-equivalent in
$\mathcal {I}$-equivalent in ![]() $\mathrm {Ch}^{\mathcal {I}}_{\mathbb {Z}}[\mathcal {C}]$ if and only if
$\mathrm {Ch}^{\mathcal {I}}_{\mathbb {Z}}[\mathcal {C}]$ if and only if ![]() $A^{\mathcal {I}}(X;\mathbb {Z})_{h\mathcal {I}}$ and
$A^{\mathcal {I}}(X;\mathbb {Z})_{h\mathcal {I}}$ and ![]() $A^{\mathcal {I}}(Y;\mathbb {Z})_{h\mathcal {I}}$ are quasi-isomorphic in
$A^{\mathcal {I}}(Y;\mathbb {Z})_{h\mathcal {I}}$ are quasi-isomorphic in ![]() $\mathrm {Ch}_{\mathbb {Z}}[\mathcal {E}]$, which is in turn equivalent to being quasi-isomorphic in
$\mathrm {Ch}_{\mathbb {Z}}[\mathcal {E}]$, which is in turn equivalent to being quasi-isomorphic in ![]() $\mathrm {Ch}_{\mathbb {Z}}[\mathcal {E}^{\mathrm {cof}}]$. By Theorem 6.2, this holds if and only if
$\mathrm {Ch}_{\mathbb {Z}}[\mathcal {E}^{\mathrm {cof}}]$. By Theorem 6.2, this holds if and only if ![]() $C^{*}(X;\mathbb {Z})$ and
$C^{*}(X;\mathbb {Z})$ and ![]() $C^{*}(Y;\mathbb {Z})$ are quasi-isomorphic in
$C^{*}(Y;\mathbb {Z})$ are quasi-isomorphic in ![]() $\mathrm {Ch}_{\mathbb {Z}}[\mathcal {E}^{\mathrm {cof}}]$. By [Reference MandellMan06, Main Theorem], this is the case if and only if
$\mathrm {Ch}_{\mathbb {Z}}[\mathcal {E}^{\mathrm {cof}}]$. By [Reference MandellMan06, Main Theorem], this is the case if and only if ![]() $X$ and
$X$ and ![]() $Y$ are weakly equivalent.
$Y$ are weakly equivalent.
Acknowledgements
The authors thank the referees for useful comments on an earlier version of this paper and Josefien Kuijper for bringing an error in a previous version of Lemma 3.7 to our attention.