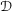1 Introduction
Let
![]() $G$
be a complex reductive group with Langlands dual
$G$
be a complex reductive group with Langlands dual
![]() $G^{\vee }$
. Thanks to Kazhdan–Lusztig [Reference Kazhdan and LusztigKL87], the affine Hecke algebra of
$G^{\vee }$
. Thanks to Kazhdan–Lusztig [Reference Kazhdan and LusztigKL87], the affine Hecke algebra of
![]() $G^{\vee }$
admits a spectral description in terms of the
$G^{\vee }$
admits a spectral description in terms of the
![]() $K$
-group of equivariant coherent sheaves on the Steinberg variety of
$K$
-group of equivariant coherent sheaves on the Steinberg variety of
![]() $G$
, which results in a classification of irreducible representations (the Deligne–Langlands conjecture). Thanks to Bezrukavnikov [Reference BezrukavnikovBez16], the affine Hecke category similarly admits a spectral description in terms of the category of equivariant coherent sheaves on the Steinberg variety, which one might hope to apply to describe the representation theory of the affine Hecke category. The main results of this paper are the calculation of the categorical center and trace of the affine Hecke category starting from this spectral presentation. The resulting categories comprise coherent sheaves on the commuting stack, the derived stack of
$G$
, which results in a classification of irreducible representations (the Deligne–Langlands conjecture). Thanks to Bezrukavnikov [Reference BezrukavnikovBez16], the affine Hecke category similarly admits a spectral description in terms of the category of equivariant coherent sheaves on the Steinberg variety, which one might hope to apply to describe the representation theory of the affine Hecke category. The main results of this paper are the calculation of the categorical center and trace of the affine Hecke category starting from this spectral presentation. The resulting categories comprise coherent sheaves on the commuting stack, the derived stack of
![]() $G$
-local systems on the two-torus, satisfying prescribed support conditions, in particular singular support conditions that appear in recent advances in the geometric Langlands program [Reference Arinkin and GaitsgoryAG15].
$G$
-local systems on the two-torus, satisfying prescribed support conditions, in particular singular support conditions that appear in recent advances in the geometric Langlands program [Reference Arinkin and GaitsgoryAG15].
It is known that the categorical center [Reference Bezrukavnikov, Finkelberg and OstrikBFO12, Reference Ben-Zvi and NadlerBN09] and trace [Reference Ben-Zvi and NadlerBN09] of the finite Hecke category are equivalent to Lusztig’s character sheaves. Thus, one can view the results of this paper as giving a spectral construction of the putative category of affine character sheaves as the geometric Langlands category in genus one. The automorphic geometry of affine character sheaves continues to be the subject of much ongoing work, motivated by representation theory of groups over local fields, with recent notable advances by Lusztig [Reference LusztigLus12, Reference LusztigLus14] and Bezrukavnikov et al. [Reference Bezrukavnikov, Kazhdan and VarshavskyBKV15] (the latter use the center of the affine Hecke category as a model for affine character sheaves). It is the natural home to a huge wealth of enumerative questions in representation theory and gauge theory (see, for example, [Reference Schiffmann and VasserotSV11, Reference Schiffmann and VasserotSV12, Reference Ben-Zvi and NadlerBN13b]).
Independently of specific applications, our proofs develop new descent techniques of broad applicability to coherent sheaves in derived algebraic geometry and
![]() ${\mathcal{D}}$
-modules in microlocal geometry. In this introduction, we first explain the general techniques and then their specific application to the affine Hecke category. We conclude with a brief further discussion of the place of this work within geometric representation theory.
${\mathcal{D}}$
-modules in microlocal geometry. In this introduction, we first explain the general techniques and then their specific application to the affine Hecke category. We conclude with a brief further discussion of the place of this work within geometric representation theory.
We will work throughout over a field
![]() $k$
of characteristic zero. All constructions and terminology will refer to natural derived enhancements. For example, we will use the term category to represent pre-triangulated
$k$
of characteristic zero. All constructions and terminology will refer to natural derived enhancements. For example, we will use the term category to represent pre-triangulated
![]() $k$
-linear dg category or stable
$k$
-linear dg category or stable
![]() $k$
-linear
$k$
-linear
![]() $\infty$
category.
$\infty$
category.
1.1 Singular support
To any coherent
![]() ${\mathcal{D}}$
-module
${\mathcal{D}}$
-module
![]() ${\mathcal{M}}$
on a smooth scheme
${\mathcal{M}}$
on a smooth scheme
![]() $Z$
, one can associate a closed conic coisotropic subvariety
$Z$
, one can associate a closed conic coisotropic subvariety
![]() $\unicode[STIX]{x1D707}({\mathcal{M}})\subset T^{\ast }Z$
called the singular support of
$\unicode[STIX]{x1D707}({\mathcal{M}})\subset T^{\ast }Z$
called the singular support of
![]() ${\mathcal{M}}$
. The intersection of the singular support with the zero-section is the traditional support of
${\mathcal{M}}$
. The intersection of the singular support with the zero-section is the traditional support of
![]() ${\mathcal{M}}$
, and
${\mathcal{M}}$
, and
![]() ${\mathcal{M}}$
is a vector bundle with flat connection if and only if the singular support lies in the zero-section. In general, the singular support records those codirections in which the propagation of sections of
${\mathcal{M}}$
is a vector bundle with flat connection if and only if the singular support lies in the zero-section. In general, the singular support records those codirections in which the propagation of sections of
![]() ${\mathcal{M}}$
are obstructed. In more traditional language, if one thinks of
${\mathcal{M}}$
are obstructed. In more traditional language, if one thinks of
![]() ${\mathcal{M}}$
as a generalized system of linear partial differential equations (PDEs), then the singular support comprises the wavefronts of distributional solutions.
${\mathcal{M}}$
as a generalized system of linear partial differential equations (PDEs), then the singular support comprises the wavefronts of distributional solutions.
Important categories of
![]() ${\mathcal{D}}$
-modules are cut out by singular support conditions: holonomic
${\mathcal{D}}$
-modules are cut out by singular support conditions: holonomic
![]() ${\mathcal{D}}$
-modules are those whose singular support is of minimal dimension and hence Lagrangian; Lusztig’s character sheaves are adjoint-equivariant
${\mathcal{D}}$
-modules are those whose singular support is of minimal dimension and hence Lagrangian; Lusztig’s character sheaves are adjoint-equivariant
![]() ${\mathcal{D}}$
-modules on a reductive group with nilpotent singular support. As is familiar with linear PDEs, many aspects of
${\mathcal{D}}$
-modules on a reductive group with nilpotent singular support. As is familiar with linear PDEs, many aspects of
![]() ${\mathcal{D}}$
-modules, such as their classifications and functoriality, are best understood by viewing them microlocally via singular support.
${\mathcal{D}}$
-modules, such as their classifications and functoriality, are best understood by viewing them microlocally via singular support.
Recent advances in the geometric Langlands program [Reference Arinkin and GaitsgoryAG15], building upon the study of categorical support in [Reference Benson, Iyengar and KrauseBIK08], have brought sharpened attention to and deepened understanding of a parallel theory of singular support for coherent sheaves. We will continue by briefly highlighting some of the key ideas in this story, with a further discussion to be found in § 2.
The natural working context is now not a smooth scheme but a quasi-smooth derived scheme. Recall that a derived scheme
![]() $Z$
is quasi-smooth if and only if it is a derived local complete intersection in the sense that it is Zariski-locally the derived zero-locus of a finite collection of polynomials. Equivalently, a derived scheme
$Z$
is quasi-smooth if and only if it is a derived local complete intersection in the sense that it is Zariski-locally the derived zero-locus of a finite collection of polynomials. Equivalently, a derived scheme
![]() $Z$
is quasi-smooth if and only if its cotangent complex
$Z$
is quasi-smooth if and only if its cotangent complex
![]() $\mathbb{L}_{Z}$
is perfect of tor-amplitude
$\mathbb{L}_{Z}$
is perfect of tor-amplitude
![]() $[-1,0]$
. More generally, it is possible to expand the working context to include derived stacks that are quasi-smooth in the sense that they admit a smooth atlas of quasi-smooth derived schemes.
$[-1,0]$
. More generally, it is possible to expand the working context to include derived stacks that are quasi-smooth in the sense that they admit a smooth atlas of quasi-smooth derived schemes.
To any quasi-smooth derived stack
![]() $Z$
, with underlying classical stack
$Z$
, with underlying classical stack
![]() $Z^{\text{cl}}$
, one can attach its shifted cotangent bundle
$Z^{\text{cl}}$
, one can attach its shifted cotangent bundle
The shifted cotangent bundle
![]() $T_{Z}^{\ast -1}$
is a classical stack with a natural map
$T_{Z}^{\ast -1}$
is a classical stack with a natural map
![]() $T_{Z}^{\ast -1}\rightarrow Z^{\text{cl}}$
with fibers the shift into degree
$T_{Z}^{\ast -1}\rightarrow Z^{\text{cl}}$
with fibers the shift into degree
![]() $0$
of the degree
$0$
of the degree
![]() $-1$
cohomology of
$-1$
cohomology of
![]() $\mathbb{L}_{Z}$
. There is a natural closed embedding
$\mathbb{L}_{Z}$
. There is a natural closed embedding
![]() $Z^{\text{cl}}\subset T_{Z}^{\ast -1}$
of the zero-section which is an isomorphism over the smooth locus of
$Z^{\text{cl}}\subset T_{Z}^{\ast -1}$
of the zero-section which is an isomorphism over the smooth locus of
![]() $Z$
.
$Z$
.
Let
![]() $\operatorname{DCoh}(Z)$
denote the derived category of coherent complexes on
$\operatorname{DCoh}(Z)$
denote the derived category of coherent complexes on
![]() $Z$
, and
$Z$
, and
![]() $\operatorname{Perf}(Z)$
the derived category of perfect complexes. Functions on the shifted cotangent bundle
$\operatorname{Perf}(Z)$
the derived category of perfect complexes. Functions on the shifted cotangent bundle
![]() $T_{Z}^{\ast -1}$
naturally map to the graded center of the homotopy category of
$T_{Z}^{\ast -1}$
naturally map to the graded center of the homotopy category of
![]() $\operatorname{DCoh}(Z)$
. In this way, any coherent complex
$\operatorname{DCoh}(Z)$
. In this way, any coherent complex
![]() ${\mathcal{M}}\in \operatorname{DCoh}(Z)$
has a natural singular support
${\mathcal{M}}\in \operatorname{DCoh}(Z)$
has a natural singular support
![]() $\unicode[STIX]{x1D707}({\mathcal{M}})\subset T_{Z}^{\ast -1}$
that is a closed conic subset. The singular support
$\unicode[STIX]{x1D707}({\mathcal{M}})\subset T_{Z}^{\ast -1}$
that is a closed conic subset. The singular support
![]() $\unicode[STIX]{x1D707}(M)$
records the failure of
$\unicode[STIX]{x1D707}(M)$
records the failure of
![]() ${\mathcal{M}}$
to be a perfect complex:
${\mathcal{M}}$
to be a perfect complex:
![]() $\unicode[STIX]{x1D707}({\mathcal{M}})\cap Z^{\text{cl}}$
is the traditional support of
$\unicode[STIX]{x1D707}({\mathcal{M}})\cap Z^{\text{cl}}$
is the traditional support of
![]() ${\mathcal{M}}$
, and
${\mathcal{M}}$
, and
![]() ${\mathcal{M}}\in \operatorname{Perf}(Z)$
if and only if
${\mathcal{M}}\in \operatorname{Perf}(Z)$
if and only if
![]() $\unicode[STIX]{x1D707}({\mathcal{M}})\subset Z^{\text{cl}}$
. More precisely, the singular support
$\unicode[STIX]{x1D707}({\mathcal{M}})\subset Z^{\text{cl}}$
. More precisely, the singular support
![]() $\unicode[STIX]{x1D707}({\mathcal{M}})$
measures codirections of smoothings of
$\unicode[STIX]{x1D707}({\mathcal{M}})$
measures codirections of smoothings of
![]() $Z$
in which
$Z$
in which
![]() ${\mathcal{M}}$
is obstructed from extending as a coherent complex (see Remark 2.1.3). To any conic Zariski-closed subset
${\mathcal{M}}$
is obstructed from extending as a coherent complex (see Remark 2.1.3). To any conic Zariski-closed subset
![]() $\unicode[STIX]{x1D6EC}\subset T_{Z}^{\ast -1}$
, there is a full subcategory
$\unicode[STIX]{x1D6EC}\subset T_{Z}^{\ast -1}$
, there is a full subcategory
consisting of coherent sheaves
![]() ${\mathcal{M}}$
with singular support
${\mathcal{M}}$
with singular support
![]() $\unicode[STIX]{x1D707}({\mathcal{M}})\in \unicode[STIX]{x1D6EC}$
. Provided
$\unicode[STIX]{x1D707}({\mathcal{M}})\in \unicode[STIX]{x1D6EC}$
. Provided
![]() $\unicode[STIX]{x1D6EC}$
contains the zero-section
$\unicode[STIX]{x1D6EC}$
contains the zero-section
![]() $Z^{\text{cl}}$
, we also have
$Z^{\text{cl}}$
, we also have
Coherent complexes with interesting singular support arise from pushforward along proper but not smooth maps. A map of quasi-smooth stacks
![]() $f:W\rightarrow Z$
induces a correspondence
$f:W\rightarrow Z$
induces a correspondence
In analogy with traditional microlocal subsets, one can pushforward and pullback support conditions by taking them across the correspondence. One can measure the singularities of the map via its characteristic locus, the closed conic subset of covectors that pullback to the zero-section
Assuming
![]() $f$
is proper, pushing forward perfect complexes along
$f$
is proper, pushing forward perfect complexes along
![]() $f$
produces coherent complexes with singularities in
$f$
produces coherent complexes with singularities in
![]() $\unicode[STIX]{x1D6EC}_{f}\subset T_{Z}^{\ast -1}$
.
$\unicode[STIX]{x1D6EC}_{f}\subset T_{Z}^{\ast -1}$
.
The appearance of singular support in this paper will result from studying descent along proper but not smooth maps. A main technical tool will be a new descent theory for coherent complexes with prescribed singular support. The arguments apply equally well in the more familiar setting of
![]() ${\mathcal{D}}$
-modules and provide a new microlocal descent theory there as well.
${\mathcal{D}}$
-modules and provide a new microlocal descent theory there as well.
1.2 Convolution categories
Next, we introduce the general formalism of convolution categories of coherent complexes. We then state our main results about the calculations of their monoidal centers and traces.
Let
![]() $p:X\rightarrow Y$
be a proper map of derived stacks. We will ultimately apply this to simple concrete examples, but in general assume that
$p:X\rightarrow Y$
be a proper map of derived stacks. We will ultimately apply this to simple concrete examples, but in general assume that
![]() $X,Y$
are reasonable (perfect stacks over
$X,Y$
are reasonable (perfect stacks over
![]() $k$
in the sense of [Reference Ben-Zvi, Francis and NadlerBFN10], in particular, quasi-compact with affine diagonal) and that
$k$
in the sense of [Reference Ben-Zvi, Francis and NadlerBFN10], in particular, quasi-compact with affine diagonal) and that
![]() $X$
is smooth.
$X$
is smooth.
In [Reference Ben-Zvi, Nadler and PreygelBNP], we prove general representability results for functors between categories of coherent sheaves as integral transforms with coherent kernels. In our present setting, we find that the integral transform construction provides a canonical equivalence
Here the functor category consists of exact
![]() $\operatorname{Perf}(Y)$
-linear functors where
$\operatorname{Perf}(Y)$
-linear functors where
![]() $\operatorname{Perf}(Y)$
is monoidal and
$\operatorname{Perf}(Y)$
is monoidal and
![]() $\operatorname{DCoh}(X)$
is a module with respect to the tensor product. Note that the functor category is naturally monoidal with respect to composition of functors and has a natural module
$\operatorname{DCoh}(X)$
is a module with respect to the tensor product. Note that the functor category is naturally monoidal with respect to composition of functors and has a natural module
![]() $\operatorname{DCoh}(X)$
.
$\operatorname{DCoh}(X)$
.
Since
![]() $X$
is smooth, the diagonal
$X$
is smooth, the diagonal
![]() $\unicode[STIX]{x1D6E5}:X\rightarrow X\times X$
has finite tor-dimension, so that convolution equips the category of integral kernels
$\unicode[STIX]{x1D6E5}:X\rightarrow X\times X$
has finite tor-dimension, so that convolution equips the category of integral kernels
![]() $\operatorname{DCoh}(X\times _{Y}X)$
with a natural monoidal structure
$\operatorname{DCoh}(X\times _{Y}X)$
with a natural monoidal structure
Moreover, convolution also makes
![]() $\operatorname{DCoh}(X)$
into a natural
$\operatorname{DCoh}(X)$
into a natural
![]() $\operatorname{DCoh}(X\times _{Y}X)$
-module
$\operatorname{DCoh}(X\times _{Y}X)$
-module
We have the following basic compatibility.
Proposition 1.2.1. The integral transform construction is naturally a monoidal equivalence
compatible with actions on the module
![]() $\operatorname{DCoh}(X)$
.
$\operatorname{DCoh}(X)$
.
Remark 1.2.2. One can also equip
![]() $\operatorname{DCoh}(X\times _{Y}X)$
with the alternative
$\operatorname{DCoh}(X\times _{Y}X)$
with the alternative
![]() $!$
-convolution structure
$!$
-convolution structure
![]() $\mathscr{F}_{1}\ast ^{!}\mathscr{F}_{2}=\unicode[STIX]{x1D70B}_{13\ast }\unicode[STIX]{x1D6FF}_{23}^{!}(\mathscr{F}_{1}\boxtimes \mathscr{F}_{2})$
. However, tensoring with the pullback
$\mathscr{F}_{1}\ast ^{!}\mathscr{F}_{2}=\unicode[STIX]{x1D70B}_{13\ast }\unicode[STIX]{x1D6FF}_{23}^{!}(\mathscr{F}_{1}\boxtimes \mathscr{F}_{2})$
. However, tensoring with the pullback
![]() $p_{2}^{\ast }\unicode[STIX]{x1D714}_{X}$
of the dualizing complex intertwines the two monoidal structures. Likewise, tensoring with
$p_{2}^{\ast }\unicode[STIX]{x1D714}_{X}$
of the dualizing complex intertwines the two monoidal structures. Likewise, tensoring with
![]() $\unicode[STIX]{x1D714}_{X}$
intertwines the two module structures on
$\unicode[STIX]{x1D714}_{X}$
intertwines the two module structures on
![]() $\operatorname{DCoh}(X)$
. Note, however, that this does not intertwine the two natural self-dualities on
$\operatorname{DCoh}(X)$
. Note, however, that this does not intertwine the two natural self-dualities on
![]() $\operatorname{Perf}(X)\simeq \operatorname{DCoh}(X)$
unless
$\operatorname{Perf}(X)\simeq \operatorname{DCoh}(X)$
unless
![]() $X$
is Calabi–Yau, in which case the two monoidal structures coincide.
$X$
is Calabi–Yau, in which case the two monoidal structures coincide.
A natural challenge in geometric representation theory is to understand the module theory of the convolution category
![]() $\operatorname{DCoh}(X\times _{Y}X)$
. It provides a highly structured version of the module theory of the affine Hecke algebra. In this paper, we will take the initial fundamental step and calculate its monoidal center and trace.
$\operatorname{DCoh}(X\times _{Y}X)$
. It provides a highly structured version of the module theory of the affine Hecke algebra. In this paper, we will take the initial fundamental step and calculate its monoidal center and trace.
Definition 1.2.3. Let
![]() ${\mathcal{A}}$
be an algebra object in a symmetric monoidal
${\mathcal{A}}$
be an algebra object in a symmetric monoidal
![]() $\infty$
category
$\infty$
category
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
-
(1) The center (or Hochschild cohomology) is the morphism of bimodules object
It comes with a natural $$\begin{eqnarray}\mathit{Z}({\mathcal{A}})=\operatorname{Hom}_{{\mathcal{A}}^{\text{op}}\otimes {\mathcal{A}}}({\mathcal{A}},{\mathcal{A}})\in {\mathcal{C}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathit{Z}({\mathcal{A}})=\operatorname{Hom}_{{\mathcal{A}}^{\text{op}}\otimes {\mathcal{A}}}({\mathcal{A}},{\mathcal{A}})\in {\mathcal{C}}.\end{eqnarray}$$
 $E_{2}$
-monoidal structure and universal central map
$E_{2}$
-monoidal structure and universal central map
 $\mathit{Z}({\mathcal{A}})\rightarrow {\mathcal{A}}$
.
$\mathit{Z}({\mathcal{A}})\rightarrow {\mathcal{A}}$
.
-
(2) The trace (or Hochschild homology) is the tensor of bimodules object
It comes with a natural $$\begin{eqnarray}\text{Tr}({\mathcal{A}})={\mathcal{A}}\otimes _{{\mathcal{A}}^{\text{op}}\otimes {\mathcal{A}}}{\mathcal{A}}\in {\mathcal{C}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Tr}({\mathcal{A}})={\mathcal{A}}\otimes _{{\mathcal{A}}^{\text{op}}\otimes {\mathcal{A}}}{\mathcal{A}}\in {\mathcal{C}}.\end{eqnarray}$$
 $S^{1}$
-action and universal trace map
$S^{1}$
-action and universal trace map
 ${\mathcal{A}}\rightarrow \text{Tr}({\mathcal{A}})$
.
${\mathcal{A}}\rightarrow \text{Tr}({\mathcal{A}})$
.
Remark 1.2.4. We refer the reader to [Reference LurieLur, §§ 5.3 and 6.1] for the
![]() $E_{2}$
-structure on the center (Deligne conjecture) and
$E_{2}$
-structure on the center (Deligne conjecture) and
![]() $S^{1}$
-action on the trace (cyclic structure).
$S^{1}$
-action on the trace (cyclic structure).
Remark 1.2.5. We will apply the above definitions to
![]() $\operatorname{DCoh}(X\times _{Y}X)$
considered as an algebra object in small stable categories. One could also pass to large categories and consider the cocompletion of ind-coherent sheaves
$\operatorname{DCoh}(X\times _{Y}X)$
considered as an algebra object in small stable categories. One could also pass to large categories and consider the cocompletion of ind-coherent sheaves
![]() $\operatorname{QC}^{!}(X\times _{Y}X)=\operatorname{Ind}\operatorname{DCoh}(X\times _{Y}X)$
. The center is sensitive to the difference in context, while the trace is not: the trace of the cocompletion is canonically equivalent to the cocompletion of the trace. We do not address the center of the cocompleted category here.
$\operatorname{QC}^{!}(X\times _{Y}X)=\operatorname{Ind}\operatorname{DCoh}(X\times _{Y}X)$
. The center is sensitive to the difference in context, while the trace is not: the trace of the cocompletion is canonically equivalent to the cocompletion of the trace. We do not address the center of the cocompleted category here.
The geometric avatar of the above definitions is the loop space (it can be realized as a trace in a suitable nonlinear setting).
Definition 1.2.6. The loop space of a derived stack
![]() $Y$
is the derived mapping stack
$Y$
is the derived mapping stack
Example 1.2.7. For
![]() $G$
a group and
$G$
a group and
![]() $Y=BG$
the classifying stack, we have
$Y=BG$
the classifying stack, we have
![]() $LY\simeq G/G$
the adjoint quotient.
$LY\simeq G/G$
the adjoint quotient.
The geometric avatar of the universal central map and trace map is the correspondence
It corresponds to the cobordism with corners (the ‘whistle diagram’ in topological field theory) between an interval with marked boundary and the circle.
Example 1.2.8. For
![]() $H\subset G$
a subgroup, and the natural map
$H\subset G$
a subgroup, and the natural map
![]() $X=BH\rightarrow Y=BG$
, the correspondence becomes
$X=BH\rightarrow Y=BG$
, the correspondence becomes
where the latter two terms are adjoint quotients.
It is shown in [Reference Ben-Zvi, Francis and NadlerBFN10] that the resulting transforms
![]() $\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FF}^{\ast }$
and
$\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FF}^{\ast }$
and
![]() $\unicode[STIX]{x1D6FF}_{\ast }\unicode[STIX]{x1D70B}^{\ast }$
on quasi-coherent sheaves induce respective equivalences
$\unicode[STIX]{x1D6FF}_{\ast }\unicode[STIX]{x1D70B}^{\ast }$
on quasi-coherent sheaves induce respective equivalences
One can view our main results as a refinement for coherent sheaves in the presence of singularities. Let us first discuss the center where we need only impose traditional support conditions.
Definition 1.2.9. Let
![]() $\operatorname{DCoh}_{\text{prop}/Y}(LY)\subset \operatorname{DCoh}(LY)$
denote the full subcategory of coherent sheaves that are proper over
$\operatorname{DCoh}_{\text{prop}/Y}(LY)\subset \operatorname{DCoh}(LY)$
denote the full subcategory of coherent sheaves that are proper over
![]() $Y$
in the sense that their pushforward to
$Y$
in the sense that their pushforward to
![]() $Y$
is coherent (equivalently, their support is proper over
$Y$
is coherent (equivalently, their support is proper over
![]() $Y$
since we assume
$Y$
since we assume
![]() $Y$
has affine diagonal, hence
$Y$
has affine diagonal, hence
![]() $LY$
is affine over
$LY$
is affine over
![]() $Y$
).
$Y$
).
An initial justification for the above definition is the fact that the functor
![]() $\unicode[STIX]{x1D6FF}_{\ast }\unicode[STIX]{x1D70B}^{\ast }:\operatorname{QC}(LY)\rightarrow \operatorname{QC}(X\times _{Y}X)$
naturally restricts to a functor
$\unicode[STIX]{x1D6FF}_{\ast }\unicode[STIX]{x1D70B}^{\ast }:\operatorname{QC}(LY)\rightarrow \operatorname{QC}(X\times _{Y}X)$
naturally restricts to a functor
![]() $\unicode[STIX]{x1D6FF}_{\ast }\unicode[STIX]{x1D70B}^{\ast }:\operatorname{DCoh}_{\text{prop}/Y}(LY)\rightarrow \operatorname{DCoh}(X\times _{Y}X)$
.
$\unicode[STIX]{x1D6FF}_{\ast }\unicode[STIX]{x1D70B}^{\ast }:\operatorname{DCoh}_{\text{prop}/Y}(LY)\rightarrow \operatorname{DCoh}(X\times _{Y}X)$
.
The following theorem is our first main result. Its proof appeals to a substantial part of the theory of integral transforms for coherent sheaves developed in the companion paper [Reference Ben-Zvi, Nadler and PreygelBNP].
Theorem 1.2.10. Suppose
![]() $p:X\rightarrow Y$
is a proper, surjective map of derived stacks with
$p:X\rightarrow Y$
is a proper, surjective map of derived stacks with
![]() $X,Y$
smooth.
$X,Y$
smooth.
Then the functor
![]() $\unicode[STIX]{x1D6FF}_{\ast }\unicode[STIX]{x1D70B}^{\ast }:\operatorname{DCoh}_{\text{prop}/Y}(Y)\rightarrow \operatorname{DCoh}(X\times _{Y}X)$
is the universal central map underlying a canonical equivalence of
$\unicode[STIX]{x1D6FF}_{\ast }\unicode[STIX]{x1D70B}^{\ast }:\operatorname{DCoh}_{\text{prop}/Y}(Y)\rightarrow \operatorname{DCoh}(X\times _{Y}X)$
is the universal central map underlying a canonical equivalence of
![]() $E_{2}$
-monoidal categories
$E_{2}$
-monoidal categories
Now let us turn to the trace where we will need to consider singular support conditions. Define the support condition
![]() $\unicode[STIX]{x1D6EC}_{X/Y}\subset T_{LY}^{\ast -1}$
(see § 2 for a precise discussion) to be the pull–push of support conditions
$\unicode[STIX]{x1D6EC}_{X/Y}\subset T_{LY}^{\ast -1}$
(see § 2 for a precise discussion) to be the pull–push of support conditions
Definition 1.2.11. Let
![]() $\operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{X/Y}}(LY)\subset \operatorname{DCoh}(LY)$
denote the full subcategory of coherent complexes whose microlocal support lies in
$\operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{X/Y}}(LY)\subset \operatorname{DCoh}(LY)$
denote the full subcategory of coherent complexes whose microlocal support lies in
![]() $\unicode[STIX]{x1D6EC}_{X/Y}\subset T_{LY}^{\ast -1}$
.
$\unicode[STIX]{x1D6EC}_{X/Y}\subset T_{LY}^{\ast -1}$
.
An initial justification for the above definition is the fact that the functor
![]() $\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FF}^{\ast }:\operatorname{QC}(X\times _{Y}X)\rightarrow \operatorname{QC}(LY)$
naturally restricts to a functor
$\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FF}^{\ast }:\operatorname{QC}(X\times _{Y}X)\rightarrow \operatorname{QC}(LY)$
naturally restricts to a functor
![]() $\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FF}^{\ast }:\operatorname{DCoh}(X\times _{Y}X)\rightarrow \operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{X/Y}}(LY)$
.
$\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FF}^{\ast }:\operatorname{DCoh}(X\times _{Y}X)\rightarrow \operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{X/Y}}(LY)$
.
The following theorem is our second main result. Its proof appeals to the microlocal descent theory developed in this paper and outlined in the next section.
Theorem 1.2.12. Suppose
![]() $p:X\rightarrow Y$
is a proper, surjective and quasi-smooth map of derived stacks with
$p:X\rightarrow Y$
is a proper, surjective and quasi-smooth map of derived stacks with
![]() $X,Y$
smooth.
$X,Y$
smooth.
Then the functor
![]() $\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FF}^{\ast }:\operatorname{DCoh}(X\times _{Y}X)\rightarrow \operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{X/Y}}(LY)$
is the universal trace map underlying a canonical equivalence of
$\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FF}^{\ast }:\operatorname{DCoh}(X\times _{Y}X)\rightarrow \operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{X/Y}}(LY)$
is the universal trace map underlying a canonical equivalence of
![]() $S^{1}$
-categories
$S^{1}$
-categories
Remark 1.2.13. As mentioned earlier, the trace is not sensitive to whether we pass to cocomplete categories: the trace of the cocompletion is canonically equivalent to the cocompletion of the trace. Thus, the above theorem also implies the equivalence for ind-coherent sheaves
1.3 Base change and descent with support
Before continuing to applications, let us highlight the microlocal descent theory developed in § 2 that contributes to the proof of Theorem 1.2.12. It is of independent interest and has broader applicability to
![]() ${\mathcal{D}}$
-modules as well as coherent sheaves.
${\mathcal{D}}$
-modules as well as coherent sheaves.
When working with fixed support conditions, natural functors on coherent sheaves need not respect the prescribed support conditions. For example, recall that perfect complexes are precisely coherent complexes with singular support in the zero-section. In general, pushforward of perfect complexes along a proper map takes perfect complexes to coherent complexes that are not perfect. If we insist on working with perfect complexes, then we must ‘correct’ pushforwards so their singular support lies in the zero-section. One fallout is that standard identities such as base change need not hold for such modified functors.
In § 2, we introduce general geometric situations where base change holds for functors with prescribed support conditions. This is a key step in establishing a general descent pattern (with respect to both pullback and pushforward) for coherent sheaves with prescribed support. A natural framework for such results is the geometry of pairs
![]() $(X,\unicode[STIX]{x1D6EC}_{X})$
of a quasi-smooth derived stack
$(X,\unicode[STIX]{x1D6EC}_{X})$
of a quasi-smooth derived stack
![]() $X$
and a conic Zariski-closed subset
$X$
and a conic Zariski-closed subset
![]() $\unicode[STIX]{x1D6EC}_{X}\subset T_{X}^{\ast -1}$
. Morphisms are maps of pairs
$\unicode[STIX]{x1D6EC}_{X}\subset T_{X}^{\ast -1}$
. Morphisms are maps of pairs
![]() $(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
given by a map
$(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
given by a map
![]() $X\rightarrow Y$
whose induced microlocal correspondence
$X\rightarrow Y$
whose induced microlocal correspondence
takes the support condition of the domain to that of the target
![]() $f_{\ast }\unicode[STIX]{x1D6EC}_{X}=\tilde{f}((df^{\ast })^{-1}(\unicode[STIX]{x1D6EC}_{X}))\subset \unicode[STIX]{x1D6EC}_{Y}$
. Note there is also a natural pullback
$f_{\ast }\unicode[STIX]{x1D6EC}_{X}=\tilde{f}((df^{\ast })^{-1}(\unicode[STIX]{x1D6EC}_{X}))\subset \unicode[STIX]{x1D6EC}_{Y}$
. Note there is also a natural pullback
![]() $f^{!}\unicode[STIX]{x1D6EC}_{Y}=df^{\ast }(\tilde{f}^{-1}(\unicode[STIX]{x1D6EC}_{Y}))\subset T_{X}^{\ast -1}$
.
$f^{!}\unicode[STIX]{x1D6EC}_{Y}=df^{\ast }(\tilde{f}^{-1}(\unicode[STIX]{x1D6EC}_{Y}))\subset T_{X}^{\ast -1}$
.
To understand descent, we first derive a general form of base change with prescribed support.
Definition 1.3.1. A strict Cartesian diagram of pairs is a Cartesian diagram of quasi-smooth derived stacks which is also a commutative diagram of maps of pairs

Furthermore, the pullbacks of support conditions should satisfy the strictness condition
Remark 1.3.2. Let us mention in a simple traditional setting the meaning of a map of pairs and what kind of notion strictness is. Take
![]() $f:X\rightarrow Y$
a smooth map of smooth manifolds, and consider the associated Lagrangian correspondence
$f:X\rightarrow Y$
a smooth map of smooth manifolds, and consider the associated Lagrangian correspondence
Fix support conditions
![]() $\unicode[STIX]{x1D6EC}_{X}\subset T^{\ast }X,\unicode[STIX]{x1D6EC}_{Y}\subset T^{\ast }Y$
. Then
$\unicode[STIX]{x1D6EC}_{X}\subset T^{\ast }X,\unicode[STIX]{x1D6EC}_{Y}\subset T^{\ast }Y$
. Then
![]() $f$
is a map of traditional pairs if the correspondence takes the support condition of the domain to that of the target:
$f$
is a map of traditional pairs if the correspondence takes the support condition of the domain to that of the target:
![]() $f_{\ast }(\unicode[STIX]{x1D6EC}_{X})=\tilde{f}((f^{\ast })^{-1}(\unicode[STIX]{x1D6EC}_{X}))\subset \unicode[STIX]{x1D6EC}_{Y}$
. If
$f_{\ast }(\unicode[STIX]{x1D6EC}_{X})=\tilde{f}((f^{\ast })^{-1}(\unicode[STIX]{x1D6EC}_{X}))\subset \unicode[STIX]{x1D6EC}_{Y}$
. If
![]() $f$
is a fibration, then
$f$
is a fibration, then
![]() $f$
is a strict map of traditional pairs if the same additionally holds in the opposite direction:
$f$
is a strict map of traditional pairs if the same additionally holds in the opposite direction:
![]() $f^{!}(\unicode[STIX]{x1D6EC}_{Y})=f^{\ast }(\tilde{f}^{-1}(\unicode[STIX]{x1D6EC}_{Y}))\subset \unicode[STIX]{x1D6EC}_{X}$
.
$f^{!}(\unicode[STIX]{x1D6EC}_{Y})=f^{\ast }(\tilde{f}^{-1}(\unicode[STIX]{x1D6EC}_{Y}))\subset \unicode[STIX]{x1D6EC}_{X}$
.
In Propositions 2.3.7 and 2.3.8, we prove that for strict Cartesian diagrams of pairs with suitable properness and quasi-smoothness assumptions, both dual forms of base-change identities hold. These base-change identities allow us to prove descent theorems for both pullbacks and pushforwards by applying the Beck–Chevalley Condition [Reference LurieLur, Corollary 6.2.4.3]. Given an augmented simplicial diagram
![]() $f:(X_{\bullet },\unicode[STIX]{x1D6EC}_{\bullet })\rightarrow (X_{-1},\unicode[STIX]{x1D6EC}_{-1})$
of maps of pairs, we refer to the induced diagrams
$f:(X_{\bullet },\unicode[STIX]{x1D6EC}_{\bullet })\rightarrow (X_{-1},\unicode[STIX]{x1D6EC}_{-1})$
of maps of pairs, we refer to the induced diagrams

as the Beck–Chevalley squares. We then prove the following in Theorem 2.4.1.
Theorem 1.3.3. Suppose
![]() $f:(X_{\bullet },\unicode[STIX]{x1D6EC}_{\bullet })\rightarrow (X_{-1},\unicode[STIX]{x1D6EC}_{-1})$
is an augmented simplicial diagram of maps of pairs with all stacks quasi-smooth and maps proper. Suppose further that the following points apply.
$f:(X_{\bullet },\unicode[STIX]{x1D6EC}_{\bullet })\rightarrow (X_{-1},\unicode[STIX]{x1D6EC}_{-1})$
is an augmented simplicial diagram of maps of pairs with all stacks quasi-smooth and maps proper. Suppose further that the following points apply.
-
(i) The face maps are quasi-smooth.
-
(ii) All Beck–Chevalley squares are strict Cartesian diagrams of pairs.
-
(iii) Pullback with prescribed support along the augmentation
is conservative (for example, as holds when
 $f_{\ast }\unicode[STIX]{x1D6EC}_{0}=\unicode[STIX]{x1D6EC}_{-1}$
).
$f_{\ast }\unicode[STIX]{x1D6EC}_{0}=\unicode[STIX]{x1D6EC}_{-1}$
).
Then the augmentation provides an equivalence with the totalization of the cosimplicial category furnished by pullbacks with support conditions:
If in addition, each of the
![]() $\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{k}}^{!}(X_{k})$
is compactly generated for
$\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{k}}^{!}(X_{k})$
is compactly generated for
![]() $k\geqslant 0$
, then the same is true for
$k\geqslant 0$
, then the same is true for
![]() $k=-1$
, and the augmentation provides an equivalence with the geometric realization of the simplicial category furnished by pushforwards:
$k=-1$
, and the augmentation provides an equivalence with the geometric realization of the simplicial category furnished by pushforwards:
Remark 1.3.4. In the theorem, the criterion
![]() $f_{\ast }\unicode[STIX]{x1D6EC}_{0}=\unicode[STIX]{x1D6EC}_{-1}$
for the conservativity of the pullback with prescribed support along the augmentation is a reformulation of [Reference Arinkin and GaitsgoryAG15, Theorem 7.8.2].
$f_{\ast }\unicode[STIX]{x1D6EC}_{0}=\unicode[STIX]{x1D6EC}_{-1}$
for the conservativity of the pullback with prescribed support along the augmentation is a reformulation of [Reference Arinkin and GaitsgoryAG15, Theorem 7.8.2].
The arguments in the proof of the above theorem may be equally well implemented in the alternative setting of
![]() ${\mathcal{D}}$
-modules. Namely, with analogous geometric hypotheses, the proof holds with
${\mathcal{D}}$
-modules. Namely, with analogous geometric hypotheses, the proof holds with
![]() ${\mathcal{D}}$
-modules with prescribed singular support substituted for coherent sheaves with prescribed singular support. As far as we know, this is a new result going beyond the descent patterns appearing in [Reference Beilinson and DrinfeldBD] and should have broad utility. For example, closely tied to the applications of this paper, it can be used to provide an alternative proof of one of the main results of [Reference Ben-Zvi and NadlerBN09] identifying the categorical trace of the finite Hecke category with character sheaves.
${\mathcal{D}}$
-modules with prescribed singular support substituted for coherent sheaves with prescribed singular support. As far as we know, this is a new result going beyond the descent patterns appearing in [Reference Beilinson and DrinfeldBD] and should have broad utility. For example, closely tied to the applications of this paper, it can be used to provide an alternative proof of one of the main results of [Reference Ben-Zvi and NadlerBN09] identifying the categorical trace of the finite Hecke category with character sheaves.
To state the version of the preceding theorem for
![]() ${\mathcal{D}}$
-modules, we only need to change our microlocal setting back to the usual cotangent bundle. The natural framework is now the geometry of traditional pairs
${\mathcal{D}}$
-modules, we only need to change our microlocal setting back to the usual cotangent bundle. The natural framework is now the geometry of traditional pairs
![]() $(X,\unicode[STIX]{x1D6EC})$
of a smooth derived stack
$(X,\unicode[STIX]{x1D6EC})$
of a smooth derived stack
![]() $X$
and a conic Zariski-closed subset
$X$
and a conic Zariski-closed subset
![]() $\unicode[STIX]{x1D6EC}\subset T^{\ast }X$
.
$\unicode[STIX]{x1D6EC}\subset T^{\ast }X$
.
Let
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D6EC}}(X)$
denote the full subcategory of the ind-completion of coherent
${\mathcal{D}}_{\unicode[STIX]{x1D6EC}}(X)$
denote the full subcategory of the ind-completion of coherent
![]() ${\mathcal{D}}$
-modules comprising objects with singular support lying in
${\mathcal{D}}$
-modules comprising objects with singular support lying in
![]() $\unicode[STIX]{x1D6EC}\subset T^{\ast }X$
. We refer the reader to [Reference Gaitsgory and RozenblyumGR] for the necessary foundations for the following theorem, in particular the
$\unicode[STIX]{x1D6EC}\subset T^{\ast }X$
. We refer the reader to [Reference Gaitsgory and RozenblyumGR] for the necessary foundations for the following theorem, in particular the
![]() $!$
-functoriality of
$!$
-functoriality of
![]() ${\mathcal{D}}$
-modules viewed as crystals. Its proof is formally the same as that of Theorem 1.3.3, and we will not return to
${\mathcal{D}}$
-modules viewed as crystals. Its proof is formally the same as that of Theorem 1.3.3, and we will not return to
![]() ${\mathcal{D}}$
-modules in the rest of the paper.
${\mathcal{D}}$
-modules in the rest of the paper.
Theorem 1.3.5. Suppose
![]() $f:(X_{\bullet },\unicode[STIX]{x1D6EC}_{\bullet })\rightarrow (X_{-1},\unicode[STIX]{x1D6EC}_{-1})$
is an augmented simplicial diagram of maps of traditional pairs with all stacks smooth and maps proper. Suppose further that:
$f:(X_{\bullet },\unicode[STIX]{x1D6EC}_{\bullet })\rightarrow (X_{-1},\unicode[STIX]{x1D6EC}_{-1})$
is an augmented simplicial diagram of maps of traditional pairs with all stacks smooth and maps proper. Suppose further that:
-
(i) the face maps are smooth;
-
(ii) all Beck–Chevalley squares are strict Cartesian diagrams of pairs;
-
(iii) pullback with prescribed support along the augmentation
is conservative.
Then the augmentation provides an equivalence with the totalization of the cosimplicial category furnished by pullbacks with support conditions:
Remark 1.3.6. In the descent theorem for coherent sheaves, we were able to give a criterion on support for the conservativity of pullback along the augmentation. We were also able to identify compact objects and give a pushforward formulation of descent on small categories. We are unsure if the analogous results hold for
![]() ${\mathcal{D}}$
-modules in complete generality, though there are broad situations where they do.
${\mathcal{D}}$
-modules in complete generality, though there are broad situations where they do.
1.4 Application to affine Hecke categories
Let us now turn to the motivating application for the development of the preceding theory.
Let
![]() $G$
be a complex reductive group and
$G$
be a complex reductive group and
![]() $B\subset G$
a Borel subgroup. Let
$B\subset G$
a Borel subgroup. Let
![]() $q:BB\rightarrow BG$
denote the natural induction map of classifying stacks. Passing to loop spaces, we obtain the Grothendieck–Springer map of adjoint quotients
$q:BB\rightarrow BG$
denote the natural induction map of classifying stacks. Passing to loop spaces, we obtain the Grothendieck–Springer map of adjoint quotients
where
![]() $\widetilde{G}$
classifies pairs of a Borel subgroup
$\widetilde{G}$
classifies pairs of a Borel subgroup
![]() $B^{\prime }\subset G$
and a group element
$B^{\prime }\subset G$
and a group element
![]() $g\in B^{\prime }$
, and
$g\in B^{\prime }$
, and
![]() $Lq$
projects to the group element and forgets the Borel subgroup.
$Lq$
projects to the group element and forgets the Borel subgroup.
Now we apply the preceding theory with
![]() $X=B/B$
,
$X=B/B$
,
![]() $Y=G/G$
, and
$Y=G/G$
, and
![]() $p=Lq$
. Note that
$p=Lq$
. Note that
![]() $B/B$
and
$B/B$
and
![]() $G/G$
are smooth, and
$G/G$
are smooth, and
![]() $p:B/B\rightarrow G/G$
is projective. Note as well that our starting point already involves loop spaces, though that structure plays no role with respect to our general results.
$p:B/B\rightarrow G/G$
is projective. Note as well that our starting point already involves loop spaces, though that structure plays no role with respect to our general results.
Definition 1.4.1. (1) The global Steinberg stack is the fiber product
(2) The global affine Hecke category is the small stable monoidal category
Remark 1.4.2. One can interpret the loop space
![]() $L(BG)\simeq G/G$
as the moduli stack of
$L(BG)\simeq G/G$
as the moduli stack of
![]() $G$
-local systems on the circle
$G$
-local systems on the circle
![]() $S^{1}$
. Similarly, one can interpret the global Steinberg stack
$S^{1}$
. Similarly, one can interpret the global Steinberg stack
![]() $\text{St}_{G}\simeq L(B\backslash G/B)$
as the moduli of
$\text{St}_{G}\simeq L(B\backslash G/B)$
as the moduli of
![]() $G$
-local systems on the cylinder
$G$
-local systems on the cylinder
![]() $S^{1}\times I$
with
$S^{1}\times I$
with
![]() $B$
-reductions at the boundary circles
$B$
-reductions at the boundary circles
![]() $S^{1}\times \unicode[STIX]{x2202}I$
.
$S^{1}\times \unicode[STIX]{x2202}I$
.
We will state the form our general results take when applied to the affine Hecke category.
Definition 1.4.3. The commuting stack is the moduli of local systems on the two-torus
![]() $T=S^{1}\times S^{1}$
or, equivalently, the twice-iterated loop space
$T=S^{1}\times S^{1}$
or, equivalently, the twice-iterated loop space
Remark 1.4.4. Unlike the Steinberg stack itself, the commuting stack has a nontrivial derived structure and must be treated as a derived stack.
Let
![]() $\mathfrak{g}$
denote the Lie algebra of
$\mathfrak{g}$
denote the Lie algebra of
![]() $G$
. The fiber of the cotangent complex of
$G$
. The fiber of the cotangent complex of
![]() $\operatorname{Loc}_{G}(T)$
at a local system
$\operatorname{Loc}_{G}(T)$
at a local system
![]() $\mathscr{P}$
can be calculated by the de Rham cochains
$\mathscr{P}$
can be calculated by the de Rham cochains
![]() $C^{\ast }(T,\mathfrak{g}_{\mathscr{P}}^{\ast })[1]$
, where
$C^{\ast }(T,\mathfrak{g}_{\mathscr{P}}^{\ast })[1]$
, where
![]() $\mathfrak{g}_{\mathscr{P}}^{\ast }$
denotes the coadjoint bundle of
$\mathfrak{g}_{\mathscr{P}}^{\ast }$
denotes the coadjoint bundle of
![]() $\mathscr{P}$
. Focusing on the degree
$\mathscr{P}$
. Focusing on the degree
![]() $-1$
term coming from the commutator equation, we see that there is a natural map
$-1$
term coming from the commutator equation, we see that there is a natural map
Let
![]() $\mathfrak{h}$
denote the Lie algebra of the universal Cartan of
$\mathfrak{h}$
denote the Lie algebra of the universal Cartan of
![]() $G$
, and
$G$
, and
![]() $W$
the Weyl group. Recall the dual characteristic polynomial map or, equivalently, the projection to the coadjoint quotient
$W$
the Weyl group. Recall the dual characteristic polynomial map or, equivalently, the projection to the coadjoint quotient
Define the global nilpotent cone
![]() $\mathscr{N}\subset T_{\operatorname{Loc}_{G}(T)}^{\ast -1}$
to be the closed conic subset given by the inverse image of zero under the composition
$\mathscr{N}\subset T_{\operatorname{Loc}_{G}(T)}^{\ast -1}$
to be the closed conic subset given by the inverse image of zero under the composition
Definition 1.4.5. (1) Let
![]() $\operatorname{DCoh}_{\mathscr{P}}(\operatorname{Loc}_{G}(T))\subset \operatorname{DCoh}(\operatorname{Loc}_{G}(T))$
denote the full subcategory of coherent sheaves whose pushforward along the restriction map
$\operatorname{DCoh}_{\mathscr{P}}(\operatorname{Loc}_{G}(T))\subset \operatorname{DCoh}(\operatorname{Loc}_{G}(T))$
denote the full subcategory of coherent sheaves whose pushforward along the restriction map
![]() $\operatorname{Loc}_{G}(T)\rightarrow \operatorname{Loc}_{G}(S^{1})$
along the first loop
$\operatorname{Loc}_{G}(T)\rightarrow \operatorname{Loc}_{G}(S^{1})$
along the first loop
![]() $S^{1}\rightarrow T$
is coherent.
$S^{1}\rightarrow T$
is coherent.
(2) Let
![]() $\operatorname{DCoh}_{\mathscr{N}}(\operatorname{Loc}_{G}(T))\subset \operatorname{DCoh}(\operatorname{Loc}_{G}(T))$
denote the full subcategory of coherent complexes whose singular support lies in the global nilpotent cone
$\operatorname{DCoh}_{\mathscr{N}}(\operatorname{Loc}_{G}(T))\subset \operatorname{DCoh}(\operatorname{Loc}_{G}(T))$
denote the full subcategory of coherent complexes whose singular support lies in the global nilpotent cone
![]() $\mathscr{N}\subset T_{\operatorname{Loc}_{G}(T)}^{\ast -1}$
.
$\mathscr{N}\subset T_{\operatorname{Loc}_{G}(T)}^{\ast -1}$
.
Theorem 1.4.6.
![]() $(1)$
There is a canonical monoidal equivalence
$(1)$
There is a canonical monoidal equivalence
![]() $(2)$
There is a canonical
$(2)$
There is a canonical
![]() $E_{2}$
-monoidal identification of the center
$E_{2}$
-monoidal identification of the center
![]() $(3)$
There is a canonical
$(3)$
There is a canonical
![]() $S^{1}$
-equivariant identification of the trace
$S^{1}$
-equivariant identification of the trace
Remark 1.4.7. Let us point out a particularly curious aspect of the theorem.
On the one hand, the description of the center is strongly asymmetric between the two loops of
![]() $T$
. This is not surprising considering the two loops play different roles: the first is implicit in the adjoint quotients
$T$
. This is not surprising considering the two loops play different roles: the first is implicit in the adjoint quotients
![]() $L(BG)\simeq G/G,L(BB)\simeq B/B$
and hence in the global Steinberg stack as well
$L(BG)\simeq G/G,L(BB)\simeq B/B$
and hence in the global Steinberg stack as well
![]() $\text{St}_{G}=L(B\backslash G/B)$
; the second arises in the geometric identification of the center.
$\text{St}_{G}=L(B\backslash G/B)$
; the second arises in the geometric identification of the center.
On the other hand, the description of the trace is symmetric in the two loops.
Finally, our arguments also apply to more traditional versions of the affine Hecke category where we linearize and constrain our focus to nilpotent elements. Fix the isomorphism
![]() $\mathfrak{g}^{\ast }\simeq \mathfrak{g}$
of an invariant inner product. Let
$\mathfrak{g}^{\ast }\simeq \mathfrak{g}$
of an invariant inner product. Let
![]() ${\mathcal{B}}=G/B$
denote the flag variety and
${\mathcal{B}}=G/B$
denote the flag variety and
![]() $T^{\ast }{\mathcal{B}}\rightarrow \mathfrak{g}^{\ast }\simeq \mathfrak{g}$
the Springer/moment map.
$T^{\ast }{\mathcal{B}}\rightarrow \mathfrak{g}^{\ast }\simeq \mathfrak{g}$
the Springer/moment map.
Let us introduce the unipotent Steinberg stack
Note that
![]() $\text{St}_{G}^{\text{u}}$
has a nontrivial derived structure since we work over
$\text{St}_{G}^{\text{u}}$
has a nontrivial derived structure since we work over
![]() $\mathfrak{g}$
rather than the nilpotent cone. Note as well that we could equivalently work over the formal completion of
$\mathfrak{g}$
rather than the nilpotent cone. Note as well that we could equivalently work over the formal completion of
![]() $\mathfrak{g}$
along the nilpotent cone. Introduce the unipotent affine Hecke category
$\mathfrak{g}$
along the nilpotent cone. Introduce the unipotent affine Hecke category
and the unipotent commuting stack
of local systems where the first monodromy
![]() $g_{1}\in {\hat{G}}_{\text{u}}$
is in the formal neighborhood of the unipotent elements
$g_{1}\in {\hat{G}}_{\text{u}}$
is in the formal neighborhood of the unipotent elements
![]() $G_{\text{u}}\subset G$
. Now compatibly with Theorem 1.4.6, our methods provide the following result.
$G_{\text{u}}\subset G$
. Now compatibly with Theorem 1.4.6, our methods provide the following result.
Theorem 1.4.8. There are canonical identifications
which are
![]() $E_{2}$
-monoidal and
$E_{2}$
-monoidal and
![]() $S^{1}$
-equivariant, respectively.
$S^{1}$
-equivariant, respectively.
Note that there is no singular support condition on the trace category (unlike in the global case above, coherent sheaves on the unipotent Steinberg stack
![]() $\text{St}_{G}^{\text{u}}$
are not forced to have nilpotent singular support).
$\text{St}_{G}^{\text{u}}$
are not forced to have nilpotent singular support).
Furthermore, one can introduce the natural
![]() $\mathbb{G}_{m}$
-dilation action on
$\mathbb{G}_{m}$
-dilation action on
![]() $\mathfrak{g}$
and the induced action on
$\mathfrak{g}$
and the induced action on
![]() $\text{St}_{G}^{\text{u}}$
. Introduce the
$\text{St}_{G}^{\text{u}}$
. Introduce the
![]() $\mathbb{G}_{m}$
-equivariant unipotent affine Hecke category
$\mathbb{G}_{m}$
-equivariant unipotent affine Hecke category
and the twisted unipotent commuting stack
where the first monodromy
![]() $g_{1}\in {\hat{G}}_{\text{u}}$
is in the formal neighborhood of the unipotent elements
$g_{1}\in {\hat{G}}_{\text{u}}$
is in the formal neighborhood of the unipotent elements
![]() $G_{\text{u}}\subset G$
, and
$G_{\text{u}}\subset G$
, and
![]() $(g_{1}^{-1})^{z}\in {\hat{G}}_{\text{u}}$
denotes the dilation of its inverse by the scalar
$(g_{1}^{-1})^{z}\in {\hat{G}}_{\text{u}}$
denotes the dilation of its inverse by the scalar
![]() $z\in \mathbb{G}_{m}$
. Now our methods provide the following theorem.
$z\in \mathbb{G}_{m}$
. Now our methods provide the following theorem.
Theorem 1.4.9. There are canonical identifications
which are
![]() $E_{2}$
-monoidal and
$E_{2}$
-monoidal and
![]() $S^{1}$
-equivariant, respectively.
$S^{1}$
-equivariant, respectively.
1.4.1 Hecke categories, character sheaves, and geometric Langlands
We conclude this section with a brief, informal discussion of the place of Theorem 1.4.6, and its variants, within geometric representation theory. To match with the conventions of the subject, and for the purposes of this section only, the reductive group denoted above by
![]() $G$
will be denoted
$G$
will be denoted
![]() $G^{\vee }$
since it will arise naturally as a Langlands dual group.
$G^{\vee }$
since it will arise naturally as a Langlands dual group.
The unipotent Steinberg stack
![]() $\text{St}_{G^{\vee }}^{\text{u}}$
plays the central role in Kazhdan–Lusztig’s solution [Reference Kazhdan and LusztigKL87] of the Deligne–Langlands conjecture on representations of affine Hecke algebras (see also [Reference Chriss and GinzburgCG97]): the Grothendieck group of
$\text{St}_{G^{\vee }}^{\text{u}}$
plays the central role in Kazhdan–Lusztig’s solution [Reference Kazhdan and LusztigKL87] of the Deligne–Langlands conjecture on representations of affine Hecke algebras (see also [Reference Chriss and GinzburgCG97]): the Grothendieck group of
![]() $\mathbb{G}_{m}$
-equivariant coherent sheaves on
$\mathbb{G}_{m}$
-equivariant coherent sheaves on
![]() $\text{St}_{G^{\vee }}^{\text{u}}$
is isomorphic to the affine Hecke algebra of
$\text{St}_{G^{\vee }}^{\text{u}}$
is isomorphic to the affine Hecke algebra of
![]() $G$
. This enables one to classify irreducible representations of the affine Hecke algebra in terms of
$G$
. This enables one to classify irreducible representations of the affine Hecke algebra in terms of
![]() $q$
-commuting pairs.
$q$
-commuting pairs.
Bezrukavnikov [Reference BezrukavnikovBez16] has categorified the Kazhdan–Lusztig realization of the affine Hecke algebra: the standard categorification in terms of mixed sheaves on the affine flag variety of
![]() $G$
is equivalent to the categorification by
$G$
is equivalent to the categorification by
![]() $\mathbb{G}_{m}$
-equivariant coherent sheaves on
$\mathbb{G}_{m}$
-equivariant coherent sheaves on
![]() $\text{St}_{G^{\vee }}^{\text{u}}$
. The affine Hecke category appears naturally in the geometric Langlands program as the modifications acting on sheaves on moduli stacks of
$\text{St}_{G^{\vee }}^{\text{u}}$
. The affine Hecke category appears naturally in the geometric Langlands program as the modifications acting on sheaves on moduli stacks of
![]() $G$
-bundles with parabolic structure. Bezrukavnikov’s theorem realizes the geometric Langlands duality for these modifications or, in other words, the tamely ramified generalization of the geometric Satake theorem. It is the centerpiece in the geometric approach to a wide variety of problems in representation theory [Reference BezrukavnikovBez06].
$G$
-bundles with parabolic structure. Bezrukavnikov’s theorem realizes the geometric Langlands duality for these modifications or, in other words, the tamely ramified generalization of the geometric Satake theorem. It is the centerpiece in the geometric approach to a wide variety of problems in representation theory [Reference BezrukavnikovBez06].
With geometric Langlands and other natural problems in mind, it is meaningful to study the representation theory of the affine Hecke category itself. By abstract nonsense, any dualizable module of a monoidal category has a character that is an object in the trace category. Thus, by Theorem 1.4.6 and its variants, characters of dualizable modules of the affine Hecke category give coherent sheaves with nilpotent singular support on the commuting stack
![]() $\operatorname{Loc}_{G^{\vee }}(T)$
and its unipotent and twisted variants. Note that this is consonant with the Deligne–Langlands classification of representations of the affine Hecke algebra in terms of
$\operatorname{Loc}_{G^{\vee }}(T)$
and its unipotent and twisted variants. Note that this is consonant with the Deligne–Langlands classification of representations of the affine Hecke algebra in terms of
![]() $q$
-commuting pairs. (This relation between the categorified and classical will be pursued in [Reference Ben-Zvi, Helm and NadlerBHN14].)
$q$
-commuting pairs. (This relation between the categorified and classical will be pursued in [Reference Ben-Zvi, Helm and NadlerBHN14].)
It is also natural to relate Theorem 1.4.6 to the character theory of the finite Hecke category of Borel-biequivariant
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $G^{\vee }$
. The main result of [Reference Ben-Zvi and NadlerBN09] identifies the monoidal center and trace of the finite Hecke category with the category of unipotent character sheaves on
$G^{\vee }$
. The main result of [Reference Ben-Zvi and NadlerBN09] identifies the monoidal center and trace of the finite Hecke category with the category of unipotent character sheaves on
![]() $G^{\vee }$
, that is, adjoint-equivariant
$G^{\vee }$
, that is, adjoint-equivariant
![]() ${\mathcal{D}}$
-modules on
${\mathcal{D}}$
-modules on
![]() $G^{\vee }$
with nilpotent singular support and trivial generalized central character. The relation between this and Theorem 1.4.6 is given by the results of [Reference Ben-Zvi and NadlerBN12, Reference Ben-Zvi and NadlerBN13a]. Namely, coherent sheaves on a loop stack, such as the Steinberg stack
$G^{\vee }$
with nilpotent singular support and trivial generalized central character. The relation between this and Theorem 1.4.6 is given by the results of [Reference Ben-Zvi and NadlerBN12, Reference Ben-Zvi and NadlerBN13a]. Namely, coherent sheaves on a loop stack, such as the Steinberg stack
![]() $\text{St}_{G^{\vee }}=L(B^{\vee }\backslash G^{\vee }/B^{\vee })$
or commuting stack
$\text{St}_{G^{\vee }}=L(B^{\vee }\backslash G^{\vee }/B^{\vee })$
or commuting stack
![]() $\operatorname{Loc}_{G^{\vee }}(T^{2})=L(G^{\vee }/G^{\vee })$
, recover
$\operatorname{Loc}_{G^{\vee }}(T^{2})=L(G^{\vee }/G^{\vee })$
, recover
![]() ${\mathcal{D}}$
-modules on the stack via the process of
${\mathcal{D}}$
-modules on the stack via the process of
![]() $S^{1}$
-localization and restriction to small loops. This supports the perspective that
$S^{1}$
-localization and restriction to small loops. This supports the perspective that
![]() $\operatorname{DCoh}_{\mathscr{N}}(\operatorname{Loc}_{G}(T))$
is the spectral realization of the putative category of ‘affine character sheaves’ for the
$\operatorname{DCoh}_{\mathscr{N}}(\operatorname{Loc}_{G}(T))$
is the spectral realization of the putative category of ‘affine character sheaves’ for the
![]() $p$
-adic group associated to
$p$
-adic group associated to
![]() $G$
.
$G$
.
Finally, the trace category
![]() $\operatorname{DCoh}_{\mathscr{N}}(\operatorname{Loc}_{G^{\vee }}(T))$
is also closely related to the genus one case of the geometric Langlands conjecture. As formulated in [Reference Arinkin and GaitsgoryAG15], the spectral side of the geometric Langlands conjecture on a smooth projective curve
$\operatorname{DCoh}_{\mathscr{N}}(\operatorname{Loc}_{G^{\vee }}(T))$
is also closely related to the genus one case of the geometric Langlands conjecture. As formulated in [Reference Arinkin and GaitsgoryAG15], the spectral side of the geometric Langlands conjecture on a smooth projective curve
![]() $C$
is the category
$C$
is the category
![]() $\operatorname{DCoh}_{\mathscr{N}}(\text{Conn}_{G^{\vee }}(C))$
of coherent sheaves with nilpotent singular support on the derived stack of flat
$\operatorname{DCoh}_{\mathscr{N}}(\text{Conn}_{G^{\vee }}(C))$
of coherent sheaves with nilpotent singular support on the derived stack of flat
![]() $G^{\vee }$
-connections on
$G^{\vee }$
-connections on
![]() $C$
. Note that the de Rham space
$C$
. Note that the de Rham space
![]() $\text{Conn}_{G^{\vee }}(C)$
can be identified analytically, though not algebraically, with the Betti space
$\text{Conn}_{G^{\vee }}(C)$
can be identified analytically, though not algebraically, with the Betti space
![]() $\operatorname{Loc}_{G^{\vee }}(C)$
. However, unlike the de Rham space, the Betti space and, hence, the category
$\operatorname{Loc}_{G^{\vee }}(C)$
. However, unlike the de Rham space, the Betti space and, hence, the category
![]() $\operatorname{DCoh}_{\mathscr{N}}(\operatorname{Loc}_{G^{\vee }}(C))$
is a topological invariant of
$\operatorname{DCoh}_{\mathscr{N}}(\operatorname{Loc}_{G^{\vee }}(C))$
is a topological invariant of
![]() $C$
. Thus, the category
$C$
. Thus, the category
![]() $\operatorname{DCoh}_{\mathscr{N}}(\operatorname{Loc}_{G^{\vee }}(T))$
provides a topological version of the genus one geometric Langlands spectral category, and Theorem 1.4.6 ties it to the representation theory of the affine Hecke category.
$\operatorname{DCoh}_{\mathscr{N}}(\operatorname{Loc}_{G^{\vee }}(T))$
provides a topological version of the genus one geometric Langlands spectral category, and Theorem 1.4.6 ties it to the representation theory of the affine Hecke category.
1.5 Standing assumptions
Unless otherwise noted, our standing assumptions are as follows. We work over a characteristic zero base field
![]() $k$
. By a category we mean a
$k$
. By a category we mean a
![]() $k$
-linear stable dg category or
$k$
-linear stable dg category or
![]() $k$
-linear stable
$k$
-linear stable
![]() $\infty$
category. By a stack
$\infty$
category. By a stack
![]() $\mathscr{X}$
, we mean a derived stack over
$\mathscr{X}$
, we mean a derived stack over
![]() $k$
which is quasi-compact, almost of finite-presentation, and with affine diagonal. This implies that
$k$
which is quasi-compact, almost of finite-presentation, and with affine diagonal. This implies that
![]() $\operatorname{QC}^{!}(\mathscr{X})\simeq \operatorname{Ind}\operatorname{DCoh}(\mathscr{X})$
by [Reference Drinfeld and GaitsgoryDG13]. We further assume that our stack is perfect in the sense of [Reference Ben-Zvi, Francis and NadlerBFN10], so that
$\operatorname{QC}^{!}(\mathscr{X})\simeq \operatorname{Ind}\operatorname{DCoh}(\mathscr{X})$
by [Reference Drinfeld and GaitsgoryDG13]. We further assume that our stack is perfect in the sense of [Reference Ben-Zvi, Francis and NadlerBFN10], so that
![]() $\operatorname{QC}(\mathscr{X})\simeq \operatorname{Ind}\operatorname{Perf}(\mathscr{X})$
.
$\operatorname{QC}(\mathscr{X})\simeq \operatorname{Ind}\operatorname{Perf}(\mathscr{X})$
.
2 Base change and descent with support
2.1 Preliminaries
We begin by collecting some basic notions about the singular support of coherent complexes (see [Reference Arinkin and GaitsgoryAG15] for a comprehensive account).
2.1.1 Odd cotangent bundle
Let
![]() $X$
be a quasi-smooth derived stack and
$X$
be a quasi-smooth derived stack and
![]() $\mathbb{L}_{X}$
its cotangent complex.
$\mathbb{L}_{X}$
its cotangent complex.
Let
![]() $X_{\text{cl}}$
denote the underlying classical stack of
$X_{\text{cl}}$
denote the underlying classical stack of
![]() $X$
. Introduce the shifted cotangent complex
$X$
. Introduce the shifted cotangent complex
There is a natural affine projection
![]() $T_{X}^{\ast -1}\rightarrow X_{\text{cl}}$
with fiberwise
$T_{X}^{\ast -1}\rightarrow X_{\text{cl}}$
with fiberwise
![]() $\mathbb{G}_{m}$
-action and the fiber
$\mathbb{G}_{m}$
-action and the fiber
![]() $T_{X}^{\ast -1}|_{x}$
at a point
$T_{X}^{\ast -1}|_{x}$
at a point
![]() $x\in X_{\text{cl}}$
is the degree
$x\in X_{\text{cl}}$
is the degree
![]() $-1$
cohomology of
$-1$
cohomology of
![]() $\mathbb{L}_{X}|_{x}$
. Informally, one can think of
$\mathbb{L}_{X}|_{x}$
. Informally, one can think of
![]() $T_{X}^{\ast -1}\rightarrow X_{\text{cl}}$
as a bundle of vector spaces of varying dimensions. We denote by
$T_{X}^{\ast -1}\rightarrow X_{\text{cl}}$
as a bundle of vector spaces of varying dimensions. We denote by
![]() $\{0\}_{X}\subset T_{X}^{\ast -1}$
the zero-section.
$\{0\}_{X}\subset T_{X}^{\ast -1}$
the zero-section.
Example 2.1.1. If
![]() $Z$
is a smooth scheme, and
$Z$
is a smooth scheme, and
![]() $X=LZ=\operatorname{Map}(S^{1},Z)$
is its loop space, then
$X=LZ=\operatorname{Map}(S^{1},Z)$
is its loop space, then
![]() $T_{X}^{\ast -1}\rightarrow X_{\text{cl}}$
is the usual cotangent bundle
$T_{X}^{\ast -1}\rightarrow X_{\text{cl}}$
is the usual cotangent bundle
![]() $T_{Z}^{\ast }\rightarrow Z$
.
$T_{Z}^{\ast }\rightarrow Z$
.
Example 2.1.2. If
![]() $X=BG$
is a classifying stack, then
$X=BG$
is a classifying stack, then
![]() $T_{X}^{\ast -1}\simeq \mathfrak{g}^{\ast }/G\rightarrow BG$
is the coadjoint quotient.
$T_{X}^{\ast -1}\simeq \mathfrak{g}^{\ast }/G\rightarrow BG$
is the coadjoint quotient.
2.1.2 Microlocalization
Let
![]() $X$
be a quasi-smooth derived stack. An important invariant of any
$X$
be a quasi-smooth derived stack. An important invariant of any
![]() $\mathscr{F}\in \operatorname{QC}^{!}(X)$
is its singular support
$\mathscr{F}\in \operatorname{QC}^{!}(X)$
is its singular support
When
![]() $\mathscr{F}\in \operatorname{DCoh}(X)$
, it is a conic Zariski-closed subset and, in general, it is a union of conic Zariski-closed subsets.
$\mathscr{F}\in \operatorname{DCoh}(X)$
, it is a conic Zariski-closed subset and, in general, it is a union of conic Zariski-closed subsets.
Singular support is a smooth-local notion and given by the following construction for
![]() $X$
affine (see also the description of Remark 2.1.3). There is a natural map of graded commutative
$X$
affine (see also the description of Remark 2.1.3). There is a natural map of graded commutative
![]() ${\mathcal{O}}(X)$
-algebras
${\mathcal{O}}(X)$
-algebras
to the even Hochschild cohomology restricting to maps
In turn, there is natural map from
![]() $\mathit{HH}^{\text{ev}}(X)$
to the graded center of the homotopy category of
$\mathit{HH}^{\text{ev}}(X)$
to the graded center of the homotopy category of
![]() $\operatorname{QC}^{!}(X)$
. Thus, for any objects
$\operatorname{QC}^{!}(X)$
. Thus, for any objects
![]() $\mathscr{F}_{1},\mathscr{F}_{2}\in \operatorname{QC}^{!}(X)$
, the graded vector space
$\mathscr{F}_{1},\mathscr{F}_{2}\in \operatorname{QC}^{!}(X)$
, the graded vector space
![]() $H^{\ast }(\operatorname{Hom}(\mathscr{F}_{1},\mathscr{F}_{2}))$
is naturally a graded
$H^{\ast }(\operatorname{Hom}(\mathscr{F}_{1},\mathscr{F}_{2}))$
is naturally a graded
![]() ${\mathcal{O}}(T_{X}^{\ast -1})$
-module.
${\mathcal{O}}(T_{X}^{\ast -1})$
-module.
The singular support
![]() $\operatorname{supp}\mathscr{F}\subset T_{X}^{\ast -1}$
of an object
$\operatorname{supp}\mathscr{F}\subset T_{X}^{\ast -1}$
of an object
![]() $\mathscr{F}\in \operatorname{DCoh}(X)$
is the support of
$\mathscr{F}\in \operatorname{DCoh}(X)$
is the support of
![]() $H^{\ast }(\operatorname{End}(\mathscr{F}))$
as an
$H^{\ast }(\operatorname{End}(\mathscr{F}))$
as an
![]() ${\mathcal{O}}(T_{X}^{\ast -1})$
-module. More generally, when
${\mathcal{O}}(T_{X}^{\ast -1})$
-module. More generally, when
![]() $\operatorname{QC}^{!}(X)$
is compactly generated (as in our applications), the singular support
$\operatorname{QC}^{!}(X)$
is compactly generated (as in our applications), the singular support
![]() $\operatorname{supp}\mathscr{F}\subset T_{X}^{\ast -1}$
of an object
$\operatorname{supp}\mathscr{F}\subset T_{X}^{\ast -1}$
of an object
![]() $\mathscr{F}\in \operatorname{QC}^{!}(X)$
is the union of the supports of
$\mathscr{F}\in \operatorname{QC}^{!}(X)$
is the union of the supports of
![]() $H^{\ast }(\operatorname{Hom}(\mathscr{F}_{\unicode[STIX]{x1D6FC}},\mathscr{F}))$
as an
$H^{\ast }(\operatorname{Hom}(\mathscr{F}_{\unicode[STIX]{x1D6FC}},\mathscr{F}))$
as an
![]() ${\mathcal{O}}(T_{X}^{\ast -1})$
-module as
${\mathcal{O}}(T_{X}^{\ast -1})$
-module as
![]() $\mathscr{F}_{\unicode[STIX]{x1D6FC}}\in \operatorname{DCoh}(X)$
ranges over a collection of compact generators. More generally still, when
$\mathscr{F}_{\unicode[STIX]{x1D6FC}}\in \operatorname{DCoh}(X)$
ranges over a collection of compact generators. More generally still, when
![]() $\operatorname{QC}^{!}(X)$
is not necessarily compactly generated, there is an umbrella notion of singular support via localization for which we refer the reader to [Reference Arinkin and GaitsgoryAG15].
$\operatorname{QC}^{!}(X)$
is not necessarily compactly generated, there is an umbrella notion of singular support via localization for which we refer the reader to [Reference Arinkin and GaitsgoryAG15].
Let
![]() $\operatorname{Con}X$
denote the set of conic Zariski-closed subsets of
$\operatorname{Con}X$
denote the set of conic Zariski-closed subsets of
![]() $T_{X}^{\ast -1}$
. For any
$T_{X}^{\ast -1}$
. For any
![]() $\unicode[STIX]{x1D6EC}\in \operatorname{Con}X$
, one defines the full subcategory
$\unicode[STIX]{x1D6EC}\in \operatorname{Con}X$
, one defines the full subcategory
of ind-coherent complexes supported along
![]() $\unicode[STIX]{x1D6EC}$
. The inclusion
$\unicode[STIX]{x1D6EC}$
. The inclusion
![]() $i_{\unicode[STIX]{x1D6EC}}$
admits a right adjoint
$i_{\unicode[STIX]{x1D6EC}}$
admits a right adjoint
We will often regard
![]() $\operatorname{QC}_{\unicode[STIX]{x1D6EC}}^{!}(X)$
as a subcategory of
$\operatorname{QC}_{\unicode[STIX]{x1D6EC}}^{!}(X)$
as a subcategory of
![]() $\operatorname{QC}^{!}(X)$
via the embedding
$\operatorname{QC}^{!}(X)$
via the embedding
![]() $i_{\unicode[STIX]{x1D6EC}}$
, and also regard
$i_{\unicode[STIX]{x1D6EC}}$
, and also regard
![]() $\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}}$
as an endofunctor of
$\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}}$
as an endofunctor of
![]() $\operatorname{QC}^{!}(X)$
. We will often say an object of
$\operatorname{QC}^{!}(X)$
. We will often say an object of
![]() $\operatorname{QC}^{!}(X)$
is
$\operatorname{QC}^{!}(X)$
is
![]() $\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}}$
-local to convey it lies in
$\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}}$
-local to convey it lies in
![]() $\operatorname{QC}_{\unicode[STIX]{x1D6EC}}^{!}(X)$
.
$\operatorname{QC}_{\unicode[STIX]{x1D6EC}}^{!}(X)$
.
We set
![]() $\operatorname{DCoh}_{\unicode[STIX]{x1D6EC}}(X)=\operatorname{DCoh}(X)\cap \operatorname{QC}_{\unicode[STIX]{x1D6EC}}^{!}(X)$
. By [Reference Arinkin and GaitsgoryAG15, Corollary 8.2.8], for global complete intersection stacks (in the sense of [Reference Arinkin and GaitsgoryAG15, § 8.2]), we have
$\operatorname{DCoh}_{\unicode[STIX]{x1D6EC}}(X)=\operatorname{DCoh}(X)\cap \operatorname{QC}_{\unicode[STIX]{x1D6EC}}^{!}(X)$
. By [Reference Arinkin and GaitsgoryAG15, Corollary 8.2.8], for global complete intersection stacks (in the sense of [Reference Arinkin and GaitsgoryAG15, § 8.2]), we have
![]() $\operatorname{QC}_{\unicode[STIX]{x1D6EC}}^{!}(X)=\operatorname{Ind}\operatorname{DCoh}_{\unicode[STIX]{x1D6EC}}(X)$
.
$\operatorname{QC}_{\unicode[STIX]{x1D6EC}}^{!}(X)=\operatorname{Ind}\operatorname{DCoh}_{\unicode[STIX]{x1D6EC}}(X)$
.
Remark 2.1.3. For
![]() $\mathscr{F}\in \operatorname{DCoh}X$
, one has
$\mathscr{F}\in \operatorname{DCoh}X$
, one has
![]() $\operatorname{supp}\mathscr{F}\subset \{0\}_{X}$
if and only if
$\operatorname{supp}\mathscr{F}\subset \{0\}_{X}$
if and only if
![]() $\mathscr{F}\in \operatorname{Perf}X$
. This observation can be upgraded to a geometric description of
$\mathscr{F}\in \operatorname{Perf}X$
. This observation can be upgraded to a geometric description of
![]() $\operatorname{supp}\mathscr{F}$
as follows.
$\operatorname{supp}\mathscr{F}$
as follows.
Suppose that
![]() $\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow X$
is a geometric point, and that in a neighborhood of
$\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow X$
is a geometric point, and that in a neighborhood of
![]() $\unicode[STIX]{x1D702}$
, one has a presentation of
$\unicode[STIX]{x1D702}$
, one has a presentation of
![]() $X$
as an iterated fiber
$X$
as an iterated fiber

where
![]() $M$
is affine and smooth. Then one can interpret
$M$
is affine and smooth. Then one can interpret
![]() $df_{1}$
as a section of
$df_{1}$
as a section of
![]() $T^{\ast -1}X$
and one has
$T^{\ast -1}X$
and one has
if and only if
![]() $\mathscr{F}$
is contained in the smallest thick subcategory of
$\mathscr{F}$
is contained in the smallest thick subcategory of
![]() $\operatorname{DCoh}X$
generated by pullbacks from
$\operatorname{DCoh}X$
generated by pullbacks from
![]() $\operatorname{DCoh}X^{\prime }$
. Informally speaking, this is the case when ‘
$\operatorname{DCoh}X^{\prime }$
. Informally speaking, this is the case when ‘
![]() $\mathscr{F}$
extends in the
$\mathscr{F}$
extends in the
![]() $f_{1}$
direction near
$f_{1}$
direction near
![]() $\unicode[STIX]{x1D702}$
’.
$\unicode[STIX]{x1D702}$
’.
Lemma 2.1.4. For
![]() $\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }\in \operatorname{Con}X$
, there is a natural equivalence
$\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6EC}^{\prime }\in \operatorname{Con}X$
, there is a natural equivalence
![]() $\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}}\circ \text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}^{\prime }}\simeq \text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}\cap \unicode[STIX]{x1D6EC}^{\prime }}$
.
$\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}}\circ \text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}^{\prime }}\simeq \text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}\cap \unicode[STIX]{x1D6EC}^{\prime }}$
.
Proof. See [Reference Arinkin and GaitsgoryAG15, Proposition 2.2.6]. ◻
2.1.3 Functoriality
Associated to a map
![]() $f:X\rightarrow Y$
is a correspondence
$f:X\rightarrow Y$
is a correspondence
Definition 2.1.5. Let
![]() $f:X\rightarrow Y$
be a map of quasi-smooth stacks.
$f:X\rightarrow Y$
be a map of quasi-smooth stacks.
-
(i) Given a subset
 $U\subset T_{X}^{\ast -1}$
, we may form the subset If
$U\subset T_{X}^{\ast -1}$
, we may form the subset If $$\begin{eqnarray}f_{\ast }U=\tilde{f}((df^{\ast })^{-1}(U))\subset T_{Y}^{\ast -1}.\end{eqnarray}$$
$$\begin{eqnarray}f_{\ast }U=\tilde{f}((df^{\ast })^{-1}(U))\subset T_{Y}^{\ast -1}.\end{eqnarray}$$
 $f:X\rightarrow Y$
is proper, then
$f:X\rightarrow Y$
is proper, then
 $\tilde{f}$
is proper, and this defines a map
$\tilde{f}$
is proper, and this defines a map 
-
(ii) Given a subset
 $V\subset T_{Y}^{\ast -1}$
, we may form the subset If
$V\subset T_{Y}^{\ast -1}$
, we may form the subset If $$\begin{eqnarray}f^{!}V=df^{\ast }(X\times _{Y}V)\subset T_{X}^{\ast -1}.\end{eqnarray}$$
$$\begin{eqnarray}f^{!}V=df^{\ast }(X\times _{Y}V)\subset T_{X}^{\ast -1}.\end{eqnarray}$$
 $f:X\rightarrow Y$
is quasi-smooth, then
$f:X\rightarrow Y$
is quasi-smooth, then
 $df^{\ast }$
is a closed immersion, and this defines a map
$df^{\ast }$
is a closed immersion, and this defines a map
Lemma 2.1.6. Let
![]() $f:X\rightarrow Y$
be a map of quasi-smooth stacks.
$f:X\rightarrow Y$
be a map of quasi-smooth stacks.
-
(i) Suppose that
 $\mathscr{F}\in \operatorname{QC}^{!}(X)$
and that
$\mathscr{F}\in \operatorname{QC}^{!}(X)$
and that
 $f$
is schematic and quasi-compact. Then, we have Thus, if
$f$
is schematic and quasi-compact. Then, we have Thus, if $$\begin{eqnarray}\operatorname{supp}f_{\ast }\mathscr{F}\subset f_{\ast }\operatorname{supp}\mathscr{F}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{supp}f_{\ast }\mathscr{F}\subset f_{\ast }\operatorname{supp}\mathscr{F}.\end{eqnarray}$$
 $\tilde{f}_{\ast }\unicode[STIX]{x1D6EC}_{X}\subset \unicode[STIX]{x1D6EC}_{Y},$
then
$\tilde{f}_{\ast }\unicode[STIX]{x1D6EC}_{X}\subset \unicode[STIX]{x1D6EC}_{Y},$
then  $$\begin{eqnarray}f_{\ast }(\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X}}^{!}(X))\subset \operatorname{QC}_{\unicode[STIX]{x1D6EC}_{Y}}^{!}(Y).\end{eqnarray}$$
$$\begin{eqnarray}f_{\ast }(\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X}}^{!}(X))\subset \operatorname{QC}_{\unicode[STIX]{x1D6EC}_{Y}}^{!}(Y).\end{eqnarray}$$
-
(ii) Suppose that
 $\mathscr{F}\in \operatorname{QC}^{!}(Y)$
. Then, we have Thus, if
$\mathscr{F}\in \operatorname{QC}^{!}(Y)$
. Then, we have Thus, if $$\begin{eqnarray}\operatorname{supp}f^{!}\mathscr{F}\subset f^{!}\operatorname{supp}\mathscr{F}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{supp}f^{!}\mathscr{F}\subset f^{!}\operatorname{supp}\mathscr{F}.\end{eqnarray}$$
 $f^{!}\unicode[STIX]{x1D6EC}_{Y}\subset \unicode[STIX]{x1D6EC}_{X},$
then
$f^{!}\unicode[STIX]{x1D6EC}_{Y}\subset \unicode[STIX]{x1D6EC}_{X},$
then  $$\begin{eqnarray}f^{!}(\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{Y}}^{!}(Y))\subset \operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X}}^{!}(X).\end{eqnarray}$$
$$\begin{eqnarray}f^{!}(\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{Y}}^{!}(Y))\subset \operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X}}^{!}(X).\end{eqnarray}$$
Proof. See [Reference Arinkin and GaitsgoryAG15, Proposition 7.1.3]. ◻
We have the following partial converse to Lemma 2.1.6.
Proposition 2.1.7. Let
![]() $f:X\rightarrow Y$
be a map of quasi-smooth stacks.
$f:X\rightarrow Y$
be a map of quasi-smooth stacks.
-
(i) Suppose that
 $f$
is schematic and proper. Then
$f$
is schematic and proper. Then
 $\operatorname{QC}_{f_{\ast }\unicode[STIX]{x1D6EC}_{X}}^{!}(X)$
is the smallest full subcategory of
$\operatorname{QC}_{f_{\ast }\unicode[STIX]{x1D6EC}_{X}}^{!}(X)$
is the smallest full subcategory of
 $\operatorname{QC}^{!}(Y)$
containing the essential image
$\operatorname{QC}^{!}(Y)$
containing the essential image
 $f_{\ast }(\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X}}^{!}(X))$
and closed under colimits.
$f_{\ast }(\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X}}^{!}(X))$
and closed under colimits. -
(ii) Suppose that
 $f$
is quasi-smooth. Then
$f$
is quasi-smooth. Then
 $\operatorname{QC}_{f^{!}\unicode[STIX]{x1D6EC}_{Y}}^{!}(X)$
is the smallest full subcategory of
$\operatorname{QC}_{f^{!}\unicode[STIX]{x1D6EC}_{Y}}^{!}(X)$
is the smallest full subcategory of
 $\operatorname{QC}^{!}(X)$
containing the essential image
$\operatorname{QC}^{!}(X)$
containing the essential image
 $f^{!}(\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{Y}}^{!}(Y))$
and closed under colimits and tensoring by objects of
$f^{!}(\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{Y}}^{!}(Y))$
and closed under colimits and tensoring by objects of
 $\operatorname{QC}(X)$
.
$\operatorname{QC}(X)$
.
Proof. See [Reference Arinkin and GaitsgoryAG15, Theorem 7.8.2] for assertion (i) and [Reference Arinkin and GaitsgoryAG15, Corollary 7.6.2] for assertion (ii). ◻
2.1.4 Relative tensor products
Proposition 2.1.8. Let
![]() $X_{1},X_{2}$
be quasi-smooth stacks over a smooth separated base
$X_{1},X_{2}$
be quasi-smooth stacks over a smooth separated base
![]() $Y$
. Then the functor of exterior product over
$Y$
. Then the functor of exterior product over
![]() $Y$
induces an equivalence
$Y$
induces an equivalence

where
![]() $\unicode[STIX]{x1D6EC}=i^{!}(T_{X_{1}\times X_{2}}^{\ast -1})$
for
$\unicode[STIX]{x1D6EC}=i^{!}(T_{X_{1}\times X_{2}}^{\ast -1})$
for
![]() $i:X_{1}\times _{Y}X_{2}\rightarrow X_{1}\times X_{2}$
.
$i:X_{1}\times _{Y}X_{2}\rightarrow X_{1}\times X_{2}$
.
Proof. Recall by [Reference PreygelPre11, Proposition B.1.1] that
![]() $\boxtimes _{Y}$
is fully faithful. By [Reference PreygelPre11, Theorem B.2.4] exterior products over
$\boxtimes _{Y}$
is fully faithful. By [Reference PreygelPre11, Theorem B.2.4] exterior products over
![]() $k$
generate
$k$
generate
![]() $\operatorname{DCoh}(X_{1}\times X_{2})$
. Observe that
$\operatorname{DCoh}(X_{1}\times X_{2})$
. Observe that
![]() $i$
is an affine quasi-smooth morphism between quasi-smooth stacks, since it is a base change of the diagonal of
$i$
is an affine quasi-smooth morphism between quasi-smooth stacks, since it is a base change of the diagonal of
![]() $Y$
. Thus, the proof of [Reference Arinkin and GaitsgoryAG15, Proposition 7.6.4] implies that the essential image of
$Y$
. Thus, the proof of [Reference Arinkin and GaitsgoryAG15, Proposition 7.6.4] implies that the essential image of
![]() $i^{\ast }$
generates
$i^{\ast }$
generates
![]() $\operatorname{DCoh}_{Y}(X_{1}\times _{Y}X_{2})$
.◻
$\operatorname{DCoh}_{Y}(X_{1}\times _{Y}X_{2})$
.◻
2.2 Maps of pairs
Definition 2.2.1. Let
![]() $X,Y$
be quasi-smooth stacks, and
$X,Y$
be quasi-smooth stacks, and
![]() $\unicode[STIX]{x1D6EC}_{X}\in \operatorname{Con}X,\unicode[STIX]{x1D6EC}_{Y}\in \operatorname{Con}Y$
.
$\unicode[STIX]{x1D6EC}_{X}\in \operatorname{Con}X,\unicode[STIX]{x1D6EC}_{Y}\in \operatorname{Con}Y$
.
Define a map of pairs
![]() $f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
to be a map
$f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
to be a map
![]() $f:X\rightarrow Y$
such that
$f:X\rightarrow Y$
such that
![]() $f_{\ast }\unicode[STIX]{x1D6EC}_{X}\subset \unicode[STIX]{x1D6EC}_{Y}.$
$f_{\ast }\unicode[STIX]{x1D6EC}_{X}\subset \unicode[STIX]{x1D6EC}_{Y}.$
In this case, we say ‘
![]() $f$
takes
$f$
takes
![]() $\unicode[STIX]{x1D6EC}_{X}$
to
$\unicode[STIX]{x1D6EC}_{X}$
to
![]() $\unicode[STIX]{x1D6EC}_{Y}$
’.
$\unicode[STIX]{x1D6EC}_{Y}$
’.
Remark 2.2.2. Returning to the correspondence (Equation (1)), let us spell out the above definition.
For a map of pairs
![]() $f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
, we require
$f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
, we require
If
![]() $f:X\rightarrow Y$
is quasi-smooth, so that
$f:X\rightarrow Y$
is quasi-smooth, so that
![]() $df^{\ast }$
is a closed immersion, then we can equivalently require
$df^{\ast }$
is a closed immersion, then we can equivalently require
With our previous notation, this can be rephrased in the form
Lemma 2.2.3. If
![]() $f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
is a map of pairs, then
$f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
is a map of pairs, then
![]() $f_{\ast }$
takes
$f_{\ast }$
takes
![]() $\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{X}}$
-local objects to
$\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{X}}$
-local objects to
![]() $\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{Y}}$
-local objects. If
$\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{Y}}$
-local objects. If
![]() $f$
is proper and quasi-smooth, then
$f$
is proper and quasi-smooth, then
![]() $f$
provides a map of pairs
$f$
provides a map of pairs
![]() $f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
if and only if
$f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
if and only if
![]() $f_{\ast }\operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{X}}(X)\subset \operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{Y}}(Y)$
.
$f_{\ast }\operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{X}}(X)\subset \operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{Y}}(Y)$
.
Proof. Both assertions are immediate from Lemma 2.1.6. ◻
Definition 2.2.4. Let
![]() $X,Y$
be quasi-smooth stacks, and
$X,Y$
be quasi-smooth stacks, and
![]() $\unicode[STIX]{x1D6EC}_{X}\in \operatorname{Con}X,\unicode[STIX]{x1D6EC}_{Y}\in \operatorname{Con}Y$
.
$\unicode[STIX]{x1D6EC}_{X}\in \operatorname{Con}X,\unicode[STIX]{x1D6EC}_{Y}\in \operatorname{Con}Y$
.
Define a strict map of pairs
![]() $f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
to be a map
$f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
to be a map
![]() $f:X\rightarrow Y$
such that
$f:X\rightarrow Y$
such that
In this case, we say ‘the
![]() $f$
-preimage of
$f$
-preimage of
![]() $\unicode[STIX]{x1D6EC}_{Y}$
is precisely
$\unicode[STIX]{x1D6EC}_{Y}$
is precisely
![]() $\unicode[STIX]{x1D6EC}_{X}$
’.
$\unicode[STIX]{x1D6EC}_{X}$
’.
Remark 2.2.5. If
![]() $f:X\rightarrow Y$
is quasi-smooth, so that
$f:X\rightarrow Y$
is quasi-smooth, so that
![]() $df^{\ast }$
is a closed immersion, then
$df^{\ast }$
is a closed immersion, then
![]() $f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
is a strict map of pairs if and only if
$f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
is a strict map of pairs if and only if
With our previous notation, this can be rephrased in the form
In practice, the above definition is too restrictive.
Definition 2.2.6. Let
![]() $X,Y$
be quasi-smooth stacks, and
$X,Y$
be quasi-smooth stacks, and
![]() $\unicode[STIX]{x1D6EC}_{X},\unicode[STIX]{x1D6EC}_{X}^{\prime }\in \operatorname{Con}X,\unicode[STIX]{x1D6EC}_{Y}\in \operatorname{Con}Y$
.
$\unicode[STIX]{x1D6EC}_{X},\unicode[STIX]{x1D6EC}_{X}^{\prime }\in \operatorname{Con}X,\unicode[STIX]{x1D6EC}_{Y}\in \operatorname{Con}Y$
.
A map
![]() $f:X\rightarrow Y$
is said to be a strict map of pairs
$f:X\rightarrow Y$
is said to be a strict map of pairs
![]() $f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
along
$f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
along
![]() $\unicode[STIX]{x1D6EC}_{X}^{\prime }$
if we have
$\unicode[STIX]{x1D6EC}_{X}^{\prime }$
if we have
In this case, we say ‘along
![]() $\unicode[STIX]{x1D6EC}_{X}^{\prime }$
, the
$\unicode[STIX]{x1D6EC}_{X}^{\prime }$
, the
![]() $f$
-preimage of
$f$
-preimage of
![]() $\unicode[STIX]{x1D6EC}_{Y}$
is precisely
$\unicode[STIX]{x1D6EC}_{Y}$
is precisely
![]() $\unicode[STIX]{x1D6EC}_{X}$
’.
$\unicode[STIX]{x1D6EC}_{X}$
’.
Remark 2.2.7. If
![]() $f:X\rightarrow Y$
is quasi-smooth, so that
$f:X\rightarrow Y$
is quasi-smooth, so that
![]() $df^{\ast }$
is a closed immersion, then
$df^{\ast }$
is a closed immersion, then
![]() $f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
is a strict map of pairs along
$f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
is a strict map of pairs along
![]() $\unicode[STIX]{x1D6EC}_{X}^{\prime }$
if and only if
$\unicode[STIX]{x1D6EC}_{X}^{\prime }$
if and only if
With our previous notation, this can be rephrased in the form
If, in addition,
![]() $f:X\rightarrow Y$
is already known to be a map of pairs
$f:X\rightarrow Y$
is already known to be a map of pairs
![]() $f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
, so that
$f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
, so that
then it is strict along
![]() $\unicode[STIX]{x1D6EC}_{X}^{\prime }$
if and only if
$\unicode[STIX]{x1D6EC}_{X}^{\prime }$
if and only if
2.3 Base change with support
Lemma 2.3.1. Let
![]() $X,Y$
be quasi-smooth stacks, and
$X,Y$
be quasi-smooth stacks, and
![]() $\unicode[STIX]{x1D6EC}_{X},\unicode[STIX]{x1D6EC}_{X}^{\prime }\in \operatorname{Con}X,\unicode[STIX]{x1D6EC}_{Y}\in \operatorname{Con}Y$
.
$\unicode[STIX]{x1D6EC}_{X},\unicode[STIX]{x1D6EC}_{X}^{\prime }\in \operatorname{Con}X,\unicode[STIX]{x1D6EC}_{Y}\in \operatorname{Con}Y$
.
Suppose that
![]() $f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
is a quasi-smooth map of pairs.
$f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
is a quasi-smooth map of pairs.
Then there is a natural morphism
of functors
![]() $\operatorname{QC}^{!}(X)\rightarrow \operatorname{QC}_{\unicode[STIX]{x1D6EC}_{Y}}^{!}(Y)$
.
$\operatorname{QC}^{!}(X)\rightarrow \operatorname{QC}_{\unicode[STIX]{x1D6EC}_{Y}}^{!}(Y)$
.
Furthermore, if
![]() $f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
is strict along
$f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
is strict along
![]() $\unicode[STIX]{x1D6EC}_{X}^{\prime }$
, then the above morphism is an equivalence when restricted to the full subcategory
$\unicode[STIX]{x1D6EC}_{X}^{\prime }$
, then the above morphism is an equivalence when restricted to the full subcategory
Proof. First, from the counit
![]() $i_{\unicode[STIX]{x1D6EC}_{X}}\circ R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{X}}\rightarrow 1$
, we obtain a map
$i_{\unicode[STIX]{x1D6EC}_{X}}\circ R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{X}}\rightarrow 1$
, we obtain a map
![]() $f_{\ast }\circ R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{X}}\rightarrow f_{\ast }$
. Since
$f_{\ast }\circ R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{X}}\rightarrow f_{\ast }$
. Since
![]() $f$
is a map of pairs,
$f$
is a map of pairs,
![]() $f_{\ast }\circ R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{X}}$
lands in the
$f_{\ast }\circ R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{X}}$
lands in the
![]() $R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{Y}}$
-local objects. Thus,
$R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{Y}}$
-local objects. Thus,
![]() $f_{\ast }\circ R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{X}}\rightarrow f_{\ast }$
factors through
$f_{\ast }\circ R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{X}}\rightarrow f_{\ast }$
factors through
![]() $R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{Y}}\circ f_{\ast }$
.
$R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{Y}}\circ f_{\ast }$
.
Now assume
![]() $f$
is strict along
$f$
is strict along
![]() $\unicode[STIX]{x1D6EC}_{X}^{\prime }$
. We must show that the map
$\unicode[STIX]{x1D6EC}_{X}^{\prime }$
. We must show that the map
is an equivalence on
![]() $\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X}^{\prime }}^{!}(X)$
.
$\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X}^{\prime }}^{!}(X)$
.
Suppose
![]() $\mathscr{F}\in \operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X}^{\prime }}^{!}(X)$
. We must show that the natural map
$\mathscr{F}\in \operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X}^{\prime }}^{!}(X)$
. We must show that the natural map
is an
![]() $R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{Y}}$
-equivalence. Equivalently, we must show that the induced map
$R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{Y}}$
-equivalence. Equivalently, we must show that the induced map
is an equivalence for all
![]() $\mathscr{K}\in \operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{Y}}(Y)$
.
$\mathscr{K}\in \operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{Y}}(Y)$
.
Since
![]() $f$
is quasi-smooth,
$f$
is quasi-smooth,
![]() $f^{\ast }$
exists and is left adjoint to
$f^{\ast }$
exists and is left adjoint to
![]() $f_{\ast }$
, so the above is equivalent to showing that
$f_{\ast }$
, so the above is equivalent to showing that
is an equivalence.
By Lemma 2.1.6 and the comparison between
![]() $f^{\ast }$
and
$f^{\ast }$
and
![]() $f^{!}$
for quasi-smooth maps (thanks to the fact that
$f^{!}$
for quasi-smooth maps (thanks to the fact that
![]() $f$
is quasi-smooth, hence Gorenstein), we have
$f$
is quasi-smooth, hence Gorenstein), we have
![]() $f^{\ast }\mathscr{K}\in \operatorname{QC}_{f^{!}\unicode[STIX]{x1D6EC}_{Y}}^{!}(X)$
, and thus the above map is equivalent to a map
$f^{\ast }\mathscr{K}\in \operatorname{QC}_{f^{!}\unicode[STIX]{x1D6EC}_{Y}}^{!}(X)$
, and thus the above map is equivalent to a map
Finally, since
![]() $\mathscr{F}$
is already
$\mathscr{F}$
is already
![]() $R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{X}^{\prime }}$
-local, by Lemma 2.1.4 we have that
$R\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{X}^{\prime }}$
-local, by Lemma 2.1.4 we have that
The strictness of
![]() $f$
along
$f$
along
![]() $\unicode[STIX]{x1D6EC}_{X}^{\prime }$
precisely guarantees that
$\unicode[STIX]{x1D6EC}_{X}^{\prime }$
precisely guarantees that
Definition 2.3.2. Suppose
![]() $f:X\rightarrow Y$
is a map of quasi-smooth stacks.
$f:X\rightarrow Y$
is a map of quasi-smooth stacks.
Fix
![]() $\unicode[STIX]{x1D6EC}_{X}\in \operatorname{Con}X$
,
$\unicode[STIX]{x1D6EC}_{X}\in \operatorname{Con}X$
,
![]() $\unicode[STIX]{x1D6EC}_{Y}\in \operatorname{Con}Y$
, and define functors with support conditions
$\unicode[STIX]{x1D6EC}_{Y}\in \operatorname{Con}Y$
, and define functors with support conditions
Remark 2.3.3. If
![]() $f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
is a map of pairs, then
$f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
is a map of pairs, then
![]() $f_{\ast }\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X}}^{!}(X)\subset \operatorname{QC}_{\unicode[STIX]{x1D6EC}_{Y}}^{!}(Y)$
, so we need not apply
$f_{\ast }\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X}}^{!}(X)\subset \operatorname{QC}_{\unicode[STIX]{x1D6EC}_{Y}}^{!}(Y)$
, so we need not apply
![]() $\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{Y}}$
in the definition of
$\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}_{Y}}$
in the definition of
![]() $\mathfrak{f}_{\ast }$
. In other words,
$\mathfrak{f}_{\ast }$
. In other words,
![]() $\mathfrak{f}_{\ast }\simeq f_{\ast }\circ i_{\unicode[STIX]{x1D6EC}_{X}}$
and, hence,
$\mathfrak{f}_{\ast }\simeq f_{\ast }\circ i_{\unicode[STIX]{x1D6EC}_{X}}$
and, hence,
![]() $\mathfrak{f}_{\ast }$
preserves compact objects. Thus, if, in addition,
$\mathfrak{f}_{\ast }$
preserves compact objects. Thus, if, in addition,
![]() $f$
is proper, the right adjoint to
$f$
is proper, the right adjoint to
![]() $\mathfrak{f}_{\ast }\simeq f_{\ast }\circ i_{\unicode[STIX]{x1D6EC}_{X}}$
coincides with
$\mathfrak{f}_{\ast }\simeq f_{\ast }\circ i_{\unicode[STIX]{x1D6EC}_{X}}$
coincides with
![]() $\mathfrak{f}^{!}$
. (Note that we still must apply
$\mathfrak{f}^{!}$
. (Note that we still must apply
![]() $\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}}$
in the definition of
$\text{R}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D6EC}}$
in the definition of
![]() $\mathfrak{f}^{!}$
in general: if
$\mathfrak{f}^{!}$
in general: if
![]() $f$
is proper but a support condition is not satisfied, then
$f$
is proper but a support condition is not satisfied, then
![]() $f^{!}$
need not be right adjoint to
$f^{!}$
need not be right adjoint to
![]() $\mathfrak{f}_{\ast }$
.Footnote
1
)
$\mathfrak{f}_{\ast }$
.Footnote
1
)
Similarly, suppose
![]() $f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
and
$f:(X,\unicode[STIX]{x1D6EC}_{X})\rightarrow (Y,\unicode[STIX]{x1D6EC}_{Y})$
and
![]() $g:(Y,\unicode[STIX]{x1D6EC}_{Y})\rightarrow (Z,\unicode[STIX]{x1D6EC}_{Z})$
are proper maps of pairs. Then
$g:(Y,\unicode[STIX]{x1D6EC}_{Y})\rightarrow (Z,\unicode[STIX]{x1D6EC}_{Z})$
are proper maps of pairs. Then
![]() $h=g\circ f$
is also a proper map of pairs, and there is a natural equivalence
$h=g\circ f$
is also a proper map of pairs, and there is a natural equivalence
![]() $\mathfrak{h}_{\ast }\simeq \mathfrak{g}_{\ast }\circ \mathfrak{f}_{\ast }$
. By the above discussion, this follows from functoriality of the usual pushforwards. Moreover, taking right adjoints, we obtain a natural equivalence
$\mathfrak{h}_{\ast }\simeq \mathfrak{g}_{\ast }\circ \mathfrak{f}_{\ast }$
. By the above discussion, this follows from functoriality of the usual pushforwards. Moreover, taking right adjoints, we obtain a natural equivalence
![]() $\mathfrak{h}^{!}\simeq \mathfrak{f}^{!}\circ \mathfrak{g}^{!}$
.
$\mathfrak{h}^{!}\simeq \mathfrak{f}^{!}\circ \mathfrak{g}^{!}$
.
It will be crucial for us to study ‘base change’ for these functors with support conditions. First, we recall the following general context for discussing base-change equivalences from [Reference LurieLur, Definition 6.2.3.13].
Definition 2.3.4. Suppose we are given a diagram of
![]() $\infty$
-categories
$\infty$
-categories

which commutes up to a specified equivalence
-
(1) We say that the square is left adjointable if the functors
 $G$
and
$G$
and
 $G^{\prime }$
admit left adjoints
$G^{\prime }$
admit left adjoints
 $F$
and
$F$
and
 $F^{\prime }$
, and base change holds: the composite transformationis an equivalence, where
$F^{\prime }$
, and base change holds: the composite transformationis an equivalence, where
 $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
 $\unicode[STIX]{x1D716}$
are the respective unit and counit of adjunctions.
$\unicode[STIX]{x1D716}$
are the respective unit and counit of adjunctions.
-
(2) Dually, the square is right adjointable if the functors
 $G$
and
$G$
and
 $G^{\prime }$
admit right adjoints
$G^{\prime }$
admit right adjoints
 $H$
and
$H$
and
 $H^{\prime }$
, and the composite transformationis an equivalence, where
$H^{\prime }$
, and the composite transformationis an equivalence, where
 $\unicode[STIX]{x1D702}$
and
$\unicode[STIX]{x1D702}$
and
 $\unicode[STIX]{x1D716}$
are the respective unit and counit of adjunctions.
$\unicode[STIX]{x1D716}$
are the respective unit and counit of adjunctions.
Definition 2.3.5. A strict Cartesian diagram of pairs is a Cartesian diagram of quasi-smooth stacks which is also a commutative diagram of maps of pairs

satisfying the strictness condition
Remark 2.3.6. If
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
are in addition assumed quasi-smooth, then by Remark 2.2.7 the strictness condition
$p_{2}$
are in addition assumed quasi-smooth, then by Remark 2.2.7 the strictness condition
![]() $\unicode[STIX]{x1D6EC}_{Z}\supset p_{1}^{!}\unicode[STIX]{x1D6EC}_{X}\cap p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}$
above is equivalent to any of the following:
$\unicode[STIX]{x1D6EC}_{Z}\supset p_{1}^{!}\unicode[STIX]{x1D6EC}_{X}\cap p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}$
above is equivalent to any of the following:
-
∙
 $p_{1}$
is strict along
$p_{1}$
is strict along
 $p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}$
;
$p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}$
; -
∙
 $p_{2}$
is strict along
$p_{2}$
is strict along
 $p_{1}^{!}\unicode[STIX]{x1D6EC}_{X}$
.
$p_{1}^{!}\unicode[STIX]{x1D6EC}_{X}$
.
Proper base change can be worded as a right adjointability condition.
Proposition 2.3.7. Consider a strict Cartesian diagram of pairs

Assume:
-
∙
 $p$
is proper (and consequently so is
$p$
is proper (and consequently so is
 $p_{2}$
);
$p_{2}$
); -
∙
 $p_{1}$
is quasi-smooth.
$p_{1}$
is quasi-smooth.
Then:
-
(i) we have adjunctions

-
(ii) the diagram of pushforwards
admits a natural equivalence and is right adjointable, i.e. the resulting base-change morphism
and is right adjointable, i.e. the resulting base-change morphism is an equivalence.
is an equivalence.
Proof. Point (i) and the functoriality equivalence of point (ii) are immediate from Remark 2.3.3. The adjointability morphism of point (ii) is the composite
Note that the second arrow is an equivalence by the usual base-change theorem for
![]() $\operatorname{QC}^{!}$
. To see that the first arrow is an equivalence we apply Lemma 2.3.1 as follows.
$\operatorname{QC}^{!}$
. To see that the first arrow is an equivalence we apply Lemma 2.3.1 as follows.
Note that the essential image of
![]() $p_{2}^{!}$
on
$p_{2}^{!}$
on
![]() $\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X^{\prime }}}^{!}(X^{\prime })$
lies in
$\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{X^{\prime }}}^{!}(X^{\prime })$
lies in
![]() $\operatorname{QC}_{p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}}^{!}(Z)$
by Lemma 2.1.6. Since
$\operatorname{QC}_{p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}}^{!}(Z)$
by Lemma 2.1.6. Since
![]() $p_{2}$
is not assumed quasi-smooth,
$p_{2}$
is not assumed quasi-smooth,
![]() $p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}$
need not be closed and by
$p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}$
need not be closed and by
![]() $\operatorname{QC}_{p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}}^{!}(Z)$
we mean the subcategory of
$\operatorname{QC}_{p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}}^{!}(Z)$
we mean the subcategory of
![]() $\operatorname{QC}^{!}(Z)$
generated under colimits by all coherent complexes on
$\operatorname{QC}^{!}(Z)$
generated under colimits by all coherent complexes on
![]() $Z$
whose microsupport is contained in a conical closed subset contained in
$Z$
whose microsupport is contained in a conical closed subset contained in
![]() $p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}$
. Thus, it is enough to show that the natural morphism
$p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}$
. Thus, it is enough to show that the natural morphism
is an equivalence on
![]() $\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{Z}^{\prime }}^{!}(Z)$
for each
$\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{Z}^{\prime }}^{!}(Z)$
for each
![]() $\unicode[STIX]{x1D6EC}_{Z}^{\prime }\in \operatorname{Con}Z$
contained in
$\unicode[STIX]{x1D6EC}_{Z}^{\prime }\in \operatorname{Con}Z$
contained in
![]() $p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}$
.
$p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}$
.
Since the diagram is a strict Cartesian diagram of pairs and
![]() $p_{1}$
is quasi-smooth, Remark 2.2.7 implies that
$p_{1}$
is quasi-smooth, Remark 2.2.7 implies that
![]() $p_{1}$
is strict along
$p_{1}$
is strict along
![]() $p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}$
and thus along each such
$p_{2}^{!}\unicode[STIX]{x1D6EC}_{X^{\prime }}$
and thus along each such
![]() $\unicode[STIX]{x1D6EC}_{Z}^{\prime }$
. Lemma 2.3.1 now completes the proof.Footnote
2
◻
$\unicode[STIX]{x1D6EC}_{Z}^{\prime }$
. Lemma 2.3.1 now completes the proof.Footnote
2
◻
With slightly more stringent conditions, we can interpret the (dual) base-change equivalence as an adjointability statement for the diagram of
![]() $!$
-pullbacks (instead of pushforwards).
$!$
-pullbacks (instead of pushforwards).
Proposition 2.3.8. Consider a strict Cartesian diagram of pairs

Assume:
-
∙
 $p$
and
$p$
and
 $q$
are proper (and consequently so are
$q$
are proper (and consequently so are
 $p_{1}$
and
$p_{1}$
and
 $p_{2}$
);
$p_{2}$
); -
∙
 $p_{2}$
is quasi-smooth.
$p_{2}$
is quasi-smooth.
Then:
-
(i) we have adjunctions


-
(ii) the diagram of pushforwards
admits a natural equivalence

-
(iii) the diagram of pullbacks
admits a natural equivalence and is left adjointable, i.e. the resulting base-change morphism
and is left adjointable, i.e. the resulting base-change morphism $$\begin{eqnarray}\mathfrak{p}_{1}^{!}\circ \mathfrak{p}^{!}\simeq \mathfrak{q}^{!}\circ \mathfrak{p}_{2}^{!}\end{eqnarray}$$
is an equivalence.
$$\begin{eqnarray}\mathfrak{p}_{1}^{!}\circ \mathfrak{p}^{!}\simeq \mathfrak{q}^{!}\circ \mathfrak{p}_{2}^{!}\end{eqnarray}$$
is an equivalence.
Proof. Points (i) and (ii) are immediate from Remark 2.3.3. The functoriality equivalence of point (iii) then results from taking right adjoints.
The adjointability equivalence of point (iii) is the composite
The second arrow is an equivalence by base change for
![]() $\operatorname{QC}^{!}$
; the first arrow is an equivalence by applying Lemma 2.3.1 to
$\operatorname{QC}^{!}$
; the first arrow is an equivalence by applying Lemma 2.3.1 to
![]() $p_{2}$
, which is quasi-smooth and strict along each conical closed subset contained in
$p_{2}$
, which is quasi-smooth and strict along each conical closed subset contained in
![]() $p_{1}^{!}\unicode[STIX]{x1D6EC}_{X}$
, analogous to the argument in Proposition 2.3.7.◻
$p_{1}^{!}\unicode[STIX]{x1D6EC}_{X}$
, analogous to the argument in Proposition 2.3.7.◻
2.4 Descent with support
Let
![]() $\unicode[STIX]{x1D6E5}$
denote the simplex category of non-empty totally ordered finite sets
$\unicode[STIX]{x1D6E5}$
denote the simplex category of non-empty totally ordered finite sets
![]() $[n]=\{0\rightarrow 1\rightarrow \cdots \rightarrow n\}$
, and
$[n]=\{0\rightarrow 1\rightarrow \cdots \rightarrow n\}$
, and
![]() $\unicode[STIX]{x1D6E5}_{+}$
the augmented simplex category of (possibly empty) totally ordered finite sets, so in other words
$\unicode[STIX]{x1D6E5}_{+}$
the augmented simplex category of (possibly empty) totally ordered finite sets, so in other words
![]() $\unicode[STIX]{x1D6E5}$
adjoined the initial object given by the empty set
$\unicode[STIX]{x1D6E5}$
adjoined the initial object given by the empty set
![]() $[-1]=\emptyset$
.
$[-1]=\emptyset$
.
Recall that a simplicial object or diagram of a category
![]() ${\mathcal{C}}$
is a functor
${\mathcal{C}}$
is a functor
![]() $\unicode[STIX]{x1D6E5}^{\text{op}}\rightarrow {\mathcal{C}}$
, traditionally denoted by
$\unicode[STIX]{x1D6E5}^{\text{op}}\rightarrow {\mathcal{C}}$
, traditionally denoted by
![]() $X_{\bullet }$
, where we understand
$X_{\bullet }$
, where we understand
![]() $X_{n}\in {\mathcal{C}}$
to be the value of the functor on
$X_{n}\in {\mathcal{C}}$
to be the value of the functor on
![]() $[n]$
. An augmented simplicial object is a functor
$[n]$
. An augmented simplicial object is a functor
![]() $\unicode[STIX]{x1D6E5}_{+}^{\text{op}}\rightarrow {\mathcal{C}}$
, traditionally denoted by
$\unicode[STIX]{x1D6E5}_{+}^{\text{op}}\rightarrow {\mathcal{C}}$
, traditionally denoted by
![]() $X_{\bullet }\rightarrow X_{-1}$
, where we understand
$X_{\bullet }\rightarrow X_{-1}$
, where we understand
![]() $X_{-1}\in {\mathcal{C}}$
to be the value of the functor on
$X_{-1}\in {\mathcal{C}}$
to be the value of the functor on
![]() $[-1]$
.
$[-1]$
.
Recall that in
![]() $\unicode[STIX]{x1D6E5}_{+}$
the injections
$\unicode[STIX]{x1D6E5}_{+}$
the injections
![]() $[n]\rightarrow [n+1]$
(respectively, surjections
$[n]\rightarrow [n+1]$
(respectively, surjections
![]() $[n+1]\rightarrow [n]$
), and the induced maps
$[n+1]\rightarrow [n]$
), and the induced maps
![]() $X_{n+1}\rightarrow X_{n}$
(respectively,
$X_{n+1}\rightarrow X_{n}$
(respectively,
![]() $X_{n}\rightarrow X_{n+1}$
) of an augmented simplicial object, are called the face (respectively, degeneracy) maps. In particular, we have the distinguished face map
$X_{n}\rightarrow X_{n+1}$
) of an augmented simplicial object, are called the face (respectively, degeneracy) maps. In particular, we have the distinguished face map
![]() $d_{0}:X_{n+1}\rightarrow X_{n}$
induced by the injection
$d_{0}:X_{n+1}\rightarrow X_{n}$
induced by the injection
![]() $[n]\rightarrow [n+1]$
whose image does not contain
$[n]\rightarrow [n+1]$
whose image does not contain
![]() $0\in [n+1]$
.
$0\in [n+1]$
.
Theorem 2.4.1. Suppose
![]() $f:(X_{\bullet },\unicode[STIX]{x1D6EC}_{\bullet })\rightarrow (X_{-1},\unicode[STIX]{x1D6EC}_{-1})$
is an augmented simplicial diagram of maps of pairs with all stacks quasi-smooth and maps proper. Suppose further that the following points apply.
$f:(X_{\bullet },\unicode[STIX]{x1D6EC}_{\bullet })\rightarrow (X_{-1},\unicode[STIX]{x1D6EC}_{-1})$
is an augmented simplicial diagram of maps of pairs with all stacks quasi-smooth and maps proper. Suppose further that the following points apply.
-
(i) The face maps are quasi-smooth.
-
(ii) For any map
 $g:[m]\rightarrow [n]$
in
$g:[m]\rightarrow [n]$
in
 $\unicode[STIX]{x1D6E5}_{+}$
, the induced commutative squareis a strict Cartesian diagram of pairs.
$\unicode[STIX]{x1D6E5}_{+}$
, the induced commutative squareis a strict Cartesian diagram of pairs.
-
(iii) Pullback along the augmentation
is conservative.
Then the augmentation provides an equivalence with the totalization of the cosimplicial category furnished by
![]() $!$
-pullbacks with support conditions
$!$
-pullbacks with support conditions
Proof. The first equivalence for the totalization is an application of the Beck–Chevalley condition [Reference LurieLur, Corollary 6.2.4.3] applied to the augmented cosimplicial category
The left adjointability required therein is precisely obtained by applying Proposition 2.3.8 to the diagram appearing in condition (ii) of the theorem. By hypothesis, the maps of the diagram are all proper maps of pairs,
![]() $d_{0}$
is quasi-smooth since it is a face map, and the required strictness condition holds. Thus, by Proposition 2.3.8, we have the left adjointability of the diagram
$d_{0}$
is quasi-smooth since it is a face map, and the required strictness condition holds. Thus, by Proposition 2.3.8, we have the left adjointability of the diagram

Corollary 2.4.2. With the assumptions of Theorem 2.4.1, suppose furthermore that each
![]() $\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{k}}^{!}(X_{k})$
is compactly generated for each
$\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{k}}^{!}(X_{k})$
is compactly generated for each
![]() $k\geqslant 0$
. (This holds, for instance, if each
$k\geqslant 0$
. (This holds, for instance, if each
![]() $X_{k}$
is a global complete intersection in the sense of [Reference Arinkin and GaitsgoryAG15, § 9].) Then, the same holds for
$X_{k}$
is a global complete intersection in the sense of [Reference Arinkin and GaitsgoryAG15, § 9].) Then, the same holds for
![]() $k=-1$
and pushforward along the augmentation provides an equivalence
$k=-1$
and pushforward along the augmentation provides an equivalence
Proof. By the previous theorem and the anti-equivalence of
![]() $\Pr ^{L}$
and
$\Pr ^{L}$
and
![]() $\Pr ^{R}$
(the
$\Pr ^{R}$
(the
![]() $\infty$
-categories of presentable
$\infty$
-categories of presentable
![]() $\infty$
-categories with morphisms left adjoints or respectively right adjoints), the augmented simplicial diagram
$\infty$
-categories with morphisms left adjoints or respectively right adjoints), the augmented simplicial diagram
is a geometric realization diagram in
![]() $\Pr ^{L}$
. The argument of [Reference Arinkin and GaitsgoryAG15, Corollary 9.2.8] identifies
$\Pr ^{L}$
. The argument of [Reference Arinkin and GaitsgoryAG15, Corollary 9.2.8] identifies
![]() $\operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{k}}(X_{k})$
with the compact objects of
$\operatorname{DCoh}_{\unicode[STIX]{x1D6EC}_{k}}(X_{k})$
with the compact objects of
![]() $\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{k}}^{!}(X_{k})$
. Hence, since the structure maps are proper and maps of pairs, the corresponding pushforwards preserve compact objects. The result now follows from the fact the colimit of small categories exists, and the formation of
$\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{k}}^{!}(X_{k})$
. Hence, since the structure maps are proper and maps of pairs, the corresponding pushforwards preserve compact objects. The result now follows from the fact the colimit of small categories exists, and the formation of
![]() $\operatorname{Ind}$
preserves colimits and is conservative.◻
$\operatorname{Ind}$
preserves colimits and is conservative.◻
In our further developments and applications in subsequent sections, we will appeal to Theorem 2.4.1 and verify its hypotheses directly. Before continuing on, let us record the following simple consequence.
Corollary 2.4.3. Suppose
![]() $S$
is quasi-smooth, and
$S$
is quasi-smooth, and
![]() $\unicode[STIX]{x1D70B}:X\rightarrow S$
is proper and quasi-smooth. Then there is a natural equivalence
$\unicode[STIX]{x1D70B}:X\rightarrow S$
is proper and quasi-smooth. Then there is a natural equivalence
Proof. For each
![]() $\bullet \geqslant -1$
, we have the identification
$\bullet \geqslant -1$
, we have the identification
The left-hand side furnishes the terms of a natural cosimplicial diagram with functors
![]() $f_{\bullet }^{\ast }$
; the right-hand side furnishes the terms of a natural cosimplicial diagram with functors
$f_{\bullet }^{\ast }$
; the right-hand side furnishes the terms of a natural cosimplicial diagram with functors
![]() $\mathfrak{f}_{\bullet }^{!}$
. One readily checks that the latter satisfies the requirements of the preceding theorem. Thus, it only remains to note that the two diagrams are intertwined by the alternative equivalences
$\mathfrak{f}_{\bullet }^{!}$
. One readily checks that the latter satisfies the requirements of the preceding theorem. Thus, it only remains to note that the two diagrams are intertwined by the alternative equivalences
3 Centers and traces of convolution categories
We will calculate the center and trace categories of functor categories with the composition monoidal structure or equivalently integral kernel categories with the convolution monoidal structure.
3.1 Preliminaries
Definition 3.1.1. Let
![]() ${\mathcal{A}}$
be an algebra object in a symmetric monoidal
${\mathcal{A}}$
be an algebra object in a symmetric monoidal
![]() $\infty$
category
$\infty$
category
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
-
(1) The center (or Hochschild cohomology) is the morphism of bimodules object
It comes with a natural $$\begin{eqnarray}\mathit{Z}({\mathcal{A}})=\operatorname{Hom}_{{\mathcal{A}}^{\text{op}}\otimes {\mathcal{A}}}({\mathcal{A}},{\mathcal{A}})\in {\mathcal{C}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathit{Z}({\mathcal{A}})=\operatorname{Hom}_{{\mathcal{A}}^{\text{op}}\otimes {\mathcal{A}}}({\mathcal{A}},{\mathcal{A}})\in {\mathcal{C}}.\end{eqnarray}$$
 $E_{2}$
-monoidal structure and universal central map
$E_{2}$
-monoidal structure and universal central map
 $\mathit{Z}({\mathcal{A}})\rightarrow {\mathcal{A}}$
.
$\mathit{Z}({\mathcal{A}})\rightarrow {\mathcal{A}}$
.
-
(2) The trace (or Hochschild homology) is the tensor of bimodules object
It comes with a natural $$\begin{eqnarray}\text{Tr}({\mathcal{A}})={\mathcal{A}}\otimes _{{\mathcal{A}}^{\text{op}}\otimes {\mathcal{A}}}{\mathcal{A}}\in {\mathcal{C}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Tr}({\mathcal{A}})={\mathcal{A}}\otimes _{{\mathcal{A}}^{\text{op}}\otimes {\mathcal{A}}}{\mathcal{A}}\in {\mathcal{C}}.\end{eqnarray}$$
 $S^{1}$
-action and universal trace map
$S^{1}$
-action and universal trace map
 ${\mathcal{A}}\rightarrow \text{Tr}({\mathcal{A}})$
.
${\mathcal{A}}\rightarrow \text{Tr}({\mathcal{A}})$
.
Remark 3.1.2. We refer the reader to [Reference LurieLur, §§ 5.3 and 6.1] for the
![]() $E_{2}$
-structure on the center (Deligne conjecture) and
$E_{2}$
-structure on the center (Deligne conjecture) and
![]() $S^{1}$
-action on the trace (cyclic structure).
$S^{1}$
-action on the trace (cyclic structure).
3.2 Convolution categories
Let
![]() $p:X\rightarrow Y$
be a map of derived stacks, with
$p:X\rightarrow Y$
be a map of derived stacks, with
![]() $Y$
perfect and
$Y$
perfect and
![]() $p$
a relative quasi-compact separated algebraic space, so that [Reference Ben-Zvi, Nadler and PreygelBNP, Theorem 3.0.4] provides an equivalence
$p$
a relative quasi-compact separated algebraic space, so that [Reference Ben-Zvi, Nadler and PreygelBNP, Theorem 3.0.4] provides an equivalence
Here we write
![]() $p_{2}-\text{prop}$
instead of
$p_{2}-\text{prop}$
instead of
![]() $\text{prop}/X$
to distinguish the second factor so there is no ambiguity.
$\text{prop}/X$
to distinguish the second factor so there is no ambiguity.
Assume, in addition,
![]() $X$
is smooth. Then, on the one hand,
$X$
is smooth. Then, on the one hand,
![]() $\operatorname{DCoh}X\simeq \operatorname{Perf}X$
, so that the functor category of the right-hand side
$\operatorname{DCoh}X\simeq \operatorname{Perf}X$
, so that the functor category of the right-hand side
has a natural monoidal structure given by composition of linear functors, along with a natural module
![]() $\operatorname{Perf}X$
. On the other hand, the diagonal
$\operatorname{Perf}X$
. On the other hand, the diagonal
![]() $\unicode[STIX]{x1D6E5}:X\rightarrow X\times X$
has finite tor-dimension, so that convolution equips the left-hand side
$\unicode[STIX]{x1D6E5}:X\rightarrow X\times X$
has finite tor-dimension, so that convolution equips the left-hand side
![]() $\operatorname{DCoh}_{p_{2}-\text{prop}}(X\times _{Y}X)$
with a natural monoidal structure
$\operatorname{DCoh}_{p_{2}-\text{prop}}(X\times _{Y}X)$
with a natural monoidal structure
Moreover, convolution equips
![]() $\operatorname{Perf}X$
with a natural
$\operatorname{Perf}X$
with a natural
![]() $\operatorname{DCoh}_{p_{2}-\text{prop}}(X\times _{Y}X)$
-module structure
$\operatorname{DCoh}_{p_{2}-\text{prop}}(X\times _{Y}X)$
-module structure
(Note that
![]() $p_{2}$
-properness ensures that the convolution of coherent complexes and action on coherent complexes are well defined.)
$p_{2}$
-properness ensures that the convolution of coherent complexes and action on coherent complexes are well defined.)
Proposition 3.2.1. Assume
![]() $X$
is smooth.
$X$
is smooth.
Then the above equivalence is naturally a monoidal equivalence
compatibly with actions on the module
![]() $\operatorname{Perf}X$
.
$\operatorname{Perf}X$
.
Proof. Standard base-change identities enhance the equivalence
to a monoidal equivalence compatible with the actions on the module
![]() $\operatorname{QC}(X)$
. The asserted monoidal equivalence is simply the restriction to full subcategories.◻
$\operatorname{QC}(X)$
. The asserted monoidal equivalence is simply the restriction to full subcategories.◻
Corollary 3.2.2. Assume
![]() $p:X\rightarrow Y$
is proper and
$p:X\rightarrow Y$
is proper and
![]() $X$
is smooth.
$X$
is smooth.
Then the above equivalence is naturally a monoidal equivalence
compatibly with actions on the module
![]() $\operatorname{Perf}X$
.
$\operatorname{Perf}X$
.
3.3 Traces of convolution categories
Let us return to the setting of § 2.
Assume now that
![]() $X,Y$
are smooth and
$X,Y$
are smooth and
![]() $p:X\rightarrow Y$
is proper (and automatically quasi-smooth).
$p:X\rightarrow Y$
is proper (and automatically quasi-smooth).
Let
![]() $LY=\operatorname{Map}(S^{1},Y)$
denote the loop space of
$LY=\operatorname{Map}(S^{1},Y)$
denote the loop space of
![]() $Y$
. Recall the fundamental correspondence
$Y$
. Recall the fundamental correspondence
Define the support condition
![]() $\unicode[STIX]{x1D6EC}_{X/Y}\in \operatorname{Con}LY$
to be the pull–push of support conditions
$\unicode[STIX]{x1D6EC}_{X/Y}\in \operatorname{Con}LY$
to be the pull–push of support conditions
Theorem 3.3.1. Let
![]() $X,Y$
be smooth and
$X,Y$
be smooth and
![]() $p:X\rightarrow Y$
proper, quasi-smooth, and surjective.
$p:X\rightarrow Y$
proper, quasi-smooth, and surjective.
There is a natural cyclic identification of the trace
Proof. For notational convenience, set
![]() ${\mathcal{A}}=\operatorname{DCoh}(X\times _{Y}X)$
and
${\mathcal{A}}=\operatorname{DCoh}(X\times _{Y}X)$
and
![]() ${\mathcal{B}}=\operatorname{Perf}X$
. Observe that pushforward along the relative diagonal
${\mathcal{B}}=\operatorname{Perf}X$
. Observe that pushforward along the relative diagonal
![]() $\unicode[STIX]{x1D6E5}_{\ast }:{\mathcal{B}}\rightarrow {\mathcal{A}}$
is monoidal, and thus we may regard
$\unicode[STIX]{x1D6E5}_{\ast }:{\mathcal{B}}\rightarrow {\mathcal{A}}$
is monoidal, and thus we may regard
![]() ${\mathcal{A}}$
as an algebra in
${\mathcal{A}}$
as an algebra in
![]() ${\mathcal{B}}$
-bimodules.
${\mathcal{B}}$
-bimodules.
Given an algebra
![]() ${\mathcal{A}}$
in
${\mathcal{A}}$
in
![]() ${\mathcal{B}}$
-bimodules, we have its relative bar resolution
${\mathcal{B}}$
-bimodules, we have its relative bar resolution
which can be used to calculate its trace
We will access the trace as the geometric realization of the simplicial object
Unwinding the notation and using the canonical identity
![]() $\operatorname{Perf}(X)^{\otimes k}\simeq \operatorname{Perf}(X^{k})$
, we find the simplicial category
$\operatorname{Perf}(X)^{\otimes k}\simeq \operatorname{Perf}(X^{k})$
, we find the simplicial category
Next we introduce the augmented simplicial diagram of derived stacks
To spell this out, identifying
![]() $[n]=\{0,\ldots ,n\}$
with the
$[n]=\{0,\ldots ,n\}$
with the
![]() $(n+1)$
th roots of unity in
$(n+1)$
th roots of unity in
![]() $S^{1}$
, we take the relative mapping space
$S^{1}$
, we take the relative mapping space
The simplicial structure maps come from the cosimplicial structure of the sources
![]() $[n]{\hookrightarrow}S^{1}$
. Colloquially speaking, a point of
$[n]{\hookrightarrow}S^{1}$
. Colloquially speaking, a point of
![]() $Z_{n}$
is a necklace of
$Z_{n}$
is a necklace of
![]() $n+1$
points of
$n+1$
points of
![]() $X$
whose images in
$X$
whose images in
![]() $Y$
are connected by a cycle of paths; the simplicial structure maps come from forgetting or repeating points.
$Y$
are connected by a cycle of paths; the simplicial structure maps come from forgetting or repeating points.

Figure 1. Schematic illustration of
![]() $Z_{n}$
and
$Z_{n}$
and
![]() $W_{n}$
.
$W_{n}$
.
There is an evident fully faithful map of simplicial diagrams
where the simplicial structure maps of the latter are pushforwards. To identify the essential image, introduce the natural level-wise maps
obtained by taking relative diagonals, or colloquially speaking, breaking apart necklaces. Then by repeated application of Proposition 2.1.8, we have an identification of the essential image
Thus, we obtain an identification of simplicial diagrams
Now it remains to verify that the hypotheses of Theorem 2.4.1 and Corollary 2.4.2 are satisfied for the augmented simplicial diagram
(1) Proper simplicial maps, quasi-smooth face maps, and requisite Cartesian squares. Leaving aside support conditions for the moment, the augmented simplicial diagram
![]() $Z_{\bullet }\rightarrow LY$
is nothing more than the Cech nerve of the map
$Z_{\bullet }\rightarrow LY$
is nothing more than the Cech nerve of the map
![]() $Z_{0}=X\times _{Y}LY\rightarrow LY$
, which, in turn, is a base change of the map
$Z_{0}=X\times _{Y}LY\rightarrow LY$
, which, in turn, is a base change of the map
![]() $p:X\rightarrow Y$
. Thus, the face maps are proper and quasi-smooth (since
$p:X\rightarrow Y$
. Thus, the face maps are proper and quasi-smooth (since
![]() $p$
is proper and quasi-smooth), the degeneracy maps are also proper (since
$p$
is proper and quasi-smooth), the degeneracy maps are also proper (since
![]() $p$
is representable and separated), and the requisite squares are Cartesian (since
$p$
is representable and separated), and the requisite squares are Cartesian (since
![]() $Z_{\bullet }\rightarrow LY$
is a Cech nerve).
$Z_{\bullet }\rightarrow LY$
is a Cech nerve).
(2) Strictness condition. Proposition 3.3.8 below verifies that the strictness condition is satisfied.
(3) Conservativity. Let
![]() $p:Z_{0}=X\times _{Y}LY\rightarrow LY$
be the augmentation. Note that
$p:Z_{0}=X\times _{Y}LY\rightarrow LY$
be the augmentation. Note that
![]() $p$
is a representable proper map, so that applying [Reference Arinkin and GaitsgoryAG15, Theorem 7.2.8], we are reduced to verifying that
$p$
is a representable proper map, so that applying [Reference Arinkin and GaitsgoryAG15, Theorem 7.2.8], we are reduced to verifying that
However, this is precisely the definition of
![]() $\unicode[STIX]{x1D6EC}_{X/Y}$
.
$\unicode[STIX]{x1D6EC}_{X/Y}$
.
(4) Compact generation. We must also verify that
![]() $\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{n}}^{!}(Z_{n})$
is compactly generated for each
$\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{n}}^{!}(Z_{n})$
is compactly generated for each
![]() $n\geqslant 0$
. Imitating the above argument, we see that the essential image of
$n\geqslant 0$
. Imitating the above argument, we see that the essential image of
is precisely
![]() $\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{n}}^{!}(Z_{n})$
. Thus, it is enough to observe that each of
$\operatorname{QC}_{\unicode[STIX]{x1D6EC}_{n}}^{!}(Z_{n})$
. Thus, it is enough to observe that each of
![]() $\operatorname{QC}(X)\simeq \operatorname{QC}^{!}(X)$
and
$\operatorname{QC}(X)\simeq \operatorname{QC}^{!}(X)$
and
![]() $\operatorname{QC}^{!}(X\times _{Y}X)$
are compactly generated (recall our standing assumptions), and that all the monoidal/module structure maps preserve compact objects so that the various tensor products are also compactly generated. This latter assertion follows from the smoothness and properness assumptions that we have, as was already implicit in the formula (2).
$\operatorname{QC}^{!}(X\times _{Y}X)$
are compactly generated (recall our standing assumptions), and that all the monoidal/module structure maps preserve compact objects so that the various tensor products are also compactly generated. This latter assertion follows from the smoothness and properness assumptions that we have, as was already implicit in the formula (2).
This concludes the proof of Theorem 3.3.1 with the proof of Proposition 3.3.8 to appear below.◻
3.3.1 Analysis of support conditions
The goal of this and the next subsection is to establish Proposition 3.3.8. We continue with the notation introduced in the proof of Theorem 3.3.1. In this subsection, we record useful identifications of the support conditions
![]() $\unicode[STIX]{x1D6EC}_{n}\subset T^{\ast -1}Z_{n}$
, in particular, their geometric fibers over
$\unicode[STIX]{x1D6EC}_{n}\subset T^{\ast -1}Z_{n}$
, in particular, their geometric fibers over
![]() $Z_{n}$
.
$Z_{n}$
.
First, we record the following evident descriptions of the geometric points of
![]() $Z_{n}$
and
$Z_{n}$
and
![]() $W_{n}$
. Note that while
$W_{n}$
. Note that while
![]() $Y(k)$
is a space, the fiber product
$Y(k)$
is a space, the fiber product
![]() $(X\times _{Y}y)(k)$
for
$(X\times _{Y}y)(k)$
for
![]() $y\in Y(k)$
is, in fact, a set.
$y\in Y(k)$
is, in fact, a set.
Lemma 3.3.2. Each geometric point
![]() $\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow Z_{n}$
may be represented (not necessarily uniquely) as a tuple
$\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow Z_{n}$
may be represented (not necessarily uniquely) as a tuple
![]() $(y;x_{0},\ldots ,x_{n};\ell )$
where
$(y;x_{0},\ldots ,x_{n};\ell )$
where
Lemma 3.3.3. Each geometric point
![]() $\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow W_{n}$
may be represented (not necessarily uniquely) as a tuple
$\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow W_{n}$
may be represented (not necessarily uniquely) as a tuple
![]() $(y_{0},\ldots ,y_{n};x_{0},x_{0}^{\prime };\ldots ;x_{n},x_{n}^{\prime })$
, where
$(y_{0},\ldots ,y_{n};x_{0},x_{0}^{\prime };\ldots ;x_{n},x_{n}^{\prime })$
, where
In terms of such representatives, the map
![]() $q_{n}:Z_{n}\rightarrow W_{n}$
is given by
$q_{n}:Z_{n}\rightarrow W_{n}$
is given by
where
![]() $\ell \circ x_{0}\in (X\times _{Y}\{y\})(k)$
denotes the pair
$\ell \circ x_{0}\in (X\times _{Y}\{y\})(k)$
denotes the pair
![]() $(x_{0},y)\in (X\times \{y\})(k)$
but where the given identification
$(x_{0},y)\in (X\times \{y\})(k)$
but where the given identification
![]() $p(x_{0})\sim y\in Y(k)$
is twisted by the automorphism
$p(x_{0})\sim y\in Y(k)$
is twisted by the automorphism
![]() $\ell \in \operatorname{Aut}_{Y(k)(y)}$
.
$\ell \in \operatorname{Aut}_{Y(k)(y)}$
.
Next, we have the following description of the geometric fibers of
![]() $T^{\ast -1}Z_{n}\rightarrow Z_{n}$
.
$T^{\ast -1}Z_{n}\rightarrow Z_{n}$
.
Lemma 3.3.4. Fix a geometric point
![]() $\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow Z_{n}$
and a representative
$\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow Z_{n}$
and a representative
![]() $(y;x_{0},\ldots ,x_{n};\ell )$
of it. Then we have an identification of the fiber
$(y;x_{0},\ldots ,x_{n};\ell )$
of it. Then we have an identification of the fiber
 $$\begin{eqnarray}(T^{\ast -1}Z_{n})|_{\unicode[STIX]{x1D702}}=\left\{(v_{0},\ldots ,v_{n})\in (\unicode[STIX]{x1D6FA}_{Y}|_{y})^{\oplus (n+1)}:\begin{array}{@{}c@{}}(dp^{\ast })_{x_{0}}(d\ell ^{\ast }(v_{n}))=(dp^{\ast })_{x_{0}}(v_{0})\\ (dp^{\ast })_{x_{1}}(v_{0})=(dp^{\ast })_{x_{1}}(v_{1})\\ \cdots \\ (dp^{\ast })_{x_{n}}(v_{n-1})=(dp^{\ast })_{x_{n}}(v_{n})\end{array}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}(T^{\ast -1}Z_{n})|_{\unicode[STIX]{x1D702}}=\left\{(v_{0},\ldots ,v_{n})\in (\unicode[STIX]{x1D6FA}_{Y}|_{y})^{\oplus (n+1)}:\begin{array}{@{}c@{}}(dp^{\ast })_{x_{0}}(d\ell ^{\ast }(v_{n}))=(dp^{\ast })_{x_{0}}(v_{0})\\ (dp^{\ast })_{x_{1}}(v_{0})=(dp^{\ast })_{x_{1}}(v_{1})\\ \cdots \\ (dp^{\ast })_{x_{n}}(v_{n-1})=(dp^{\ast })_{x_{n}}(v_{n})\end{array}\right\}.\end{eqnarray}$$
Proof. Let us return to the necklace description of
![]() $Z_{n}$
where we place
$Z_{n}$
where we place
![]() $X$
at each vertex and
$X$
at each vertex and
![]() $Y$
along each edge so that
$Y$
along each edge so that
![]() $Z_{n}$
is the limit of the resulting finite diagram. Formation of cotangent complexes takes finite limits to finite colimits. Thus, the fiber
$Z_{n}$
is the limit of the resulting finite diagram. Formation of cotangent complexes takes finite limits to finite colimits. Thus, the fiber
![]() $\mathbb{L}_{Z_{n}}$
at a point is the colimit of the diagram where we place the appropriate fiber of
$\mathbb{L}_{Z_{n}}$
at a point is the colimit of the diagram where we place the appropriate fiber of
![]() $\mathbb{L}_{X}$
at each vertex and that of
$\mathbb{L}_{X}$
at each vertex and that of
![]() $\mathbb{L}_{Y}$
along each edge. Since
$\mathbb{L}_{Y}$
along each edge. Since
![]() $X$
and
$X$
and
![]() $Y$
are assumed to be smooth, we find that the fiber is the colimit of the diagram
$Y$
are assumed to be smooth, we find that the fiber is the colimit of the diagram

Taking homology gives the asserted description. ◻
Next, we record a similar though elementary description for the geometric fibers of
![]() $T^{\ast -1}W_{n}\rightarrow W_{n}$
.
$T^{\ast -1}W_{n}\rightarrow W_{n}$
.
Lemma 3.3.5. Fix a geometric point
![]() $\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow W_{n}$
and a representative
$\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow W_{n}$
and a representative
![]() $(y_{0},\ldots ,y_{n};x_{0},x_{0}^{\prime };\ldots ;x_{n},x_{n}^{\prime })$
of it. Then we have an identification of the fiber
$(y_{0},\ldots ,y_{n};x_{0},x_{0}^{\prime };\ldots ;x_{n},x_{n}^{\prime })$
of it. Then we have an identification of the fiber
 $$\begin{eqnarray}(T^{\ast -1}W_{n})|_{\unicode[STIX]{x1D702}}=\left\{(v_{0},\ldots ,v_{n})\in (\unicode[STIX]{x1D6FA}_{Y}|_{y})^{\oplus (n+1)}:\begin{array}{@{}c@{}}(dp^{\ast })_{x_{0}}(v_{0})=(dp^{\ast })_{x_{0}^{\prime }}(v_{0})=0\\ \cdots \\ (dp^{\ast })_{x_{n}}(v_{n})=(dp^{\ast })_{x_{n}^{\prime }}(v_{n})=0\end{array}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}(T^{\ast -1}W_{n})|_{\unicode[STIX]{x1D702}}=\left\{(v_{0},\ldots ,v_{n})\in (\unicode[STIX]{x1D6FA}_{Y}|_{y})^{\oplus (n+1)}:\begin{array}{@{}c@{}}(dp^{\ast })_{x_{0}}(v_{0})=(dp^{\ast })_{x_{0}^{\prime }}(v_{0})=0\\ \cdots \\ (dp^{\ast })_{x_{n}}(v_{n})=(dp^{\ast })_{x_{n}^{\prime }}(v_{n})=0\end{array}\right\}.\end{eqnarray}$$
Finally, we arrive at the following description of the geometric fibers of
![]() $\unicode[STIX]{x1D6EC}_{n}\rightarrow Z_{n}$
.
$\unicode[STIX]{x1D6EC}_{n}\rightarrow Z_{n}$
.
Lemma 3.3.6. Fix a geometric point
![]() $\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow Z_{n}$
and a representative
$\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow Z_{n}$
and a representative
![]() $(y;x_{0},\ldots ,x_{n};\ell )$
of it.
$(y;x_{0},\ldots ,x_{n};\ell )$
of it.
In terms of our previous identification of
![]() $(T^{\ast -1}Z_{n})_{\unicode[STIX]{x1D702}}$
, we have an identification of the fiber
$(T^{\ast -1}Z_{n})_{\unicode[STIX]{x1D702}}$
, we have an identification of the fiber
 $$\begin{eqnarray}(\unicode[STIX]{x1D6EC}_{n})|_{\unicode[STIX]{x1D702}}=\left\{(v_{0},\ldots ,v_{n})\in \unicode[STIX]{x1D6FA}_{Y}|_{y}^{\oplus (n+1)}:\begin{array}{@{}c@{}}(dp^{\ast })_{x_{0}}(d\ell ^{\ast }(v_{n}))=(dp^{\ast })_{x_{0}}(v_{0})=0\\ (dp^{\ast })_{x_{1}}(v_{0})=(dp^{\ast })_{x_{1}}(v_{1})=0\\ \cdots \\ (dp^{\ast })_{x_{n}}(v_{n-1})=(dp^{\ast })_{x_{n}}(v_{n})=0\end{array}\right\}\subset (T^{\ast -1}Z_{n})|_{\unicode[STIX]{x1D702}}.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6EC}_{n})|_{\unicode[STIX]{x1D702}}=\left\{(v_{0},\ldots ,v_{n})\in \unicode[STIX]{x1D6FA}_{Y}|_{y}^{\oplus (n+1)}:\begin{array}{@{}c@{}}(dp^{\ast })_{x_{0}}(d\ell ^{\ast }(v_{n}))=(dp^{\ast })_{x_{0}}(v_{0})=0\\ (dp^{\ast })_{x_{1}}(v_{0})=(dp^{\ast })_{x_{1}}(v_{1})=0\\ \cdots \\ (dp^{\ast })_{x_{n}}(v_{n-1})=(dp^{\ast })_{x_{n}}(v_{n})=0\end{array}\right\}\subset (T^{\ast -1}Z_{n})|_{\unicode[STIX]{x1D702}}.\end{eqnarray}$$
Proof. Let
![]() $\unicode[STIX]{x1D702}^{\prime }=q_{n}(\unicode[STIX]{x1D702})$
. Under our previous identifications, the pullback map
$\unicode[STIX]{x1D702}^{\prime }=q_{n}(\unicode[STIX]{x1D702})$
. Under our previous identifications, the pullback map
restricted to the fibers
is given by the identity
Thus, the assertion follows from our previous identifications. ◻
Remark 3.3.7. The previous lemmas state that
is cut out by the additional equations
3.3.2 Verification of strictness condition
We continue with the notation introduced in the proof of Theorem 3.3.1. Our goal is to complete the proof of the theorem by establishing the following.
Proposition 3.3.8. The diagram

is a strict Cartesian diagram of pairs.
We will prove the proposition in two steps: first for face maps in Lemma 3.3.9 and then in general.
Lemma 3.3.9. Proposition 3.3.8 holds when
![]() $g$
corresponds to a face map (order-preserving inclusion).
$g$
corresponds to a face map (order-preserving inclusion).
Proof. We will prove that the inclusion holds over each geometric point
![]() $\unicode[STIX]{x1D702}\in Z_{n+1}(k)$
via explicit formulas for the relevant subspaces of
$\unicode[STIX]{x1D702}\in Z_{n+1}(k)$
via explicit formulas for the relevant subspaces of
![]() $(T^{\ast -1}Z_{n+1})|_{\unicode[STIX]{x1D702}}$
. To do this, given any injection
$(T^{\ast -1}Z_{n+1})|_{\unicode[STIX]{x1D702}}$
. To do this, given any injection
![]() $\unicode[STIX]{x1D713}:[m]\rightarrow [n]$
, we will give a fiberwise description of the induced map
$\unicode[STIX]{x1D713}:[m]\rightarrow [n]$
, we will give a fiberwise description of the induced map
We will provide explicit formulas below, but first let us give a more informal description.
Informal description. Suppose
![]() $\unicode[STIX]{x1D702}\in Z_{n}(k)$
is represented by a tuple
$\unicode[STIX]{x1D702}\in Z_{n}(k)$
is represented by a tuple
![]() $(s;x_{0},\ldots ,x_{n};\ell )$
as in Lemma 3.3.2. Then its image
$(s;x_{0},\ldots ,x_{n};\ell )$
as in Lemma 3.3.2. Then its image
![]() $\bar{\unicode[STIX]{x1D702}}\in Z_{m}(k)$
is given by forgetting some
$\bar{\unicode[STIX]{x1D702}}\in Z_{m}(k)$
is given by forgetting some
![]() $x_{i}$
as prescribed by
$x_{i}$
as prescribed by
![]() $\unicode[STIX]{x1D713}$
. The map of fibers
$\unicode[STIX]{x1D713}$
. The map of fibers
is given in terms of a tuple
![]() $(v_{0},\ldots ,v_{m})$
as in Lemma 3.3.4 by repeating entries (as in the formula for
$(v_{0},\ldots ,v_{m})$
as in Lemma 3.3.4 by repeating entries (as in the formula for
![]() $(\tilde{g})!$
below) with
$(\tilde{g})!$
below) with
![]() $d\ell ^{\ast }$
inserted when looping around (as in the formula for
$d\ell ^{\ast }$
inserted when looping around (as in the formula for
![]() $(d_{0})^{!}$
below). The resulting element may be depicted graphically as follows:
$(d_{0})^{!}$
below). The resulting element may be depicted graphically as follows:
Here the arrows represent summands of the linear condition cutting out
![]() $(T^{\ast -1}Z_{m})|_{\unicode[STIX]{x1D702}}$
.
$(T^{\ast -1}Z_{m})|_{\unicode[STIX]{x1D702}}$
.
Formulas. Using the above description, at a geometric point
![]() $\unicode[STIX]{x1D702}\in Z_{n+1}(k)$
, we find that
$\unicode[STIX]{x1D702}\in Z_{n+1}(k)$
, we find that
 $$\begin{eqnarray}\displaystyle & & \displaystyle ((d_{0})^{!}\unicode[STIX]{x1D6EC}_{n})|_{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{(v_{0},\ldots ,v_{n+1})\in (\unicode[STIX]{x1D6FA}_{Y}|_{y})^{\oplus (n+1)}:\begin{array}{@{}c@{}}v_{0}=d\ell ^{\ast }(v_{n+1})\\ (d\unicode[STIX]{x1D70B}^{\ast })_{x_{i}}(v_{i-1})=(dp^{\ast })_{x_{i}}(v_{i})=0\quad \text{for }1\leqslant i\leqslant n+1\end{array}\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle ((d_{0})^{!}\unicode[STIX]{x1D6EC}_{n})|_{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{(v_{0},\ldots ,v_{n+1})\in (\unicode[STIX]{x1D6FA}_{Y}|_{y})^{\oplus (n+1)}:\begin{array}{@{}c@{}}v_{0}=d\ell ^{\ast }(v_{n+1})\\ (d\unicode[STIX]{x1D70B}^{\ast })_{x_{i}}(v_{i-1})=(dp^{\ast })_{x_{i}}(v_{i})=0\quad \text{for }1\leqslant i\leqslant n+1\end{array}\right\}.\nonumber\end{eqnarray}$$
For
![]() $\unicode[STIX]{x1D713}:[m]\rightarrow [n]$
the face map inducing
$\unicode[STIX]{x1D713}:[m]\rightarrow [n]$
the face map inducing
![]() $g$
, the simplicial map
$g$
, the simplicial map
![]() $\tilde{\unicode[STIX]{x1D713}}:[m+1]\rightarrow [n+1]$
inducing
$\tilde{\unicode[STIX]{x1D713}}:[m+1]\rightarrow [n+1]$
inducing
![]() $\tilde{g}$
is given by
$\tilde{g}$
is given by
![]() $\tilde{\unicode[STIX]{x1D713}}(0)=0$
and
$\tilde{\unicode[STIX]{x1D713}}(0)=0$
and
![]() $\tilde{\unicode[STIX]{x1D713}}(i)=1+\unicode[STIX]{x1D719}(i-1)$
, for
$\tilde{\unicode[STIX]{x1D713}}(i)=1+\unicode[STIX]{x1D719}(i-1)$
, for
![]() $i\geqslant 1$
. Let
$i\geqslant 1$
. Let
![]() $\operatorname{im}\tilde{\unicode[STIX]{x1D713}}\subset [n+1]$
denote the image of
$\operatorname{im}\tilde{\unicode[STIX]{x1D713}}\subset [n+1]$
denote the image of
![]() $\tilde{\unicode[STIX]{x1D713}}$
, and define
$\tilde{\unicode[STIX]{x1D713}}$
, and define
![]() $a:[n+1]\rightarrow \operatorname{im}\tilde{\unicode[STIX]{x1D713}}$
by setting
$a:[n+1]\rightarrow \operatorname{im}\tilde{\unicode[STIX]{x1D713}}$
by setting
![]() $a(i)=\sup \{\tilde{\unicode[STIX]{x1D713}}(j):\tilde{\unicode[STIX]{x1D713}}(j)\leqslant i\}$
. Then we find that
$a(i)=\sup \{\tilde{\unicode[STIX]{x1D713}}(j):\tilde{\unicode[STIX]{x1D713}}(j)\leqslant i\}$
. Then we find that
 $$\begin{eqnarray}\displaystyle & & \displaystyle ((\tilde{g})^{!}\unicode[STIX]{x1D6EC}_{m+1})|_{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{(v_{0},\ldots ,v_{n+1})\in (\unicode[STIX]{x1D6FA}_{Y}|_{y})^{\oplus (n+1)}:\begin{array}{@{}c@{}}v_{i}=v_{a(i)},\text{ for }i\in [n+1]\setminus \operatorname{im}\tilde{\unicode[STIX]{x1D713}}\\ (dp^{\ast })_{x_{i}}(v_{i-1})=(d\unicode[STIX]{x1D70B}^{\ast })_{x_{i}}(v_{i})=0,\text{ for }i\in \operatorname{im}\tilde{\unicode[STIX]{x1D713}}\end{array}\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle ((\tilde{g})^{!}\unicode[STIX]{x1D6EC}_{m+1})|_{\unicode[STIX]{x1D702}}\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{(v_{0},\ldots ,v_{n+1})\in (\unicode[STIX]{x1D6FA}_{Y}|_{y})^{\oplus (n+1)}:\begin{array}{@{}c@{}}v_{i}=v_{a(i)},\text{ for }i\in [n+1]\setminus \operatorname{im}\tilde{\unicode[STIX]{x1D713}}\\ (dp^{\ast })_{x_{i}}(v_{i-1})=(d\unicode[STIX]{x1D70B}^{\ast })_{x_{i}}(v_{i})=0,\text{ for }i\in \operatorname{im}\tilde{\unicode[STIX]{x1D713}}\end{array}\right\}.\nonumber\end{eqnarray}$$
Since
![]() $0\in \operatorname{im}\tilde{\unicode[STIX]{x1D713}}$
, we conclude that
$0\in \operatorname{im}\tilde{\unicode[STIX]{x1D713}}$
, we conclude that
We are now ready to complete the proof of Proposition 3.3.8 for an arbitrary simplicial structure map.
Proof of Proposition 3.3.8.
Let
![]() $\unicode[STIX]{x1D713}:[m]\rightarrow [n]$
be the simplicial map inducing
$\unicode[STIX]{x1D713}:[m]\rightarrow [n]$
be the simplicial map inducing
![]() $g$
. It uniquely factors
$g$
. It uniquely factors
as a surjection followed by an injection. This gives rise to an extended diagram

where
![]() $p$
corresponds to the injection
$p$
corresponds to the injection
![]() $\unicode[STIX]{x1D704}$
, and
$\unicode[STIX]{x1D704}$
, and
![]() $q$
corresponds to the surjection
$q$
corresponds to the surjection
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
We need to show that the large square satisfies the required strictness. By the previous lemma, we know that the top square satisfies the required strictness. Thus, it suffices to show that
![]() $(\tilde{q})^{!}\unicode[STIX]{x1D6EC}_{m+1}=\unicode[STIX]{x1D6EC}_{k+1}$
since then
$(\tilde{q})^{!}\unicode[STIX]{x1D6EC}_{m+1}=\unicode[STIX]{x1D6EC}_{k+1}$
since then
and we are reduced to applying the previous lemma to the top square.
To do this, as in the proof of the previous lemma, over each geometric point
![]() $\unicode[STIX]{x1D702}\in Z_{k+1}(k)$
, we will give a description of the induced map of fibers
$\unicode[STIX]{x1D702}\in Z_{k+1}(k)$
, we will give a description of the induced map of fibers
Define
![]() $\unicode[STIX]{x1D70B}^{\prime }:[k]\rightarrow [m]$
to be the section of
$\unicode[STIX]{x1D70B}^{\prime }:[k]\rightarrow [m]$
to be the section of
![]() $\unicode[STIX]{x1D70B}$
given by its break points
$\unicode[STIX]{x1D70B}$
given by its break points
Then, in terms of the identifications of Lemma 3.3.4, the pullback map admits the description
Note that this is no longer a closed immersion, and instead admits a section by repeating terms.
It is now elementary to see that
![]() $(\tilde{q})^{!}\unicode[STIX]{x1D6EC}_{m+1}=\unicode[STIX]{x1D6EC}_{k+1}$
. On the one hand, the inclusion
$(\tilde{q})^{!}\unicode[STIX]{x1D6EC}_{m+1}=\unicode[STIX]{x1D6EC}_{k+1}$
. On the one hand, the inclusion
![]() $(\tilde{q})^{!}\unicode[STIX]{x1D6EC}_{m+1}\subset \unicode[STIX]{x1D6EC}_{k+1}$
is evident. On the other hand, the inclusion
$(\tilde{q})^{!}\unicode[STIX]{x1D6EC}_{m+1}\subset \unicode[STIX]{x1D6EC}_{k+1}$
is evident. On the other hand, the inclusion
![]() $(\tilde{q})^{!}\unicode[STIX]{x1D6EC}_{m+1}\supset \unicode[STIX]{x1D6EC}_{k+1}$
follows from the fact that the noted section takes
$(\tilde{q})^{!}\unicode[STIX]{x1D6EC}_{m+1}\supset \unicode[STIX]{x1D6EC}_{k+1}$
follows from the fact that the noted section takes
![]() $\unicode[STIX]{x1D6EC}_{k+1}$
into
$\unicode[STIX]{x1D6EC}_{k+1}$
into
![]() $\unicode[STIX]{x1D6EC}_{m+1}$
.
$\unicode[STIX]{x1D6EC}_{m+1}$
.
This completes the proof of Proposition 3.3.8 and, in turn, that of Theorem 3.3.1. ◻
3.4 Centers of convolution categories
Corollary 3.2.2 states that
![]() $\operatorname{DCoh}(X\times _{Y}X)$
is like a ‘matrix’ or endomorphism algebra for
$\operatorname{DCoh}(X\times _{Y}X)$
is like a ‘matrix’ or endomorphism algebra for
![]() $\operatorname{Perf}(X)$
over
$\operatorname{Perf}(X)$
over
![]() $\operatorname{Perf}(Y)$
. In linear algebra, it is not hard to show that the center/Hochschild cohomology of
$\operatorname{Perf}(Y)$
. In linear algebra, it is not hard to show that the center/Hochschild cohomology of
![]() $\operatorname{End}_{R}(M)$
will be the same as that of
$\operatorname{End}_{R}(M)$
will be the same as that of
![]() $R$
so long as
$R$
so long as
![]() $M$
‘sees’ all of
$M$
‘sees’ all of
![]() $R$
(e.g. if
$R$
(e.g. if
![]() $R$
is a retract of
$R$
is a retract of
![]() $M$
). The main result of this section will be a categorified version of this in the special case of convolution categories. The proof will not so abstract, but rather will use the ‘functional analysis’ for categories such as
$M$
). The main result of this section will be a categorified version of this in the special case of convolution categories. The proof will not so abstract, but rather will use the ‘functional analysis’ for categories such as
![]() $\operatorname{DCoh}$
developed in [Reference Ben-Zvi, Nadler and PreygelBNP].
$\operatorname{DCoh}$
developed in [Reference Ben-Zvi, Nadler and PreygelBNP].
To explain the situation, let us start with
![]() $p:X\rightarrow Y$
a surjective map of perfect stacks.
$p:X\rightarrow Y$
a surjective map of perfect stacks.
Observe that the loop space
![]() $LY=\operatorname{Map}(S^{1},Y)$
comes equipped with a natural basepoint map
$LY=\operatorname{Map}(S^{1},Y)$
comes equipped with a natural basepoint map
![]() $e:LY\rightarrow Y$
as well as rotational
$e:LY\rightarrow Y$
as well as rotational
![]() $S^{1}$
-action. We fix once and for all the identification
$S^{1}$
-action. We fix once and for all the identification
so that
![]() $e$
corresponds to the first projection (which is equivalent to the second projection, though in two different ways).
$e$
corresponds to the first projection (which is equivalent to the second projection, though in two different ways).
The category
![]() $\operatorname{QC}(LY)$
has a natural
$\operatorname{QC}(LY)$
has a natural
![]() $E_{2}$
-monoidal structure and the pushforward functor
$E_{2}$
-monoidal structure and the pushforward functor
realizes
![]() $\operatorname{QC}(LY)$
as the center of
$\operatorname{QC}(LY)$
as the center of
![]() $\operatorname{QC}(Y)$
. More generally, recall the fundamental correspondence
$\operatorname{QC}(Y)$
. More generally, recall the fundamental correspondence
The pullback–pushforward functor
also realizes
![]() $\operatorname{QC}(LY)$
as the center of
$\operatorname{QC}(LY)$
as the center of
![]() $\operatorname{QC}(X\times _{Y}X)$
.
$\operatorname{QC}(X\times _{Y}X)$
.
For the above assertions, see [Reference Ben-Zvi, Francis and NadlerBFN10]. In the following, we give an outline of a proof.
Let us recall some generalities seen in the proof of Theorem 3.3.1. For notational convenience, set
![]() ${\mathcal{A}}=\operatorname{QC}(X\times _{Y}X)$
and
${\mathcal{A}}=\operatorname{QC}(X\times _{Y}X)$
and
![]() ${\mathcal{B}}=\operatorname{QC}(X)$
. Observe that pushforward along the relative diagonal
${\mathcal{B}}=\operatorname{QC}(X)$
. Observe that pushforward along the relative diagonal
![]() $\unicode[STIX]{x1D6E5}_{\ast }:{\mathcal{B}}\rightarrow {\mathcal{A}}$
is monoidal, and thus we may regard
$\unicode[STIX]{x1D6E5}_{\ast }:{\mathcal{B}}\rightarrow {\mathcal{A}}$
is monoidal, and thus we may regard
![]() ${\mathcal{A}}$
as an algebra in
${\mathcal{A}}$
as an algebra in
![]() ${\mathcal{B}}$
-bimodules.
${\mathcal{B}}$
-bimodules.
Given an algebra
![]() ${\mathcal{A}}$
in
${\mathcal{A}}$
in
![]() ${\mathcal{B}}$
-bimodules, we have its relative bar resolution
${\mathcal{B}}$
-bimodules, we have its relative bar resolution
which can be used to calculate its center
We will access the center as the totalization of the cosimplicial object
Unwinding the notation and using the canonical identity
![]() $\operatorname{QC}(X)^{\otimes k}\simeq \operatorname{QC}(X^{k})$
, we find the cosimplicial category
$\operatorname{QC}(X)^{\otimes k}\simeq \operatorname{QC}(X^{k})$
, we find the cosimplicial category
Using the canonical identity of functors with integral transforms, we find further
where the cosimplicial structure maps are given by
![]() $\ast$
-pullback functors. Thus, with any assumptions for which descent holds (see, for example, Corollary 2.4.3), one has the identification
$\ast$
-pullback functors. Thus, with any assumptions for which descent holds (see, for example, Corollary 2.4.3), one has the identification
Now let us return to small categories of coherent sheaves. Suppose now that
![]() $X$
and
$X$
and
![]() $Y$
are smooth and
$Y$
are smooth and
![]() $p:X\rightarrow Y$
is proper and surjective. Observe that the
$p:X\rightarrow Y$
is proper and surjective. Observe that the
![]() $E_{2}$
-monoidal structure on
$E_{2}$
-monoidal structure on
![]() $\operatorname{QC}(LY)$
preserves the full subcategory
$\operatorname{QC}(LY)$
preserves the full subcategory
of coherent complexes with support proper over
![]() $Y$
(or, equivalently, proper over
$Y$
(or, equivalently, proper over
![]() $Y$
with respect to the second projection). It consists precisely of those complexes taken via
$Y$
with respect to the second projection). It consists precisely of those complexes taken via
![]() $e_{\ast }$
to the full subcategory
$e_{\ast }$
to the full subcategory
![]() $\operatorname{Perf}Y\subset \operatorname{QC}(Y)$
.
$\operatorname{Perf}Y\subset \operatorname{QC}(Y)$
.
Theorem 3.4.1. Let
![]() $X,Y$
be smooth and
$X,Y$
be smooth and
![]() $p:X\rightarrow Y$
be proper and surjective.
$p:X\rightarrow Y$
be proper and surjective.
There is a natural
![]() $E_{2}$
-identification
$E_{2}$
-identification
Proof. As explained above, via the relative bar resolution for the monoidal map
![]() $\unicode[STIX]{x1D6E5}_{\ast }:\operatorname{QC}(X)\rightarrow \operatorname{QC}(X\times _{Y}X)$
, we may calculate
$\unicode[STIX]{x1D6E5}_{\ast }:\operatorname{QC}(X)\rightarrow \operatorname{QC}(X\times _{Y}X)$
, we may calculate
![]() $\mathit{Z}(\operatorname{QC}(X\times _{Y}X))$
as the totalization of the cosimplicial diagram
$\mathit{Z}(\operatorname{QC}(X\times _{Y}X))$
as the totalization of the cosimplicial diagram
Likewise, via the relative bar resolution for the monoidal map
![]() $\unicode[STIX]{x1D6E5}_{\ast }:\operatorname{Perf}X\rightarrow \operatorname{DCoh}(X\times _{Y}X)$
, we may calculate
$\unicode[STIX]{x1D6E5}_{\ast }:\operatorname{Perf}X\rightarrow \operatorname{DCoh}(X\times _{Y}X)$
, we may calculate
![]() $\mathit{Z}(\operatorname{DCoh}(X\times _{Y}X))$
as the totalization of the cosimplicial diagram
$\mathit{Z}(\operatorname{DCoh}(X\times _{Y}X))$
as the totalization of the cosimplicial diagram
By [Reference Ben-Zvi, Nadler and PreygelBNP, § 5.3], the natural map of cosimplicial diagrams
is fully faithful at each term and, thus, we have a fully faithful inclusion
The essential image consists of objects that land in
![]() $c^{0}\subset {\mathcal{C}}^{0}$
under the coaugmentation map
$c^{0}\subset {\mathcal{C}}^{0}$
under the coaugmentation map
![]() $\operatorname{Tot}{\mathcal{C}}^{\bullet }\rightarrow {\mathcal{C}}^{0}$
. In other words, it consists of
$\operatorname{Tot}{\mathcal{C}}^{\bullet }\rightarrow {\mathcal{C}}^{0}$
. In other words, it consists of
![]() $\mathscr{F}\in \operatorname{QC}(LY)$
such that
$\mathscr{F}\in \operatorname{QC}(LY)$
such that
![]() $\unicode[STIX]{x1D6FF}_{\ast }p^{\ast }\mathscr{F}\in \operatorname{QC}(X\times _{Y}X)$
, in fact, lies in
$\unicode[STIX]{x1D6FF}_{\ast }p^{\ast }\mathscr{F}\in \operatorname{QC}(X\times _{Y}X)$
, in fact, lies in
![]() $\operatorname{DCoh}(X\times _{Y}X)$
. We must check that this is equivalent to
$\operatorname{DCoh}(X\times _{Y}X)$
. We must check that this is equivalent to
![]() $\mathscr{F}\in \operatorname{DCoh}_{\text{prop}/Y}(LY)$
.
$\mathscr{F}\in \operatorname{DCoh}_{\text{prop}/Y}(LY)$
.
First, note that
![]() $\mathscr{F}\in \operatorname{DCoh}(LY)$
if and only if
$\mathscr{F}\in \operatorname{DCoh}(LY)$
if and only if
![]() $p^{\ast }\mathscr{F}\in \operatorname{DCoh}(X\times _{Y}LY)$
.
$p^{\ast }\mathscr{F}\in \operatorname{DCoh}(X\times _{Y}LY)$
.
Let us write
![]() $W\subset LY$
for the support of
$W\subset LY$
for the support of
![]() $\mathscr{F}$
so that
$\mathscr{F}$
so that
![]() $p^{-1}W=X\times _{Y}W\subset X\times _{Y}LY$
is the support of
$p^{-1}W=X\times _{Y}W\subset X\times _{Y}LY$
is the support of
![]() $p^{\ast }\mathscr{F}$
. Note that
$p^{\ast }\mathscr{F}$
. Note that
![]() $W\rightarrow Y$
is proper if and only if
$W\rightarrow Y$
is proper if and only if
![]() $p^{-1}W\rightarrow Y$
is proper since
$p^{-1}W\rightarrow Y$
is proper since
![]() $X\rightarrow Y$
is proper.
$X\rightarrow Y$
is proper.
Since
![]() $\unicode[STIX]{x1D6FF}$
is affine, we have that
$\unicode[STIX]{x1D6FF}$
is affine, we have that
![]() $\unicode[STIX]{x1D6FF}_{\ast }p^{\ast }\mathscr{F}\in \operatorname{DCoh}(X\times _{Y}X)$
if and only if
$\unicode[STIX]{x1D6FF}_{\ast }p^{\ast }\mathscr{F}\in \operatorname{DCoh}(X\times _{Y}X)$
if and only if
![]() $p^{\ast }\mathscr{F}\in \operatorname{DCoh}(X\times _{Y}LY)$
and
$p^{\ast }\mathscr{F}\in \operatorname{DCoh}(X\times _{Y}LY)$
and
![]() $p^{-1}W\rightarrow X\times _{Y}X$
is proper.
$p^{-1}W\rightarrow X\times _{Y}X$
is proper.
Finally, consider the diagram
where the second map is proper since
![]() $X\rightarrow Y$
is proper. Thus,
$X\rightarrow Y$
is proper. Thus,
![]() $p^{-1}W\rightarrow X\times _{Y}X$
is proper if and only if
$p^{-1}W\rightarrow X\times _{Y}X$
is proper if and only if
![]() $p^{-1}W\rightarrow Y$
and, hence,
$p^{-1}W\rightarrow Y$
and, hence,
![]() $W\rightarrow Y$
is proper.
$W\rightarrow Y$
is proper.
We conclude that
![]() $\unicode[STIX]{x1D6FF}_{\ast }p^{\ast }\mathscr{F}\in \operatorname{DCoh}(X\times _{Y}X)$
if and only if
$\unicode[STIX]{x1D6FF}_{\ast }p^{\ast }\mathscr{F}\in \operatorname{DCoh}(X\times _{Y}X)$
if and only if
![]() $\mathscr{F}\in \operatorname{DCoh}(LY)$
with proper support over
$\mathscr{F}\in \operatorname{DCoh}(LY)$
with proper support over
![]() $Y$
.◻
$Y$
.◻
Remark 3.4.2. Since the theorem is the restriction of the parallel result for quasi-coherent sheaves, the central functor
is given by the pullback–pushforward functor
![]() $p_{\ast }\unicode[STIX]{x1D6FF}^{\ast }$
along the fundamental correspondence
$p_{\ast }\unicode[STIX]{x1D6FF}^{\ast }$
along the fundamental correspondence
4 Application: affine Hecke category
We turn now to our motivating application for the development of the preceding theory.
4.1 Global affine Hecke category
Let
![]() $G$
be a complex reductive group and
$G$
be a complex reductive group and
![]() $B\subset G$
a Borel subgroup. Let
$B\subset G$
a Borel subgroup. Let
![]() $q:BB\rightarrow BG$
denote the natural induction map of classifying stacks. Passing to loop spaces, we obtain the Grothendieck–Springer map of adjoint quotients
$q:BB\rightarrow BG$
denote the natural induction map of classifying stacks. Passing to loop spaces, we obtain the Grothendieck–Springer map of adjoint quotients
where
![]() $\widetilde{G}$
classifies pairs of a Borel subgroup
$\widetilde{G}$
classifies pairs of a Borel subgroup
![]() $B^{\prime }\subset G$
and a group element
$B^{\prime }\subset G$
and a group element
![]() $g\in B^{\prime }$
, and
$g\in B^{\prime }$
, and
![]() $Lq$
projects to the group element and forgets the Borel subgroup.
$Lq$
projects to the group element and forgets the Borel subgroup.
Now we apply the preceding theory with
![]() $X=B/B$
,
$X=B/B$
,
![]() $Y=G/G$
, and
$Y=G/G$
, and
![]() $p=Lq$
. Note that
$p=Lq$
. Note that
![]() $X=B/B$
and
$X=B/B$
and
![]() $Y=G/G$
are smooth, and
$Y=G/G$
are smooth, and
![]() $p:B/B\rightarrow G/G$
is proper. Note as well that our starting point already involves loop spaces, though that structure plays no role with respect to our general results.
$p:B/B\rightarrow G/G$
is proper. Note as well that our starting point already involves loop spaces, though that structure plays no role with respect to our general results.
Definition 4.1.1. Let
![]() $G$
be a complex reductive group and
$G$
be a complex reductive group and
![]() $B\subset G$
a Borel subgroup.
$B\subset G$
a Borel subgroup.
-
(i) The global Steinberg stack is the fiber product
 $$\begin{eqnarray}\text{St}_{G}=B/B\times _{G/G}B/B.\end{eqnarray}$$
$$\begin{eqnarray}\text{St}_{G}=B/B\times _{G/G}B/B.\end{eqnarray}$$
-
(ii) The global affine Hecke category is the small stable monoidal category
 $$\begin{eqnarray}{\mathcal{H}}_{G}^{\text{aff}}=\operatorname{DCoh}(\text{St}_{G}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}_{G}^{\text{aff}}=\operatorname{DCoh}(\text{St}_{G}).\end{eqnarray}$$
Applying Corollary 3.2.2, we immediately obtain the following theorem.
Theorem 4.1.2. There is a natural monoidal equivalence
compatible with actions on the module
![]() $\operatorname{Perf}(B/B)$
.
$\operatorname{Perf}(B/B)$
.
4.2 Local systems
One can interpret the loop space
![]() $L(BG)\simeq G/G$
as the moduli stack of
$L(BG)\simeq G/G$
as the moduli stack of
![]() $G$
-local systems on the circle
$G$
-local systems on the circle
![]() $S^{1}$
. Similarly, one can interpret the global Steinberg stack
$S^{1}$
. Similarly, one can interpret the global Steinberg stack
![]() $\text{St}_{G}$
as the moduli of
$\text{St}_{G}$
as the moduli of
![]() $G$
-local systems on the cylinder
$G$
-local systems on the cylinder
![]() $S^{1}\times I$
with
$S^{1}\times I$
with
![]() $B$
-reductions at the boundary circles
$B$
-reductions at the boundary circles
![]() $S^{1}\times \unicode[STIX]{x2202}I$
.
$S^{1}\times \unicode[STIX]{x2202}I$
.
Definition 4.2.1. The commuting stack
![]() $\operatorname{Loc}_{G}(T)$
is the moduli of
$\operatorname{Loc}_{G}(T)$
is the moduli of
![]() $G$
-local systems on the two-torus
$G$
-local systems on the two-torus
![]() $T=S^{1}\times S^{1}$
or, equivalently, the twice-iterated loop space
$T=S^{1}\times S^{1}$
or, equivalently, the twice-iterated loop space
Remark 4.2.2. The name commuting stack comes from the presentation
One should be careful to understand that the commutator equation needs to be imposed in a derived sense.
Let
![]() $\mathfrak{g}$
denote the Lie algebra of
$\mathfrak{g}$
denote the Lie algebra of
![]() $G$
. The fiber of the cotangent complex of
$G$
. The fiber of the cotangent complex of
![]() $\operatorname{Loc}_{G}(T)$
at a local system
$\operatorname{Loc}_{G}(T)$
at a local system
![]() $\mathscr{P}$
can be calculated by the de Rham cochains
$\mathscr{P}$
can be calculated by the de Rham cochains
![]() $C^{\ast }(T,\mathfrak{g}_{\mathscr{P}}^{\ast })[1]$
, where
$C^{\ast }(T,\mathfrak{g}_{\mathscr{P}}^{\ast })[1]$
, where
![]() $\mathfrak{g}_{\mathscr{P}}^{\ast }$
denotes the coadjoint bundle of
$\mathfrak{g}_{\mathscr{P}}^{\ast }$
denotes the coadjoint bundle of
![]() $\mathscr{P}$
. Focusing on the degree
$\mathscr{P}$
. Focusing on the degree
![]() $-1$
term coming from the commutator equation, we see that there is a natural map
$-1$
term coming from the commutator equation, we see that there is a natural map
Let
![]() $\mathfrak{h}$
denote the Lie algebra of the universal Cartan of
$\mathfrak{h}$
denote the Lie algebra of the universal Cartan of
![]() $G$
, and
$G$
, and
![]() $W$
the Weyl group. Recall the dual characteristic polynomial map or, equivalently, the projection to the coadjoint quotient
$W$
the Weyl group. Recall the dual characteristic polynomial map or, equivalently, the projection to the coadjoint quotient
Definition 4.2.3. The global nilpotent cone
![]() $\mathscr{N}\subset T_{\operatorname{Loc}_{G}(T)}^{\ast -1}$
is the conic closed subset given by the inverse-image of zero under the composition
$\mathscr{N}\subset T_{\operatorname{Loc}_{G}(T)}^{\ast -1}$
is the conic closed subset given by the inverse-image of zero under the composition
4.3 Center of affine Hecke category
Starting from the loop space
![]() $\operatorname{Loc}_{G}(S^{1})\simeq L(BG)\simeq G/G$
, we have arrived at the commuting stack
$\operatorname{Loc}_{G}(S^{1})\simeq L(BG)\simeq G/G$
, we have arrived at the commuting stack
![]() $\operatorname{Loc}_{G}(T)\simeq L(L(BG))$
by taking loops again. Thus there is a natural asymmetry to the construction: we will distinguish the projection to the first loop or, in other words, the basepoint of the second loop
$\operatorname{Loc}_{G}(T)\simeq L(L(BG))$
by taking loops again. Thus there is a natural asymmetry to the construction: we will distinguish the projection to the first loop or, in other words, the basepoint of the second loop
Following our general results, we introduce the full subcategory
of coherent complexes with proper support along the projection to the first loop.
Applying Corollary 3.4.1, we immediately obtain the following theorem.
Theorem 4.3.1. There is a natural
![]() $E_{2}$
-monoidal identification of the center
$E_{2}$
-monoidal identification of the center
Remark 4.3.2. The description of the center is manifestly not
![]() $\operatorname{SL}_{2}(\mathbb{Z})$
-equivariant in contrast to that of the trace calculated below.
$\operatorname{SL}_{2}(\mathbb{Z})$
-equivariant in contrast to that of the trace calculated below.
4.4 Trace of affine Hecke category
Recall that we have introduced the global nilpotent cone
![]() $\mathscr{N}\subset T_{\operatorname{Loc}_{G}(T)}^{\ast -1}$
, and can consider the corresponding full subcategory
$\mathscr{N}\subset T_{\operatorname{Loc}_{G}(T)}^{\ast -1}$
, and can consider the corresponding full subcategory
of coherent complexes supported along it. All of these constructions are manifestly
![]() $\operatorname{SL}_{2}(\mathbb{Z})$
-equivariant.
$\operatorname{SL}_{2}(\mathbb{Z})$
-equivariant.
Theorem 4.4.1. There is a canonical
![]() $S^{1}$
-equivariant identification of the trace
$S^{1}$
-equivariant identification of the trace
Proof. Set
![]() $X=L(BB)\simeq B/B$
,
$X=L(BB)\simeq B/B$
,
![]() $Y=L(BG)\simeq G/G$
, and
$Y=L(BG)\simeq G/G$
, and
![]() $p=Lq$
for
$p=Lq$
for
![]() $q:BB\rightarrow BG$
.
$q:BB\rightarrow BG$
.
Applying Theorem 3.3.1, it remains to identify the support condition
![]() $\unicode[STIX]{x1D6EC}_{X/Y}\subset T_{LY}^{\ast -1}$
as described therein with the global nilpotent locus
$\unicode[STIX]{x1D6EC}_{X/Y}\subset T_{LY}^{\ast -1}$
as described therein with the global nilpotent locus
![]() $\mathscr{N}\subset T_{\operatorname{Loc}_{G}(T)}^{\ast -1}$
.
$\mathscr{N}\subset T_{\operatorname{Loc}_{G}(T)}^{\ast -1}$
.
Recall
![]() $\mathfrak{g}$
denotes the Lie algebra of
$\mathfrak{g}$
denotes the Lie algebra of
![]() $G$
. Let
$G$
. Let
![]() $\mathfrak{b}$
denote the Lie algebra of
$\mathfrak{b}$
denote the Lie algebra of
![]() $B$
. Let
$B$
. Let
![]() $N\subset B$
denote the maximal unipotent subgroup, and
$N\subset B$
denote the maximal unipotent subgroup, and
![]() $\mathfrak{n}$
its Lie algebra. Fix an invariant inner product on
$\mathfrak{n}$
its Lie algebra. Fix an invariant inner product on
![]() $\mathfrak{g}$
, so that we have an identification
$\mathfrak{g}$
, so that we have an identification
![]() $\mathfrak{g}\simeq \mathfrak{g}^{\ast }$
and, in particular, an identification
$\mathfrak{g}\simeq \mathfrak{g}^{\ast }$
and, in particular, an identification
![]() $\mathfrak{n}=\ker (\mathfrak{g}^{\ast }\rightarrow \mathfrak{b}^{\ast })$
.
$\mathfrak{n}=\ker (\mathfrak{g}^{\ast }\rightarrow \mathfrak{b}^{\ast })$
.
Fix a geometric point
![]() $\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow \operatorname{Loc}_{G}(T)\simeq L(L(BG))$
given by a pair of commuting elements
$\unicode[STIX]{x1D702}:\operatorname{Spec}k\rightarrow \operatorname{Loc}_{G}(T)\simeq L(L(BG))$
given by a pair of commuting elements
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\in G\times G$
. Note that the intermediate stack
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\in G\times G$
. Note that the intermediate stack
![]() $LY\times _{Y}X$
is the moduli of
$LY\times _{Y}X$
is the moduli of
![]() $G$
-bundles on
$G$
-bundles on
![]() $S^{1}\times S^{1}$
with a
$S^{1}\times S^{1}$
with a
![]() $B$
-reduction along the first loop. Thus, we have the identifications:
$B$
-reduction along the first loop. Thus, we have the identifications:
Recall that
![]() $v\in \mathfrak{g}^{\ast }\simeq \mathfrak{g}$
is nilpotent if and only if there exists
$v\in \mathfrak{g}^{\ast }\simeq \mathfrak{g}$
is nilpotent if and only if there exists
![]() $g\in G$
such that
$g\in G$
such that
![]() $\operatorname{ad}_{g}v\in \mathfrak{n}$
. Thus we clearly have the containment:
$\operatorname{ad}_{g}v\in \mathfrak{n}$
. Thus we clearly have the containment:
Thus, it is sufficient to show that two commuting elements
![]() $v\in \mathfrak{g}$
,
$v\in \mathfrak{g}$
,
![]() $\unicode[STIX]{x1D6FC}\in G$
with
$\unicode[STIX]{x1D6FC}\in G$
with
![]() $v$
nilpotent are contained in a Borel subgroup
$v$
nilpotent are contained in a Borel subgroup
![]() $B\subset G$
. Equivalently, it is sufficient to show two such elements simultaneously fix a point of the flag variety
$B\subset G$
. Equivalently, it is sufficient to show two such elements simultaneously fix a point of the flag variety
![]() $G/B$
. Note that a nilpotent element
$G/B$
. Note that a nilpotent element
![]() $v\in \mathfrak{g}$
generates an
$v\in \mathfrak{g}$
generates an
![]() $\mathbb{A}^{1}$
-action on
$\mathbb{A}^{1}$
-action on
![]() $G/B$
, and the action preserves the fixed points of the element
$G/B$
, and the action preserves the fixed points of the element
![]() $\unicode[STIX]{x1D6FC}\in G$
. Since the fixed points of
$\unicode[STIX]{x1D6FC}\in G$
. Since the fixed points of
![]() $\unicode[STIX]{x1D6FC}$
are a non-empty projective variety, the
$\unicode[STIX]{x1D6FC}$
are a non-empty projective variety, the
![]() $\mathbb{A}^{1}$
-action must have a fixed point. This concludes the proof.◻
$\mathbb{A}^{1}$
-action must have a fixed point. This concludes the proof.◻
Remark 4.4.2. Note that the map
![]() $\operatorname{Loc}_{B}(T)\rightarrow \operatorname{Loc}_{G}(T)$
is not necessarily surjective, even though
$\operatorname{Loc}_{B}(T)\rightarrow \operatorname{Loc}_{G}(T)$
is not necessarily surjective, even though
![]() $B/B\rightarrow G/G$
always is. For example, consider
$B/B\rightarrow G/G$
always is. For example, consider
![]() $G=\operatorname{PGL}_{2}$
and two commuting elements
$G=\operatorname{PGL}_{2}$
and two commuting elements
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \operatorname{PGL}_{2}$
that are not contained in any Borel subgroup
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\in \operatorname{PGL}_{2}$
that are not contained in any Borel subgroup
![]() $B\subset G$
. However, if the derived group of
$B\subset G$
. However, if the derived group of
![]() $G$
is simply connected, then the map is in fact surjective. In this case, one can derive the global nilpotent cone
$G$
is simply connected, then the map is in fact surjective. In this case, one can derive the global nilpotent cone
![]() $\mathscr{N}\subset T_{\operatorname{Loc}_{G}(T)}^{\ast -1}$
directly from the map
$\mathscr{N}\subset T_{\operatorname{Loc}_{G}(T)}^{\ast -1}$
directly from the map
![]() $\operatorname{Loc}_{B}(T)\rightarrow \operatorname{Loc}_{G}(T)$
.
$\operatorname{Loc}_{B}(T)\rightarrow \operatorname{Loc}_{G}(T)$
.
Acknowledgements
We thank an anonymous referee for many helpful comments and suggestions about the exposition.
We gratefully acknowledge the support of NSF grants DMS-1103525 (DBZ), DMS-1319287 (DN), and an NSF Postdoctoral Fellowship (AP).