Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-04-30T12:01:43.986Z Has data issue: false hasContentIssue false
  • English
  • Français

Simple zeros of automorphic 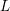$L$-functions

Part of: Discontinuous groups and automorphic forms Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  30 May 2019

Andrew R. Booker ,
Peter J. Cho  and
Myoungil Kim
Andrew R. Booker
Affiliation:
School of Mathematics, University of Bristol, University Walk, Bristol BS8 1TW, UK email andrew.booker@bristol.ac.uk
Peter J. Cho
Affiliation:
Department of Mathematical Sciences, Ulsan National Institute of Science and Technology, Ulsan, Korea email petercho@unist.ac.kr
Myoungil Kim
Affiliation:
Department of Mathematical Sciences, Ulsan National Institute of Science and Technology, Ulsan, Korea email mikim@unist.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the complete 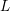$L$-function associated to any cuspidal automorphic representation of 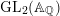$\operatorname{GL}_{2}(\mathbb{A}_{\mathbb{Q}})$ has infinitely many simple zeros.

Keywords

L-functionssimple zerosautomorphic forms

MSC classification

Primary: 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations
Secondary: 11M41: Other Dirichlet series and zeta functions
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 6 , June 2019 , pp. 1224 - 1243
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

A. R. Booker was partially supported by EPSRC grant EP/K034383/1. P. J. Cho was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2016R1D1A1B03935186). No data were created in the course of this study.

References

Booker, A. R., Simple zeros of degree 2 L-functions , J. Eur. Math. Soc. (JEMS) 18 (2016), 813–823; MR 3474457.Google Scholar
Booker, A. R. and Krishnamurthy, M., A strengthening of the GL(2) converse theorem , Compos. Math. 147 (2011), 669–715; MR 2801397.Google Scholar
Booker, A. R. and Then, H., Rapid computation of L-functions attached to Maass forms , Int. J. Number Theory 14 (2018), 1459–1485; MR 3806315.Google Scholar
Cho, P. J., Simple zeros of Maass L-functions , Int. J. Number Theory 9 (2013), 167–178; MR 2997497.Google Scholar
Conrey, J. B. and Ghosh, A., Simple zeros of the Ramanujan 𝜏-Dirichlet series , Invent. Math. 94 (1988), 403–419; MR 958837.Google Scholar
Duke, W., Friedlander, J. B. and Iwaniec, H., The subconvexity problem for Artin L-functions , Invent. Math. 149 (2002), 489–577; MR 1923476.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of integrals, series, and products, eighth edition (Elsevier/Academic Press, Amsterdam, 2015), translated from the Russian. Translation edited and with a preface by D. Zwillinger and V. Moll, revised from the seventh edition [MR 2360010]; MR 3307944.Google Scholar
Jacquet, H. and Shalika, J. A., A non-vanishing theorem for zeta functions of GL n , Invent. Math. 38 (1976/77), 1–16; MR 0432596.Google Scholar
Kim, H. H., Functoriality for the exterior square of GL4 and the symmetric fourth of GL2 , J. Amer. Math. Soc. 16 (2003), 139–183. With Appendix 1 by D. Ramakrishnan and Appendix 2 by Kim and P. Sarnak; MR 1937203.Google Scholar
Liu, J. and Ye, Y., Perron’s formula and the prime number theorem for automorphic L-functions , Pure Appl. Math. Q. 3 (2007), 481–497. Special issue in honor of L. Simon. Part 1; MR 2340051.Google Scholar