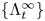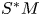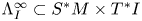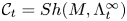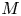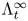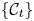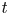Motivation and results
Let ![]() $M$ be a smooth manifold, and let
$M$ be a smooth manifold, and let ![]() $Sh(M)$ be the co-complete differential graded (dg) derived category of weakly constructible sheaves on
$Sh(M)$ be the co-complete differential graded (dg) derived category of weakly constructible sheaves on ![]() $M$ with coefficient in
$M$ with coefficient in ![]() $\mathbb {C}$. In [Reference Kashiwara and SchapiraKS13, Reference TamarkinTam08, Reference Guillermou, Kashiwara and SchapiraGKS12] it is proved that contact isotopy of the cosphere bundle
$\mathbb {C}$. In [Reference Kashiwara and SchapiraKS13, Reference TamarkinTam08, Reference Guillermou, Kashiwara and SchapiraGKS12] it is proved that contact isotopy of the cosphere bundle ![]() $T^\infty M=(T^*M - T^*_M M)/\mathbb {R}_+$ acts on
$T^\infty M=(T^*M - T^*_M M)/\mathbb {R}_+$ acts on ![]() $Sh(M)$ as equivalences of categories. In this paper, we consider a (singular) Legendrian
$Sh(M)$ as equivalences of categories. In this paper, we consider a (singular) Legendrian ![]() $\Lambda ^\infty \subset T^\infty M$ and the full subcategory
$\Lambda ^\infty \subset T^\infty M$ and the full subcategory ![]() $Sh(M, \Lambda ^\infty )$ consisting of sheaves
$Sh(M, \Lambda ^\infty )$ consisting of sheaves ![]() $F$ with singular support at infinity,
$F$ with singular support at infinity, ![]() $SS^\infty (F) = (SS(F) - T^*_M M)/\mathbb {R}_+$, contained in
$SS^\infty (F) = (SS(F) - T^*_M M)/\mathbb {R}_+$, contained in ![]() $\Lambda ^\infty$. We define a notion of isotopy for the singular Legendrian
$\Lambda ^\infty$. We define a notion of isotopy for the singular Legendrian ![]() $\Lambda ^\infty$ and prove that the category
$\Lambda ^\infty$ and prove that the category ![]() $Sh(M, \Lambda ^\infty )$ remains invariant under such an isotopy.
$Sh(M, \Lambda ^\infty )$ remains invariant under such an isotopy.
Such invariances of constructible sheaf categories are possible because constructible sheaves are closely related to Lagrangians in ![]() $T^*M$ (see [Reference Nadler and ZaslowNZ09, Reference Ganatra, Pardon and ShendeGPS18a, Reference Nadler and ShendeNS20]) and hence enjoy the flexibility of symplectic geometry. More precisely, the full subcategory of compact objects in
$T^*M$ (see [Reference Nadler and ZaslowNZ09, Reference Ganatra, Pardon and ShendeGPS18a, Reference Nadler and ShendeNS20]) and hence enjoy the flexibility of symplectic geometry. More precisely, the full subcategory of compact objects in ![]() $Sh(M, \Lambda ^\infty )$, denoted by
$Sh(M, \Lambda ^\infty )$, denoted by ![]() $Sh^{\rm w}(M, \Lambda ^\infty )$, is equivalent to the wrapped Fukaya category of the pair
$Sh^{\rm w}(M, \Lambda ^\infty )$, is equivalent to the wrapped Fukaya category of the pair ![]() $(T^*M, \Lambda ^\infty )$ (see [Reference Ganatra, Pardon and ShendeGPS18a, Reference Nadler and ShendeNS20]),
$(T^*M, \Lambda ^\infty )$ (see [Reference Ganatra, Pardon and ShendeGPS18a, Reference Nadler and ShendeNS20]),
where the superscript ‘w’ stands for ‘wrapped’. The traditional constructible sheaves with bounded cohomologies ![]() $Sh^{pp}(M, \Lambda ^\infty )$ can be recovered as perfect modules [Reference NadlerNad16],
$Sh^{pp}(M, \Lambda ^\infty )$ can be recovered as perfect modules [Reference NadlerNad16],
There is an analogous result in the wrapped Fukaya category for Liouville sectors [Reference Ganatra, Pardon and ShendeGPS18b, Theorem 1.4]: given a Liouville domain ![]() $W$ with a ‘stop’
$W$ with a ‘stop’ ![]() $S \subset \partial W$, if the contact complement
$S \subset \partial W$, if the contact complement ![]() $\partial W \backslash S$ remains invariant up to contact isotopy as
$\partial W \backslash S$ remains invariant up to contact isotopy as ![]() $S$ moves, then the wrapped Fukaya category
$S$ moves, then the wrapped Fukaya category ![]() $\operatorname {Fuk}^{\rm w}(W, S)$ is invariant. Hence, combined with the comparison results of [Reference Ganatra, Pardon and ShendeGPS18a, Reference Nadler and ShendeNS20], we get that
$\operatorname {Fuk}^{\rm w}(W, S)$ is invariant. Hence, combined with the comparison results of [Reference Ganatra, Pardon and ShendeGPS18a, Reference Nadler and ShendeNS20], we get that ![]() $Sh(M, \Lambda ^\infty )$ is invariant as long as
$Sh(M, \Lambda ^\infty )$ is invariant as long as ![]() $T^\infty M \backslash \Lambda ^\infty$ is invariant up to contact isotopy.
$T^\infty M \backslash \Lambda ^\infty$ is invariant up to contact isotopy.
This paper gives a similar sufficient condition using ‘isotopy’ of ![]() $\Lambda ^\infty$: we replace
$\Lambda ^\infty$: we replace ![]() $\Lambda ^\infty$ by a tube
$\Lambda ^\infty$ by a tube ![]() $U=U(\Lambda ^\infty )$ around the Legendrian
$U=U(\Lambda ^\infty )$ around the Legendrian ![]() $\Lambda ^\infty$, and we equip
$\Lambda ^\infty$, and we equip ![]() $U$ with a contact flow
$U$ with a contact flow ![]() $X$ that shrinks the tube
$X$ that shrinks the tube ![]() $U$ back to
$U$ back to ![]() $\Lambda ^\infty$ (Definition 0.2). Although
$\Lambda ^\infty$ (Definition 0.2). Although ![]() $\Lambda ^\infty$ may be singular, the data of
$\Lambda ^\infty$ may be singular, the data of ![]() $(U,X)$ are smooth, so we can talk about isotopies of
$(U,X)$ are smooth, so we can talk about isotopies of ![]() $(U,X)$. The relation to the complement
$(U,X)$. The relation to the complement ![]() $T^\infty M \backslash \Lambda ^\infty$ is that if
$T^\infty M \backslash \Lambda ^\infty$ is that if ![]() $(U_t, X_t)$ varies smoothly, then the complements
$(U_t, X_t)$ varies smoothly, then the complements ![]() $\{T^\infty M \backslash \Lambda ^\infty _t\}_t$ are contactomorphic, where
$\{T^\infty M \backslash \Lambda ^\infty _t\}_t$ are contactomorphic, where ![]() $\Lambda ^\infty _t$ is the limit of
$\Lambda ^\infty _t$ is the limit of ![]() $U_t$ under the shrinking flow
$U_t$ under the shrinking flow ![]() $X_t$.
$X_t$.
To state the main theorem precisely, we need some definitions.
Let ![]() $(C, \alpha )$ be a contact manifold with a contact 1-form
$(C, \alpha )$ be a contact manifold with a contact 1-form ![]() $\alpha$.
$\alpha$.
Definition 0.1 A singular Legendrian ![]() $\mathcal {L} \subset C$ is a Whitney stratifiable subspace such that its top-dimensional strata are smooth Legendrians and the closure of the union of the top-dimensional strata is
$\mathcal {L} \subset C$ is a Whitney stratifiable subspace such that its top-dimensional strata are smooth Legendrians and the closure of the union of the top-dimensional strata is ![]() $\mathcal {L}$.
$\mathcal {L}$.
Definition 0.2 Let ![]() $\mathcal {L} \subset C$ be a singular Legendrian. A convex tube
$\mathcal {L} \subset C$ be a singular Legendrian. A convex tube ![]() $(U,X)$ around
$(U,X)$ around ![]() $\mathcal {L}$ is an open subset
$\mathcal {L}$ is an open subset ![]() $U$ containing
$U$ containing ![]() $\mathcal {L}$ with smooth boundary
$\mathcal {L}$ with smooth boundary ![]() $\partial U$ and a contact vector field
$\partial U$ and a contact vector field ![]() $X$ transverse to
$X$ transverse to ![]() $\partial U$ and pointing inward to
$\partial U$ and pointing inward to ![]() $\partial U$, such that
$\partial U$, such that ![]() $\mathcal {L}_X(\alpha ) = -\alpha$ and
$\mathcal {L}_X(\alpha ) = -\alpha$ and ![]() $\bigcap _{u > 0} X^u(U) = \mathcal {L}$, where
$\bigcap _{u > 0} X^u(U) = \mathcal {L}$, where ![]() $X^u$ is the time-
$X^u$ is the time-![]() $u$ flow of
$u$ flow of ![]() $X$.
$X$.
Definition 0.3 Let ![]() $I \subset \mathbb {R}$ be a closed interval and
$I \subset \mathbb {R}$ be a closed interval and ![]() $\{(U_t, X_t, \mathcal {L}_t)\}_{t \in I}$ a family of singular Legendrians
$\{(U_t, X_t, \mathcal {L}_t)\}_{t \in I}$ a family of singular Legendrians ![]() $\mathcal {L}_t$ with convex tubes
$\mathcal {L}_t$ with convex tubes ![]() $(U_t, X_t)$. If
$(U_t, X_t)$. If ![]() $\partial U_t$ and
$\partial U_t$ and ![]() $X_t$ vary smoothly with
$X_t$ vary smoothly with ![]() $t$, we say that
$t$, we say that ![]() $\{(U_t, X_t, \mathcal {L}_t)\}_{t \in I}$ is an isotopy of convex tubes over
$\{(U_t, X_t, \mathcal {L}_t)\}_{t \in I}$ is an isotopy of convex tubes over ![]() $I$.
$I$.
Let ![]() $M$ be a smooth manifold with Riemannian metric
$M$ be a smooth manifold with Riemannian metric ![]() $g$. Let
$g$. Let ![]() $S^*M \subset T^*M$ be the unit cosphere bundle, and let
$S^*M \subset T^*M$ be the unit cosphere bundle, and let ![]() $\alpha = \lambda |_{S^*M}$ be a contact 1-form on
$\alpha = \lambda |_{S^*M}$ be a contact 1-form on ![]() $S^*M$ where
$S^*M$ where ![]() $\lambda$ is the Liouville 1-form on
$\lambda$ is the Liouville 1-form on ![]() $T^*M$ (e.g.
$T^*M$ (e.g. ![]() $\lambda = p\,dx$ on
$\lambda = p\,dx$ on ![]() $T^*\mathbb {R}$). We identify
$T^*\mathbb {R}$). We identify ![]() $S^*M$ with
$S^*M$ with ![]() $T^\infty M$. We equip
$T^\infty M$. We equip ![]() $S^*M \times T^*I$ with the contact form
$S^*M \times T^*I$ with the contact form ![]() $\widetilde \alpha = \alpha + \tau \,dt$, where
$\widetilde \alpha = \alpha + \tau \,dt$, where ![]() $t$ is the coordinate of
$t$ is the coordinate of ![]() $I$ and
$I$ and ![]() $\tau$ is the coordinate on the cotangent fiber. Then the composition
$\tau$ is the coordinate on the cotangent fiber. Then the composition ![]() $S^*M \times T^*I \hookrightarrow \dot {T}^*(M \times I) \to T^\infty (M \times I)$ is an open immersion and contactomorphism, with image
$S^*M \times T^*I \hookrightarrow \dot {T}^*(M \times I) \to T^\infty (M \times I)$ is an open immersion and contactomorphism, with image ![]() $(x, t; [p, \tau ]) \in T^\infty (M \times I)$ where
$(x, t; [p, \tau ]) \in T^\infty (M \times I)$ where ![]() $p \neq 0$.
$p \neq 0$.
Definition 0.4 Let ![]() $I \subset \mathbb {R}$ be a closed interval. A strong isotopy of Legendrians in
$I \subset \mathbb {R}$ be a closed interval. A strong isotopy of Legendrians in ![]() $S^*M$ over
$S^*M$ over ![]() $I$ is a Legendrian
$I$ is a Legendrian ![]() $\mathcal {L}_I \subset S^*M \times T^*I$. A strong isotopy of convex tubes is a convex tube
$\mathcal {L}_I \subset S^*M \times T^*I$. A strong isotopy of convex tubes is a convex tube ![]() $(U_I, X_I)$ of
$(U_I, X_I)$ of ![]() $\mathcal {L}_I$ such that
$\mathcal {L}_I$ such that ![]() $X_I$ preserves the fibers of
$X_I$ preserves the fibers of ![]() $S^*M \times T^*I \to I$.
$S^*M \times T^*I \to I$.
Our main result is the following.
Theorem 0.5 If ![]() $(U_I, X_I)$ is a strong isotopy of convex tubes around
$(U_I, X_I)$ is a strong isotopy of convex tubes around ![]() $\mathcal {L}_I$ in
$\mathcal {L}_I$ in ![]() $S^*M \times T^*I$, then for any
$S^*M \times T^*I$, then for any ![]() $t \in I$ we have an equivalence of categories
$t \in I$ we have an equivalence of categories
where ![]() $\iota _t: M_t = M \times \{t\} \hookrightarrow M_I = M \times I$ is the inclusion of the slice over
$\iota _t: M_t = M \times \{t\} \hookrightarrow M_I = M \times I$ is the inclusion of the slice over ![]() $t$.
$t$.
Given a strong isotopy of Legendrians ![]() $\mathcal {L}_I$, we prove that to construct a tube thickening
$\mathcal {L}_I$, we prove that to construct a tube thickening ![]() $(U_I, X_I)$ it suffices to construct a Liouville hypersurface thickening of each slice
$(U_I, X_I)$ it suffices to construct a Liouville hypersurface thickening of each slice ![]() $\mathcal {L}_t$ (see Proposition 1.14).
$\mathcal {L}_t$ (see Proposition 1.14).
Although the result is expected given the analogous result in Fukaya category, and it is superseded by the recent paper [Reference Nadler and ShendeNS20], we hope that its purely sheaf-theoretic proof and the simpler cotangent bundle setting make the presentation of this result still worthwhile.
Previous work
We first recall the sheaf quantization of a contact isotopy of ![]() $S^*M$.
$S^*M$.
Theorem 0.6 [Reference Guillermou, Kashiwara and SchapiraGKS12, Theorem 3.7 and Proposition 3.12]
Let ![]() $I$ be an open interval containing
$I$ be an open interval containing ![]() $0$, and let
$0$, and let ![]() $\varphi : I \times T^\infty M\to T^\infty M$ be a smooth map with
$\varphi : I \times T^\infty M\to T^\infty M$ be a smooth map with ![]() $\varphi _t=\varphi (t,-)$. Assume
$\varphi _t=\varphi (t,-)$. Assume ![]() $\varphi$ is such that (i)
$\varphi$ is such that (i) ![]() $\varphi _0=\mathrm {id}$ and (ii)
$\varphi _0=\mathrm {id}$ and (ii) ![]() $\varphi _t$ are contactomorphisms for all
$\varphi _t$ are contactomorphisms for all ![]() $t \in I$. Then for each
$t \in I$. Then for each ![]() $t \in I$ we have the equivalences of categories
$t \in I$ we have the equivalences of categories
Note that any isotopy of smooth Legendrians can be extended to a contact isotopy of the ambient manifold. In general, we have the following corollary.
Corollary 0.7 If an isotopy of Legendrians ![]() $\{\Lambda ^\infty _t\}_{t \in I}$ can be embedded into an isotopy
$\{\Lambda ^\infty _t\}_{t \in I}$ can be embedded into an isotopy ![]() $\{\varphi _t\}_{t \in I}:S^*M \to S^*M$ of the contact manifold, that is,
$\{\varphi _t\}_{t \in I}:S^*M \to S^*M$ of the contact manifold, that is, ![]() $\Lambda ^\infty _t = \varphi _t(\Lambda ^\infty _0)$, then we have an equivalence of categories
$\Lambda ^\infty _t = \varphi _t(\Lambda ^\infty _0)$, then we have an equivalence of categories
For a deformation of singular Legendrians, there is one necessary condition for the invariance of categories, due to Nadler [Reference NadlerNad15].
Definition 0.8 (Displaceable Legendrian)
Let ![]() $(S^* M, \alpha )$ be the unit cosphere bundle of a Riemannian manifold
$(S^* M, \alpha )$ be the unit cosphere bundle of a Riemannian manifold ![]() $M$ with Reeb vector field
$M$ with Reeb vector field ![]() $R$ and time-
$R$ and time-![]() $t$ Reeb flow
$t$ Reeb flow ![]() $R^t$. A Legendrian
$R^t$. A Legendrian ![]() $\mathcal {L} \subset S^* M$ is
$\mathcal {L} \subset S^* M$ is ![]() $\epsilon$-displaceable for
$\epsilon$-displaceable for ![]() $R$ and for some
$R$ and for some ![]() $\epsilon >0$ if
$\epsilon >0$ if
We say that a family of Legendrians ![]() $\{\mathcal {L}_t\}$ is uniformly
$\{\mathcal {L}_t\}$ is uniformly ![]() $\epsilon$-displaceable for
$\epsilon$-displaceable for ![]() $R$ and for some
$R$ and for some ![]() $\epsilon >0$ if each
$\epsilon >0$ if each ![]() $\mathcal {L}_t$ is
$\mathcal {L}_t$ is ![]() $\epsilon$-displaceable.
$\epsilon$-displaceable.
If a family of Legendrians ![]() $\{\mathcal {L}_t\}$ can be upgraded to an isotopy of convex tubes
$\{\mathcal {L}_t\}$ can be upgraded to an isotopy of convex tubes ![]() $\{U_t, X_t, \mathcal {L}_t\}$, then
$\{U_t, X_t, \mathcal {L}_t\}$, then ![]() $\{\mathcal {L}_t\}$ is uniformly displaceable (Proposition 1.9).
$\{\mathcal {L}_t\}$ is uniformly displaceable (Proposition 1.9).
Example 0.9 Consider the example in Figure 1.

Figure 1. The deformation to the right is uniformly displaceable, and the one to the left is not, due to the appearance of a new short Reeb chord (marked by a thick line); cf. [Reference NadlerNad15, Example 1.5].
The category of constructible sheaves for the three diagrams comprises the representations of the following commutative diagrams (where each region corresponds to a vertex and an arrow between vertices goes against the direction of the hair).

A sketch of the proof
Given a convex tube ![]() $(U,X)$ of a Legendrian
$(U,X)$ of a Legendrian ![]() $\mathcal {L} \subset S^*M$, we may define a projection functor as the ‘limit’ of the flow
$\mathcal {L} \subset S^*M$, we may define a projection functor as the ‘limit’ of the flow ![]() $X$:
$X$:
where ![]() $Sh(M, U)$ stands for the category of constructible sheaves with
$Sh(M, U)$ stands for the category of constructible sheaves with ![]() $SS^\infty (F) \subset U$ and the limit is defined using the nearby cycle functor in § 2.6.
$SS^\infty (F) \subset U$ and the limit is defined using the nearby cycle functor in § 2.6.
Let ![]() $(U_I, X_I, \mathcal {L}_I)$ be a strong isotopy of convex tubes in
$(U_I, X_I, \mathcal {L}_I)$ be a strong isotopy of convex tubes in ![]() $S^*M \times T^*I$, and let
$S^*M \times T^*I$, and let ![]() $\{(U_t, X_t, \mathcal {L}_t)\}$ be the slices. Let
$\{(U_t, X_t, \mathcal {L}_t)\}$ be the slices. Let ![]() $F_t \in Sh(M, \mathcal {L}_t)$. We will extend
$F_t \in Sh(M, \mathcal {L}_t)$. We will extend ![]() $F_t$ to a sheaf
$F_t$ to a sheaf ![]() $F_I \subset Sh(M \times I, \mathcal {L}_I)$ such that
$F_I \subset Sh(M \times I, \mathcal {L}_I)$ such that ![]() $F_I|_t=F_t$.
$F_I|_t=F_t$.
We first show that such an extension is unique (if it exists); this is equivalent to showing that the restriction functor ![]() $Sh(M, \mathcal {L}_I) \to Sh(M, \mathcal {L}_t)$ is fully faithful (Proposition 3.1), that is,
$Sh(M, \mathcal {L}_I) \to Sh(M, \mathcal {L}_t)$ is fully faithful (Proposition 3.1), that is,
One needs to show that ![]() $\mathcal {H}om(F_I, G_I)(M \times (a,b))$ is independent of the size of the interval, so that one can interpolate from
$\mathcal {H}om(F_I, G_I)(M \times (a,b))$ is independent of the size of the interval, so that one can interpolate from ![]() $(a,b) = I$ to an infinitesimally small neighborhood around
$(a,b) = I$ to an infinitesimally small neighborhood around ![]() $t$. The key technical point is to use the uniform displaceability condition to perturb
$t$. The key technical point is to use the uniform displaceability condition to perturb ![]() $G_I$ slicewise by positive Reeb flow for time
$G_I$ slicewise by positive Reeb flow for time ![]() $s$,
$s$, ![]() $G_I \to K_s^!G_I$, to separate
$G_I \to K_s^!G_I$, to separate ![]() $SS^\infty (F_I)$ and
$SS^\infty (F_I)$ and ![]() $SS^\infty (K_s^!G_I)$.
$SS^\infty (K_s^!G_I)$.
We then show that such an extension exists locally; that is, given ![]() $F_t$, we can find a small neighborhood
$F_t$, we can find a small neighborhood ![]() $J = (t-\delta, t+\delta )$ such that
$J = (t-\delta, t+\delta )$ such that ![]() $\mathcal {L}_t \times T^*_J J \subset U_J = U_I \cap S^*M \times T^*J$ and extend
$\mathcal {L}_t \times T^*_J J \subset U_J = U_I \cap S^*M \times T^*J$ and extend ![]() $F_t$ on
$F_t$ on ![]() $M_t$ to
$M_t$ to ![]() $F_J$ on
$F_J$ on ![]() $M_J$ by defining
$M_J$ by defining ![]() $F_J = \Pi _{\mathcal {L}_J}(F_t \boxtimes \mathbb {C}_J)$.
$F_J = \Pi _{\mathcal {L}_J}(F_t \boxtimes \mathbb {C}_J)$.
Finally, we use the uniqueness of extension to patch together the local extensions, and thus we get the global extension result (cf. [Reference Guillermou, Kashiwara and SchapiraGKS12, Lemma 1.13]).
Notation
We use ![]() $Sh(M)$ to denote the co-complete dg derived category of weakly constructible sheaves. With an abuse of notation, we use ‘constructible sheaf’ to mean a cohomologically constructible complex of sheaves. All the functors
$Sh(M)$ to denote the co-complete dg derived category of weakly constructible sheaves. With an abuse of notation, we use ‘constructible sheaf’ to mean a cohomologically constructible complex of sheaves. All the functors ![]() $f_*, f^*, f_!, \mathcal {H}om$ etc. are derived.
$f_*, f^*, f_!, \mathcal {H}om$ etc. are derived.
1. Convex tubes and isotopy
1.1 Basics of contact geometry
We recall the definition of co-oriented contact manifold as follows. Let ![]() $C$ be a
$C$ be a ![]() $(2n+1)$-dimensional manifold, and let
$(2n+1)$-dimensional manifold, and let ![]() $\xi \subset TC$ be a rank-
$\xi \subset TC$ be a rank-![]() $2n$ sub-bundle such that there exists a
$2n$ sub-bundle such that there exists a ![]() $1$-form (contact
$1$-form (contact ![]() $1$-form)
$1$-form) ![]() $\alpha$ (up to multiplication by a non-negative function) satisfying
$\alpha$ (up to multiplication by a non-negative function) satisfying ![]() $\xi = \ker \alpha$ and
$\xi = \ker \alpha$ and ![]() $\alpha \wedge (d\alpha )^n \neq 0$. If we fix such an
$\alpha \wedge (d\alpha )^n \neq 0$. If we fix such an ![]() $\alpha$, we have a Reeb vector field
$\alpha$, we have a Reeb vector field ![]() $R_\alpha$ given by
$R_\alpha$ given by
We remark that different choices of ![]() $\alpha$ will lead to different choices of
$\alpha$ will lead to different choices of ![]() $R_\alpha$.
$R_\alpha$.
A contact vector field ![]() $X$ is a vector field on
$X$ is a vector field on ![]() $C$ that preserves the sub-bundle
$C$ that preserves the sub-bundle ![]() $\xi$.
$\xi$.
Definition 1.1 Given a smooth function ![]() $H: C \to \mathbb {R}$, the contact Hamiltonian vector field
$H: C \to \mathbb {R}$, the contact Hamiltonian vector field ![]() $X_H$ is uniquely determined by the conditions
$X_H$ is uniquely determined by the conditions
 \begin{equation} \begin{cases} \langle X_H, \alpha \rangle = H ,\\ \iota_{X_H} \,d \alpha = \langle dH, R \rangle \alpha - d H .\end{cases} \end{equation}
\begin{equation} \begin{cases} \langle X_H, \alpha \rangle = H ,\\ \iota_{X_H} \,d \alpha = \langle dH, R \rangle \alpha - d H .\end{cases} \end{equation} The Reeb vector field is a special case of ![]() $X_H$ where
$X_H$ where ![]() $H=1$.
$H=1$.
Proposition 1.2 [Reference GeigesGei08, Theorem 2.3.1]
With a fixed choice of contact form ![]() $\alpha$, there is a one-to-one correspondence between the contact vector field
$\alpha$, there is a one-to-one correspondence between the contact vector field ![]() $X$ and smooth functions
$X$ and smooth functions ![]() $H: C \to \mathbb {R}$. The correspondence is given by
$H: C \to \mathbb {R}$. The correspondence is given by
Unlike symplectic Hamiltonian vector fields, ![]() $X_H$ does not preserve the level sets of
$X_H$ does not preserve the level sets of ![]() $H$.
$H$.
Lemma 1.3 We have that
In particular, ![]() $X_H$ preserves the zero set of
$X_H$ preserves the zero set of ![]() $H$.
$H$.
Proof. Apply ![]() $\iota _{X_H}$ to the second line of (3) and then use the first line.
$\iota _{X_H}$ to the second line of (3) and then use the first line.
We also have the Lie derivative of ![]() $\alpha$ along
$\alpha$ along ![]() $X_H$,
$X_H$,
Proposition 1.4 If ![]() $\mathcal {L} \subset C$ is a germ of a smooth Legendrian and
$\mathcal {L} \subset C$ is a germ of a smooth Legendrian and ![]() $H$ is any locally defined function vanishing on
$H$ is any locally defined function vanishing on ![]() $\mathcal {L}$, then the contact flow
$\mathcal {L}$, then the contact flow ![]() $X_H$ is tangential to
$X_H$ is tangential to ![]() $\mathcal {L}$.
$\mathcal {L}$.
Proof. To show that ![]() $X_H$ is tangential to
$X_H$ is tangential to ![]() $\mathcal {L}$ at
$\mathcal {L}$ at ![]() $p \in \mathcal {L}$, we only need to show that for any tangent vector
$p \in \mathcal {L}$, we only need to show that for any tangent vector ![]() $v \in T_p \mathcal {L}$ we have
$v \in T_p \mathcal {L}$ we have ![]() $d \alpha (X_H, v) = 0$ and
$d \alpha (X_H, v) = 0$ and ![]() $\alpha (X_H)|_p=0$, because these two conditions imply
$\alpha (X_H)|_p=0$, because these two conditions imply ![]() $X_H \in (T_p \mathcal {L})^{\perp _{d\alpha }} \cap \ker (\alpha )= T_p \mathcal {L}$. Indeed,
$X_H \in (T_p \mathcal {L})^{\perp _{d\alpha }} \cap \ker (\alpha )= T_p \mathcal {L}$. Indeed, ![]() $\alpha (X_H)|_p= H(p) = 0$ and
$\alpha (X_H)|_p= H(p) = 0$ and
Hence ![]() $X_H$ is tangential to
$X_H$ is tangential to ![]() $\mathcal {L}$.
$\mathcal {L}$.
Example 1.5 Let ![]() $M$ be a smooth manifold, and let
$M$ be a smooth manifold, and let ![]() $T^*M$ the cotangent bundle with canonical Liouville
$T^*M$ the cotangent bundle with canonical Liouville ![]() $1$-form
$1$-form ![]() $\lambda$ and symplectic
$\lambda$ and symplectic ![]() $2$-form
$2$-form ![]() $\omega =d\lambda$. If we put local Darboux coordinates
$\omega =d\lambda$. If we put local Darboux coordinates ![]() $(q,p)=(q_1,\ldots, q_m; p_1, \ldots, p_m)$ on
$(q,p)=(q_1,\ldots, q_m; p_1, \ldots, p_m)$ on ![]() $T^*M$, where
$T^*M$, where ![]() $m=\dim _\mathbb {R} M$, then
$m=\dim _\mathbb {R} M$, then ![]() $\lambda = \sum _{i=1}^m p_i \,dq_i$ and
$\lambda = \sum _{i=1}^m p_i \,dq_i$ and ![]() $\omega = \sum _i\,dp_i \wedge dq_i$, and we will suppress the indices and summation and write simply
$\omega = \sum _i\,dp_i \wedge dq_i$, and we will suppress the indices and summation and write simply ![]() $\lambda = p\,dq$ and
$\lambda = p\,dq$ and ![]() $\omega = dp\,dq$. Also define
$\omega = dp\,dq$. Also define ![]() $\dot {T}^*M = T^*M \backslash T^*_M M$ and
$\dot {T}^*M = T^*M \backslash T^*_M M$ and ![]() $T^\infty M = \dot {T}^*M / \mathbb {R}_{>0}$. The Liouville vector field for
$T^\infty M = \dot {T}^*M / \mathbb {R}_{>0}$. The Liouville vector field for ![]() $\lambda$ is defined by
$\lambda$ is defined by ![]() $\iota _{V_\lambda } \omega = \lambda$, and here it is given by
$\iota _{V_\lambda } \omega = \lambda$, and here it is given by ![]() $V_\lambda = p \partial _p$. On
$V_\lambda = p \partial _p$. On ![]() $T(\dot {T}^*M)$, the symplectic orthogonal to the Liouville vector field defines a distribution
$T(\dot {T}^*M)$, the symplectic orthogonal to the Liouville vector field defines a distribution
which projects to a canonical contact distribution ![]() $\xi$ on
$\xi$ on ![]() $T^\infty M$. Let
$T^\infty M$. Let ![]() $g$ be any Riemannian metric on
$g$ be any Riemannian metric on ![]() $M$; then
$M$; then ![]() $T^*M$ has an induced norm. Let
$T^*M$ has an induced norm. Let ![]() $S^*M = \{ (q, p) \in T^*M : |p|=1\}$ be the unit cosphere bundle with contact form
$S^*M = \{ (q, p) \in T^*M : |p|=1\}$ be the unit cosphere bundle with contact form ![]() $\alpha = \lambda |_{S^*M}$; then the contact distribution can also be written as
$\alpha = \lambda |_{S^*M}$; then the contact distribution can also be written as ![]() $\xi = \ker (\alpha )$.
$\xi = \ker (\alpha )$.
Define the symplectization of ![]() $(C, \xi = \ker \alpha )$ by
$(C, \xi = \ker \alpha )$ by
We have the projection along ![]() $\mathbb {R}_u$ and the inclusion of zero-section
$\mathbb {R}_u$ and the inclusion of zero-section
A different choice of ![]() $\alpha$ would give rise to the same
$\alpha$ would give rise to the same ![]() $S$ up to a fiber-preserving symplectomorphism that identifies the ‘zero-section’
$S$ up to a fiber-preserving symplectomorphism that identifies the ‘zero-section’ ![]() $\text {Im} (\iota _C)$.
$\text {Im} (\iota _C)$.
A Hamiltonian function ![]() $H: C \to \mathbb {R}$ can be extended to a homogeneous degree-one function
$H: C \to \mathbb {R}$ can be extended to a homogeneous degree-one function ![]() $\widetilde H: S \to \mathbb {R}$ by setting
$\widetilde H: S \to \mathbb {R}$ by setting ![]() $\widetilde H =e^u H$. Then the symplectic Hamiltonian vector field
$\widetilde H =e^u H$. Then the symplectic Hamiltonian vector field ![]() $\xi _{\widetilde H}$, given by
$\xi _{\widetilde H}$, given by ![]() $\omega _S(-, \xi _{\widetilde H}) = d \widetilde H(-)$, preserves the fiber of
$\omega _S(-, \xi _{\widetilde H}) = d \widetilde H(-)$, preserves the fiber of ![]() $\pi _S$ and descends to
$\pi _S$ and descends to ![]() $X_H$.
$X_H$.
1.2 Convex tubes
Recall the definition of convex tubes in Definition 0.2.
Definition 1.6 A Liouville hypersurface thickening of a singular Legendrian ![]() $\mathcal {L}$ is a hypersurface
$\mathcal {L}$ is a hypersurface ![]() $\mathcal {H} \supset \mathcal {L}$ such that
$\mathcal {H} \supset \mathcal {L}$ such that ![]() $(\mathcal {H}, \alpha |_\mathcal {H})$ is a Liouville domain with the Liouville skeleton being
$(\mathcal {H}, \alpha |_\mathcal {H})$ is a Liouville domain with the Liouville skeleton being ![]() $\mathcal {L}$.
$\mathcal {L}$.
First we show that a Liouville hypersurface thickening can be upgraded to a convex tube thickening of ![]() $\mathcal {L}$.
$\mathcal {L}$.
Proposition 1.7 Let ![]() $\mathcal {L}$ be a singular Legendrian with a Liouville hypersurface thickening
$\mathcal {L}$ be a singular Legendrian with a Liouville hypersurface thickening ![]() $\mathcal {H}$. Then
$\mathcal {H}$. Then ![]() $\mathcal {L}$ admits a convex tube
$\mathcal {L}$ admits a convex tube ![]() $(U, X)$, where the contact vector field
$(U, X)$, where the contact vector field ![]() $X$ preserves
$X$ preserves ![]() $\mathcal {H}$ and
$\mathcal {H}$ and ![]() $X$ restricted to
$X$ restricted to ![]() $\mathcal {H}$ is the downward Liouville flow of
$\mathcal {H}$ is the downward Liouville flow of ![]() $\mathcal {H}$.
$\mathcal {H}$.
Proof. Let ![]() $\epsilon >0$ be small enough that for any
$\epsilon >0$ be small enough that for any ![]() $0< s<\epsilon$ we have
$0< s<\epsilon$ we have ![]() $\mathcal {H} \cap R^s \mathcal {H} = \emptyset$. Then define
$\mathcal {H} \cap R^s \mathcal {H} = \emptyset$. Then define ![]() $U = \bigcup _{|s| \leqslant \epsilon /2} R^s \mathcal {H} \simeq \mathcal {H} \times (-\epsilon /2, +\epsilon /2)$, and let
$U = \bigcup _{|s| \leqslant \epsilon /2} R^s \mathcal {H} \simeq \mathcal {H} \times (-\epsilon /2, +\epsilon /2)$, and let ![]() $h: U \to (-\epsilon /2, +\epsilon /2)$ be the projection. Then
$h: U \to (-\epsilon /2, +\epsilon /2)$ be the projection. Then ![]() $X = X_h$ shrinks
$X = X_h$ shrinks ![]() $U$ to
$U$ to ![]() $\mathcal {L}$ and restricts to the downward Liouville flow on
$\mathcal {L}$ and restricts to the downward Liouville flow on ![]() $\mathcal {H}$. One may smooth the corner of
$\mathcal {H}$. One may smooth the corner of ![]() $U$ and achieve transversality of
$U$ and achieve transversality of ![]() $X$ with
$X$ with ![]() $\partial U$.
$\partial U$.
Conversely, we show that each convex tube ![]() $(U,X)$ around
$(U,X)$ around ![]() $\mathcal {L}$ determines a Liouville thickening.
$\mathcal {L}$ determines a Liouville thickening.
Proposition 1.8 Let ![]() $(U,X)$ be a convex tube around
$(U,X)$ be a convex tube around ![]() $\mathcal {L}$. Let
$\mathcal {L}$. Let ![]() $h=\alpha (X)$ and
$h=\alpha (X)$ and ![]() $\mathcal {H}= h^{-1}(0) \subset U$. Then
$\mathcal {H}= h^{-1}(0) \subset U$. Then ![]() $\mathcal {H}$ is a Liouville thickening of
$\mathcal {H}$ is a Liouville thickening of ![]() $\mathcal {L}$.
$\mathcal {L}$.
Proof. Since ![]() $X = X_h$ preserves
$X = X_h$ preserves ![]() $\mathcal {H}$ and shrinks
$\mathcal {H}$ and shrinks ![]() $\mathcal {H}$ to
$\mathcal {H}$ to ![]() $\mathcal {L}$, we only need to show that
$\mathcal {L}$, we only need to show that ![]() $\mathcal {H}$ is transverse to
$\mathcal {H}$ is transverse to ![]() $R$ and
$R$ and ![]() $X$ is the downward Liouville flow on
$X$ is the downward Liouville flow on ![]() $\mathcal {H}$.
$\mathcal {H}$.
Since ![]() $\mathcal {L}_X(\alpha )=\langle R, dh \rangle \alpha = -\alpha$, we have
$\mathcal {L}_X(\alpha )=\langle R, dh \rangle \alpha = -\alpha$, we have ![]() $R(h)=-1$. Thus
$R(h)=-1$. Thus ![]() $R$ is transversal to the level sets of
$R$ is transversal to the level sets of ![]() $h$, in particular
$h$, in particular ![]() $\mathcal {H}$. Hence
$\mathcal {H}$. Hence ![]() $d\alpha$ is non-degenerate on
$d\alpha$ is non-degenerate on ![]() $\mathcal {H}$, so
$\mathcal {H}$, so ![]() $\mathcal {H}$ is exact symplectic. Let
$\mathcal {H}$ is exact symplectic. Let ![]() $\lambda = \alpha |_\mathcal {H}, \omega = d\lambda$. When we restrict to
$\lambda = \alpha |_\mathcal {H}, \omega = d\lambda$. When we restrict to ![]() $T\mathcal {H}$, we have
$T\mathcal {H}$, we have
and hence ![]() $X_h$ is the downward Liouville flow on
$X_h$ is the downward Liouville flow on ![]() $\mathcal {H}$.
$\mathcal {H}$.
Proposition 1.9 Let ![]() $(U,X)$ be a convex tube of
$(U,X)$ be a convex tube of ![]() $\mathcal {L}$. Then
$\mathcal {L}$. Then ![]() $\mathcal {L}$ is displaceable (see Definition 0.8). Similarly, let
$\mathcal {L}$ is displaceable (see Definition 0.8). Similarly, let ![]() $I=[0,1]$ and let
$I=[0,1]$ and let ![]() $(U_I, X_I)$ be a strong isotopy of convex tubes for
$(U_I, X_I)$ be a strong isotopy of convex tubes for ![]() $\mathcal {L}_I$. Then the family of Legendrians
$\mathcal {L}_I$. Then the family of Legendrians ![]() $\mathcal {L}_t$ are uniformly displaceable.
$\mathcal {L}_t$ are uniformly displaceable.
Proof. Let ![]() $h =\alpha (X)$ be the Hamiltonian function generating
$h =\alpha (X)$ be the Hamiltonian function generating ![]() $X$. Then
$X$. Then ![]() $h$ vanishes on
$h$ vanishes on ![]() $\mathcal {L}$, and by the normalization condition we have
$\mathcal {L}$, and by the normalization condition we have ![]() $R(h)=-1$. If there is a Reeb chord
$R(h)=-1$. If there is a Reeb chord ![]() $\gamma : [0, T] \to C$ contained in
$\gamma : [0, T] \to C$ contained in ![]() $U$ and ending on
$U$ and ending on ![]() $\mathcal {L}$, then we have
$\mathcal {L}$, then we have
But on the other hand we also have
 \[ \int_0^T \dot{\gamma}(dh) \,dt = \int_\gamma \,dh = h(\gamma(T)) - h(\gamma(0)) = 0, \]
\[ \int_0^T \dot{\gamma}(dh) \,dt = \int_\gamma \,dh = h(\gamma(T)) - h(\gamma(0)) = 0, \]
since ![]() $\gamma (T) \in \mathcal {L}$,
$\gamma (T) \in \mathcal {L}$, ![]() $\gamma (0) \in \mathcal {L}$ and
$\gamma (0) \in \mathcal {L}$ and ![]() $h|_\mathcal {L} = 0$. Thus, there is no Reeb chord ending on
$h|_\mathcal {L} = 0$. Thus, there is no Reeb chord ending on ![]() $\mathcal {L}$ and contained in
$\mathcal {L}$ and contained in ![]() $U$. For any
$U$. For any ![]() $x \in \mathcal {L}$, let
$x \in \mathcal {L}$, let ![]() $t(x) = \inf \{t \in \mathbb {R}: R^t(x) \notin U\}$; then
$t(x) = \inf \{t \in \mathbb {R}: R^t(x) \notin U\}$; then ![]() $t(x)>0$ and is continuous on
$t(x)>0$ and is continuous on ![]() $\mathcal {L}$. Let
$\mathcal {L}$. Let ![]() $\epsilon =\inf \{t(x): x \in \mathcal {L}\}$; since
$\epsilon =\inf \{t(x): x \in \mathcal {L}\}$; since ![]() $\mathcal {L}$ is compact,
$\mathcal {L}$ is compact, ![]() $\epsilon >0$. Then
$\epsilon >0$. Then ![]() $\mathcal {L}$ is displaceable.
$\mathcal {L}$ is displaceable.
For the uniformly displaceable statement, note that ![]() $I=[0,1]$ is compact and
$I=[0,1]$ is compact and ![]() $\epsilon (t)$ for
$\epsilon (t)$ for ![]() $(U_t,X_t)$ is continuous in
$(U_t,X_t)$ is continuous in ![]() $t$; hence
$t$; hence ![]() $\epsilon = \inf \{\epsilon (t)\}>0$.
$\epsilon = \inf \{\epsilon (t)\}>0$.
1.3 The construction of strong isotopies of convex tubes
Consider the unit cosphere bundle ![]() $(S^*M, \alpha )$ and a closed interval
$(S^*M, \alpha )$ and a closed interval ![]() $I \subset \mathbb {R}$. Let a point in
$I \subset \mathbb {R}$. Let a point in ![]() $S^*M$ be denoted by
$S^*M$ be denoted by ![]() $(x,p) \in T^*M$ with
$(x,p) \in T^*M$ with ![]() $|p| = 1$. Let a point in
$|p| = 1$. Let a point in ![]() $T^*I$ be denoted by
$T^*I$ be denoted by ![]() $(t, \tau ) \in I \times \mathbb {R}$. Let
$(t, \tau ) \in I \times \mathbb {R}$. Let ![]() $S^*M \times T^*I$ be equipped with the contact 1-form
$S^*M \times T^*I$ be equipped with the contact 1-form
Let ![]() $\pi _t: S^*M \times T^*I \to I$.
$\pi _t: S^*M \times T^*I \to I$.
Proposition 1.10 The Reeb flow ![]() $R_I$ on
$R_I$ on ![]() $S^*M \times T^*I$ for
$S^*M \times T^*I$ for ![]() $\alpha _I$ is the pullback of the Reeb flow
$\alpha _I$ is the pullback of the Reeb flow ![]() $R$ on
$R$ on ![]() $S^*M$.
$S^*M$.
Proof. Let ![]() $R$ denote the pullback to
$R$ denote the pullback to ![]() $S^*M \times T^*I$. We may verify that
$S^*M \times T^*I$. We may verify that ![]() $\iota _R(\alpha _I)=1$ and
$\iota _R(\alpha _I)=1$ and ![]() $\iota _R(d \alpha _I) = 0$.
$\iota _R(d \alpha _I) = 0$.
Let ![]() $\mathcal {L}_I$ be a strong isotopy of Legendrians. Let
$\mathcal {L}_I$ be a strong isotopy of Legendrians. Let
Lemma 1.11 We have that ![]() $\mathcal {L}_t$ is a singular Legendrian in
$\mathcal {L}_t$ is a singular Legendrian in ![]() $S^*M$.
$S^*M$.
Proof. Take any ![]() $p \in \mathcal {L}_t$ that is the image of a point
$p \in \mathcal {L}_t$ that is the image of a point ![]() $\widetilde p$ in the smooth loci
$\widetilde p$ in the smooth loci ![]() $\mathcal {L}_I^{sm}$; any tangent vector
$\mathcal {L}_I^{sm}$; any tangent vector ![]() $v \in T_p \mathcal {L}_t$ can be lifted to
$v \in T_p \mathcal {L}_t$ can be lifted to ![]() $\widetilde v \in T_{\widetilde p} \mathcal {L}_I$. Concretely,
$\widetilde v \in T_{\widetilde p} \mathcal {L}_I$. Concretely, ![]() $\widetilde v = v + c \partial _\tau$. Since
$\widetilde v = v + c \partial _\tau$. Since ![]() $0 = (\alpha + \tau \, dt) (\widetilde v) = \alpha (v)$, we see that
$0 = (\alpha + \tau \, dt) (\widetilde v) = \alpha (v)$, we see that ![]() $T_p \mathcal {L}_t$ is in
$T_p \mathcal {L}_t$ is in ![]() $\ker (\alpha )$. Hence a dense open part of
$\ker (\alpha )$. Hence a dense open part of ![]() $\mathcal {L}_t$ is Legendrian, and thus
$\mathcal {L}_t$ is Legendrian, and thus ![]() $\mathcal {L}_t$ is a singular Legendrian.
$\mathcal {L}_t$ is a singular Legendrian.
Let ![]() $(U_I, X_I, \mathcal {L}_I)$ be a strong isotopy of convex tubes. First we define the restriction to
$(U_I, X_I, \mathcal {L}_I)$ be a strong isotopy of convex tubes. First we define the restriction to ![]() $S^*M \times T_t^* I$. Since
$S^*M \times T_t^* I$. Since ![]() $X_I$ preserves the
$X_I$ preserves the ![]() $t$ coordinate, for each
$t$ coordinate, for each ![]() $t$ we have the vector field
$t$ we have the vector field
Also define the restriction
Next, we define ![]() $(U_t, X_t)$. Define the projection map
$(U_t, X_t)$. Define the projection map ![]() $\hat \pi _t: S^*M \times T^*_t I \to S^*M$ and write
$\hat \pi _t: S^*M \times T^*_t I \to S^*M$ and write
Let ![]() $h_I = \alpha _I(X_I)$; since
$h_I = \alpha _I(X_I)$; since ![]() $X_I$ has no
$X_I$ has no ![]() $\partial _t$ component,
$\partial _t$ component, ![]() $\partial _\tau h_I=0$ and hence
$\partial _\tau h_I=0$ and hence ![]() $h_I$ is independent of
$h_I$ is independent of ![]() $\tau$. For each
$\tau$. For each ![]() $t \in I$ we define
$t \in I$ we define
and we let ![]() $X_t$ be the contact vector field generated by
$X_t$ be the contact vector field generated by ![]() $h_t$.
$h_t$.
Proposition 1.12 With the above setup, we have
Proof. We split a tangent vector ![]() $v$ on
$v$ on ![]() $S^*M \times T^*I$ into two components as
$S^*M \times T^*I$ into two components as ![]() $v = v_1 + v_2$, where
$v = v_1 + v_2$, where ![]() $v_1$ and
$v_1$ and ![]() $v_2$ are along the
$v_2$ are along the ![]() $S^*M$ and
$S^*M$ and ![]() $T^*I$ factors, respectively. Similarly, we decompose
$T^*I$ factors, respectively. Similarly, we decompose ![]() $X_I$ as
$X_I$ as ![]() $X_I = X_{I,1} + X_{I,2}$, where
$X_I = X_{I,1} + X_{I,2}$, where ![]() $X_{I,2} = a \,\partial _\tau$.
$X_{I,2} = a \,\partial _\tau$.
By the definition of ![]() $X_I$, we have
$X_I$, we have
and
which we will refer to as the first and second equations below.
Since ![]() $\tau \,dt(X_{I,2}) = 0$, the first equation becomes
$\tau \,dt(X_{I,2}) = 0$, the first equation becomes
For the second equation, if we restrict to the tangent space on ![]() $S^*M$, we have
$S^*M$, we have
Thus ![]() $X_{I,1} = X_t$ is the contact vector field on
$X_{I,1} = X_t$ is the contact vector field on ![]() $S^*M$ generated by
$S^*M$ generated by ![]() $h_t(x,p)$.
$h_t(x,p)$.
Finally, if we restrict the second equation to the tangent space of ![]() $T^*I$, we get
$T^*I$, we get
If we plug in ![]() $X_{I,2} = a \partial _t$ and
$X_{I,2} = a \partial _t$ and ![]() $\langle R, h_I \rangle = -1$, we get the desired result.
$\langle R, h_I \rangle = -1$, we get the desired result.
Proposition 1.13 For any ![]() $t \in I$, the
$t \in I$, the ![]() $(U_t, X_t)$ defined above is a convex tube for
$(U_t, X_t)$ defined above is a convex tube for ![]() $\mathcal {L}_t$. Furthermore, the family
$\mathcal {L}_t$. Furthermore, the family ![]() $\{(U_t, X_t)\}_t$ varies smoothly with
$\{(U_t, X_t)\}_t$ varies smoothly with ![]() $t$ and hence is an isotopy of convex tubes for
$t$ and hence is an isotopy of convex tubes for ![]() $\{\mathcal {L}_t\}$.
$\{\mathcal {L}_t\}$.
Proof. From Proposition 1.12 we know that the flow of ![]() $\hat {X}_t$ preserves the fibers of
$\hat {X}_t$ preserves the fibers of ![]() $S^*M \times T_t^* I \to S^*M$ and the induced flow on
$S^*M \times T_t^* I \to S^*M$ and the induced flow on ![]() $S^*M$ is generated by
$S^*M$ is generated by ![]() $X_t$. Since the flow of
$X_t$. Since the flow of ![]() $\hat {X}_t$ shrinks
$\hat {X}_t$ shrinks ![]() $\hat U_t$ to
$\hat U_t$ to ![]() $\hat {\mathcal {L}}_t$, i.e.
$\hat {\mathcal {L}}_t$, i.e. ![]() $\hat {\mathcal {L}}_t = \bigcap _{u > 0} \hat {X}_t^u \hat U_t$, the sequence of open sets
$\hat {\mathcal {L}}_t = \bigcap _{u > 0} \hat {X}_t^u \hat U_t$, the sequence of open sets ![]() $\hat {X}_t^u \hat U_t$ is monotonically decreasing in
$\hat {X}_t^u \hat U_t$ is monotonically decreasing in ![]() $u$; furthermore,
$u$; furthermore, ![]() $\hat \pi _t(\hat {X}_t^u \hat U_t) = X_t^u (U_t)$, so we have
$\hat \pi _t(\hat {X}_t^u \hat U_t) = X_t^u (U_t)$, so we have
The final proposition allows us to upgrade from an isotopy of Liouville hypersurfaces to a strong isotopy of convex tubes.
Proposition 1.14 If ![]() $\mathcal {L}_I$ is a Legendrian in
$\mathcal {L}_I$ is a Legendrian in ![]() $S^*M \times T^*I$ and if
$S^*M \times T^*I$ and if ![]() $\{\mathcal {H}_t\}$ is a smooth family of Liouville hypersurfaces in
$\{\mathcal {H}_t\}$ is a smooth family of Liouville hypersurfaces in ![]() $S^*M$ such that
$S^*M$ such that ![]() $\mathcal {L}_t$ is the skeleton of
$\mathcal {L}_t$ is the skeleton of ![]() $\mathcal {H}_t$, then we have a strong isotopy of convex tubes
$\mathcal {H}_t$, then we have a strong isotopy of convex tubes ![]() $(U_I, X_I)$ around
$(U_I, X_I)$ around ![]() $\mathcal {L}_I$.
$\mathcal {L}_I$.
Proof. First we use ![]() $\mathcal {H}_t$ to get a family of convex tubes
$\mathcal {H}_t$ to get a family of convex tubes ![]() $(U_t, X_t)$ and the associated Hamiltonian functions
$(U_t, X_t)$ and the associated Hamiltonian functions ![]() $h_t$, where
$h_t$, where ![]() $h_t|_{\mathcal {H}_t}=0$ and
$h_t|_{\mathcal {H}_t}=0$ and ![]() $R(h_t)=-1$. The family of functions
$R(h_t)=-1$. The family of functions ![]() $h_t$ determines the lifted function
$h_t$ determines the lifted function ![]() $h_I(x,p,t,\tau ) = h_t(x,p)$ which is defined when
$h_I(x,p,t,\tau ) = h_t(x,p)$ which is defined when ![]() $(x,p) \in U_t$. In turn,
$(x,p) \in U_t$. In turn, ![]() $h_I$ determines the contact vector field
$h_I$ determines the contact vector field ![]() $X_I$, which restricts to the fiber
$X_I$, which restricts to the fiber ![]() $S^*M \times T^*_t I$ as given by Proposition 1.12. Thus, we only need to specify the subset
$S^*M \times T^*_t I$ as given by Proposition 1.12. Thus, we only need to specify the subset ![]() $\hat U_t \subset U_t \times T^*_t I$ such that its boundary
$\hat U_t \subset U_t \times T^*_t I$ such that its boundary ![]() $\partial \hat U_t$ is transverse to the vector field
$\partial \hat U_t$ is transverse to the vector field ![]() $\hat X_t$ and it is compressed by the flow of
$\hat X_t$ and it is compressed by the flow of ![]() $\hat X_t$ to
$\hat X_t$ to ![]() $\hat {\mathcal {L}}_t = \mathcal {L}_I \cap S^*M \times T^*_t I$.
$\hat {\mathcal {L}}_t = \mathcal {L}_I \cap S^*M \times T^*_t I$.
Let
and let
Then the flow ![]() $\hat X_t$ is transverse to the boundary
$\hat X_t$ is transverse to the boundary ![]() $\partial U_t$. We only need to show that
$\partial U_t$. We only need to show that ![]() $\bigcap _{u>0} \hat X_t^u(\hat U_t) = \hat {\mathcal {L}}_t$. Since
$\bigcap _{u>0} \hat X_t^u(\hat U_t) = \hat {\mathcal {L}}_t$. Since ![]() $\hat U_t \to U_t$ with fiber
$\hat U_t \to U_t$ with fiber ![]() $(-C, C)$,
$(-C, C)$, ![]() $\hat X_t$ restricted to the fiber gives the equation for
$\hat X_t$ restricted to the fiber gives the equation for ![]() $\tau$ as
$\tau$ as
This is a contracting flow with unit contraction rate in the sense that for any initial condition ![]() $(\tau _1, \tau _2)$ at
$(\tau _1, \tau _2)$ at ![]() $u=0$ we have
$u=0$ we have ![]() $\tau _1(u)-\tau _2(u) = (\tau _1 - \tau _2) e^{-u}$ for
$\tau _1(u)-\tau _2(u) = (\tau _1 - \tau _2) e^{-u}$ for ![]() $u>0$.
$u>0$.
Under the projection map ![]() $\hat \pi _t: S^*M \times T_t^*I \to S^*M$, we have the surjection
$\hat \pi _t: S^*M \times T_t^*I \to S^*M$, we have the surjection
and by the contracting property of the flow ![]() $\hat X_t$, the fiber can consist of only one point; thus
$\hat X_t$, the fiber can consist of only one point; thus ![]() $\hat \pi _t: \hat {\mathcal {L}}'_t \to \mathcal {L}_t$ is a bijection.
$\hat \pi _t: \hat {\mathcal {L}}'_t \to \mathcal {L}_t$ is a bijection.
Let ![]() $U_I = \bigcup _{t \in I} \hat U_t \subset S^*M \times T^*I$, and put the slices
$U_I = \bigcup _{t \in I} \hat U_t \subset S^*M \times T^*I$, and put the slices ![]() $\hat {\mathcal {L}}'_t$ together into
$\hat {\mathcal {L}}'_t$ together into ![]() $\mathcal {L}'_I = \bigcap _{u > 0} X_I^u U_I$. Recall
$\mathcal {L}'_I = \bigcap _{u > 0} X_I^u U_I$. Recall ![]() $\hat \pi : S^*M \times T^*I \to S^*M \times I$; then
$\hat \pi : S^*M \times T^*I \to S^*M \times I$; then ![]() $\hat \pi (\mathcal {L}_I) = \hat \pi (\mathcal {L}'_I)$ and
$\hat \pi (\mathcal {L}_I) = \hat \pi (\mathcal {L}'_I)$ and ![]() $\mathcal {L}'_I$ is homeomorphic to its image. Since a smooth family of smooth Legendrians in
$\mathcal {L}'_I$ is homeomorphic to its image. Since a smooth family of smooth Legendrians in ![]() $S^*M \times I$ has a unique lift to
$S^*M \times I$ has a unique lift to ![]() $S^*M \times T^*I$,
$S^*M \times T^*I$, ![]() $\:\mathcal {L}_I$ and
$\:\mathcal {L}_I$ and ![]() $\mathcal {L}'_I$ agree over the smooth loci of
$\mathcal {L}'_I$ agree over the smooth loci of ![]() $\hat \pi (\mathcal {L}_I)$. Since
$\hat \pi (\mathcal {L}_I)$. Since ![]() $\mathcal {L}_I$ is the closure of its smooth part, we have
$\mathcal {L}_I$ is the closure of its smooth part, we have ![]() $\mathcal {L}_I = \mathcal {L}'_I$, finishing the proof of the proposition.
$\mathcal {L}_I = \mathcal {L}'_I$, finishing the proof of the proposition.
2. Non-characteristic isotopy of sheaves
2.1 Constructible sheaves
We give a quick working definition of constructible sheaves used in this paper, and refer to [Reference Kashiwara and SchapiraKS13] for a proper treatment. A constructible sheaf ![]() $F$ on
$F$ on ![]() $M$ is a sheaf valued in a chain complex of
$M$ is a sheaf valued in a chain complex of ![]() $\mathbb {C}$-vector spaces, such that its cohomology is locally constant with finite rank with respect to some Whitney stratificationFootnote 1
$\mathbb {C}$-vector spaces, such that its cohomology is locally constant with finite rank with respect to some Whitney stratificationFootnote 1 ![]() $\mathcal {S} = \{\mathcal {S}_\alpha \}_{\alpha \in A}$ on
$\mathcal {S} = \{\mathcal {S}_\alpha \}_{\alpha \in A}$ on ![]() $M$, where the
$M$, where the ![]() $\mathcal {S}_\alpha$ are disjoint locally closed smooth submanifolds with a nice adjacency condition and
$\mathcal {S}_\alpha$ are disjoint locally closed smooth submanifolds with a nice adjacency condition and ![]() $M= \bigsqcup _{\alpha \in A} \mathcal {S}_\alpha$. The singular support
$M= \bigsqcup _{\alpha \in A} \mathcal {S}_\alpha$. The singular support ![]() $SS(F)$ of
$SS(F)$ of ![]() $F$ is a closed conical Lagrangian in
$F$ is a closed conical Lagrangian in ![]() $T^*M$, contained in
$T^*M$, contained in ![]() $\bigcup _{\alpha \in A} T_{\mathcal {S}_\alpha }^* M$, such that
$\bigcup _{\alpha \in A} T_{\mathcal {S}_\alpha }^* M$, such that ![]() $SS(F) \cap T^*_M M$ equals the support of
$SS(F) \cap T^*_M M$ equals the support of ![]() $F$ and
$F$ and ![]() $(p,q) \in SS(F) \backslash T^*_M M$ if there exists a locally defined function
$(p,q) \in SS(F) \backslash T^*_M M$ if there exists a locally defined function ![]() $f$ with
$f$ with ![]() $f(q)=0$ and
$f(q)=0$ and ![]() $df(q)=p$ such that the restriction map
$df(q)=p$ such that the restriction map ![]() $F(B_\epsilon (q) \cap \{f<\delta \}) \to F(B_\epsilon (q) \cap \{f<-\delta \})$ fails to be a quasi-isomorphism for
$F(B_\epsilon (q) \cap \{f<\delta \}) \to F(B_\epsilon (q) \cap \{f<-\delta \})$ fails to be a quasi-isomorphism for ![]() $0 < \delta \ll \epsilon \ll 1$. We denote by
$0 < \delta \ll \epsilon \ll 1$. We denote by ![]() $SS^\infty (F) = SS(F) \cap S^*M$ the singular support of
$SS^\infty (F) = SS(F) \cap S^*M$ the singular support of ![]() $F$ at infinity.
$F$ at infinity.
If ![]() $\Lambda \subset T^*M$ is a conical Lagrangian containing the zero-section (as assumed throughout this paper), we write
$\Lambda \subset T^*M$ is a conical Lagrangian containing the zero-section (as assumed throughout this paper), we write ![]() $Sh(M, \Lambda ^\infty )$ for the dg derived category of constructible sheaves with object
$Sh(M, \Lambda ^\infty )$ for the dg derived category of constructible sheaves with object ![]() $F$ satisfying
$F$ satisfying ![]() $SS^\infty (F) \subset \Lambda ^\infty$.
$SS^\infty (F) \subset \Lambda ^\infty$.
Example 2.1 On ![]() $\mathbb {R}$, let
$\mathbb {R}$, let ![]() $\mathbb {C}_{[0,1]}$ (respectively
$\mathbb {C}_{[0,1]}$ (respectively ![]() $\mathbb {C}_{(0,1)}$) denote the constant sheaf with stalk
$\mathbb {C}_{(0,1)}$) denote the constant sheaf with stalk ![]() $\mathbb {C}$ on
$\mathbb {C}$ on ![]() $[0,1]$ (respectively on
$[0,1]$ (respectively on ![]() $(0,1)$) and zero stalk elsewhere. Then the singular supports of
$(0,1)$) and zero stalk elsewhere. Then the singular supports of ![]() $\mathbb {C}_{[0,1]}$ and
$\mathbb {C}_{[0,1]}$ and ![]() $\mathbb {C}_{(0,1)}$ in
$\mathbb {C}_{(0,1)}$ in ![]() $T^*\mathbb {R}$ are
$T^*\mathbb {R}$ are

Example 2.2 Let ![]() $j: U=B(0,1) \hookrightarrow \mathbb {R}^2$ be the inclusion of an open unit ball in
$j: U=B(0,1) \hookrightarrow \mathbb {R}^2$ be the inclusion of an open unit ball in ![]() $\mathbb {R}^2$. Then
$\mathbb {R}^2$. Then ![]() $j_* \mathbb {C}_U$ is supported on the closed set
$j_* \mathbb {C}_U$ is supported on the closed set ![]() $\overline U$, with singular support at infinity as
$\overline U$, with singular support at infinity as

And ![]() $j_! \mathbb {C}_U$ is supported on the open set
$j_! \mathbb {C}_U$ is supported on the open set ![]() $U$, with singular support at infinity given by
$U$, with singular support at infinity given by

Here the Legendrians are represented by co-oriented hypersurfaces in ![]() $\mathbb {R}^2$ with hairs indicating the co-orientation.
$\mathbb {R}^2$ with hairs indicating the co-orientation.
2.2 Operation on sheaves
In this subsection, we deviate from our running convention and use ![]() $Sh(X)$ to denote the co-complete dg derived category of sheaves on
$Sh(X)$ to denote the co-complete dg derived category of sheaves on ![]() $X$ without any constructibility condition. Let
$X$ without any constructibility condition. Let ![]() $f: Y \to X$ be a map of real analytic manifolds. Then we have the following pairs of adjoint functors:
$f: Y \to X$ be a map of real analytic manifolds. Then we have the following pairs of adjoint functors:
 \begin{align*} - \otimes F&{:}\, Sh(X) \leftrightarrow Sh(X) {:}\, \mathcal{H}om(F, -),\\ f^*&{:}\, Sh(X) \leftrightarrow Sh(Y) {:}\, f_* ,\\ f_!&{:}\, Sh(Y) \leftrightarrow Sh(X){:}\, f^!. \end{align*}
\begin{align*} - \otimes F&{:}\, Sh(X) \leftrightarrow Sh(X) {:}\, \mathcal{H}om(F, -),\\ f^*&{:}\, Sh(X) \leftrightarrow Sh(Y) {:}\, f_* ,\\ f_!&{:}\, Sh(Y) \leftrightarrow Sh(X){:}\, f^!. \end{align*}
Given an open subset ![]() $U$ of
$U$ of ![]() $X$ and its closed complement
$X$ and its closed complement ![]() $Z$,
$Z$,
we have ![]() $j^* = j^!$ and
$j^* = j^!$ and ![]() $i_*=i_!$. Furthermore, there are exact triangles
$i_*=i_!$. Furthermore, there are exact triangles
These are sheaf-theoretic incarnations of excisions: upon applying to the constant sheaf on ![]() $X$ and taking global sections, we get
$X$ and taking global sections, we get
Let ![]() $X_i$,
$X_i$, ![]() $i=1,2$, be spaces, and let
$i=1,2$, be spaces, and let ![]() $K \in Sh(X_1 \times X_2)$. We define the pair of adjoint functors
$K \in Sh(X_1 \times X_2)$. We define the pair of adjoint functors
In [Reference Kashiwara and SchapiraKS13], ![]() $K_! = \Phi _K$ and
$K_! = \Phi _K$ and ![]() $K^!=\Psi _K$ with
$K^!=\Psi _K$ with ![]() $X_1$ and
$X_1$ and ![]() $X_2$ switched. The notation here is suggestive of their being adjoint functors.
$X_2$ switched. The notation here is suggestive of their being adjoint functors.
2.3 Isotopy of constructible sheaves
Let ![]() $I =(a,b) \subset \mathbb {R}$. For any
$I =(a,b) \subset \mathbb {R}$. For any ![]() $t \in I$, let
$t \in I$, let
be the inclusion of the ![]() $t$-slice
$t$-slice ![]() $M_t$ into the total space
$M_t$ into the total space ![]() $M_I$, and let
$M_I$, and let ![]() $\pi _I: M_I \to I$ be the projection. Let
$\pi _I: M_I \to I$ be the projection. Let ![]() $\mathbb {C}_{M_t}$ be the constant sheaf on
$\mathbb {C}_{M_t}$ be the constant sheaf on ![]() $M_t$ with stalk
$M_t$ with stalk ![]() $\mathbb {C}$. We then have
$\mathbb {C}$. We then have
Definition 2.3 Let ![]() $M$ be a smooth manifold and
$M$ be a smooth manifold and ![]() $I$ a closed interval of
$I$ a closed interval of ![]() $\mathbb {R}$.
$\mathbb {R}$.
(i) An isotopy of (constructible) sheaves is a constructible sheaf
 $F_I \in Sh(M \times I)$ such that
$F_I \in Sh(M \times I)$ such that  $SS^\infty (F_I)$ is a strong isotopy of Legendrians in
$SS^\infty (F_I)$ is a strong isotopy of Legendrians in  $S^*M \times T^* I$ (Definition 0.4). Equivalently, for any
$S^*M \times T^* I$ (Definition 0.4). Equivalently, for any  $t \in I$ we have
If
$t \in I$ we have
If \[ SS^\infty(F_I) \cap SS^\infty(\mathbb{C}_{M_t}) = \emptyset. \]
\[ SS^\infty(F_I) \cap SS^\infty(\mathbb{C}_{M_t}) = \emptyset. \]
 $F_I$ is an isotopy of sheaves, then for any
$F_I$ is an isotopy of sheaves, then for any  $t \in I$ we denote the restriction of
$t \in I$ we denote the restriction of  $F_I$ at
$F_I$ at  $t$ by
$t$ by
 \[ F_t: = F_I|_{M_t} \in Sh(M). \]
\[ F_t: = F_I|_{M_t} \in Sh(M). \]
(ii) Two isotopies of sheaves
 $F_I, G_I \in Sh(M \times I)$ are said to be non-characteristic if
$F_I, G_I \in Sh(M \times I)$ are said to be non-characteristic if
 \[ SS^\infty(F_I)|_t \cap SS^\infty(G_I)|_t = \emptyset \quad \text{for all }t \in I. \]
\[ SS^\infty(F_I)|_t \cap SS^\infty(G_I)|_t = \emptyset \quad \text{for all }t \in I. \]
Some easy-to-check properties are the following.
Proposition 2.4 Let ![]() $M$ be a compact real analytic manifold.
$M$ be a compact real analytic manifold.
(1) If
 $F_I$ is an isotopy of sheaves and
$F_I$ is an isotopy of sheaves and  $\Lambda ^\infty _I = SS^\infty (F_I)$, then
$\Lambda ^\infty _I = SS^\infty (F_I)$, then
 \[ SS^\infty(F_t) \subset \Lambda^\infty_t. \]
\[ SS^\infty(F_t) \subset \Lambda^\infty_t. \]
(2) If
 $F_I$ is an isotopy of sheaves and
$F_I$ is an isotopy of sheaves and  $\pi _I: M_I \to I$, then
$\pi _I: M_I \to I$, then  $(\pi _I)_* F_I$ is a local system on
$(\pi _I)_* F_I$ is a local system on  $I$.
$I$.
2.4 Invariance of morphisms under non-characteristic isotopies
We use the same notation for ![]() $M_I=M \times I, \,M_t, \,\mathbb {C}_{M_t}$ etc. as in the previous subsection.
$M_I=M \times I, \,M_t, \,\mathbb {C}_{M_t}$ etc. as in the previous subsection.
Lemma 2.5 Let ![]() $F \in Sh(M)$ and let
$F \in Sh(M)$ and let ![]() $\varphi : M \to \mathbb {R}$ be a
$\varphi : M \to \mathbb {R}$ be a ![]() $C^1$ function such that
$C^1$ function such that ![]() $d\varphi (x)\neq 0$ for
$d\varphi (x)\neq 0$ for ![]() $x \in \varphi ^{-1}([0,1])$.
$x \in \varphi ^{-1}([0,1])$.
(1) For
 $s \in (0,1)$ let
$s \in (0,1)$ let  $U_s = \{x: \varphi (x) < s \}$, and let
$U_s = \{x: \varphi (x) < s \}$, and let  $U_1 = \bigcup _{s} U_s$. If
then
$U_1 = \bigcup _{s} U_s$. If
then \[ SS^\infty(\mathbb{C}_{U_s}) \cap SS^\infty(F) = \emptyset \quad \text{for all } 0< s<1, \]
\[ SS^\infty(\mathbb{C}_{U_s}) \cap SS^\infty(F) = \emptyset \quad \text{for all } 0< s<1, \]
 \[ \operatorname{Hom}(\mathbb{C}_{U_1}, F) \xrightarrow{\sim} \operatorname{Hom}(\mathbb{C}_{U_s}, F)\quad \text{for all } 0< s<1. \]
\[ \operatorname{Hom}(\mathbb{C}_{U_1}, F) \xrightarrow{\sim} \operatorname{Hom}(\mathbb{C}_{U_s}, F)\quad \text{for all } 0< s<1. \]
(2) For
 $s \in (0,1)$ let
$s \in (0,1)$ let  $Z_s = \{x: \varphi (x) \leqslant s \}$, and let
$Z_s = \{x: \varphi (x) \leqslant s \}$, and let  $Z_0 = \bigcap _{s} Z_s$. If
then
$Z_0 = \bigcap _{s} Z_s$. If
then \[ SS^\infty(\mathbb{C}_{Z_s}) \cap SS^\infty(F) = \emptyset\quad \text{for all } 0< s<1, \]
\[ SS^\infty(\mathbb{C}_{Z_s}) \cap SS^\infty(F) = \emptyset\quad \text{for all } 0< s<1, \]
 \[ \operatorname{Hom}(\mathbb{C}_{Z_s}, F) \xrightarrow{\sim} \operatorname{Hom}(\mathbb{C}_{Z_0}, F)\quad \text{for all } 0< s<1. \]
\[ \operatorname{Hom}(\mathbb{C}_{Z_s}, F) \xrightarrow{\sim} \operatorname{Hom}(\mathbb{C}_{Z_0}, F)\quad \text{for all } 0< s<1. \]
Proof. Assertion (1) is a special case of [Reference Guillermou, Kashiwara and SchapiraGKS12, Proposition 1.8]. Assertion (2) follows from (1) and the fact that
The following lemma is also often used.
Lemma 2.6 (Petrowsky theorem for sheaves [Reference Kashiwara and SchapiraKS13])
Let ![]() $F, G \in Sh(M)$ be (cohomologically) constructible complexes of sheaves. If
$F, G \in Sh(M)$ be (cohomologically) constructible complexes of sheaves. If ![]() $SS^\infty (F) \cap SS^\infty (G) = \emptyset$, then the natural morphism
$SS^\infty (F) \cap SS^\infty (G) = \emptyset$, then the natural morphism
is an isomorphism.
Corollary 2.7 If ![]() $F_I$ is an isotopy of sheaves, then
$F_I$ is an isotopy of sheaves, then
Proposition 2.8 Let ![]() $G_I$ and
$G_I$ and ![]() $F_I$ be non-characteristic isotopies of sheaves; then
$F_I$ be non-characteristic isotopies of sheaves; then ![]() $\mathcal {H}om(F_I, G_I)$ is an isotopy of sheaves. In particular,
$\mathcal {H}om(F_I, G_I)$ is an isotopy of sheaves. In particular,
Proof. As ![]() $G_I$ and
$G_I$ and ![]() $F_I$ being non-characteristic implies
$F_I$ being non-characteristic implies ![]() $SS^\infty (G_I) \cap SS^\infty (F_I) = \emptyset$, we can bound the singular support of the hom-sheaf as [Reference Kashiwara and SchapiraKS13]
$SS^\infty (G_I) \cap SS^\infty (F_I) = \emptyset$, we can bound the singular support of the hom-sheaf as [Reference Kashiwara and SchapiraKS13]
Again, using that ![]() $G_I$ and
$G_I$ and ![]() $F_I$ are non-characteristic, we obtain
$F_I$ are non-characteristic, we obtain
Hence ![]() $\mathcal {H}om(F_I, G_I)$ is an isotopy of sheaves. For the second statement, we have
$\mathcal {H}om(F_I, G_I)$ is an isotopy of sheaves. For the second statement, we have
 \begin{align} \operatorname{Hom}(F_t, G_t) &= \operatorname{Hom}({j_t}^* F_I, {j_t}^* G_I) \simeq \operatorname{Hom}(F_I, {j_t}_* j_t^* G_I) \simeq \operatorname{Hom}(F_I, \mathbb{C}_{M_t} \otimes G_I) \nonumber\\ &\simeq \operatorname{Hom}(F_I, \mathcal{H}om(\mathbb{C}_{M_t}, G_I)[1]) \simeq \operatorname{Hom}(\mathbb{C}_{M_t}, \mathcal{H}om(F_I, G_I))[1] \nonumber\\ &\simeq \operatorname{Hom}(\mathbb{C}_t, \pi_{I*} \mathcal{H}om(F_I, G_I))[1] \simeq [\pi_{I*} \mathcal{H}om(F_I, G_I)]_t . \end{align}
\begin{align} \operatorname{Hom}(F_t, G_t) &= \operatorname{Hom}({j_t}^* F_I, {j_t}^* G_I) \simeq \operatorname{Hom}(F_I, {j_t}_* j_t^* G_I) \simeq \operatorname{Hom}(F_I, \mathbb{C}_{M_t} \otimes G_I) \nonumber\\ &\simeq \operatorname{Hom}(F_I, \mathcal{H}om(\mathbb{C}_{M_t}, G_I)[1]) \simeq \operatorname{Hom}(\mathbb{C}_{M_t}, \mathcal{H}om(F_I, G_I))[1] \nonumber\\ &\simeq \operatorname{Hom}(\mathbb{C}_t, \pi_{I*} \mathcal{H}om(F_I, G_I))[1] \simeq [\pi_{I*} \mathcal{H}om(F_I, G_I)]_t . \end{align}
The result then follows since ![]() $\pi _{I*}(\mathcal {H}om(F_I, G_I))$ is a local system.
$\pi _{I*}(\mathcal {H}om(F_I, G_I))$ is a local system.
2.5 Invariance of morphisms under Reeb perturbations
Sometimes we want to vary ![]() $G$ and
$G$ and ![]() $F$ while preserving
$F$ while preserving ![]() $\operatorname {Hom}(F,G)$, but
$\operatorname {Hom}(F,G)$, but ![]() $SS^\infty (G) \cap SS^\infty (F) \neq \emptyset$, e.g.
$SS^\infty (G) \cap SS^\infty (F) \neq \emptyset$, e.g. ![]() $F=G$. Here we borrow an idea from the infinitesimally wrapped Fukaya category [Reference Nadler and ZaslowNZ09], namely that to compute
$F=G$. Here we borrow an idea from the infinitesimally wrapped Fukaya category [Reference Nadler and ZaslowNZ09], namely that to compute ![]() $\operatorname {Hom}_{Fuk}( L_1, L_2)$ one needs to perform a perturbation to separate
$\operatorname {Hom}_{Fuk}( L_1, L_2)$ one needs to perform a perturbation to separate ![]() $L_1$ and
$L_1$ and ![]() $L_2$ at infinity; one can perturb
$L_2$ at infinity; one can perturb ![]() $L_2 \leadsto R^t L_2$ or
$L_2 \leadsto R^t L_2$ or ![]() $L_1 \leadsto R^{-t} L_1$, where
$L_1 \leadsto R^{-t} L_1$, where ![]() $R^t$ is the unit-speed geodesic flow on
$R^t$ is the unit-speed geodesic flow on ![]() $T^*M$ (smoothed near the zero-section) for positive small times
$T^*M$ (smoothed near the zero-section) for positive small times ![]() $t$, small enough that no new intersections are created between
$t$, small enough that no new intersections are created between ![]() $L_1$ and
$L_1$ and ![]() $L_2$ at infinity.
$L_2$ at infinity.
Fix a Riemannian metric ![]() $g$ on
$g$ on ![]() $M$ and identify
$M$ and identify ![]() $S^*M$ with
$S^*M$ with ![]() $T^\infty M$, so that the Reeb flow
$T^\infty M$, so that the Reeb flow ![]() $R^t$ is the unit-speed geodesic flow. Let
$R^t$ is the unit-speed geodesic flow. Let ![]() $r_{\rm inj}(M, g)$ be the injective radius of
$r_{\rm inj}(M, g)$ be the injective radius of ![]() $(M,g)$. Let
$(M,g)$. Let ![]() $\hat R^t$ be the GKS quantization of
$\hat R^t$ be the GKS quantization of ![]() $R^t$. The rest of this subsection will be devoted to proving the following proposition.
$R^t$. The rest of this subsection will be devoted to proving the following proposition.
Proposition 2.9 Let ![]() $\Lambda ^\infty \subset T^\infty M$ be a Legendrian, and let
$\Lambda ^\infty \subset T^\infty M$ be a Legendrian, and let ![]() $0 < \epsilon < r_{\rm inj}(M, g)$ be small enough that
$0 < \epsilon < r_{\rm inj}(M, g)$ be small enough that
(1) For any
 $F \in Sh(M, \Lambda )$ and
$F \in Sh(M, \Lambda )$ and  $0\leqslant t<\epsilon$, we have a canonical morphism
$0\leqslant t<\epsilon$, we have a canonical morphism
 \[ F \to \hat R^t F. \]
\[ F \to \hat R^t F. \]
(2) For any
 $F,G \in Sh(M, \Lambda )$ and
$F,G \in Sh(M, \Lambda )$ and  $0 \leqslant t<\epsilon$, we have canonical quasi-isomorphisms
$0 \leqslant t<\epsilon$, we have canonical quasi-isomorphisms
 \[ \operatorname{Hom}(F, G) \xrightarrow{\sim} \operatorname{Hom}(F, \hat R^t G), \quad \operatorname{Hom}(F, G) \xrightarrow{\sim} \operatorname{Hom}(\hat R^{-t}F, G). \]
\[ \operatorname{Hom}(F, G) \xrightarrow{\sim} \operatorname{Hom}(F, \hat R^t G), \quad \operatorname{Hom}(F, G) \xrightarrow{\sim} \operatorname{Hom}(\hat R^{-t}F, G). \]
Proof. For any ![]() $0\leqslant t < \epsilon$, define
$0\leqslant t < \epsilon$, define
Then, from [Reference Guillermou, Kashiwara and SchapiraGKS12], we have
and
where ![]() $\pi _1$ and
$\pi _1$ and ![]() $\pi _2$ are the projections from
$\pi _2$ are the projections from ![]() $M \times M$ to the first and second factors, and
$M \times M$ to the first and second factors, and ![]() $\mathcal {H}om$ is the (dg derived) sheaf-hom. From the canonical restriction morphism
$\mathcal {H}om$ is the (dg derived) sheaf-hom. From the canonical restriction morphism ![]() $K_t \to K_0=\mathbb {C}_\Delta$, where
$K_t \to K_0=\mathbb {C}_\Delta$, where ![]() $\Delta \subset M \times M$ is the diagonal subset, we have
$\Delta \subset M \times M$ is the diagonal subset, we have
For statement (2) of the proposition, we first prove the following lemma.
Lemma 2.10 We have that
Proof. We identify the contact infinity ![]() $T^\infty M$ with the unit cosphere bundle
$T^\infty M$ with the unit cosphere bundle ![]() $S^*M$. Assume that the intersection is non-empty and contains the point
$S^*M$. Assume that the intersection is non-empty and contains the point ![]() $(x_1, x_2, p_1, p_2)$. Since
$(x_1, x_2, p_1, p_2)$. Since ![]() $(x_1, x_2; p_1, p_2) \in SS^\infty (K_t)$, we have
$(x_1, x_2; p_1, p_2) \in SS^\infty (K_t)$, we have
Since ![]() $t < \epsilon < r_{\rm inj}(M,g)$, there is a unique length-
$t < \epsilon < r_{\rm inj}(M,g)$, there is a unique length-![]() $t$ geodesic
$t$ geodesic ![]() $\gamma$ connecting
$\gamma$ connecting ![]() $x_1$ and
$x_1$ and ![]() $x_2$, and
$x_2$, and ![]() $p_i$ is the unit tangent vector along
$p_i$ is the unit tangent vector along ![]() $\gamma$ at
$\gamma$ at ![]() $x_i$ pointing to the interior of the geodesic,
$x_i$ pointing to the interior of the geodesic,
Hence the geodesic flow on ![]() $S^*M$ relates
$S^*M$ relates ![]() $(x_i, p_i)$ via
$(x_i, p_i)$ via
On the other hand, since ![]() $(x_1, x_2; p_1, p_2) \in SS^\infty (\mathcal {H}om(\pi _1^*F, \pi _2^! G))$, we have
$(x_1, x_2; p_1, p_2) \in SS^\infty (\mathcal {H}om(\pi _1^*F, \pi _2^! G))$, we have
Hence, combining (8) and (9), we have
This contradicts the displaceability of ![]() $\Lambda ^\infty$ for
$\Lambda ^\infty$ for ![]() $t < \epsilon$.
$t < \epsilon$.
Now we come back to the proof of Proposition 2.9. We have
 \begin{align*} \operatorname{Hom}(F, G) &\simeq \Gamma(M, \mathcal{H}om(F,G)) \\ &\simeq \Gamma(M \times M, \mathcal{H}om(\mathbb{C}_\Delta, \mathcal{H}om(\pi_1^*F,\pi_2^!G))) \\ &\xrightarrow{\sim} \Gamma(M \times M, \mathcal{H}om(K_t, \mathcal{H}om(\pi_1^*F,\pi_2^!G))) \\ &\simeq \Gamma(M \times M, \mathcal{H}om(\pi_1^*F, \mathcal{H}om(K_t,\pi_2^!G))) \\ &\simeq \Gamma(M, \mathcal{H}om(F, \pi_{1*}\mathcal{H}om(K_t,\pi_2^!G))) \\ &\simeq \operatorname{Hom}(F, \hat R^t G), \end{align*}
\begin{align*} \operatorname{Hom}(F, G) &\simeq \Gamma(M, \mathcal{H}om(F,G)) \\ &\simeq \Gamma(M \times M, \mathcal{H}om(\mathbb{C}_\Delta, \mathcal{H}om(\pi_1^*F,\pi_2^!G))) \\ &\xrightarrow{\sim} \Gamma(M \times M, \mathcal{H}om(K_t, \mathcal{H}om(\pi_1^*F,\pi_2^!G))) \\ &\simeq \Gamma(M \times M, \mathcal{H}om(\pi_1^*F, \mathcal{H}om(K_t,\pi_2^!G))) \\ &\simeq \Gamma(M, \mathcal{H}om(F, \pi_{1*}\mathcal{H}om(K_t,\pi_2^!G))) \\ &\simeq \operatorname{Hom}(F, \hat R^t G), \end{align*}
where in the third step we used the canonical morphism ![]() $K_t \to \mathbb {C}_\Delta$ when replacing
$K_t \to \mathbb {C}_\Delta$ when replacing ![]() $\mathbb {C}_\Delta$ by
$\mathbb {C}_\Delta$ by ![]() $K_t$, and used Lemmas 2.10 and 2.5(2) to show that it is a quasi-isomorphism.
$K_t$, and used Lemmas 2.10 and 2.5(2) to show that it is a quasi-isomorphism.
We will use the following purely sheaf-theoretic statement later to study the family of GKS quantization.
Proposition 2.11 Let ![]() $I=(0,1)$, and let
$I=(0,1)$, and let ![]() $K_I \in Sh(M \times M \times I)$ be an isotopy of sheaves such that
$K_I \in Sh(M \times M \times I)$ be an isotopy of sheaves such that ![]() $K_t = \mathbb {C}_{\Delta _t}$ for some closed subsets
$K_t = \mathbb {C}_{\Delta _t}$ for some closed subsets ![]() $\{\Delta _t\}_{0< t<1}$ satisfying
$\{\Delta _t\}_{0< t<1}$ satisfying
Let ![]() $F, G \in Sh(M, \Lambda )$, and let
$F, G \in Sh(M, \Lambda )$, and let ![]() $\mathcal {H}om(\pi _1^*F,\pi _2^!G) \in Sh(M \times M)$ be the hom-sheaf. Assume that
$\mathcal {H}om(\pi _1^*F,\pi _2^!G) \in Sh(M \times M)$ be the hom-sheaf. Assume that
then
where ![]() $K_t^!, K_{t!}$ are defined in (5).
$K_t^!, K_{t!}$ are defined in (5).
The proof is exactly the same as that of Proposition 2.9(2), where the condition provided in Lemma 2.10 is put into the hypothesis, so we do not repeat it here.
2.6 Limit of contact isotopy
Let ![]() $I=(0,1)$ and define the inclusions
$I=(0,1)$ and define the inclusions
Proposition 2.12 [Reference Treumann, Williams and ZaslowTWZ19, Lemma 7.1]
Let ![]() $F_I \in Sh(M_I)$ be an isotopy of constructible sheaves, and let
$F_I \in Sh(M_I)$ be an isotopy of constructible sheaves, and let ![]() $\Lambda ^\infty _I = SS^\infty (F_I)$. Suppose the family
$\Lambda ^\infty _I = SS^\infty (F_I)$. Suppose the family ![]() ${(\Lambda _t^\infty, t)} \subset T^\infty M \times (0,1)$ has a closure in
${(\Lambda _t^\infty, t)} \subset T^\infty M \times (0,1)$ has a closure in ![]() $T^\infty M \times [0,1)$ whose intersection with
$T^\infty M \times [0,1)$ whose intersection with ![]() $T^\infty M \times \{0\}$ is a Legendrian
$T^\infty M \times \{0\}$ is a Legendrian ![]() $\Lambda _0^\infty$. Then the sheaf
$\Lambda _0^\infty$. Then the sheaf
has ![]() $SS^\infty (F_0) \subset \Lambda ^\infty _0$.
$SS^\infty (F_0) \subset \Lambda ^\infty _0$.
Proof. These are corollaries of results in [Reference Kashiwara and SchapiraKS13]. By [Reference Kashiwara and SchapiraKS13, Theorem 6.3.1], a point ![]() $(x,p; 0, -1) \in \dot T^*M \times T^*\mathbb {R}$ belongs to
$(x,p; 0, -1) \in \dot T^*M \times T^*\mathbb {R}$ belongs to ![]() $SS((j_I)_* F_I)$ only if
$SS((j_I)_* F_I)$ only if ![]() $(x,p)$ is the limit of a sequence of points
$(x,p)$ is the limit of a sequence of points ![]() $(x_n, p_n) \in \Lambda _{t_n}$ where
$(x_n, p_n) \in \Lambda _{t_n}$ where ![]() $t_n \to 0$, i.e.
$t_n \to 0$, i.e. ![]() $(x,p) \in \Lambda _0$. By [Reference Kashiwara and SchapiraKS13, Proposition 5.4.5],
$(x,p) \in \Lambda _0$. By [Reference Kashiwara and SchapiraKS13, Proposition 5.4.5], ![]() $SS(F_0) \subset SS((j_I)_* F_I)|_0 = \Lambda _0$; hence
$SS(F_0) \subset SS((j_I)_* F_I)|_0 = \Lambda _0$; hence ![]() $SS^\infty (F_0) \subset \Lambda _0^\infty$.
$SS^\infty (F_0) \subset \Lambda _0^\infty$.
Let ![]() $(U,X)$ be a convex tube for a Legendrian
$(U,X)$ be a convex tube for a Legendrian ![]() $\mathcal {L} \subset S^*M$. Let
$\mathcal {L} \subset S^*M$. Let ![]() $X$ be extended from a neighborhood of
$X$ be extended from a neighborhood of ![]() $\bar U$ to all of
$\bar U$ to all of ![]() $S^*M$. Let
$S^*M$. Let
be the sheaf quantization of the flow ![]() $X$, and let
$X$, and let
Then we define the functor ![]() $\Pi _X: = ({\rm id}_M \times j_\infty )^* \circ ({\rm id}_M \times j_{[0,\infty )})_* \circ \hat X^{[0,\infty )}: Sh(M) \to Sh(M).$
$\Pi _X: = ({\rm id}_M \times j_\infty )^* \circ ({\rm id}_M \times j_{[0,\infty )})_* \circ \hat X^{[0,\infty )}: Sh(M) \to Sh(M).$
Let ![]() $Sh(M, U)$ denote the subcategory of
$Sh(M, U)$ denote the subcategory of ![]() $Sh(M)$ consisting of sheaves
$Sh(M)$ consisting of sheaves ![]() $F$ with
$F$ with ![]() $SS^\infty (F) \subset U$.
$SS^\infty (F) \subset U$.
Proposition 2.13 When restricted to ![]() $Sh(M, U)$, we have that
$Sh(M, U)$, we have that
Proof. This follows from the definition of a convex tube and Proposition 2.12.
3. Existence and uniqueness of the extension
In this section we prove our main result, Theorem 0.5. In this section, we will sometimes identify ![]() $\Lambda ^\infty _t \subset T^\infty M$ with
$\Lambda ^\infty _t \subset T^\infty M$ with ![]() $\mathcal {L}_t \subset S^*M$ and identify Reeb flow with geodesic flow.
$\mathcal {L}_t \subset S^*M$ and identify Reeb flow with geodesic flow.
3.1 Uniqueness of extension
Recall from Proposition 1.9 that existence of strong isotopy of convex tubes implies uniform displaceability of the family ![]() $\{\mathcal {L}_t\}$.
$\{\mathcal {L}_t\}$.
Proposition 3.1 Let ![]() $\Lambda ^\infty _t$ be a family of Legendrians in
$\Lambda ^\infty _t$ be a family of Legendrians in ![]() $T^\infty M$ that are uniformly displaceable with parameter
$T^\infty M$ that are uniformly displaceable with parameter ![]() $\epsilon$. Then the restriction functor
$\epsilon$. Then the restriction functor ![]() $\iota _t^*$ is fully faithful for all
$\iota _t^*$ is fully faithful for all ![]() $t$.
$t$.
Proof. For ![]() $0 \leqslant s < \epsilon$ we define a family of kernels in
$0 \leqslant s < \epsilon$ we define a family of kernels in ![]() $Sh((M_1 \times I_1) \times (M_2 \times I_2))$ as
$Sh((M_1 \times I_1) \times (M_2 \times I_2))$ as
One can check that ![]() $K_s$ generates the slicewise geodesic flow, i.e. if
$K_s$ generates the slicewise geodesic flow, i.e. if ![]() $F_I \in Sh(M_I)$ and
$F_I \in Sh(M_I)$ and
then
where ![]() $\pi _i$ is the projection from
$\pi _i$ is the projection from ![]() $(M_1 \times I_1) \times (M_2 \times I_2)$ to
$(M_1 \times I_1) \times (M_2 \times I_2)$ to ![]() $M_i \times I_i$ and
$M_i \times I_i$ and ![]() $R^s$ is the Reeb (geodesic) flow for time
$R^s$ is the Reeb (geodesic) flow for time ![]() $s$.
$s$.
We first prove the following claim: for any ![]() $F_I, G_I \in Sh(M_I, \Lambda ^\infty _I)$,
$F_I, G_I \in Sh(M_I, \Lambda ^\infty _I)$,
It suffices to prove the case for the right endpoint ![]() $b$. To use the estimate of the singular support of the hom-sheaf, we would like to perturb
$b$. To use the estimate of the singular support of the hom-sheaf, we would like to perturb ![]() $G_I$ by the fiberwise Reeb flow.
$G_I$ by the fiberwise Reeb flow.
Lemma 3.2 For any ![]() $0< s<\epsilon$,
$0< s<\epsilon$,
Furthermore, ![]() $\operatorname {Hom}(\mathbb {C}_{M \times \{t\}}, \mathcal {H}om(F_I, K_s^!G_I))$ is independent of
$\operatorname {Hom}(\mathbb {C}_{M \times \{t\}}, \mathcal {H}om(F_I, K_s^!G_I))$ is independent of ![]() $t$. The same is true if we replace
$t$. The same is true if we replace ![]() $\{t\}$ by any subinterval, e.g.
$\{t\}$ by any subinterval, e.g. ![]() $[a,b]$ and
$[a,b]$ and ![]() $(a,b)$ of
$(a,b)$ of ![]() $I$.
$I$.
Proof. Unwinding the definition of ![]() $K_s^!$, we have
$K_s^!$, we have
 \begin{align*} &\operatorname{Hom}(\mathbb{C}_{M \times \{t\}}, \mathcal{H}om(F_I, K_s^!G_I)) \\ &\quad=\operatorname{Hom}(\mathbb{C}_{M \times \{t\}}, \mathcal{H}om(F_I, \pi_{1*} \mathcal{H}om(K_s, \pi_2^! G_I))) \\ &\quad=\operatorname{Hom}(\mathbb{C}_{M \times \{t\}}, \pi_{1*} \mathcal{H}om(\pi_1^* F_I, \mathcal{H}om(K_s, \pi_2^! G_I))) \\ &\quad=\operatorname{Hom}(\pi_1^* \mathbb{C}_{M \times \{t\}}, \mathcal{H}om(K_s, \mathcal{H}om(\pi_1^* F_I, \pi_2^! G_I))). \end{align*}
\begin{align*} &\operatorname{Hom}(\mathbb{C}_{M \times \{t\}}, \mathcal{H}om(F_I, K_s^!G_I)) \\ &\quad=\operatorname{Hom}(\mathbb{C}_{M \times \{t\}}, \mathcal{H}om(F_I, \pi_{1*} \mathcal{H}om(K_s, \pi_2^! G_I))) \\ &\quad=\operatorname{Hom}(\mathbb{C}_{M \times \{t\}}, \pi_{1*} \mathcal{H}om(\pi_1^* F_I, \mathcal{H}om(K_s, \pi_2^! G_I))) \\ &\quad=\operatorname{Hom}(\pi_1^* \mathbb{C}_{M \times \{t\}}, \mathcal{H}om(K_s, \mathcal{H}om(\pi_1^* F_I, \pi_2^! G_I))). \end{align*}
We claim that
The verification is straightforward, though a bit tedious, and we leave it to the reader.
From this claim and the fact that
 \begin{align*} &\operatorname{Hom}(\pi_1^* \mathbb{C}_{M \times \{t\}}, \mathcal{H}om(K_s, \mathcal{H}om(\pi_1^* F_I, \pi_2^! G_I)))\\ &\quad \simeq \operatorname{Hom}(\pi_1^* \mathbb{C}_{M \times \{t\}} \otimes K_s, \mathcal{H}om(\pi_1^* F_I, \pi_2^! G_I)), \end{align*}
\begin{align*} &\operatorname{Hom}(\pi_1^* \mathbb{C}_{M \times \{t\}}, \mathcal{H}om(K_s, \mathcal{H}om(\pi_1^* F_I, \pi_2^! G_I)))\\ &\quad \simeq \operatorname{Hom}(\pi_1^* \mathbb{C}_{M \times \{t\}} \otimes K_s, \mathcal{H}om(\pi_1^* F_I, \pi_2^! G_I)), \end{align*}
we may apply Lemma 2.5(2) on the shrinking closed set to get
for all ![]() $0< s<\epsilon$. This proves the first statement of the lemma.
$0< s<\epsilon$. This proves the first statement of the lemma.
The statement about independence of ![]() $t$ follows from (12) and Proposition 2.8.
$t$ follows from (12) and Proposition 2.8.
The subinterval case can be proved similarly, and we omit the details.
Now we finish proving the proposition. By Lemma 3.2,
is independent of ![]() $(a,b)$, so we may shrink from
$(a,b)$, so we may shrink from ![]() $(0,1)$ to an arbitrary small neighborhood of
$(0,1)$ to an arbitrary small neighborhood of ![]() $t$. Then we have
$t$. Then we have
 \begin{align*} \operatorname{Hom}(F_I, G_I) &\simeq [\pi_{I*} (\mathcal{H}om(F_I, G_I))]_t \simeq [\pi_{I*} (\mathcal{H}om(F_I, K_s^! G_I))]_t \\ &\simeq \operatorname{Hom}(\iota_t^*F_I,\iota_t^* K_s^! G_I) \simeq \operatorname{Hom}(F_t,R^s G_t) \simeq \operatorname{Hom}( F_t, G_t), \end{align*}
\begin{align*} \operatorname{Hom}(F_I, G_I) &\simeq [\pi_{I*} (\mathcal{H}om(F_I, G_I))]_t \simeq [\pi_{I*} (\mathcal{H}om(F_I, K_s^! G_I))]_t \\ &\simeq \operatorname{Hom}(\iota_t^*F_I,\iota_t^* K_s^! G_I) \simeq \operatorname{Hom}(F_t,R^s G_t) \simeq \operatorname{Hom}( F_t, G_t), \end{align*}
where ![]() $0< s<\epsilon$ and we have used a small Reeb perturbation to make
$0< s<\epsilon$ and we have used a small Reeb perturbation to make ![]() $F_I, K_s^! G_I$ a non-characteristic isotopy of sheaves and then applied (6) from the proof of Proposition 2.8.
$F_I, K_s^! G_I$ a non-characteristic isotopy of sheaves and then applied (6) from the proof of Proposition 2.8.
Proposition 3.3 Let ![]() $\{\Lambda ^\infty _t\}$ be a family of Legendrians in
$\{\Lambda ^\infty _t\}$ be a family of Legendrians in ![]() $T^\infty M$ that are uniformly displaceable with parameter
$T^\infty M$ that are uniformly displaceable with parameter ![]() $\epsilon$. For a given
$\epsilon$. For a given ![]() $t$, let
$t$, let ![]() $F_t \in Sh(M, \Lambda ^\infty _t)$. Suppose we have
$F_t \in Sh(M, \Lambda ^\infty _t)$. Suppose we have ![]() $F'_I$ and
$F'_I$ and ![]() $F''_I$ in
$F''_I$ in ![]() $Sh(M_I, \Lambda ^\infty _I)$ and isomorphisms
$Sh(M_I, \Lambda ^\infty _I)$ and isomorphisms
Then there exists a canonical isomorphism
such that ![]() $\Phi |_{t} = g^{-1} \circ f: F'_I|_t \to F''_I|_t$.
$\Phi |_{t} = g^{-1} \circ f: F'_I|_t \to F''_I|_t$.
Proof. The proof follows from Proposition 3.1 by standard arguments.
3.2 Existence of local extension
Proposition 3.4 Let ![]() $I=[0,1]$. Let
$I=[0,1]$. Let ![]() $\mathcal {L}_I$ be a strong isotopy of Legendrians in
$\mathcal {L}_I$ be a strong isotopy of Legendrians in ![]() $S^*M \times T^*I$ with the slice over
$S^*M \times T^*I$ with the slice over ![]() $t$ denoted by
$t$ denoted by ![]() $\mathcal {L}_t$. Let
$\mathcal {L}_t$. Let ![]() $(U_I, X_I)$ be a strong isotopy of convex tubes for
$(U_I, X_I)$ be a strong isotopy of convex tubes for ![]() $\mathcal {L}_I$. Then for any
$\mathcal {L}_I$. Then for any ![]() $t \in I$ and
$t \in I$ and ![]() $F_t \in Sh(M, \mathcal {L}_t)$, there exists an interval
$F_t \in Sh(M, \mathcal {L}_t)$, there exists an interval ![]() $J \supset t$ and
$J \supset t$ and ![]() $F_J \in Sh(M_J, \mathcal {L}_J)$ such that
$F_J \in Sh(M_J, \mathcal {L}_J)$ such that ![]() $F_J|_t = F_t$, where
$F_J|_t = F_t$, where ![]() $M_J = M \times J$ and
$M_J = M \times J$ and ![]() $\mathcal {L}_J = \mathcal {L}_I \cap S^*M \times T^*J$.
$\mathcal {L}_J = \mathcal {L}_I \cap S^*M \times T^*J$.
Proof. For any interval ![]() $J \subset I$, let
$J \subset I$, let ![]() $U_J = U_I \cap S^*M \times T^*J$. Then for small enough
$U_J = U_I \cap S^*M \times T^*J$. Then for small enough ![]() $J$ containing
$J$ containing ![]() $t$, we have
$t$, we have ![]() $\mathcal {L}_{t} \times T^*_J J \subset U_J$. Let
$\mathcal {L}_{t} \times T^*_J J \subset U_J$. Let ![]() $X_J$ denote the restriction of
$X_J$ denote the restriction of ![]() $X_I$ to
$X_I$ to ![]() $X_J$; then if we define (see Proposition 2.13 for definition of
$X_J$; then if we define (see Proposition 2.13 for definition of ![]() $\Pi _{U,X}$)
$\Pi _{U,X}$)
we have ![]() $F_J|_t = F_t$ and
$F_J|_t = F_t$ and ![]() $SS^\infty (F_J) \in \mathcal {L}_J$.
$SS^\infty (F_J) \in \mathcal {L}_J$.
3.3 Proof of Theorem 0.5
By the local extension result (Proposition 3.4) and uniqueness of extension result, for any ![]() $t \in I=[0,1]$ and
$t \in I=[0,1]$ and ![]() $F_t \in Sh(M, \mathcal {L}_t)$ we can extend
$F_t \in Sh(M, \mathcal {L}_t)$ we can extend ![]() $F_t$ to
$F_t$ to ![]() $F_I \in Sh(M_I, \mathcal {L}_I)$ such that
$F_I \in Sh(M_I, \mathcal {L}_I)$ such that ![]() $F_I|_t=F_t$. Hence the functor
$F_I|_t=F_t$. Hence the functor ![]() $\iota _t^*$ is fully faithful (Proposition 3.1) and essentially surjective; thus it is an equivalence.
$\iota _t^*$ is fully faithful (Proposition 3.1) and essentially surjective; thus it is an equivalence.
Acknowledgements
I would like to thank E. Zaslow for the statement and proof of Proposition 2.12, and D. Nadler, V. Shende, P. Schapira and S. Guillermou for their interest and inspiring discussions. I would also like to thank the anonymous referee who pointed out a serious gap in an earlier version of the manuscript and provided many useful comments for improving the paper.