No CrossRef data available.
Article contents
Sets of special subvarieties of bounded degree
Part of:
Cycles and subschemes
Published online by Cambridge University Press: 14 March 2023
Abstract
Let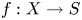 
$f : X \to S$ be a family of smooth projective algebraic varieties over a smooth connected quasi-projective base 
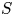$S$, and let 
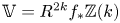$\mathbb {V} = R^{2k} f_{*} \mathbb {Z}(k)$ be the integral variation of Hodge structure coming from degree 
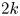$2k$ cohomology it induces. Associated to 
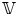$\mathbb {V}$ one has the so-called Hodge locus 
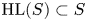$\textrm {HL}(S) \subset S$, which is a countable union of ‘special’ algebraic subvarieties of 
$S$ parametrizing those fibres of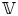 
$\mathbb {V}$ possessing extra Hodge tensors (and so, conjecturally, those fibres of 
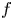$f$ possessing extra algebraic cycles). The special subvarieties belong to a larger class of so-called weakly special subvarieties, which are subvarieties of 
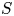$S$ maximal for their algebraic monodromy groups. For each positive integer 
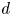$d$, we give an algorithm to compute the set of all weakly special subvarieties 
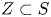$Z \subset S$ of degree at most 
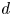$d$ (with the degree taken relative to a choice of projective compactification 
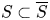$S \subset \overline {S}$ and very ample line bundle 
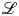$\mathcal {L}$ on 
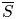$\overline {S}$). As a corollary of our algorithm we prove conjectures of Daw–Ren and Daw–Javanpeykar–Kühne on the finiteness of sets of special and weakly special subvarieties of bounded degree.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
Ayad, A., Complexité de la résolution des systèmes algébriques paramétriques, PhD thesis, Université Rennes 1, 2006.Google Scholar
Ayad, A., On computing absolutely irreducible components of algebraic varieties with parameters, Computing 89 (2010), 45–68.Google Scholar
Bakker, B. and Tsimerman, J., The Ax–Schanuel conjecture for variations of Hodge structures, Invent. Math. 217 (2017), 77–94.CrossRefGoogle Scholar
Barakat, M. and Lange-Hegermann, M., An algorithmic approach to Chevalley's Theorem on images of rational morphisms between affine varieties, Math. Comp. 91 (2022), 451–490.Google Scholar
Bayer, D. and Stillman, M., Computation of Hilbert functions, J. Symbolic Comput. 14 (1992), 31–50.CrossRefGoogle Scholar
Beauville, A., Le groupe de monodromie des familles universelles d'hypersurfaces et d'intersections complètes, in Complex analysis and algebraic geometry (Springer, 1986), 8–18.Google Scholar
Benjamin, B., Klingler, B. and Tsimerman, J., Tame topology of arithmetic quotients and algebraicity of Hodge loci, Amer. Math. Soc. 33 (2020), 917–939.Google Scholar
Binyamini, G. and Daw, C., Effective computations for weakly optimal subvarieties, J. Eur. Math. Soc. (JEMS), to appear. Preprint (2021), arXiv:2105.12760.Google Scholar
Blechschmidt, I., An elementary and constructive proof of Grothendieck's generic freeness lemma, Preprint (2018), arXiv:1807.01231.Google Scholar
Cattani, E., Deligne, P. and Kaplan, A., On the locus of Hodge Classes, J. Amer. Math. Soc. 8 (1994), 483–506.Google Scholar
Daw, C., Javanpeykar, A. and Kühne, L., Effective estimates for the degrees of maximal special subvarieties, Selecta Math. (N.S.) 26 (2020), 1–31.Google Scholar
Daw, C. and Ren, J., Applications of the hyperbolic Ax–Schanuel conjecture, Compos. Math. 154 (2018), 1843–1888.CrossRefGoogle Scholar
de Graaf, W. A., Constructing algebraic groups from their Lie algebras, J. Symbolic Comput. 44 (2009), 1223–1233.CrossRefGoogle Scholar
de Graaf, W. A., Constructing semisimple subalgebras of semisimple Lie algebras, J. Algebra 325 (2011), 416–430.CrossRefGoogle Scholar
Grothendieck, A., Éléments de géométrie algébrique : IV. Étude locale des schémas et des morphismes de schémas, Troisième partie, Publ. Math. Inst. Hautes Études Sci. 28 (1966), 5–255.Google Scholar
Enolski, V. and Richter, P., Periods of hyperelliptic integrals expressed in terms of 
$\theta$-constants by means of Thomae formulae, Philos. Trans. Roy. Soc. A 366 (2008), 1005–1024.CrossRefGoogle ScholarPubMed
$\theta$-constants by means of Thomae formulae, Philos. Trans. Roy. Soc. A 366 (2008), 1005–1024.CrossRefGoogle ScholarPubMedGreen, M., Griffiths, P. and Kerr, M., Mumford–Tate groups and domains: their geometry and arithmetic (AM-183) (Princeton University Press, 2012).Google Scholar
Grothendieck, A., Techniques de construction en géométrie analytique. VI. Étude locale des morphismes : germes d'espaces analytiques, platitude, morphismes simples, Séminaire Henri Cartan 13 (1960–1961), talk:13.Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, 2013).Google Scholar
Katz, N. M. and Oda, T., On the differentiation of De Rham cohomology classes with respect to parameters, J. Math. Kyoto Univ. 8 (1968), 199–213.Google Scholar
Klingler, B. and Otwinowska, A., On the closure of the Hodge locus of positive period dimension, Invent. Math. 225 (2021), 857–883.CrossRefGoogle Scholar
Klingler, B., Otwinowska, A. and Urbanik, D., On the fields of definition of Hodge loci, Ann. Sci. Éc. Norm. Supér. (4), to appear. Preprint (2020), arXiv:2010.03359.Google Scholar
Klingler, B., Ullmo, E. and Yafaev, A., Bi-algebraic geometry and the André–Oort conjecture, in Algebraic geometry: Salt Lake City 2015, Proceedings of Symposia in Pure Mathematics, vol. 97.2 (American Mathematical Society, 2018), 319–359.Google Scholar
Krick, T. and Logar, A., An algorithm for the computation of the radical of an ideal in the ring of polynomials, in International Symposium on Applied Algebra, Algebraic Algorithms, and Error-Correcting Codes (Springer. 1991), 195–205.CrossRefGoogle Scholar
Lombardi, H. and Quitté, C., Commutative algebra: constructive methods – finite projective modules, Algebra and Applications, vol. 20 (Springer, 2015).Google Scholar
Peterzil, Y. and Starchenko, S., Complex analytic geometry in a nonstandard setting, in Model theory with applications to algebra and analysis, London Mathematical Society Lecture Note Series, vol. 349 (Cambridge University Press, 2008), 117–166.Google Scholar
Scheiblechner, P., Castelnuovo–Mumford regularity and computing the de Rham cohomology of smooth projective varieties, Found. Comput. Math. 12 (2012), 541–571.Google Scholar
Schmid, W., Variation of Hodge structure: the singularities of the period mapping, Invent. Math. 22 (1973), 211–320.Google Scholar
The Stacks Project Authors. Stacks Project (2020), https://stacks.math.columbia.edu.Google Scholar
Starr, J., Counting Hilbert polynomials of projective varieties. MathOverflow. URL: https://mathoverflow.net/q/264428 (version: 2017-04-13).Google Scholar
Swinarski, D., Equations of Riemann surfaces with automorphisms. Higher genus curves in mathematical physics and arithmetic geometry, Contemp. Math. 703 (2018), 33–46.CrossRefGoogle Scholar
Urbanik, D., On the transcendence of period images, J. Differential Geom., to appear. Preprint (2021), arXiv:2106.09342.Google Scholar
Voisin, C., Hodge loci, in Handbook of moduli, vol. III (International Press, Boston, MA, 2012), 507–546.Google Scholar
Weibel, C. A., An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, vol. 38 (Cambridge University Press, 1994).CrossRefGoogle Scholar
Wibmer, M., Gröbner bases for families of affine or projective schemes, J. Symbolic Comput. 42 (2007), 803–834.Google Scholar
Yves, A., Mumford–Tate groups of mixed Hodge structures and the theorem of the fixed part, Compos. Math. 82 (1992), 1–24.Google Scholar