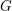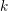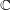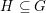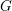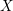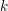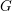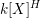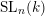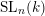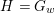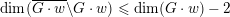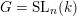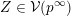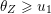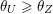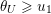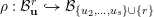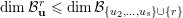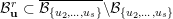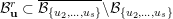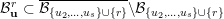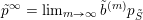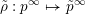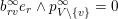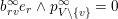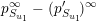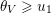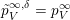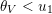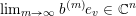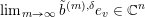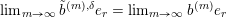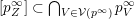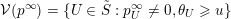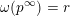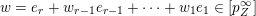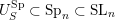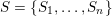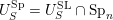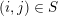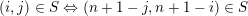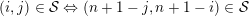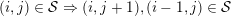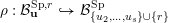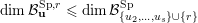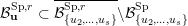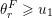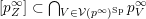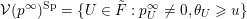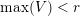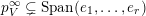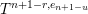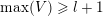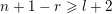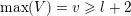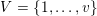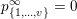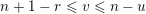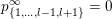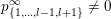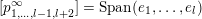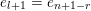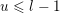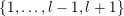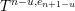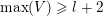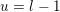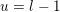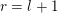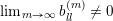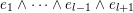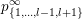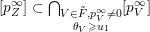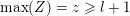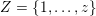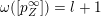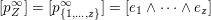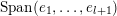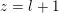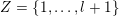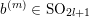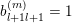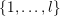1 Introduction
Let
![]() $k$
be an algebraically closed subfield of
$k$
be an algebraically closed subfield of
![]() $\mathbb{C}$
of characteristic zero,
$\mathbb{C}$
of characteristic zero,
![]() $G$
an affine algebraic group over
$G$
an affine algebraic group over
![]() $k$
, and
$k$
, and
![]() $X$
an affine
$X$
an affine
![]() $k$
-variety on which
$k$
-variety on which
![]() $G$
acts rationally. There is an induced action of
$G$
acts rationally. There is an induced action of
![]() $G$
on the coordinate ring
$G$
on the coordinate ring
![]() $k[X]$
given by
$k[X]$
given by
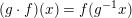 $(g\cdot f)(x)=f(g^{-1}x)$
for
$(g\cdot f)(x)=f(g^{-1}x)$
for
![]() $g\in G$
,
$g\in G$
,
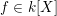 $f\in k[X]$
and
$f\in k[X]$
and
![]() $x\in X$
. The invariant subalgebra is
$x\in X$
. The invariant subalgebra is
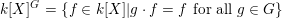 $k[X]^{G}=\{f\in k[X]|g\cdot f=f~\text{for all}~g\in G\}$
. Invariant theory studies the structure of this algebra and one of its fundamental problems is to characterise those actions where
$k[X]^{G}=\{f\in k[X]|g\cdot f=f~\text{for all}~g\in G\}$
. Invariant theory studies the structure of this algebra and one of its fundamental problems is to characterise those actions where
![]() $k[X]^{G}$
is finitely generated.
$k[X]^{G}$
is finitely generated.
When
![]() $G$
is reductive
$G$
is reductive
![]() $k[X]^{G}$
is finitely generated, due to Mumford [Reference Mumford, Fogarty and KirwanMFK94], Nagata [Reference NagataNag65] and Haboush [Reference HaboushHab75]. Since Nagata’s counterexample from 1958 [Reference NagataNag65] we know that for nonreductive groups the invariant algebra is not necessarily finitely generated. In fact Popov [Reference PopovPop79] proved that finite generation for arbitrary ring
$k[X]^{G}$
is finitely generated, due to Mumford [Reference Mumford, Fogarty and KirwanMFK94], Nagata [Reference NagataNag65] and Haboush [Reference HaboushHab75]. Since Nagata’s counterexample from 1958 [Reference NagataNag65] we know that for nonreductive groups the invariant algebra is not necessarily finitely generated. In fact Popov [Reference PopovPop79] proved that finite generation for arbitrary ring
![]() $k[X]^{G}$
implies that
$k[X]^{G}$
implies that
![]() $G$
is reductive.
$G$
is reductive.
Invariant rings for nonreductive group actions have been extensively studied over the last 60 years. Finite generation has been proved in many interesting situations; however, characterisation of those actions with finitely generated invariant rings is still seems to be hopeless. Weitzenböck in [Reference WeitzenbockWei32] (and later Seshadri [Reference SeshadriSes61]) proved that finite generation holds if
![]() $G$
is the additive group
$G$
is the additive group
![]() $k^{+}$
of an algebraically closed field
$k^{+}$
of an algebraically closed field
![]() $k$
of characteristic 0,
$k$
of characteristic 0,
![]() $X$
is an affine
$X$
is an affine
![]() $k$
-space and the action of
$k$
-space and the action of
![]() $k^{+}$
on
$k^{+}$
on
![]() $X$
extends to
$X$
extends to
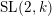 $\operatorname{SL}(2,k)$
. Later Hochschild, Mostow and Grosshans generalised this result by showing that if
$\operatorname{SL}(2,k)$
. Later Hochschild, Mostow and Grosshans generalised this result by showing that if
![]() $G$
is reductive,
$G$
is reductive,
![]() $H$
is the unipotent radical of some parabolic subgroup of
$H$
is the unipotent radical of some parabolic subgroup of
![]() $G$
and
$G$
and
![]() $G$
acts rationally on
$G$
acts rationally on
![]() $X$
, then
$X$
, then
![]() $k[X]^{H}$
is finitely generated (see [Reference Hochschield and MostowHM73, Reference GrosshansGro83]). Recently, Bérczi et al. [Reference Bérczi, Doran, Hawes and KirwanBDHK16b] showed finite generation for invariant rings of certain
$k[X]^{H}$
is finitely generated (see [Reference Hochschield and MostowHM73, Reference GrosshansGro83]). Recently, Bérczi et al. [Reference Bérczi, Doran, Hawes and KirwanBDHK16b] showed finite generation for invariant rings of certain
![]() $\mathbb{C}^{\ast }$
-extensions of unipotent groups. This rather general result follows from extension of Mumford’s reductive geometric invariant theory to a wide class of nonreductive groups, see [Reference Bérczi, Doran, Hawes and KirwanBDHK16a, Reference Bérczi, Doran, Hawes, Kirwan, Ji, Papadopoulos and YauBDHK] for details.
$\mathbb{C}^{\ast }$
-extensions of unipotent groups. This rather general result follows from extension of Mumford’s reductive geometric invariant theory to a wide class of nonreductive groups, see [Reference Bérczi, Doran, Hawes and KirwanBDHK16a, Reference Bérczi, Doran, Hawes, Kirwan, Ji, Papadopoulos and YauBDHK] for details.
Natural generalisations of parabolic subgroups of the reductive group
![]() $G$
are the subgroups normalised by a maximal torus of
$G$
are the subgroups normalised by a maximal torus of
![]() $G$
: these are generated by root subgroups corresponding to a closed set of positive roots and we call them regular subgroups. The following conjecture was formulated almost simultaneously in the late 1970s by Popov and Pommerening.
$G$
: these are generated by root subgroups corresponding to a closed set of positive roots and we call them regular subgroups. The following conjecture was formulated almost simultaneously in the late 1970s by Popov and Pommerening.
Conjecture 1.1 (Popov, Pommerening).
Let
![]() $G$
be a reductive group over
$G$
be a reductive group over
![]() $k$
, and let
$k$
, and let
![]() $H\subset G$
be an observable subgroup normalised by a maximal torus of
$H\subset G$
be an observable subgroup normalised by a maximal torus of
![]() $G$
. Then for any affine
$G$
. Then for any affine
![]() $G$
-variety
$G$
-variety
![]() $X$
the algebra of invariants
$X$
the algebra of invariants
![]() $k[X]^{H}$
is finitely generated.
$k[X]^{H}$
is finitely generated.
Note that
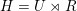 $H=U\rtimes R$
can be written as the semidirect product of its unipotent radical
$H=U\rtimes R$
can be written as the semidirect product of its unipotent radical
![]() $U$
and a reductive group
$U$
and a reductive group
![]() $R$
. Since
$R$
. Since
![]() $U\leqslant H$
is a characteristic subgroup, if the maximal torus normalises
$U\leqslant H$
is a characteristic subgroup, if the maximal torus normalises
![]() $H$
then it normalises
$H$
then it normalises
![]() $U$
as well. Moreover,
$U$
as well. Moreover,
 $$\begin{eqnarray}k[X]^{H}=[k[X]^{U}]^{R}\end{eqnarray}$$
$$\begin{eqnarray}k[X]^{H}=[k[X]^{U}]^{R}\end{eqnarray}$$
holds for any
![]() $H$
-variety
$H$
-variety
![]() $X$
, so we can restrict our study to the unipotent part
$X$
, so we can restrict our study to the unipotent part
![]() $U$
and the corresponding invariant ring
$U$
and the corresponding invariant ring
![]() $k[X]^{U}$
. Furthermore, if
$k[X]^{U}$
. Furthermore, if
![]() $G$
is any linear algebraic group and
$G$
is any linear algebraic group and
![]() $H\subset G$
is a closed subgroup and
$H\subset G$
is a closed subgroup and
![]() $X$
is an affine
$X$
is an affine
![]() $G$
-variety, then
$G$
-variety, then
 $$\begin{eqnarray}k[X]^{H}=(k[G]^{H}\otimes k[X])^{G}\end{eqnarray}$$
$$\begin{eqnarray}k[X]^{H}=(k[G]^{H}\otimes k[X])^{G}\end{eqnarray}$$
holds for the invariant rings. This is called the transfer principle, which goes back to the nineteenth century. In its modern form, it appeared in Grosshans [Reference GrosshansGro73] and Popov [Reference PopovPop87]. In particular, if
![]() $G$
is reductive, then finite generation of
$G$
is reductive, then finite generation of
![]() $k[G]^{U}$
implies finite generation of
$k[G]^{U}$
implies finite generation of
![]() $k[X]^{U}$
and
$k[X]^{U}$
and
![]() $k[X]^{H}$
.
$k[X]^{H}$
.
The question can be further reduced to connected, simply connected, simple reductive groups, see [Reference TanTan89a, Reference GrosshansGro97]. Unipotent subgroups of these normalised by a maximal torus
![]() $T$
can be parametrized by ‘(quasi-)closed’ subsets
$T$
can be parametrized by ‘(quasi-)closed’ subsets
 $S\subset R^{+}$
of the set
$S\subset R^{+}$
of the set
![]() $R^{+}$
of positive roots of
$R^{+}$
of positive roots of
![]() $G$
relative to some Borel subgroup containing
$G$
relative to some Borel subgroup containing
![]() $T$
. If
$T$
. If
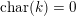 $\text{char}(k)=0$
, then quasi-closed and closed subsets are the same: a subset
$\text{char}(k)=0$
, then quasi-closed and closed subsets are the same: a subset
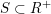 $S\subset R^{+}$
is closed if the subgroup
$S\subset R^{+}$
is closed if the subgroup
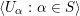 $\langle U_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in S\rangle$
generated by the root subgroups in
$\langle U_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in S\rangle$
generated by the root subgroups in
![]() $S$
does not contain any
$S$
does not contain any
![]() $U_{\unicode[STIX]{x1D6FD}}$
with
$U_{\unicode[STIX]{x1D6FD}}$
with
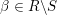 $\unicode[STIX]{x1D6FD}\in R\setminus S$
. Then the unipotent group
$\unicode[STIX]{x1D6FD}\in R\setminus S$
. Then the unipotent group
 $$\begin{eqnarray}U_{S}=\langle U_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in S\rangle\end{eqnarray}$$
$$\begin{eqnarray}U_{S}=\langle U_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in S\rangle\end{eqnarray}$$
is normalised by the maximal torus
![]() $T$
, and all unipotent subgroups of
$T$
, and all unipotent subgroups of
![]() $G$
with this property have this form for some closed subset
$G$
with this property have this form for some closed subset
![]() $S$
(cf. [Reference TanTan88, Reference TanTan89a]).
$S$
(cf. [Reference TanTan88, Reference TanTan89a]).
When
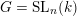 $G=\operatorname{SL}_{n}(k)$
we can assume that
$G=\operatorname{SL}_{n}(k)$
we can assume that
![]() $U_{S}$
is unipotent upper triangular subgroup normalised by the diagonal maximal torus. Let
$U_{S}$
is unipotent upper triangular subgroup normalised by the diagonal maximal torus. Let
 $B_{n}\subset \operatorname{SL}_{n}(k)$
be the upper Borel subgroup; then the positive roots are
$B_{n}\subset \operatorname{SL}_{n}(k)$
be the upper Borel subgroup; then the positive roots are
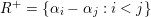 $R^{+}=\{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}:i<j\}$
, where
$R^{+}=\{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}:i<j\}$
, where
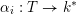 $\unicode[STIX]{x1D6FC}_{i}:T\rightarrow k^{\ast }$
is the character of the maximal diagonal torus
$\unicode[STIX]{x1D6FC}_{i}:T\rightarrow k^{\ast }$
is the character of the maximal diagonal torus
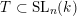 $T\subset \operatorname{SL}_{n}(k)$
sending a torus element to its
$T\subset \operatorname{SL}_{n}(k)$
sending a torus element to its
![]() $(i,i)$
entry. Then
$(i,i)$
entry. Then
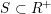 $S\subset R^{+}$
is closed if and only if it is the incidence matrix of a strict ordering of the set
$S\subset R^{+}$
is closed if and only if it is the incidence matrix of a strict ordering of the set
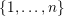 $\{1,\ldots ,n\}$
, that is,
$\{1,\ldots ,n\}$
, that is,
 $$\begin{eqnarray}(i,j),\quad (j,k)\in S\Rightarrow (i,k)\in S.\end{eqnarray}$$
$$\begin{eqnarray}(i,j),\quad (j,k)\in S\Rightarrow (i,k)\in S.\end{eqnarray}$$
The corresponding unipotent subgroup
![]() $U_{S}$
is upper triangular with ones on the diagonal and zeros at the entries
$U_{S}$
is upper triangular with ones on the diagonal and zeros at the entries
![]() $(i,j)$
where
$(i,j)$
where
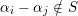 $\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\notin S$
. For example, for
$\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\notin S$
. For example, for
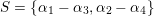 $S=\{\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{3},\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FC}_{4}\}$
$S=\{\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{3},\unicode[STIX]{x1D6FC}_{2}-\unicode[STIX]{x1D6FC}_{4}\}$

We will often refer to elements of
![]() $S$
with pairs
$S$
with pairs
![]() $(i,j)$
instead of
$(i,j)$
instead of
![]() $\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}$
. We introduce the following special type of regular subgroups.
$\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}$
. We introduce the following special type of regular subgroups.
(i) A regular subgroup
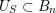 $U_{S}\subset B_{n}$
is called left (respectively right) Borel-regular if its Lie algebra
$U_{S}\subset B_{n}$
is called left (respectively right) Borel-regular if its Lie algebra
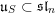 $\mathfrak{u}_{S}\subset \mathfrak{sl}_{n}$
is closed under multiplication on the left (respectively right) by
$\mathfrak{u}_{S}\subset \mathfrak{sl}_{n}$
is closed under multiplication on the left (respectively right) by
![]() $B_{n}$
. In a left Borel-regular subgroup the nondiagonal elements of
$B_{n}$
. In a left Borel-regular subgroup the nondiagonal elements of
![]() $S$
form a vertical ‘barcode’, that is
$S$
form a vertical ‘barcode’, that is
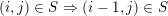 $(i,j)\in S\Rightarrow (i-1,j)\in S$
holds and
$(i,j)\in S\Rightarrow (i-1,j)\in S$
holds and
![]() $S$
can be parametrized by the sequence of positions of the lowest free parameter in each column:
$S$
can be parametrized by the sequence of positions of the lowest free parameter in each column:

(ii) We call a subgroup
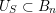 $U_{S}\subset B_{n}$
Borel-regular if it is left and right Borel-regular at the same time. Equivalently, it is normalised by
$U_{S}\subset B_{n}$
Borel-regular if it is left and right Borel-regular at the same time. Equivalently, it is normalised by
![]() $B_{n}$
. This means that
$B_{n}$
. This means that
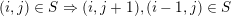 $(i,j)\in S\Rightarrow (i,j+1),(i-1,j)\in S$
, and hence Borel-regular subgroups are those left Borel-regular subgroups which correspond to some increasing sequence, e.g.
$(i,j)\in S\Rightarrow (i,j+1),(i-1,j)\in S$
, and hence Borel-regular subgroups are those left Borel-regular subgroups which correspond to some increasing sequence, e.g.

Unipotent radicals of parabolic subgroups are special Borel-regular subgroups where all blocks ‘touch’ the main diagonal.
Borel-regular subgroups can be defined in any linear algebraic group
![]() $G$
: these are the regular subgroups normalised by some Borel subgroup of
$G$
: these are the regular subgroups normalised by some Borel subgroup of
![]() $G$
. These are subgroups of the form
$G$
. These are subgroups of the form
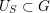 $U_{S}\subset G$
where
$U_{S}\subset G$
where
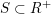 $S\subset R^{+}$
is closed under shifting by elements of
$S\subset R^{+}$
is closed under shifting by elements of
![]() $R^{+}$
, i.e.
$R^{+}$
, i.e.
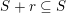 $S+r\subseteq S$
for any
$S+r\subseteq S$
for any
![]() $r\in R^{+}$
.
$r\in R^{+}$
.
(iii) In particular, the symplectic group
![]() $\operatorname{Sp}_{n}(k)$
and orthogonal group
$\operatorname{Sp}_{n}(k)$
and orthogonal group
![]() $\operatorname{SO}_{n}(k)$
have Borel-compatible embeddings into
$\operatorname{SO}_{n}(k)$
have Borel-compatible embeddings into
![]() $\operatorname{SL}_{n}(k)$
, that is, a choice of Borel subgroups
$\operatorname{SL}_{n}(k)$
, that is, a choice of Borel subgroups
![]() $B_{\text{Sp}_{n}}$
and
$B_{\text{Sp}_{n}}$
and
![]() $B_{\text{SO}_{n}}$
whose image sit in the upper Borel
$B_{\text{SO}_{n}}$
whose image sit in the upper Borel
![]() $B_{n}$
of
$B_{n}$
of
![]() $\operatorname{SL}_{n}(k)$
. The image of the maximal torus in
$\operatorname{SL}_{n}(k)$
. The image of the maximal torus in
![]() $\operatorname{Sp}_{n}(k)$
and
$\operatorname{Sp}_{n}(k)$
and
![]() $\operatorname{SO}_{n}(k)$
consists of diagonal matrices
$\operatorname{SO}_{n}(k)$
consists of diagonal matrices
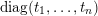 $\operatorname{diag}(t_{1},\ldots ,t_{n})$
satisfying
$\operatorname{diag}(t_{1},\ldots ,t_{n})$
satisfying
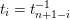 $t_{i}=t_{n+1-i}^{-1}$
, see §§ 5.2, 5.3 for the details. The positive roots are
$t_{i}=t_{n+1-i}^{-1}$
, see §§ 5.2, 5.3 for the details. The positive roots are
 $$\begin{eqnarray}R^{+}=\left\{\begin{array}{@{}ll@{}}\{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i\leqslant j\leqslant l}\quad & \text{for}~\,\text{Sp}_{2l},\\ \{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\quad & \text{for}~\,\text{SO}_{2l},\\ \{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}\}_{1\leqslant i\leqslant l}\quad & \text{for}~\,\text{SO}_{2l+1}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}R^{+}=\left\{\begin{array}{@{}ll@{}}\{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i\leqslant j\leqslant l}\quad & \text{for}~\,\text{Sp}_{2l},\\ \{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\quad & \text{for}~\,\text{SO}_{2l},\\ \{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}\}_{1\leqslant i\leqslant l}\quad & \text{for}~\,\text{SO}_{2l+1}.\end{array}\right.\end{eqnarray}$$
We call the Borel-regular subgroup
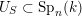 $U_{S}\subset \operatorname{Sp}_{n}(k)$
fat Borel-regular if
$U_{S}\subset \operatorname{Sp}_{n}(k)$
fat Borel-regular if
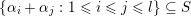 $\{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}:1\leqslant i\leqslant j\leqslant l\}\subseteq S$
. Similarly,
$\{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}:1\leqslant i\leqslant j\leqslant l\}\subseteq S$
. Similarly,
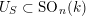 $U_{S}\subset \operatorname{SO}_{n}(k)$
is fat if
$U_{S}\subset \operatorname{SO}_{n}(k)$
is fat if
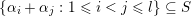 $\{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}:1\leqslant i<j\leqslant l\}\subseteq S$
when
$\{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}:1\leqslant i<j\leqslant l\}\subseteq S$
when
![]() $n=2l$
and
$n=2l$
and
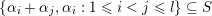 $\{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FC}_{i}:1\leqslant i<j\leqslant l\}\subseteq S$
when
$\{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FC}_{i}:1\leqslant i<j\leqslant l\}\subseteq S$
when
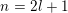 $n=2l+1$
. We will see that if
$n=2l+1$
. We will see that if
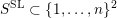 $S^{\text{SL}}\subset \{1,\ldots ,n\}^{2}$
collects the possible nonzero entries of a fat Borel-regular subgroup
$S^{\text{SL}}\subset \{1,\ldots ,n\}^{2}$
collects the possible nonzero entries of a fat Borel-regular subgroup
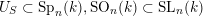 $U_{S}\subset \operatorname{Sp}_{n}(k),\operatorname{SO}_{n}(k)\subset \operatorname{SL}_{n}(k)$
, then
$U_{S}\subset \operatorname{Sp}_{n}(k),\operatorname{SO}_{n}(k)\subset \operatorname{SL}_{n}(k)$
, then
![]() $U_{S}$
is Borel regular in
$U_{S}$
is Borel regular in
![]() $\operatorname{SL}_{n}(k)$
such that
$\operatorname{SL}_{n}(k)$
such that
![]() $S$
is a ‘fat’ domain in the sense that it contains the top right quarter of
$S$
is a ‘fat’ domain in the sense that it contains the top right quarter of
![]() $\operatorname{SL}_{n}$
:
$\operatorname{SL}_{n}$
:

Machinery for proving finite generation for algebra of invariants is quite limited. However, there exists a standard criterion, called the Grosshans criterion [Reference GrosshansGro73, Reference GrosshansGro97] for proving the finite generation of
![]() $k[G]^{H}$
, where
$k[G]^{H}$
, where
![]() $H\subset G$
is observable in the sense that
$H\subset G$
is observable in the sense that
 $$\begin{eqnarray}H=\{g\in G:f(xg)=f(x)~\text{for all}~x\in G~\text{and}~f\in k[G]^{H}\}.\end{eqnarray}$$
$$\begin{eqnarray}H=\{g\in G:f(xg)=f(x)~\text{for all}~x\in G~\text{and}~f\in k[G]^{H}\}.\end{eqnarray}$$
Note that the action of
![]() $H$
on
$H$
on
![]() $G$
is by right translation. In this case the finite generation of
$G$
is by right translation. In this case the finite generation of
![]() $k[G]^{H}$
is equivalent to the existence of a finite-dimensional affine (left)
$k[G]^{H}$
is equivalent to the existence of a finite-dimensional affine (left)
![]() $G$
-module
$G$
-module
![]() ${\mathcal{W}}$
and some
${\mathcal{W}}$
and some
![]() $w\in {\mathcal{W}}$
such that
$w\in {\mathcal{W}}$
such that
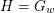 $H=G_{w}$
is the stabiliser of
$H=G_{w}$
is the stabiliser of
![]() $w$
and
$w$
and
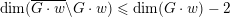 $\dim (\overline{G\cdot w}\setminus G\cdot w)\leqslant \dim (G\cdot w)-2$
. Such subgroups
$\dim (\overline{G\cdot w}\setminus G\cdot w)\leqslant \dim (G\cdot w)-2$
. Such subgroups
![]() $H$
are called Grosshans subgroups of
$H$
are called Grosshans subgroups of
![]() $G$
and we call the pair
$G$
and we call the pair
![]() $({\mathcal{W}},w)$
a Grosshans pair for
$({\mathcal{W}},w)$
a Grosshans pair for
![]() $H$
.
$H$
.
The main results of this paper are the following two theorems.
Theorem 1.2. If
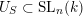 $U_{S}\subset \operatorname{SL}_{n}(k)$
is a left (respectively right) Borel-regular subgroup, then
$U_{S}\subset \operatorname{SL}_{n}(k)$
is a left (respectively right) Borel-regular subgroup, then
![]() $U_{S}$
is a Grosshans subgroup of
$U_{S}$
is a Grosshans subgroup of
![]() $\operatorname{SL}_{n}(k)$
. Therefore every linear action of
$\operatorname{SL}_{n}(k)$
. Therefore every linear action of
![]() $U_{S}$
on an affine or projective variety which extends to a linear action of
$U_{S}$
on an affine or projective variety which extends to a linear action of
![]() $G$
has a finitely generated algebra of invariants. In particular this gives an affirmative answer to the Popov–Pommerening conjecture for left (respectively right) Borel-regular subgroups of
$G$
has a finitely generated algebra of invariants. In particular this gives an affirmative answer to the Popov–Pommerening conjecture for left (respectively right) Borel-regular subgroups of
![]() $\operatorname{SL}_{n}(k)$
.
$\operatorname{SL}_{n}(k)$
.
Theorem 1.3. Let
![]() $G$
be a linear reductive group over
$G$
be a linear reductive group over
![]() $k$
of type
$k$
of type
![]() $B$
or
$B$
or
![]() $D$
and
$D$
and
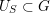 $U_{S}\subset G$
a fat Borel-regular subgroup. Then
$U_{S}\subset G$
a fat Borel-regular subgroup. Then
![]() $U_{S}$
is a Grosshans subgroup of
$U_{S}$
is a Grosshans subgroup of
![]() $G$
. In particular this gives an affirmative answer to the Popov–Pommerening conjecture for fat Borel-regular subgroups of symplectic and orthogonal Lie groups.
$G$
. In particular this gives an affirmative answer to the Popov–Pommerening conjecture for fat Borel-regular subgroups of symplectic and orthogonal Lie groups.
The Popov–Pommerening conjecture was known before in a few special cases. In a series of papers Tan [Reference TanTan88, Reference TanTan89a, Reference TanTan89b] proved it for all simple groups of Dynkin type
![]() $A_{n}$
with
$A_{n}$
with
![]() $n\leqslant 4$
, and for groups of type
$n\leqslant 4$
, and for groups of type
![]() $B_{2}$
and
$B_{2}$
and
![]() $G_{2}$
. Grosshans in [Reference GrosshansGro97] confirmed the conjecture for unipotent radicals of parabolic subgroups and in [Reference GrosshansGro86] for those
$G_{2}$
. Grosshans in [Reference GrosshansGro97] confirmed the conjecture for unipotent radicals of parabolic subgroups and in [Reference GrosshansGro86] for those
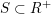 $S\subset R^{+}$
where
$S\subset R^{+}$
where
![]() $R^{+}\setminus S$
is a linearly independent set over
$R^{+}\setminus S$
is a linearly independent set over
![]() $\mathbb{Q}$
. Pommerening [Reference PommereningPom87b] proved the conjecture for a large class of subgroups of
$\mathbb{Q}$
. Pommerening [Reference PommereningPom87b] proved the conjecture for a large class of subgroups of
![]() $\operatorname{GL}_{n}(k)$
by giving a generating set of the invariant ring
$\operatorname{GL}_{n}(k)$
by giving a generating set of the invariant ring
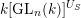 $k[\operatorname{GL}_{n}(k)]^{U_{S}}$
, but these cases only cover very special block regular subgroups. For more details on the history of the problem see [Reference GrosshansGro97] and the survey papers [Reference TanTan89a, Reference Pommerening and KohPom87a, Reference GrosshansGro10]. After finishing the first version of this paper, Popov kindly drew my attention to the unpublished PhD thesis of A’Campo-Neuen [Reference A’Campo-NeuenA’Ca94] where the Popov–Pomerening conjecture is proved for Borel-regular subgroups of
$k[\operatorname{GL}_{n}(k)]^{U_{S}}$
, but these cases only cover very special block regular subgroups. For more details on the history of the problem see [Reference GrosshansGro97] and the survey papers [Reference TanTan89a, Reference Pommerening and KohPom87a, Reference GrosshansGro10]. After finishing the first version of this paper, Popov kindly drew my attention to the unpublished PhD thesis of A’Campo-Neuen [Reference A’Campo-NeuenA’Ca94] where the Popov–Pomerening conjecture is proved for Borel-regular subgroups of
![]() $\operatorname{SL}_{n}(k)$
; this is a special case of our Theorem 1.3.
$\operatorname{SL}_{n}(k)$
; this is a special case of our Theorem 1.3.
The layout of this paper is the following. We will work with
![]() $k=\mathbb{C}$
, but all arguments work for any algebraically closed field
$k=\mathbb{C}$
, but all arguments work for any algebraically closed field
![]() $k$
of characteristic zero which is a subfield of
$k$
of characteristic zero which is a subfield of
![]() $\mathbb{C}$
. We start with a short introduction of Grosshans subgroups in § 2. In § 3 we construct for any regular subgroup
$\mathbb{C}$
. We start with a short introduction of Grosshans subgroups in § 2. In § 3 we construct for any regular subgroup
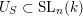 $U_{S}\subset \operatorname{SL}_{n}(k)$
corresponding to the closed subset
$U_{S}\subset \operatorname{SL}_{n}(k)$
corresponding to the closed subset
 $S\subseteq R^{+}$
a subset family
$S\subseteq R^{+}$
a subset family
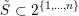 $\tilde{S}\subset 2^{\{1,\ldots ,n\}}$
and an affine
$\tilde{S}\subset 2^{\{1,\ldots ,n\}}$
and an affine
![]() $\operatorname{SL}_{n}(k)$
-module
$\operatorname{SL}_{n}(k)$
-module
![]() ${\mathcal{W}}_{\tilde{S}}$
with a point
${\mathcal{W}}_{\tilde{S}}$
with a point
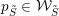 $p_{\tilde{S}}\in {\mathcal{W}}_{\tilde{S}}$
whose stabiliser is isomorphic to
$p_{\tilde{S}}\in {\mathcal{W}}_{\tilde{S}}$
whose stabiliser is isomorphic to
![]() $U_{S}$
.
$U_{S}$
.
In § 4 we prove that the constructed pair
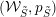 $({\mathcal{W}}_{\tilde{S}},p_{\tilde{S}})$
is a Grosshans pair if
$({\mathcal{W}}_{\tilde{S}},p_{\tilde{S}})$
is a Grosshans pair if
![]() $U_{S}$
is left Borel-regular. An outline of the proof is as follows. When the field of definition is
$U_{S}$
is left Borel-regular. An outline of the proof is as follows. When the field of definition is
![]() $\mathbb{C}$
, the Zariski-closure of an orbit is the Euclidean closure, see [Reference BorelBor91]. Therefore every boundary point in
$\mathbb{C}$
, the Zariski-closure of an orbit is the Euclidean closure, see [Reference BorelBor91]. Therefore every boundary point in
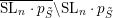 $\overline{\operatorname{SL}_{n}\cdot p_{\tilde{S}}}\setminus \operatorname{SL}_{n}\cdot p_{\tilde{S}}$
can be written as a limit
$\overline{\operatorname{SL}_{n}\cdot p_{\tilde{S}}}\setminus \operatorname{SL}_{n}\cdot p_{\tilde{S}}$
can be written as a limit
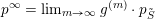 $p^{\infty }=\lim _{m\rightarrow \infty }g^{(m)}\cdot p_{\tilde{S}}$
for some sequence
$p^{\infty }=\lim _{m\rightarrow \infty }g^{(m)}\cdot p_{\tilde{S}}$
for some sequence
 $(g^{(m)})\subset \operatorname{SL}_{n}$
. When
$(g^{(m)})\subset \operatorname{SL}_{n}$
. When
![]() $k=\mathbb{C}$
, however,
$k=\mathbb{C}$
, however,
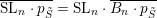 $\overline{\operatorname{SL}_{n}\cdot p_{\tilde{S}}}=\operatorname{SL}_{n}\cdot \overline{B_{n}\cdot p_{\tilde{S}}}$
holds because
$\overline{\operatorname{SL}_{n}\cdot p_{\tilde{S}}}=\operatorname{SL}_{n}\cdot \overline{B_{n}\cdot p_{\tilde{S}}}$
holds because
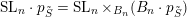 $\operatorname{SL}_{n}\cdot p_{\tilde{S}}=\operatorname{SL}_{n}\times _{B_{n}}(B_{n}\cdot p_{\tilde{S}})$
fibres over
$\operatorname{SL}_{n}\cdot p_{\tilde{S}}=\operatorname{SL}_{n}\times _{B_{n}}(B_{n}\cdot p_{\tilde{S}})$
fibres over
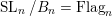 $\operatorname{SL}_{n}/B_{n}=\text{Flag}_{n}$
, the complete flag variety, which is closed. Therefore we can study the boundary of the Borel orbit instead. We construct a cover
$\operatorname{SL}_{n}/B_{n}=\text{Flag}_{n}$
, the complete flag variety, which is closed. Therefore we can study the boundary of the Borel orbit instead. We construct a cover
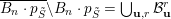 $\overline{B_{n}\cdot p_{\tilde{S}}}\setminus B_{n}\cdot p_{\tilde{S}}=\bigcup _{\mathbf{u},r}{\mathcal{B}}_{\mathbf{u}}^{r}$
with Borel-invariant boundary subsets
$\overline{B_{n}\cdot p_{\tilde{S}}}\setminus B_{n}\cdot p_{\tilde{S}}=\bigcup _{\mathbf{u},r}{\mathcal{B}}_{\mathbf{u}}^{r}$
with Borel-invariant boundary subsets
![]() ${\mathcal{B}}_{\mathbf{u}}^{r}$
indexed by an array
${\mathcal{B}}_{\mathbf{u}}^{r}$
indexed by an array
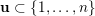 $\mathbf{u}\subset \{1,\ldots ,n\}$
and an integer
$\mathbf{u}\subset \{1,\ldots ,n\}$
and an integer
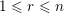 $1\leqslant r\leqslant n$
. We prove that for all
$1\leqslant r\leqslant n$
. We prove that for all
![]() $\mathbf{u},r$
either: (1)
$\mathbf{u},r$
either: (1)
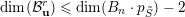 $\dim ({\mathcal{B}}_{\mathbf{u}}^{r})\leqslant \dim (B_{n}\cdot p_{\tilde{S}})-2$
; or (2) every point of
$\dim ({\mathcal{B}}_{\mathbf{u}}^{r})\leqslant \dim (B_{n}\cdot p_{\tilde{S}})-2$
; or (2) every point of
![]() ${\mathcal{B}}_{\mathbf{u}}^{r}$
is fixed by a one-dimensional subgroup of the opposite Borel
${\mathcal{B}}_{\mathbf{u}}^{r}$
is fixed by a one-dimensional subgroup of the opposite Borel
![]() $B^{op}$
. In both cases we can easily deduce that
$B^{op}$
. In both cases we can easily deduce that
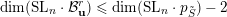 $\dim (\operatorname{SL}_{n}\cdot {\mathcal{B}}_{\mathbf{u}}^{r})\leqslant \dim (\operatorname{SL}_{n}\cdot p_{\tilde{S}})-2$
.
$\dim (\operatorname{SL}_{n}\cdot {\mathcal{B}}_{\mathbf{u}}^{r})\leqslant \dim (\operatorname{SL}_{n}\cdot p_{\tilde{S}})-2$
.
In § 5 we study Borel regular subgroup of classical groups. In particular, in § 5.2 we define a Borel-compatible embedding of
![]() $\operatorname{Sp}_{n}(k)$
into
$\operatorname{Sp}_{n}(k)$
into
![]() $\operatorname{SL}_{n}(k)$
and using this embedding we parametrize Borel regular subgroups of
$\operatorname{SL}_{n}(k)$
and using this embedding we parametrize Borel regular subgroups of
![]() $\operatorname{Sp}_{n}(k)$
with root subsets
$\operatorname{Sp}_{n}(k)$
with root subsets
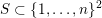 $S\subset \{1,\ldots ,n\}^{2}$
again. We define the symplectic fundamental domain
$S\subset \{1,\ldots ,n\}^{2}$
again. We define the symplectic fundamental domain
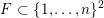 $F\subset \{1,\ldots ,n\}^{2}$
corresponding to
$F\subset \{1,\ldots ,n\}^{2}$
corresponding to
![]() $S$
and define the pair
$S$
and define the pair
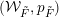 $({\mathcal{W}}_{\tilde{F}},p_{\tilde{F}})$
where the stabiliser of
$({\mathcal{W}}_{\tilde{F}},p_{\tilde{F}})$
where the stabiliser of
![]() $p_{\tilde{F}}$
in
$p_{\tilde{F}}$
in
![]() $\operatorname{Sp}_{n}(k)$
is
$\operatorname{Sp}_{n}(k)$
is
![]() $U_{S}$
. Finally, we prove Theorem 1.3 for symplectic groups. Section 5.3 follows the same line for the orthogonal groups
$U_{S}$
. Finally, we prove Theorem 1.3 for symplectic groups. Section 5.3 follows the same line for the orthogonal groups
![]() $\operatorname{SO}_{n}$
for odd and even
$\operatorname{SO}_{n}$
for odd and even
![]() $n$
and proves Theorem 1.3 for orthogonal groups.
$n$
and proves Theorem 1.3 for orthogonal groups.
We conjecture that
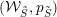 $({\mathcal{W}}_{\tilde{S}},p_{\tilde{S}})$
is a Grosshans pair for arbitrary regular subgroup
$({\mathcal{W}}_{\tilde{S}},p_{\tilde{S}})$
is a Grosshans pair for arbitrary regular subgroup
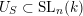 $U_{S}\subset \operatorname{SL}_{n}(k)$
, not just for left Borel-regular subgroups. Unfortunately we cannot prove this in full generality. What we conjecture is that all boundary components of
$U_{S}\subset \operatorname{SL}_{n}(k)$
, not just for left Borel-regular subgroups. Unfortunately we cannot prove this in full generality. What we conjecture is that all boundary components of
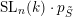 $\operatorname{SL}_{n}(k)\cdot p_{\tilde{S}}$
have codimension at least two in its closure in
$\operatorname{SL}_{n}(k)\cdot p_{\tilde{S}}$
have codimension at least two in its closure in
![]() ${\mathcal{W}}_{\tilde{S}}$
. In § 6 we prove this for a special class of boundary components. We define the toric closure of the orbit
${\mathcal{W}}_{\tilde{S}}$
. In § 6 we prove this for a special class of boundary components. We define the toric closure of the orbit
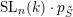 $\operatorname{SL}_{n}(k)\cdot p_{\tilde{S}}$
as
$\operatorname{SL}_{n}(k)\cdot p_{\tilde{S}}$
as
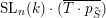 $\operatorname{SL}_{n}(k)\cdot (\overline{T\cdot p_{\tilde{S}}})$
and prove that the toric boundary components are small.
$\operatorname{SL}_{n}(k)\cdot (\overline{T\cdot p_{\tilde{S}}})$
and prove that the toric boundary components are small.
Theorem 1.4 (Partial answer to the Popov–Pommerening conjecture for general
 $S$
).
$S$
).
Let
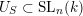 $U_{S}\subset \operatorname{SL}_{n}(k)$
be a regular subgroup corresponding to the closed subset
$U_{S}\subset \operatorname{SL}_{n}(k)$
be a regular subgroup corresponding to the closed subset
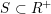 $S\subset R^{+}$
. Then the toric boundary components of the orbit
$S\subset R^{+}$
. Then the toric boundary components of the orbit
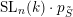 $\operatorname{SL}_{n}(k)\cdot p_{\tilde{S}}$
have codimension at least
$\operatorname{SL}_{n}(k)\cdot p_{\tilde{S}}$
have codimension at least
![]() $2$
in the orbit closure, that is
$2$
in the orbit closure, that is
 $$\begin{eqnarray}\dim (\operatorname{SL}_{n}(k)\cdot (\overline{T\cdot p_{\tilde{S}}})\setminus \operatorname{SL}_{n}(k)\cdot p_{\tilde{S}})\leqslant \dim (\operatorname{SL}_{n}(k)\cdot p_{\tilde{S}})-2.\end{eqnarray}$$
$$\begin{eqnarray}\dim (\operatorname{SL}_{n}(k)\cdot (\overline{T\cdot p_{\tilde{S}}})\setminus \operatorname{SL}_{n}(k)\cdot p_{\tilde{S}})\leqslant \dim (\operatorname{SL}_{n}(k)\cdot p_{\tilde{S}})-2.\end{eqnarray}$$
We finish the paper with some remarks in § 7 on the relation of our approach to configuration varieties and Bott–Samelson varieties.
2 Grosshans subgroups
Let
![]() $G$
be reductive algebraic group over an algebraically closed field
$G$
be reductive algebraic group over an algebraically closed field
![]() $k$
.
$k$
.
Definition 2.1. A subgroup
![]() $H\subset G$
is called Grosshans subgroup if
$H\subset G$
is called Grosshans subgroup if
![]() $k[X]^{H}$
finitely generated for any affine variety
$k[X]^{H}$
finitely generated for any affine variety
![]() $X$
endowed with a linear action of
$X$
endowed with a linear action of
![]() $G$
.
$G$
.
Theorem 2.2 (Grosshans criterion [Reference GrosshansGro97]).
Let
![]() $G$
be a reductive group over an algebraically closed field, and
$G$
be a reductive group over an algebraically closed field, and
![]() $H$
an observable subgroup, that is,
$H$
an observable subgroup, that is,
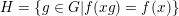 $H=\{g\in G|f(xg)=f(x)\}$
for all
$H=\{g\in G|f(xg)=f(x)\}$
for all
![]() $x\in G$
and
$x\in G$
and
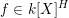 $f\in k[X]^{H}$
. Then the following conditions are equivalent:
$f\in k[X]^{H}$
. Then the following conditions are equivalent:
-
(i)
 $H$
is a Grosshans subgroup of
$H$
is a Grosshans subgroup of
 $G$
;
$G$
; -
(ii)
 $k[G]^{H}$
is a finitely generated
$k[G]^{H}$
is a finitely generated
 $k$
-algebra, where
$k$
-algebra, where
 $H$
acts via right translations;
$H$
acts via right translations; -
(iii) there is a finite-dimensional left
 $G$
-module
$G$
-module
 ${\mathcal{W}}$
and some
${\mathcal{W}}$
and some
 $w\in {\mathcal{W}}$
such that
$w\in {\mathcal{W}}$
such that
 $H=G_{w}$
is the stabiliser of
$H=G_{w}$
is the stabiliser of
 $w$
(and therefore
$w$
(and therefore
 $G/H$
is a homogeneous space
$G/H$
is a homogeneous space
 $G\cdot w$
) and
$G\cdot w$
) and
 $\dim (\overline{G\cdot w}\setminus G\cdot w)\leqslant \dim (G\cdot w)-2$
.
$\dim (\overline{G\cdot w}\setminus G\cdot w)\leqslant \dim (G\cdot w)-2$
.
Definition 2.3. A pair
![]() $({\mathcal{W}},w)$
where
$({\mathcal{W}},w)$
where
![]() ${\mathcal{W}}$
is a finite-dimensional
${\mathcal{W}}$
is a finite-dimensional
![]() $G$
-module and
$G$
-module and
![]() $w\in {\mathcal{W}}$
is a point satisfying the Grosshans criterion is called a Grosshans pair.
$w\in {\mathcal{W}}$
is a point satisfying the Grosshans criterion is called a Grosshans pair.
3 Construction of Grosshans pairs for
 $G=\operatorname{SL}_{n}(k)$
$G=\operatorname{SL}_{n}(k)$
For the rest of the paper we restrict our attention to the
![]() $k=\mathbb{C}$
case, but all arguments work for any algebraically closed field
$k=\mathbb{C}$
case, but all arguments work for any algebraically closed field
![]() $k$
of characteristic zero which is a subfield of
$k$
of characteristic zero which is a subfield of
![]() $\mathbb{C}$
. We will often use the shorthand notation
$\mathbb{C}$
. We will often use the shorthand notation
![]() $\operatorname{SL}_{n}$
for
$\operatorname{SL}_{n}$
for
![]() $\operatorname{SL}_{n}(\mathbb{C})$
.
$\operatorname{SL}_{n}(\mathbb{C})$
.
In this section we assume that
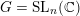 $G=\operatorname{SL}_{n}(\mathbb{C})$
and let
$G=\operatorname{SL}_{n}(\mathbb{C})$
and let
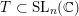 $T\subset \operatorname{SL}_{n}(\mathbb{C})$
be the diagonal maximal torus and
$T\subset \operatorname{SL}_{n}(\mathbb{C})$
be the diagonal maximal torus and
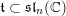 $\mathfrak{t}\subset \mathfrak{sl}_{n}(\mathbb{C})$
the Cartan subalgebra of diagonal matrices. Let
$\mathfrak{t}\subset \mathfrak{sl}_{n}(\mathbb{C})$
the Cartan subalgebra of diagonal matrices. Let
![]() $\unicode[STIX]{x1D6FC}_{i}\in \mathfrak{t}^{\ast }$
be the dual of
$\unicode[STIX]{x1D6FC}_{i}\in \mathfrak{t}^{\ast }$
be the dual of
![]() $E_{ii}\in \mathfrak{t}$
where
$E_{ii}\in \mathfrak{t}$
where
![]() $E_{ii}$
is the matrix of the endomorphism which fixes the
$E_{ii}$
is the matrix of the endomorphism which fixes the
![]() $i$
th basis vector and kills all other basis vectors. Let
$i$
th basis vector and kills all other basis vectors. Let
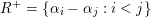 $R^{+}=\{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}:i<j\}$
be the set of positive roots and
$R^{+}=\{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}:i<j\}$
be the set of positive roots and
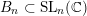 $B_{n}\subset \operatorname{SL}_{n}(\mathbb{C})$
be the corresponding upper Borel subgroup. The one-dimensional root subgroup
$B_{n}\subset \operatorname{SL}_{n}(\mathbb{C})$
be the corresponding upper Borel subgroup. The one-dimensional root subgroup
![]() $U_{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}}$
consists of unipotent matrices with the only nonzero off-diagonal entry sitting at
$U_{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}}$
consists of unipotent matrices with the only nonzero off-diagonal entry sitting at
![]() $(i,j)$
.
$(i,j)$
.
A subset
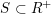 $S\subset R^{+}$
of the root system is closed if and only if the following transitivity conditions hold for all
$S\subset R^{+}$
of the root system is closed if and only if the following transitivity conditions hold for all
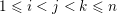 $1\leqslant i<j<k\leqslant n$
:
$1\leqslant i<j<k\leqslant n$
:
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j},\quad \unicode[STIX]{x1D6FC}_{j}-\unicode[STIX]{x1D6FC}_{k}\in S\Rightarrow \unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{k}\in S.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j},\quad \unicode[STIX]{x1D6FC}_{j}-\unicode[STIX]{x1D6FC}_{k}\in S\Rightarrow \unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{k}\in S.\end{eqnarray}$$
Define the unipotent subgroup
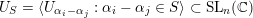 $$\begin{eqnarray}U_{S}=\langle U_{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}}:\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\in S\rangle \subset \operatorname{SL}_{n}(\mathbb{C})\end{eqnarray}$$
$$\begin{eqnarray}U_{S}=\langle U_{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}}:\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\in S\rangle \subset \operatorname{SL}_{n}(\mathbb{C})\end{eqnarray}$$
generated by the root subgroups
![]() $U_{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}}$
. Then
$U_{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}}$
. Then
![]() $U_{S}$
is unipotent with independent parameters at the entries indexed by
$U_{S}$
is unipotent with independent parameters at the entries indexed by
![]() $S$
and it is normalised by the maximal diagonal torus in
$S$
and it is normalised by the maximal diagonal torus in
![]() $\operatorname{SL}_{n}(\mathbb{C})$
, and all unipotent subgroups normalised by this torus have this form.
$\operatorname{SL}_{n}(\mathbb{C})$
, and all unipotent subgroups normalised by this torus have this form.
For
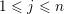 $1\leqslant j\leqslant n$
let
$1\leqslant j\leqslant n$
let
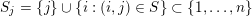 $S_{j}=\{j\}\cup \{i:(i,j)\in S\}\subset \{1,\ldots ,n\}$
collect the positions of the (possibly) nonzero entries in the
$S_{j}=\{j\}\cup \{i:(i,j)\in S\}\subset \{1,\ldots ,n\}$
collect the positions of the (possibly) nonzero entries in the
![]() $j$
th column of
$j$
th column of
![]() $U_{S}$
. In the example (2) of the Introduction
$U_{S}$
. In the example (2) of the Introduction
 $$\begin{eqnarray}S_{1}=\{1\},\quad S_{2}=\{2\},\quad S_{3}=\{1,3\},\quad S_{4}=\{2,4\}.\end{eqnarray}$$
$$\begin{eqnarray}S_{1}=\{1\},\quad S_{2}=\{2\},\quad S_{3}=\{1,3\},\quad S_{4}=\{2,4\}.\end{eqnarray}$$
Fix a basis
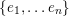 $\{e_{1},\ldots e_{n}\}$
of
$\{e_{1},\ldots e_{n}\}$
of
![]() $\mathbb{C}^{n}$
compatible with
$\mathbb{C}^{n}$
compatible with
![]() $B_{n}$
, that is,
$B_{n}$
, that is,
![]() $B_{n}$
preserves the subspace
$B_{n}$
preserves the subspace
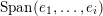 $\operatorname{Span}(e_{1},\ldots ,e_{i})$
for
$\operatorname{Span}(e_{1},\ldots ,e_{i})$
for
 $1\leqslant i\leqslant n$
. For a subset
$1\leqslant i\leqslant n$
. For a subset
 $Z\subset \{1,\ldots ,n\}$
we set
$Z\subset \{1,\ldots ,n\}$
we set
 $$\begin{eqnarray}p_{Z}=\wedge _{z\in Z}e_{z}\in \wedge ^{|Z|}\mathbb{C}^{n}\end{eqnarray}$$
$$\begin{eqnarray}p_{Z}=\wedge _{z\in Z}e_{z}\in \wedge ^{|Z|}\mathbb{C}^{n}\end{eqnarray}$$
where
![]() $|Z|$
is the cardinality of
$|Z|$
is the cardinality of
![]() $Z$
. Define the point
$Z$
. Define the point
 $$\begin{eqnarray}p_{S}=\bigoplus _{j=1}^{n}p_{S_{j}}=\bigoplus _{j=1}^{n}\wedge _{i\in S_{j}}e_{i}\in {\mathcal{W}}_{S}\end{eqnarray}$$
$$\begin{eqnarray}p_{S}=\bigoplus _{j=1}^{n}p_{S_{j}}=\bigoplus _{j=1}^{n}\wedge _{i\in S_{j}}e_{i}\in {\mathcal{W}}_{S}\end{eqnarray}$$
where
 $$\begin{eqnarray}{\mathcal{W}}_{S}=\bigoplus _{j=1}^{n}\wedge ^{|S_{j}|}\mathbb{C}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{S}=\bigoplus _{j=1}^{n}\wedge ^{|S_{j}|}\mathbb{C}^{n}.\end{eqnarray}$$
In the example (2)
 $$\begin{eqnarray}p_{S}=e_{1}\oplus e_{2}\oplus (e_{1}\wedge e_{3})\oplus (e_{2}\wedge e_{4})\in \mathbb{C}^{S}=\mathbb{C}^{4}\oplus \mathbb{C}^{4}\oplus \wedge ^{2}\mathbb{C}^{4}\oplus \wedge ^{2}\mathbb{C}^{4}.\end{eqnarray}$$
$$\begin{eqnarray}p_{S}=e_{1}\oplus e_{2}\oplus (e_{1}\wedge e_{3})\oplus (e_{2}\wedge e_{4})\in \mathbb{C}^{S}=\mathbb{C}^{4}\oplus \mathbb{C}^{4}\oplus \wedge ^{2}\mathbb{C}^{4}\oplus \wedge ^{2}\mathbb{C}^{4}.\end{eqnarray}$$
Theorem 3.1. The stabiliser of
![]() $p_{S}$
in
$p_{S}$
in
![]() $\operatorname{SL}_{n}$
is
$\operatorname{SL}_{n}$
is
![]() $U_{S}$
.
$U_{S}$
.
Proof. Let
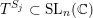 $T^{S_{j}}\subset \operatorname{SL}_{n}(\mathbb{C})$
denote the diagonal torus
$T^{S_{j}}\subset \operatorname{SL}_{n}(\mathbb{C})$
denote the diagonal torus
 $$\begin{eqnarray}T^{S_{j}}=\{\operatorname{diag}(a_{1},\ldots ,a_{n}):\unicode[STIX]{x1D6F1}_{i\in S_{j}}a_{i}=\unicode[STIX]{x1D6F1}_{i\notin S_{j}}a_{i}=1\}.\end{eqnarray}$$
$$\begin{eqnarray}T^{S_{j}}=\{\operatorname{diag}(a_{1},\ldots ,a_{n}):\unicode[STIX]{x1D6F1}_{i\in S_{j}}a_{i}=\unicode[STIX]{x1D6F1}_{i\notin S_{j}}a_{i}=1\}.\end{eqnarray}$$
The stabiliser of
![]() $p_{S}$
is the intersection of the stabilisers of its direct summands. The stabiliser in
$p_{S}$
is the intersection of the stabilisers of its direct summands. The stabiliser in
![]() $\operatorname{SL}_{n}(\mathbb{C})$
of the direct summand
$\operatorname{SL}_{n}(\mathbb{C})$
of the direct summand
![]() $\wedge _{i\in S_{j}}e_{i}$
is the semidirect product
$\wedge _{i\in S_{j}}e_{i}$
is the semidirect product
 $$\begin{eqnarray}U_{S}^{j}=\langle U_{\unicode[STIX]{x1D6FC}_{a}-\unicode[STIX]{x1D6FC}_{b}}:(a\neq b,a,b\in S_{j})~\text{or}~(a\neq b,b\notin S_{j})\rangle \rtimes T^{S_{j}}.\end{eqnarray}$$
$$\begin{eqnarray}U_{S}^{j}=\langle U_{\unicode[STIX]{x1D6FC}_{a}-\unicode[STIX]{x1D6FC}_{b}}:(a\neq b,a,b\in S_{j})~\text{or}~(a\neq b,b\notin S_{j})\rangle \rtimes T^{S_{j}}.\end{eqnarray}$$
Now
![]() $j\in S_{j}$
for
$j\in S_{j}$
for
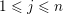 $1\leqslant j\leqslant n$
and by (3) the intersection is
$1\leqslant j\leqslant n$
and by (3) the intersection is
 $$\begin{eqnarray}\mathop{\bigcap }_{j=1}^{n}U_{S}^{j}=\langle U_{\unicode[STIX]{x1D6FC}_{a}-\unicode[STIX]{x1D6FC}_{b}}:a<b,a\in S_{b}\rangle \rtimes \biggl(\mathop{\bigcap }_{j=1}^{n}T^{S_{j}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\bigcap }_{j=1}^{n}U_{S}^{j}=\langle U_{\unicode[STIX]{x1D6FC}_{a}-\unicode[STIX]{x1D6FC}_{b}}:a<b,a\in S_{b}\rangle \rtimes \biggl(\mathop{\bigcap }_{j=1}^{n}T^{S_{j}}\biggr).\end{eqnarray}$$
Since
![]() $j\in S_{j}$
and
$j\in S_{j}$
and
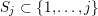 $S_{j}\subset \{1,\ldots ,j\}$
for all
$S_{j}\subset \{1,\ldots ,j\}$
for all
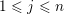 $1\leqslant j\leqslant n$
we have by induction on
$1\leqslant j\leqslant n$
we have by induction on
![]() $n$
that
$n$
that
 $$\begin{eqnarray}\mathop{\bigcap }_{j=1}^{n}T^{S_{j}}=\{\operatorname{diag}(a_{1},\ldots ,a_{n}):a_{1}=1,\unicode[STIX]{x1D6F1}_{i\in S_{2}}a_{i}=1,\ldots ,\unicode[STIX]{x1D6F1}_{i\in S_{n}}a_{i}=1\}=1,\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\bigcap }_{j=1}^{n}T^{S_{j}}=\{\operatorname{diag}(a_{1},\ldots ,a_{n}):a_{1}=1,\unicode[STIX]{x1D6F1}_{i\in S_{2}}a_{i}=1,\ldots ,\unicode[STIX]{x1D6F1}_{i\in S_{n}}a_{i}=1\}=1,\end{eqnarray}$$
and therefore
 $$\begin{eqnarray}\mathop{\bigcap }_{j=1}^{n}U_{S}^{j}=\langle U_{\unicode[STIX]{x1D6FC}_{a}-\unicode[STIX]{x1D6FC}_{b}}:b<a,b\in S_{a}\rangle =U_{S}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\bigcap }_{j=1}^{n}U_{S}^{j}=\langle U_{\unicode[STIX]{x1D6FC}_{a}-\unicode[STIX]{x1D6FC}_{b}}:b<a,b\in S_{a}\rangle =U_{S}\end{eqnarray}$$
by definition. ◻
Corollary 3.2. The map
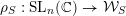 $\unicode[STIX]{x1D70C}_{S}:\operatorname{SL}_{n}(\mathbb{C})\rightarrow {\mathcal{W}}_{S}$
defined as
$\unicode[STIX]{x1D70C}_{S}:\operatorname{SL}_{n}(\mathbb{C})\rightarrow {\mathcal{W}}_{S}$
defined as
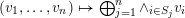 $(v_{1},\ldots ,v_{n})\mapsto \bigoplus _{j=1}^{n}\wedge _{i\in S_{j}}v_{i}$
on a matrix with column vectors
$(v_{1},\ldots ,v_{n})\mapsto \bigoplus _{j=1}^{n}\wedge _{i\in S_{j}}v_{i}$
on a matrix with column vectors
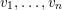 $v_{1},\ldots ,v_{n}$
is invariant under the right multiplication action of
$v_{1},\ldots ,v_{n}$
is invariant under the right multiplication action of
![]() $U_{S}$
on
$U_{S}$
on
![]() $\operatorname{SL}_{n}(\mathbb{C})$
and the induced map
$\operatorname{SL}_{n}(\mathbb{C})$
and the induced map
 $$\begin{eqnarray}\operatorname{SL}_{n}(\mathbb{C})/U_{S}{\hookrightarrow}{\mathcal{W}}_{S}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{SL}_{n}(\mathbb{C})/U_{S}{\hookrightarrow}{\mathcal{W}}_{S}\end{eqnarray}$$
on the set of
![]() $U_{S}$
-orbits is injective and
$U_{S}$
-orbits is injective and
![]() $\operatorname{SL}_{n}(\mathbb{C})$
-equivariant with respect to the left multiplication action of
$\operatorname{SL}_{n}(\mathbb{C})$
-equivariant with respect to the left multiplication action of
![]() $\operatorname{SL}_{n}(\mathbb{C})$
on
$\operatorname{SL}_{n}(\mathbb{C})$
on
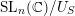 $\operatorname{SL}_{n}(\mathbb{C})/U_{S}$
.
$\operatorname{SL}_{n}(\mathbb{C})/U_{S}$
.
Example 3.3. This example shows that
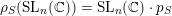 $\unicode[STIX]{x1D70C}_{S}(\operatorname{SL}_{n}(\mathbb{C}))=\operatorname{SL}_{n}(\mathbb{C})\cdot p_{S}$
might have codimension 1 boundary components in
$\unicode[STIX]{x1D70C}_{S}(\operatorname{SL}_{n}(\mathbb{C}))=\operatorname{SL}_{n}(\mathbb{C})\cdot p_{S}$
might have codimension 1 boundary components in
![]() ${\mathcal{W}}_{S}$
. Take
${\mathcal{W}}_{S}$
. Take
 $$\begin{eqnarray}p_{S}=e_{1}\oplus (e_{1}\wedge e_{2})\oplus (e_{1}\wedge e_{3})\oplus (e_{1}\wedge e_{2}\wedge e_{3}\wedge e_{4})\in \mathbb{C}^{4}\oplus \wedge ^{2}\mathbb{C}^{4}\oplus \wedge ^{2}\mathbb{C}^{4}\oplus \wedge ^{4}\mathbb{C}^{4}\end{eqnarray}$$
$$\begin{eqnarray}p_{S}=e_{1}\oplus (e_{1}\wedge e_{2})\oplus (e_{1}\wedge e_{3})\oplus (e_{1}\wedge e_{2}\wedge e_{3}\wedge e_{4})\in \mathbb{C}^{4}\oplus \wedge ^{2}\mathbb{C}^{4}\oplus \wedge ^{2}\mathbb{C}^{4}\oplus \wedge ^{4}\mathbb{C}^{4}\end{eqnarray}$$
corresponding to the group

Then
 $$\begin{eqnarray}\lim _{t\rightarrow 0}\left(\begin{array}{@{}cccc@{}}t & 0 & 0 & 0\\ 0 & t^{-1} & 0 & 0\\ 0 & 0 & t^{-1} & 0\\ 0 & 0 & 0 & t\end{array}\right)\cdot p_{S}=0\oplus (e_{1}\wedge e_{2})\oplus (e_{1}\wedge e_{3})\oplus (e_{1}\wedge e_{2}\wedge e_{3}\wedge e_{4}),\end{eqnarray}$$
$$\begin{eqnarray}\lim _{t\rightarrow 0}\left(\begin{array}{@{}cccc@{}}t & 0 & 0 & 0\\ 0 & t^{-1} & 0 & 0\\ 0 & 0 & t^{-1} & 0\\ 0 & 0 & 0 & t\end{array}\right)\cdot p_{S}=0\oplus (e_{1}\wedge e_{2})\oplus (e_{1}\wedge e_{3})\oplus (e_{1}\wedge e_{2}\wedge e_{3}\wedge e_{4}),\end{eqnarray}$$
whose stabiliser in
![]() $\operatorname{SL}_{n}(\mathbb{C})$
is
$\operatorname{SL}_{n}(\mathbb{C})$
is
 $$\begin{eqnarray}\left\{\left(\begin{array}{@{}cccc@{}}a & b & c & d\\ 0 & a^{-1} & 0 & e\\ 0 & 0 & a^{-1} & f\\ 0 & 0 & 0 & a\end{array}\right):a\in \mathbb{C}^{\ast },b,c,d,e,f\in \mathbb{C}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left\{\left(\begin{array}{@{}cccc@{}}a & b & c & d\\ 0 & a^{-1} & 0 & e\\ 0 & 0 & a^{-1} & f\\ 0 & 0 & 0 & a\end{array}\right):a\in \mathbb{C}^{\ast },b,c,d,e,f\in \mathbb{C}\right\}\end{eqnarray}$$
which has dimension one plus the dimension of
![]() $U_{S}$
, and therefore this boundary orbit has codimension 1 in
$U_{S}$
, and therefore this boundary orbit has codimension 1 in
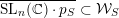 $\overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{S}}\subset {\mathcal{W}}_{S}$
.
$\overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{S}}\subset {\mathcal{W}}_{S}$
.
To make things even worse, in this example we have infinitely many boundary orbits, which means that it is not enough to study the boundary orbits and their stabilisers to prove the Grosshans property. Indeed,
 $$\begin{eqnarray}\lim _{t\rightarrow 0}\left(\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 1 & \unicode[STIX]{x1D6FC} & 0\\ 0 & 0 & t & 0\\ 0 & 0 & 0 & t^{-1}\end{array}\right)\cdot p_{S}=e_{1}\oplus (e_{1}\wedge e_{2})\oplus \unicode[STIX]{x1D6FC}(e_{1}\wedge e_{2})\oplus (e_{1}\wedge e_{2}\wedge e_{3}\wedge e_{4}),\end{eqnarray}$$
$$\begin{eqnarray}\lim _{t\rightarrow 0}\left(\begin{array}{@{}cccc@{}}1 & 0 & 0 & 0\\ 0 & 1 & \unicode[STIX]{x1D6FC} & 0\\ 0 & 0 & t & 0\\ 0 & 0 & 0 & t^{-1}\end{array}\right)\cdot p_{S}=e_{1}\oplus (e_{1}\wedge e_{2})\oplus \unicode[STIX]{x1D6FC}(e_{1}\wedge e_{2})\oplus (e_{1}\wedge e_{2}\wedge e_{3}\wedge e_{4}),\end{eqnarray}$$
and for different
![]() $\unicode[STIX]{x1D6FC}$
values these boundary points sit in different
$\unicode[STIX]{x1D6FC}$
values these boundary points sit in different
![]() $\operatorname{SL}_{n}(k)$
orbits.
$\operatorname{SL}_{n}(k)$
orbits.
Let
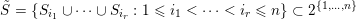 $\tilde{S}=\{S_{i_{1}}\cup \cdots \cup S_{i_{r}}:1\leqslant i_{1}<\cdots <i_{r}\leqslant n\}\subset 2^{\{1,\ldots ,n\}}$
be the family of all possible unions of the
$\tilde{S}=\{S_{i_{1}}\cup \cdots \cup S_{i_{r}}:1\leqslant i_{1}<\cdots <i_{r}\leqslant n\}\subset 2^{\{1,\ldots ,n\}}$
be the family of all possible unions of the
![]() $S_{j}$
. Recall from (1) that the stars in the box form of
$S_{j}$
. Recall from (1) that the stars in the box form of
![]() $U_{S}$
form an incidence matrix of a partial order of
$U_{S}$
form an incidence matrix of a partial order of
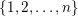 $\{1,2,\ldots ,n\}$
, that is,
$\{1,2,\ldots ,n\}$
, that is,
 $$\begin{eqnarray}i\in S_{j},\quad j\in S_{k}\Rightarrow i\in S_{k}\end{eqnarray}$$
$$\begin{eqnarray}i\in S_{j},\quad j\in S_{k}\Rightarrow i\in S_{k}\end{eqnarray}$$
holds for
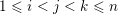 $1\leqslant i<j<k\leqslant n$
and therefore for
$1\leqslant i<j<k\leqslant n$
and therefore for
![]() $i<j$
,
$i<j$
,
 $$\begin{eqnarray}S_{i}\cap S_{j}=\mathop{\bigcup }_{k\in S_{i}\cap S_{j}}S_{k}.\end{eqnarray}$$
$$\begin{eqnarray}S_{i}\cap S_{j}=\mathop{\bigcup }_{k\in S_{i}\cap S_{j}}S_{k}.\end{eqnarray}$$
Hence
![]() $\tilde{S}$
is a so-called ring family, that is, closed under intersections and finite unions:
$\tilde{S}$
is a so-called ring family, that is, closed under intersections and finite unions:
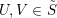 $U,V\in \tilde{S}$
implies
$U,V\in \tilde{S}$
implies
![]() $U\cap V$
,
$U\cap V$
,
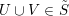 $U\cup V\in \tilde{S}$
. The point
$U\cup V\in \tilde{S}$
. The point
 $$\begin{eqnarray}p_{\tilde{S}}=\bigoplus _{U\in \tilde{S}}\wedge _{i\in U}e_{i}\in {\mathcal{W}}_{\tilde{S}}\end{eqnarray}$$
$$\begin{eqnarray}p_{\tilde{S}}=\bigoplus _{U\in \tilde{S}}\wedge _{i\in U}e_{i}\in {\mathcal{W}}_{\tilde{S}}\end{eqnarray}$$
where
 $$\begin{eqnarray}{\mathcal{W}}_{\tilde{S}}=\bigoplus _{U\in \tilde{S}}\wedge ^{|U|}\mathbb{C}^{n}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}_{\tilde{S}}=\bigoplus _{U\in \tilde{S}}\wedge ^{|U|}\mathbb{C}^{n}\end{eqnarray}$$
has the same stabiliser as
![]() $p_{S}$
, that is, Theorem 3.1 implies the following.
$p_{S}$
, that is, Theorem 3.1 implies the following.
Corollary 3.4. The stabiliser of
![]() $p_{\tilde{S}}$
in
$p_{\tilde{S}}$
in
![]() $\operatorname{SL}_{n}$
is
$\operatorname{SL}_{n}$
is
![]() $U_{S}$
.
$U_{S}$
.
In our example (2) we have
 $$\begin{eqnarray}\tilde{S}=\{\{1\},\{2\},\{1,3\},\{2,4\},\{1,2\},\{1,2,3\},\{1,2,4\},\{1,2,3,4\}\}\end{eqnarray}$$
$$\begin{eqnarray}\tilde{S}=\{\{1\},\{2\},\{1,3\},\{2,4\},\{1,2\},\{1,2,3\},\{1,2,4\},\{1,2,3,4\}\}\end{eqnarray}$$
and
 $$\begin{eqnarray}p_{\tilde{S}}=e_{1}\oplus e_{2}\oplus (e_{1}\wedge e_{3})\oplus (e_{2}\wedge e_{4})\oplus (e_{1}\wedge e_{2})\oplus (e_{1}\wedge e_{2}\wedge e_{3})\oplus (e_{1}\wedge e_{2}\wedge e_{4})\oplus (e_{1}\wedge e_{2}\wedge e_{3}\wedge e_{4}).\end{eqnarray}$$
$$\begin{eqnarray}p_{\tilde{S}}=e_{1}\oplus e_{2}\oplus (e_{1}\wedge e_{3})\oplus (e_{2}\wedge e_{4})\oplus (e_{1}\wedge e_{2})\oplus (e_{1}\wedge e_{2}\wedge e_{3})\oplus (e_{1}\wedge e_{2}\wedge e_{4})\oplus (e_{1}\wedge e_{2}\wedge e_{3}\wedge e_{4}).\end{eqnarray}$$
Conjecture 3.5. The pair
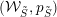 $({\mathcal{W}}_{\tilde{S}},p_{\tilde{S}})$
is a Grosshans pair for the group
$({\mathcal{W}}_{\tilde{S}},p_{\tilde{S}})$
is a Grosshans pair for the group
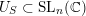 $U_{S}\subset \operatorname{SL}_{n}(\mathbb{C})$
, that is, the boundary components of the orbit
$U_{S}\subset \operatorname{SL}_{n}(\mathbb{C})$
, that is, the boundary components of the orbit
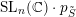 $\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}$
have codimension at least
$\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}$
have codimension at least
![]() $2$
in its closure:
$2$
in its closure:
 $$\begin{eqnarray}\dim (\overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}}\setminus \operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}})\leqslant \dim (\overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}})-2.\end{eqnarray}$$
$$\begin{eqnarray}\dim (\overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}}\setminus \operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}})\leqslant \dim (\overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}})-2.\end{eqnarray}$$
4 Left Borel-regular subgroups of
 $\operatorname{SL}_{n}(k)$
$\operatorname{SL}_{n}(k)$
In this section we prove Theorem 1.2. As we already mentioned in the introduction of § 3, we only consider the
![]() $k=\mathbb{C}$
case but the arguments work for any algebraically closed field
$k=\mathbb{C}$
case but the arguments work for any algebraically closed field
![]() $k$
of characteristic zero which is a subfield of
$k$
of characteristic zero which is a subfield of
![]() $\mathbb{C}$
.
$\mathbb{C}$
.
Recall from the Introduction that a left Borel-regular subgroup
 $U_{S}\subset \operatorname{SL}_{n}(\mathbb{C})$
is determined by a sequence
$U_{S}\subset \operatorname{SL}_{n}(\mathbb{C})$
is determined by a sequence
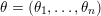 $\unicode[STIX]{x1D703}=(\unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n})$
such that
$\unicode[STIX]{x1D703}=(\unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n})$
such that
 $0\leqslant \unicode[STIX]{x1D703}_{i}<i$
and the corresponding closed root subset
$0\leqslant \unicode[STIX]{x1D703}_{i}<i$
and the corresponding closed root subset
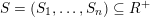 $S=(S_{1},\ldots ,S_{n})\subseteq R^{+}$
has the form
$S=(S_{1},\ldots ,S_{n})\subseteq R^{+}$
has the form
 $$\begin{eqnarray}S_{i}=\left\{\begin{array}{@{}ll@{}}\{1,\ldots \unicode[STIX]{x1D703}_{i},i\}\quad & \text{when}~\unicode[STIX]{x1D703}_{i}>0,\\ \{i\}\quad & \text{when}~\unicode[STIX]{x1D703}_{i}=0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}S_{i}=\left\{\begin{array}{@{}ll@{}}\{1,\ldots \unicode[STIX]{x1D703}_{i},i\}\quad & \text{when}~\unicode[STIX]{x1D703}_{i}>0,\\ \{i\}\quad & \text{when}~\unicode[STIX]{x1D703}_{i}=0.\end{array}\right.\end{eqnarray}$$
For a subset
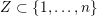 $Z\subset \{1,\ldots ,n\}$
we define
$Z\subset \{1,\ldots ,n\}$
we define
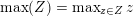 $\max (Z)=\max _{z\in Z}z$
to be its maximal element and we let
$\max (Z)=\max _{z\in Z}z$
to be its maximal element and we let
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{Z}:=\max _{z\in Z}\unicode[STIX]{x1D703}_{z}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{Z}:=\max _{z\in Z}\unicode[STIX]{x1D703}_{z}.\end{eqnarray}$$
Elements of the generated ring family
![]() $\tilde{S}$
are formed by unions of the
$\tilde{S}$
are formed by unions of the
![]() $S_{i}$
and for a subset
$S_{i}$
and for a subset
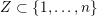 $Z\subset \{1,\ldots ,n\}$
the corresponding element of
$Z\subset \{1,\ldots ,n\}$
the corresponding element of
![]() $\tilde{S}$
is
$\tilde{S}$
is
 $$\begin{eqnarray}S_{Z}=\mathop{\bigcup }_{z\in Z}S_{z}=\{1,\ldots ,\unicode[STIX]{x1D703}_{Z}\}\cup \{z\in Z:z>\unicode[STIX]{x1D703}_{Z}\}.\end{eqnarray}$$
$$\begin{eqnarray}S_{Z}=\mathop{\bigcup }_{z\in Z}S_{z}=\{1,\ldots ,\unicode[STIX]{x1D703}_{Z}\}\cup \{z\in Z:z>\unicode[STIX]{x1D703}_{Z}\}.\end{eqnarray}$$
That is, (6) tells us that
![]() $S_{Z}$
contains all integers between 1 and
$S_{Z}$
contains all integers between 1 and
![]() $\unicode[STIX]{x1D703}_{Z}$
along with those elements of
$\unicode[STIX]{x1D703}_{Z}$
along with those elements of
![]() $Z$
which are bigger than
$Z$
which are bigger than
![]() $\unicode[STIX]{x1D703}_{Z}$
. In other words, if
$\unicode[STIX]{x1D703}_{Z}$
. In other words, if
![]() $Z\in \tilde{S}$
with
$Z\in \tilde{S}$
with
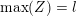 $\max (Z)=l$
, then there exist integers
$\max (Z)=l$
, then there exist integers
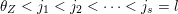 $\unicode[STIX]{x1D703}_{Z}<j_{1}<j_{2}<\cdots <j_{s}=l$
such that
$\unicode[STIX]{x1D703}_{Z}<j_{1}<j_{2}<\cdots <j_{s}=l$
such that
 $$\begin{eqnarray}Z=\{1,\ldots ,\unicode[STIX]{x1D703}_{Z},j_{1},\ldots ,j_{s}=l\},\end{eqnarray}$$
$$\begin{eqnarray}Z=\{1,\ldots ,\unicode[STIX]{x1D703}_{Z},j_{1},\ldots ,j_{s}=l\},\end{eqnarray}$$
see Figure 1 for an example.

Figure 1. The group corresponding to the sequence
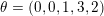 $\unicode[STIX]{x1D703}=(0,0,1,3,2)$
. Elements of
$\unicode[STIX]{x1D703}=(0,0,1,3,2)$
. Elements of
![]() $\tilde{S}$
are
$\tilde{S}$
are
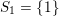 $S_{1}=\{1\}$
,
$S_{1}=\{1\}$
,
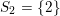 $S_{2}=\{2\}$
,
$S_{2}=\{2\}$
,
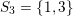 $S_{3}=\{1,3\}$
,
$S_{3}=\{1,3\}$
,
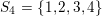 $S_{4}=\{1,2,3,4\}$
,
$S_{4}=\{1,2,3,4\}$
,
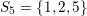 $S_{5}=\{1,2,5\}$
,
$S_{5}=\{1,2,5\}$
,
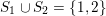 $S_{1}\cup S_{2}=\{1,2\}$
,
$S_{1}\cup S_{2}=\{1,2\}$
,
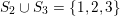 $S_{2}\cup S_{3}=\{1,2,3\}$
,
$S_{2}\cup S_{3}=\{1,2,3\}$
,
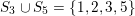 $S_{3}\cup S_{5}=\{1,2,3,5\}$
and
$S_{3}\cup S_{5}=\{1,2,3,5\}$
and
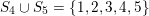 $S_{4}\cup S_{5}=\{1,2,3,4,5\}$
.
$S_{4}\cup S_{5}=\{1,2,3,4,5\}$
.
Remark 4.1. Borel-regular subgroups are by definition left and right Borel-regular and they correspond to monotone increasing sequences
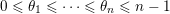 $0\leqslant \unicode[STIX]{x1D703}_{1}\leqslant \cdots \leqslant \unicode[STIX]{x1D703}_{n}\leqslant n-1$
, therefore
$0\leqslant \unicode[STIX]{x1D703}_{1}\leqslant \cdots \leqslant \unicode[STIX]{x1D703}_{n}\leqslant n-1$
, therefore
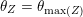 $\unicode[STIX]{x1D703}_{Z}=\unicode[STIX]{x1D703}_{\text{max}(Z)}$
holds.
$\unicode[STIX]{x1D703}_{Z}=\unicode[STIX]{x1D703}_{\text{max}(Z)}$
holds.
The boundary points in
![]() $\overline{B_{n}\cdot p_{\tilde{S}}}$
are limits of the form
$\overline{B_{n}\cdot p_{\tilde{S}}}$
are limits of the form
 $$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }\left(\begin{array}{@{}cccc@{}}b_{11}^{(m)} & b_{12}^{(m)} & \cdots \, & b_{1n}^{(m)}\\ 0 & b_{22}^{(m)} & & \\ & & \ddots & \\ 0 & & & b_{nn}^{(m)}\end{array}\right)\cdot p_{\tilde{S}}.\end{eqnarray}$$
$$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }\left(\begin{array}{@{}cccc@{}}b_{11}^{(m)} & b_{12}^{(m)} & \cdots \, & b_{1n}^{(m)}\\ 0 & b_{22}^{(m)} & & \\ & & \ddots & \\ 0 & & & b_{nn}^{(m)}\end{array}\right)\cdot p_{\tilde{S}}.\end{eqnarray}$$
The sequence
![]() $(b^{(m)})$
in (8) is not unique: different sequences can define the same limit point
$(b^{(m)})$
in (8) is not unique: different sequences can define the same limit point
![]() $p^{\infty }$
. However, any sequence
$p^{\infty }$
. However, any sequence
![]() $(b^{(m)})$
has a (not unique) subsequence
$(b^{(m)})$
has a (not unique) subsequence
 $(b^{(m_{s})})_{s=1}^{\infty }$
such that for all
$(b^{(m_{s})})_{s=1}^{\infty }$
such that for all
![]() $1\leqslant i$
,
$1\leqslant i$
,
![]() $j\leqslant n$
either
$j\leqslant n$
either
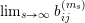 $\lim _{s\rightarrow \infty }b_{ij}^{(m_{s})}$
exists or the modulus
$\lim _{s\rightarrow \infty }b_{ij}^{(m_{s})}$
exists or the modulus
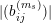 $|(b_{ij}^{(m_{s})})|$
tends to infinity. Then we can use this subsequence in (8) to define
$|(b_{ij}^{(m_{s})})|$
tends to infinity. Then we can use this subsequence in (8) to define
![]() $p^{\infty }$
, see Definition 4.2 below.
$p^{\infty }$
, see Definition 4.2 below.
Next observe that if
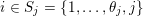 $i\in S_{j}=\{1,\ldots ,\unicode[STIX]{x1D703}_{j},j\}$
for some
$i\in S_{j}=\{1,\ldots ,\unicode[STIX]{x1D703}_{j},j\}$
for some
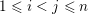 $1\leqslant i<j\leqslant n$
, then
$1\leqslant i<j\leqslant n$
, then
![]() $b^{(m)}p_{\tilde{S}}$
is independent of the value of
$b^{(m)}p_{\tilde{S}}$
is independent of the value of
![]() $b_{ij}^{(m)}$
. Indeed, for a
$b_{ij}^{(m)}$
. Indeed, for a
![]() $Z\in \tilde{S}$
of the form (7) the expression for
$Z\in \tilde{S}$
of the form (7) the expression for
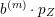 $b^{(m)}\cdot p_{Z}$
contains
$b^{(m)}\cdot p_{Z}$
contains
![]() $b_{ij}^{(m)}$
only if
$b_{ij}^{(m)}$
only if
![]() $j\in Z$
. However, if
$j\in Z$
. However, if
![]() $j\in Z$
then
$j\in Z$
then
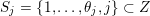 $S_{j}=\{1,\ldots ,\unicode[STIX]{x1D703}_{j},j\}\subset Z$
and since
$S_{j}=\{1,\ldots ,\unicode[STIX]{x1D703}_{j},j\}\subset Z$
and since
![]() $i\leqslant \unicode[STIX]{x1D703}_{j}$
we have
$i\leqslant \unicode[STIX]{x1D703}_{j}$
we have
![]() $i\in Z$
. Therefore
$i\in Z$
. Therefore
 $$\begin{eqnarray}b^{(m)}\cdot p_{Z}=\cdots \wedge \underbrace{(b_{jj}^{(m)}e_{j}+\cdots +b_{ij}^{(m)}e_{i}+\cdots \,)}_{b^{(m)}\cdot e_{j}}\wedge \cdots \wedge \underbrace{(b_{ii}^{(m)}e_{i}+b_{i-1i}^{(m)}e_{i-1}+\cdots \,)}_{b^{(m)}\cdot e_{i}}\wedge \cdots\end{eqnarray}$$
$$\begin{eqnarray}b^{(m)}\cdot p_{Z}=\cdots \wedge \underbrace{(b_{jj}^{(m)}e_{j}+\cdots +b_{ij}^{(m)}e_{i}+\cdots \,)}_{b^{(m)}\cdot e_{j}}\wedge \cdots \wedge \underbrace{(b_{ii}^{(m)}e_{i}+b_{i-1i}^{(m)}e_{i-1}+\cdots \,)}_{b^{(m)}\cdot e_{i}}\wedge \cdots\end{eqnarray}$$
and
![]() $b_{ij}^{(m)}$
vanishes by taking the wedge product.
$b_{ij}^{(m)}$
vanishes by taking the wedge product.
This means that changing the value of
![]() $b_{ij}^{(m)}$
will not change the point
$b_{ij}^{(m)}$
will not change the point
![]() $b^{(m)}p_{\tilde{S}}$
so we may assume without loss of generality that
$b^{(m)}p_{\tilde{S}}$
so we may assume without loss of generality that
 $$\begin{eqnarray}b_{ij}^{(m)}=0~\text{holds for all}~m~\text{and}~1\leqslant i<j\leqslant n~\text{such that}~i\in S_{j}.\end{eqnarray}$$
$$\begin{eqnarray}b_{ij}^{(m)}=0~\text{holds for all}~m~\text{and}~1\leqslant i<j\leqslant n~\text{such that}~i\in S_{j}.\end{eqnarray}$$
Definition 4.2. We call a sequence
![]() $(b^{(m)})$
of matrices normalised if it satisfies (9) and for all
$(b^{(m)})$
of matrices normalised if it satisfies (9) and for all
![]() $1\leqslant i$
,
$1\leqslant i$
,
![]() $j\leqslant n$
either
$j\leqslant n$
either
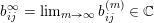 $b_{ij}^{\infty }=\lim _{m\rightarrow \infty }b_{ij}^{(m)}\in \mathbb{C}$
exists or
$b_{ij}^{\infty }=\lim _{m\rightarrow \infty }b_{ij}^{(m)}\in \mathbb{C}$
exists or
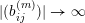 $|(b_{ij}^{(m)})|\rightarrow \infty$
as
$|(b_{ij}^{(m)})|\rightarrow \infty$
as
 $m\rightarrow \infty$
. In the latter case we write
$m\rightarrow \infty$
. In the latter case we write
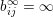 $b_{ij}^{\infty }=\infty$
. The vanishing spectrum of the normalised sequence
$b_{ij}^{\infty }=\infty$
. The vanishing spectrum of the normalised sequence
![]() $(b^{(m)})$
is defined as
$(b^{(m)})$
is defined as
 $$\begin{eqnarray}\operatorname{VSpec}(b^{(m)})=\Bigl\{i:\lim _{m\rightarrow \infty }b_{ii}^{(m)}=0\Bigr\}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{VSpec}(b^{(m)})=\Bigl\{i:\lim _{m\rightarrow \infty }b_{ii}^{(m)}=0\Bigr\}.\end{eqnarray}$$
In short, the proof of Theorem 1.2 will follow an induction argument on the size of the vanishing rank of the normalised sequence in (8) which defines
![]() $p^{\infty }$
.
$p^{\infty }$
.
Definition 4.3. Let
![]() ${\mathcal{B}}_{\mathbf{u}}$
denote the set of boundary points in
${\mathcal{B}}_{\mathbf{u}}$
denote the set of boundary points in
![]() $\overline{B_{n}\cdot p_{\tilde{S}}}$
which are limits of the form (8) with vanishing diagonal entries indexed by the array
$\overline{B_{n}\cdot p_{\tilde{S}}}$
which are limits of the form (8) with vanishing diagonal entries indexed by the array
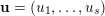 $\mathbf{u}=(u_{1},\ldots ,u_{s})$
, that is,
$\mathbf{u}=(u_{1},\ldots ,u_{s})$
, that is,
 $$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}=\Bigl\{p^{\infty }\,\in \,\overline{B_{n}\cdot p_{\tilde{S}}}:\exists ~\text{normalised sequence}~(b^{(m)})~\text{s.t.}~p^{\infty }\,=\,\lim _{m\rightarrow \infty }\!b^{(m)}\,\cdot \,p_{\tilde{S}}~\text{and}~\text{VSpec}(b^{(m)})\,=\,\mathbf{u}\Bigr\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}=\Bigl\{p^{\infty }\,\in \,\overline{B_{n}\cdot p_{\tilde{S}}}:\exists ~\text{normalised sequence}~(b^{(m)})~\text{s.t.}~p^{\infty }\,=\,\lim _{m\rightarrow \infty }\!b^{(m)}\,\cdot \,p_{\tilde{S}}~\text{and}~\text{VSpec}(b^{(m)})\,=\,\mathbf{u}\Bigr\}.\end{eqnarray}$$
As we noted above, every boundary point
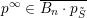 $p^{\infty }\in \overline{B_{n}\cdot p_{\tilde{S}}}$
is the limit of the form (8) for a normalised
$p^{\infty }\in \overline{B_{n}\cdot p_{\tilde{S}}}$
is the limit of the form (8) for a normalised
![]() $(b^{(m)})$
and therefore
$(b^{(m)})$
and therefore
 $$\begin{eqnarray}\overline{B_{n}\cdot p_{\tilde{S}}}=\mathop{\bigcup }_{\mathbf{u}\in 2^{\{1,\ldots ,n\}}}{\mathcal{B}}_{\mathbf{u}}.\end{eqnarray}$$
$$\begin{eqnarray}\overline{B_{n}\cdot p_{\tilde{S}}}=\mathop{\bigcup }_{\mathbf{u}\in 2^{\{1,\ldots ,n\}}}{\mathcal{B}}_{\mathbf{u}}.\end{eqnarray}$$
According to the next Lemma
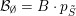 ${\mathcal{B}}_{\emptyset }=B\cdot p_{\tilde{S}}$
is the Borel orbit.
${\mathcal{B}}_{\emptyset }=B\cdot p_{\tilde{S}}$
is the Borel orbit.
Lemma 4.4.
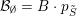 ${\mathcal{B}}_{\emptyset }=B\cdot p_{\tilde{S}}$
is equal to the Borel orbit of
${\mathcal{B}}_{\emptyset }=B\cdot p_{\tilde{S}}$
is equal to the Borel orbit of
![]() $p_{\tilde{S}}$
in
$p_{\tilde{S}}$
in
![]() ${\mathcal{W}}_{\tilde{S}}$
.
${\mathcal{W}}_{\tilde{S}}$
.
First proof.
We use the following fact about solvable groups.
Let
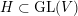 $H\subset \operatorname{GL}(V)$
be a solvable algebraic group and let
$H\subset \operatorname{GL}(V)$
be a solvable algebraic group and let
![]() $v\in V$
. Then there is an
$v\in V$
. Then there is an
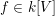 $f\in k[V]$
and a character
$f\in k[V]$
and a character
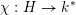 $\unicode[STIX]{x1D712}:H\rightarrow k^{\ast }$
such that
$\unicode[STIX]{x1D712}:H\rightarrow k^{\ast }$
such that
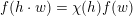 $f(h\cdot w)=\unicode[STIX]{x1D712}(h)f(w)$
holds for all
$f(h\cdot w)=\unicode[STIX]{x1D712}(h)f(w)$
holds for all
![]() $b\in B$
,
$b\in B$
,
![]() $w\in V$
and
$w\in V$
and
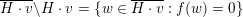 $\overline{H\cdot v}\setminus H\cdot v=\{w\in \overline{H\cdot v}:f(w)=0\}$
.
$\overline{H\cdot v}\setminus H\cdot v=\{w\in \overline{H\cdot v}:f(w)=0\}$
.
We apply this result with the Borel
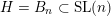 $H=B_{n}\subset \operatorname{SL}(n)$
. Let
$H=B_{n}\subset \operatorname{SL}(n)$
. Let
![]() $(b^{(m)})$
be a sequence such that
$(b^{(m)})$
be a sequence such that
 $$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}\in \overline{B_{n}\cdot p_{\tilde{S}}}\setminus B_{n}\cdot p_{\tilde{S}}.\end{eqnarray}$$
$$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}\in \overline{B_{n}\cdot p_{\tilde{S}}}\setminus B_{n}\cdot p_{\tilde{S}}.\end{eqnarray}$$
Let
![]() $f$
be as above, vanishing on
$f$
be as above, vanishing on
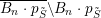 $\overline{B_{n}\cdot p_{\tilde{S}}}\setminus B_{n}\cdot p_{\tilde{S}}$
. Then
$\overline{B_{n}\cdot p_{\tilde{S}}}\setminus B_{n}\cdot p_{\tilde{S}}$
. Then
 $$\begin{eqnarray}0=f(p^{\infty })=\lim _{m\rightarrow \infty }f(b^{(m)}\cdot p_{\tilde{S}})=\lim _{m\rightarrow \infty }\unicode[STIX]{x1D712}(b^{(m)})f(p_{\tilde{S}}).\end{eqnarray}$$
$$\begin{eqnarray}0=f(p^{\infty })=\lim _{m\rightarrow \infty }f(b^{(m)}\cdot p_{\tilde{S}})=\lim _{m\rightarrow \infty }\unicode[STIX]{x1D712}(b^{(m)})f(p_{\tilde{S}}).\end{eqnarray}$$
Since
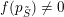 $f(p_{\tilde{S}})\neq 0$
, we must have
$f(p_{\tilde{S}})\neq 0$
, we must have
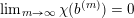 $\lim _{m\rightarrow \infty }\unicode[STIX]{x1D712}(b^{(m)})=0$
so
$\lim _{m\rightarrow \infty }\unicode[STIX]{x1D712}(b^{(m)})=0$
so
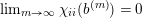 $\lim _{m\rightarrow \infty }\unicode[STIX]{x1D712}_{ii}(b^{(m)})=0$
for some
$\lim _{m\rightarrow \infty }\unicode[STIX]{x1D712}_{ii}(b^{(m)})=0$
for some
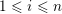 $1\leqslant i\leqslant n$
.◻
$1\leqslant i\leqslant n$
.◻
We give a second, longer proof because its main idea will turn up in the proof of Theorem 1.4 in § 6 again.
Second proof.
Let
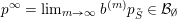 $p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}\in {\mathcal{B}}_{\emptyset }$
be defined by the normalised sequence
$p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}\in {\mathcal{B}}_{\emptyset }$
be defined by the normalised sequence
![]() $(b^{(m)})$
such that
$(b^{(m)})$
such that
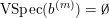 $\operatorname{VSpec}(b^{(m)})=\emptyset$
. By definition for all
$\operatorname{VSpec}(b^{(m)})=\emptyset$
. By definition for all
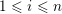 $1\leqslant i\leqslant n$
either
$1\leqslant i\leqslant n$
either
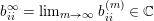 $b_{ii}^{\infty }=\lim _{m\rightarrow \infty }b_{ii}^{(m)}\in \mathbb{C}$
exists or
$b_{ii}^{\infty }=\lim _{m\rightarrow \infty }b_{ii}^{(m)}\in \mathbb{C}$
exists or
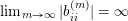 $\lim _{m\rightarrow \infty }|b_{ii}^{(m)}|=\infty$
. Since
$\lim _{m\rightarrow \infty }|b_{ii}^{(m)}|=\infty$
. Since
 $$\begin{eqnarray}b_{11}^{(m)}\cdot \ldots \cdot b_{nn}^{(m)}=1~\text{holds for all}~m,\end{eqnarray}$$
$$\begin{eqnarray}b_{11}^{(m)}\cdot \ldots \cdot b_{nn}^{(m)}=1~\text{holds for all}~m,\end{eqnarray}$$
if
 $b_{ii}^{(m)}\rightarrow \infty$
for some
$b_{ii}^{(m)}\rightarrow \infty$
for some
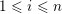 $1\leqslant i\leqslant n$
, then for some
$1\leqslant i\leqslant n$
, then for some
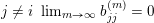 $j\neq i~\lim _{m\rightarrow \infty }b_{jj}^{(m)}=0$
so
$j\neq i~\lim _{m\rightarrow \infty }b_{jj}^{(m)}=0$
so
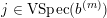 $j\in \operatorname{VSpec}(b^{(m)})$
, a contradiction. This proves that
$j\in \operatorname{VSpec}(b^{(m)})$
, a contradiction. This proves that
 $$\begin{eqnarray}b_{ii}^{\infty }=\lim _{m\rightarrow \infty }b_{ii}^{(m)}\in \mathbb{C}\setminus \{0\}\quad \text{for}~1\leqslant i\leqslant n.\end{eqnarray}$$
$$\begin{eqnarray}b_{ii}^{\infty }=\lim _{m\rightarrow \infty }b_{ii}^{(m)}\in \mathbb{C}\setminus \{0\}\quad \text{for}~1\leqslant i\leqslant n.\end{eqnarray}$$
Assume that some off-diagonal entries of the normalised sequence
![]() $(b^{(m)})$
are not convergent and let
$(b^{(m)})$
are not convergent and let
 $$\begin{eqnarray}v=\min \{j:\exists i\notin S_{j}~\text{such that}~i<j~\text{and}~b_{ij}^{\infty }=\infty \}\end{eqnarray}$$
$$\begin{eqnarray}v=\min \{j:\exists i\notin S_{j}~\text{such that}~i<j~\text{and}~b_{ij}^{\infty }=\infty \}\end{eqnarray}$$
be the leftmost column containing such entries and choose a
![]() $u<v$
,
$u<v$
,
![]() $u\notin S_{v}$
such that
$u\notin S_{v}$
such that
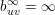 $b_{uv}^{\infty }=\infty$
. Then due to (9) the coefficient of
$b_{uv}^{\infty }=\infty$
. Then due to (9) the coefficient of
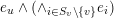 $e_{u}\wedge (\wedge _{i\in S_{v}\setminus \{v\}}e_{i})$
in
$e_{u}\wedge (\wedge _{i\in S_{v}\setminus \{v\}}e_{i})$
in
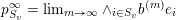 $p_{S_{v}}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{i\in S_{v}}b^{(m)}e_{i}$
would be
$p_{S_{v}}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{i\in S_{v}}b^{(m)}e_{i}$
would be
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }b_{uv}^{(m)}\cdot \mathop{\prod }_{i\in S_{v}\setminus \{v\}}b_{ii}^{\infty }=\infty ,\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }b_{uv}^{(m)}\cdot \mathop{\prod }_{i\in S_{v}\setminus \{v\}}b_{ii}^{\infty }=\infty ,\end{eqnarray}$$
a contradiction. Hence
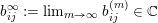 $b_{ij}^{\infty }:=\lim _{m\rightarrow \infty }b_{ij}^{(m)}\in \mathbb{C}$
exists for all
$b_{ij}^{\infty }:=\lim _{m\rightarrow \infty }b_{ij}^{(m)}\in \mathbb{C}$
exists for all
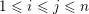 $1\leqslant i\leqslant j\leqslant n$
and
$1\leqslant i\leqslant j\leqslant n$
and
![]() $b_{ii}^{\infty }\neq 0$
so
$b_{ii}^{\infty }\neq 0$
so
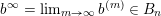 $b^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}\in B_{n}$
exists and
$b^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}\in B_{n}$
exists and
 $$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}\cdot p_{\tilde{S}}=b^{\infty }\cdot p_{\tilde{S}}\in B_{n}\cdot p_{\tilde{S}}.\Box\end{eqnarray}$$
$$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}\cdot p_{\tilde{S}}=b^{\infty }\cdot p_{\tilde{S}}\in B_{n}\cdot p_{\tilde{S}}.\Box\end{eqnarray}$$
When
![]() $\mathbf{u}$
is nonempty, the corresponding set
$\mathbf{u}$
is nonempty, the corresponding set
![]() ${\mathcal{B}}_{\mathbf{u}}$
is algebraic and
${\mathcal{B}}_{\mathbf{u}}$
is algebraic and
![]() $B_{n}$
-invariant as the following lemma shows.
$B_{n}$
-invariant as the following lemma shows.
Lemma 4.5. If
![]() $\mathbf{u}\neq \emptyset$
, then
$\mathbf{u}\neq \emptyset$
, then
![]() ${\mathcal{B}}_{\mathbf{u}}$
is a
${\mathcal{B}}_{\mathbf{u}}$
is a
![]() $B_{n}$
-invariant subvariety of
$B_{n}$
-invariant subvariety of
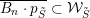 $\overline{B_{n}\cdot p_{\tilde{S}}}\subset {\mathcal{W}}_{\tilde{S}}$
.
$\overline{B_{n}\cdot p_{\tilde{S}}}\subset {\mathcal{W}}_{\tilde{S}}$
.
Proof. Let
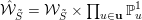 $\hat{{\mathcal{W}}}_{\tilde{S}}={\mathcal{W}}_{\tilde{S}}\times \prod _{u\in \mathbf{u}}\mathbb{P}_{u}^{1}$
denote the product of the affine ambient space
$\hat{{\mathcal{W}}}_{\tilde{S}}={\mathcal{W}}_{\tilde{S}}\times \prod _{u\in \mathbf{u}}\mathbb{P}_{u}^{1}$
denote the product of the affine ambient space
![]() ${\mathcal{W}}_{\tilde{S}}$
with a copy of
${\mathcal{W}}_{\tilde{S}}$
with a copy of
![]() $\mathbb{P}^{1}$
for every element of
$\mathbb{P}^{1}$
for every element of
![]() $\mathbf{u}$
. We endow
$\mathbf{u}$
. We endow
![]() $\mathbb{P}_{u}^{1}$
with a
$\mathbb{P}_{u}^{1}$
with a
![]() $B_{n}$
action as follows: for
$B_{n}$
action as follows: for
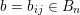 $b=b_{ij}\in B_{n}$
we let
$b=b_{ij}\in B_{n}$
we let
 $b\cdot [x:y]=[x:b_{uu}y]$
for
$b\cdot [x:y]=[x:b_{uu}y]$
for
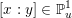 $[x:y]\in \mathbb{P}_{u}^{1}$
. Define the point
$[x:y]\in \mathbb{P}_{u}^{1}$
. Define the point
 $$\begin{eqnarray}\hat{p}_{\tilde{S}}=p_{\tilde{S}}\times \mathop{\prod }_{u\in \mathbf{u}}[1:1]\in \hat{{\mathcal{W}}}_{\tilde{S}}\end{eqnarray}$$
$$\begin{eqnarray}\hat{p}_{\tilde{S}}=p_{\tilde{S}}\times \mathop{\prod }_{u\in \mathbf{u}}[1:1]\in \hat{{\mathcal{W}}}_{\tilde{S}}\end{eqnarray}$$
and take the orbit closure
![]() $\overline{B_{n}\cdot \hat{p}_{\tilde{S}}}$
in
$\overline{B_{n}\cdot \hat{p}_{\tilde{S}}}$
in
![]() $\hat{{\mathcal{W}}}_{\tilde{S}}$
. If
$\hat{{\mathcal{W}}}_{\tilde{S}}$
. If
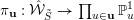 $\unicode[STIX]{x1D70B}_{\mathbf{u}}:\hat{{\mathcal{W}}}_{\tilde{S}}\rightarrow \prod _{u\in \mathbf{u}}\mathbb{P}_{u}^{1}$
denotes the projection, then
$\unicode[STIX]{x1D70B}_{\mathbf{u}}:\hat{{\mathcal{W}}}_{\tilde{S}}\rightarrow \prod _{u\in \mathbf{u}}\mathbb{P}_{u}^{1}$
denotes the projection, then
 $$\begin{eqnarray}\hat{{\mathcal{B}}}_{\mathbf{u}}=\unicode[STIX]{x1D70B}_{\mathbf{u}}^{-1}\biggl(\mathop{\prod }_{u\in \mathbf{u}}[1:0]\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\hat{{\mathcal{B}}}_{\mathbf{u}}=\unicode[STIX]{x1D70B}_{\mathbf{u}}^{-1}\biggl(\mathop{\prod }_{u\in \mathbf{u}}[1:0]\biggr)\end{eqnarray}$$
is a Zariski closed subset of
![]() $\hat{{\mathcal{W}}}_{\tilde{S}}$
and by definition its image under the projection
$\hat{{\mathcal{W}}}_{\tilde{S}}$
and by definition its image under the projection
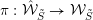 $\unicode[STIX]{x1D70B}:\hat{{\mathcal{W}}}_{\tilde{S}}\rightarrow {\mathcal{W}}_{\tilde{S}}$
is equal to
$\unicode[STIX]{x1D70B}:\hat{{\mathcal{W}}}_{\tilde{S}}\rightarrow {\mathcal{W}}_{\tilde{S}}$
is equal to
![]() ${\mathcal{B}}_{\mathbf{u}}$
. This image is, however, constructible as the image of a closed set. Even more, since the projection is a closed morphism, it takes Zariski closed subsets onto Zariski closed sets. The
${\mathcal{B}}_{\mathbf{u}}$
. This image is, however, constructible as the image of a closed set. Even more, since the projection is a closed morphism, it takes Zariski closed subsets onto Zariski closed sets. The
![]() $B_{n}$
-invariance of
$B_{n}$
-invariance of
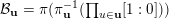 ${\mathcal{B}}_{\mathbf{u}}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D70B}_{\mathbf{u}}^{-1}(\prod _{u\in \mathbf{u}}[1:0]))$
follows from
${\mathcal{B}}_{\mathbf{u}}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D70B}_{\mathbf{u}}^{-1}(\prod _{u\in \mathbf{u}}[1:0]))$
follows from
![]() $B_{n}$
-equivariance of the projections and
$B_{n}$
-equivariance of the projections and
![]() $B_{n}$
-invariance of the point
$B_{n}$
-invariance of the point
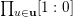 $\prod _{u\in \mathbf{u}}[1:0]$
(that is, this is a
$\prod _{u\in \mathbf{u}}[1:0]$
(that is, this is a
![]() $B_{n}$
-fixed point).◻
$B_{n}$
-fixed point).◻
Definition 4.6. Let
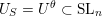 $U_{S}=U^{\unicode[STIX]{x1D703}}\subset \operatorname{SL}_{n}$
be a left Borel-regular subgroup and
$U_{S}=U^{\unicode[STIX]{x1D703}}\subset \operatorname{SL}_{n}$
be a left Borel-regular subgroup and
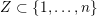 $Z\subset \{1,\ldots ,n\}$
. We say that the integer
$Z\subset \{1,\ldots ,n\}$
. We say that the integer
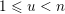 $1\leqslant u<n$
is covered by
$1\leqslant u<n$
is covered by
![]() $Z$
if
$Z$
if
![]() $u\leqslant \unicode[STIX]{x1D703}_{Z}$
. We say that
$u\leqslant \unicode[STIX]{x1D703}_{Z}$
. We say that
![]() $u$
is covered by
$u$
is covered by
![]() $S$
if it is covered by at least one of
$S$
if it is covered by at least one of
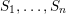 $S_{1},\ldots ,S_{n}$
, that is,
$S_{1},\ldots ,S_{n}$
, that is,
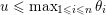 $u\leqslant \max _{1\leqslant i\leqslant n}\unicode[STIX]{x1D703}_{i}$
. The subset
$u\leqslant \max _{1\leqslant i\leqslant n}\unicode[STIX]{x1D703}_{i}$
. The subset
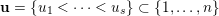 $\mathbf{u}=\{u_{1}<\cdots <u_{s}\}\subset \{1,\ldots ,n\}$
is covered by
$\mathbf{u}=\{u_{1}<\cdots <u_{s}\}\subset \{1,\ldots ,n\}$
is covered by
![]() $S$
if all elements of it are covered by
$S$
if all elements of it are covered by
![]() $S$
.
$S$
.
Example 4.7. In Figure 1,
![]() $S_{4}$
covers 1, 2, 3 and
$S_{4}$
covers 1, 2, 3 and
![]() $S_{5}$
covers 1 and 2. Moreover,
$S_{5}$
covers 1 and 2. Moreover,
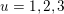 $u=1,2,3$
are covered by
$u=1,2,3$
are covered by
![]() $S$
, but
$S$
, but
![]() $u=4$
is not covered. Therefore any subset
$u=4$
is not covered. Therefore any subset
![]() $\mathbf{u}$
of
$\mathbf{u}$
of
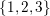 $\{1,2,3\}$
is covered by
$\{1,2,3\}$
is covered by
![]() $S$
and the subsets containing 4 are not covered by
$S$
and the subsets containing 4 are not covered by
![]() $S$
.
$S$
.
Let
![]() $Z\in \tilde{S}$
and let
$Z\in \tilde{S}$
and let
![]() $b^{(m)}$
be a normalised sequence. In what follows we will work with subspaces of
$b^{(m)}$
be a normalised sequence. In what follows we will work with subspaces of
![]() $\mathbb{C}^{n}$
determined by
$\mathbb{C}^{n}$
determined by
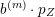 $b^{(m)}\cdot p_{Z}$
and the limit of these subspaces.
$b^{(m)}\cdot p_{Z}$
and the limit of these subspaces.
Definition 4.8. For the nonzero vectors
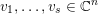 $v_{1},\ldots ,v_{s}\in \mathbb{C}^{n}$
let
$v_{1},\ldots ,v_{s}\in \mathbb{C}^{n}$
let
 $$\begin{eqnarray}[v_{1}\wedge \cdots \wedge v_{s}]\in \operatorname{Gr}_{s}(\mathbb{C}^{n})\end{eqnarray}$$
$$\begin{eqnarray}[v_{1}\wedge \cdots \wedge v_{s}]\in \operatorname{Gr}_{s}(\mathbb{C}^{n})\end{eqnarray}$$
denote the subspace spanned by them. In particular, for a subset
![]() $Z\in \tilde{S}$
we let
$Z\in \tilde{S}$
we let
 $$\begin{eqnarray}[p_{Z}]=[\wedge _{z\in Z}e_{z}]\in \operatorname{Gr}_{|Z|}\mathbb{C}^{n}\end{eqnarray}$$
$$\begin{eqnarray}[p_{Z}]=[\wedge _{z\in Z}e_{z}]\in \operatorname{Gr}_{|Z|}\mathbb{C}^{n}\end{eqnarray}$$
and
 $$\begin{eqnarray}[p_{Z}^{\infty }]=\lim _{m\rightarrow \infty }[b^{(m)}\cdot p_{Z}]\end{eqnarray}$$
$$\begin{eqnarray}[p_{Z}^{\infty }]=\lim _{m\rightarrow \infty }[b^{(m)}\cdot p_{Z}]\end{eqnarray}$$
denotes the limit in
 $\operatorname{Gr}_{|Z|}(\mathbb{C}^{n})$
.
$\operatorname{Gr}_{|Z|}(\mathbb{C}^{n})$
.
Remark 4.9. If
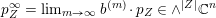 $p_{Z}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}\,\cdot \,p_{Z}\in \wedge ^{|Z|}\mathbb{C}^{n}$
exists, then either
$p_{Z}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}\,\cdot \,p_{Z}\in \wedge ^{|Z|}\mathbb{C}^{n}$
exists, then either
![]() $p_{Z}^{\infty }=0$
or it is a decomposable vector, i.e.
$p_{Z}^{\infty }=0$
or it is a decomposable vector, i.e.
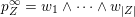 $p_{Z}^{\infty }=w_{1}\wedge \cdots \wedge w_{|Z|}$
for some nonzero vectors
$p_{Z}^{\infty }=w_{1}\wedge \cdots \wedge w_{|Z|}$
for some nonzero vectors
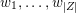 $w_{1},\ldots ,w_{|Z|}$
. To see this, note that the Veronese map
$w_{1},\ldots ,w_{|Z|}$
. To see this, note that the Veronese map
 $$\begin{eqnarray}\unicode[STIX]{x1D707}:\operatorname{Gr}_{|Z|}(\mathbb{C}^{n}){\hookrightarrow}\mathbb{P}(\wedge ^{|Z|}\mathbb{C}^{n})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}:\operatorname{Gr}_{|Z|}(\mathbb{C}^{n}){\hookrightarrow}\mathbb{P}(\wedge ^{|Z|}\mathbb{C}^{n})\end{eqnarray}$$
is a closed embedding and the set of decomposable vectors in
![]() $\wedge ^{|Z|}\mathbb{C}^{n}$
forms the affine cone over the image of
$\wedge ^{|Z|}\mathbb{C}^{n}$
forms the affine cone over the image of
![]() $\unicode[STIX]{x1D707}$
and therefore this set is closed. Hence the limit of decomposable elements in
$\unicode[STIX]{x1D707}$
and therefore this set is closed. Hence the limit of decomposable elements in
![]() $\wedge ^{n}\mathbb{C}^{n}$
is either decomposable or zero. Moreover, if
$\wedge ^{n}\mathbb{C}^{n}$
is either decomposable or zero. Moreover, if
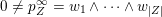 $0\neq p_{Z}^{\infty }=w_{1}\wedge \cdots \wedge w_{|Z|}$
, then the subspace
$0\neq p_{Z}^{\infty }=w_{1}\wedge \cdots \wedge w_{|Z|}$
, then the subspace
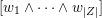 $[w_{1}\wedge \cdots \wedge w_{|Z|}]$
is equal to the limit defined in (10).
$[w_{1}\wedge \cdots \wedge w_{|Z|}]$
is equal to the limit defined in (10).
The following technical lemma will be used repeatedly in this section.
Lemma 4.10. Let
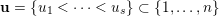 $\mathbf{u}=\{u_{1}<\cdots <u_{s}\}\subset \{1,\ldots ,n\}$
be an arbitrary subset. Let
$\mathbf{u}=\{u_{1}<\cdots <u_{s}\}\subset \{1,\ldots ,n\}$
be an arbitrary subset. Let
 $$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}=\bigoplus _{U\in \tilde{S}}p_{U}^{\infty }\in {\mathcal{B}}_{\boldsymbol{ u}}\end{eqnarray}$$
$$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}=\bigoplus _{U\in \tilde{S}}p_{U}^{\infty }\in {\mathcal{B}}_{\boldsymbol{ u}}\end{eqnarray}$$
be a limit point defined by the normalised sequence
![]() $(b^{(m)})$
such that
$(b^{(m)})$
such that
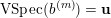 $\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
. If
$\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
. If
![]() $\unicode[STIX]{x1D703}_{i}<u_{1}$
for some
$\unicode[STIX]{x1D703}_{i}<u_{1}$
for some
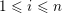 $1\leqslant i\leqslant n$
, then
$1\leqslant i\leqslant n$
, then
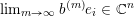 $\lim _{m\rightarrow \infty }b^{(m)}e_{i}\in \mathbb{C}^{n}$
exists.
$\lim _{m\rightarrow \infty }b^{(m)}e_{i}\in \mathbb{C}^{n}$
exists.
Proof. Assume
![]() $\unicode[STIX]{x1D703}_{i}<u_{1}$
but
$\unicode[STIX]{x1D703}_{i}<u_{1}$
but
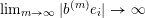 $\lim _{m\rightarrow \infty }|b^{(m)}e_{i}|\rightarrow \infty$
and
$\lim _{m\rightarrow \infty }|b^{(m)}e_{i}|\rightarrow \infty$
and
![]() $i$
is the smallest index with this property. Then
$i$
is the smallest index with this property. Then
 $e_{j}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}e_{j}\in \mathbb{C}^{n}$
for
$e_{j}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}e_{j}\in \mathbb{C}^{n}$
for
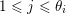 $1\leqslant j\leqslant \unicode[STIX]{x1D703}_{i}$
, because in this case
$1\leqslant j\leqslant \unicode[STIX]{x1D703}_{i}$
, because in this case
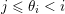 $j\leqslant \unicode[STIX]{x1D703}_{i}<i$
so
$j\leqslant \unicode[STIX]{x1D703}_{i}<i$
so
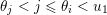 $\unicode[STIX]{x1D703}_{j}<j\leqslant \unicode[STIX]{x1D703}_{i}<u_{1}$
and the limit exists by the minimality of
$\unicode[STIX]{x1D703}_{j}<j\leqslant \unicode[STIX]{x1D703}_{i}<u_{1}$
and the limit exists by the minimality of
![]() $i$
. Then
$i$
. Then
 $$\begin{eqnarray}p_{S_{i}}^{\infty }=\wedge _{j=1}^{\unicode[STIX]{x1D703}_{i}}e_{j}^{\infty }\wedge \lim _{m\rightarrow \infty }b^{(m)}e_{i}\end{eqnarray}$$
$$\begin{eqnarray}p_{S_{i}}^{\infty }=\wedge _{j=1}^{\unicode[STIX]{x1D703}_{i}}e_{j}^{\infty }\wedge \lim _{m\rightarrow \infty }b^{(m)}e_{i}\end{eqnarray}$$
does not exist, a contradiction. ◻
Remark 4.11. Note that
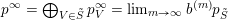 $p^{\infty }=\bigoplus _{V\in \tilde{S}}p_{V}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}$
can be an element of several different
$p^{\infty }=\bigoplus _{V\in \tilde{S}}p_{V}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}$
can be an element of several different
![]() ${\mathcal{B}}_{\mathbf{u}}$
, that is,
${\mathcal{B}}_{\mathbf{u}}$
, that is,
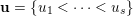 $\mathbf{u}=\{u_{1}<\cdots <u_{s}\}$
is not uniquely determined by
$\mathbf{u}=\{u_{1}<\cdots <u_{s}\}$
is not uniquely determined by
![]() $p^{\infty }$
. However, Lemma 4.10 implies that
$p^{\infty }$
. However, Lemma 4.10 implies that
![]() $p^{\infty }$
determines
$p^{\infty }$
determines
![]() $u_{1}$
at least:
$u_{1}$
at least:
![]() $u_{1}$
signs the first diagonal entry of
$u_{1}$
signs the first diagonal entry of
![]() $b^{(m)}$
which tends to 0 as
$b^{(m)}$
which tends to 0 as
 $m\rightarrow \infty$
and all previous diagonal entries tend to a nonzero constant. Therefore
$m\rightarrow \infty$
and all previous diagonal entries tend to a nonzero constant. Therefore
 $$\begin{eqnarray}u_{1}=\min \{j:p_{\{1,\ldots ,j\}}^{\infty }=0\}\end{eqnarray}$$
$$\begin{eqnarray}u_{1}=\min \{j:p_{\{1,\ldots ,j\}}^{\infty }=0\}\end{eqnarray}$$
is the common minimal element of the vanishing spectra which define
![]() $p^{\infty }$
.
$p^{\infty }$
.
Lemma 4.12. Let
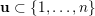 $\mathbf{u}\subset \{1,\ldots ,n\}$
be a subset and assume
$\mathbf{u}\subset \{1,\ldots ,n\}$
be a subset and assume
![]() ${\mathcal{B}}_{\mathbf{u}}$
is nonempty. Then
${\mathcal{B}}_{\mathbf{u}}$
is nonempty. Then
![]() $\mathbf{u}$
is covered by
$\mathbf{u}$
is covered by
![]() $S$
.
$S$
.
Proof. Let
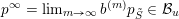 $p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}\in {\mathcal{B}}_{u}$
be a point defined by a normalised sequence
$p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}\in {\mathcal{B}}_{u}$
be a point defined by a normalised sequence
![]() $(b^{(m)})$
with
$(b^{(m)})$
with
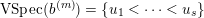 $\operatorname{VSpec}(b^{(m)})=\{u_{1}<\cdots <u_{s}\}$
. Assume that
$\operatorname{VSpec}(b^{(m)})=\{u_{1}<\cdots <u_{s}\}$
. Assume that
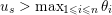 $u_{s}>\max _{1\leqslant i\leqslant n}\unicode[STIX]{x1D703}_{i}$
. Then
$u_{s}>\max _{1\leqslant i\leqslant n}\unicode[STIX]{x1D703}_{i}$
. Then
 $$\begin{eqnarray}V=\{1,\ldots ,n\}\setminus \{u_{s}\}=\mathop{\bigcup }_{i\in \{1,\ldots ,n\}\setminus \{u_{s}\}}S_{i}\in \tilde{S}\end{eqnarray}$$
$$\begin{eqnarray}V=\{1,\ldots ,n\}\setminus \{u_{s}\}=\mathop{\bigcup }_{i\in \{1,\ldots ,n\}\setminus \{u_{s}\}}S_{i}\in \tilde{S}\end{eqnarray}$$
and the coefficient of
![]() $\wedge _{i\in V}e_{i}$
in
$\wedge _{i\in V}e_{i}$
in
![]() $p_{V}^{\infty }$
is
$p_{V}^{\infty }$
is
 $$\begin{eqnarray}p_{V}^{\infty }[\wedge _{i\in V}e_{i}]=\lim _{m\rightarrow \infty }\mathop{\prod }_{i\in V}b_{ii}^{(m)}=\lim _{m\rightarrow \infty }\frac{1}{b_{u_{s}u_{s}}^{(m)}}=\infty ,\end{eqnarray}$$
$$\begin{eqnarray}p_{V}^{\infty }[\wedge _{i\in V}e_{i}]=\lim _{m\rightarrow \infty }\mathop{\prod }_{i\in V}b_{ii}^{(m)}=\lim _{m\rightarrow \infty }\frac{1}{b_{u_{s}u_{s}}^{(m)}}=\infty ,\end{eqnarray}$$
a contradiction. Here we used that
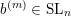 $b^{(m)}\in \operatorname{SL}_{n}$
and hence
$b^{(m)}\in \operatorname{SL}_{n}$
and hence
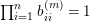 $\prod _{i=1}^{n}b_{ii}^{(m)}=1$
for all
$\prod _{i=1}^{n}b_{ii}^{(m)}=1$
for all
![]() $m$
.◻
$m$
.◻
Definition 4.13. Let
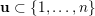 $\mathbf{u}\subset \{1,\ldots ,n\}$
be a subset covered by
$\mathbf{u}\subset \{1,\ldots ,n\}$
be a subset covered by
![]() $S$
and let
$S$
and let
 $p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}=\bigoplus _{U\in \tilde{S}}p_{U}^{\infty }\in {\mathcal{B}}_{\mathbf{u}}$
be a boundary point defined by the normalised sequence
$p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}=\bigoplus _{U\in \tilde{S}}p_{U}^{\infty }\in {\mathcal{B}}_{\mathbf{u}}$
be a boundary point defined by the normalised sequence
![]() $(b^{(m)})$
with
$(b^{(m)})$
with
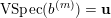 $\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
. Let
$\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
. Let
![]() ${\mathcal{V}}(p^{\infty })$
denote the set of those elements in
${\mathcal{V}}(p^{\infty })$
denote the set of those elements in
![]() $\tilde{S}$
which cover
$\tilde{S}$
which cover
![]() $u_{1}$
and the corresponding term of
$u_{1}$
and the corresponding term of
![]() $p^{\infty }$
is nonzero, that is
$p^{\infty }$
is nonzero, that is
 $$\begin{eqnarray}{\mathcal{V}}(p^{\infty })=\{U\in \tilde{S}:p_{U}^{\infty }\neq 0,\unicode[STIX]{x1D703}_{U}\geqslant u_{1}\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{V}}(p^{\infty })=\{U\in \tilde{S}:p_{U}^{\infty }\neq 0,\unicode[STIX]{x1D703}_{U}\geqslant u_{1}\}.\end{eqnarray}$$
According to Remark 4.11 this set is determined by
![]() $p^{\infty }$
. It is nonempty: indeed,
$p^{\infty }$
. It is nonempty: indeed,
![]() $\mathbf{u}$
is covered by assumption and therefore
$\mathbf{u}$
is covered by assumption and therefore
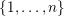 $\{1,\ldots ,n\}$
covers it. Moreover
$\{1,\ldots ,n\}$
covers it. Moreover
 $$\begin{eqnarray}p_{\{1,\ldots ,n\}}^{\infty }=\lim _{m\rightarrow \infty }\det (b^{(m)})e_{1}\wedge \cdots \wedge e_{n}=e_{1}\wedge \cdots \wedge e_{n}\neq 0,\end{eqnarray}$$
$$\begin{eqnarray}p_{\{1,\ldots ,n\}}^{\infty }=\lim _{m\rightarrow \infty }\det (b^{(m)})e_{1}\wedge \cdots \wedge e_{n}=e_{1}\wedge \cdots \wedge e_{n}\neq 0,\end{eqnarray}$$
so
 $\{1,\ldots ,n\}\in {\mathcal{V}}(p^{\infty })$
. Now define the partial order
$\{1,\ldots ,n\}\in {\mathcal{V}}(p^{\infty })$
. Now define the partial order
![]() $\preccurlyeq$
on the elements of
$\preccurlyeq$
on the elements of
![]() ${\mathcal{V}}(p^{\infty })$
as follows. For
${\mathcal{V}}(p^{\infty })$
as follows. For
![]() $U$
,
$U$
,
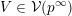 $V\in {\mathcal{V}}(p^{\infty })$
we write
$V\in {\mathcal{V}}(p^{\infty })$
we write
![]() $U\preccurlyeq V$
if
$U\preccurlyeq V$
if
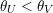 $\unicode[STIX]{x1D703}_{U}<\unicode[STIX]{x1D703}_{V}$
or
$\unicode[STIX]{x1D703}_{U}<\unicode[STIX]{x1D703}_{V}$
or
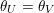 $\unicode[STIX]{x1D703}_{U}=\unicode[STIX]{x1D703}_{V}$
but
$\unicode[STIX]{x1D703}_{U}=\unicode[STIX]{x1D703}_{V}$
but
![]() $U\subseteq V$
. Let
$U\subseteq V$
. Let
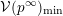 ${\mathcal{V}}(p^{\infty })_{\text{min}}$
denote the set of minimal elements of
${\mathcal{V}}(p^{\infty })_{\text{min}}$
denote the set of minimal elements of
![]() ${\mathcal{V}}(p^{\infty })$
with respect to
${\mathcal{V}}(p^{\infty })$
with respect to
![]() $\preccurlyeq$
. We call elements of
$\preccurlyeq$
. We call elements of
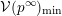 ${\mathcal{V}}(p^{\infty })_{\text{min}}$
minimal for
${\mathcal{V}}(p^{\infty })_{\text{min}}$
minimal for
![]() $p^{\infty }$
.
$p^{\infty }$
.
A central part of our argument is the following technical proposition.
Proposition 4.14. Let
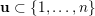 $\mathbf{u}\subset \{1,\ldots ,n\}$
be a subset covered by
$\mathbf{u}\subset \{1,\ldots ,n\}$
be a subset covered by
![]() $S$
and
$S$
and
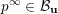 $p^{\infty }\in {\mathcal{B}}_{\mathbf{u}}$
. If
$p^{\infty }\in {\mathcal{B}}_{\mathbf{u}}$
. If
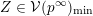 $Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
, then
$Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
, then
 $$\begin{eqnarray}[p_{Z}^{\infty }]\subset \mathop{\bigcap }_{V\in {\mathcal{V}}(p^{\infty })}[p_{V}^{\infty }].\end{eqnarray}$$
$$\begin{eqnarray}[p_{Z}^{\infty }]\subset \mathop{\bigcap }_{V\in {\mathcal{V}}(p^{\infty })}[p_{V}^{\infty }].\end{eqnarray}$$
Proof. By definition we can write
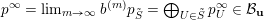 $p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}=\bigoplus _{U\in \tilde{S}}p_{U}^{\infty }\in {\mathcal{B}}_{\mathbf{u}}$
as a limit point where
$p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}=\bigoplus _{U\in \tilde{S}}p_{U}^{\infty }\in {\mathcal{B}}_{\mathbf{u}}$
as a limit point where
![]() $(b^{(m)})$
is normalised and
$(b^{(m)})$
is normalised and
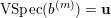 $\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
. By definition
$\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
. By definition
 $Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
satisfies the following properties:
$Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
satisfies the following properties:
-
(i)
 $Z\in {\mathcal{V}}(p^{\infty })$
, that is,
$Z\in {\mathcal{V}}(p^{\infty })$
, that is,
 $p_{Z}^{\infty }\neq 0$
and
$p_{Z}^{\infty }\neq 0$
and
 $\unicode[STIX]{x1D703}_{Z}\geqslant u_{1}$
;
$\unicode[STIX]{x1D703}_{Z}\geqslant u_{1}$
; -
(ii) if
 $p_{U}^{\infty }\neq 0$
and
$p_{U}^{\infty }\neq 0$
and
 $\unicode[STIX]{x1D703}_{U}\geqslant u_{1}$
for some
$\unicode[STIX]{x1D703}_{U}\geqslant u_{1}$
for some
 $U\in \tilde{S}$
, then
$U\in \tilde{S}$
, then
 $\unicode[STIX]{x1D703}_{U}\geqslant \unicode[STIX]{x1D703}_{Z}$
holds;
$\unicode[STIX]{x1D703}_{U}\geqslant \unicode[STIX]{x1D703}_{Z}$
holds; -
(iii) if
 $U\in \tilde{S}$
,
$U\in \tilde{S}$
,
 $\unicode[STIX]{x1D703}_{U}\geqslant u_{1}$
and
$\unicode[STIX]{x1D703}_{U}\geqslant u_{1}$
and
 $U\subsetneq Z$
, then
$U\subsetneq Z$
, then
 $p_{U}^{\infty }=0$
.
$p_{U}^{\infty }=0$
.
Here (ii) and (iii) together say that
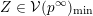 $Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
. Assume there is a
$Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
. Assume there is a
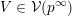 $V\in {\mathcal{V}}(p^{\infty })$
such that
$V\in {\mathcal{V}}(p^{\infty })$
such that
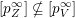 $[p_{Z}^{\infty }]\nsubseteq [p_{V}^{\infty }]$
. By definition
$[p_{Z}^{\infty }]\nsubseteq [p_{V}^{\infty }]$
. By definition
 $$\begin{eqnarray}p_{Z}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{z\in Z}b^{(m)}e_{z}\quad \text{and}\quad p_{V}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{v\in V}b^{(m)}e_{v},\end{eqnarray}$$
$$\begin{eqnarray}p_{Z}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{z\in Z}b^{(m)}e_{z}\quad \text{and}\quad p_{V}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{v\in V}b^{(m)}e_{v},\end{eqnarray}$$
therefore
![]() $Z\subset V$
would imply that
$Z\subset V$
would imply that
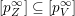 $[p_{Z}^{\infty }]\subseteq [p_{V}^{\infty }]$
. So
$[p_{Z}^{\infty }]\subseteq [p_{V}^{\infty }]$
. So
![]() $Z\setminus V$
must be nonempty.
$Z\setminus V$
must be nonempty.
Fix a hermitian form
![]() $(\cdot ,\cdot )$
on
$(\cdot ,\cdot )$
on
![]() $\mathbb{C}^{n}$
and let
$\mathbb{C}^{n}$
and let
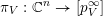 $\unicode[STIX]{x1D70B}_{V}:\mathbb{C}^{n}\rightarrow [p_{V}^{\infty }]$
denote the projection to the subspace
$\unicode[STIX]{x1D70B}_{V}:\mathbb{C}^{n}\rightarrow [p_{V}^{\infty }]$
denote the projection to the subspace
![]() $[p_{V}^{\infty }]$
. For
$[p_{V}^{\infty }]$
. For
![]() $w\in \mathbb{C}^{n}$
let
$w\in \mathbb{C}^{n}$
let
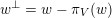 $w^{\bot }=w-\unicode[STIX]{x1D70B}_{V}(w)$
denote the orthogonal component.
$w^{\bot }=w-\unicode[STIX]{x1D70B}_{V}(w)$
denote the orthogonal component.
In Corollary 4.17 below we show that if we drop any subset
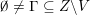 $\emptyset \neq \unicode[STIX]{x1D6E4}\subseteq Z\setminus V$
from
$\emptyset \neq \unicode[STIX]{x1D6E4}\subseteq Z\setminus V$
from
![]() $Z$
, then the smaller subset
$Z$
, then the smaller subset
![]() $Z\setminus \unicode[STIX]{x1D6E4}$
is still in
$Z\setminus \unicode[STIX]{x1D6E4}$
is still in
![]() $\tilde{S}$
. We claim that
$\tilde{S}$
. We claim that
 $$\begin{eqnarray}p_{Z\setminus \unicode[STIX]{x1D6E4}}^{\infty }=0\quad \text{for all}~\emptyset \neq \unicode[STIX]{x1D6E4}\subseteq Z\setminus V.\end{eqnarray}$$
$$\begin{eqnarray}p_{Z\setminus \unicode[STIX]{x1D6E4}}^{\infty }=0\quad \text{for all}~\emptyset \neq \unicode[STIX]{x1D6E4}\subseteq Z\setminus V.\end{eqnarray}$$
Indeed, if
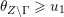 $\unicode[STIX]{x1D703}_{Z\setminus \unicode[STIX]{x1D6E4}}\geqslant u_{1}$
, then this is property (iii) above. If
$\unicode[STIX]{x1D703}_{Z\setminus \unicode[STIX]{x1D6E4}}\geqslant u_{1}$
, then this is property (iii) above. If
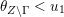 $\unicode[STIX]{x1D703}_{Z\setminus \unicode[STIX]{x1D6E4}}<u_{1}$
, then, by Lemma 4.10,
$\unicode[STIX]{x1D703}_{Z\setminus \unicode[STIX]{x1D6E4}}<u_{1}$
, then, by Lemma 4.10,
 $$\begin{eqnarray}e_{z}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}e_{z}\in \mathbb{C}^{n}\quad \text{exists for all}~z\in Z\setminus \unicode[STIX]{x1D6E4}.\end{eqnarray}$$
$$\begin{eqnarray}e_{z}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}e_{z}\in \mathbb{C}^{n}\quad \text{exists for all}~z\in Z\setminus \unicode[STIX]{x1D6E4}.\end{eqnarray}$$
Moreover,
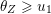 $\unicode[STIX]{x1D703}_{Z}\geqslant u_{1}$
and hence
$\unicode[STIX]{x1D703}_{Z}\geqslant u_{1}$
and hence
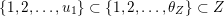 $\{1,2,\ldots ,u_{1}\}\subset \{1,2,\ldots ,\unicode[STIX]{x1D703}_{Z}\}\subset Z$
. On the other hand property (ii) tells us that
$\{1,2,\ldots ,u_{1}\}\subset \{1,2,\ldots ,\unicode[STIX]{x1D703}_{Z}\}\subset Z$
. On the other hand property (ii) tells us that
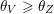 $\unicode[STIX]{x1D703}_{V}\geqslant \unicode[STIX]{x1D703}_{Z}$
and therefore
$\unicode[STIX]{x1D703}_{V}\geqslant \unicode[STIX]{x1D703}_{Z}$
and therefore
 $$\begin{eqnarray}\{1,2,\ldots ,\unicode[STIX]{x1D703}_{Z}\}\subseteq \{1,2,\ldots ,\unicode[STIX]{x1D703}_{V}\}\subset V\end{eqnarray}$$
$$\begin{eqnarray}\{1,2,\ldots ,\unicode[STIX]{x1D703}_{Z}\}\subseteq \{1,2,\ldots ,\unicode[STIX]{x1D703}_{V}\}\subset V\end{eqnarray}$$
which implies that
 $$\begin{eqnarray}\{1,2,\ldots ,u_{1}\}\subset Z\setminus \unicode[STIX]{x1D6E4}\end{eqnarray}$$
$$\begin{eqnarray}\{1,2,\ldots ,u_{1}\}\subset Z\setminus \unicode[STIX]{x1D6E4}\end{eqnarray}$$
and therefore
 $$\begin{eqnarray}p_{Z\setminus \unicode[STIX]{x1D6E4}}^{\infty }=e_{u_{1}}^{\infty }\wedge (\wedge _{z\in Z\setminus \{\unicode[STIX]{x1D6E4}\cup \{u_{1}\}\}}e_{z}^{\infty })=b_{u_{1}u_{1}}^{\infty }e_{u_{1}}\wedge b_{u_{1}-1u_{1}-1}^{\infty }e_{u_{1}-1}\wedge \cdots \wedge b_{11}^{\infty }e_{1}\wedge (\wedge _{z\in Z\setminus \{\unicode[STIX]{x1D6E4}\cup \{1,\ldots ,u_{1}\}\}}e_{z}^{\infty }).\end{eqnarray}$$
$$\begin{eqnarray}p_{Z\setminus \unicode[STIX]{x1D6E4}}^{\infty }=e_{u_{1}}^{\infty }\wedge (\wedge _{z\in Z\setminus \{\unicode[STIX]{x1D6E4}\cup \{u_{1}\}\}}e_{z}^{\infty })=b_{u_{1}u_{1}}^{\infty }e_{u_{1}}\wedge b_{u_{1}-1u_{1}-1}^{\infty }e_{u_{1}-1}\wedge \cdots \wedge b_{11}^{\infty }e_{1}\wedge (\wedge _{z\in Z\setminus \{\unicode[STIX]{x1D6E4}\cup \{1,\ldots ,u_{1}\}\}}e_{z}^{\infty }).\end{eqnarray}$$
But
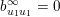 $b_{u_{1}u_{1}}^{\infty }=0$
and by (13) all other terms are finite so this wedge product is 0 and (12) is proved.
$b_{u_{1}u_{1}}^{\infty }=0$
and by (13) all other terms are finite so this wedge product is 0 and (12) is proved.
Then (12) implies that
 $$\begin{eqnarray}0=\unicode[STIX]{x1D70B}_{V}(p_{Z\setminus \unicode[STIX]{x1D6E4}}^{\infty })=\lim _{m\rightarrow \infty }\wedge _{j\in Z\setminus \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70B}_{V}(b^{(m)}\cdot e_{j})\quad \text{for all}~\emptyset \neq \unicode[STIX]{x1D6E4}\subseteq Z\setminus V.\end{eqnarray}$$
$$\begin{eqnarray}0=\unicode[STIX]{x1D70B}_{V}(p_{Z\setminus \unicode[STIX]{x1D6E4}}^{\infty })=\lim _{m\rightarrow \infty }\wedge _{j\in Z\setminus \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70B}_{V}(b^{(m)}\cdot e_{j})\quad \text{for all}~\emptyset \neq \unicode[STIX]{x1D6E4}\subseteq Z\setminus V.\end{eqnarray}$$
Hence
 $$\begin{eqnarray}\displaystyle p_{Z}^{\infty } & = & \displaystyle {\lim _{m\rightarrow \infty }\,\bigoplus }_{\unicode[STIX]{x1D6E4}\subseteq Z\setminus V}\,\bigwedge _{j\in \unicode[STIX]{x1D6E4}}b^{(m)}e_{j}^{\bot }\wedge \bigwedge _{j\in Z\setminus \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70B}_{V}(b^{(m)}\cdot e_{j})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}_{V}(p_{Z}^{\infty })\oplus {\lim _{m\rightarrow \infty }\,\bigoplus }_{\emptyset \neq \unicode[STIX]{x1D6E4}\subseteq Z\setminus V}\,\bigwedge _{j\in \unicode[STIX]{x1D6E4}}b^{(m)}e_{j}^{\bot }\wedge \bigwedge _{j\in Z\setminus \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70B}_{V}(b^{(m)}\cdot e_{j}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{Z}^{\infty } & = & \displaystyle {\lim _{m\rightarrow \infty }\,\bigoplus }_{\unicode[STIX]{x1D6E4}\subseteq Z\setminus V}\,\bigwedge _{j\in \unicode[STIX]{x1D6E4}}b^{(m)}e_{j}^{\bot }\wedge \bigwedge _{j\in Z\setminus \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70B}_{V}(b^{(m)}\cdot e_{j})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70B}_{V}(p_{Z}^{\infty })\oplus {\lim _{m\rightarrow \infty }\,\bigoplus }_{\emptyset \neq \unicode[STIX]{x1D6E4}\subseteq Z\setminus V}\,\bigwedge _{j\in \unicode[STIX]{x1D6E4}}b^{(m)}e_{j}^{\bot }\wedge \bigwedge _{j\in Z\setminus \unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D70B}_{V}(b^{(m)}\cdot e_{j}).\nonumber\end{eqnarray}$$
By (14) all terms corresponding to nonempty
![]() $\unicode[STIX]{x1D6E4}$
vanish and therefore
$\unicode[STIX]{x1D6E4}$
vanish and therefore
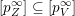 $[p_{Z}^{\infty }]\subseteq [p_{V}^{\infty }]$
unless there is a
$[p_{Z}^{\infty }]\subseteq [p_{V}^{\infty }]$
unless there is a
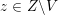 $z\in Z\setminus V$
such that the limit norm
$z\in Z\setminus V$
such that the limit norm
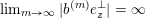 $\lim _{m\rightarrow \infty }|b^{(m)}e_{z}^{\bot }|=\infty$
.
$\lim _{m\rightarrow \infty }|b^{(m)}e_{z}^{\bot }|=\infty$
.
However,
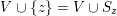 $V\cup \{z\}=V\cup S_{z}$
because
$V\cup \{z\}=V\cup S_{z}$
because
![]() $z\in Z$
and
$z\in Z$
and
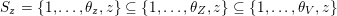 $S_{z}=\{1,\ldots ,\unicode[STIX]{x1D703}_{z},z\}\subseteq \{1,\ldots ,\unicode[STIX]{x1D703}_{Z},z\}\subseteq \{1,\ldots ,\unicode[STIX]{x1D703}_{V},z\}$
since
$S_{z}=\{1,\ldots ,\unicode[STIX]{x1D703}_{z},z\}\subseteq \{1,\ldots ,\unicode[STIX]{x1D703}_{Z},z\}\subseteq \{1,\ldots ,\unicode[STIX]{x1D703}_{V},z\}$
since
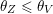 $\unicode[STIX]{x1D703}_{Z}\leqslant \unicode[STIX]{x1D703}_{V}$
by property (ii). Therefore
$\unicode[STIX]{x1D703}_{Z}\leqslant \unicode[STIX]{x1D703}_{V}$
by property (ii). Therefore
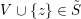 $V\cup \{z\}\in \tilde{S}$
and then
$V\cup \{z\}\in \tilde{S}$
and then
 $$\begin{eqnarray}p_{V\cup \{z\}}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}e_{z}^{\bot }\wedge p_{V}^{\infty }\end{eqnarray}$$
$$\begin{eqnarray}p_{V\cup \{z\}}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}e_{z}^{\bot }\wedge p_{V}^{\infty }\end{eqnarray}$$
does not exist (the limit is not finite), which is a contradiction. So
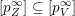 $[p_{Z}^{\infty }]\subseteq [p_{V}^{\infty }]$
holds, and Proposition 4.14 is proved.◻
$[p_{Z}^{\infty }]\subseteq [p_{V}^{\infty }]$
holds, and Proposition 4.14 is proved.◻
Corollary 4.15. Assume
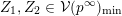 $Z_{1},Z_{2}\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
are minimal subsets for
$Z_{1},Z_{2}\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
are minimal subsets for
![]() $p^{\infty }$
. Then
$p^{\infty }$
. Then
 $[p_{Z_{1}}^{\infty }]=[p_{Z_{2}}^{\infty }]$
.
$[p_{Z_{1}}^{\infty }]=[p_{Z_{2}}^{\infty }]$
.
Proof. As
![]() $Z_{1}$
and
$Z_{1}$
and
![]() $Z_{2}$
are both in
$Z_{2}$
are both in
![]() ${\mathcal{V}}(p^{\infty })$
, by Proposition 4.14 we have
${\mathcal{V}}(p^{\infty })$
, by Proposition 4.14 we have
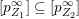 $[p_{Z_{1}}^{\infty }]\subseteq [p_{Z_{2}}^{\infty }]$
and
$[p_{Z_{1}}^{\infty }]\subseteq [p_{Z_{2}}^{\infty }]$
and
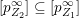 $[p_{Z_{2}}^{\infty }]\subseteq [p_{Z_{1}}^{\infty }]$
.◻
$[p_{Z_{2}}^{\infty }]\subseteq [p_{Z_{1}}^{\infty }]$
.◻
Here are the small technical statements on
![]() $\tilde{S}$
we used in the proof of Proposition 4.14.
$\tilde{S}$
we used in the proof of Proposition 4.14.
Lemma 4.16. Let
![]() $Z\in \tilde{S}$
and let
$Z\in \tilde{S}$
and let
![]() $z\in Z$
be an element such that
$z\in Z$
be an element such that
![]() $z>\unicode[STIX]{x1D703}_{Z}$
. Then
$z>\unicode[STIX]{x1D703}_{Z}$
. Then
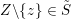 $Z\setminus \{z\}\in \tilde{S}$
.
$Z\setminus \{z\}\in \tilde{S}$
.
Proof. It suffices to show that
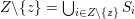 $Z\setminus \{z\}=\bigcup _{i\in Z\setminus \{z\}}S_{i}$
. The direction
$Z\setminus \{z\}=\bigcup _{i\in Z\setminus \{z\}}S_{i}$
. The direction
![]() $\subseteq$
is clear as
$\subseteq$
is clear as
![]() $i\in S_{i}$
for all
$i\in S_{i}$
for all
![]() $i$
. For
$i$
. For
![]() $\supseteq$
note that if
$\supseteq$
note that if
 $i\in Z\setminus \{z\}$
and
$i\in Z\setminus \{z\}$
and
![]() $z>\unicode[STIX]{x1D703}_{Z}$
, then
$z>\unicode[STIX]{x1D703}_{Z}$
, then
 $$\begin{eqnarray}S_{i}=\{1,2,\ldots ,\unicode[STIX]{x1D703}_{i}\}\cup \{i\}\subset \{1,2,\ldots ,\unicode[STIX]{x1D703}_{Z}\}\cup \{i\}\subseteq Z\setminus \{z\}.\Box\end{eqnarray}$$
$$\begin{eqnarray}S_{i}=\{1,2,\ldots ,\unicode[STIX]{x1D703}_{i}\}\cup \{i\}\subset \{1,2,\ldots ,\unicode[STIX]{x1D703}_{Z}\}\cup \{i\}\subseteq Z\setminus \{z\}.\Box\end{eqnarray}$$
Corollary 4.17. If
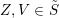 $Z,V\in \tilde{S}$
such that
$Z,V\in \tilde{S}$
such that
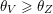 $\unicode[STIX]{x1D703}_{V}\geqslant \unicode[STIX]{x1D703}_{Z}$
, then for any
$\unicode[STIX]{x1D703}_{V}\geqslant \unicode[STIX]{x1D703}_{Z}$
, then for any
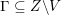 $\unicode[STIX]{x1D6E4}\subseteq Z\setminus V$
we have
$\unicode[STIX]{x1D6E4}\subseteq Z\setminus V$
we have
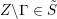 $Z\setminus \unicode[STIX]{x1D6E4}\in \tilde{S}$
.
$Z\setminus \unicode[STIX]{x1D6E4}\in \tilde{S}$
.
Proof. Since
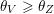 $\unicode[STIX]{x1D703}_{V}\geqslant \unicode[STIX]{x1D703}_{Z}$
, any
$\unicode[STIX]{x1D703}_{V}\geqslant \unicode[STIX]{x1D703}_{Z}$
, any
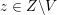 $z\in Z\setminus V$
must satisfy
$z\in Z\setminus V$
must satisfy
![]() $z>\unicode[STIX]{x1D703}_{Z}$
and the statement follows from Lemma 4.16.◻
$z>\unicode[STIX]{x1D703}_{Z}$
and the statement follows from Lemma 4.16.◻
Definition 4.18. Let
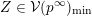 $Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
be a minimal subset for
$Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
be a minimal subset for
![]() $p^{\infty }$
. By Corollary 4.15 the subspace
$p^{\infty }$
. By Corollary 4.15 the subspace
![]() $[p_{Z}^{\infty }]$
is independent of the choice of
$[p_{Z}^{\infty }]$
is independent of the choice of
![]() $Z$
and depends only on
$Z$
and depends only on
![]() $p^{\infty }$
. Assume that
$p^{\infty }$
. Assume that
 $[p_{Z}^{\infty }]\subset \operatorname{Span}(e_{1},\ldots ,e_{r})$
but
$[p_{Z}^{\infty }]\subset \operatorname{Span}(e_{1},\ldots ,e_{r})$
but
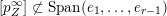 $[p_{Z}^{\infty }]\not \subset \operatorname{Span}(e_{1},\ldots ,e_{r-1})$
for some
$[p_{Z}^{\infty }]\not \subset \operatorname{Span}(e_{1},\ldots ,e_{r-1})$
for some
![]() $r$
. We call this
$r$
. We call this
![]() $r$
the width of
$r$
the width of
![]() $p^{\infty }$
and denote it by
$p^{\infty }$
and denote it by
![]() $\unicode[STIX]{x1D714}(p^{\infty })$
. We will also say that
$\unicode[STIX]{x1D714}(p^{\infty })$
. We will also say that
![]() $[p_{Z}^{\infty }]$
has width
$[p_{Z}^{\infty }]$
has width
![]() $r$
. Note that
$r$
. Note that
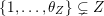 $\{1,\ldots ,\unicode[STIX]{x1D703}_{Z}\}\subsetneq Z$
and hence
$\{1,\ldots ,\unicode[STIX]{x1D703}_{Z}\}\subsetneq Z$
and hence
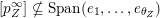 $[p_{Z}^{\infty }]\nsubseteq \operatorname{Span}(e_{1},\ldots ,e_{\unicode[STIX]{x1D703}_{Z}})$
, which by definition means that
$[p_{Z}^{\infty }]\nsubseteq \operatorname{Span}(e_{1},\ldots ,e_{\unicode[STIX]{x1D703}_{Z}})$
, which by definition means that
 $\unicode[STIX]{x1D703}_{Z}<\unicode[STIX]{x1D714}(p^{\infty })$
. We get that
$\unicode[STIX]{x1D703}_{Z}<\unicode[STIX]{x1D714}(p^{\infty })$
. We get that
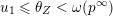 $u_{1}\leqslant \unicode[STIX]{x1D703}_{Z}<\unicode[STIX]{x1D714}(p^{\infty })$
. Let
$u_{1}\leqslant \unicode[STIX]{x1D703}_{Z}<\unicode[STIX]{x1D714}(p^{\infty })$
. Let
 $$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{r}=\{p^{\infty }\in {\mathcal{B}}_{\boldsymbol{ u}}:\unicode[STIX]{x1D714}(p^{\infty })=r\}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{r}=\{p^{\infty }\in {\mathcal{B}}_{\boldsymbol{ u}}:\unicode[STIX]{x1D714}(p^{\infty })=r\}\end{eqnarray}$$
denote the set of points in
![]() ${\mathcal{B}}_{\mathbf{u}}$
of width
${\mathcal{B}}_{\mathbf{u}}$
of width
![]() $r$
.
$r$
.
Remark 4.19. Since the property
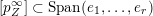 $[p_{Z}^{\infty }]\subset \operatorname{Span}(e_{1},\ldots ,e_{r})$
is closed and
$[p_{Z}^{\infty }]\subset \operatorname{Span}(e_{1},\ldots ,e_{r})$
is closed and
![]() $B_{n}$
-invariant, the set
$B_{n}$
-invariant, the set
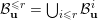 ${\mathcal{B}}_{\mathbf{u}}^{{\leqslant}r}=\bigcup _{i\leqslant r}{\mathcal{B}}_{\mathbf{u}}^{i}$
is closed and
${\mathcal{B}}_{\mathbf{u}}^{{\leqslant}r}=\bigcup _{i\leqslant r}{\mathcal{B}}_{\mathbf{u}}^{i}$
is closed and
![]() $B_{n}$
-invariant and therefore
$B_{n}$
-invariant and therefore
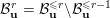 ${\mathcal{B}}_{\mathbf{u}}^{r}={\mathcal{B}}_{\mathbf{u}}^{{\leqslant}r}\setminus {\mathcal{B}}_{\mathbf{u}}^{{\leqslant}r-1}$
is quasi-affine and
${\mathcal{B}}_{\mathbf{u}}^{r}={\mathcal{B}}_{\mathbf{u}}^{{\leqslant}r}\setminus {\mathcal{B}}_{\mathbf{u}}^{{\leqslant}r-1}$
is quasi-affine and
![]() $B_{n}$
-invariant.
$B_{n}$
-invariant.
We have then a (not necessarily disjoint) finite decomposition
 $$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}=\mathop{\bigcup }_{u_{1}<r}{\mathcal{B}}_{\mathbf{u}}^{r}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}=\mathop{\bigcup }_{u_{1}<r}{\mathcal{B}}_{\mathbf{u}}^{r}.\end{eqnarray}$$
Remark 4.20. Points of the boundary sets
![]() ${\mathcal{B}}_{\mathbf{u}}^{r}$
are defined as limits of normalised sequences and hence the stratification
${\mathcal{B}}_{\mathbf{u}}^{r}$
are defined as limits of normalised sequences and hence the stratification
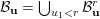 ${\mathcal{B}}_{\mathbf{u}}=\bigcup _{u_{1}<r}{\mathcal{B}}_{\mathbf{u}}^{r}$
a priori depends on the choice of the basis
${\mathcal{B}}_{\mathbf{u}}=\bigcup _{u_{1}<r}{\mathcal{B}}_{\mathbf{u}}^{r}$
a priori depends on the choice of the basis
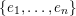 $\{e_{1},\ldots ,e_{n}\}$
of
$\{e_{1},\ldots ,e_{n}\}$
of
![]() $\mathbb{C}^{n}$
. Let us indicate this dependence temporarily as
$\mathbb{C}^{n}$
. Let us indicate this dependence temporarily as
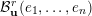 ${\mathcal{B}}_{\mathbf{u}}^{r}(e_{1},\ldots ,e_{n})$
. We show that changing this basis with a unipotent element of the Borel
${\mathcal{B}}_{\mathbf{u}}^{r}(e_{1},\ldots ,e_{n})$
. We show that changing this basis with a unipotent element of the Borel
![]() $B_{n}$
leaves all
$B_{n}$
leaves all
![]() ${\mathcal{B}}_{\mathbf{u}}^{r}$
unchanged. More precisely, let
${\mathcal{B}}_{\mathbf{u}}^{r}$
unchanged. More precisely, let
![]() $A\in B_{n}$
define the new basis
$A\in B_{n}$
define the new basis
 $$\begin{eqnarray}\bar{e}_{i}=A\cdot e_{i}\quad \text{for}~i=1,\ldots ,n.\end{eqnarray}$$
$$\begin{eqnarray}\bar{e}_{i}=A\cdot e_{i}\quad \text{for}~i=1,\ldots ,n.\end{eqnarray}$$
Let
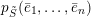 $p_{\tilde{S}}(\bar{e}_{1},\ldots ,\bar{e}_{n})$
denote the base point
$p_{\tilde{S}}(\bar{e}_{1},\ldots ,\bar{e}_{n})$
denote the base point
![]() $p_{\tilde{S}}$
written in the new basis. Then
$p_{\tilde{S}}$
written in the new basis. Then
 $$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}=\lim _{m\rightarrow \infty }(Ab^{(m)}A^{-1})p_{\tilde{S}}(\bar{e}_{1},\ldots ,\bar{e}_{n}).\end{eqnarray}$$
$$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}=\lim _{m\rightarrow \infty }(Ab^{(m)}A^{-1})p_{\tilde{S}}(\bar{e}_{1},\ldots ,\bar{e}_{n}).\end{eqnarray}$$
If
![]() $A$
is unipotent, then the new sequence
$A$
is unipotent, then the new sequence
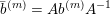 $\bar{b}^{(m)}=Ab^{(m)}A^{-1}$
has the same vanishing spectrum
$\bar{b}^{(m)}=Ab^{(m)}A^{-1}$
has the same vanishing spectrum
![]() $\mathbf{u}$
. Moreover, since
$\mathbf{u}$
. Moreover, since
 $$\begin{eqnarray}\operatorname{Span}(e_{1},\ldots ,e_{i})=\operatorname{Span}(\bar{e}_{1},\ldots ,\bar{e}_{i})\quad \text{for}~1\leqslant i\leqslant n,\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Span}(e_{1},\ldots ,e_{i})=\operatorname{Span}(\bar{e}_{1},\ldots ,\bar{e}_{i})\quad \text{for}~1\leqslant i\leqslant n,\end{eqnarray}$$
the width of
![]() $[p_{Z}^{\infty }]$
in this new basis is
$[p_{Z}^{\infty }]$
in this new basis is
![]() $r$
again. Therefore
$r$
again. Therefore
 $$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{r}(e_{1},\ldots e_{n})={\mathcal{B}}_{\mathbf{u}}^{r}(\bar{e}_{1},\ldots ,\bar{e}_{n})\quad \text{for all}~\mathbf{u},r.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{r}(e_{1},\ldots e_{n})={\mathcal{B}}_{\mathbf{u}}^{r}(\bar{e}_{1},\ldots ,\bar{e}_{n})\quad \text{for all}~\mathbf{u},r.\end{eqnarray}$$
In short, changing the basis with a unipotent element of the Borel will leave the subsets
![]() ${\mathcal{B}}_{\mathbf{u}}^{r}$
unchanged.
${\mathcal{B}}_{\mathbf{u}}^{r}$
unchanged.
Remark 4.21. Let
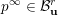 $p^{\infty }\in {\mathcal{B}}_{\mathbf{u}}^{r}$
and
$p^{\infty }\in {\mathcal{B}}_{\mathbf{u}}^{r}$
and
 $Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
. By definition this means that
$Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
. By definition this means that
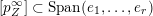 $[p_{Z}^{\infty }]\subset \operatorname{Span}(e_{1},\ldots ,e_{r})$
but
$[p_{Z}^{\infty }]\subset \operatorname{Span}(e_{1},\ldots ,e_{r})$
but
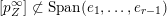 $[p_{Z}^{\infty }]\not \subset \operatorname{Span}(e_{1},\ldots ,e_{r-1})$
so there is a vector
$[p_{Z}^{\infty }]\not \subset \operatorname{Span}(e_{1},\ldots ,e_{r-1})$
so there is a vector
 $$\begin{eqnarray}w=e_{r}+w_{r-1}e_{r-1}+\cdots +w_{1}e_{1}\in [p_{Z}^{\infty }].\end{eqnarray}$$
$$\begin{eqnarray}w=e_{r}+w_{r-1}e_{r-1}+\cdots +w_{1}e_{1}\in [p_{Z}^{\infty }].\end{eqnarray}$$
This
![]() $w$
is not necessarily unique, we fix one. The base change
$w$
is not necessarily unique, we fix one. The base change
 $$\begin{eqnarray}\overline{e}_{i}=\left\{\begin{array}{@{}ll@{}}e_{i}\quad & \text{if}~i\neq r,\\ e_{r}+w_{r-1}e_{r-1}+\cdots +w_{1}e_{1}\quad & \text{if}~i=r,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\overline{e}_{i}=\left\{\begin{array}{@{}ll@{}}e_{i}\quad & \text{if}~i\neq r,\\ e_{r}+w_{r-1}e_{r-1}+\cdots +w_{1}e_{1}\quad & \text{if}~i=r,\end{array}\right.\end{eqnarray}$$
is defined by a unipotent element of
![]() $B_{n}$
. According to Remark 4.20 changing
$B_{n}$
. According to Remark 4.20 changing
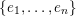 $\{e_{1},\ldots ,e_{n}\}$
to the new basis
$\{e_{1},\ldots ,e_{n}\}$
to the new basis
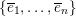 $\{\overline{e}_{1},\ldots ,\overline{e}_{n}\}$
leaves the boundary sets
$\{\overline{e}_{1},\ldots ,\overline{e}_{n}\}$
leaves the boundary sets
![]() ${\mathcal{B}}_{\mathbf{u}}^{r}$
unchanged for all
${\mathcal{B}}_{\mathbf{u}}^{r}$
unchanged for all
![]() $\mathbf{u}$
and
$\mathbf{u}$
and
![]() $r$
but in this new basis
$r$
but in this new basis
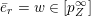 $\bar{e}_{r}=w\in [p_{Z}^{\infty }]$
holds.
$\bar{e}_{r}=w\in [p_{Z}^{\infty }]$
holds.
Proposition 4.22. Let
![]() $s\geqslant 2$
and
$s\geqslant 2$
and
 $\mathbf{u}=\{u_{1}<\cdots <u_{s}\}$
be a subset covered by
$\mathbf{u}=\{u_{1}<\cdots <u_{s}\}$
be a subset covered by
![]() $S$
. Then we have the following.
$S$
. Then we have the following.
-
(a) If
 $r\notin \mathbf{u}$
and
$r\notin \mathbf{u}$
and
 $\unicode[STIX]{x1D703}_{r}<u_{1}$
, then there is a continuous injection
$\unicode[STIX]{x1D703}_{r}<u_{1}$
, then there is a continuous injection
 $\unicode[STIX]{x1D70C}:{\mathcal{B}}_{\mathbf{u}}^{r}{\hookrightarrow}{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
and therefore
$\unicode[STIX]{x1D70C}:{\mathcal{B}}_{\mathbf{u}}^{r}{\hookrightarrow}{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
and therefore
 $\dim {\mathcal{B}}_{\mathbf{u}}^{r}\leqslant \dim {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
.
$\dim {\mathcal{B}}_{\mathbf{u}}^{r}\leqslant \dim {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
. -
(b) If
 $r\in \mathbf{u}$
, then
$r\in \mathbf{u}$
, then
 ${\mathcal{B}}_{\mathbf{u}}^{r}\subset \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}}\setminus {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}$
.
${\mathcal{B}}_{\mathbf{u}}^{r}\subset \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}}\setminus {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}$
. -
(c) If
 $r\notin \mathbf{u}$
and
$r\notin \mathbf{u}$
and
 $\unicode[STIX]{x1D703}_{r}\geqslant u_{1}$
, then
$\unicode[STIX]{x1D703}_{r}\geqslant u_{1}$
, then
 ${\mathcal{B}}_{\mathbf{u}}^{r}\subset \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}}\setminus {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}$
or
${\mathcal{B}}_{\mathbf{u}}^{r}\subset \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}}\setminus {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}$
or
 ${\mathcal{B}}_{\mathbf{u}}^{r}\subset \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}}\setminus {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
.
${\mathcal{B}}_{\mathbf{u}}^{r}\subset \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}}\setminus {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
.
Proof. To prove (a) assume that
![]() $r\notin \mathbf{u}$
and
$r\notin \mathbf{u}$
and
![]() $\unicode[STIX]{x1D703}_{r}<u_{1}$
. Let
$\unicode[STIX]{x1D703}_{r}<u_{1}$
. Let
 $$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}=\bigoplus _{U\in \tilde{S}}p_{U}^{\infty }\in {\mathcal{B}}_{\boldsymbol{ u}}^{r}\end{eqnarray}$$
$$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{S}}=\bigoplus _{U\in \tilde{S}}p_{U}^{\infty }\in {\mathcal{B}}_{\boldsymbol{ u}}^{r}\end{eqnarray}$$
be a limit point such that
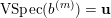 $\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
and
$\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
and
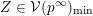 $Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
. By Remark 4.21 we can assume that
$Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
. By Remark 4.21 we can assume that
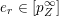 $e_{r}\in [p_{Z}^{\infty }]$
.
$e_{r}\in [p_{Z}^{\infty }]$
.
According to Lemma 4.10
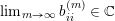 $\lim _{m\rightarrow \infty }b_{ii}^{(m)}\in \mathbb{C}$
exists whenever
$\lim _{m\rightarrow \infty }b_{ii}^{(m)}\in \mathbb{C}$
exists whenever
![]() $\unicode[STIX]{x1D703}_{i}<u_{1}$
and, since
$\unicode[STIX]{x1D703}_{i}<u_{1}$
and, since
![]() $r\notin \mathbf{u}$
, this limit is nonzero for
$r\notin \mathbf{u}$
, this limit is nonzero for
![]() $i=r$
:
$i=r$
:
 $$\begin{eqnarray}b_{rr}^{\infty }:=\lim _{m\rightarrow \infty }b_{rr}^{(m)}\in \mathbb{C}\setminus \{0\}.\end{eqnarray}$$
$$\begin{eqnarray}b_{rr}^{\infty }:=\lim _{m\rightarrow \infty }b_{rr}^{(m)}\in \mathbb{C}\setminus \{0\}.\end{eqnarray}$$
Define the modified sequence
 $$\begin{eqnarray}\tilde{b}_{ij}^{(m)}=\left\{\begin{array}{@{}ll@{}}b_{rr}^{\infty },\quad & (i,j)=(u_{1},u_{1}),\\ {\displaystyle \frac{1}{b_{rr}^{\infty }}}\cdot b_{rr}^{(m)}\cdot b_{u_{1}u_{1}}^{(m)},\quad & (i,j)=(r,r),\\ {\displaystyle \frac{1}{b_{rr}^{\infty }}}\cdot b_{rj}^{(m)}\cdot b_{u_{1},u_{1}}^{(m)}\quad & \text{for}~i=r~\text{and}~j>r~\text{with}~\unicode[STIX]{x1D703}_{j}\geqslant u_{1},\\ b_{ij}^{(m)}\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{b}_{ij}^{(m)}=\left\{\begin{array}{@{}ll@{}}b_{rr}^{\infty },\quad & (i,j)=(u_{1},u_{1}),\\ {\displaystyle \frac{1}{b_{rr}^{\infty }}}\cdot b_{rr}^{(m)}\cdot b_{u_{1}u_{1}}^{(m)},\quad & (i,j)=(r,r),\\ {\displaystyle \frac{1}{b_{rr}^{\infty }}}\cdot b_{rj}^{(m)}\cdot b_{u_{1},u_{1}}^{(m)}\quad & \text{for}~i=r~\text{and}~j>r~\text{with}~\unicode[STIX]{x1D703}_{j}\geqslant u_{1},\\ b_{ij}^{(m)}\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
In short, we fix the diagonal entry
![]() $b_{u_{1}u_{1}}^{(m)}$
to be the nonzero constant
$b_{u_{1}u_{1}}^{(m)}$
to be the nonzero constant
![]() $b_{rr}^{\infty }$
and multiply the entries in the
$b_{rr}^{\infty }$
and multiply the entries in the
![]() $r$
th row of those columns which cover
$r$
th row of those columns which cover
![]() $u_{1}$
by
$u_{1}$
by
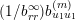 $(1/b_{rr}^{\infty })b_{u_{1}u_{1}}^{(m)}$
. Then the new sequence still sits in
$(1/b_{rr}^{\infty })b_{u_{1}u_{1}}^{(m)}$
. Then the new sequence still sits in
![]() $\operatorname{SL}_{n}(\mathbb{C})$
and part (a) of Proposition 4.22 follows from the following three statements:
$\operatorname{SL}_{n}(\mathbb{C})$
and part (a) of Proposition 4.22 follows from the following three statements:
-
(i)
 $\tilde{p}^{\infty }=\lim _{m\rightarrow \infty }\tilde{b}^{(m)}p_{\tilde{S}}$
exists and therefore the map
$\tilde{p}^{\infty }=\lim _{m\rightarrow \infty }\tilde{b}^{(m)}p_{\tilde{S}}$
exists and therefore the map
 $\tilde{\unicode[STIX]{x1D70C}}:p^{\infty }\mapsto \tilde{p}^{\infty }$
is well defined;
$\tilde{\unicode[STIX]{x1D70C}}:p^{\infty }\mapsto \tilde{p}^{\infty }$
is well defined; -
(ii)
 $\tilde{p}^{\infty }\in {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
;
$\tilde{p}^{\infty }\in {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
; -
(iii)
 $\tilde{\unicode[STIX]{x1D70C}}:p^{\infty }\mapsto \tilde{p}^{\infty }$
is injective.
$\tilde{\unicode[STIX]{x1D70C}}:p^{\infty }\mapsto \tilde{p}^{\infty }$
is injective.
To prove (i) and (ii) we first show that
 $$\begin{eqnarray}\text{if}~\unicode[STIX]{x1D703}_{V}\geqslant u_{1}\quad \text{then}~\tilde{p}_{V}^{\infty }=p_{V}^{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}\text{if}~\unicode[STIX]{x1D703}_{V}\geqslant u_{1}\quad \text{then}~\tilde{p}_{V}^{\infty }=p_{V}^{\infty }.\end{eqnarray}$$
Note that in this case
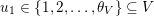 $u_{1}\in \{1,2,\ldots ,\unicode[STIX]{x1D703}_{V}\}\subseteq V$
and therefore
$u_{1}\in \{1,2,\ldots ,\unicode[STIX]{x1D703}_{V}\}\subseteq V$
and therefore
 $$\begin{eqnarray}p_{V}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{v\in V}b^{(m)}e_{v}=\lim _{m\rightarrow \infty }\biggl(\unicode[STIX]{x1D6F1}_{i=1}^{\unicode[STIX]{x1D703}_{V}}b_{ii}^{(m)}\bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{V}}e_{i}\wedge \bigwedge _{\unicode[STIX]{x1D703}_{V}<v\in V}b^{(m)}e_{v}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}p_{V}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{v\in V}b^{(m)}e_{v}=\lim _{m\rightarrow \infty }\biggl(\unicode[STIX]{x1D6F1}_{i=1}^{\unicode[STIX]{x1D703}_{V}}b_{ii}^{(m)}\bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{V}}e_{i}\wedge \bigwedge _{\unicode[STIX]{x1D703}_{V}<v\in V}b^{(m)}e_{v}\biggr).\end{eqnarray}$$
First we study the case when
![]() $r\leqslant \unicode[STIX]{x1D703}_{V}$
. If
$r\leqslant \unicode[STIX]{x1D703}_{V}$
. If
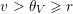 $v>\unicode[STIX]{x1D703}_{V}\geqslant r$
, then
$v>\unicode[STIX]{x1D703}_{V}\geqslant r$
, then
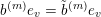 $b^{(m)}e_{v}=\tilde{b}^{(m)}e_{v}$
, and therefore the second product remains the same by changing
$b^{(m)}e_{v}=\tilde{b}^{(m)}e_{v}$
, and therefore the second product remains the same by changing
![]() $b^{(m)}$
to
$b^{(m)}$
to
![]() $\tilde{b}^{(m)}$
. The product
$\tilde{b}^{(m)}$
. The product
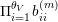 $\unicode[STIX]{x1D6F1}_{i=1}^{\unicode[STIX]{x1D703}_{V}}b_{ii}^{(m)}$
of the first
$\unicode[STIX]{x1D6F1}_{i=1}^{\unicode[STIX]{x1D703}_{V}}b_{ii}^{(m)}$
of the first
![]() $\unicode[STIX]{x1D703}_{V}$
diagonal entries in
$\unicode[STIX]{x1D703}_{V}$
diagonal entries in
![]() $b^{(m)}$
and
$b^{(m)}$
and
![]() $\tilde{b}^{(m)}$
are again equal, so the first product does not change either, giving us
$\tilde{b}^{(m)}$
are again equal, so the first product does not change either, giving us
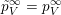 $\tilde{p}_{V}^{\infty }=p_{V}^{\infty }$
.
$\tilde{p}_{V}^{\infty }=p_{V}^{\infty }$
.
Assume now that
![]() $r>\unicode[STIX]{x1D703}_{V}$
and recall that
$r>\unicode[STIX]{x1D703}_{V}$
and recall that
 $e_{r}\in [p_{Z}^{\infty }]\subset [p_{V}^{\infty }]$
. Hence the term
$e_{r}\in [p_{Z}^{\infty }]\subset [p_{V}^{\infty }]$
. Hence the term
![]() $e_{r}$
must be selected in each term of the expansion of the second product, that is, if
$e_{r}$
must be selected in each term of the expansion of the second product, that is, if
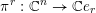 $\unicode[STIX]{x1D70B}^{r}:\mathbb{C}^{n}\rightarrow \mathbb{C}e_{r}$
denotes the projection of a vector to the line spanned by
$\unicode[STIX]{x1D70B}^{r}:\mathbb{C}^{n}\rightarrow \mathbb{C}e_{r}$
denotes the projection of a vector to the line spanned by
![]() $e_{r}$
, then
$e_{r}$
, then
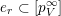 $e_{r}\subset [p_{V}^{\infty }]$
implies that
$e_{r}\subset [p_{V}^{\infty }]$
implies that
 $$\begin{eqnarray}\displaystyle p_{V}^{\infty } & = & \displaystyle \lim _{m\rightarrow \infty }\mathop{\sum }_{v\in V}\biggl(\unicode[STIX]{x1D70B}^{r}(b^{(m)}e_{v})\wedge \bigwedge _{i\in V\setminus v}b^{(m)}e_{i}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \lim _{m\rightarrow \infty }\unicode[STIX]{x1D6F1}_{i=1}^{\unicode[STIX]{x1D703}_{V}}b_{ii}^{(m)}\bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{V}}e_{i}\wedge \mathop{\sum }_{r\leqslant v\in V}\biggl(b_{rv}^{(m)}e_{r}\wedge \bigwedge _{\unicode[STIX]{x1D703}_{V}<i\in V\setminus \{v\}}b^{(m)}e_{i}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{V}^{\infty } & = & \displaystyle \lim _{m\rightarrow \infty }\mathop{\sum }_{v\in V}\biggl(\unicode[STIX]{x1D70B}^{r}(b^{(m)}e_{v})\wedge \bigwedge _{i\in V\setminus v}b^{(m)}e_{i}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \lim _{m\rightarrow \infty }\unicode[STIX]{x1D6F1}_{i=1}^{\unicode[STIX]{x1D703}_{V}}b_{ii}^{(m)}\bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{V}}e_{i}\wedge \mathop{\sum }_{r\leqslant v\in V}\biggl(b_{rv}^{(m)}e_{r}\wedge \bigwedge _{\unicode[STIX]{x1D703}_{V}<i\in V\setminus \{v\}}b^{(m)}e_{i}\biggr).\end{eqnarray}$$
It is easy to see that if
![]() $r\leqslant v$
and
$r\leqslant v$
and
![]() $\unicode[STIX]{x1D703}_{v}<u_{1}$
, then the corresponding term in the direct sum on the right-hand side has zero contribution. Indeed, by Lemma 4.10
$\unicode[STIX]{x1D703}_{v}<u_{1}$
, then the corresponding term in the direct sum on the right-hand side has zero contribution. Indeed, by Lemma 4.10
 $$\begin{eqnarray}b_{rv}^{\infty }=\lim _{m\rightarrow \infty }b_{rv}^{(m)}\in \mathbb{C}\quad \text{for}~r\leqslant v,\unicode[STIX]{x1D703}_{v}<u_{1}.\end{eqnarray}$$
$$\begin{eqnarray}b_{rv}^{\infty }=\lim _{m\rightarrow \infty }b_{rv}^{(m)}\in \mathbb{C}\quad \text{for}~r\leqslant v,\unicode[STIX]{x1D703}_{v}<u_{1}.\end{eqnarray}$$
On the other hand
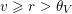 $v\geqslant r>\unicode[STIX]{x1D703}_{V}$
holds and therefore by Lemma 4.16
$v\geqslant r>\unicode[STIX]{x1D703}_{V}$
holds and therefore by Lemma 4.16
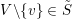 $V\setminus \{v\}\in \tilde{S}$
. Moreover, since
$V\setminus \{v\}\in \tilde{S}$
. Moreover, since
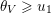 $\unicode[STIX]{x1D703}_{V}\geqslant u_{1}$
but
$\unicode[STIX]{x1D703}_{V}\geqslant u_{1}$
but
![]() $\unicode[STIX]{x1D703}_{v}<u_{1}$
, we must have
$\unicode[STIX]{x1D703}_{v}<u_{1}$
, we must have
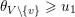 $\unicode[STIX]{x1D703}_{V\setminus \{v\}}\geqslant u_{1}$
. Now, we have the following.
$\unicode[STIX]{x1D703}_{V\setminus \{v\}}\geqslant u_{1}$
. Now, we have the following.
-
– If
 $p_{V\setminus \{v\}}^{\infty }=0$
, then by (18) we have
$p_{V\setminus \{v\}}^{\infty }=0$
, then by (18) we have
 $b_{rv}^{\infty }e_{r}\wedge p_{V\setminus \{v\}}^{\infty }=0$
.
$b_{rv}^{\infty }e_{r}\wedge p_{V\setminus \{v\}}^{\infty }=0$
. -
– If
 $p_{V\setminus \{v\}}^{\infty }\neq 0$
, then by Proposition 4.14
$p_{V\setminus \{v\}}^{\infty }\neq 0$
, then by Proposition 4.14
 $e_{r}\in [p_{Z}^{\infty }]\subset [p_{V\setminus \{v\}}^{\infty }]$
and therefore by (18) we have
$e_{r}\in [p_{Z}^{\infty }]\subset [p_{V\setminus \{v\}}^{\infty }]$
and therefore by (18) we have
 $b_{rv}^{\infty }e_{r}\wedge p_{V\setminus \{v\}}^{\infty }=0$
again.
$b_{rv}^{\infty }e_{r}\wedge p_{V\setminus \{v\}}^{\infty }=0$
again.
In both cases we get
 $$\begin{eqnarray}0=b_{rv}^{\infty }e_{r}\wedge p_{V\setminus \{v\}}^{\infty }=\lim _{m\rightarrow \infty }(\unicode[STIX]{x1D6F1}_{i=1}^{\unicode[STIX]{x1D703}_{V}}b_{ii}^{(m)})\bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{V}}e_{i}\wedge \biggl(b_{rv}^{\infty }e_{r}\wedge \bigwedge _{\unicode[STIX]{x1D703}_{V}<i\in V\setminus \{v\}}b^{(m)}e_{i}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}0=b_{rv}^{\infty }e_{r}\wedge p_{V\setminus \{v\}}^{\infty }=\lim _{m\rightarrow \infty }(\unicode[STIX]{x1D6F1}_{i=1}^{\unicode[STIX]{x1D703}_{V}}b_{ii}^{(m)})\bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{V}}e_{i}\wedge \biggl(b_{rv}^{\infty }e_{r}\wedge \bigwedge _{\unicode[STIX]{x1D703}_{V}<i\in V\setminus \{v\}}b^{(m)}e_{i}\biggr).\end{eqnarray}$$
So in (17) only those terms have nonzero contributions where
![]() $\unicode[STIX]{x1D703}_{v}\geqslant u_{1}$
and
$\unicode[STIX]{x1D703}_{v}\geqslant u_{1}$
and
 $$\begin{eqnarray}p_{V}^{\infty }=\lim _{m\rightarrow \infty }\biggl(\unicode[STIX]{x1D6F1}_{i=1}^{\unicode[STIX]{x1D703}_{V}}b_{ii}^{(m)}\bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{V}}e_{i}\wedge \mathop{\sum }_{\substack{ \unicode[STIX]{x1D703}_{v}\geqslant u_{1} \\ r\leqslant v\in V}}\biggl(b_{rv}^{(m)}e_{r}\wedge \bigwedge _{\unicode[STIX]{x1D703}_{V}<i\in V\setminus \{v\}}b^{(m)}e_{i}\biggr)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}p_{V}^{\infty }=\lim _{m\rightarrow \infty }\biggl(\unicode[STIX]{x1D6F1}_{i=1}^{\unicode[STIX]{x1D703}_{V}}b_{ii}^{(m)}\bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{V}}e_{i}\wedge \mathop{\sum }_{\substack{ \unicode[STIX]{x1D703}_{v}\geqslant u_{1} \\ r\leqslant v\in V}}\biggl(b_{rv}^{(m)}e_{r}\wedge \bigwedge _{\unicode[STIX]{x1D703}_{V}<i\in V\setminus \{v\}}b^{(m)}e_{i}\biggr)\biggr).\end{eqnarray}$$
Replacing
![]() $b^{(m)}$
with
$b^{(m)}$
with
![]() $\tilde{b}^{(m)}$
clearly does not change the right-hand side, so
$\tilde{b}^{(m)}$
clearly does not change the right-hand side, so
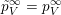 $\tilde{p}_{V}^{\infty }=p_{V}^{\infty }$
is proved for this case too. We have completed the proof of (16).
$\tilde{p}_{V}^{\infty }=p_{V}^{\infty }$
is proved for this case too. We have completed the proof of (16).
Next, if
![]() $V\in \tilde{S}$
but
$V\in \tilde{S}$
but
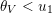 $\unicode[STIX]{x1D703}_{V}<u_{1}$
, then
$\unicode[STIX]{x1D703}_{V}<u_{1}$
, then
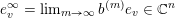 $e_{v}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}e_{v}\in \mathbb{C}^{n}$
exists for all
$e_{v}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}e_{v}\in \mathbb{C}^{n}$
exists for all
![]() $v\in V$
by Lemma 4.10 and therefore
$v\in V$
by Lemma 4.10 and therefore
 $$\begin{eqnarray}p_{V}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{v\in V}b^{(m)}e_{v}=\wedge _{v\in V}e_{v}^{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}p_{V}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{v\in V}b^{(m)}e_{v}=\wedge _{v\in V}e_{v}^{\infty }.\end{eqnarray}$$
Similarly
 $$\begin{eqnarray}\tilde{p}_{V}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{v\in V}\tilde{b}^{(m)}e_{v}=\wedge _{v\in V}\tilde{e}_{v}^{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{p}_{V}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{v\in V}\tilde{b}^{(m)}e_{v}=\wedge _{v\in V}\tilde{e}_{v}^{\infty }.\end{eqnarray}$$
where
 $$\begin{eqnarray}\tilde{e}_{v}^{\infty }=\lim _{m\rightarrow \infty }\tilde{b}^{(m)}e_{v}=\left\{\begin{array}{@{}ll@{}}e_{v}^{\infty },\quad & v\neq u_{1},r,\\ e_{v}^{\infty }+b_{rr}^{\infty }e_{u_{1}},\quad & v=u_{1},\\ \unicode[STIX]{x1D70B}^{r-1}(e_{r}^{\infty }),\quad & v=r,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{e}_{v}^{\infty }=\lim _{m\rightarrow \infty }\tilde{b}^{(m)}e_{v}=\left\{\begin{array}{@{}ll@{}}e_{v}^{\infty },\quad & v\neq u_{1},r,\\ e_{v}^{\infty }+b_{rr}^{\infty }e_{u_{1}},\quad & v=u_{1},\\ \unicode[STIX]{x1D70B}^{r-1}(e_{r}^{\infty }),\quad & v=r,\end{array}\right.\end{eqnarray}$$
where
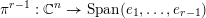 $\unicode[STIX]{x1D70B}^{r-1}:\mathbb{C}^{n}\rightarrow \operatorname{Span}(e_{1},\ldots ,e_{r-1})$
is the projection. This is because
$\unicode[STIX]{x1D70B}^{r-1}:\mathbb{C}^{n}\rightarrow \operatorname{Span}(e_{1},\ldots ,e_{r-1})$
is the projection. This is because
 $\lim _{m\rightarrow \infty }b_{u_{1},u_{1}}^{(m)}=0$
by definition and the last coordinate of
$\lim _{m\rightarrow \infty }b_{u_{1},u_{1}}^{(m)}=0$
by definition and the last coordinate of
![]() $b^{(m)}e_{r}$
tends to 0:
$b^{(m)}e_{r}$
tends to 0:
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }\frac{1}{b_{rr}^{\infty }}\cdot b_{rr}^{(m)}\cdot b_{u_{1}u_{1}}^{(m)}=0.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }\frac{1}{b_{rr}^{\infty }}\cdot b_{rr}^{(m)}\cdot b_{u_{1}u_{1}}^{(m)}=0.\end{eqnarray}$$
This means that
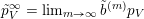 $\tilde{p}_{V}^{\infty }=\lim _{m\rightarrow \infty }\tilde{b}^{(m)}p_{V}$
exists for all
$\tilde{p}_{V}^{\infty }=\lim _{m\rightarrow \infty }\tilde{b}^{(m)}p_{V}$
exists for all
![]() $V\in \tilde{S}$
and
$V\in \tilde{S}$
and
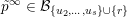 $\tilde{p}^{\infty }\in {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
.
$\tilde{p}^{\infty }\in {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
.
Note that, formally, the equation for
![]() $\tilde{e}_{v}^{\infty }$
depends on the sequence
$\tilde{e}_{v}^{\infty }$
depends on the sequence
![]() $b^{(m)}$
and in particular on
$b^{(m)}$
and in particular on
![]() $b_{rr}^{\infty }$
. However: (i) since
$b_{rr}^{\infty }$
. However: (i) since
![]() $\unicode[STIX]{x1D703}_{r}\leqslant u_{1}$
we have
$\unicode[STIX]{x1D703}_{r}\leqslant u_{1}$
we have
 $p_{1,\ldots ,\unicode[STIX]{x1D703}_{r}}^{\infty }\neq 0$
and; (ii)
$p_{1,\ldots ,\unicode[STIX]{x1D703}_{r}}^{\infty }\neq 0$
and; (ii)
![]() $r\notin \mathbf{u}$
by assumption and therefore
$r\notin \mathbf{u}$
by assumption and therefore
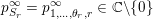 $p_{S_{r}}^{\infty }=p_{1,\ldots ,\unicode[STIX]{x1D703}_{r},r}^{\infty }\in \mathbb{C}\setminus \{0\}$
. Now
$p_{S_{r}}^{\infty }=p_{1,\ldots ,\unicode[STIX]{x1D703}_{r},r}^{\infty }\in \mathbb{C}\setminus \{0\}$
. Now
 $$\begin{eqnarray}b_{rr}^{\infty }=\frac{\lim _{m\rightarrow \infty }b_{11}^{(m)}\ldots b_{\unicode[STIX]{x1D703}_{r}\unicode[STIX]{x1D703}_{r}}^{(m)}b_{rr}^{(m)}}{\lim _{m\rightarrow \infty }b_{11}^{(m)}\ldots b_{\unicode[STIX]{x1D703}_{r}\unicode[STIX]{x1D703}_{r}}^{(m)}}\end{eqnarray}$$
$$\begin{eqnarray}b_{rr}^{\infty }=\frac{\lim _{m\rightarrow \infty }b_{11}^{(m)}\ldots b_{\unicode[STIX]{x1D703}_{r}\unicode[STIX]{x1D703}_{r}}^{(m)}b_{rr}^{(m)}}{\lim _{m\rightarrow \infty }b_{11}^{(m)}\ldots b_{\unicode[STIX]{x1D703}_{r}\unicode[STIX]{x1D703}_{r}}^{(m)}}\end{eqnarray}$$
is a rational function of
![]() $p^{\infty }$
, where the numerator is a coordinate of
$p^{\infty }$
, where the numerator is a coordinate of
![]() $p_{S_{r}}^{\infty }$
and therefore finite by (ii) and the denominator is the coefficient of
$p_{S_{r}}^{\infty }$
and therefore finite by (ii) and the denominator is the coefficient of
![]() $p_{1,\ldots ,\unicode[STIX]{x1D703}_{r}}^{\infty }$
and therefore nonzero and finite by (i). This proves the map
$p_{1,\ldots ,\unicode[STIX]{x1D703}_{r}}^{\infty }$
and therefore nonzero and finite by (i). This proves the map
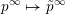 $p^{\infty }\mapsto \tilde{p}^{\infty }$
is well defined and continuous.
$p^{\infty }\mapsto \tilde{p}^{\infty }$
is well defined and continuous.
To prove (iii) (the injectivity of
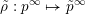 $\tilde{\unicode[STIX]{x1D70C}}:p^{\infty }\mapsto \tilde{p}^{\infty }$
) note that by (16)
$\tilde{\unicode[STIX]{x1D70C}}:p^{\infty }\mapsto \tilde{p}^{\infty }$
) note that by (16)
 $$\begin{eqnarray}p_{V}^{\infty }=\tilde{p}_{V}^{\infty }\quad \text{whenever}~\unicode[STIX]{x1D703}_{V}\geqslant u_{1}\end{eqnarray}$$
$$\begin{eqnarray}p_{V}^{\infty }=\tilde{p}_{V}^{\infty }\quad \text{whenever}~\unicode[STIX]{x1D703}_{V}\geqslant u_{1}\end{eqnarray}$$
so
![]() $\tilde{\unicode[STIX]{x1D70C}}$
is the identity (and therefore injective) on these coordinates. It remains to check injectivity on the other coordinates.
$\tilde{\unicode[STIX]{x1D70C}}$
is the identity (and therefore injective) on these coordinates. It remains to check injectivity on the other coordinates.
Take two points
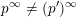 $p^{\infty }\neq (p^{\prime })^{\infty }$
in
$p^{\infty }\neq (p^{\prime })^{\infty }$
in
![]() ${\mathcal{B}}_{\mathbf{u}}^{r}$
such that
${\mathcal{B}}_{\mathbf{u}}^{r}$
such that
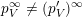 $p_{V}^{\infty }\neq (p_{V}^{\prime })^{\infty }$
for some
$p_{V}^{\infty }\neq (p_{V}^{\prime })^{\infty }$
for some
![]() $V$
with
$V$
with
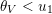 $\unicode[STIX]{x1D703}_{V}<u_{1}$
. This means that
$\unicode[STIX]{x1D703}_{V}<u_{1}$
. This means that
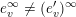 $e_{v}^{\infty }\neq (e_{v}^{\prime })^{\infty }$
for some
$e_{v}^{\infty }\neq (e_{v}^{\prime })^{\infty }$
for some
![]() $v\in V$
satisfying
$v\in V$
satisfying
![]() $\unicode[STIX]{x1D703}_{v}<u_{1}$
. Let
$\unicode[STIX]{x1D703}_{v}<u_{1}$
. Let
![]() $v$
be minimal with this property. Then
$v$
be minimal with this property. Then
 $$\begin{eqnarray}p_{S_{v}}^{\infty }-(p_{S_{v}}^{\prime })^{\infty }=(e_{v}^{\infty }-(e_{v}^{\prime })^{\infty })\wedge \bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{v}}b_{ii}^{\infty }e_{i}\neq 0\end{eqnarray}$$
$$\begin{eqnarray}p_{S_{v}}^{\infty }-(p_{S_{v}}^{\prime })^{\infty }=(e_{v}^{\infty }-(e_{v}^{\prime })^{\infty })\wedge \bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{v}}b_{ii}^{\infty }e_{i}\neq 0\end{eqnarray}$$
and using (19) we have the following cases.
-
– If
 $v\neq u_{1},r$
, then
$v\neq u_{1},r$
, then
 $\tilde{p}_{S_{v}}^{\infty }-(\tilde{p}_{S_{v}}^{\prime })^{\infty }=p_{S_{v}}^{\infty }-(p_{S_{v}}^{\prime })^{\infty }\neq 0$
.
$\tilde{p}_{S_{v}}^{\infty }-(\tilde{p}_{S_{v}}^{\prime })^{\infty }=p_{S_{v}}^{\infty }-(p_{S_{v}}^{\prime })^{\infty }\neq 0$
. -
– If
 $v=u_{1}$
, then
$v=u_{1}$
, then
 $\tilde{p}_{S_{u_{1}}}^{\infty }-(\tilde{p}_{S_{u_{1}}}^{\prime }\!)^{\infty }=p_{S_{u_{1}}}^{\infty }-(p_{S_{u_{1}}}^{\prime }\!)^{\infty }+(b_{rr}^{\infty }-(b_{rr}^{\prime })^{\infty })e_{u_{1}}\wedge \bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{u_{1}}}b_{ii}^{\infty }e_{i}\neq 0$
because
$\tilde{p}_{S_{u_{1}}}^{\infty }-(\tilde{p}_{S_{u_{1}}}^{\prime }\!)^{\infty }=p_{S_{u_{1}}}^{\infty }-(p_{S_{u_{1}}}^{\prime }\!)^{\infty }+(b_{rr}^{\infty }-(b_{rr}^{\prime })^{\infty })e_{u_{1}}\wedge \bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{u_{1}}}b_{ii}^{\infty }e_{i}\neq 0$
because
 $p_{S_{u_{1}}}^{\infty }-(p_{S_{u_{1}}}^{\prime }\!)^{\infty }$
does not contain
$p_{S_{u_{1}}}^{\infty }-(p_{S_{u_{1}}}^{\prime }\!)^{\infty }$
does not contain
 $e_{u_{1}}$
due to the fact that
$e_{u_{1}}$
due to the fact that
 $b_{u_{1},u_{1}}^{\infty }=0$
.
$b_{u_{1},u_{1}}^{\infty }=0$
. -
– If
 $v=r$
, then
$v=r$
, then
 $\tilde{p}_{S_{r}}^{\infty }-(\tilde{p}_{S_{r}}^{\prime })^{\infty }=\unicode[STIX]{x1D70B}^{r-1}(e_{r}^{\infty }-(e_{r}^{\prime })^{\infty })\wedge \bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{r}}b_{ii}^{\infty }$
, and if this is
$\tilde{p}_{S_{r}}^{\infty }-(\tilde{p}_{S_{r}}^{\prime })^{\infty }=\unicode[STIX]{x1D70B}^{r-1}(e_{r}^{\infty }-(e_{r}^{\prime })^{\infty })\wedge \bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{r}}b_{ii}^{\infty }$
, and if this is
 $0$
, then the
$0$
, then the
 $e_{r}$
coordinate of
$e_{r}$
coordinate of
 $e_{r}^{\infty }$
and
$e_{r}^{\infty }$
and
 $(e_{r}^{\prime })^{\infty }$
are not equal, that is,
$(e_{r}^{\prime })^{\infty }$
are not equal, that is,
 $b_{rr}^{\infty }-(b_{rr}^{\prime })^{\infty }\neq 0$
. But then again, as in the previous case we have
$b_{rr}^{\infty }-(b_{rr}^{\prime })^{\infty }\neq 0$
. But then again, as in the previous case we have  $$\begin{eqnarray}\tilde{p}_{S_{u_{1}}}^{\infty }-(\tilde{p}_{S_{u_{1}}}^{\prime }\!)^{\infty }=p_{S_{u_{1}}}^{\infty }-(p_{S_{u_{1}}}^{\prime }\!)^{\infty }+(b_{rr}^{\infty }-(b_{rr}^{\prime })^{\infty })e_{u_{1}}\wedge \bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{v}}b_{ii}^{\infty }e_{i}\neq 0.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{p}_{S_{u_{1}}}^{\infty }-(\tilde{p}_{S_{u_{1}}}^{\prime }\!)^{\infty }=p_{S_{u_{1}}}^{\infty }-(p_{S_{u_{1}}}^{\prime }\!)^{\infty }+(b_{rr}^{\infty }-(b_{rr}^{\prime })^{\infty })e_{u_{1}}\wedge \bigwedge _{i=1}^{\unicode[STIX]{x1D703}_{v}}b_{ii}^{\infty }e_{i}\neq 0.\end{eqnarray}$$
In any case,
![]() $\tilde{p}^{\infty }$
and
$\tilde{p}^{\infty }$
and
![]() $(\tilde{p}^{\prime })^{\infty }$
differ in at least one term, proving injectivity of
$(\tilde{p}^{\prime })^{\infty }$
differ in at least one term, proving injectivity of
![]() $\tilde{\unicode[STIX]{x1D70C}}$
.
$\tilde{\unicode[STIX]{x1D70C}}$
.
Next we prove (b) and (c) of Proposition 4.22 simultaneously. Assume that
![]() $r\in \mathbf{u}$
or
$r\in \mathbf{u}$
or
![]() $\unicode[STIX]{x1D703}_{r}\geqslant u_{1}$
. The problem with this case is that
$\unicode[STIX]{x1D703}_{r}\geqslant u_{1}$
. The problem with this case is that
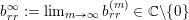 $b_{rr}^{\infty }:=\lim _{m\rightarrow \infty }b_{rr}^{(m)}\in \mathbb{C}\setminus \{0\}$
does not necessarily hold any more and the limit can be
$b_{rr}^{\infty }:=\lim _{m\rightarrow \infty }b_{rr}^{(m)}\in \mathbb{C}\setminus \{0\}$
does not necessarily hold any more and the limit can be
![]() $\infty$
or 0. In both cases
$\infty$
or 0. In both cases
![]() $\tilde{b}^{(m)}$
is ill defined in (15).
$\tilde{b}^{(m)}$
is ill defined in (15).
Fix a nonzero
![]() $\unicode[STIX]{x1D6FF}\in \mathbb{C}$
and define the sequence
$\unicode[STIX]{x1D6FF}\in \mathbb{C}$
and define the sequence
 $$\begin{eqnarray}\tilde{b}_{ij}^{(m),\unicode[STIX]{x1D6FF}}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FF},\quad & (i,j)=(u_{1},u_{1}),\\ {\displaystyle \frac{1}{\unicode[STIX]{x1D6FF}}}b_{rr}^{(m)}\cdot b_{u_{1}u_{1}}^{(m)},\quad & (i,j)=(r,r),\\ {\displaystyle \frac{1}{\unicode[STIX]{x1D6FF}}}b_{rj}^{(m)}\cdot b_{u_{1},u_{1}}^{(m)}\quad & \text{if}~i=r,j>r~\text{and}~\unicode[STIX]{x1D703}_{j}\geqslant u_{1},\\ b_{ij}^{(m)}\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{b}_{ij}^{(m),\unicode[STIX]{x1D6FF}}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FF},\quad & (i,j)=(u_{1},u_{1}),\\ {\displaystyle \frac{1}{\unicode[STIX]{x1D6FF}}}b_{rr}^{(m)}\cdot b_{u_{1}u_{1}}^{(m)},\quad & (i,j)=(r,r),\\ {\displaystyle \frac{1}{\unicode[STIX]{x1D6FF}}}b_{rj}^{(m)}\cdot b_{u_{1},u_{1}}^{(m)}\quad & \text{if}~i=r,j>r~\text{and}~\unicode[STIX]{x1D703}_{j}\geqslant u_{1},\\ b_{ij}^{(m)}\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
In short, we increase the diagonal entry
![]() $b_{u_{1}u_{1}}^{(m)}$
to be constant
$b_{u_{1}u_{1}}^{(m)}$
to be constant
![]() $\unicode[STIX]{x1D6FF}$
and multiply the entries in the
$\unicode[STIX]{x1D6FF}$
and multiply the entries in the
![]() $r$
th row above the diagonal by
$r$
th row above the diagonal by
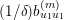 $(1/\unicode[STIX]{x1D6FF})b_{u_{1}u_{1}}^{(m)}$
whenever
$(1/\unicode[STIX]{x1D6FF})b_{u_{1}u_{1}}^{(m)}$
whenever
![]() $\unicode[STIX]{x1D703}_{j}\geqslant u_{1}$
. Then the new sequence still sits in
$\unicode[STIX]{x1D703}_{j}\geqslant u_{1}$
. Then the new sequence still sits in
![]() $\operatorname{SL}_{n}(\mathbb{C})$
. If
$\operatorname{SL}_{n}(\mathbb{C})$
. If
![]() $r\in \mathbf{u}$
, then
$r\in \mathbf{u}$
, then
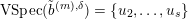 $\operatorname{VSpec}(\tilde{b}^{(m),\unicode[STIX]{x1D6FF}})=\{u_{2},\ldots ,u_{s}\}$
. If
$\operatorname{VSpec}(\tilde{b}^{(m),\unicode[STIX]{x1D6FF}})=\{u_{2},\ldots ,u_{s}\}$
. If
![]() $r\notin \mathbf{u}$
and
$r\notin \mathbf{u}$
and
![]() $\unicode[STIX]{x1D703}_{r}\geqslant u_{1}$
, then
$\unicode[STIX]{x1D703}_{r}\geqslant u_{1}$
, then
 $$\begin{eqnarray}\operatorname{VSpec}(\tilde{b}^{(m),\unicode[STIX]{x1D6FF}})=\left\{\begin{array}{@{}ll@{}}\{u_{2},\ldots ,u_{s}\}\quad & \displaystyle \text{if}~\lim _{m\rightarrow \infty }b_{rr}^{(m)}b_{u_{1}u_{1}}^{(m)}\neq 0,\\ \{u_{2},\ldots ,u_{s}\}\cup \{r\}\quad & \displaystyle \text{if}~\lim _{m\rightarrow \infty }b_{rr}^{(m)}b_{u_{1}u_{1}}^{(m)}=0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{VSpec}(\tilde{b}^{(m),\unicode[STIX]{x1D6FF}})=\left\{\begin{array}{@{}ll@{}}\{u_{2},\ldots ,u_{s}\}\quad & \displaystyle \text{if}~\lim _{m\rightarrow \infty }b_{rr}^{(m)}b_{u_{1}u_{1}}^{(m)}\neq 0,\\ \{u_{2},\ldots ,u_{s}\}\cup \{r\}\quad & \displaystyle \text{if}~\lim _{m\rightarrow \infty }b_{rr}^{(m)}b_{u_{1}u_{1}}^{(m)}=0.\end{array}\right.\end{eqnarray}$$
In any case, if the limit exists, then
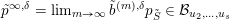 $\tilde{p}^{\infty ,\unicode[STIX]{x1D6FF}}=\lim _{m\rightarrow \infty }\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}p_{\tilde{S}}\in {\mathcal{B}}_{u_{2},\ldots ,u_{s}}$
or
$\tilde{p}^{\infty ,\unicode[STIX]{x1D6FF}}=\lim _{m\rightarrow \infty }\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}p_{\tilde{S}}\in {\mathcal{B}}_{u_{2},\ldots ,u_{s}}$
or
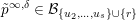 $\tilde{p}^{\infty ,\unicode[STIX]{x1D6FF}}\in {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
.
$\tilde{p}^{\infty ,\unicode[STIX]{x1D6FF}}\in {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
.
The same argument as for part (a) shows the following.
-
– If
 $V\in \tilde{S}$
with
$V\in \tilde{S}$
with
 $\unicode[STIX]{x1D703}_{V}\geqslant u_{1}$
, then
$\unicode[STIX]{x1D703}_{V}\geqslant u_{1}$
, then
 $\tilde{p}_{V}^{\infty ,\unicode[STIX]{x1D6FF}}=p_{V}^{\infty }$
.
$\tilde{p}_{V}^{\infty ,\unicode[STIX]{x1D6FF}}=p_{V}^{\infty }$
. -
– If
 $V\in \tilde{S}$
with
$V\in \tilde{S}$
with
 $\unicode[STIX]{x1D703}_{V}<u_{1}$
, then
$\unicode[STIX]{x1D703}_{V}<u_{1}$
, then
 $\lim _{m\rightarrow \infty }b^{(m)}e_{v}\in \mathbb{C}^{n}$
and
$\lim _{m\rightarrow \infty }b^{(m)}e_{v}\in \mathbb{C}^{n}$
and
 $\lim _{m\rightarrow \infty }\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}e_{v}\in \mathbb{C}^{n}$
exists for all
$\lim _{m\rightarrow \infty }\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}e_{v}\in \mathbb{C}^{n}$
exists for all
 $v\in V$
by Lemma 4.10 and therefore and the same holds with
$v\in V$
by Lemma 4.10 and therefore and the same holds with $$\begin{eqnarray}p_{V}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{v\in V}b^{(m)}e_{v}=\wedge _{v\in V}\lim _{m\rightarrow \infty }b^{(m)}e_{v}\end{eqnarray}$$
$$\begin{eqnarray}p_{V}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{v\in V}b^{(m)}e_{v}=\wedge _{v\in V}\lim _{m\rightarrow \infty }b^{(m)}e_{v}\end{eqnarray}$$
 $b^{(m)}$
replaced by
$b^{(m)}$
replaced by
 $\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}$
. But for
$\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}$
. But for
 $v\in V$
we have Note that the first line holds for
$v\in V$
we have Note that the first line holds for $$\begin{eqnarray}\lim _{m\rightarrow \infty }\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}e_{v}=\left\{\begin{array}{@{}ll@{}}\displaystyle \lim _{m\rightarrow \infty }b^{(m)}e_{v},\quad & v\neq u_{1},\\ \displaystyle \lim _{m\rightarrow \infty }b^{(m)}e_{u_{1}}+\unicode[STIX]{x1D6FF}e_{u_{1}},\quad & v=u_{1}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}e_{v}=\left\{\begin{array}{@{}ll@{}}\displaystyle \lim _{m\rightarrow \infty }b^{(m)}e_{v},\quad & v\neq u_{1},\\ \displaystyle \lim _{m\rightarrow \infty }b^{(m)}e_{u_{1}}+\unicode[STIX]{x1D6FF}e_{u_{1}},\quad & v=u_{1}.\end{array}\right.\end{eqnarray}$$
 $v=r$
too, that is,
$v=r$
too, that is,
 $\lim _{m\rightarrow \infty }\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}e_{r}=\lim _{m\rightarrow \infty }b^{(m)}e_{r}$
. We assumed that
$\lim _{m\rightarrow \infty }\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}e_{r}=\lim _{m\rightarrow \infty }b^{(m)}e_{r}$
. We assumed that
 $v\in V$
, but if
$v\in V$
, but if
 $\unicode[STIX]{x1D703}_{r}>u_{1}$
, then
$\unicode[STIX]{x1D703}_{r}>u_{1}$
, then
 $r\notin V$
since
$r\notin V$
since
 $\unicode[STIX]{x1D703}_{V}<u_{1}$
by assumption. So the other condition must hold, that is,
$\unicode[STIX]{x1D703}_{V}<u_{1}$
by assumption. So the other condition must hold, that is,
 $r\in \mathbf{u}$
, and then
$r\in \mathbf{u}$
, and then
 $\tilde{b}_{rr}^{\infty }=b_{rr}^{\infty }=0$
and therefore
$\tilde{b}_{rr}^{\infty }=b_{rr}^{\infty }=0$
and therefore
 $\lim _{m\rightarrow \infty }\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}e_{r}=\lim _{m\rightarrow \infty }b^{(m)}e_{r}=\unicode[STIX]{x1D70B}^{r-1}(e_{r}^{\infty })$
.
$\lim _{m\rightarrow \infty }\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}e_{r}=\lim _{m\rightarrow \infty }b^{(m)}e_{r}=\unicode[STIX]{x1D70B}^{r-1}(e_{r}^{\infty })$
.
In particular, when
 $\unicode[STIX]{x1D6FF}\rightarrow 0$
the point
$\unicode[STIX]{x1D6FF}\rightarrow 0$
the point
 $\tilde{p}_{V}^{\infty ,\unicode[STIX]{x1D6FF}}$
tends to
$\tilde{p}_{V}^{\infty ,\unicode[STIX]{x1D6FF}}$
tends to
 $p_{V}^{\infty }$
.
$p_{V}^{\infty }$
.
In short,
 $$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\tilde{p}^{\infty ,\unicode[STIX]{x1D6FF}}=p^{\infty }\end{eqnarray}$$
$$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\tilde{p}^{\infty ,\unicode[STIX]{x1D6FF}}=p^{\infty }\end{eqnarray}$$
and therefore
 $$\begin{eqnarray}p^{\infty }\in \left\{\begin{array}{@{}ll@{}}\overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}}\quad & \text{if}~r\in \mathbf{u},\\ \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}}~\text{or}~\overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}}\quad & \text{if}~\unicode[STIX]{x1D703}_{r}\geqslant u_{1}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}p^{\infty }\in \left\{\begin{array}{@{}ll@{}}\overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}}\quad & \text{if}~r\in \mathbf{u},\\ \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}}~\text{or}~\overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}}\quad & \text{if}~\unicode[STIX]{x1D703}_{r}\geqslant u_{1}.\end{array}\right.\end{eqnarray}$$
But
 $p^{\infty }\in {\mathcal{B}}_{\{u_{1},\ldots ,u_{s}\}}$
so
$p^{\infty }\in {\mathcal{B}}_{\{u_{1},\ldots ,u_{s}\}}$
so
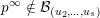 $p^{\infty }\notin {\mathcal{B}}_{(u_{2},\ldots ,u_{s})}$
and
$p^{\infty }\notin {\mathcal{B}}_{(u_{2},\ldots ,u_{s})}$
and
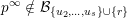 $p^{\infty }\notin {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
and we are done.◻
$p^{\infty }\notin {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}$
and we are done.◻
We are ready to finish the proof of Theorem 1.2 for
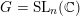 $G=\operatorname{SL}_{n}(\mathbb{C})$
. The key observation is that in Proposition 4.22 the smallest element of the vanishing spectrum
$G=\operatorname{SL}_{n}(\mathbb{C})$
. The key observation is that in Proposition 4.22 the smallest element of the vanishing spectrum
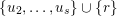 $\{u_{2},\ldots ,u_{s}\}\cup \{r\}$
, which is either
$\{u_{2},\ldots ,u_{s}\}\cup \{r\}$
, which is either
![]() $r$
or
$r$
or
![]() $u_{2}$
, is strictly bigger than
$u_{2}$
, is strictly bigger than
![]() $u_{1}$
.
$u_{1}$
.
To make this idea more formal, we introduce an order among the various
![]() $\mathbf{u}$
as follows: we say that
$\mathbf{u}$
as follows: we say that
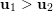 $\mathbf{u}_{1}>\mathbf{u}_{2}$
if either
$\mathbf{u}_{1}>\mathbf{u}_{2}$
if either
![]() $\mathbf{u}_{1}$
is shorter than
$\mathbf{u}_{1}$
is shorter than
![]() $\mathbf{u}_{2}$
or has a larger smallest element when
$\mathbf{u}_{2}$
or has a larger smallest element when
![]() $\mathbf{u}_{1}$
and
$\mathbf{u}_{1}$
and
![]() $\mathbf{u}_{2}$
have the same length. For given
$\mathbf{u}_{2}$
have the same length. For given
![]() $\mathbf{u}$
and
$\mathbf{u}$
and
![]() $r$
choose
$r$
choose
![]() $\hat{\mathbf{u}}(r)$
so that
$\hat{\mathbf{u}}(r)$
so that
![]() $\hat{\mathbf{u}}(r)$
is largest among those vanishing spectra for which
$\hat{\mathbf{u}}(r)$
is largest among those vanishing spectra for which
![]() ${\mathcal{B}}_{\mathbf{u}}^{r}$
admits a continuous injection into
${\mathcal{B}}_{\mathbf{u}}^{r}$
admits a continuous injection into
![]() ${\mathcal{B}}_{\hat{\mathbf{u}}(r)}$
.
${\mathcal{B}}_{\hat{\mathbf{u}}(r)}$
.
According to Proposition 4.22 either the length of
![]() $\hat{\mathbf{u}}(r)$
must be one, or one of (b) and (c) holds, in which case
$\hat{\mathbf{u}}(r)$
must be one, or one of (b) and (c) holds, in which case
![]() ${\mathcal{B}}_{\mathbf{u}}^{r}$
sits in the boundary of a boundary component and therefore has codimension at least 2 in
${\mathcal{B}}_{\mathbf{u}}^{r}$
sits in the boundary of a boundary component and therefore has codimension at least 2 in
![]() $\overline{B\cdot p_{\tilde{S}}}$
. So Theorem 1.2 is reduced to the special case when
$\overline{B\cdot p_{\tilde{S}}}$
. So Theorem 1.2 is reduced to the special case when
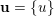 $\mathbf{u}=\{u\}$
has a single element. In order to handle this case we need one more definition.
$\mathbf{u}=\{u\}$
has a single element. In order to handle this case we need one more definition.
Definition 4.23. Let
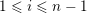 $1\leqslant i\leqslant n-1$
be an integer and
$1\leqslant i\leqslant n-1$
be an integer and
![]() $v\in \mathbb{C}^{n}$
such that
$v\in \mathbb{C}^{n}$
such that
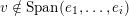 $v\notin \operatorname{Span}(e_{1},\ldots ,e_{i})$
. A point
$v\notin \operatorname{Span}(e_{1},\ldots ,e_{i})$
. A point
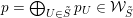 $p=\bigoplus _{U\in \tilde{S}}p_{U}\in {\mathcal{W}}_{\tilde{S}}$
is called
$p=\bigoplus _{U\in \tilde{S}}p_{U}\in {\mathcal{W}}_{\tilde{S}}$
is called
![]() $(i,v)$
-fixed if the stabiliser
$(i,v)$
-fixed if the stabiliser
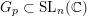 $G_{p}\subset \operatorname{SL}_{n}(\mathbb{C})$
of
$G_{p}\subset \operatorname{SL}_{n}(\mathbb{C})$
of
![]() $p$
contains the one-parameter subgroup
$p$
contains the one-parameter subgroup
 $$\begin{eqnarray}T^{i,v}(\unicode[STIX]{x1D706}):e_{j}\mapsto \left\{\begin{array}{@{}ll@{}}e_{j},\quad & j\neq i,\\ e_{i}+\unicode[STIX]{x1D706}v,\quad & j=i,\end{array}\right.\quad \text{for}~\unicode[STIX]{x1D706}\in \mathbb{C}.\end{eqnarray}$$
$$\begin{eqnarray}T^{i,v}(\unicode[STIX]{x1D706}):e_{j}\mapsto \left\{\begin{array}{@{}ll@{}}e_{j},\quad & j\neq i,\\ e_{i}+\unicode[STIX]{x1D706}v,\quad & j=i,\end{array}\right.\quad \text{for}~\unicode[STIX]{x1D706}\in \mathbb{C}.\end{eqnarray}$$
A subset
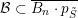 ${\mathcal{B}}\subset \overline{B_{n}\cdot p_{\tilde{S}}}$
is called
${\mathcal{B}}\subset \overline{B_{n}\cdot p_{\tilde{S}}}$
is called
![]() $i$
-fixed if every point of
$i$
-fixed if every point of
![]() ${\mathcal{B}}$
is
${\mathcal{B}}$
is
![]() $(i,v)$
-fixed for some
$(i,v)$
-fixed for some
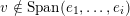 $v\notin \operatorname{Span}(e_{1},\ldots ,e_{i})$
.
$v\notin \operatorname{Span}(e_{1},\ldots ,e_{i})$
.
Lemma 4.24. Let
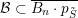 ${\mathcal{B}}\subset \overline{B_{n}\cdot p_{\tilde{S}}}$
be an
${\mathcal{B}}\subset \overline{B_{n}\cdot p_{\tilde{S}}}$
be an
![]() $i$
-fixed Borel invariant subvariety for some
$i$
-fixed Borel invariant subvariety for some
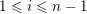 $1\leqslant i\leqslant n-1$
. Then
$1\leqslant i\leqslant n-1$
. Then
 $$\begin{eqnarray}\dim \overline{\operatorname{SL}_{n}(\mathbb{C})\cdot {\mathcal{B}}}\leqslant \dim \overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}}-2.\end{eqnarray}$$
$$\begin{eqnarray}\dim \overline{\operatorname{SL}_{n}(\mathbb{C})\cdot {\mathcal{B}}}\leqslant \dim \overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}}-2.\end{eqnarray}$$
Proof. Consider the map
 $$\begin{eqnarray}\unicode[STIX]{x1D711}:\operatorname{SL}_{n}(\mathbb{C})\times {\mathcal{B}}\rightarrow {\mathcal{W}}_{\tilde{S}},\quad \unicode[STIX]{x1D711}(g,w)\mapsto g\cdot w.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}:\operatorname{SL}_{n}(\mathbb{C})\times {\mathcal{B}}\rightarrow {\mathcal{W}}_{\tilde{S}},\quad \unicode[STIX]{x1D711}(g,w)\mapsto g\cdot w.\end{eqnarray}$$
Choose
![]() $w\in {\mathcal{B}}$
and let
$w\in {\mathcal{B}}$
and let
![]() $T^{i,w}(\unicode[STIX]{x1D706})$
be the corresponding one-parameter subgroup as in Definition 4.23. Since
$T^{i,w}(\unicode[STIX]{x1D706})$
be the corresponding one-parameter subgroup as in Definition 4.23. Since
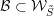 ${\mathcal{B}}\subset {\mathcal{W}}_{\tilde{S}}$
is Borel-invariant, the fibre
${\mathcal{B}}\subset {\mathcal{W}}_{\tilde{S}}$
is Borel-invariant, the fibre
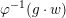 $\unicode[STIX]{x1D711}^{-1}(g\cdot w)$
contains
$\unicode[STIX]{x1D711}^{-1}(g\cdot w)$
contains
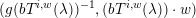 $(g(bT^{i,w}(\unicode[STIX]{x1D706}))^{-1},(bT^{i,w}(\unicode[STIX]{x1D706}))\cdot w)$
for
$(g(bT^{i,w}(\unicode[STIX]{x1D706}))^{-1},(bT^{i,w}(\unicode[STIX]{x1D706}))\cdot w)$
for
![]() $b\in B_{n}$
,
$b\in B_{n}$
,
![]() $\unicode[STIX]{x1D706}\in \mathbb{C}$
. Since
$\unicode[STIX]{x1D706}\in \mathbb{C}$
. Since
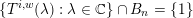 $\{T^{i,w}(\unicode[STIX]{x1D706}):\unicode[STIX]{x1D706}\in \mathbb{C}\}\cap B_{n}=\{1\}$
,
$\{T^{i,w}(\unicode[STIX]{x1D706}):\unicode[STIX]{x1D706}\in \mathbb{C}\}\cap B_{n}=\{1\}$
,
 $$\begin{eqnarray}\dim (\{bT^{i,w}(\unicode[STIX]{x1D706}):b\in B_{n},\unicode[STIX]{x1D706}\in \mathbb{C}\})=\dim (B_{n})+1\end{eqnarray}$$
$$\begin{eqnarray}\dim (\{bT^{i,w}(\unicode[STIX]{x1D706}):b\in B_{n},\unicode[STIX]{x1D706}\in \mathbb{C}\})=\dim (B_{n})+1\end{eqnarray}$$
and we get
 $$\begin{eqnarray}\displaystyle \dim (\operatorname{Im}(\unicode[STIX]{x1D711})) & = & \displaystyle \dim \operatorname{SL}_{n}(\mathbb{C})+\dim {\mathcal{B}}-\dim (\text{fibre})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \dim \operatorname{SL}_{n}(\mathbb{C})+\dim \overline{B_{n}\cdot p_{\tilde{S}}}-1-(\dim (B_{n})+1)\nonumber\\ \displaystyle & = & \displaystyle \dim \operatorname{SL}_{n}(\mathbb{C})/U_{S}-2=\dim \overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}}-2.\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim (\operatorname{Im}(\unicode[STIX]{x1D711})) & = & \displaystyle \dim \operatorname{SL}_{n}(\mathbb{C})+\dim {\mathcal{B}}-\dim (\text{fibre})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \dim \operatorname{SL}_{n}(\mathbb{C})+\dim \overline{B_{n}\cdot p_{\tilde{S}}}-1-(\dim (B_{n})+1)\nonumber\\ \displaystyle & = & \displaystyle \dim \operatorname{SL}_{n}(\mathbb{C})/U_{S}-2=\dim \overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}}-2.\Box \nonumber\end{eqnarray}$$
Lemma 4.25. Let
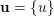 $\mathbf{u}=\{u\}$
have one element and
$\mathbf{u}=\{u\}$
have one element and
![]() $r>u$
. Then
$r>u$
. Then
![]() ${\mathcal{B}}_{u}^{r}$
is
${\mathcal{B}}_{u}^{r}$
is
![]() $u$
-fixed and therefore by Lemma 4.24
$u$
-fixed and therefore by Lemma 4.24
 $$\begin{eqnarray}\dim \overline{\operatorname{SL}_{n}(\mathbb{C}){\mathcal{B}}_{u}^{r}}\leqslant \dim \overline{\operatorname{SL}_{n}(\mathbb{C})p_{S}}-2.\end{eqnarray}$$
$$\begin{eqnarray}\dim \overline{\operatorname{SL}_{n}(\mathbb{C}){\mathcal{B}}_{u}^{r}}\leqslant \dim \overline{\operatorname{SL}_{n}(\mathbb{C})p_{S}}-2.\end{eqnarray}$$
Proof. Let
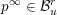 $p^{\infty }\in {\mathcal{B}}_{u}^{r}$
and
$p^{\infty }\in {\mathcal{B}}_{u}^{r}$
and
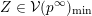 $Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
. By Proposition 4.14 we have:
$Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
. By Proposition 4.14 we have:
-
(i)
 $[p_{Z}^{\infty }]\subset \bigcap _{V\in {\mathcal{V}}(p^{\infty })}p_{V}^{\infty }$
where
$[p_{Z}^{\infty }]\subset \bigcap _{V\in {\mathcal{V}}(p^{\infty })}p_{V}^{\infty }$
where
 ${\mathcal{V}}(p^{\infty })=\{U\in \tilde{S}:p_{U}^{\infty }\neq 0,\unicode[STIX]{x1D703}_{U}\geqslant u\}$
;
${\mathcal{V}}(p^{\infty })=\{U\in \tilde{S}:p_{U}^{\infty }\neq 0,\unicode[STIX]{x1D703}_{U}\geqslant u\}$
; -
(ii)
 $\unicode[STIX]{x1D714}(p^{\infty })=r$
, and hence there is a vector
$\unicode[STIX]{x1D714}(p^{\infty })=r$
, and hence there is a vector
 $w=e_{r}+w_{r-1}e_{r-1}+\cdots +w_{1}e_{1}\in [p_{Z}^{\infty }]$
.
$w=e_{r}+w_{r-1}e_{r-1}+\cdots +w_{1}e_{1}\in [p_{Z}^{\infty }]$
.
By Lemma 4.10
 $$\begin{eqnarray}e_{j}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}e_{j}=\unicode[STIX]{x1D707}_{jj}e_{j}+\cdots +\unicode[STIX]{x1D707}_{1j}e_{1}\quad \text{exists when}~\unicode[STIX]{x1D703}_{j}<u\end{eqnarray}$$
$$\begin{eqnarray}e_{j}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}e_{j}=\unicode[STIX]{x1D707}_{jj}e_{j}+\cdots +\unicode[STIX]{x1D707}_{1j}e_{1}\quad \text{exists when}~\unicode[STIX]{x1D703}_{j}<u\end{eqnarray}$$
and in particular, since only
![]() $b_{uu}^{(m)}$
tends to zero among the diagonal entries, we have
$b_{uu}^{(m)}$
tends to zero among the diagonal entries, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{jj}\neq 0\quad \text{when}~\unicode[STIX]{x1D703}_{j}<u.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{jj}\neq 0\quad \text{when}~\unicode[STIX]{x1D703}_{j}<u.\end{eqnarray}$$
Therefore the linear base change
 $$\begin{eqnarray}A:\tilde{e}_{j}:=\left\{\begin{array}{@{}ll@{}}e_{j}^{\infty },\quad & j\neq u,\unicode[STIX]{x1D703}_{j}<u,\\ e_{u},\quad & j=u,\\ w,\quad & j=r,\\ e_{j}\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}A:\tilde{e}_{j}:=\left\{\begin{array}{@{}ll@{}}e_{j}^{\infty },\quad & j\neq u,\unicode[STIX]{x1D703}_{j}<u,\\ e_{u},\quad & j=u,\\ w,\quad & j=r,\\ e_{j}\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
sits in the Borel
![]() $B_{\text{SL}_{n}}$
. Since
$B_{\text{SL}_{n}}$
. Since
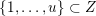 $\{1,\ldots ,u\}\subset Z$
, by (i) and (ii) above we have
$\{1,\ldots ,u\}\subset Z$
, by (i) and (ii) above we have
 $$\begin{eqnarray}\operatorname{Span}(e_{1},\ldots ,e_{u},w)=\operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u},\tilde{e}_{r})\subseteq [p_{Z}^{\infty }]\subseteq [p_{V}^{\infty }]\quad \text{for all}~V\in \tilde{S}~\text{with}~p_{V}^{\infty }\neq 0,\unicode[STIX]{x1D703}_{V}\geqslant u.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Span}(e_{1},\ldots ,e_{u},w)=\operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u},\tilde{e}_{r})\subseteq [p_{Z}^{\infty }]\subseteq [p_{V}^{\infty }]\quad \text{for all}~V\in \tilde{S}~\text{with}~p_{V}^{\infty }\neq 0,\unicode[STIX]{x1D703}_{V}\geqslant u.\end{eqnarray}$$
If
![]() $\unicode[STIX]{x1D703}_{V}<u$
, then by Lemma 4.10 again
$\unicode[STIX]{x1D703}_{V}<u$
, then by Lemma 4.10 again
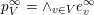 $p_{V}^{\infty }=\wedge _{v\in V}e_{v}^{\infty }$
. But
$p_{V}^{\infty }=\wedge _{v\in V}e_{v}^{\infty }$
. But
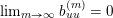 $\lim _{m\rightarrow \infty }b_{uu}^{(m)}=0$
and hence
$\lim _{m\rightarrow \infty }b_{uu}^{(m)}=0$
and hence
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }b^{(m)}e_{u}\subseteq \operatorname{Span}(e_{1},\ldots ,e_{u-1})=\operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u-1}).\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }b^{(m)}e_{u}\subseteq \operatorname{Span}(e_{1},\ldots ,e_{u-1})=\operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u-1}).\end{eqnarray}$$
Note that since
![]() $\unicode[STIX]{x1D703}_{V}<u$
, we have
$\unicode[STIX]{x1D703}_{V}<u$
, we have
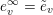 $e_{v}^{\infty }=\tilde{e}_{v}$
for all
$e_{v}^{\infty }=\tilde{e}_{v}$
for all
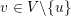 $v\in V\setminus \{u\}$
. Therefore
$v\in V\setminus \{u\}$
. Therefore
 $$\begin{eqnarray}[p_{V}^{\infty }]\subset \operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u-1},\tilde{e}_{u+1},\ldots ,\tilde{e}_{n})\quad \text{for all}~V\in \tilde{S}~\text{with}~p_{V}^{\infty }\neq 0,\unicode[STIX]{x1D703}_{V}<u.\end{eqnarray}$$
$$\begin{eqnarray}[p_{V}^{\infty }]\subset \operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u-1},\tilde{e}_{u+1},\ldots ,\tilde{e}_{n})\quad \text{for all}~V\in \tilde{S}~\text{with}~p_{V}^{\infty }\neq 0,\unicode[STIX]{x1D703}_{V}<u.\end{eqnarray}$$
From (23) and (22) it follows that the one-parameter subgroup
 $$\begin{eqnarray}\tilde{T}^{u,\tilde{e}_{r}}(\unicode[STIX]{x1D706}):\tilde{e}_{j}\mapsto \left\{\begin{array}{@{}ll@{}}\tilde{e}_{j},\quad & j\neq u,\\ \tilde{e}_{u}+\unicode[STIX]{x1D706}\tilde{e}_{r},\quad & j=u,\end{array}\right.\quad \text{for}~\unicode[STIX]{x1D706}\in \mathbb{C}\end{eqnarray}$$
$$\begin{eqnarray}\tilde{T}^{u,\tilde{e}_{r}}(\unicode[STIX]{x1D706}):\tilde{e}_{j}\mapsto \left\{\begin{array}{@{}ll@{}}\tilde{e}_{j},\quad & j\neq u,\\ \tilde{e}_{u}+\unicode[STIX]{x1D706}\tilde{e}_{r},\quad & j=u,\end{array}\right.\quad \text{for}~\unicode[STIX]{x1D706}\in \mathbb{C}\end{eqnarray}$$
stabilises
![]() $p^{\infty }$
so
$p^{\infty }$
so
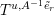 $T^{u,A^{-1}\tilde{e}_{r}}$
stabilises
$T^{u,A^{-1}\tilde{e}_{r}}$
stabilises
![]() $p^{\infty }$
in the old basis, proving that it is
$p^{\infty }$
in the old basis, proving that it is
![]() $u$
-fixed.◻
$u$
-fixed.◻
5 Borel-regular subgroups of classical groups
In this section, again, we restrict our attention to the
![]() $k=\mathbb{C}$
case, but all arguments work for any algebraically closed field
$k=\mathbb{C}$
case, but all arguments work for any algebraically closed field
![]() $k$
of characteristic zero which is a subfield of
$k$
of characteristic zero which is a subfield of
![]() $\mathbb{C}$
. We will often use the shorthand notation
$\mathbb{C}$
. We will often use the shorthand notation
![]() $\operatorname{Sp}_{n}$
for
$\operatorname{Sp}_{n}$
for
![]() $\operatorname{Sp}_{n}(\mathbb{C})$
and
$\operatorname{Sp}_{n}(\mathbb{C})$
and
![]() $\operatorname{SO}_{n}$
for
$\operatorname{SO}_{n}$
for
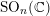 $\operatorname{SO}_{n}(\mathbb{C})$
.
$\operatorname{SO}_{n}(\mathbb{C})$
.
Recall from the Introduction that a Borel-regular subgroup of a linear algebraic group is a subgroup normalised by a Borel subgroup. They have the form
![]() $U_{S}$
corresponding to closed root subsets
$U_{S}$
corresponding to closed root subsets
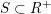 $S\subset R^{+}$
which are also closed under shifting by elements of
$S\subset R^{+}$
which are also closed under shifting by elements of
![]() $R^{+}$
, i.e.
$R^{+}$
, i.e.
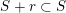 $S+r\subset S$
for any
$S+r\subset S$
for any
![]() $r\in R^{+}$
.
$r\in R^{+}$
.
5.1 Borel-regular subgroups of
 $\operatorname{SL}_{n}$
$\operatorname{SL}_{n}$
When
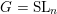 $G=\operatorname{SL}_{n}$
this means that
$G=\operatorname{SL}_{n}$
this means that
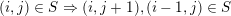 $(i,j)\in S\Rightarrow (i,j+1),(i-1,j)\in S$
, and hence Borel-regular subgroups have the form
$(i,j)\in S\Rightarrow (i,j+1),(i-1,j)\in S$
, and hence Borel-regular subgroups have the form

where the positions of free parameters are encoded by a monotone increasing sequence
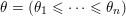 $\unicode[STIX]{x1D703}=(\unicode[STIX]{x1D703}_{1}\leqslant \cdots \leqslant \unicode[STIX]{x1D703}_{n})$
satisfying
$\unicode[STIX]{x1D703}=(\unicode[STIX]{x1D703}_{1}\leqslant \cdots \leqslant \unicode[STIX]{x1D703}_{n})$
satisfying
![]() $\unicode[STIX]{x1D703}_{i}<i$
. This sequence then corresponds to the root subset
$\unicode[STIX]{x1D703}_{i}<i$
. This sequence then corresponds to the root subset
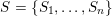 $S=\{S_{1},\ldots ,S_{n}\}$
where
$S=\{S_{1},\ldots ,S_{n}\}$
where
 $S_{i}=\{1,\ldots ,\unicode[STIX]{x1D703}_{i},i\}$
. Note that a subgroup of
$S_{i}=\{1,\ldots ,\unicode[STIX]{x1D703}_{i},i\}$
. Note that a subgroup of
![]() $\operatorname{SL}_{n}$
is Borel regular if and only if it is left and right Borel regular at the same time. Therefore the Popov–Pommerening conjecture for Borel-regular subgroups of
$\operatorname{SL}_{n}$
is Borel regular if and only if it is left and right Borel regular at the same time. Therefore the Popov–Pommerening conjecture for Borel-regular subgroups of
![]() $\operatorname{SL}_{n}$
is a special case of Theorem 1.2.
$\operatorname{SL}_{n}$
is a special case of Theorem 1.2.
5.2 Borel-regular subgroups of symplectic groups
Let
![]() $V$
be a
$V$
be a
![]() $n=2l$
-dimensional complex vector space and
$n=2l$
-dimensional complex vector space and
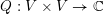 $Q:V\times V\rightarrow \mathbb{C}$
a nondegenerate skew-symmetric bilinear form on
$Q:V\times V\rightarrow \mathbb{C}$
a nondegenerate skew-symmetric bilinear form on
![]() $V$
. The symplectic Lie group is then
$V$
. The symplectic Lie group is then
 $$\begin{eqnarray}\operatorname{Sp}_{n}(V)=\{A\in \operatorname{SL}_{n}(\mathbb{C}):Q(Av,Aw)=Q(v,w)~\text{for all}~v,w\in V\},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sp}_{n}(V)=\{A\in \operatorname{SL}_{n}(\mathbb{C}):Q(Av,Aw)=Q(v,w)~\text{for all}~v,w\in V\},\end{eqnarray}$$
and the corresponding symplectic Lie algebra is
 $$\begin{eqnarray}\mathfrak{sp}_{n}(V)=\{A\in \mathfrak{sl}_{n}(\mathbb{C}):Q(Av,w)+Q(v,Aw)=0~\text{for all}~v,w\in V\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{sp}_{n}(V)=\{A\in \mathfrak{sl}_{n}(\mathbb{C}):Q(Av,w)+Q(v,Aw)=0~\text{for all}~v,w\in V\}.\end{eqnarray}$$
To get a compatible embedding of
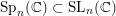 $\operatorname{Sp}_{n}(\mathbb{C})\subset \operatorname{SL}_{n}(\mathbb{C})$
with diagonal maximal torus and which preserves the standard Borel of upper triangular matrices in
$\operatorname{Sp}_{n}(\mathbb{C})\subset \operatorname{SL}_{n}(\mathbb{C})$
with diagonal maximal torus and which preserves the standard Borel of upper triangular matrices in
![]() $\operatorname{SL}_{n}$
, we take a basis
$\operatorname{SL}_{n}$
, we take a basis
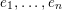 $e_{1},\ldots ,e_{n}$
of
$e_{1},\ldots ,e_{n}$
of
![]() $V$
such that
$V$
such that
![]() $Q$
is given by the matrix
$Q$
is given by the matrix
![]() $M$
in the form
$M$
in the form
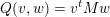 $Q(v,w)=v^{t}Mw$
where
$Q(v,w)=v^{t}Mw$
where
![]() $M$
is the antidiagonal
$M$
is the antidiagonal
![]() $n\times n$
matrix with two antidiagonal
$n\times n$
matrix with two antidiagonal
![]() $l\times l$
blocks:
$l\times l$
blocks:

For a diagonal matrix
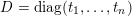 $D=\operatorname{diag}(t_{1},\ldots ,t_{n})$
, the condition to lie in
$D=\operatorname{diag}(t_{1},\ldots ,t_{n})$
, the condition to lie in
![]() $\operatorname{Sp}_{n}$
is
$\operatorname{Sp}_{n}$
is
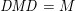 $\mathit{DMD}=M$
. Since
$\mathit{DMD}=M$
. Since

this happens exactly when
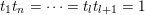 $t_{1}t_{n}=\cdots =t_{l}t_{l+1}=1$
. Hence the maximal torus in
$t_{1}t_{n}=\cdots =t_{l}t_{l+1}=1$
. Hence the maximal torus in
![]() $\operatorname{Sp}_{n}$
is
$\operatorname{Sp}_{n}$
is
 $$\begin{eqnarray}T_{\text{Sp}_{n}}=\left\{\left(\begin{array}{@{}cccccc@{}}t_{1} & & & & & \\ & \ddots & & & & \\ & & t_{l} & & & \\ & & & t_{l}^{-1} & & \\ & & & & \ddots & \\ & & & & & t_{1}^{-1}\end{array}\right):t_{1},\ldots ,t_{l}\in \mathbb{C}^{\ast }\right\}\end{eqnarray}$$
$$\begin{eqnarray}T_{\text{Sp}_{n}}=\left\{\left(\begin{array}{@{}cccccc@{}}t_{1} & & & & & \\ & \ddots & & & & \\ & & t_{l} & & & \\ & & & t_{l}^{-1} & & \\ & & & & \ddots & \\ & & & & & t_{1}^{-1}\end{array}\right):t_{1},\ldots ,t_{l}\in \mathbb{C}^{\ast }\right\}\end{eqnarray}$$
and the rank of
![]() $\operatorname{Sp}_{2l}$
is
$\operatorname{Sp}_{2l}$
is
![]() $l$
. For
$l$
. For
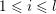 $1\leqslant i\leqslant l$
define the character
$1\leqslant i\leqslant l$
define the character
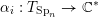 $\unicode[STIX]{x1D6FC}_{i}:T_{\text{Sp}_{n}}\rightarrow \mathbb{C}^{\ast }$
by
$\unicode[STIX]{x1D6FC}_{i}:T_{\text{Sp}_{n}}\rightarrow \mathbb{C}^{\ast }$
by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i}(\operatorname{diag}(t_{1},t_{2},\ldots ,t_{2}^{-1},t_{1}^{-1}))=t_{i}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i}(\operatorname{diag}(t_{1},t_{2},\ldots ,t_{2}^{-1},t_{1}^{-1}))=t_{i}\end{eqnarray}$$
and the cocharacter
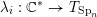 $\unicode[STIX]{x1D706}_{i}:\mathbb{C}^{\ast }\rightarrow T_{\text{Sp}_{n}}$
by
$\unicode[STIX]{x1D706}_{i}:\mathbb{C}^{\ast }\rightarrow T_{\text{Sp}_{n}}$
by
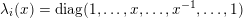 $\unicode[STIX]{x1D706}_{i}(x)=\operatorname{diag}(1,\ldots ,x,\ldots ,x^{-1},\ldots ,1)$
with
$\unicode[STIX]{x1D706}_{i}(x)=\operatorname{diag}(1,\ldots ,x,\ldots ,x^{-1},\ldots ,1)$
with
![]() $x$
at the
$x$
at the
![]() $i$
th position. Then
$i$
th position. Then
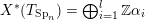 $X^{\ast }(T_{\text{Sp}_{n}})=\bigoplus _{i=1}^{l}\mathbb{Z}\unicode[STIX]{x1D6FC}_{i}$
and
$X^{\ast }(T_{\text{Sp}_{n}})=\bigoplus _{i=1}^{l}\mathbb{Z}\unicode[STIX]{x1D6FC}_{i}$
and
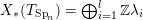 $X_{\ast }(T_{\text{Sp}_{n}})=\bigoplus _{i=1}^{l}\mathbb{Z}\unicode[STIX]{x1D706}_{i}$
with dual pairing
$X_{\ast }(T_{\text{Sp}_{n}})=\bigoplus _{i=1}^{l}\mathbb{Z}\unicode[STIX]{x1D706}_{i}$
with dual pairing
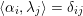 $\langle \unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D706}_{j}\rangle =\unicode[STIX]{x1D6FF}_{ij}$
.
$\langle \unicode[STIX]{x1D6FC}_{i},\unicode[STIX]{x1D706}_{j}\rangle =\unicode[STIX]{x1D6FF}_{ij}$
.
For an
![]() $n\times n$
matrix
$n\times n$
matrix
 $A=(a_{ij})$
let
$A=(a_{ij})$
let
 $A^{at}=(a_{ij}^{at})$
denote its antidiagonal-transpose, that is
$A^{at}=(a_{ij}^{at})$
denote its antidiagonal-transpose, that is
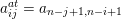 $a_{ij}^{at}=a_{n-j+1,n-i+1}$
. Computing
$a_{ij}^{at}=a_{n-j+1,n-i+1}$
. Computing
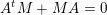 $A^{t}M+MA=0$
shows that the Lie algebra
$A^{t}M+MA=0$
shows that the Lie algebra
![]() $\mathfrak{sp}_{n}$
consists of matrices of the form
$\mathfrak{sp}_{n}$
consists of matrices of the form
 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}A & B\\ C & -A^{at}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}A & B\\ C & -A^{at}\end{array}\right)\end{eqnarray}$$
where
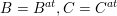 $B=B^{at},C=C^{at}$
.
$B=B^{at},C=C^{at}$
.
Remark 5.1. In particular this means that any Lie algebra element
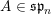 $A\in \mathfrak{sp}_{n}$
is uniquely determined by its entries
$A\in \mathfrak{sp}_{n}$
is uniquely determined by its entries
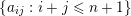 $\{a_{ij}:i+j\leqslant n+1\}$
sitting above and on the antidiagonal.
$\{a_{ij}:i+j\leqslant n+1\}$
sitting above and on the antidiagonal.
The Cartan subalgebra
![]() $\mathfrak{h}\subset \mathfrak{sp}_{n}$
is
$\mathfrak{h}\subset \mathfrak{sp}_{n}$
is
![]() $l$
-dimensional, spanned by the diagonal matrices
$l$
-dimensional, spanned by the diagonal matrices
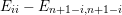 $E_{ii}-E_{n+1-i,n+1-i}$
whose dual is
$E_{ii}-E_{n+1-i,n+1-i}$
whose dual is
![]() $\unicode[STIX]{x1D6FC}_{i}$
. Here, as before,
$\unicode[STIX]{x1D6FC}_{i}$
. Here, as before,
![]() $E_{ii}$
is the matrix with 1 in the diagonal entry
$E_{ii}$
is the matrix with 1 in the diagonal entry
![]() $(i,i)$
and 0 elsewhere. The roots of
$(i,i)$
and 0 elsewhere. The roots of
![]() $\operatorname{Sp}_{n}$
are
$\operatorname{Sp}_{n}$
are
 $$\begin{eqnarray}R=\{\pm \unicode[STIX]{x1D6FC}_{i}\pm \unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i,j\leqslant l}\end{eqnarray}$$
$$\begin{eqnarray}R=\{\pm \unicode[STIX]{x1D6FC}_{i}\pm \unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i,j\leqslant l}\end{eqnarray}$$
and the positive roots are
 $$\begin{eqnarray}R^{+}=\{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\}_{i<j}\cup \{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\}_{i\leqslant j}.\end{eqnarray}$$
$$\begin{eqnarray}R^{+}=\{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\}_{i<j}\cup \{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\}_{i\leqslant j}.\end{eqnarray}$$
Therefore the Lie algebra of the corresponding Borel subgroup consists of matrices of the form
 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}A & B\\ 0 & -A^{at}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}A & B\\ 0 & -A^{at}\end{array}\right)\end{eqnarray}$$
where
![]() $A$
is upper triangular and
$A$
is upper triangular and
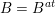 $B=B^{at}$
.
$B=B^{at}$
.
All one-dimensional positive root subspaces
![]() $\mathfrak{g}_{\unicode[STIX]{x1D6FC}}$
have the form
$\mathfrak{g}_{\unicode[STIX]{x1D6FC}}$
have the form
 $$\begin{eqnarray}\mathfrak{g}_{\unicode[STIX]{x1D6FC}}=\left\{\left(\begin{array}{@{}cccc@{}}0 & & x & \\ & 0 & & (x~\text{or}~-x)\\ & & 0 & \\ & & & 0\end{array}\right):x\in \mathbb{C}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{g}_{\unicode[STIX]{x1D6FC}}=\left\{\left(\begin{array}{@{}cccc@{}}0 & & x & \\ & 0 & & (x~\text{or}~-x)\\ & & 0 & \\ & & & 0\end{array}\right):x\in \mathbb{C}\right\}\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle & x~\text{sits at}~(i,j)~\text{and}~-x~\text{sits at}~(n+1-j,n+1-i)~\text{if}~\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}, & \displaystyle \nonumber\\ \displaystyle & x~\text{sits at}~(i,n+1-j)~\text{and}~x~\text{sits at}~(j,n+1-i)~\text{if}~\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j},i\neq j, & \displaystyle \nonumber\\ \displaystyle & x~\text{sits at}~(i,n+1-i)~\text{if}~\unicode[STIX]{x1D6FC}=2\unicode[STIX]{x1D6FC}_{i}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & x~\text{sits at}~(i,j)~\text{and}~-x~\text{sits at}~(n+1-j,n+1-i)~\text{if}~\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}, & \displaystyle \nonumber\\ \displaystyle & x~\text{sits at}~(i,n+1-j)~\text{and}~x~\text{sits at}~(j,n+1-i)~\text{if}~\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j},i\neq j, & \displaystyle \nonumber\\ \displaystyle & x~\text{sits at}~(i,n+1-i)~\text{if}~\unicode[STIX]{x1D6FC}=2\unicode[STIX]{x1D6FC}_{i}. & \displaystyle \nonumber\end{eqnarray}$$
The corresponding root subgroups
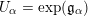 $U_{\unicode[STIX]{x1D6FC}}=\exp (\mathfrak{g}_{\unicode[STIX]{x1D6FC}})$
have the same form with ones on the diagonal. Figure 2 shows the positive root spaces and root subgroups for
$U_{\unicode[STIX]{x1D6FC}}=\exp (\mathfrak{g}_{\unicode[STIX]{x1D6FC}})$
have the same form with ones on the diagonal. Figure 2 shows the positive root spaces and root subgroups for
![]() $n=4$
.
$n=4$
.
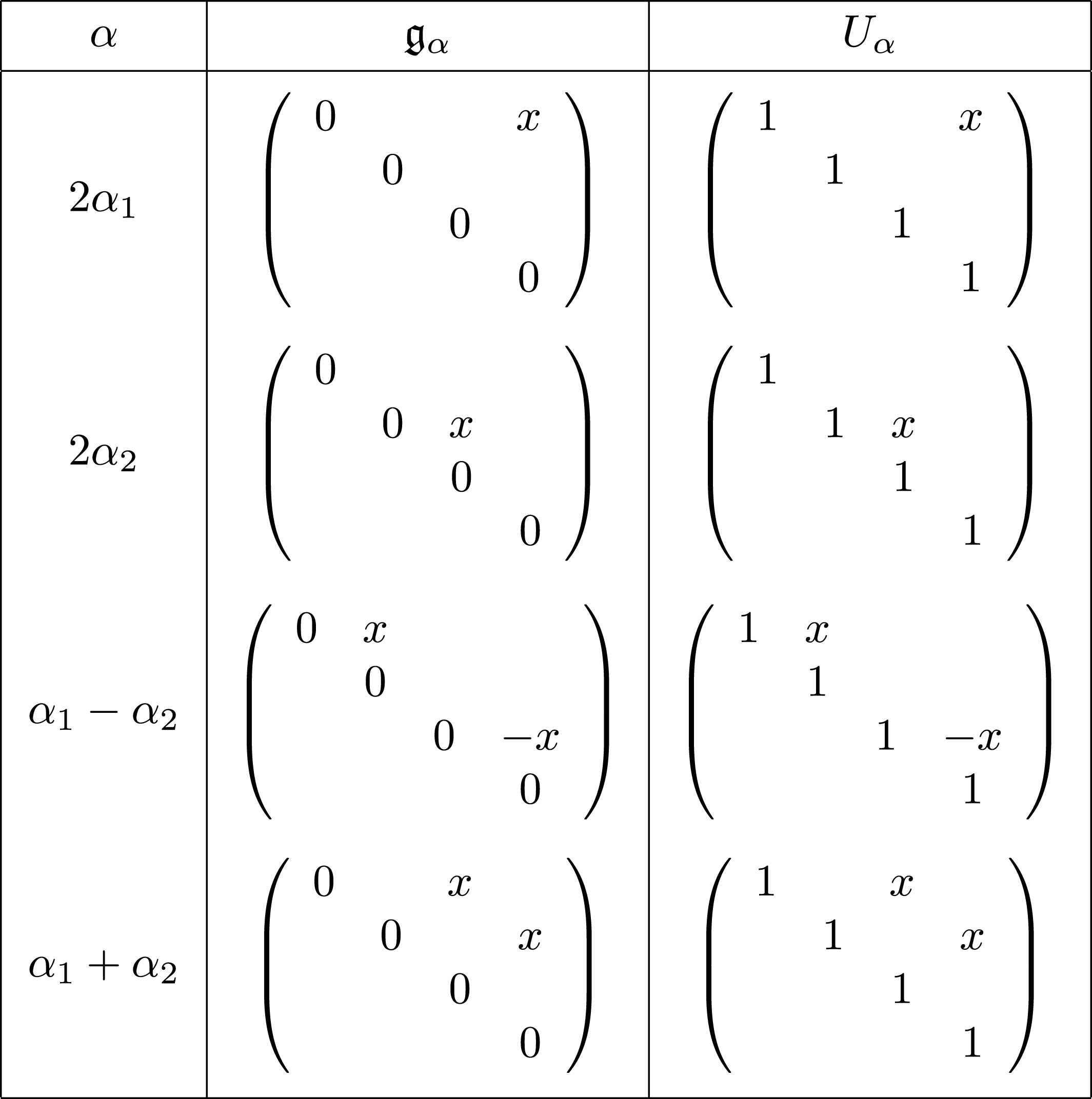
Figure 2. Root subspaces and root subgroups of
![]() $\operatorname{Sp}_{4}$
.
$\operatorname{Sp}_{4}$
.
Definition 5.2. For a closed subset
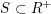 $S\subset R^{+}$
let
$S\subset R^{+}$
let
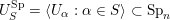 $U_{S}^{\text{Sp}}=\langle U_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in S\rangle \subset \operatorname{Sp}_{n}$
be the corresponding unipotent subgroup generated by the root subgroups in
$U_{S}^{\text{Sp}}=\langle U_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in S\rangle \subset \operatorname{Sp}_{n}$
be the corresponding unipotent subgroup generated by the root subgroups in
![]() $\operatorname{Sp}_{n}$
, normalised by the maximal diagonal torus in
$\operatorname{Sp}_{n}$
, normalised by the maximal diagonal torus in
![]() $\operatorname{Sp}_{n}$
. We define the family
$\operatorname{Sp}_{n}$
. We define the family
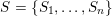 $S=\{S_{1},\ldots ,S_{n}\}$
of subsets of
$S=\{S_{1},\ldots ,S_{n}\}$
of subsets of
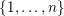 $\{1,\ldots ,n\}$
in such way that
$\{1,\ldots ,n\}$
in such way that
![]() $S_{i}$
collects all possible nonzero entries in the
$S_{i}$
collects all possible nonzero entries in the
![]() $j$
th column in
$j$
th column in
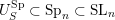 $U_{S}^{\text{Sp}}\subset \operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
, that is
$U_{S}^{\text{Sp}}\subset \operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
, that is
 $$\begin{eqnarray}S_{j}=\{i:\exists u\in U_{S}^{\text{Sp}}\subset \operatorname{Sp}_{n}\subset \operatorname{SL}_{n}~\text{such that}~u_{ij}\neq 0\}.\end{eqnarray}$$
$$\begin{eqnarray}S_{j}=\{i:\exists u\in U_{S}^{\text{Sp}}\subset \operatorname{Sp}_{n}\subset \operatorname{SL}_{n}~\text{such that}~u_{ij}\neq 0\}.\end{eqnarray}$$
These subsets can be described using the roots in
![]() $S$
as follows:
$S$
as follows:
 $$\begin{eqnarray}S_{j}=\left\{\begin{array}{@{}ll@{}}\{j\}\cup \{i:\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\in S\}\quad & \text{for}~1\leqslant j\leqslant l,\\ \{j\}\cup \{i:\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{n+1-j}~\text{or}~\unicode[STIX]{x1D6FC}_{j}+\unicode[STIX]{x1D6FC}_{n+1-i}~\text{or}~\unicode[STIX]{x1D6FC}_{n+1-j}-\unicode[STIX]{x1D6FC}_{n+1-i}~\text{is in}~S\}\quad & \text{for}~l+1\leqslant j\leqslant 2l.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}S_{j}=\left\{\begin{array}{@{}ll@{}}\{j\}\cup \{i:\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\in S\}\quad & \text{for}~1\leqslant j\leqslant l,\\ \{j\}\cup \{i:\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{n+1-j}~\text{or}~\unicode[STIX]{x1D6FC}_{j}+\unicode[STIX]{x1D6FC}_{n+1-i}~\text{or}~\unicode[STIX]{x1D6FC}_{n+1-j}-\unicode[STIX]{x1D6FC}_{n+1-i}~\text{is in}~S\}\quad & \text{for}~l+1\leqslant j\leqslant 2l.\end{array}\right.\end{eqnarray}$$
In what follows, we will use the same notation
![]() $S$
for a set of positive roots for
$S$
for a set of positive roots for
![]() $\operatorname{Sp}_{n}$
, for the corresponding subset family
$\operatorname{Sp}_{n}$
, for the corresponding subset family
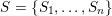 $S=\{S_{1},\ldots ,S_{n}\}$
and the corresponding set of entries
$S=\{S_{1},\ldots ,S_{n}\}$
and the corresponding set of entries
 $$\begin{eqnarray}S=\{(i,j)\in \{1,\ldots ,n\}\times \{1,\ldots ,n\}:i\in S_{j}\}\end{eqnarray}$$
$$\begin{eqnarray}S=\{(i,j)\in \{1,\ldots ,n\}\times \{1,\ldots ,n\}:i\in S_{j}\}\end{eqnarray}$$
indexing all possibly nonzero entries of
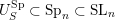 $U_{S}^{\text{Sp}}\subset \operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
.
$U_{S}^{\text{Sp}}\subset \operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
.
Example 5.3. For
![]() $\operatorname{Sp}_{4}$
the closed subset
$\operatorname{Sp}_{4}$
the closed subset
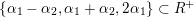 $\{\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2},2\unicode[STIX]{x1D6FC}_{1}\}\subset R^{+}$
defines the regular subgroup
$\{\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2},2\unicode[STIX]{x1D6FC}_{1}\}\subset R^{+}$
defines the regular subgroup
 $$\begin{eqnarray}U_{S}^{\text{Sp}}=\left\{\left(\begin{array}{@{}cccc@{}}1 & a & b & c\\ 0 & 1 & 0 & b\\ 0 & 0 & 1 & -a\\ 0 & 0 & 0 & 1\end{array}\right):a,b,c\in \mathbb{C}\right\}\subset \operatorname{Sp}_{4}(\mathbb{C})\end{eqnarray}$$
$$\begin{eqnarray}U_{S}^{\text{Sp}}=\left\{\left(\begin{array}{@{}cccc@{}}1 & a & b & c\\ 0 & 1 & 0 & b\\ 0 & 0 & 1 & -a\\ 0 & 0 & 0 & 1\end{array}\right):a,b,c\in \mathbb{C}\right\}\subset \operatorname{Sp}_{4}(\mathbb{C})\end{eqnarray}$$
with the corresponding subset family
 $$\begin{eqnarray}S_{1}=\{1\},\quad S_{2}=\{1,2\},\quad S_{3}=\{1,3\},\quad S_{4}=\{1,2,3,4\}.\end{eqnarray}$$
$$\begin{eqnarray}S_{1}=\{1\},\quad S_{2}=\{1,2\},\quad S_{3}=\{1,3\},\quad S_{4}=\{1,2,3,4\}.\end{eqnarray}$$
Lemma 5.4.
-
(i) If
 $U_{S}^{\text{Sp}}\subset \operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
is a Borel-regular subgroup, then the subset family
$U_{S}^{\text{Sp}}\subset \operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
is a Borel-regular subgroup, then the subset family
 $S=\{S_{1},\ldots ,S_{n}\}$
defines a Borel regular subgroup
$S=\{S_{1},\ldots ,S_{n}\}$
defines a Borel regular subgroup
 $U_{S}^{\text{SL}}$
of
$U_{S}^{\text{SL}}$
of
 $\operatorname{SL}_{n}$
such that
$\operatorname{SL}_{n}$
such that
 $U_{S}^{\text{Sp}}=U_{S}^{\text{SL}}\cap \operatorname{Sp}_{n}$
. Equivalently, if
$U_{S}^{\text{Sp}}=U_{S}^{\text{SL}}\cap \operatorname{Sp}_{n}$
. Equivalently, if
 $(i,j)\in S$
, then
$(i,j)\in S$
, then
 $(i-1,j),(i,j+1)\in S$
.
$(i-1,j),(i,j+1)\in S$
. -
(ii) The set
 $S$
is symmetric about the antidiagonal:
$S$
is symmetric about the antidiagonal:
 $(i,j)\in S\Leftrightarrow (n+1-j,n+1-i)\in S$
.
$(i,j)\in S\Leftrightarrow (n+1-j,n+1-i)\in S$
.
Proof. (i) Follows from the fact that the embedding
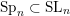 $\operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
preserves the Borel subgroup of upper triangular matrices in
$\operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
preserves the Borel subgroup of upper triangular matrices in
![]() $\operatorname{SL}_{n}$
. Positive root subspaces of
$\operatorname{SL}_{n}$
. Positive root subspaces of
![]() $\operatorname{SL}_{n}$
correspond to entries above the diagonal, and every such entry defines a unique positive root subspace of
$\operatorname{SL}_{n}$
correspond to entries above the diagonal, and every such entry defines a unique positive root subspace of
![]() $\operatorname{Sp}_{n}$
.
$\operatorname{Sp}_{n}$
.
(ii) Follows from the symmetry of the Lie algebra
![]() $\mathfrak{sp}_{n}$
in
$\mathfrak{sp}_{n}$
in
![]() $\mathfrak{sl}_{n}$
: all root subspaces are symmetric about the antidiagonal in
$\mathfrak{sl}_{n}$
: all root subspaces are symmetric about the antidiagonal in
![]() $\mathfrak{sl}_{n}$
.◻
$\mathfrak{sl}_{n}$
.◻
Example 5.5. In
![]() $\operatorname{Sp}_{4}$
the subset
$\operatorname{Sp}_{4}$
the subset
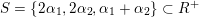 $S=\{2\unicode[STIX]{x1D6FC}_{1},2\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}\}\subset R^{+}$
is closed under addition of positive roots and therefore defines a Borel-regular subgroup
$S=\{2\unicode[STIX]{x1D6FC}_{1},2\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}\}\subset R^{+}$
is closed under addition of positive roots and therefore defines a Borel-regular subgroup
 $$\begin{eqnarray}U_{S}^{\text{Sp}}=\left\{\left(\begin{array}{@{}cccc@{}}1 & 0 & a & b\\ 0 & 1 & c & a\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right):a,b,c\in \mathbb{C}\right\}\subset \operatorname{Sp}_{4}(\mathbb{C}).\end{eqnarray}$$
$$\begin{eqnarray}U_{S}^{\text{Sp}}=\left\{\left(\begin{array}{@{}cccc@{}}1 & 0 & a & b\\ 0 & 1 & c & a\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right):a,b,c\in \mathbb{C}\right\}\subset \operatorname{Sp}_{4}(\mathbb{C}).\end{eqnarray}$$
The corresponding subset family is
 $$\begin{eqnarray}S_{1}=\{1\},\quad S_{2}=\{2\},\quad S_{3}=\{1,2,3\},\quad S_{4}=\{1,2,4\}\end{eqnarray}$$
$$\begin{eqnarray}S_{1}=\{1\},\quad S_{2}=\{2\},\quad S_{3}=\{1,2,3\},\quad S_{4}=\{1,2,4\}\end{eqnarray}$$
which defines the Borel-regular subgroup
 $$\begin{eqnarray}U_{S}^{\text{SL}}=\left\{\left(\begin{array}{@{}cccc@{}}1 & 0 & a & b\\ 0 & 1 & c & d\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right):a,b,c,d\in \mathbb{C}\right\}\subset \operatorname{SL}_{4}.\end{eqnarray}$$
$$\begin{eqnarray}U_{S}^{\text{SL}}=\left\{\left(\begin{array}{@{}cccc@{}}1 & 0 & a & b\\ 0 & 1 & c & d\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right):a,b,c,d\in \mathbb{C}\right\}\subset \operatorname{SL}_{4}.\end{eqnarray}$$
Lemma 5.4 implies that
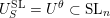 $U_{S}^{\text{SL}}=U^{\unicode[STIX]{x1D703}}\subset \operatorname{SL}_{n}$
corresponds to some monotone increasing sequence
$U_{S}^{\text{SL}}=U^{\unicode[STIX]{x1D703}}\subset \operatorname{SL}_{n}$
corresponds to some monotone increasing sequence
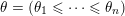 $\unicode[STIX]{x1D703}=(\unicode[STIX]{x1D703}_{1}\leqslant \cdots \leqslant \unicode[STIX]{x1D703}_{n})$
where
$\unicode[STIX]{x1D703}=(\unicode[STIX]{x1D703}_{1}\leqslant \cdots \leqslant \unicode[STIX]{x1D703}_{n})$
where
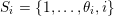 $S_{i}=\{1,\ldots ,\unicode[STIX]{x1D703}_{i},i\}$
. Due to the antidiagonal symmetry there is a unique integer
$S_{i}=\{1,\ldots ,\unicode[STIX]{x1D703}_{i},i\}$
. Due to the antidiagonal symmetry there is a unique integer
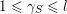 $1\leqslant \unicode[STIX]{x1D6FE}_{S}\leqslant l$
which satisfies that
$1\leqslant \unicode[STIX]{x1D6FE}_{S}\leqslant l$
which satisfies that
 $$\begin{eqnarray}(\unicode[STIX]{x1D6FE}_{S},n+1-\unicode[STIX]{x1D6FE}_{S})\in S\quad \text{but}~(\unicode[STIX]{x1D6FE}_{S}+1,n-\unicode[STIX]{x1D6FE}_{S})\notin S.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FE}_{S},n+1-\unicode[STIX]{x1D6FE}_{S})\in S\quad \text{but}~(\unicode[STIX]{x1D6FE}_{S}+1,n-\unicode[STIX]{x1D6FE}_{S})\notin S.\end{eqnarray}$$
We call
![]() $\unicode[STIX]{x1D6FE}_{S}$
the crossing point of
$\unicode[STIX]{x1D6FE}_{S}$
the crossing point of
![]() $S$
because the boundary of the region of free parameters intersect the antidiagonal at the point
$S$
because the boundary of the region of free parameters intersect the antidiagonal at the point
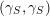 $(\unicode[STIX]{x1D6FE}_{S},\unicode[STIX]{x1D6FE}_{S})$
, see Figure 3 for an example.
$(\unicode[STIX]{x1D6FE}_{S},\unicode[STIX]{x1D6FE}_{S})$
, see Figure 3 for an example.

Figure 3. A domain
![]() $S$
symmetric about the antidiagonal with crossing point
$S$
symmetric about the antidiagonal with crossing point
![]() $\unicode[STIX]{x1D6FE}_{S}=3$
and its symplectic fundamental domain.
$\unicode[STIX]{x1D6FE}_{S}=3$
and its symplectic fundamental domain.
Definition 5.6. Let
 $S=(S_{1},\ldots ,S_{n})\subset \{1,\ldots ,n\}\times \{1,\ldots ,n\}$
be a domain which is:
$S=(S_{1},\ldots ,S_{n})\subset \{1,\ldots ,n\}\times \{1,\ldots ,n\}$
be a domain which is:
-
(i) symmetric about the antidiagonal, that is
 $(i,j)\in {\mathcal{S}}\Leftrightarrow (n+1-j,n+1-i)\in {\mathcal{S}}$
;
$(i,j)\in {\mathcal{S}}\Leftrightarrow (n+1-j,n+1-i)\in {\mathcal{S}}$
; -
(ii) Borel-regular, that is,
 $(i,j)\in {\mathcal{S}}\Rightarrow (i,j+1),(i-1,j)\in {\mathcal{S}}$
.
$(i,j)\in {\mathcal{S}}\Rightarrow (i,j+1),(i-1,j)\in {\mathcal{S}}$
.
We define the symplectic fundamental domain to be
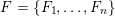 $F=\{F_{1},\ldots ,F_{n}\}$
such that
$F=\{F_{1},\ldots ,F_{n}\}$
such that
 $$\begin{eqnarray}F_{i}=\left\{\begin{array}{@{}ll@{}}S_{i},\quad & i\leqslant n-\unicode[STIX]{x1D6FE}_{{\mathcal{S}}},\\ \{1,2,\ldots ,i\},\quad & i>n-\unicode[STIX]{x1D6FE}_{{\mathcal{S}}}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}F_{i}=\left\{\begin{array}{@{}ll@{}}S_{i},\quad & i\leqslant n-\unicode[STIX]{x1D6FE}_{{\mathcal{S}}},\\ \{1,2,\ldots ,i\},\quad & i>n-\unicode[STIX]{x1D6FE}_{{\mathcal{S}}}.\end{array}\right.\end{eqnarray}$$
Note that
![]() $F$
is no longer symmetric about the antidiagonal but it remains Borel regular and
$F$
is no longer symmetric about the antidiagonal but it remains Borel regular and
 $U_{F}=U^{\unicode[STIX]{x1D703}_{F}}$
corresponds to the modified sequence
$U_{F}=U^{\unicode[STIX]{x1D703}_{F}}$
corresponds to the modified sequence
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{F}=\{\unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n-\unicode[STIX]{x1D6FE}_{S}},n-\unicode[STIX]{x1D6FE}_{S},\ldots ,n-1\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{F}=\{\unicode[STIX]{x1D703}_{1},\ldots ,\unicode[STIX]{x1D703}_{n-\unicode[STIX]{x1D6FE}_{S}},n-\unicode[STIX]{x1D6FE}_{S},\ldots ,n-1\}.\end{eqnarray}$$
See Figure 3 for an example. Recall that we fixed a basis
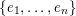 $\{e_{1},\ldots ,e_{n}\}$
of
$\{e_{1},\ldots ,e_{n}\}$
of
![]() $\mathbb{C}^{n}$
to get the embedding
$\mathbb{C}^{n}$
to get the embedding
 $\operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
of the right form. The corresponding point
$\operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
of the right form. The corresponding point
 $$\begin{eqnarray}p_{F}=\bigoplus _{U\in F}\wedge _{i\in U}e_{i}\in {\mathcal{W}}_{F}=\bigoplus _{U\in F}\wedge ^{|U|}\mathbb{C}^{n}\end{eqnarray}$$
$$\begin{eqnarray}p_{F}=\bigoplus _{U\in F}\wedge _{i\in U}e_{i}\in {\mathcal{W}}_{F}=\bigoplus _{U\in F}\wedge ^{|U|}\mathbb{C}^{n}\end{eqnarray}$$
has the right stabiliser in
![]() $\operatorname{Sp}_{n}$
according to the following.
$\operatorname{Sp}_{n}$
according to the following.
Theorem 5.7. The stabiliser of
![]() $p_{F}$
in
$p_{F}$
in
![]() $\operatorname{Sp}_{n}$
is
$\operatorname{Sp}_{n}$
is
![]() $U_{S}^{\text{Sp}}$
.
$U_{S}^{\text{Sp}}$
.
Proof. Let
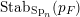 $\operatorname{Stab}_{\text{Sp}_{n}}(p_{F})$
(respectively
$\operatorname{Stab}_{\text{Sp}_{n}}(p_{F})$
(respectively
 $\operatorname{Stab}_{\text{SL}_{n}}(p_{F})$
) denote the stabiliser of
$\operatorname{Stab}_{\text{SL}_{n}}(p_{F})$
) denote the stabiliser of
![]() $p_{F}$
in
$p_{F}$
in
![]() $\operatorname{Sp}_{n}$
(respectively
$\operatorname{Sp}_{n}$
(respectively
![]() $\operatorname{SL}_{n}$
). Then
$\operatorname{SL}_{n}$
). Then
 $$\begin{eqnarray}\operatorname{Stab}_{\text{Sp}_{n}}(p_{F})=\operatorname{Stab}_{\text{SL}_{n}}(p_{F})\cap \text{Sp}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Stab}_{\text{Sp}_{n}}(p_{F})=\operatorname{Stab}_{\text{SL}_{n}}(p_{F})\cap \text{Sp}_{n}.\end{eqnarray}$$
But, according to Lemma 3.1,
 $\operatorname{Stab}_{\text{SL}_{n}}(p_{F})=U_{F}^{\text{SL}}$
and due to the antidiagonal symmetry of
$\operatorname{Stab}_{\text{SL}_{n}}(p_{F})=U_{F}^{\text{SL}}$
and due to the antidiagonal symmetry of
![]() $\operatorname{Sp}_{n}$
,
$\operatorname{Sp}_{n}$
,
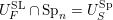 $U_{F}^{\text{SL}}\cap \operatorname{Sp}_{n}=U_{S}^{\text{Sp}}$
, which proves the statement.◻
$U_{F}^{\text{SL}}\cap \operatorname{Sp}_{n}=U_{S}^{\text{Sp}}$
, which proves the statement.◻
We define the symplectic Grosshans pair using the corresponding ring family as before:
 $$\begin{eqnarray}\tilde{F}=\{F_{i_{1}}\cup \cdots \cup F_{i_{r}}:1\leqslant i_{1}<\cdots <i_{r}\leqslant n\}\subset 2^{\{1,\ldots ,n\}}\end{eqnarray}$$
$$\begin{eqnarray}\tilde{F}=\{F_{i_{1}}\cup \cdots \cup F_{i_{r}}:1\leqslant i_{1}<\cdots <i_{r}\leqslant n\}\subset 2^{\{1,\ldots ,n\}}\end{eqnarray}$$
and then
 $$\begin{eqnarray}p_{\tilde{F}}=\bigoplus _{U\in \tilde{F}}\wedge _{i\in U}e_{i}\in {\mathcal{W}}_{\tilde{F}}=\bigoplus _{U\in \tilde{F}}\wedge ^{|U|}\mathbb{C}^{n}\end{eqnarray}$$
$$\begin{eqnarray}p_{\tilde{F}}=\bigoplus _{U\in \tilde{F}}\wedge _{i\in U}e_{i}\in {\mathcal{W}}_{\tilde{F}}=\bigoplus _{U\in \tilde{F}}\wedge ^{|U|}\mathbb{C}^{n}\end{eqnarray}$$
has the same stabiliser in
![]() $\operatorname{Sp}_{n}$
as
$\operatorname{Sp}_{n}$
as
![]() $p_{F}$
.
$p_{F}$
.
Corollary 5.8. The stabiliser of
![]() $p_{\tilde{F}}$
in
$p_{\tilde{F}}$
in
![]() $\operatorname{Sp}_{n}$
is
$\operatorname{Sp}_{n}$
is
![]() $U_{S}^{\text{Sp}}$
.
$U_{S}^{\text{Sp}}$
.
Recall the definition of a fat Borel subgroup from the Introduction: for
![]() $\operatorname{Sp}_{2l}$
these are the Borel-regular subgroups which contain
$\operatorname{Sp}_{2l}$
these are the Borel-regular subgroups which contain
 $\{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}:1\leqslant i<j\leqslant l\}$
. In particular, these contain
$\{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}:1\leqslant i<j\leqslant l\}$
. In particular, these contain
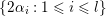 $\{2\unicode[STIX]{x1D6FC}_{i}:1\leqslant i\leqslant l\}$
and ‘fatness’ is equivalent to saying that the crossing point is
$\{2\unicode[STIX]{x1D6FC}_{i}:1\leqslant i\leqslant l\}$
and ‘fatness’ is equivalent to saying that the crossing point is
![]() $\unicode[STIX]{x1D6FE}_{S}=l$
.
$\unicode[STIX]{x1D6FE}_{S}=l$
.
Theorem 5.9. Let
![]() $n=2l$
and
$n=2l$
and
 $F=\{F_{1},\ldots ,F_{n}\}$
be the symplectic fundamental domain corresponding to a Borel-regular subgroup
$F=\{F_{1},\ldots ,F_{n}\}$
be the symplectic fundamental domain corresponding to a Borel-regular subgroup
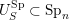 $U_{S}^{\text{Sp}}\subset \operatorname{Sp}_{n}$
with
$U_{S}^{\text{Sp}}\subset \operatorname{Sp}_{n}$
with
![]() $\unicode[STIX]{x1D6FE}_{S}=l$
. Then the pair
$\unicode[STIX]{x1D6FE}_{S}=l$
. Then the pair
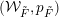 $({\mathcal{W}}_{\tilde{F}},p_{\tilde{F}})$
is a Grosshans pair for
$({\mathcal{W}}_{\tilde{F}},p_{\tilde{F}})$
is a Grosshans pair for
![]() $U_{S}^{\text{Sp}}$
. This proves Theorem 1.3 for symplectic groups.
$U_{S}^{\text{Sp}}$
. This proves Theorem 1.3 for symplectic groups.
We devote the rest of this section to the proof of Theorem 5.9. Note that
![]() $\unicode[STIX]{x1D6FE}_{S}=l$
is equivalent to saying that the top right quarter
$\unicode[STIX]{x1D6FE}_{S}=l$
is equivalent to saying that the top right quarter
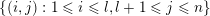 $\{(i,j):1\leqslant i\leqslant l,l+1\leqslant j\leqslant n\}$
belongs to
$\{(i,j):1\leqslant i\leqslant l,l+1\leqslant j\leqslant n\}$
belongs to
![]() $F$
. In other words
$F$
. In other words
![]() $F$
corresponds to a sequence
$F$
corresponds to a sequence
 $$\begin{eqnarray}\unicode[STIX]{x1D703}^{F}=(\unicode[STIX]{x1D703}_{1}\leqslant \cdots \leqslant \unicode[STIX]{x1D703}_{l},l,l+1,\ldots ,n-1).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}^{F}=(\unicode[STIX]{x1D703}_{1}\leqslant \cdots \leqslant \unicode[STIX]{x1D703}_{l},l,l+1,\ldots ,n-1).\end{eqnarray}$$
See Figure 4 for an example.

Figure 4. The fundamental domain of a fat Borel-regular subgroup of
![]() $\operatorname{Sp}_{8}$
. Here
$\operatorname{Sp}_{8}$
. Here
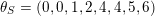 $\unicode[STIX]{x1D703}_{S}=(0,0,1,2,4,4,5,6)$
and
$\unicode[STIX]{x1D703}_{S}=(0,0,1,2,4,4,5,6)$
and
 $\unicode[STIX]{x1D703}_{F}=(0,0,1,2,4,5,6,7)$
.
$\unicode[STIX]{x1D703}_{F}=(0,0,1,2,4,5,6,7)$
.
Recall that elements of the Borel
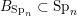 $B_{\text{Sp}_{n}}\subset \operatorname{Sp}_{n}$
have the form
$B_{\text{Sp}_{n}}\subset \operatorname{Sp}_{n}$
have the form
 $$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}b_{11} & b_{12} & \cdots \, & b_{1n}\\ 0 & b_{22} & & \\ & & \ddots & b_{n-1n}\\ 0 & & 0 & b_{nn}\end{array}\right)\quad \text{where}~b_{ii}=b_{n+1-i,n+1-i}^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}b_{11} & b_{12} & \cdots \, & b_{1n}\\ 0 & b_{22} & & \\ & & \ddots & b_{n-1n}\\ 0 & & 0 & b_{nn}\end{array}\right)\quad \text{where}~b_{ii}=b_{n+1-i,n+1-i}^{-1}\end{eqnarray}$$
and the off-diagonal entries
![]() $b_{ij}$
are not independent, but we will not use the exact form of these entries in this argument. The boundary points in
$b_{ij}$
are not independent, but we will not use the exact form of these entries in this argument. The boundary points in
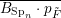 $\overline{B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}}$
are limits of the form
$\overline{B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}}$
are limits of the form
 $$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}\cdot p_{\tilde{F}},\end{eqnarray}$$
$$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}\cdot p_{\tilde{F}},\end{eqnarray}$$
where
![]() $(b^{(m)})$
is a normalised sequence in the sense of Definition 4.2. We define the vanishing spectrum and the sets
$(b^{(m)})$
is a normalised sequence in the sense of Definition 4.2. We define the vanishing spectrum and the sets
![]() $B_{\mathbf{u}}^{\text{Sp}}$
exactly the same way as they are defined for
$B_{\mathbf{u}}^{\text{Sp}}$
exactly the same way as they are defined for
![]() $\operatorname{SL}_{n}$
in Definitions 4.2 and 4.3, that is, for
$\operatorname{SL}_{n}$
in Definitions 4.2 and 4.3, that is, for
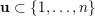 $\mathbf{u}\subset \{1,\ldots ,n\}$
we let
$\mathbf{u}\subset \{1,\ldots ,n\}$
we let
 $$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}=\Big\{p^{\infty }\,\in \,\overline{B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}}:\exists ~\text{norm. seq.}~(b^{(m)})\subset \operatorname{Sp}_{n}~\text{s.t.}~p^{\infty }=\lim _{m\rightarrow \infty }\!b^{(m)}\,\cdot \,p_{\tilde{F}}~\text{and}~\text{VSpec}(b^{(m)})\,=\,\mathbf{u}\Big\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}=\Big\{p^{\infty }\,\in \,\overline{B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}}:\exists ~\text{norm. seq.}~(b^{(m)})\subset \operatorname{Sp}_{n}~\text{s.t.}~p^{\infty }=\lim _{m\rightarrow \infty }\!b^{(m)}\,\cdot \,p_{\tilde{F}}~\text{and}~\text{VSpec}(b^{(m)})\,=\,\mathbf{u}\Big\}.\end{eqnarray}$$
The embedding
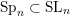 $\operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
implies that
$\operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
implies that
 $$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}\subseteq {\mathcal{B}}_{\boldsymbol{ u}}^{\text{SL}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}\subseteq {\mathcal{B}}_{\boldsymbol{ u}}^{\text{SL}}.\end{eqnarray}$$
Note that the first proof of Lemma 4.4 applies for the symplectic case and therefore
 $$\begin{eqnarray}{\mathcal{B}}_{\emptyset }^{\text{Sp}}=B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\emptyset }^{\text{Sp}}=B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}.\end{eqnarray}$$
This means that, again, all boundary points sit in a
![]() $B_{\mathbf{u}}^{\text{Sp}}$
with some nonempty
$B_{\mathbf{u}}^{\text{Sp}}$
with some nonempty
![]() $\mathbf{u}$
:
$\mathbf{u}$
:
 $$\begin{eqnarray}\overline{B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}}\setminus B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}\subset \mathop{\bigcup }_{\mathbf{u}\neq \emptyset }{\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}.\end{eqnarray}$$
$$\begin{eqnarray}\overline{B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}}\setminus B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}\subset \mathop{\bigcup }_{\mathbf{u}\neq \emptyset }{\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}.\end{eqnarray}$$
In what follows we adapt the argument developed for left Borel regular subgroups of
![]() $\operatorname{SL}_{n}$
to Borel regular subgroups of
$\operatorname{SL}_{n}$
to Borel regular subgroups of
![]() $\operatorname{Sp}_{n}$
. We start with two remarks on notations and definitions.
$\operatorname{Sp}_{n}$
. We start with two remarks on notations and definitions.
-
(i) Since
 $\unicode[STIX]{x1D703}^{F}$
is monotone increasing,
$\unicode[STIX]{x1D703}^{F}$
is monotone increasing,
 $\unicode[STIX]{x1D703}_{Z}^{F}=\unicode[STIX]{x1D703}_{\max (Z)}^{F}$
holds for all
$\unicode[STIX]{x1D703}_{Z}^{F}=\unicode[STIX]{x1D703}_{\max (Z)}^{F}$
holds for all
 $Z\subseteq \{1,\ldots ,n\}$
.
$Z\subseteq \{1,\ldots ,n\}$
. -
(ii) Since
 $\unicode[STIX]{x1D703}_{n}^{F}=n$
, every subset
$\unicode[STIX]{x1D703}_{n}^{F}=n$
, every subset
 $\mathbf{u}$
is automatically covered in the sense of Definition 4.6.
$\mathbf{u}$
is automatically covered in the sense of Definition 4.6.
We have the following stronger version of Lemma 4.12.
Lemma 5.10. If
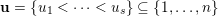 $\mathbf{u}=\{u_{1}<\cdots <u_{s}\}\subseteq \{1,\ldots ,n\}$
is such that
$\mathbf{u}=\{u_{1}<\cdots <u_{s}\}\subseteq \{1,\ldots ,n\}$
is such that
![]() $u_{1}>l$
, then
$u_{1}>l$
, then
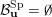 ${\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}=\emptyset$
.
${\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}=\emptyset$
.
Proof. Let
![]() $(b^{(m)})$
be a normalised sequence with vanishing spectrum
$(b^{(m)})$
be a normalised sequence with vanishing spectrum
![]() $\mathbf{u}$
. If
$\mathbf{u}$
. If
 $u_{1}\geqslant l+1$
, or equivalently
$u_{1}\geqslant l+1$
, or equivalently
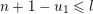 $n+1-u_{1}\leqslant l$
, then the relation
$n+1-u_{1}\leqslant l$
, then the relation
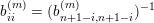 $b_{ii}^{(m)}=(b_{n+1-i,n+1-i}^{(m)})^{-1}$
implies that
$b_{ii}^{(m)}=(b_{n+1-i,n+1-i}^{(m)})^{-1}$
implies that
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }b_{ii}^{(m)}\neq 0\quad \text{for}~1\leqslant i<n+1-u_{1}\quad \text{and}\quad \lim _{m\rightarrow \infty }|b_{n+1-u_{1},n+1-u_{1}}^{(m)}|=\infty .\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }b_{ii}^{(m)}\neq 0\quad \text{for}~1\leqslant i<n+1-u_{1}\quad \text{and}\quad \lim _{m\rightarrow \infty }|b_{n+1-u_{1},n+1-u_{1}}^{(m)}|=\infty .\end{eqnarray}$$
However,
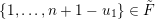 $\{1,\ldots ,n+1-u_{1}\}\in \tilde{F}$
and
$\{1,\ldots ,n+1-u_{1}\}\in \tilde{F}$
and
 $$\begin{eqnarray}p_{\{1,\ldots ,n+1-u_{1}\}}^{\infty }=\lim _{m\rightarrow \infty }\biggl(\mathop{\prod }_{i=1}^{n+1-u_{1}}b_{ii}^{(m)}\biggr)\cdot \wedge _{i=1}^{n+1-u_{1}}e_{i}\end{eqnarray}$$
$$\begin{eqnarray}p_{\{1,\ldots ,n+1-u_{1}\}}^{\infty }=\lim _{m\rightarrow \infty }\biggl(\mathop{\prod }_{i=1}^{n+1-u_{1}}b_{ii}^{(m)}\biggr)\cdot \wedge _{i=1}^{n+1-u_{1}}e_{i}\end{eqnarray}$$
is not bounded, so this coordinate of
![]() $p^{\infty }$
does not exist, a contradiction.◻
$p^{\infty }$
does not exist, a contradiction.◻
Let
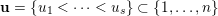 $\mathbf{u}=\{u_{1}<\cdots <u_{s}\}\subset \{1,\ldots ,n\}$
be a subset with
$\mathbf{u}=\{u_{1}<\cdots <u_{s}\}\subset \{1,\ldots ,n\}$
be a subset with
![]() $u_{1}\leqslant l$
and let
$u_{1}\leqslant l$
and let
 $$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{F}}=\bigoplus _{U\in \tilde{F}}p_{U}^{\infty }\in {\mathcal{B}}_{\boldsymbol{ u}}^{\text{Sp}}\end{eqnarray}$$
$$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{F}}=\bigoplus _{U\in \tilde{F}}p_{U}^{\infty }\in {\mathcal{B}}_{\boldsymbol{ u}}^{\text{Sp}}\end{eqnarray}$$
be a limit point defined by the normalised sequence
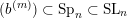 $(b^{(m)})\subset \operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
such that
$(b^{(m)})\subset \operatorname{Sp}_{n}\subset \operatorname{SL}_{n}$
such that
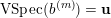 $\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
. Note that
$\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
. Note that
![]() $(b^{(m)})$
is a normalised sequence in the Borel
$(b^{(m)})$
is a normalised sequence in the Borel
![]() $B_{\text{SL}_{n}}$
of
$B_{\text{SL}_{n}}$
of
![]() $\operatorname{SL}_{n}$
too, and therefore we can restate Lemma 4.10.
$\operatorname{SL}_{n}$
too, and therefore we can restate Lemma 4.10.
Lemma 5.11. Let
 $\mathbf{u}=\{u_{1}<\cdots <u_{s}\}\subset \{1,\ldots ,n\}$
be a subset with
$\mathbf{u}=\{u_{1}<\cdots <u_{s}\}\subset \{1,\ldots ,n\}$
be a subset with
![]() $u_{1}\leqslant l$
. Let
$u_{1}\leqslant l$
. Let
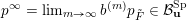 $p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{F}}\in {\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}$
be a limit point defined by the normalised sequence
$p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{F}}\in {\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}$
be a limit point defined by the normalised sequence
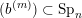 $(b^{(m)})\subset \operatorname{Sp}_{n}$
such that
$(b^{(m)})\subset \operatorname{Sp}_{n}$
such that
 $\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
. If
$\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
. If
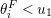 $\unicode[STIX]{x1D703}_{i}^{F}<u_{1}$
for some
$\unicode[STIX]{x1D703}_{i}^{F}<u_{1}$
for some
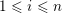 $1\leqslant i\leqslant n$
, then
$1\leqslant i\leqslant n$
, then
 $\lim _{m\rightarrow \infty }b^{(m)}e_{i}\in \mathbb{C}^{n}$
exists.
$\lim _{m\rightarrow \infty }b^{(m)}e_{i}\in \mathbb{C}^{n}$
exists.
We define in accordance with Definition 4.13 the set
 $$\begin{eqnarray}{\mathcal{V}}(p^{\infty })=\{U\in \tilde{F}:p_{U}^{\infty }\neq 0,\unicode[STIX]{x1D703}_{U}^{F}\geqslant u_{1}\}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{V}}(p^{\infty })=\{U\in \tilde{F}:p_{U}^{\infty }\neq 0,\unicode[STIX]{x1D703}_{U}^{F}\geqslant u_{1}\}\end{eqnarray}$$
and
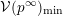 ${\mathcal{V}}(p^{\infty })_{\text{min}}$
using the same order. Proposition 4.14 tells something about points in
${\mathcal{V}}(p^{\infty })_{\text{min}}$
using the same order. Proposition 4.14 tells something about points in
![]() ${\mathcal{B}}_{\mathbf{u}}^{\text{SL}}$
and since
${\mathcal{B}}_{\mathbf{u}}^{\text{SL}}$
and since
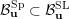 ${\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}\subset {\mathcal{B}}_{\mathbf{u}}^{\text{SL}}$
these properties hold for points in
${\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}\subset {\mathcal{B}}_{\mathbf{u}}^{\text{SL}}$
these properties hold for points in
![]() ${\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}$
too. In short we have the following analog of Proposition 4.14.
${\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}$
too. In short we have the following analog of Proposition 4.14.
Proposition 5.12. Let
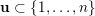 $\mathbf{u}\subset \{1,\ldots ,n\}$
be a subset with
$\mathbf{u}\subset \{1,\ldots ,n\}$
be a subset with
![]() $u_{1}\leqslant l$
, covered by
$u_{1}\leqslant l$
, covered by
![]() $\tilde{F}$
and
$\tilde{F}$
and
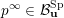 $p^{\infty }\in {\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}$
. If
$p^{\infty }\in {\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}$
. If
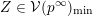 $Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
, then
$Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}$
, then
 $$\begin{eqnarray}[p_{Z}^{\infty }]\subset \mathop{\bigcap }_{V\in {\mathcal{V}}(p^{\infty })}[p_{V}^{\infty }].\end{eqnarray}$$
$$\begin{eqnarray}[p_{Z}^{\infty }]\subset \mathop{\bigcap }_{V\in {\mathcal{V}}(p^{\infty })}[p_{V}^{\infty }].\end{eqnarray}$$
Using Definition 4.18 we can talk about the width
![]() $\unicode[STIX]{x1D714}(p^{\infty })$
of a boundary point
$\unicode[STIX]{x1D714}(p^{\infty })$
of a boundary point
![]() $p^{\infty }$
and let
$p^{\infty }$
and let
 $$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}=\{p^{\infty }\in {\mathcal{B}}_{\boldsymbol{ u}}^{\text{Sp}}:\unicode[STIX]{x1D714}(p^{\infty })=r\}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}=\{p^{\infty }\in {\mathcal{B}}_{\boldsymbol{ u}}^{\text{Sp}}:\unicode[STIX]{x1D714}(p^{\infty })=r\}\end{eqnarray}$$
denote the set of points in
![]() ${\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}$
of width
${\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}$
of width
![]() $r$
. Then we have a (not necessary disjoint) finite decomposition
$r$
. Then we have a (not necessary disjoint) finite decomposition
 $$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}=\mathop{\bigcup }_{u_{1}<r}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp}}=\mathop{\bigcup }_{u_{1}<r}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}.\end{eqnarray}$$
Remark 4.20 on unipotent base change remains valid if we choose our base change matrix
![]() $A$
from
$A$
from
![]() $B_{\text{Sp}_{n}}$
, and such a base change will leave
$B_{\text{Sp}_{n}}$
, and such a base change will leave
![]() ${\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}$
intact for all
${\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}$
intact for all
![]() $\mathbf{u}$
and
$\mathbf{u}$
and
![]() $r$
. As a corollary we have the following analog of Remark 4.21.
$r$
. As a corollary we have the following analog of Remark 4.21.
Remark 5.13. Let
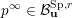 $p^{\infty }\in {\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}$
and
$p^{\infty }\in {\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}$
and
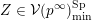 $Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}^{\text{Sp}}$
. By definition this means that
$Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}^{\text{Sp}}$
. By definition this means that
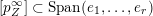 $[p_{Z}^{\infty }]\subset \operatorname{Span}(e_{1},\ldots ,e_{r})$
but
$[p_{Z}^{\infty }]\subset \operatorname{Span}(e_{1},\ldots ,e_{r})$
but
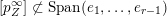 $[p_{Z}^{\infty }]\not \subset \operatorname{Span}(e_{1},\ldots ,e_{r-1})$
so there is a vector
$[p_{Z}^{\infty }]\not \subset \operatorname{Span}(e_{1},\ldots ,e_{r-1})$
so there is a vector
 $$\begin{eqnarray}w=e_{r}+w_{r-1}e_{r-1}+\cdots +w_{1}e_{1}\in [p_{Z}^{\infty }].\end{eqnarray}$$
$$\begin{eqnarray}w=e_{r}+w_{r-1}e_{r-1}+\cdots +w_{1}e_{1}\in [p_{Z}^{\infty }].\end{eqnarray}$$
Define the Lie algebra element
 $$\begin{eqnarray}X^{w}:=\left(\begin{array}{@{}ccccccccc@{}}0 & & & w_{1} & & & & & \\ & \ddots & & \vdots & & & & & \\ & & & w_{r-1} & & & & & \\ & & & 0 & & & & & \\ & & & & \ddots & & & & \\ & & & & & 0 & -w_{r-1} & \cdots \, & -w_{1}\\ & & & & & & \ddots & & \\ & & & & & & & & 0\end{array}\right)\in \mathfrak{sp}_{n},\end{eqnarray}$$
$$\begin{eqnarray}X^{w}:=\left(\begin{array}{@{}ccccccccc@{}}0 & & & w_{1} & & & & & \\ & \ddots & & \vdots & & & & & \\ & & & w_{r-1} & & & & & \\ & & & 0 & & & & & \\ & & & & \ddots & & & & \\ & & & & & 0 & -w_{r-1} & \cdots \, & -w_{1}\\ & & & & & & \ddots & & \\ & & & & & & & & 0\end{array}\right)\in \mathfrak{sp}_{n},\end{eqnarray}$$
where we put
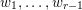 $w_{1},\ldots ,w_{r-1}$
into the
$w_{1},\ldots ,w_{r-1}$
into the
![]() $r$
th column and
$r$
th column and
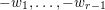 $-w_{1},\ldots ,-w_{r-1}$
into the
$-w_{1},\ldots ,-w_{r-1}$
into the
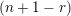 $(n+1-r)$
th row.
$(n+1-r)$
th row.
![]() $X^{w}$
sits in the Lie algebra of
$X^{w}$
sits in the Lie algebra of
![]() $B_{\text{Sp}_{n}}$
and
$B_{\text{Sp}_{n}}$
and
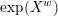 $\exp (X^{w})$
is a unipotent element of
$\exp (X^{w})$
is a unipotent element of
![]() $B_{\text{Sp}_{n}}$
. This defines the new basis
$B_{\text{Sp}_{n}}$
. This defines the new basis
 $\bar{e}_{i}=\exp (X^{w})\cdot e_{i}$
. Let
$\bar{e}_{i}=\exp (X^{w})\cdot e_{i}$
. Let
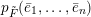 $p_{\tilde{F}}(\bar{e}_{1},\ldots ,\bar{e}_{n})$
denote the base point
$p_{\tilde{F}}(\bar{e}_{1},\ldots ,\bar{e}_{n})$
denote the base point
![]() $p_{\tilde{F}}$
written in the new basis. Then
$p_{\tilde{F}}$
written in the new basis. Then
 $$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{F}}=\lim _{m\rightarrow \infty }(\exp (X^{w})b^{(m)}\exp (-X^{w}))p_{\tilde{F}}(\bar{e}_{1},\ldots ,\bar{e}_{n}).\end{eqnarray}$$
$$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{F}}=\lim _{m\rightarrow \infty }(\exp (X^{w})b^{(m)}\exp (-X^{w}))p_{\tilde{F}}(\bar{e}_{1},\ldots ,\bar{e}_{n}).\end{eqnarray}$$
Similarly to Remark 4.20 we note that since
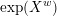 $\exp (X^{w})$
is unipotent, the new sequence
$\exp (X^{w})$
is unipotent, the new sequence
 $$\begin{eqnarray}\tilde{b}^{(m)}=\exp (X^{w})b^{(m)}\exp (-X^{w})\end{eqnarray}$$
$$\begin{eqnarray}\tilde{b}^{(m)}=\exp (X^{w})b^{(m)}\exp (-X^{w})\end{eqnarray}$$
has the same vanishing spectrum
![]() $\mathbf{u}$
and
$\mathbf{u}$
and
![]() $[p_{Z}^{\infty }]$
in this new basis has width
$[p_{Z}^{\infty }]$
in this new basis has width
![]() $r$
again and therefore
$r$
again and therefore
 $$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}(e_{1},\ldots ,e_{n})={\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}(\bar{e}_{1},\ldots ,\bar{e}_{n})\quad \text{for all}~\mathbf{u},r.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}(e_{1},\ldots ,e_{n})={\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}(\bar{e}_{1},\ldots ,\bar{e}_{n})\quad \text{for all}~\mathbf{u},r.\end{eqnarray}$$
In this new basis, however,
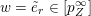 $w=\tilde{e}_{r}\in [p_{Z}^{\infty }]$
holds.
$w=\tilde{e}_{r}\in [p_{Z}^{\infty }]$
holds.
The cornerstone of our argument for
![]() $\operatorname{SL}(n)$
was Proposition 4.22 on the structure of the subsets
$\operatorname{SL}(n)$
was Proposition 4.22 on the structure of the subsets
![]() ${\mathcal{B}}_{\mathbf{u}}^{r}$
. The same proposition remains true for
${\mathcal{B}}_{\mathbf{u}}^{r}$
. The same proposition remains true for
![]() $\operatorname{Sp}_{n}$
, but we need a careful review of the proof which was based on proper modifications of the sequence
$\operatorname{Sp}_{n}$
, but we need a careful review of the proof which was based on proper modifications of the sequence
![]() $(b^{(m)})$
: the problem with the original argument is that the modified sequence sits in
$(b^{(m)})$
: the problem with the original argument is that the modified sequence sits in
![]() $\operatorname{SL}(n)$
but not necessarily in
$\operatorname{SL}(n)$
but not necessarily in
![]() $\operatorname{Sp}_{n}$
.
$\operatorname{Sp}_{n}$
.
Proposition 5.14. Let
![]() $s\geqslant 2$
and
$s\geqslant 2$
and
 $\mathbf{u}=\{u_{1}<\cdots <u_{s}\}$
be a subset with
$\mathbf{u}=\{u_{1}<\cdots <u_{s}\}$
be a subset with
![]() $u_{1}\leqslant l$
. Then we have the following.
$u_{1}\leqslant l$
. Then we have the following.
-
(a) If
 $r\notin \mathbf{u}$
and
$r\notin \mathbf{u}$
and
 $\unicode[STIX]{x1D703}_{r}^{F}<u_{1}$
, then there is a continuous injection
$\unicode[STIX]{x1D703}_{r}^{F}<u_{1}$
, then there is a continuous injection
 $\unicode[STIX]{x1D70C}:{\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}{\hookrightarrow}{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}^{\text{Sp}}$
and therefore
$\unicode[STIX]{x1D70C}:{\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}{\hookrightarrow}{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}^{\text{Sp}}$
and therefore
 $\dim {\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}\leqslant \dim {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}^{\text{Sp}}$
.
$\dim {\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}\leqslant \dim {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}^{\text{Sp}}$
. -
(b) If
 $r\in \mathbf{u}$
, then
$r\in \mathbf{u}$
, then
 ${\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}\subset \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp},r}}\setminus {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp}}$
.
${\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}\subset \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp},r}}\setminus {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp}}$
. -
(c) If
 $r\notin \mathbf{u}$
and
$r\notin \mathbf{u}$
and
 $\unicode[STIX]{x1D703}_{r}^{F}\geqslant u_{1}$
, then
$\unicode[STIX]{x1D703}_{r}^{F}\geqslant u_{1}$
, then  $$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}\subset \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp}}}\setminus {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp}}\quad \text{or}\quad {\mathcal{B}}_{\boldsymbol{ u}}^{\text{Sp},r}\subset \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}^{\text{Sp}}}\setminus {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}^{\text{Sp}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}\subset \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp}}}\setminus {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp}}\quad \text{or}\quad {\mathcal{B}}_{\boldsymbol{ u}}^{\text{Sp},r}\subset \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}^{\text{Sp}}}\setminus {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}^{\text{Sp}}.\end{eqnarray}$$
Proof. To prove (a) assume that
![]() $r\notin \mathbf{u}$
and
$r\notin \mathbf{u}$
and
 $\unicode[STIX]{x1D703}_{r}^{F}<u_{1}$
. Let
$\unicode[STIX]{x1D703}_{r}^{F}<u_{1}$
. Let
 $$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{F}}=\bigoplus _{U\in \tilde{F}}p_{U}^{\infty }\in {\mathcal{B}}_{\boldsymbol{ u}}^{\text{Sp},r}\end{eqnarray}$$
$$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{F}}=\bigoplus _{U\in \tilde{F}}p_{U}^{\infty }\in {\mathcal{B}}_{\boldsymbol{ u}}^{\text{Sp},r}\end{eqnarray}$$
be a limit point such that
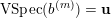 $\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
and
$\operatorname{VSpec}(b^{(m)})=\mathbf{u}$
and
 $Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}^{\text{Sp}}$
. According to Remark 5.13 we can assume that
$Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}^{\text{Sp}}$
. According to Remark 5.13 we can assume that
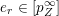 $e_{r}\in [p_{Z}^{\infty }]$
.
$e_{r}\in [p_{Z}^{\infty }]$
.
By Proposition 5.12,
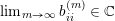 $\lim _{m\rightarrow \infty }b_{ii}^{(m)}\in \mathbb{C}$
exists whenever
$\lim _{m\rightarrow \infty }b_{ii}^{(m)}\in \mathbb{C}$
exists whenever
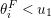 $\unicode[STIX]{x1D703}_{i}^{F}<u_{1}$
and since
$\unicode[STIX]{x1D703}_{i}^{F}<u_{1}$
and since
![]() $r\notin \mathbf{u}$
, this limit is nonzero for
$r\notin \mathbf{u}$
, this limit is nonzero for
![]() $i=r$
:
$i=r$
:
 $$\begin{eqnarray}b_{rr}^{\infty }:=\lim _{m\rightarrow \infty }b_{rr}^{(m)}\in \mathbb{C}\setminus \{0\}.\end{eqnarray}$$
$$\begin{eqnarray}b_{rr}^{\infty }:=\lim _{m\rightarrow \infty }b_{rr}^{(m)}\in \mathbb{C}\setminus \{0\}.\end{eqnarray}$$
We define the entries
![]() $\hat{b}_{ij}^{(m)}$
of a modified sequence
$\hat{b}_{ij}^{(m)}$
of a modified sequence
![]() $\hat{b}^{(m)}$
for
$\hat{b}^{(m)}$
for
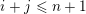 $i+j\leqslant n+1$
as follows:
$i+j\leqslant n+1$
as follows:
 $$\begin{eqnarray}\hat{b}_{ij}^{(m)}=\left\{\begin{array}{@{}ll@{}}b_{rr}^{\infty },\quad & (i,j)=(u_{1},u_{1}),\\ {\displaystyle \frac{1}{b_{rr}^{\infty }}}\cdot b_{rr}^{(m)}\cdot b_{u_{1}u_{1}}^{(m)},\quad & (i,j)=(r,r),\\ {\displaystyle \frac{1}{b_{rr}^{\infty }}}\cdot b_{rj}^{(m)}\cdot b_{u_{1},u_{1}}^{(m)}\quad & \text{if}~i=r,\unicode[STIX]{x1D703}_{j}^{F}\geqslant u_{1}~\text{and}~i+j\leqslant n+1,\\ b_{ij}^{(m)}\quad & \text{otherwise whenever}~i+j\leqslant n+1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\hat{b}_{ij}^{(m)}=\left\{\begin{array}{@{}ll@{}}b_{rr}^{\infty },\quad & (i,j)=(u_{1},u_{1}),\\ {\displaystyle \frac{1}{b_{rr}^{\infty }}}\cdot b_{rr}^{(m)}\cdot b_{u_{1}u_{1}}^{(m)},\quad & (i,j)=(r,r),\\ {\displaystyle \frac{1}{b_{rr}^{\infty }}}\cdot b_{rj}^{(m)}\cdot b_{u_{1},u_{1}}^{(m)}\quad & \text{if}~i=r,\unicode[STIX]{x1D703}_{j}^{F}\geqslant u_{1}~\text{and}~i+j\leqslant n+1,\\ b_{ij}^{(m)}\quad & \text{otherwise whenever}~i+j\leqslant n+1.\end{array}\right.\end{eqnarray}$$
In short, we fix the diagonal entry
![]() $b_{u_{1}u_{1}}^{(m)}$
to be the nonzero constant
$b_{u_{1}u_{1}}^{(m)}$
to be the nonzero constant
![]() $b_{rr}^{\infty }$
and multiply by
$b_{rr}^{\infty }$
and multiply by
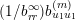 $(1/b_{rr}^{\infty })b_{u_{1}u_{1}}^{(m)}$
the entries on and above the antidiagonal in the
$(1/b_{rr}^{\infty })b_{u_{1}u_{1}}^{(m)}$
the entries on and above the antidiagonal in the
![]() $r$
th row sitting in those columns which cover
$r$
th row sitting in those columns which cover
![]() $u_{1}$
. Recall from (26) that for
$u_{1}$
. Recall from (26) that for
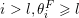 $i>l,\unicode[STIX]{x1D703}_{i}^{F}\geqslant l$
. Since by assumption
$i>l,\unicode[STIX]{x1D703}_{i}^{F}\geqslant l$
. Since by assumption
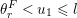 $\unicode[STIX]{x1D703}_{r}^{F}<u_{1}\leqslant l$
, we must have
$\unicode[STIX]{x1D703}_{r}^{F}<u_{1}\leqslant l$
, we must have
![]() $r\leqslant l$
. Then, according to Remark 5.1, there is a unique extension in
$r\leqslant l$
. Then, according to Remark 5.1, there is a unique extension in
![]() $\operatorname{Sp}_{n}$
of these entries to the region below the antidiagonal; we denote this matrix by
$\operatorname{Sp}_{n}$
of these entries to the region below the antidiagonal; we denote this matrix by
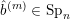 $\hat{b}^{(m)}\in \operatorname{Sp}_{n}$
.
$\hat{b}^{(m)}\in \operatorname{Sp}_{n}$
.
Remark 5.15. For
 $i+j\leqslant n+1$
the modified entries in (15) are equal to the entries in (28). In particular, the first
$i+j\leqslant n+1$
the modified entries in (15) are equal to the entries in (28). In particular, the first
![]() $l$
columns of
$l$
columns of
![]() $\tilde{b}^{(m)}$
and
$\tilde{b}^{(m)}$
and
![]() $\hat{b}^{(m)}$
are the same.
$\hat{b}^{(m)}$
are the same.
Let
 $\tilde{p}^{\infty }=\lim _{m\rightarrow \infty }\tilde{b}^{(m)}p_{\tilde{F}}$
be the limit point defined by the modified sequence (15). We show that
$\tilde{p}^{\infty }=\lim _{m\rightarrow \infty }\tilde{b}^{(m)}p_{\tilde{F}}$
be the limit point defined by the modified sequence (15). We show that
 $\tilde{p}^{\infty }=\hat{p}^{\infty }$
and hence
$\tilde{p}^{\infty }=\hat{p}^{\infty }$
and hence
![]() $\tilde{\unicode[STIX]{x1D70C}}=\hat{\unicode[STIX]{x1D70C}}$
on
$\tilde{\unicode[STIX]{x1D70C}}=\hat{\unicode[STIX]{x1D70C}}$
on
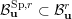 ${\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}\subset {\mathcal{B}}_{\mathbf{u}}^{r}$
and part (a) follows from Proposition 5.12(a).
${\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}\subset {\mathcal{B}}_{\mathbf{u}}^{r}$
and part (a) follows from Proposition 5.12(a).
Let
![]() $V\in \tilde{F}$
. Due to Remark 5.15
$V\in \tilde{F}$
. Due to Remark 5.15
 $$\begin{eqnarray}\hat{p}_{V}^{\infty }=\tilde{p}_{V}^{\infty }\quad \text{holds whenever}~\max (V)\leqslant l.\end{eqnarray}$$
$$\begin{eqnarray}\hat{p}_{V}^{\infty }=\tilde{p}_{V}^{\infty }\quad \text{holds whenever}~\max (V)\leqslant l.\end{eqnarray}$$
If
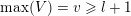 $\max (V)=v\geqslant l+1$
, then in fact
$\max (V)=v\geqslant l+1$
, then in fact
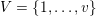 $V=\{1,\ldots ,v\}$
, and therefore using the equality
$V=\{1,\ldots ,v\}$
, and therefore using the equality
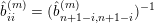 $\hat{b}_{ii}^{(m)}=(\hat{b}_{n+1-i,n+1-i}^{(m)})^{-1}$
we get
$\hat{b}_{ii}^{(m)}=(\hat{b}_{n+1-i,n+1-i}^{(m)})^{-1}$
we get
 $$\begin{eqnarray}\hat{p}_{V}^{\infty }=\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{v}\hat{b}_{ii}^{(m)}\cdot \bigwedge _{i=1}^{v}e_{i}=\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{n-v}\hat{b}_{ii}^{(m)}\cdot \bigwedge _{i=1}^{v}e_{i}=\hat{p}_{\{1,\ldots ,n-v\}}^{\infty }\wedge \bigwedge _{i=n+1-v}^{v}e_{i}.\end{eqnarray}$$
$$\begin{eqnarray}\hat{p}_{V}^{\infty }=\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{v}\hat{b}_{ii}^{(m)}\cdot \bigwedge _{i=1}^{v}e_{i}=\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{n-v}\hat{b}_{ii}^{(m)}\cdot \bigwedge _{i=1}^{v}e_{i}=\hat{p}_{\{1,\ldots ,n-v\}}^{\infty }\wedge \bigwedge _{i=n+1-v}^{v}e_{i}.\end{eqnarray}$$
Similarly,
 $$\begin{eqnarray}\tilde{p}_{V}^{\infty }=\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{v}\tilde{b}_{ii}^{(m)}\cdot \bigwedge _{i=1}^{v}e_{i}=\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{n-v}\tilde{b}_{ii}^{(m)}\cdot \bigwedge _{i=1}^{v}e_{i}=\tilde{p}_{\{1,\ldots ,n-v\}}^{\infty }\wedge \bigwedge _{i=n+1-v}^{v}e_{i}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{p}_{V}^{\infty }=\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{v}\tilde{b}_{ii}^{(m)}\cdot \bigwedge _{i=1}^{v}e_{i}=\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{n-v}\tilde{b}_{ii}^{(m)}\cdot \bigwedge _{i=1}^{v}e_{i}=\tilde{p}_{\{1,\ldots ,n-v\}}^{\infty }\wedge \bigwedge _{i=n+1-v}^{v}e_{i}.\end{eqnarray}$$
However, by (29)
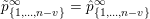 $\tilde{p}_{\{1,\ldots ,n-v\}}^{\infty }=\hat{p}_{\{1,\ldots ,n-v\}}^{\infty }$
and hence
$\tilde{p}_{\{1,\ldots ,n-v\}}^{\infty }=\hat{p}_{\{1,\ldots ,n-v\}}^{\infty }$
and hence
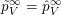 $\tilde{p}_{V}^{\infty }=\hat{p}_{V}^{\infty }$
. So
$\tilde{p}_{V}^{\infty }=\hat{p}_{V}^{\infty }$
. So
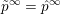 $\tilde{p}^{\infty }=\hat{p}^{\infty }$
and part (a) is proved.
$\tilde{p}^{\infty }=\hat{p}^{\infty }$
and part (a) is proved.
To prove (b) and (c) we define for
![]() $\unicode[STIX]{x1D6FF}\neq 0$
the modified sequence
$\unicode[STIX]{x1D6FF}\neq 0$
the modified sequence
 $$\begin{eqnarray}\hat{b}_{ij}^{(m),\unicode[STIX]{x1D6FF}}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FF},\quad & (i,j)=(u_{1},u_{1}),\\ {\displaystyle \frac{1}{\unicode[STIX]{x1D6FF}}}b_{rr}^{(m)}\cdot b_{u_{1}u_{1}}^{(m)}\quad & \text{if}~(i,j)=(r,r)~\text{and}~r\leqslant l,\\ {\displaystyle \frac{1}{\unicode[STIX]{x1D6FF}}}b_{rj}^{(m)}\cdot b_{u_{1},u_{1}}^{(m)}\quad & \text{if}~i=r,j\geqslant r,\unicode[STIX]{x1D703}_{j}^{F}\geqslant u_{1}~\text{and}~i+j\leqslant n+1,\\ b_{ij}^{(m)}\quad & \text{otherwise whenever}~i+j\leqslant n+1,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\hat{b}_{ij}^{(m),\unicode[STIX]{x1D6FF}}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FF},\quad & (i,j)=(u_{1},u_{1}),\\ {\displaystyle \frac{1}{\unicode[STIX]{x1D6FF}}}b_{rr}^{(m)}\cdot b_{u_{1}u_{1}}^{(m)}\quad & \text{if}~(i,j)=(r,r)~\text{and}~r\leqslant l,\\ {\displaystyle \frac{1}{\unicode[STIX]{x1D6FF}}}b_{rj}^{(m)}\cdot b_{u_{1},u_{1}}^{(m)}\quad & \text{if}~i=r,j\geqslant r,\unicode[STIX]{x1D703}_{j}^{F}\geqslant u_{1}~\text{and}~i+j\leqslant n+1,\\ b_{ij}^{(m)}\quad & \text{otherwise whenever}~i+j\leqslant n+1,\end{array}\right.\end{eqnarray}$$
and its unique extension
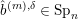 $\hat{b}^{(m),\unicode[STIX]{x1D6FF}}\in \operatorname{Sp}_{n}$
.
$\hat{b}^{(m),\unicode[STIX]{x1D6FF}}\in \operatorname{Sp}_{n}$
.
Remark 5.16. If
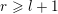 $r\geqslant l+1$
, then the second and third line in (28) are irrelevant and
$r\geqslant l+1$
, then the second and third line in (28) are irrelevant and
![]() $\hat{b}^{(m)}$
differs from
$\hat{b}^{(m)}$
differs from
![]() $b^{(m)}$
only in the
$b^{(m)}$
only in the
![]() $(u_{1},u_{1})$
and
$(u_{1},u_{1})$
and
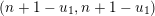 $(n+1-u_{1},n+1-u_{1})$
diagonal entries.
$(n+1-u_{1},n+1-u_{1})$
diagonal entries.
Remark 5.17. For
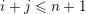 $i+j\leqslant n+1$
the modified entries in (20) are equal to the entries in (32). In particular, the first
$i+j\leqslant n+1$
the modified entries in (20) are equal to the entries in (32). In particular, the first
![]() $l$
columns of
$l$
columns of
![]() $\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}$
and
$\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}$
and
![]() $\hat{b}^{(m),\unicode[STIX]{x1D6FF}}$
are the same.
$\hat{b}^{(m),\unicode[STIX]{x1D6FF}}$
are the same.
If
![]() $r\in \mathbf{u}$
, then
$r\in \mathbf{u}$
, then
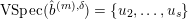 $\operatorname{VSpec}(\hat{b}^{(m),\unicode[STIX]{x1D6FF}})=\{u_{2},\ldots ,u_{s}\}$
. If
$\operatorname{VSpec}(\hat{b}^{(m),\unicode[STIX]{x1D6FF}})=\{u_{2},\ldots ,u_{s}\}$
. If
![]() $r\notin \mathbf{u}$
and
$r\notin \mathbf{u}$
and
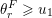 $\unicode[STIX]{x1D703}_{r}^{F}\geqslant u_{1}$
, then
$\unicode[STIX]{x1D703}_{r}^{F}\geqslant u_{1}$
, then
 $$\begin{eqnarray}\operatorname{VSpec}(\hat{b}^{(m),\unicode[STIX]{x1D6FF}})=\left\{\begin{array}{@{}ll@{}}\{u_{2},\ldots ,u_{s}\}\quad & \displaystyle \text{if}~\lim _{m\rightarrow \infty }b_{rr}^{(m)}b_{u_{1}u_{1}}^{(m)}\neq 0,\\ \{u_{2},\ldots ,u_{s}\}\cup \{r\}\quad & \displaystyle \text{if}~\lim _{m\rightarrow \infty }b_{rr}^{(m)}b_{u_{1}u_{1}}^{(m)}=0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{VSpec}(\hat{b}^{(m),\unicode[STIX]{x1D6FF}})=\left\{\begin{array}{@{}ll@{}}\{u_{2},\ldots ,u_{s}\}\quad & \displaystyle \text{if}~\lim _{m\rightarrow \infty }b_{rr}^{(m)}b_{u_{1}u_{1}}^{(m)}\neq 0,\\ \{u_{2},\ldots ,u_{s}\}\cup \{r\}\quad & \displaystyle \text{if}~\lim _{m\rightarrow \infty }b_{rr}^{(m)}b_{u_{1}u_{1}}^{(m)}=0.\end{array}\right.\end{eqnarray}$$
Let
 $\tilde{p}^{\infty ,\unicode[STIX]{x1D6FF}}=\lim _{m\rightarrow \infty }\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}p_{\tilde{F}}$
be the limit point defined by the modified sequence (20). The same argument as above shows again that
$\tilde{p}^{\infty ,\unicode[STIX]{x1D6FF}}=\lim _{m\rightarrow \infty }\tilde{b}^{(m),\unicode[STIX]{x1D6FF}}p_{\tilde{F}}$
be the limit point defined by the modified sequence (20). The same argument as above shows again that
 $$\begin{eqnarray}\hat{p}^{\infty ,\unicode[STIX]{x1D6FF}}=\tilde{p}^{\infty ,\unicode[STIX]{x1D6FF}}\quad \text{for all}~\unicode[STIX]{x1D6FF}>0\end{eqnarray}$$
$$\begin{eqnarray}\hat{p}^{\infty ,\unicode[STIX]{x1D6FF}}=\tilde{p}^{\infty ,\unicode[STIX]{x1D6FF}}\quad \text{for all}~\unicode[STIX]{x1D6FF}>0\end{eqnarray}$$
and hence by (21) we have
 $$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\hat{p}^{\infty ,\unicode[STIX]{x1D6FF}}=\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\tilde{p}^{\infty ,\unicode[STIX]{x1D6FF}}=p^{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\hat{p}^{\infty ,\unicode[STIX]{x1D6FF}}=\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\tilde{p}^{\infty ,\unicode[STIX]{x1D6FF}}=p^{\infty }.\end{eqnarray}$$
Therefore
 $$\begin{eqnarray}p^{\infty }\in \left\{\begin{array}{@{}ll@{}}\overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp}}}\quad & \text{if}~r\in \mathbf{u},\\ \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp}}}~\text{or}~\overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}^{\text{Sp}}}\quad & \text{if}~r\notin \mathbf{u}~\text{and}~\unicode[STIX]{x1D703}_{r}^{F}\geqslant u_{1}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}p^{\infty }\in \left\{\begin{array}{@{}ll@{}}\overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp}}}\quad & \text{if}~r\in \mathbf{u},\\ \overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp}}}~\text{or}~\overline{{\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}^{\text{Sp}}}\quad & \text{if}~r\notin \mathbf{u}~\text{and}~\unicode[STIX]{x1D703}_{r}^{F}\geqslant u_{1}.\end{array}\right.\end{eqnarray}$$
But
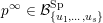 $p^{\infty }\in {\mathcal{B}}_{\{u_{1},\ldots ,u_{s}\}}^{\text{Sp}}$
so
$p^{\infty }\in {\mathcal{B}}_{\{u_{1},\ldots ,u_{s}\}}^{\text{Sp}}$
so
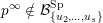 $p^{\infty }\notin {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp}}$
and
$p^{\infty }\notin {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}}^{\text{Sp}}$
and
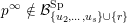 $p^{\infty }\notin {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}^{\text{Sp}}$
, and we are done.◻
$p^{\infty }\notin {\mathcal{B}}_{\{u_{2},\ldots ,u_{s}\}\cup \{r\}}^{\text{Sp}}$
, and we are done.◻
Proposition 5.14 reduces the proof of Theorem 5.9 the same way as in the
![]() $\operatorname{SL}_{n}$
case to the simple situation when
$\operatorname{SL}_{n}$
case to the simple situation when
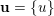 $\mathbf{u}=\{u\}$
has a single element. Before we start studying this special case we state the following analog of Lemma 4.24.
$\mathbf{u}=\{u\}$
has a single element. Before we start studying this special case we state the following analog of Lemma 4.24.
Lemma 5.18. Let
![]() $\unicode[STIX]{x1D6FC}\in R^{-}$
be a negative root. Let
$\unicode[STIX]{x1D6FC}\in R^{-}$
be a negative root. Let
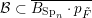 ${\mathcal{B}}\subset \overline{B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}}$
be a
${\mathcal{B}}\subset \overline{B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}}$
be a
![]() $B_{\text{Sp}_{n}}$
-invariant subvariety. Assume that for every point
$B_{\text{Sp}_{n}}$
-invariant subvariety. Assume that for every point
![]() $w\in {\mathcal{B}}$
there is an element
$w\in {\mathcal{B}}$
there is an element
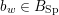 $b_{w}\in B_{\text{Sp}}$
such that
$b_{w}\in B_{\text{Sp}}$
such that
![]() $w$
is fixed by the conjugate
$w$
is fixed by the conjugate
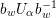 $b_{w}U_{\unicode[STIX]{x1D6FC}}b_{w}^{-1}$
of the root subgroup
$b_{w}U_{\unicode[STIX]{x1D6FC}}b_{w}^{-1}$
of the root subgroup
 $U_{\unicode[STIX]{x1D6FC}}\subset \operatorname{Sp}_{n}$
. Then
$U_{\unicode[STIX]{x1D6FC}}\subset \operatorname{Sp}_{n}$
. Then
 $$\begin{eqnarray}\dim \overline{\operatorname{Sp}_{n}\cdot {\mathcal{B}}}\leqslant \dim \overline{\operatorname{Sp}_{n}\cdot p_{\tilde{F}}}-2.\end{eqnarray}$$
$$\begin{eqnarray}\dim \overline{\operatorname{Sp}_{n}\cdot {\mathcal{B}}}\leqslant \dim \overline{\operatorname{Sp}_{n}\cdot p_{\tilde{F}}}-2.\end{eqnarray}$$
Proof. We can simply copy the proof of Lemma 4.24. Consider the map
 $$\begin{eqnarray}\unicode[STIX]{x1D711}:\operatorname{Sp}_{n}\times {\mathcal{B}}\rightarrow {\mathcal{W}}_{\tilde{F}},\quad \unicode[STIX]{x1D711}(g,w)\mapsto g\cdot w.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}:\operatorname{Sp}_{n}\times {\mathcal{B}}\rightarrow {\mathcal{W}}_{\tilde{F}},\quad \unicode[STIX]{x1D711}(g,w)\mapsto g\cdot w.\end{eqnarray}$$
Choose
![]() $w\in {\mathcal{B}}$
and let
$w\in {\mathcal{B}}$
and let
 $T^{w}=b_{w}U_{\unicode[STIX]{x1D6FC}}b_{w}^{-1}$
be the corresponding subgroup which fixes
$T^{w}=b_{w}U_{\unicode[STIX]{x1D6FC}}b_{w}^{-1}$
be the corresponding subgroup which fixes
![]() $w$
. Since
$w$
. Since
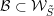 ${\mathcal{B}}\subset {\mathcal{W}}_{\tilde{S}}$
is Borel-invariant, the fibre
${\mathcal{B}}\subset {\mathcal{W}}_{\tilde{S}}$
is Borel-invariant, the fibre
 $\unicode[STIX]{x1D711}^{-1}(g\cdot w)$
contains
$\unicode[STIX]{x1D711}^{-1}(g\cdot w)$
contains
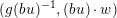 $(g(bu)^{-1},(bu)\cdot w)$
for
$(g(bu)^{-1},(bu)\cdot w)$
for
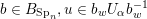 $b\in B_{\text{Sp}_{n}},u\in b_{w}U_{\unicode[STIX]{x1D6FC}}b_{w}^{-1}$
. Since
$b\in B_{\text{Sp}_{n}},u\in b_{w}U_{\unicode[STIX]{x1D6FC}}b_{w}^{-1}$
. Since
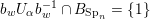 $b_{w}U_{\unicode[STIX]{x1D6FC}}b_{w}^{-1}\cap B_{\text{Sp}_{n}}=\{1\}$
,
$b_{w}U_{\unicode[STIX]{x1D6FC}}b_{w}^{-1}\cap B_{\text{Sp}_{n}}=\{1\}$
,
 $$\begin{eqnarray}\dim (\{bu:b\in B_{\text{Sp}_{n}},u\in b_{w}U_{\unicode[STIX]{x1D6FC}}b_{w}^{-1}\})=\dim (B_{\text{Sp}_{n}})+1\end{eqnarray}$$
$$\begin{eqnarray}\dim (\{bu:b\in B_{\text{Sp}_{n}},u\in b_{w}U_{\unicode[STIX]{x1D6FC}}b_{w}^{-1}\})=\dim (B_{\text{Sp}_{n}})+1\end{eqnarray}$$
and we get
 $$\begin{eqnarray}\displaystyle \dim (\operatorname{Im}(\unicode[STIX]{x1D711})) & = & \displaystyle \dim \operatorname{Sp}_{n}+\dim {\mathcal{B}}-\dim (\text{fibre})\leqslant \dim \operatorname{Sp}_{n}+\dim \overline{B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}}-1-(\dim (B_{\text{Sp}_{n}})+1)\nonumber\\ \displaystyle & = & \displaystyle \dim \operatorname{Sp}_{n}/U_{S}^{\text{Sp}}-2=\dim \overline{\operatorname{Sp}_{n}\cdot p_{\tilde{F}}}-2.\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim (\operatorname{Im}(\unicode[STIX]{x1D711})) & = & \displaystyle \dim \operatorname{Sp}_{n}+\dim {\mathcal{B}}-\dim (\text{fibre})\leqslant \dim \operatorname{Sp}_{n}+\dim \overline{B_{\text{Sp}_{n}}\cdot p_{\tilde{F}}}-1-(\dim (B_{\text{Sp}_{n}})+1)\nonumber\\ \displaystyle & = & \displaystyle \dim \operatorname{Sp}_{n}/U_{S}^{\text{Sp}}-2=\dim \overline{\operatorname{Sp}_{n}\cdot p_{\tilde{F}}}-2.\Box \nonumber\end{eqnarray}$$
First we study the sets
![]() ${\mathcal{B}}_{u}^{\text{Sp},r}$
with
${\mathcal{B}}_{u}^{\text{Sp},r}$
with
![]() $r\leqslant l$
.
$r\leqslant l$
.
Lemma 5.19. Let
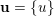 $\mathbf{u}=\{u\}$
and
$\mathbf{u}=\{u\}$
and
![]() $r$
be an integer such that
$r$
be an integer such that
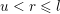 $u<r\leqslant l$
. Let
$u<r\leqslant l$
. Let
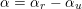 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{r}-\unicode[STIX]{x1D6FC}_{u}$
so that the corresponding root subgroup has two nonzero off-diagonal entries as in (25) where
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{r}-\unicode[STIX]{x1D6FC}_{u}$
so that the corresponding root subgroup has two nonzero off-diagonal entries as in (25) where
![]() $x$
sits in the
$x$
sits in the
![]() $(r,u)$
and
$(r,u)$
and
![]() $-x$
in the
$-x$
in the
 $(n+1-u,n+1-r)$
entry. Then every point in
$(n+1-u,n+1-r)$
entry. Then every point in
![]() ${\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}$
is fixed by a conjugate
${\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}$
is fixed by a conjugate
 $\hat{A}U_{\unicode[STIX]{x1D6FC}}\hat{A}^{-1}$
for some
$\hat{A}U_{\unicode[STIX]{x1D6FC}}\hat{A}^{-1}$
for some
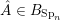 $\hat{A}\in B_{\text{Sp}_{n}}\!$
.
$\hat{A}\in B_{\text{Sp}_{n}}\!$
.
Proof. Let
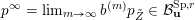 $p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{Z}}\in {\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}$
. We define the matrix
$p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{Z}}\in {\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}$
. We define the matrix
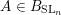 $A\in B_{\text{SL}_{n}}$
and the new matrix
$A\in B_{\text{SL}_{n}}$
and the new matrix
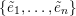 $\{\tilde{e}_{1},\ldots ,\tilde{e}_{n}\}$
satisfying (23) and (22) just as in the proof of Lemma 4.25. Since
$\{\tilde{e}_{1},\ldots ,\tilde{e}_{n}\}$
satisfying (23) and (22) just as in the proof of Lemma 4.25. Since
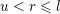 $u<r\leqslant l$
, the matrix
$u<r\leqslant l$
, the matrix
![]() $A$
has nonzero off-diagonal entries only in the first
$A$
has nonzero off-diagonal entries only in the first
![]() $l$
column and by Remark 5.1, it has a unique extension
$l$
column and by Remark 5.1, it has a unique extension
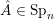 $\hat{A}\in \operatorname{Sp}_{n}$
whose entries above the antidiagonal are equal to those entries of
$\hat{A}\in \operatorname{Sp}_{n}$
whose entries above the antidiagonal are equal to those entries of
![]() $A$
.
$A$
.
We claim that
![]() $p^{\infty }$
is fixed by
$p^{\infty }$
is fixed by
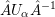 $\hat{A}U_{\unicode[STIX]{x1D6FC}}\hat{A}^{-1}$
. Equivalently,
$\hat{A}U_{\unicode[STIX]{x1D6FC}}\hat{A}^{-1}$
. Equivalently,
![]() $p^{\infty }$
is fixed by
$p^{\infty }$
is fixed by
![]() $U_{\unicode[STIX]{x1D6FC}}$
when written in the basis
$U_{\unicode[STIX]{x1D6FC}}$
when written in the basis
 $\{\tilde{e}_{1},\ldots ,\tilde{e}_{n}\}$
. Since
$\{\tilde{e}_{1},\ldots ,\tilde{e}_{n}\}$
. Since
 $U_{\unicode[STIX]{x1D6FC}}\subset \operatorname{Sp}_{n}$
has nonzero off-diagonal entries only at
$U_{\unicode[STIX]{x1D6FC}}\subset \operatorname{Sp}_{n}$
has nonzero off-diagonal entries only at
![]() $(r,u)$
and
$(r,u)$
and
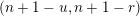 $(n+1-u,n+1-r)$
this follows if we prove that
$(n+1-u,n+1-r)$
this follows if we prove that
![]() $p^{\infty }$
is fixed by both
$p^{\infty }$
is fixed by both
![]() $T^{u,\tilde{e}_{r}}$
and
$T^{u,\tilde{e}_{r}}$
and
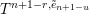 $T^{n+1-r,\tilde{e}_{n+1-u}}$
. Recall from Definition 4.23 the one-parameter subgroup
$T^{n+1-r,\tilde{e}_{n+1-u}}$
. Recall from Definition 4.23 the one-parameter subgroup
 $$\begin{eqnarray}T^{i,v}(\unicode[STIX]{x1D706}):\tilde{e}_{j}\mapsto \left\{\begin{array}{@{}ll@{}}\tilde{e}_{j},\quad & j\neq i,\\ \tilde{e}_{i}+\unicode[STIX]{x1D706}v,\quad & j=i,\end{array}\right.\quad \text{for}~\unicode[STIX]{x1D706}\in \mathbb{C}.\end{eqnarray}$$
$$\begin{eqnarray}T^{i,v}(\unicode[STIX]{x1D706}):\tilde{e}_{j}\mapsto \left\{\begin{array}{@{}ll@{}}\tilde{e}_{j},\quad & j\neq i,\\ \tilde{e}_{i}+\unicode[STIX]{x1D706}v,\quad & j=i,\end{array}\right.\quad \text{for}~\unicode[STIX]{x1D706}\in \mathbb{C}.\end{eqnarray}$$
First,
![]() $p^{\infty }$
is fixed by both
$p^{\infty }$
is fixed by both
![]() $T^{u,\tilde{e}_{r}}$
due to (22) and (23).
$T^{u,\tilde{e}_{r}}$
due to (22) and (23).
To see that
![]() $p^{\infty }$
is fixed by
$p^{\infty }$
is fixed by
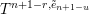 $T^{n+1-r,\tilde{e}_{n+1-u}}$
note that
$T^{n+1-r,\tilde{e}_{n+1-u}}$
note that
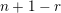 $n+1-r$
and
$n+1-r$
and
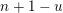 $n+1-u$
are both bigger than
$n+1-u$
are both bigger than
![]() $l$
and therefore
$l$
and therefore
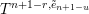 $T^{n+1-r,\tilde{e}_{n+1-u}}$
fixes
$T^{n+1-r,\tilde{e}_{n+1-u}}$
fixes
![]() $p_{V}^{\infty }$
automatically when
$p_{V}^{\infty }$
automatically when
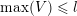 $\max (V)\leqslant l$
.
$\max (V)\leqslant l$
.
When
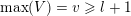 $\max (V)=v\geqslant l+1$
, then in fact
$\max (V)=v\geqslant l+1$
, then in fact
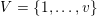 $V=\{1,\ldots ,v\}$
and therefore using the equality
$V=\{1,\ldots ,v\}$
and therefore using the equality
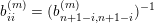 $b_{ii}^{(m)}=(b_{n+1-i,n+1-i}^{(m)})^{-1}$
and Remark 5.15 we get
$b_{ii}^{(m)}=(b_{n+1-i,n+1-i}^{(m)})^{-1}$
and Remark 5.15 we get
 $$\begin{eqnarray}p_{\{1,\ldots ,v\}}^{\infty }=\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{v}b_{ii}^{(m)}\cdot \wedge _{i=1}^{v}e_{i}=\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{n-v}b_{ii}^{(m)}\cdot \wedge _{i=1}^{v}e_{i}.\end{eqnarray}$$
$$\begin{eqnarray}p_{\{1,\ldots ,v\}}^{\infty }=\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{v}b_{ii}^{(m)}\cdot \wedge _{i=1}^{v}e_{i}=\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{n-v}b_{ii}^{(m)}\cdot \wedge _{i=1}^{v}e_{i}.\end{eqnarray}$$
Now we prove that
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{t}b_{ii}^{(m)}=0\quad \text{whenever}~u\leqslant t<r.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{t}b_{ii}^{(m)}=0\quad \text{whenever}~u\leqslant t<r.\end{eqnarray}$$
By Lemma 5.11
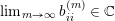 $\lim _{m\rightarrow \infty }b_{ii}^{(m)}\in \mathbb{C}$
exists when
$\lim _{m\rightarrow \infty }b_{ii}^{(m)}\in \mathbb{C}$
exists when
![]() $\unicode[STIX]{x1D703}_{i}^{F}<u$
and since
$\unicode[STIX]{x1D703}_{i}^{F}<u$
and since
![]() $\unicode[STIX]{x1D703}_{u}^{F}<u$
we have
$\unicode[STIX]{x1D703}_{u}^{F}<u$
we have
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{t}b_{ii}^{(m)}=0\quad \text{if}~u\leqslant t~\text{and}~\unicode[STIX]{x1D703}_{t}^{F}<u.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{t}b_{ii}^{(m)}=0\quad \text{if}~u\leqslant t~\text{and}~\unicode[STIX]{x1D703}_{t}^{F}<u.\end{eqnarray}$$
Now let
![]() $t<r$
such that
$t<r$
such that
![]() $\unicode[STIX]{x1D703}_{t}^{F}\geqslant u$
and take
$\unicode[STIX]{x1D703}_{t}^{F}\geqslant u$
and take
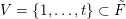 $V=\{1,\ldots ,t\}\subset \tilde{F}$
. If
$V=\{1,\ldots ,t\}\subset \tilde{F}$
. If
![]() $p_{V}^{\infty }\neq 0$
, then by definition
$p_{V}^{\infty }\neq 0$
, then by definition
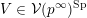 $V\in {\mathcal{V}}(p^{\infty })^{\text{Sp}}$
and therefore by Proposition 5.12
$V\in {\mathcal{V}}(p^{\infty })^{\text{Sp}}$
and therefore by Proposition 5.12
 $$\begin{eqnarray}[p_{Z}^{\infty }]\subset [p_{V}^{\infty }]=[e_{1}\wedge \cdots \wedge e_{v}],\end{eqnarray}$$
$$\begin{eqnarray}[p_{Z}^{\infty }]\subset [p_{V}^{\infty }]=[e_{1}\wedge \cdots \wedge e_{v}],\end{eqnarray}$$
which is a contradiction because
![]() $[p_{Z}^{\infty }]$
has width
$[p_{Z}^{\infty }]$
has width
![]() $r>t$
. Therefore
$r>t$
. Therefore
![]() $p_{V}^{\infty }=0$
, that is,
$p_{V}^{\infty }=0$
, that is,
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{t}b_{ii}^{(m)}=0\quad \text{if}~t<r~\text{and}~\unicode[STIX]{x1D703}_{t}^{F}\geqslant u.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }\mathop{\prod }_{i=1}^{t}b_{ii}^{(m)}=0\quad \text{if}~t<r~\text{and}~\unicode[STIX]{x1D703}_{t}^{F}\geqslant u.\end{eqnarray}$$
Putting these together we get (34). Then
 $$\begin{eqnarray}p_{\{1,\ldots ,v\}}^{\infty }=0\quad \text{for}~n-r<v\leqslant n-u.\end{eqnarray}$$
$$\begin{eqnarray}p_{\{1,\ldots ,v\}}^{\infty }=0\quad \text{for}~n-r<v\leqslant n-u.\end{eqnarray}$$
This means that
 $$\begin{eqnarray}\text{if}~p_{\{1,\ldots ,v\}}^{\infty }\neq 0~\text{then either:}~n+1-r\notin \{1,\ldots ,v\}~\text{or:}~n+1-r~\text{and}~n+1-u~\text{are both in}~\{1,\ldots ,v\}.\end{eqnarray}$$
$$\begin{eqnarray}\text{if}~p_{\{1,\ldots ,v\}}^{\infty }\neq 0~\text{then either:}~n+1-r\notin \{1,\ldots ,v\}~\text{or:}~n+1-r~\text{and}~n+1-u~\text{are both in}~\{1,\ldots ,v\}.\end{eqnarray}$$
In both cases
![]() $p_{\{1,\ldots ,v\}}^{\infty }$
is fixed by
$p_{\{1,\ldots ,v\}}^{\infty }$
is fixed by
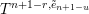 $T^{n+1-r,\tilde{e}_{n+1-u}}$
.◻
$T^{n+1-r,\tilde{e}_{n+1-u}}$
.◻
Finally we study the sets
![]() ${\mathcal{B}}_{u}^{\text{Sp},r}$
with
${\mathcal{B}}_{u}^{\text{Sp},r}$
with
![]() $r>l$
.
$r>l$
.
Lemma 5.20. Let
 $\mathbf{u}=\{u\}$
and
$\mathbf{u}=\{u\}$
and
![]() $r$
be an integer such that
$r$
be an integer such that
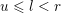 $u\leqslant l<r$
. Let
$u\leqslant l<r$
. Let
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}_{u+1}-\unicode[STIX]{x1D6FC}_{u},\quad & u\leqslant l-1,\\ -2\unicode[STIX]{x1D6FC}_{l},\quad & u=l.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FC}_{u+1}-\unicode[STIX]{x1D6FC}_{u},\quad & u\leqslant l-1,\\ -2\unicode[STIX]{x1D6FC}_{l},\quad & u=l.\end{array}\right.\end{eqnarray}$$
The corresponding negative root subgroup
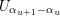 $U_{\unicode[STIX]{x1D6FC}_{u+1}-\unicode[STIX]{x1D6FC}_{u}}$
has nonzero off-diagonal entries as in (25) where
$U_{\unicode[STIX]{x1D6FC}_{u+1}-\unicode[STIX]{x1D6FC}_{u}}$
has nonzero off-diagonal entries as in (25) where
![]() $x$
sits at
$x$
sits at
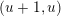 $(u+1,u)$
and
$(u+1,u)$
and
![]() $-x$
sits at
$-x$
sits at
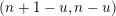 $(n+1-u,n-u)$
, whereas
$(n+1-u,n-u)$
, whereas
![]() $U_{-2\unicode[STIX]{x1D6FC}_{l}}$
has
$U_{-2\unicode[STIX]{x1D6FC}_{l}}$
has
![]() $x$
at
$x$
at
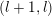 $(l+1,l)$
. Then every point in
$(l+1,l)$
. Then every point in
![]() ${\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}$
is fixed by a conjugate
${\mathcal{B}}_{\mathbf{u}}^{\text{Sp},r}$
is fixed by a conjugate
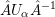 $\hat{A}U_{\unicode[STIX]{x1D6FC}}\hat{A}^{-1}$
for some
$\hat{A}U_{\unicode[STIX]{x1D6FC}}\hat{A}^{-1}$
for some
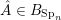 $\hat{A}\in B_{\text{Sp}_{n}}$
.
$\hat{A}\in B_{\text{Sp}_{n}}$
.
Proof. Let
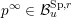 $p^{\infty }\in {\mathcal{B}}_{u}^{\text{Sp},r}$
and
$p^{\infty }\in {\mathcal{B}}_{u}^{\text{Sp},r}$
and
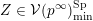 $Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}^{\text{Sp}}$
. By Proposition 5.12, we have the following:
$Z\in {\mathcal{V}}(p^{\infty })_{\text{min}}^{\text{Sp}}$
. By Proposition 5.12, we have the following:
-
(i)
 $[p_{Z}^{\infty }]\subset \bigcap _{V\in {\mathcal{V}}(p^{\infty })^{\text{Sp}}}p_{V}^{\infty }$
, where
$[p_{Z}^{\infty }]\subset \bigcap _{V\in {\mathcal{V}}(p^{\infty })^{\text{Sp}}}p_{V}^{\infty }$
, where
 ${\mathcal{V}}(p^{\infty })^{\text{Sp}}=\{U\in \tilde{F}:p_{U}^{\infty }\neq 0,\unicode[STIX]{x1D703}_{U}\geqslant u\}$
;
${\mathcal{V}}(p^{\infty })^{\text{Sp}}=\{U\in \tilde{F}:p_{U}^{\infty }\neq 0,\unicode[STIX]{x1D703}_{U}\geqslant u\}$
; -
(ii)
 $\unicode[STIX]{x1D714}(p^{\infty })=r$
, and in particular if
$\unicode[STIX]{x1D714}(p^{\infty })=r$
, and in particular if
 $\max (V)<r$
, then
$\max (V)<r$
, then
 $p_{V}^{\infty }\subsetneq \operatorname{Span}(e_{1},\ldots ,e_{r})$
and therefore
$p_{V}^{\infty }\subsetneq \operatorname{Span}(e_{1},\ldots ,e_{r})$
and therefore
 $[p_{Z}^{\infty }]$
cannot sit in
$[p_{Z}^{\infty }]$
cannot sit in
 $[p_{V}^{\infty }]$
. Therefore by (i) (37)
$[p_{V}^{\infty }]$
. Therefore by (i) (37) $$\begin{eqnarray}\text{if}~\unicode[STIX]{x1D703}_{V}^{F}\geqslant u~\text{and}~\max (V)<r,~\text{then}~p_{V}^{\infty }=0.\end{eqnarray}$$
$$\begin{eqnarray}\text{if}~\unicode[STIX]{x1D703}_{V}^{F}\geqslant u~\text{and}~\max (V)<r,~\text{then}~p_{V}^{\infty }=0.\end{eqnarray}$$
By Lemma 5.11
 $$\begin{eqnarray}e_{j}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}e_{j}=\unicode[STIX]{x1D707}_{jj}e_{j}+\cdots +\unicode[STIX]{x1D707}_{1j}e_{1}\quad \text{exists when}~\unicode[STIX]{x1D703}_{j}^{F}<u\end{eqnarray}$$
$$\begin{eqnarray}e_{j}^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}e_{j}=\unicode[STIX]{x1D707}_{jj}e_{j}+\cdots +\unicode[STIX]{x1D707}_{1j}e_{1}\quad \text{exists when}~\unicode[STIX]{x1D703}_{j}^{F}<u\end{eqnarray}$$
and in particular, since only
![]() $b_{uu}^{(m)}$
tends to zero among the diagonal entries, we have
$b_{uu}^{(m)}$
tends to zero among the diagonal entries, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{jj}\neq 0\quad \text{when}~u\neq j\leqslant l,\unicode[STIX]{x1D703}_{j}^{F}<u.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{jj}\neq 0\quad \text{when}~u\neq j\leqslant l,\unicode[STIX]{x1D703}_{j}^{F}<u.\end{eqnarray}$$
Thus we can define the new basis elements
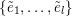 $\{\tilde{e}_{1},\ldots ,\tilde{e}_{l}\}$
as follows:
$\{\tilde{e}_{1},\ldots ,\tilde{e}_{l}\}$
as follows:
 $$\begin{eqnarray}A:\tilde{e}_{j}:=\left\{\begin{array}{@{}ll@{}}e_{j}^{\infty },\quad & u\neq j\leqslant l,\unicode[STIX]{x1D703}_{j}^{F}<u,\\ e_{u},\quad & j=u,\\ e_{j}\quad & \text{otherwise whenever}~j\leqslant l.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}A:\tilde{e}_{j}:=\left\{\begin{array}{@{}ll@{}}e_{j}^{\infty },\quad & u\neq j\leqslant l,\unicode[STIX]{x1D703}_{j}^{F}<u,\\ e_{u},\quad & j=u,\\ e_{j}\quad & \text{otherwise whenever}~j\leqslant l.\end{array}\right.\end{eqnarray}$$
According to Remark 5.1, this can be extended to a linear base change
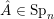 $\hat{A}\in \operatorname{Sp}_{n}$
to get a new basis
$\hat{A}\in \operatorname{Sp}_{n}$
to get a new basis
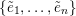 $\{\tilde{e}_{1},\ldots ,\tilde{e}_{n}\}$
.
$\{\tilde{e}_{1},\ldots ,\tilde{e}_{n}\}$
.
If
![]() $\unicode[STIX]{x1D703}_{V}^{F}<u$
, then by Lemma 5.11 again
$\unicode[STIX]{x1D703}_{V}^{F}<u$
, then by Lemma 5.11 again
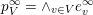 $p_{V}^{\infty }=\wedge _{v\in V}e_{v}^{\infty }$
. Since
$p_{V}^{\infty }=\wedge _{v\in V}e_{v}^{\infty }$
. Since
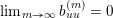 $\lim _{m\rightarrow \infty }b_{uu}^{(m)}=0$
, this means that
$\lim _{m\rightarrow \infty }b_{uu}^{(m)}=0$
, this means that
 $$\begin{eqnarray}e_{u}^{\infty }\subseteq \operatorname{Span}(e_{1},\ldots ,e_{u-1})=\operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u-1}).\end{eqnarray}$$
$$\begin{eqnarray}e_{u}^{\infty }\subseteq \operatorname{Span}(e_{1},\ldots ,e_{u-1})=\operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u-1}).\end{eqnarray}$$
If
![]() $p_{V}^{\infty }\neq 0$
and
$p_{V}^{\infty }\neq 0$
and
![]() $\unicode[STIX]{x1D703}_{V}^{F}<u$
, then
$\unicode[STIX]{x1D703}_{V}^{F}<u$
, then
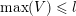 $\max (V)\leqslant l$
(this is because
$\max (V)\leqslant l$
(this is because
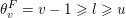 $\unicode[STIX]{x1D703}_{v}^{F}=v-1\geqslant l\geqslant u$
for
$\unicode[STIX]{x1D703}_{v}^{F}=v-1\geqslant l\geqslant u$
for
![]() $v>l$
) and therefore by (38)
$v>l$
) and therefore by (38)
 $$\begin{eqnarray}[p_{V}^{\infty }]\subset \operatorname{Span}(\tilde{e}_{v}:v\in V)\subset \operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u-1},\tilde{e}_{u+1},\ldots ,\tilde{e}_{l}).\end{eqnarray}$$
$$\begin{eqnarray}[p_{V}^{\infty }]\subset \operatorname{Span}(\tilde{e}_{v}:v\in V)\subset \operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u-1},\tilde{e}_{u+1},\ldots ,\tilde{e}_{l}).\end{eqnarray}$$
Together with (37) (and taking account of the assumption that
![]() $r>l$
) this means that
$r>l$
) this means that
 $$\begin{eqnarray}\text{if}~p_{V}^{\infty }\neq 0~\text{and}~\max (V)\leqslant l,~\text{then}~[p_{V}^{\infty }]\subset \operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u-1},\tilde{e}_{u+1},\ldots ,\tilde{e}_{l}).\end{eqnarray}$$
$$\begin{eqnarray}\text{if}~p_{V}^{\infty }\neq 0~\text{and}~\max (V)\leqslant l,~\text{then}~[p_{V}^{\infty }]\subset \operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u-1},\tilde{e}_{u+1},\ldots ,\tilde{e}_{l}).\end{eqnarray}$$
If
![]() $V\in \tilde{F}$
such that
$V\in \tilde{F}$
such that
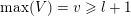 $\max (V)=v\geqslant l+1$
, then
$\max (V)=v\geqslant l+1$
, then
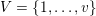 $V=\{1,\ldots ,v\}$
and therefore
$V=\{1,\ldots ,v\}$
and therefore
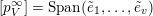 $[p_{V}^{\infty }]=\operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{v})$
. According to (35) we have
$[p_{V}^{\infty }]=\operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{v})$
. According to (35) we have
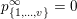 $p_{\{1,\ldots ,v\}}^{\infty }=0$
for
$p_{\{1,\ldots ,v\}}^{\infty }=0$
for
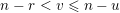 $n-r<v\leqslant n-u$
. Since
$n-r<v\leqslant n-u$
. Since
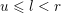 $u\leqslant l<r$
, this means in particular that
$u\leqslant l<r$
, this means in particular that
 $$\begin{eqnarray}p_{V}^{\infty }=p_{\{1,\ldots ,v\}}^{\infty }=0\quad \text{for}~l+1\leqslant v=\max (V)\leqslant n-u.\end{eqnarray}$$
$$\begin{eqnarray}p_{V}^{\infty }=p_{\{1,\ldots ,v\}}^{\infty }=0\quad \text{for}~l+1\leqslant v=\max (V)\leqslant n-u.\end{eqnarray}$$
For
 $v>n-u$
, however,
$v>n-u$
, however,
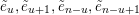 $\tilde{e}_{u},\tilde{e}_{u+1},\tilde{e}_{n-u},\tilde{e}_{n-u+1}$
are all in
$\tilde{e}_{u},\tilde{e}_{u+1},\tilde{e}_{n-u},\tilde{e}_{n-u+1}$
are all in
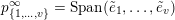 $p_{\{1,\ldots ,v\}}^{\infty }=\operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{v})$
. Together with (39) and (40) this implies that
$p_{\{1,\ldots ,v\}}^{\infty }=\operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{v})$
. Together with (39) and (40) this implies that
 $$\begin{eqnarray}\text{if}~p_{V}^{\infty }\neq 0,~\text{then}\left\{\begin{array}{@{}ll@{}}[p_{V}^{\infty }]\subset \operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u-1},\tilde{e}_{u+1},\ldots ,\tilde{e}_{l})\quad & \text{if}~\max (V)\leqslant l,\\ \operatorname{Span}(\tilde{e}_{u},\tilde{e}_{u+1},\tilde{e}_{n-u},\tilde{e}_{n-u+1})\subset p_{V}^{\infty }\quad & \text{if}~\max (V)>l.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\text{if}~p_{V}^{\infty }\neq 0,~\text{then}\left\{\begin{array}{@{}ll@{}}[p_{V}^{\infty }]\subset \operatorname{Span}(\tilde{e}_{1},\ldots ,\tilde{e}_{u-1},\tilde{e}_{u+1},\ldots ,\tilde{e}_{l})\quad & \text{if}~\max (V)\leqslant l,\\ \operatorname{Span}(\tilde{e}_{u},\tilde{e}_{u+1},\tilde{e}_{n-u},\tilde{e}_{n-u+1})\subset p_{V}^{\infty }\quad & \text{if}~\max (V)>l.\end{array}\right.\end{eqnarray}$$
Thus
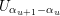 $U_{\unicode[STIX]{x1D6FC}_{u+1}-\unicode[STIX]{x1D6FC}_{u}}$
(for
$U_{\unicode[STIX]{x1D6FC}_{u+1}-\unicode[STIX]{x1D6FC}_{u}}$
(for
![]() $u<l$
) and
$u<l$
) and
![]() $U_{2\unicode[STIX]{x1D6FC}_{l}}$
(for
$U_{2\unicode[STIX]{x1D6FC}_{l}}$
(for
![]() $u=l$
) stabilises
$u=l$
) stabilises
![]() $p^{\infty }$
written in the new basis, so
$p^{\infty }$
written in the new basis, so
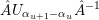 $\hat{A}U_{\unicode[STIX]{x1D6FC}_{u+1}-\unicode[STIX]{x1D6FC}_{u}}\hat{A}^{-1}$
stabilises
$\hat{A}U_{\unicode[STIX]{x1D6FC}_{u+1}-\unicode[STIX]{x1D6FC}_{u}}\hat{A}^{-1}$
stabilises
![]() $p^{\infty }$
in the old basis.◻
$p^{\infty }$
in the old basis.◻
We have finished the proof of Theorem 5.9 and hence Theorem 1.3 is proved.
5.3 Borel-regular subgroups of orthogonal groups
Let
![]() $V$
be an
$V$
be an
![]() $n$
-dimensional complex vector space and
$n$
-dimensional complex vector space and
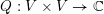 $Q:V\times V\rightarrow \mathbb{C}$
a nondegenerate, symmetric bilinear form on
$Q:V\times V\rightarrow \mathbb{C}$
a nondegenerate, symmetric bilinear form on
![]() $V$
. The orthogonal Lie group is then
$V$
. The orthogonal Lie group is then
 $$\begin{eqnarray}\operatorname{SO}_{n}(V)=\{A\in \operatorname{SL}_{n}(\mathbb{C}):Q(Av,Aw)=Q(v,w)~\text{for all}~v,w\in V\},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{SO}_{n}(V)=\{A\in \operatorname{SL}_{n}(\mathbb{C}):Q(Av,Aw)=Q(v,w)~\text{for all}~v,w\in V\},\end{eqnarray}$$
and the corresponding symplectic Lie algebra is
 $$\begin{eqnarray}\mathfrak{so}_{n}(V)=\{A\in \mathfrak{sl}_{n}(\mathbb{C}):Q(Av,w)+Q(v,Aw)=0~\text{for all}~v,w\in V\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{so}_{n}(V)=\{A\in \mathfrak{sl}_{n}(\mathbb{C}):Q(Av,w)+Q(v,Aw)=0~\text{for all}~v,w\in V\}.\end{eqnarray}$$
To get a compatible embedding of
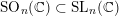 $\operatorname{SO}_{n}(\mathbb{C})\subset \operatorname{SL}_{n}(\mathbb{C})$
with diagonal maximal torus, we take a basis
$\operatorname{SO}_{n}(\mathbb{C})\subset \operatorname{SL}_{n}(\mathbb{C})$
with diagonal maximal torus, we take a basis
 $\{e_{1},\ldots ,e_{n}\}$
of
$\{e_{1},\ldots ,e_{n}\}$
of
![]() $V$
such that
$V$
such that
![]() $Q$
is given by the matrix
$Q$
is given by the matrix
![]() $M$
in the form
$M$
in the form
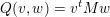 $Q(v,w)=v^{t}Mw$
, and we choose
$Q(v,w)=v^{t}Mw$
, and we choose
![]() $M$
to be the antidiagonal matrix (with
$M$
to be the antidiagonal matrix (with
![]() $n=2l$
or
$n=2l$
or
 $n=2l+1$
)
$n=2l+1$
)

For
![]() $n=2l$
,
$n=2l$
,
![]() $\operatorname{SO}_{n}$
has the same maximal torus as
$\operatorname{SO}_{n}$
has the same maximal torus as
![]() $\operatorname{Sp}_{n}$
and for
$\operatorname{Sp}_{n}$
and for
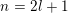 $n=2l+1$
the maximal torus consist of diagonal matrices
$n=2l+1$
the maximal torus consist of diagonal matrices
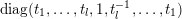 $\operatorname{diag}(t_{1},\ldots ,t_{l},1,t_{l}^{-1},\ldots ,t_{1})$
. The Lie algebra
$\operatorname{diag}(t_{1},\ldots ,t_{l},1,t_{l}^{-1},\ldots ,t_{1})$
. The Lie algebra
![]() $\mathfrak{so}_{n}$
consists of matrices of the form
$\mathfrak{so}_{n}$
consists of matrices of the form
 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}A & B\\ C & -A^{at}\end{array}\right)\quad \text{for}~n=2l\quad \text{and}\quad \left(\begin{array}{@{}ccc@{}}A & \mathbf{v} & B\\ \mathbf{w} & 0 & -\mathbf{v}^{t}J\\ C & -\mathbf{w}^{t}J & -A^{at}\end{array}\right)\quad \text{for}~n=2l+1,\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}A & B\\ C & -A^{at}\end{array}\right)\quad \text{for}~n=2l\quad \text{and}\quad \left(\begin{array}{@{}ccc@{}}A & \mathbf{v} & B\\ \mathbf{w} & 0 & -\mathbf{v}^{t}J\\ C & -\mathbf{w}^{t}J & -A^{at}\end{array}\right)\quad \text{for}~n=2l+1,\end{eqnarray}$$
where
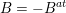 $B=-B^{at}$
,
$B=-B^{at}$
,
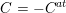 $C=-C^{at}$
and
$C=-C^{at}$
and
![]() $\mathbf{v}$
,
$\mathbf{v}$
,
![]() $\mathbf{w}$
are arrays of length
$\mathbf{w}$
are arrays of length
![]() $l$
and
$l$
and
![]() $J$
is the
$J$
is the
![]() $l\times l$
matrix with ones on the antidiagonal and zero elsewhere. In particular, the antidiagonal entries are all zero in
$l\times l$
matrix with ones on the antidiagonal and zero elsewhere. In particular, the antidiagonal entries are all zero in
![]() $\mathfrak{so}_{n}$
.
$\mathfrak{so}_{n}$
.
Remark 5.21. In particular this means again that any Lie algebra element
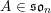 $A\in \mathfrak{so}_{n}$
is uniquely determined by its entries
$A\in \mathfrak{so}_{n}$
is uniquely determined by its entries
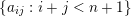 $\{a_{ij}:i+j<n+1\}$
sitting above the antidiagonal.
$\{a_{ij}:i+j<n+1\}$
sitting above the antidiagonal.
The characters and cocharacters are the same as in
![]() $\operatorname{Sp}_{n}$
and the Cartan subalgebra
$\operatorname{Sp}_{n}$
and the Cartan subalgebra
![]() $\mathfrak{h}\subset \mathfrak{so}_{n}$
is
$\mathfrak{h}\subset \mathfrak{so}_{n}$
is
![]() $l$
-dimensional spanned by the diagonal matrices
$l$
-dimensional spanned by the diagonal matrices
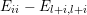 $E_{ii}-E_{l+i,l+i}$
for
$E_{ii}-E_{l+i,l+i}$
for
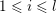 $1\leqslant i\leqslant l$
whose dual is
$1\leqslant i\leqslant l$
whose dual is
![]() $\unicode[STIX]{x1D6FC}_{i}$
. The roots are
$\unicode[STIX]{x1D6FC}_{i}$
. The roots are
 $$\begin{eqnarray}\{\pm \unicode[STIX]{x1D6FC}_{i}\pm \unicode[STIX]{x1D6FC}_{j}\}_{i<j}\quad \text{for}~n=2l\quad \text{and}\quad \{\pm \unicode[STIX]{x1D6FC}_{i}\pm \unicode[STIX]{x1D6FC}_{j}\}_{i<j}\cup \{\pm \unicode[STIX]{x1D6FC}_{i}\}\quad \text{for}~n=2l+1.\end{eqnarray}$$
$$\begin{eqnarray}\{\pm \unicode[STIX]{x1D6FC}_{i}\pm \unicode[STIX]{x1D6FC}_{j}\}_{i<j}\quad \text{for}~n=2l\quad \text{and}\quad \{\pm \unicode[STIX]{x1D6FC}_{i}\pm \unicode[STIX]{x1D6FC}_{j}\}_{i<j}\cup \{\pm \unicode[STIX]{x1D6FC}_{i}\}\quad \text{for}~n=2l+1.\end{eqnarray}$$
The positive roots are
 $$\begin{eqnarray}\displaystyle & n=2l:R^{+}=\{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}, & \displaystyle \nonumber\\ \displaystyle & n=2l+1:R^{+}=\{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}\}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & n=2l:R^{+}=\{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}, & \displaystyle \nonumber\\ \displaystyle & n=2l+1:R^{+}=\{\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}\}_{1\leqslant i<j\leqslant l}\cup \{\unicode[STIX]{x1D6FC}_{i}\}. & \displaystyle \nonumber\end{eqnarray}$$
The root vectors corresponding to the positive roots have two nonzero entries symmetric about the antidiagonal as in
![]() $\operatorname{Sp}_{n}$
but here
$\operatorname{Sp}_{n}$
but here
 $$\begin{eqnarray}\displaystyle & x~\text{sits at}~(i,j)~\text{and}~(-x)~\text{sits at}~(n+1-j,n+1-i)~\text{if}~\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}, & \displaystyle \nonumber\\ \displaystyle & x~\text{sits at}~(i,j+l)~\text{and}~(-x)~\text{sits at}~(l+1-j,n+1-i)~\text{if}~\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j},i\neq j, & \displaystyle \nonumber\\ \displaystyle & x~\text{sits at}~(i,l+1)~\text{and}~(-x)~\text{sits at}~(l+1,n+1-i)~\text{if}~\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & x~\text{sits at}~(i,j)~\text{and}~(-x)~\text{sits at}~(n+1-j,n+1-i)~\text{if}~\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}-\unicode[STIX]{x1D6FC}_{j}, & \displaystyle \nonumber\\ \displaystyle & x~\text{sits at}~(i,j+l)~\text{and}~(-x)~\text{sits at}~(l+1-j,n+1-i)~\text{if}~\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j},i\neq j, & \displaystyle \nonumber\\ \displaystyle & x~\text{sits at}~(i,l+1)~\text{and}~(-x)~\text{sits at}~(l+1,n+1-i)~\text{if}~\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{i}. & \displaystyle \nonumber\end{eqnarray}$$
For a closed subset
 $S\subset R^{+}$
let
$S\subset R^{+}$
let
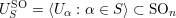 $U_{S}^{\text{SO}}=\langle U_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in S\rangle \subset \operatorname{SO}_{n}$
be the corresponding unipotent subgroup generated by the root subgroups in
$U_{S}^{\text{SO}}=\langle U_{\unicode[STIX]{x1D6FC}}:\unicode[STIX]{x1D6FC}\in S\rangle \subset \operatorname{SO}_{n}$
be the corresponding unipotent subgroup generated by the root subgroups in
![]() $\operatorname{SO}_{n}$
, normalised by the maximal diagonal torus in
$\operatorname{SO}_{n}$
, normalised by the maximal diagonal torus in
![]() $\operatorname{SO}_{n}$
. We define the family
$\operatorname{SO}_{n}$
. We define the family
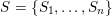 $S=\{S_{1},\ldots ,S_{n}\}$
of subsets in the same way as for
$S=\{S_{1},\ldots ,S_{n}\}$
of subsets in the same way as for
![]() $\operatorname{Sp}_{n}$
, that is,
$\operatorname{Sp}_{n}$
, that is,
![]() $S_{i}$
collects the possible nonzero entries in the
$S_{i}$
collects the possible nonzero entries in the
![]() $j$
th column in
$j$
th column in
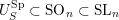 $U_{S}^{\text{Sp}}\subset \operatorname{SO}_{n}\subset \operatorname{SL}_{n}$
:
$U_{S}^{\text{Sp}}\subset \operatorname{SO}_{n}\subset \operatorname{SL}_{n}$
:
 $$\begin{eqnarray}S_{j}=\{i:\exists u\in U_{S}^{\text{SO}}\subset \operatorname{SO}_{n}\subset \operatorname{SL}_{n}~\text{such that}~u_{ij}\neq 0\}.\end{eqnarray}$$
$$\begin{eqnarray}S_{j}=\{i:\exists u\in U_{S}^{\text{SO}}\subset \operatorname{SO}_{n}\subset \operatorname{SL}_{n}~\text{such that}~u_{ij}\neq 0\}.\end{eqnarray}$$
Example 5.22. If
![]() $n=4$
and
$n=4$
and
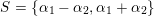 $S=\{\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}\}$
, then the corresponding subgroup
$S=\{\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}\}$
, then the corresponding subgroup
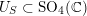 $U_{S}\subset \operatorname{SO}_{4}(\mathbb{C})$
is the maximal unipotent radical of the full upper Borel subgroup of
$U_{S}\subset \operatorname{SO}_{4}(\mathbb{C})$
is the maximal unipotent radical of the full upper Borel subgroup of
![]() $\operatorname{SO}_{4}(\mathbb{C})$
, that is,
$\operatorname{SO}_{4}(\mathbb{C})$
, that is,
 $$\begin{eqnarray}U_{S}=\left\{\left(\begin{array}{@{}cccc@{}}1 & a & b & -ab\\ 0 & 1 & 0 & -b\\ 0 & 0 & 1 & -a\\ 0 & 0 & 0 & 1\end{array}\right):a,b\in \mathbb{C}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}U_{S}=\left\{\left(\begin{array}{@{}cccc@{}}1 & a & b & -ab\\ 0 & 1 & 0 & -b\\ 0 & 0 & 1 & -a\\ 0 & 0 & 0 & 1\end{array}\right):a,b\in \mathbb{C}\right\}.\end{eqnarray}$$
Then the nonzero entries of
![]() $U_{S}$
define the sets
$U_{S}$
define the sets
 $$\begin{eqnarray}S_{1}=\{1\},\quad S_{2}=\{1,2\},\quad S_{3}=\{1,3\},\quad S_{4}=\{1,2,3,4\}.\end{eqnarray}$$
$$\begin{eqnarray}S_{1}=\{1\},\quad S_{2}=\{1,2\},\quad S_{3}=\{1,3\},\quad S_{4}=\{1,2,3,4\}.\end{eqnarray}$$
If
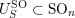 $U_{S}^{\text{SO}}\subset \operatorname{SO}_{n}$
is Borel-regular, then the regular subgroup
$U_{S}^{\text{SO}}\subset \operatorname{SO}_{n}$
is Borel-regular, then the regular subgroup
![]() $U_{S}^{\text{SL}}$
is Borel regular in
$U_{S}^{\text{SL}}$
is Borel regular in
![]() $\operatorname{SL}_{n}$
, symmetric about the antidiagonal. Therefore we can define the crossing point
$\operatorname{SL}_{n}$
, symmetric about the antidiagonal. Therefore we can define the crossing point
![]() $\unicode[STIX]{x1D6FE}_{S}$
of
$\unicode[STIX]{x1D6FE}_{S}$
of
![]() $S$
like in the symplectic case.
$S$
like in the symplectic case.
Remark 5.23. Note that in
![]() $\operatorname{SO}_{n}$
with
$\operatorname{SO}_{n}$
with
![]() $n=2l$
the entry
$n=2l$
the entry
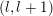 $(l,l+1)$
is always zero and therefore
$(l,l+1)$
is always zero and therefore
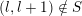 $(l,l+1)\notin S$
. This implies that
$(l,l+1)\notin S$
. This implies that
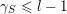 $\unicode[STIX]{x1D6FE}_{S}\leqslant l-1$
.
$\unicode[STIX]{x1D6FE}_{S}\leqslant l-1$
.
We define the orthogonal fundamental domain
![]() $F$
corresponding to a Borel-regular subset
$F$
corresponding to a Borel-regular subset
![]() $S$
symmetric about the antidiagonal the same way as in Definition 5.6. The corresponding point
$S$
symmetric about the antidiagonal the same way as in Definition 5.6. The corresponding point
![]() $p_{F}$
and therefore
$p_{F}$
and therefore
![]() $p_{\tilde{F}}$
has stabiliser
$p_{\tilde{F}}$
has stabiliser
![]() $U_{S}$
in
$U_{S}$
in
![]() $\operatorname{SO}_{n}$
.
$\operatorname{SO}_{n}$
.
Definition 5.24. We define the snipped top right quarter of
![]() $\operatorname{SL}_{n}$
as the domain
$\operatorname{SL}_{n}$
as the domain
 $$\begin{eqnarray}\mathbf{Q}=\left\{\begin{array}{@{}ll@{}}\{(i,j):1\leqslant i\leqslant l,l+1\leqslant j\leqslant n\}\setminus \{(l,l+1)\}\quad & \text{for}~n=2l,\\ \{(i,j):1\leqslant i\leqslant l+1,l+1\leqslant j\leqslant n\}\setminus \{(l+1,l+1)\}\quad & \text{for}~n=2l+1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{Q}=\left\{\begin{array}{@{}ll@{}}\{(i,j):1\leqslant i\leqslant l,l+1\leqslant j\leqslant n\}\setminus \{(l,l+1)\}\quad & \text{for}~n=2l,\\ \{(i,j):1\leqslant i\leqslant l+1,l+1\leqslant j\leqslant n\}\setminus \{(l+1,l+1)\}\quad & \text{for}~n=2l+1.\end{array}\right.\end{eqnarray}$$
We call a Borel regular subgroup
 $U_{S}^{\text{SO}}\subset \operatorname{SO}_{n}$
fat Borel regular if
$U_{S}^{\text{SO}}\subset \operatorname{SO}_{n}$
fat Borel regular if
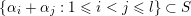 $\{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}:1\leqslant i<j\leqslant l\}\subset S$
for
$\{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j}:1\leqslant i<j\leqslant l\}\subset S$
for
![]() $n=2l$
and
$n=2l$
and
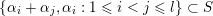 $\{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FC}_{i}:1\leqslant i<j\leqslant l\}\subset S$
for
$\{\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FC}_{i}:1\leqslant i<j\leqslant l\}\subset S$
for
 $n=2l+1$
. Equivalently, the snipped top right quarter
$n=2l+1$
. Equivalently, the snipped top right quarter
![]() $\mathbf{Q}$
is part of the free parameter domain of the corresponding
$\mathbf{Q}$
is part of the free parameter domain of the corresponding
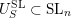 $U_{S}^{\text{SL}}\subset \operatorname{SL}_{n}$
. For examples of fat Borel regular subgroups, see Figures 5 and 6.
$U_{S}^{\text{SL}}\subset \operatorname{SL}_{n}$
. For examples of fat Borel regular subgroups, see Figures 5 and 6.

Figure 5. A fat Borel-regular subgroup for
![]() $n=8$
and its fundamental domain. Note that
$n=8$
and its fundamental domain. Note that
![]() $(4,5)$
is missing from the free parameter domain.
$(4,5)$
is missing from the free parameter domain.

Figure 6. A fat Borel-regular subgroup for
![]() $n=7$
and its fundamental domain.
$n=7$
and its fundamental domain.
Theorem 5.25. Let
![]() $n=2l$
or
$n=2l$
or
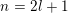 $n=2l+1$
and
$n=2l+1$
and
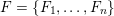 $F=\{F_{1},\ldots ,F_{n}\}$
be the orthogonal fundamental domain corresponding to a fat Borel-regular subgroup
$F=\{F_{1},\ldots ,F_{n}\}$
be the orthogonal fundamental domain corresponding to a fat Borel-regular subgroup
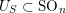 $U_{S}\subset \operatorname{SO}_{n}$
. Then the pair
$U_{S}\subset \operatorname{SO}_{n}$
. Then the pair
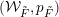 $({\mathcal{W}}_{\tilde{F}},p_{\tilde{F}})$
is a Grosshans pair for
$({\mathcal{W}}_{\tilde{F}},p_{\tilde{F}})$
is a Grosshans pair for
![]() $U_{F}$
. This proves Theorem 1.3 for orthogonal groups.
$U_{F}$
. This proves Theorem 1.3 for orthogonal groups.
Proof. First we assume
![]() $n=2l$
. The key observation is the following stronger version of Lemma 5.10.
$n=2l$
. The key observation is the following stronger version of Lemma 5.10.
Lemma 5.26. Let
![]() $n=2l$
. If
$n=2l$
. If
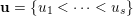 $\mathbf{u}=\{u_{1}<\cdots <u_{s}\}$
is such that
$\mathbf{u}=\{u_{1}<\cdots <u_{s}\}$
is such that
![]() $u_{1}\geqslant l$
, then
$u_{1}\geqslant l$
, then
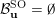 ${\mathcal{B}}_{\mathbf{u}}^{\text{SO}}=\emptyset$
.
${\mathcal{B}}_{\mathbf{u}}^{\text{SO}}=\emptyset$
.
Proof. The
![]() $u_{1}>l$
case is the same as in Lemma 5.10. Assume
$u_{1}>l$
case is the same as in Lemma 5.10. Assume
![]() $u_{1}=l$
. Then
$u_{1}=l$
. Then
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }b_{l+1l+1}^{(m)}=\lim _{m\rightarrow \infty }(b_{ll}^{(m)})^{-1}=\infty \quad \text{and}\quad \lim _{m\rightarrow \infty }b_{ii}^{(m)}\in \mathbb{C}\setminus \{0\}\quad \text{for}~1\leqslant i<l.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }b_{l+1l+1}^{(m)}=\lim _{m\rightarrow \infty }(b_{ll}^{(m)})^{-1}=\infty \quad \text{and}\quad \lim _{m\rightarrow \infty }b_{ii}^{(m)}\in \mathbb{C}\setminus \{0\}\quad \text{for}~1\leqslant i<l.\end{eqnarray}$$
Since
![]() $S$
is fat,
$S$
is fat,
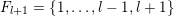 $F_{l+1}=\{1,\ldots ,l-1,l+1\}$
and the coefficient of
$F_{l+1}=\{1,\ldots ,l-1,l+1\}$
and the coefficient of
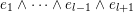 $e_{1}\wedge \cdots \wedge e_{l-1}\wedge e_{l+1}$
in
$e_{1}\wedge \cdots \wedge e_{l-1}\wedge e_{l+1}$
in
![]() $p_{F_{l+1}}^{\infty }$
is
$p_{F_{l+1}}^{\infty }$
is
 $$\begin{eqnarray}p_{S_{l+1}}^{\infty }[e_{1}\wedge \cdots \wedge e_{l-1}\wedge e_{l+1}]=\lim _{m\rightarrow \infty }b_{l+1l+1}^{(m)}\cdot \mathop{\prod }_{i=1}^{l-1}b_{ii}^{(m)}=\infty ,\end{eqnarray}$$
$$\begin{eqnarray}p_{S_{l+1}}^{\infty }[e_{1}\wedge \cdots \wedge e_{l-1}\wedge e_{l+1}]=\lim _{m\rightarrow \infty }b_{l+1l+1}^{(m)}\cdot \mathop{\prod }_{i=1}^{l-1}b_{ii}^{(m)}=\infty ,\end{eqnarray}$$
a contradiction. ◻
The proof of Theorem 5.9 applies with two minor changes for the proof of Theorem 5.25. The only difference we have to keep in mind is that for
![]() $\operatorname{SO}_{2l}$
,
$\operatorname{SO}_{2l}$
,
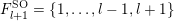 $F_{l+1}^{\text{SO}}=\{1,\ldots ,l-1,l+1\}$
whereas in
$F_{l+1}^{\text{SO}}=\{1,\ldots ,l-1,l+1\}$
whereas in
![]() $\operatorname{Sp}_{2l}$
it was
$\operatorname{Sp}_{2l}$
it was
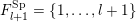 $F_{l+1}^{\text{Sp}}=\{1,\ldots ,l+1\}$
. This means that
$F_{l+1}^{\text{Sp}}=\{1,\ldots ,l+1\}$
. This means that
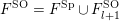 $F^{\text{SO}}=F^{\text{Sp}}\cup F_{l+1}^{\text{SO}}$
, and this extra set results in minor changes in the proof of Lemmas 5.19 and 5.20 as follows.
$F^{\text{SO}}=F^{\text{Sp}}\cup F_{l+1}^{\text{SO}}$
, and this extra set results in minor changes in the proof of Lemmas 5.19 and 5.20 as follows.
-
– In the proof of Lemma 5.19 the first part proving that
 $T^{u,e_{r}}$
fixes
$T^{u,e_{r}}$
fixes
 $p^{\infty }$
remains the same. To prove that
$p^{\infty }$
remains the same. To prove that
 $T^{n+1-r,e_{n+1-u}}$
fixes
$T^{n+1-r,e_{n+1-u}}$
fixes
 $p^{\infty }$
we only need to worry about those
$p^{\infty }$
we only need to worry about those
 $p_{V}^{\infty }$
where
$p_{V}^{\infty }$
where
 $\max (V)\geqslant l+1$
. In order to prove (36) we distinguish two cases.
$\max (V)\geqslant l+1$
. In order to prove (36) we distinguish two cases.-
(a) If
 $r\leqslant l-1$
, then
$r\leqslant l-1$
, then
 $n+1-r\geqslant l+2$
. However, for
$n+1-r\geqslant l+2$
. However, for
 $\max (V)=v\geqslant l+2$
we have
$\max (V)=v\geqslant l+2$
we have
 $V=\{1,\ldots ,v\}$
so (33) holds and therefore (34) implies that
$V=\{1,\ldots ,v\}$
so (33) holds and therefore (34) implies that
 $p_{\{1,\ldots ,v\}}^{\infty }=0$
for
$p_{\{1,\ldots ,v\}}^{\infty }=0$
for
 $n+1-r\leqslant v\leqslant n-u$
again.
$n+1-r\leqslant v\leqslant n-u$
again. -
(b) If
 $r=l$
, then either
$r=l$
, then either
 $p_{\{1,\ldots ,l-1,l+1\}}^{\infty }=0$
and the extra subset
$p_{\{1,\ldots ,l-1,l+1\}}^{\infty }=0$
and the extra subset
 $F_{l+1}^{\text{SO}}$
added to
$F_{l+1}^{\text{SO}}$
added to
 $F^{\text{Sp}}$
does not affect the proof, or
$F^{\text{Sp}}$
does not affect the proof, or
 $p_{\{1,\ldots ,l-1,l+1\}}^{\infty }\neq 0$
, but then and the only way this can happen is that
$p_{\{1,\ldots ,l-1,l+1\}}^{\infty }\neq 0$
, but then and the only way this can happen is that $$\begin{eqnarray}e_{r}\in [p_{Z}^{\infty }]\subset [p_{F_{l+1}}^{\infty }]=[p_{1,\ldots ,l-1,l+2}^{\infty }],\end{eqnarray}$$
$$\begin{eqnarray}e_{r}\in [p_{Z}^{\infty }]\subset [p_{F_{l+1}}^{\infty }]=[p_{1,\ldots ,l-1,l+2}^{\infty }],\end{eqnarray}$$
 $[p_{1,\ldots ,l-1,l+2}^{\infty }]=\operatorname{Span}(e_{1},\ldots ,e_{l})$
. But then
$[p_{1,\ldots ,l-1,l+2}^{\infty }]=\operatorname{Span}(e_{1},\ldots ,e_{l})$
. But then
 $e_{l+1}=e_{n+1-r}$
is not contained in the only problematic set
$e_{l+1}=e_{n+1-r}$
is not contained in the only problematic set
 $[p_{\{1,\ldots ,l-1,l+1\}}]^{\infty }$
and the proof of the symplectic case works here again.
$[p_{\{1,\ldots ,l-1,l+1\}}]^{\infty }$
and the proof of the symplectic case works here again.
-
-
– The second case in Lemma 5.20 does not make sense in the orthogonal case:
 $-2\unicode[STIX]{x1D6FC}_{l}$
is not a root for
$-2\unicode[STIX]{x1D6FC}_{l}$
is not a root for
 $\operatorname{SO}_{2l}$
. But Lemma 5.26 tells us that
$\operatorname{SO}_{2l}$
. But Lemma 5.26 tells us that
 $u=l$
cannot happen and in fact
$u=l$
cannot happen and in fact
 $u\leqslant l-1$
ensures that the extra set
$u\leqslant l-1$
ensures that the extra set
 $\{1,\ldots ,l-1,l+1\}$
which we added to
$\{1,\ldots ,l-1,l+1\}$
which we added to
 $F^{\text{Sp}_{2l}}$
does not affect the proof. Indeed, this is clear when
$F^{\text{Sp}_{2l}}$
does not affect the proof. Indeed, this is clear when
 $u\leqslant l-2$
because in this case
$u\leqslant l-2$
because in this case
 $n-u\geqslant l+2$
, and hence to prove that
$n-u\geqslant l+2$
, and hence to prove that
 $T^{n-u,e_{n+1-u}}$
fixes
$T^{n-u,e_{n+1-u}}$
fixes
 $p^{\infty }$
it is enough to have the following weaker version of (40): But subsets with
$p^{\infty }$
it is enough to have the following weaker version of (40): But subsets with $$\begin{eqnarray}p_{\{1,\ldots ,v\}}^{\infty }=0\quad \text{for}~l+2\leqslant v\leqslant n-u.\end{eqnarray}$$
$$\begin{eqnarray}p_{\{1,\ldots ,v\}}^{\infty }=0\quad \text{for}~l+2\leqslant v\leqslant n-u.\end{eqnarray}$$
 $\max (V)\geqslant l+2$
are the same in
$\max (V)\geqslant l+2$
are the same in
 $F^{\text{Sp}}$
and
$F^{\text{Sp}}$
and
 $F^{\text{SO}}$
and so this follows exactly the same way as (40).
$F^{\text{SO}}$
and so this follows exactly the same way as (40).
If
 $u=l-1$
and
$u=l-1$
and
 $r\geqslant l+2$
, then
$r\geqslant l+2$
, then
 $p_{\{1,\ldots ,l-1,l+1\}}^{\infty }=0$
and
$p_{\{1,\ldots ,l-1,l+1\}}^{\infty }=0$
and
 $F_{l+1}^{\text{SO}}$
does not make any difference.
$F_{l+1}^{\text{SO}}$
does not make any difference.Finally, if
 $u=l-1$
is the only element of the vanishing spectrum and
$u=l-1$
is the only element of the vanishing spectrum and
 $r=l+1$
, then
$r=l+1$
, then
 $\lim _{m\rightarrow \infty }b_{ll}^{(m)}\neq 0$
and therefore
$\lim _{m\rightarrow \infty }b_{ll}^{(m)}\neq 0$
and therefore
 $\lim _{m\rightarrow \infty }|b_{l+1l+1}^{(m)}|=\lim _{m\rightarrow \infty }|(b_{ll}^{(m)})|^{-1}<\infty$
. But then the coefficient of
$\lim _{m\rightarrow \infty }|b_{l+1l+1}^{(m)}|=\lim _{m\rightarrow \infty }|(b_{ll}^{(m)})|^{-1}<\infty$
. But then the coefficient of
 $e_{1}\wedge \cdots \wedge e_{l-1}\wedge e_{l+1}$
in
$e_{1}\wedge \cdots \wedge e_{l-1}\wedge e_{l+1}$
in
 $p_{\{1,\ldots ,l-1,l+1\}}^{\infty }$
is because the first limit is 0 (the
$p_{\{1,\ldots ,l-1,l+1\}}^{\infty }$
is because the first limit is 0 (the $$\begin{eqnarray}\lim _{m\rightarrow \infty }(b_{11}^{(m)}\cdots b_{l-1l-1}^{(m)})\cdot \lim _{m\rightarrow \infty }b_{l+1l+1}^{(m)}=0\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }(b_{11}^{(m)}\cdots b_{l-1l-1}^{(m)})\cdot \lim _{m\rightarrow \infty }b_{l+1l+1}^{(m)}=0\end{eqnarray}$$
 $l-1$
th term tends to 0, the rest to some nonzero constant) and the second limit is finite. Therefore a contradiction.
$l-1$
th term tends to 0, the rest to some nonzero constant) and the second limit is finite. Therefore a contradiction. $$\begin{eqnarray}e_{r}\in [p_{Z}^{\infty }]\subset [p_{\{1,\ldots ,l-1,l+1\}}^{\infty }]\subset [\operatorname{Span}(e_{1},\ldots ,e_{r-1})],\end{eqnarray}$$
$$\begin{eqnarray}e_{r}\in [p_{Z}^{\infty }]\subset [p_{\{1,\ldots ,l-1,l+1\}}^{\infty }]\subset [\operatorname{Span}(e_{1},\ldots ,e_{r-1})],\end{eqnarray}$$
Now assume
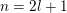 $n=2l+1$
. Since the diagonal entry
$n=2l+1$
. Since the diagonal entry
![]() $b_{l+1,l+1}^{(m)}$
is constant
$b_{l+1,l+1}^{(m)}$
is constant
![]() $1$
in
$1$
in
![]() $\operatorname{SO}_{n}$
,
$\operatorname{SO}_{n}$
,
![]() $\mathbf{u}$
cannot contain
$\mathbf{u}$
cannot contain
![]() $l+1$
and Lemma 5.10 holds without change. We furthermore add the following observation.
$l+1$
and Lemma 5.10 holds without change. We furthermore add the following observation.
Lemma 5.27.
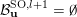 ${\mathcal{B}}_{\mathbf{u}}^{\text{SO},l+1}=\emptyset$
for arbitrary
${\mathcal{B}}_{\mathbf{u}}^{\text{SO},l+1}=\emptyset$
for arbitrary
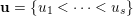 $\mathbf{u}=\{u_{1}<\cdots <u_{s}\}$
.
$\mathbf{u}=\{u_{1}<\cdots <u_{s}\}$
.
Proof. Assume
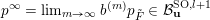 $p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{F}}\in {\mathcal{B}}_{\mathbf{u}}^{\text{SO},l+1}$
. By definition there is a
$p^{\infty }=\lim _{m\rightarrow \infty }b^{(m)}p_{\tilde{F}}\in {\mathcal{B}}_{\mathbf{u}}^{\text{SO},l+1}$
. By definition there is a
![]() $Z\in \tilde{F}$
with
$Z\in \tilde{F}$
with
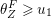 $\unicode[STIX]{x1D703}_{Z}^{F}\geqslant u_{1}$
such that
$\unicode[STIX]{x1D703}_{Z}^{F}\geqslant u_{1}$
such that
![]() $p_{Z}^{\infty }\neq 0$
and the following are true.
$p_{Z}^{\infty }\neq 0$
and the following are true.
-
(i)
 $[p_{Z}^{\infty }]\subset \bigcap _{\substack{ V\in \tilde{F},p_{V}^{\infty }\neq 0 \\ \unicode[STIX]{x1D703}_{V}\geqslant u_{1}}}[p_{V}^{\infty }]$
.
$[p_{Z}^{\infty }]\subset \bigcap _{\substack{ V\in \tilde{F},p_{V}^{\infty }\neq 0 \\ \unicode[STIX]{x1D703}_{V}\geqslant u_{1}}}[p_{V}^{\infty }]$
. -
(ii)
 $\unicode[STIX]{x1D714}([p_{Z}^{\infty }])=l+1$
. For this to happen
$\unicode[STIX]{x1D714}([p_{Z}^{\infty }])=l+1$
. For this to happen
 $\max (Z)=z\geqslant l+1$
must hold, and therefore
$\max (Z)=z\geqslant l+1$
must hold, and therefore
 $Z=\{1,\ldots ,z\}$
. But if
$Z=\{1,\ldots ,z\}$
. But if
 $\unicode[STIX]{x1D714}([p_{Z}^{\infty }])=l+1$
, then
$\unicode[STIX]{x1D714}([p_{Z}^{\infty }])=l+1$
, then
 $[p_{Z}^{\infty }]=[p_{\{1,\ldots ,z\}}^{\infty }]=[e_{1}\wedge \cdots \wedge e_{z}]$
is a subspace of
$[p_{Z}^{\infty }]=[p_{\{1,\ldots ,z\}}^{\infty }]=[e_{1}\wedge \cdots \wedge e_{z}]$
is a subspace of
 $\operatorname{Span}(e_{1},\ldots ,e_{l+1})$
by definition, which means that
$\operatorname{Span}(e_{1},\ldots ,e_{l+1})$
by definition, which means that
 $z=l+1$
and
$z=l+1$
and
 $Z=\{1,\ldots ,l+1\}$
. Then But
$Z=\{1,\ldots ,l+1\}$
. Then But $$\begin{eqnarray}0\neq p_{Z}^{\infty }=\lim _{m\rightarrow \infty }\biggl(\mathop{\prod }_{i=1}^{l+1}b_{ii}^{(m)}\biggr)\cdot \wedge _{i=1}^{l+1}e_{i}.\end{eqnarray}$$
$$\begin{eqnarray}0\neq p_{Z}^{\infty }=\lim _{m\rightarrow \infty }\biggl(\mathop{\prod }_{i=1}^{l+1}b_{ii}^{(m)}\biggr)\cdot \wedge _{i=1}^{l+1}e_{i}.\end{eqnarray}$$
 $b^{(m)}\in \operatorname{SO}_{2l+1}$
and therefore the diagonal entry
$b^{(m)}\in \operatorname{SO}_{2l+1}$
and therefore the diagonal entry
 $b_{l+1l+1}^{(m)}=1$
for all
$b_{l+1l+1}^{(m)}=1$
for all
 $m$
. Hence which means that
$m$
. Hence which means that $$\begin{eqnarray}p_{\{1,\ldots ,l\}}^{\infty }=\lim _{m\rightarrow \infty }\biggl(\mathop{\prod }_{i=1}^{l}b_{ii}^{(m)}\biggr)\cdot \wedge _{i=1}^{l}e_{i}\neq 0,\end{eqnarray}$$
$$\begin{eqnarray}p_{\{1,\ldots ,l\}}^{\infty }=\lim _{m\rightarrow \infty }\biggl(\mathop{\prod }_{i=1}^{l}b_{ii}^{(m)}\biggr)\cdot \wedge _{i=1}^{l}e_{i}\neq 0,\end{eqnarray}$$
 $\{1,\ldots ,l\}$
is a minimal subset for
$\{1,\ldots ,l\}$
is a minimal subset for
 $p^{\infty }$
contradicting the minimality of
$p^{\infty }$
contradicting the minimality of
 $Z$
with respect to
$Z$
with respect to
 $\preccurlyeq$
(see Definition 4.18) because
$\preccurlyeq$
(see Definition 4.18) because
 $\max (\{1,\ldots ,l\})=l<\max (Z)=l+1$
. ◻
$\max (\{1,\ldots ,l\})=l<\max (Z)=l+1$
. ◻
In particular, this means that either
![]() $r\leqslant l$
or
$r\leqslant l$
or
 $r\geqslant l+2$
and the proof of Theorem 5.9 applies again without change, including Lemmas 5.19 and 5.20.◻
$r\geqslant l+2$
and the proof of Theorem 5.9 applies again without change, including Lemmas 5.19 and 5.20.◻
6 A partial result for general regular subgroups of
 $\operatorname{SL}_{n}$
$\operatorname{SL}_{n}$
This section gives partial affirmative answer to the Popov–Pommerening conjecture for general regular subgroups of
![]() $\operatorname{SL}_{n}$
corresponding to arbitrary closed family
$\operatorname{SL}_{n}$
corresponding to arbitrary closed family
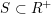 $S\subset R^{+}$
. We prove Theorem 1.4. Let
$S\subset R^{+}$
. We prove Theorem 1.4. Let
![]() $G$
be a connected, simply connected, simple linear algebraic group over the algebraically closed subfield
$G$
be a connected, simply connected, simple linear algebraic group over the algebraically closed subfield
![]() $k$
of
$k$
of
![]() $\mathbb{C}$
, and
$\mathbb{C}$
, and
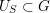 $U_{S}\subset G$
a unipotent subgroup normalised by a maximal torus
$U_{S}\subset G$
a unipotent subgroup normalised by a maximal torus
![]() $T$
of
$T$
of
![]() $G$
corresponding to the closed subset
$G$
corresponding to the closed subset
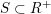 $S\subset R^{+}$
, where
$S\subset R^{+}$
, where
![]() $U_{S}$
is not necessarily block regular.
$U_{S}$
is not necessarily block regular.
Definition 6.1. We call
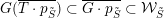 $G(\overline{T\cdot p_{\tilde{S}}})\subset \overline{G\cdot p_{\tilde{S}}}\subset {\mathcal{W}}_{\tilde{S}}$
the toric closure of
$G(\overline{T\cdot p_{\tilde{S}}})\subset \overline{G\cdot p_{\tilde{S}}}\subset {\mathcal{W}}_{\tilde{S}}$
the toric closure of
![]() $G\cdot p_{\tilde{S}}$
. Points and components of
$G\cdot p_{\tilde{S}}$
. Points and components of
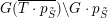 $G(\overline{T\cdot p_{\tilde{S}}})\setminus G\cdot p_{\tilde{S}}$
are called toric boundary points and components.
$G(\overline{T\cdot p_{\tilde{S}}})\setminus G\cdot p_{\tilde{S}}$
are called toric boundary points and components.
We are ready to prove Theorem 1.4 on toric boundary components. Unfortunately we cannot prove the same for nontoric boundary components, that is, components of
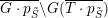 $\overline{G\cdot p_{\tilde{S}}}\setminus G(\overline{T\cdot p_{\tilde{S}}})$
.
$\overline{G\cdot p_{\tilde{S}}}\setminus G(\overline{T\cdot p_{\tilde{S}}})$
.
Proof of Theorem 1.4.
Let
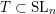 $T\subset \operatorname{SL}_{n}$
be the diagonal torus. Points of
$T\subset \operatorname{SL}_{n}$
be the diagonal torus. Points of
![]() $\overline{T\cdot p_{\tilde{S}}}$
are limits of the form
$\overline{T\cdot p_{\tilde{S}}}$
are limits of the form
 $$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }\left(\begin{array}{@{}cccc@{}}b_{11}^{(m)} & 0 & \cdots \, & 0\\ 0 & b_{22}^{(m)} & & \\ \vdots & & \ddots & 0\\ 0 & & 0 & b_{nn}^{(m)}\end{array}\right)\cdot p_{\tilde{S}}=\bigoplus _{V\in \tilde{S}}p_{V}^{\infty },\end{eqnarray}$$
$$\begin{eqnarray}p^{\infty }=\lim _{m\rightarrow \infty }\left(\begin{array}{@{}cccc@{}}b_{11}^{(m)} & 0 & \cdots \, & 0\\ 0 & b_{22}^{(m)} & & \\ \vdots & & \ddots & 0\\ 0 & & 0 & b_{nn}^{(m)}\end{array}\right)\cdot p_{\tilde{S}}=\bigoplus _{V\in \tilde{S}}p_{V}^{\infty },\end{eqnarray}$$
where
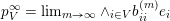 $p_{V}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{i\in V}b_{ii}^{(m)}e_{i}$
. According to Lemma 4.4 if
$p_{V}^{\infty }=\lim _{m\rightarrow \infty }\wedge _{i\in V}b_{ii}^{(m)}e_{i}$
. According to Lemma 4.4 if
![]() $p^{\infty }$
is a boundary point, that is,
$p^{\infty }$
is a boundary point, that is,
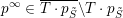 $p^{\infty }\in \overline{T\cdot p_{\tilde{S}}}\setminus T\cdot p_{\tilde{S}}$
, then there is a smallest index
$p^{\infty }\in \overline{T\cdot p_{\tilde{S}}}\setminus T\cdot p_{\tilde{S}}$
, then there is a smallest index
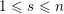 $1\leqslant s\leqslant n$
such that
$1\leqslant s\leqslant n$
such that
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }b_{ss}^{(m)}=0.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }b_{ss}^{(m)}=0.\end{eqnarray}$$
Define
 $$\begin{eqnarray}t=\min \{j:\exists V\in \tilde{S}~\text{such that}~s\in V,j=\max (V)~\text{and}~p_{V}^{\infty }\neq 0\}.\end{eqnarray}$$
$$\begin{eqnarray}t=\min \{j:\exists V\in \tilde{S}~\text{such that}~s\in V,j=\max (V)~\text{and}~p_{V}^{\infty }\neq 0\}.\end{eqnarray}$$
Note that
![]() $t$
is well defined because
$t$
is well defined because
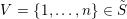 $V=\{1,\ldots ,n\}\in \tilde{S}$
and
$V=\{1,\ldots ,n\}\in \tilde{S}$
and
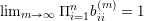 $\lim _{m\rightarrow \infty }\unicode[STIX]{x1D6F1}_{i=1}^{n}b_{ii}^{(m)}=1$
, so the defining set above is nonempty. Furthermore
$\lim _{m\rightarrow \infty }\unicode[STIX]{x1D6F1}_{i=1}^{n}b_{ii}^{(m)}=1$
, so the defining set above is nonempty. Furthermore
![]() $t>s$
holds by the minimality of
$t>s$
holds by the minimality of
![]() $s$
. We call
$s$
. We call
![]() $(s,t)$
the type of
$(s,t)$
the type of
![]() $p^{\infty }$
.
$p^{\infty }$
.
Remark 6.2. If the vanishing spectrum of
![]() $(b^{(m)})$
is
$(b^{(m)})$
is
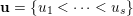 $\mathbf{u}=\{u_{1}<\cdots <u_{s}\}$
, then
$\mathbf{u}=\{u_{1}<\cdots <u_{s}\}$
, then
![]() $s=u_{1}$
and
$s=u_{1}$
and
![]() $s$
is uniquely determined by
$s$
is uniquely determined by
![]() $p^{\infty }$
according to Remark 4.11. Moreover,
$p^{\infty }$
according to Remark 4.11. Moreover,
![]() $t$
plays the role of the width of
$t$
plays the role of the width of
![]() $p^{\infty }$
and it is again determined by
$p^{\infty }$
and it is again determined by
![]() $p^{\infty }$
.
$p^{\infty }$
.
Let
![]() $Z\in \tilde{S}$
be one of the minimising subsets in the definition of
$Z\in \tilde{S}$
be one of the minimising subsets in the definition of
![]() $t$
, that is,
$t$
, that is,
 $$\begin{eqnarray}s\in Z,t=\max (Z)\quad \text{and}\quad p_{Z}^{\infty }=\lim _{m\rightarrow \infty }\unicode[STIX]{x1D6F1}_{i\in Z}b_{ii}^{(m)}\wedge _{i\in Z}e_{i}\neq 0.\end{eqnarray}$$
$$\begin{eqnarray}s\in Z,t=\max (Z)\quad \text{and}\quad p_{Z}^{\infty }=\lim _{m\rightarrow \infty }\unicode[STIX]{x1D6F1}_{i\in Z}b_{ii}^{(m)}\wedge _{i\in Z}e_{i}\neq 0.\end{eqnarray}$$
We prove that
![]() $p^{\infty }$
is
$p^{\infty }$
is
![]() $(s,e_{t})$
-fixed (see Definition 4.23). Assume there is a
$(s,e_{t})$
-fixed (see Definition 4.23). Assume there is a
![]() $V\in \tilde{S}$
such that
$V\in \tilde{S}$
such that
 $$\begin{eqnarray}p_{V}^{\infty }=\lim _{m\rightarrow \infty }\biggl(\mathop{\prod }_{i\in V}b_{ii}^{(m)}\biggr)\cdot \wedge _{i\in V}e_{i}\neq 0,\quad s\in V~\text{but}~t\notin V.\end{eqnarray}$$
$$\begin{eqnarray}p_{V}^{\infty }=\lim _{m\rightarrow \infty }\biggl(\mathop{\prod }_{i\in V}b_{ii}^{(m)}\biggr)\cdot \wedge _{i\in V}e_{i}\neq 0,\quad s\in V~\text{but}~t\notin V.\end{eqnarray}$$
Now
 $V\cup Z,V\cap Z\in \tilde{S}$
and
$V\cup Z,V\cap Z\in \tilde{S}$
and
 $$\begin{eqnarray}\lim _{m\rightarrow \infty }\mathop{\prod }_{i\in V\cup Z}b_{ii}^{(m)}=\lim _{m\rightarrow \infty }\frac{\unicode[STIX]{x1D6F1}_{i\in V}b_{ii}^{(m)}\unicode[STIX]{x1D6F1}_{i\in Z}b_{ii}^{(m)}}{\unicode[STIX]{x1D6F1}_{i\in V\cap Z}b_{ii}^{(m)}}.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{m\rightarrow \infty }\mathop{\prod }_{i\in V\cup Z}b_{ii}^{(m)}=\lim _{m\rightarrow \infty }\frac{\unicode[STIX]{x1D6F1}_{i\in V}b_{ii}^{(m)}\unicode[STIX]{x1D6F1}_{i\in Z}b_{ii}^{(m)}}{\unicode[STIX]{x1D6F1}_{i\in V\cap Z}b_{ii}^{(m)}}.\end{eqnarray}$$
The limit of the numerator is finite and nonzero from the definition of
![]() $V$
and
$V$
and
![]() $Z$
. But
$Z$
. But
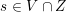 $s\in V\cap Z$
and
$s\in V\cap Z$
and
![]() $t\notin V$
so
$t\notin V$
so
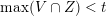 $\max (V\cap Z)<t$
and therefore by the definition of
$\max (V\cap Z)<t$
and therefore by the definition of
![]() $t$
the limit of the denominator is 0. This is a contradiction as the left-hand side is the coefficient of
$t$
the limit of the denominator is 0. This is a contradiction as the left-hand side is the coefficient of
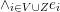 $\wedge _{i\in V\cup Z}e_{i}$
in
$\wedge _{i\in V\cup Z}e_{i}$
in
![]() $p_{V\cup Z}^{\infty }$
. So there is no
$p_{V\cup Z}^{\infty }$
. So there is no
![]() $V\in \tilde{S}$
satisfying (41), which means that
$V\in \tilde{S}$
satisfying (41), which means that
![]() $p^{\infty }$
is fixed by
$p^{\infty }$
is fixed by
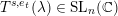 $T^{s,e_{t}}(\unicode[STIX]{x1D706})\in \operatorname{SL}_{n}(\mathbb{C})$
and therefore
$T^{s,e_{t}}(\unicode[STIX]{x1D706})\in \operatorname{SL}_{n}(\mathbb{C})$
and therefore
![]() $p^{\infty }$
is
$p^{\infty }$
is
![]() $(s,e_{t})$
-fixed. For
$(s,e_{t})$
-fixed. For
 $1\leqslant s<t\leqslant n$
let
$1\leqslant s<t\leqslant n$
let
 $$\begin{eqnarray}{\mathcal{B}}_{s,t}=\{p^{\infty }\in \overline{T\cdot p_{\tilde{S}}}\setminus T\cdot p_{\tilde{S}}:\text{the type of}~p^{\infty }~\text{is}~(s,t)\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{s,t}=\{p^{\infty }\in \overline{T\cdot p_{\tilde{S}}}\setminus T\cdot p_{\tilde{S}}:\text{the type of}~p^{\infty }~\text{is}~(s,t)\}.\end{eqnarray}$$
According to Remark 6.2 we have
 $$\begin{eqnarray}{\mathcal{B}}_{s,t}=\mathop{\bigcup }_{\mathbf{u}=\{s<u_{2}<\cdots \,\}}(\overline{T\cdot p_{\tilde{S}}}\cap {\mathcal{B}}_{\mathbf{u}}^{t})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{s,t}=\mathop{\bigcup }_{\mathbf{u}=\{s<u_{2}<\cdots \,\}}(\overline{T\cdot p_{\tilde{S}}}\cap {\mathcal{B}}_{\mathbf{u}}^{t})\end{eqnarray}$$
and therefore by Remark 4.19
![]() ${\mathcal{B}}_{s,t}$
is quasi-affine again.
${\mathcal{B}}_{s,t}$
is quasi-affine again.
Then
 $$\begin{eqnarray}\operatorname{SL}_{n}\cdot \overline{T\cdot p_{\tilde{S}}}\setminus T\cdot p_{\tilde{S}}=\mathop{\bigcup }_{1\leqslant s<t\leqslant n}\operatorname{SL}_{n}\cdot {\mathcal{B}}_{s,t}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{SL}_{n}\cdot \overline{T\cdot p_{\tilde{S}}}\setminus T\cdot p_{\tilde{S}}=\mathop{\bigcup }_{1\leqslant s<t\leqslant n}\operatorname{SL}_{n}\cdot {\mathcal{B}}_{s,t}.\end{eqnarray}$$
We adapt the proof of Lemma 4.24 to show that
 $$\begin{eqnarray}\dim (\operatorname{SL}_{n}\cdot {\mathcal{B}}_{s,t})\leqslant \dim (\operatorname{SL}_{n}\cdot p_{\tilde{S}})-2,\end{eqnarray}$$
$$\begin{eqnarray}\dim (\operatorname{SL}_{n}\cdot {\mathcal{B}}_{s,t})\leqslant \dim (\operatorname{SL}_{n}\cdot p_{\tilde{S}})-2,\end{eqnarray}$$
which implies Theorem 1.4. Let us start with the observation that
![]() ${\mathcal{B}}_{s,t}$
is
${\mathcal{B}}_{s,t}$
is
![]() $T$
-invariant and also
$T$
-invariant and also
![]() $U_{S}$
-invariant for any
$U_{S}$
-invariant for any
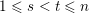 $1\leqslant s<t\leqslant n$
. This latter follows from the fact that
$1\leqslant s<t\leqslant n$
. This latter follows from the fact that
![]() $U_{S}$
is normalised by
$U_{S}$
is normalised by
![]() $T$
and fixes
$T$
and fixes
![]() $p_{\tilde{S}}$
and therefore
$p_{\tilde{S}}$
and therefore
![]() $U_{S}$
fixes each point in
$U_{S}$
fixes each point in
![]() $T\cdot p_{\tilde{S}}$
and, then, each point in
$T\cdot p_{\tilde{S}}$
and, then, each point in
![]() ${\mathcal{B}}_{s,t}$
. Consider the map
${\mathcal{B}}_{s,t}$
. Consider the map
 $$\begin{eqnarray}\unicode[STIX]{x1D711}:\operatorname{SL}_{n}(\mathbb{C})\times {\mathcal{B}}_{s,t}\rightarrow {\mathcal{W}}_{\tilde{S}},\quad \unicode[STIX]{x1D711}(g,w)\mapsto g\cdot w.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}:\operatorname{SL}_{n}(\mathbb{C})\times {\mathcal{B}}_{s,t}\rightarrow {\mathcal{W}}_{\tilde{S}},\quad \unicode[STIX]{x1D711}(g,w)\mapsto g\cdot w.\end{eqnarray}$$
Let
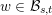 $w\in {\mathcal{B}}_{s,t}$
. Since
$w\in {\mathcal{B}}_{s,t}$
. Since
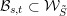 ${\mathcal{B}}_{s,t}\subset {\mathcal{W}}_{\tilde{S}}$
is
${\mathcal{B}}_{s,t}\subset {\mathcal{W}}_{\tilde{S}}$
is
![]() $U_{S}\rtimes T$
-invariant, the fibre
$U_{S}\rtimes T$
-invariant, the fibre
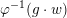 $\unicode[STIX]{x1D711}^{-1}(g\cdot w)$
contains
$\unicode[STIX]{x1D711}^{-1}(g\cdot w)$
contains
 $$\begin{eqnarray}(g(hT^{s,e_{t}}(\unicode[STIX]{x1D706}))^{-1},(hT^{s,e_{t}}(\unicode[STIX]{x1D706}))\cdot w)\end{eqnarray}$$
$$\begin{eqnarray}(g(hT^{s,e_{t}}(\unicode[STIX]{x1D706}))^{-1},(hT^{s,e_{t}}(\unicode[STIX]{x1D706}))\cdot w)\end{eqnarray}$$
for
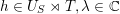 $h\in U_{S}\rtimes T,\unicode[STIX]{x1D706}\in \mathbb{C}$
. Since
$h\in U_{S}\rtimes T,\unicode[STIX]{x1D706}\in \mathbb{C}$
. Since
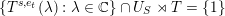 $\{T^{s,e_{t}}(\unicode[STIX]{x1D706}):\unicode[STIX]{x1D706}\in \mathbb{C}\}\cap U_{S}\rtimes T=\{1\}$
,
$\{T^{s,e_{t}}(\unicode[STIX]{x1D706}):\unicode[STIX]{x1D706}\in \mathbb{C}\}\cap U_{S}\rtimes T=\{1\}$
,
 $$\begin{eqnarray}\dim (\{hT^{s,e_{t}}(\unicode[STIX]{x1D706}):h\in U_{S}\rtimes T,\unicode[STIX]{x1D706}\in \mathbb{C}\})=\dim (U_{S})+n+1\end{eqnarray}$$
$$\begin{eqnarray}\dim (\{hT^{s,e_{t}}(\unicode[STIX]{x1D706}):h\in U_{S}\rtimes T,\unicode[STIX]{x1D706}\in \mathbb{C}\})=\dim (U_{S})+n+1\end{eqnarray}$$
and we get
 $$\begin{eqnarray}\displaystyle \dim (\operatorname{Im}(\unicode[STIX]{x1D711})) & = & \displaystyle \dim (\operatorname{SL}_{n})+\dim ({\mathcal{B}}_{s,t})-\dim (\text{fibre})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \dim (\operatorname{SL}_{n})+\dim (\overline{T\cdot p_{\tilde{S}}})-1-(\dim (U_{S})+n+1)\nonumber\\ \displaystyle & = & \displaystyle \dim \operatorname{SL}_{n}(\mathbb{C})/U_{S}-2=\dim \overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}}-2.\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim (\operatorname{Im}(\unicode[STIX]{x1D711})) & = & \displaystyle \dim (\operatorname{SL}_{n})+\dim ({\mathcal{B}}_{s,t})-\dim (\text{fibre})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \dim (\operatorname{SL}_{n})+\dim (\overline{T\cdot p_{\tilde{S}}})-1-(\dim (U_{S})+n+1)\nonumber\\ \displaystyle & = & \displaystyle \dim \operatorname{SL}_{n}(\mathbb{C})/U_{S}-2=\dim \overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}}-2.\Box \nonumber\end{eqnarray}$$
7 A remark on configuration varieties and Bott–Samelson varieties
Configuration varieties are a powerful tool in representation theory and geometry of the reductive group
![]() $G$
. If
$G$
. If
![]() $B\subset G$
is a Borel subgroup, then these varieties are certain subvarieties in the product of flag varieties
$B\subset G$
is a Borel subgroup, then these varieties are certain subvarieties in the product of flag varieties
![]() $(G/B)^{l}$
. In [Reference MagyarMag98] Magyar describes them as closures of
$(G/B)^{l}$
. In [Reference MagyarMag98] Magyar describes them as closures of
![]() $B$
-orbits in
$B$
-orbits in
![]() $(G/B)^{l}$
, which is relevant to our construction, and therefore we give a short summary in the special case when
$(G/B)^{l}$
, which is relevant to our construction, and therefore we give a short summary in the special case when
 $G=\operatorname{SL}_{n}(\mathbb{C})$
, keeping [Reference MagyarMag98] as the leading reference.
$G=\operatorname{SL}_{n}(\mathbb{C})$
, keeping [Reference MagyarMag98] as the leading reference.
Let
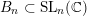 $B_{n}\subset \operatorname{SL}_{n}(\mathbb{C})$
denote the Borel of upper triangular matrices. Define a subset family to be a collection
$B_{n}\subset \operatorname{SL}_{n}(\mathbb{C})$
denote the Borel of upper triangular matrices. Define a subset family to be a collection
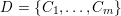 $D=\{C_{1},\ldots ,C_{m}\}$
of subsets
$D=\{C_{1},\ldots ,C_{m}\}$
of subsets
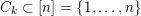 $C_{k}\subset [n]=\{1,\ldots ,n\}$
. The order is irrelevant in the family, and we do not allow repetitions. Let
$C_{k}\subset [n]=\{1,\ldots ,n\}$
. The order is irrelevant in the family, and we do not allow repetitions. Let
![]() $\mathbb{C}^{n}$
have the standard basis
$\mathbb{C}^{n}$
have the standard basis
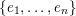 $\{e_{1},\ldots ,e_{n}\}$
and for any subset
$\{e_{1},\ldots ,e_{n}\}$
and for any subset
![]() $C\subset [n]$
define the subspace
$C\subset [n]$
define the subspace
 $$\begin{eqnarray}{\mathcal{Q}}^{C}=\operatorname{Span}_{\mathbb{ C}}\{e_{j}:j\in C\}\in \operatorname{Gr}(|C|,n).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Q}}^{C}=\operatorname{Span}_{\mathbb{ C}}\{e_{j}:j\in C\}\in \operatorname{Gr}(|C|,n).\end{eqnarray}$$
This point is fixed by the diagonal torus
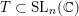 $T\subset \operatorname{SL}_{n}(\mathbb{C})$
, and so we can associate a
$T\subset \operatorname{SL}_{n}(\mathbb{C})$
, and so we can associate a
![]() $T$
-fixed point to the subset family in the product of Grassmannians:
$T$
-fixed point to the subset family in the product of Grassmannians:
 $$\begin{eqnarray}z_{D}=({\mathcal{Q}}^{C_{1}},\ldots ,{\mathcal{Q}}^{C_{m}})\in \operatorname{Gr}(D)=\operatorname{Gr}(|C_{1}|,n)\times \cdots \times \operatorname{Gr}(|C_{m}|,n).\end{eqnarray}$$
$$\begin{eqnarray}z_{D}=({\mathcal{Q}}^{C_{1}},\ldots ,{\mathcal{Q}}^{C_{m}})\in \operatorname{Gr}(D)=\operatorname{Gr}(|C_{1}|,n)\times \cdots \times \operatorname{Gr}(|C_{m}|,n).\end{eqnarray}$$
The configuration variety of
![]() $D$
is the closure of the
$D$
is the closure of the
![]() $\operatorname{SL}_{n}(\mathbb{C})$
-orbit of
$\operatorname{SL}_{n}(\mathbb{C})$
-orbit of
![]() $z_{D}$
,
$z_{D}$
,
 $$\begin{eqnarray}{\mathcal{A}}_{D}=\overline{\operatorname{SL}_{n}(\mathbb{C})\cdot z_{D}}\subset \operatorname{Gr}(D),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{D}=\overline{\operatorname{SL}_{n}(\mathbb{C})\cdot z_{D}}\subset \operatorname{Gr}(D),\end{eqnarray}$$
and the flagged configuration variety is the closure of the Borel orbit,
 $$\begin{eqnarray}{\mathcal{A}}_{D}^{B}=\overline{B_{n}\cdot z_{D}}\subset \operatorname{Gr}(D).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{D}^{B}=\overline{B_{n}\cdot z_{D}}\subset \operatorname{Gr}(D).\end{eqnarray}$$
There is an important class of subset families associated to subsets of the Weyl group
![]() $W$
of the reductive group. In the case of
$W$
of the reductive group. In the case of
![]() $\operatorname{SL}_{n}(\mathbb{C})$
, to a list of permutations
$\operatorname{SL}_{n}(\mathbb{C})$
, to a list of permutations
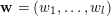 $\mathbf{w}=(w_{1},\ldots ,w_{l})$
,
$\mathbf{w}=(w_{1},\ldots ,w_{l})$
,
 $w_{k}\in W$
, and a list of indices
$w_{k}\in W$
, and a list of indices
 $\mathbf{j}=(j_{1},\ldots ,j_{l}),1\leqslant j_{k}\leqslant n$
, we associate a subset family:
$\mathbf{j}=(j_{1},\ldots ,j_{l}),1\leqslant j_{k}\leqslant n$
, we associate a subset family:
 $$\begin{eqnarray}D=D_{\mathbf{w},\mathbf{j}}=\{w_{1}[j_{1}],\ldots ,w_{l}[j_{l}]\},\end{eqnarray}$$
$$\begin{eqnarray}D=D_{\mathbf{w},\mathbf{j}}=\{w_{1}[j_{1}],\ldots ,w_{l}[j_{l}]\},\end{eqnarray}$$
where
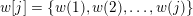 $w[j]=\{w(1),w(2),\ldots ,w(j)\}$
. Now suppose the list of indices
$w[j]=\{w(1),w(2),\ldots ,w(j)\}$
. Now suppose the list of indices
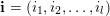 $\mathbf{i}=(i_{1},i_{2},\ldots ,i_{l})$
encodes a reduced decomposition
$\mathbf{i}=(i_{1},i_{2},\ldots ,i_{l})$
encodes a reduced decomposition
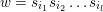 $w=s_{i_{1}}s_{i_{2}}\ldots s_{i_{l}}$
of a permutation into a minimal number of simple transpositions. Let
$w=s_{i_{1}}s_{i_{2}}\ldots s_{i_{l}}$
of a permutation into a minimal number of simple transpositions. Let
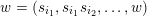 $w=(s_{i_{1}},s_{i_{1}}s_{i_{2}},\ldots ,w)$
and define the reduced chamber family
$w=(s_{i_{1}},s_{i_{1}}s_{i_{2}},\ldots ,w)$
and define the reduced chamber family
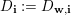 $D_{\mathbf{i}}:=D_{\mathbf{w},\mathbf{i}}$
. The full chamber family is
$D_{\mathbf{i}}:=D_{\mathbf{w},\mathbf{i}}$
. The full chamber family is
 $$\begin{eqnarray}D_{\mathbf{i}}^{+}=\{[1],[2],\ldots ,[n]\}\cup D_{\boldsymbol{ i}}.\end{eqnarray}$$
$$\begin{eqnarray}D_{\mathbf{i}}^{+}=\{[1],[2],\ldots ,[n]\}\cup D_{\boldsymbol{ i}}.\end{eqnarray}$$
A subfamily
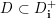 $D\subset D_{\mathbf{i}}^{+}$
is called a chamber subfamily. Leclerc and Zelevinsky in [Reference Leclerc, Zelevinsky and OlshanskiLZ98] gave a characterisation of these as follows. For two sets
$D\subset D_{\mathbf{i}}^{+}$
is called a chamber subfamily. Leclerc and Zelevinsky in [Reference Leclerc, Zelevinsky and OlshanskiLZ98] gave a characterisation of these as follows. For two sets
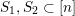 $S_{1},S_{2}\subset [n]$
we say
$S_{1},S_{2}\subset [n]$
we say
![]() $S_{1}$
is elementwise less than
$S_{1}$
is elementwise less than
![]() $S_{2}$
,
$S_{2}$
,
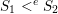 $S_{1}{<}^{e}S_{2}$
, if
$S_{1}{<}^{e}S_{2}$
, if
![]() $s_{1}<s_{2}$
for all
$s_{1}<s_{2}$
for all
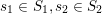 $s_{1}\in S_{1},s_{2}\in S_{2}$
. Now, a pair of subsets
$s_{1}\in S_{1},s_{2}\in S_{2}$
. Now, a pair of subsets
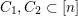 $C_{1},C_{2}\subset [n]$
is strongly separated if
$C_{1},C_{2}\subset [n]$
is strongly separated if
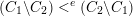 $(C_{1}\setminus C_{2}){<}^{e}(C_{2}\setminus C_{1})$
or
$(C_{1}\setminus C_{2}){<}^{e}(C_{2}\setminus C_{1})$
or
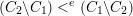 $(C_{2}\setminus C_{1}){<}^{e}(C_{1}\setminus C_{2})$
holds. A family of subsets is called strongly separated if each pair of subsets in it is strongly separated. Leclerc and Zelevinsky proved that a subset family
$(C_{2}\setminus C_{1}){<}^{e}(C_{1}\setminus C_{2})$
holds. A family of subsets is called strongly separated if each pair of subsets in it is strongly separated. Leclerc and Zelevinsky proved that a subset family
![]() $D$
is a chamber subfamily,
$D$
is a chamber subfamily,
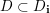 $D\subset D_{\mathbf{i}}$
for some
$D\subset D_{\mathbf{i}}$
for some
![]() $\mathbf{i}$
if and only if it is strongly separated.
$\mathbf{i}$
if and only if it is strongly separated.
If
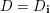 $D=D_{\mathbf{i}}$
is a chamber family, then the corresponding flagged configuration variety
$D=D_{\mathbf{i}}$
is a chamber family, then the corresponding flagged configuration variety
![]() ${\mathcal{A}}_{D}^{B}$
is called Bott–Samelson variety.
${\mathcal{A}}_{D}^{B}$
is called Bott–Samelson variety.
Very little is known about general configuration varieties. They can be badly singular; however, certain of them are well understood because they can be desexualised by Bott–Samelson varieties, which are always smooth.
The link to our construction is straightforward; if
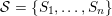 ${\mathcal{S}}=\{S_{1},\ldots ,S_{n}\}$
denotes the subset family formed from the columns of the star pattern
${\mathcal{S}}=\{S_{1},\ldots ,S_{n}\}$
denotes the subset family formed from the columns of the star pattern
![]() $S$
corresponding the regular subgroup
$S$
corresponding the regular subgroup
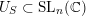 $U_{S}\subset \operatorname{SL}_{n}(\mathbb{C})$
, then there is a natural map
$U_{S}\subset \operatorname{SL}_{n}(\mathbb{C})$
, then there is a natural map
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{S}:(\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}})\rightarrow {\mathcal{A}}_{{\mathcal{S}}}\quad \text{where}~A\cdot p_{\tilde{S}}\mapsto A\cdot z_{{\mathcal{S}}}~\text{for}~A\in \operatorname{SL}_{n}(\mathbb{C}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{S}:(\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}})\rightarrow {\mathcal{A}}_{{\mathcal{S}}}\quad \text{where}~A\cdot p_{\tilde{S}}\mapsto A\cdot z_{{\mathcal{S}}}~\text{for}~A\in \operatorname{SL}_{n}(\mathbb{C}).\end{eqnarray}$$
This map does not extend to the closure. In short, our space
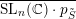 $\overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}}$
is a weighted affine configuration space where the weights are different tensor powers of
$\overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}}$
is a weighted affine configuration space where the weights are different tensor powers of
![]() $\tilde{e}_{n}$
. Unfortunately, the subset family
$\tilde{e}_{n}$
. Unfortunately, the subset family
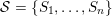 ${\mathcal{S}}=\{S_{1},\ldots ,S_{n}\}$
is not necessarily strongly separated and therefore not a chamber subfamily in general. This leaves the question of desingularization of
${\mathcal{S}}=\{S_{1},\ldots ,S_{n}\}$
is not necessarily strongly separated and therefore not a chamber subfamily in general. This leaves the question of desingularization of
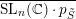 $\overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}}$
open.
$\overline{\operatorname{SL}_{n}(\mathbb{C})\cdot p_{\tilde{S}}}$
open.
Acknowledgements
I would like to thank Frances Kirwan for many helpful discussions and for listening to the details of this work. I thank Vladimir Popov for pointing out the existence of [Reference A’Campo-NeuenA’Ca94] and Frank Grosshans and Klaus Pommerening for their useful comments on the first version of this paper. Last but not least, special thanks go to the referee of this paper for the insightful comments, suggestions and remarks.